Inbreeding depression load for litter size in Entrepelado and Retinto Iberian pig varieties

Abstract

Individual-specific hidden inbreeding depression load (IDL) can be accounted for in livestock populations by appropriate best linear unbiased prediction approaches. This genetic effect has a recessive pattern and reveals when inherited in terms of identity-by-descent. Nevertheless, IDL inherits as a pure additive genetic background and can be selected using standard breeding values. The main target of this research was to evaluate IDL for litter size in 2 Iberian pig varieties (Entrepelado and Retinto) from a commercial breeding-stock. Analyses were performed on the total number of piglets born (both alive and dead) and used data from 3,200 (8.02 ± 0.04 piglets/litter) Entrepelado and 4,744 Retinto litters (8.40 ± 0.03 piglets/litter). Almost 50% of Entrepelado sows were inbred (1.7% to 25.0%), whereas this percentage reduced to 37.4% in the Retinto variety (0.2% to 25.0%). The analytical model was solved by Bayesian inference and accounted for 2 systematic effects (sow age and breed/variety of the artificial insemination boar), 2 permanent environmental effects (herd-year-season and sow), and 2 genetic effects (IDL and infinitesimal additive). In terms of posterior means (PM), additive genetic and IDL variances were similar in the Entrepelado variety (PM, 0.68 vs. 0.76 piglets², respectively) and their 95% credibility intervals (95CI) overlapped, although without including zero (0.38 to 0.94 vs. 0.15 to 1.31 piglets², respectively). The same pattern revealed in the Retinto variety, with IDL variance (PM, 0.41 piglets²; 95CI, 0.07 to 0.88 piglets²) slightly larger than the additive genetic variance (PM, 0.37 piglets²; 95CI, 0.16 to 0.59 piglets²). The relevance of IDL was also checked by a Bayes factor and the deviance information criterion, the model including this effect being clearly favored in both cases. Although the analysis assumed null genetic covariance between IDL and infinitesimal additive effects, a moderate negative correlation (−0.31) was suggested when plotting the PM of breeding values in the Entrepelado variety; a negative genetic trend for IDL was also revealed in this Iberian pig variety (−0.25 piglets for 100% inbred offspring of individuals born in 2014), whereas no trend was detected in Retinto breeding-stock. Those were the first estimates of IDL in a commercial livestock population, they giving evidence of a relevant genetic background with potential consequences on the reproductive performance of Iberian sows.

Introduction

Inbreeding depression merges 2 genetic mechanisms, a higher impact from recessive mutations and the waste of overdominance contributions (Charlesworth and Willis, 2009). This genetic phenomenon reduces biological fitness in the offspring of related individuals (Pujol et al., 2009; Leroy, 2014) and is of major concern for the conservation of small or structured populations (Saccheri et al., 1998; Ober et al., 1999). Despite its relevance, inbreeding depression has been typically simplified to the linear (or may be quadratic) regression of overall inbreeding coefficient against the phenotypic trait of interest (Leroy, 2014). In the absence of epistasis, this rough approximation omitted heterogeneity of the recessive load across population (Gulisija et al., 2006; Casellas et al., 2008), as well as the most basic rules of genetic inheritance and resemblance between relatives (Quaas, 1976). Nevertheless, all these limitations were recently overcome by a mixed model approach to predict individual-specific hidden inbreeding depression load (IDL; Casellas, 2018).

The development of organized breeding programs is scarce and relatively recent in the Iberian pig breed (Silió, 2000; Ibáñez-Escriche et al., 2014). Traditionally, this breed has distributed in many small populations with remarkable phenotypic and genomic differences as a result of genetic drift, important demographic fluctuations, and a scarce genetic flow among herds (Fabuel et al., 2004). This is the perfect substrate for inbreeding and inbreeding depression, as already reported in most of Iberian pig varieties (Silió et al., 2013; Saura et al., 2015). Within this context, an accurate prediction of IDL can become a useful step for any breeding program in the Iberian pig breed nowadays.

The aim of this study was to estimate IDL variance components for litter size in 2 Iberian pig varieties, as well as their statistical relevance. Moreover, distribution and magnitude of IDL effects were characterized as the first implementation of this analytical approach in a commercial pig population.

MATERIALS AND METHODS

All management and experimental procedures involving live animals were approved by the Research Ethics Committee of the Institut de Recerca i Tecnologia Agroalimentàries (Caldes de Montbui, Spain). Analyses were performed on existing field data obtained under standard farm management from selection nuclei. Both pedigree and productive data were collected, registered, and administrated by the personnel from INGA FOOD S.A. (Almendralejo, Badajoz, Spain).

Iberian Pig Field Data

Analyses relied on the Entrepelado and Retinto Iberian pig breeding-stocks of Inga Food SA. Both Iberian varieties actively contribute data to the Spain’s official Iberian Herdbook (Ministry of Agriculture and Fisheries, Food and Environment, Spain’s Government, Madrid, Spain), this being administered by the Spanish Association of Iberian Purebred Pig Breeders (AECERIBER; Zafra, Badajoz, Spain). The Entrepelado is a black hairy variety although piglets are born with red coat color, whereas the Retinto is the most abundant variety in the Iberian pig population, and is characterized by a reddish-brown coat color. Some authors have suggested that Entrepelado and Retinto varieties share origins, regardless of their dissimilarities (Martínez et al., 2000; Alves et al., 2006). For the creation of both selection nuclei, boars and sows from the Iberian Herdbook were purchased after weaning (30 to 35 d of age) and kept under intensive rearing conditions such as those used in selection farms of the pig industry. All genealogical and reproductive data were registered. Sows were distributed in 2 selection farms and one multiplier farm located in Extremadura (south-west Spain). Note that 3 different boar types were used in selection farms (Entrepelado, Retinto, and Torbiscal), whereas all sows in the multiplier farm were inseminated with Duroc semen. The Torbiscal Iberian variety is a reddish synthetic variety originated during 1940s by combining 4 ancestral Iberian pig strains as described by Fernández et al. (2002) and Fabuel et al. (2004).

This research focused on litter size data measured as the total number of piglets born, both alive and dead. The data set from the Entrepelado variety included 3,200 litters (8.02 ± 0.04 piglets/litter) from 739 sows, registered between years 2010 and 2017. The full pedigree included 863 individuals (69 boars and 794 sows), 51 of them being founders without known ancestors (5.91%). On the other hand, the Retinto variety had data from 4,744 litters (8.40 ± 0.03 piglets/litter) provided by 922 sows between years 2009 and 2017. A total of 1,064 individuals were registered in the pedigree file (89 boars and 975 sows), and 85 of them were founders (7.99%). Both populations were kept under a controlled mating system to minimize inbreeding.

Operational Model

Analyses focused on the prediction of hidden IDL effects, where IDL effects were defined as the expected joint impact of all the inbreeding-related polymorphisms in the genome of a given individual when homozygous in a 100% inbreed offspring. Within this context, IDL of each individual may or may not affect its own fitness (depending on whether the individual is inbred or not), and will reveal in inbred descendants, if any. Litter size data (y) from each Iberian pig variety were solved separately under the following hierarchical structure,

$${\displaystyle \begin{array}{l}{\displaystyle \mathbf{y}=\mathbf{X}\mathbf{b}+{\mathbf{Z}}_1{\mathbf{p}}_1+{\mathbf{Z}}_2{\mathbf{p}}_2+{\mathbf{Z}}_3\mathbf{a}+{\mathbf{Z}}_4\mathbf{d}+\mathbf{e},}\end{array}}$$

where b was the vector of systematic effects accounting for the parity number (1st, 2nd, 3rd, 4th, 5th, and 6th and upper parities) and the genetic type of the insemination boar (Entrepelado, Retinto, Torbiscal, and Duroc). On the other hand, p₁ was the vector of herd-year-season effects, p₂ was the vector of permanent environmental sow effects, a was the vector of infinitesimal additive genetic effects, d was the vector of IDL effects, and e was the residual term; X, Z₁, Z₂ and Z₃ and Z₄ were appropriate incidence matrices. As noted by Casellas (2018), d predicted infinitesimal IDL inherent to the genome of each individual, whereas their realization in terms of inbreeding depression of inbred offspring was linked by Z₄. This was a lower-triangular matrix where each nonzero element was a partial inbreeding coefficient obtained by Mendelian decomposition from the standard pedigree file (Caballero and Toro, 2000; García-Cortés et al., 2010). This approach splits the overall inbreeding coefficient of each individual (F_i) into the specific contribution of each relevant ancestor (F_j’) in terms of identity-by-descent. Assuming n ancestors contributing inbreeding to the ith individual, F_i = F₁’ + F₂’ + ... + F_n’.

Bayesian Inference

The model was solved within a Bayesian context by appropriately sampling from the following joint posterior distribution,

$$p\left({\mathbf{\text{b, p}}}_1,{\mathbf{\text{p}}}_2,\mathbf{\text{a, d,}}{\sigma }_{p1}{}^2,{\sigma }_{p2}{}^2,{\sigma }_a^2,{\sigma }_d^2,{\sigma }_e^2|\mathbf{\text{y}}\right)\alpha p\left(\mathbf{\text{y}}|\mathbf{\text{b}},{\mathbf{\text{p}}}_1,{\mathbf{\text{p}}}_2,\mathbf{\text{a, d, }}{\sigma }_e^2\right)p\left(\mathbf{b}\right)\mathbf{p}\left({\text{p}}_1|{\sigma }_{p1}{}^2\right)\times p\left({\sigma }_{p1}{}^2\right)p\left({\text{p}}_2|{\sigma }_{p2}{}^2\right)\mathbf{p}\left({\sigma }_2{}^2\right)p\left(\mathbf{a}|\mathbf{\text{A}},{\sigma }_a{}^2\right)\times p\left({\sigma }_a^2\right)p\left(\mathbf{d}|\mathbf{A},{\sigma }_d^2\right)p\left({\sigma }_d^2\right)p\left({\sigma }_e^2\right)$$

The conditional distribution of y was assumed multivariate normal (MVN) as follows:

$${\displaystyle \begin{array}{l}{\displaystyle p(\mathbf{y}|\mathbf{b},{\mathbf{p}}_1,{\mathbf{p}}_2,\mathbf{a},\mathbf{d},{{\mathrm{\sigma }}_e}^2)=MVN(\mathbf{X}\mathbf{b}+{\mathbf{Z}}_1{\mathbf{p}}_1+{\mathbf{Z}}_2{\mathbf{p}}_2+{\mathbf{Z}}_3\mathbf{a}+{\mathbf{Z}}_4\mathbf{d},{\mathbf{I}}_n{{\mathrm{\sigma }}_e}^2),}\end{array}}$$

where I_n was an identity matrix with dimensions equal to the number of phenotypic records and σ_e² was the residual variance. Random sources of variation were modeled under appropriate MVN distributions, (Wang et al., 1994)

$${\displaystyle \begin{array}{l}{\displaystyle \begin{array}{ll}& {\displaystyle p({\mathbf{p}}_1|{\mathrm{\sigma }}_p{{}_1}^2)=MVN({{\mathbf{0}}_p}_1|{{\mathbf{I}}_p}_1{\mathrm{\sigma }}_p{{}_1}^2),}\\ & {\displaystyle \mathrm{p}({\mathbf{p}}_2|{\mathrm{\sigma }}_p{{}_2}^2)=MVN({{\mathbf{0}}_p}_2|{{\mathbf{I}}_p}_2{\mathrm{\sigma }}_p{{}_2}^2),}\\ & {\displaystyle p(\mathbf{a}|{{\mathrm{\sigma }}_a}^2)=MVN({\mathbf{0}}_a|\mathbf{A}{{\mathrm{\sigma }}_a}^2)}\end{array}}\end{array}}$$

and

$${\displaystyle \begin{array}{l}{\displaystyle p(\mathbf{d}|\mathbf{A},{{\mathrm{\sigma }}_d}^2)=MVN({\mathbf{0}}_d|\mathbf{A}{{\mathrm{\sigma }}_d}^2).}\end{array}}$$

Although d accounted for recessive genetic effects, they were inherited as additive genetic effects (Casellas, 2018). Note that σ_ε² was the variance component of the ε effect with θ levels, 0_θ was a zeroing vector with θ rows, I_θ was a θ × θ identity matrix, and A was the numerator relationship matrix (Wright, 1922). Flat priors were assumed for systematic effects and variance components.

Inferences for all the unknown parameters in the model were made on the relevant marginal posterior distributions by Gibbs sampling (Gelfand and Smith, 1990). More specifically, 3 independent Monte Carlo Markov chains (MCMC) with 550,000 iterations were launched for each analysis, and the first 50,000 were discarded as burn-in (Raftery and Lewis, 1992).

The statistical relevance of σ_d² was tested by a Bayes factor (BF; Kass and Raftery, 1995) and the deviance information criterion (DIC; Spiegelhalter et al., 2002). The BF focuses on the ratio between the posterior probability of 2 competing models; a BF > 1 supports the numerator model, whereas a BF < 1 favors the denominator model. The model described earlier (numerator model) was compared against a model with σ_d² = 0 and d = 0 by the harmonic mean estimator developed by Newton and Raftery (1994). On the other hand, the DIC evaluates model complexity and fit; a smaller DIC value indicates a better fit and a lesser degree of complexity. Differences of at least 3 to 5 DIC units are generally considered as statistically relevant (Spiegelhalter et al., 2002).

Genetic Trend

Given that both Iberian pig varieties were under genetic selection for litter size, correlated genetic trend for IDL was also evaluated. For each variety, the average IDL of replacement boars and sows born each year was computed during the MCMC process. All animals born before 2010 were grouped in the same category and used as reference (average IDL = 0).

RESULTS AND DISCUSSION

Inbreeding Pattern

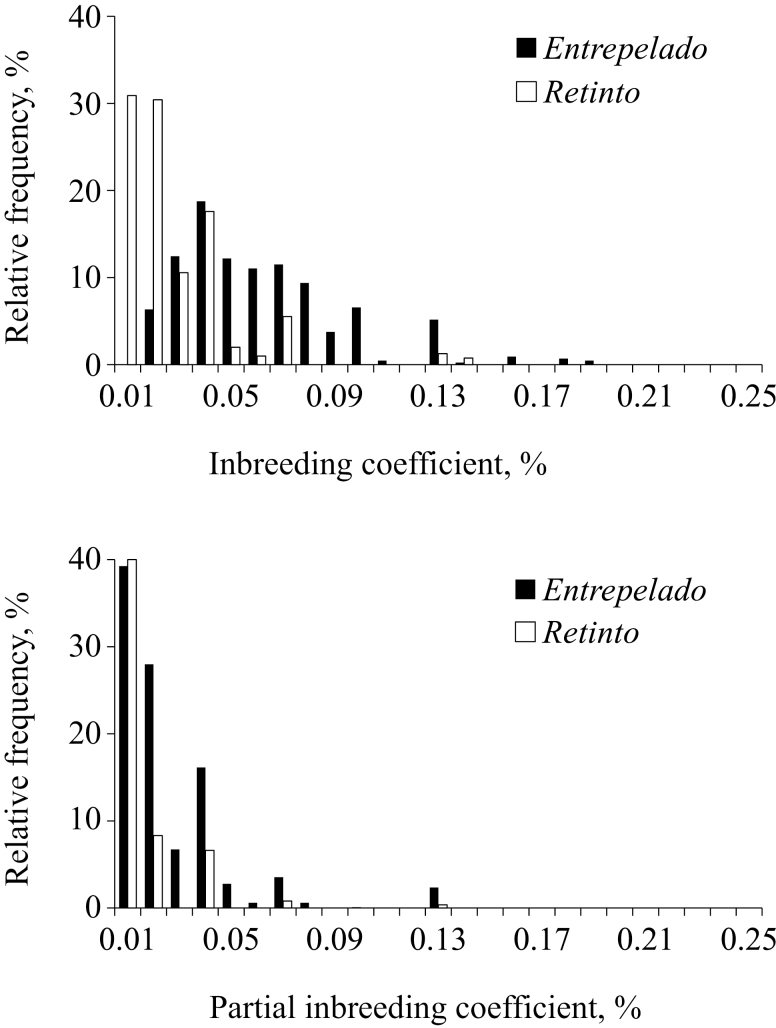
The Iberian pig is a very interesting genetic population to analyze inbreeding and inbreeding depression due to its population dynamics during the last century (Saura et al., 2013). Although Entrepelado and Retinto varieties involved in this research were founded less than a decade ago, the inbreeding coefficient averaged 0.058 and 0.025 in the whole pedigree file, respectively. Half of the Entrepelado breeding-stock (49.7%) was inbred, with inbreeding coefficients ranging from 0.017 to 0.250 (mean ± SE, 0.058 ± 0.002). The incidence of inbreeding in the Retinto variety was lower (37.4% of the breeding-stock), although it had a similar range (from 0.002 to 0.250; mean ± SE, 0.045 ± 0.002; Fig. 1A). As anticipated, inbreeding was lower than in other Iberian pig varieties, such as Torbiscal and Gamito varieties (~0.07 and ~0.30; Fernández et al., 2002) or the Guadyerbas variety (~0.4; Esteve-Codina et al., 2011; Saura et al., 2013), although this last had a pedigree that traced back more than half a century. Moreover, those varieties were kept as closed herds whereas our Entrepelado and Retinto varieties were founded less than 10 yr ago by the acquisition of individuals of different origins.

Figure 1.

Distribution of inbreeding coefficients in Entrepelado and Retinto Iberian pig varieties.

Overall inbreeding coefficients outlined above were partitioned into partial inbreeding coefficients by Mendelian decomposition (Caballero and Toro, 2000). Each partial inbreeding coefficient captured the identity-by-descent contribution of each relevant ancestor to the inbreeding coefficient of a specific individual. The Mendelian decomposition approach partitioned each inbreeding coefficient and provided between 1 and 13 partial inbreeding coefficients in the Entrepelado variety, with a total of 1,190 partial inbreeding coefficients. In a similar way, the Retinto variety provided 1,120 partial inbreeding coefficients, and the inbreeding coefficient of each inbred individual partitioned between 1 and 17 contributions. Partial inbreeding coefficients were linked to 135 and 150 ancestors from the Entrepelado and Retinto populations, respectively. Although some of them were founders, partial inbreeding coefficients are not restricted to individuals without known ancestors but link to relevant ancestors originating identity-by-descent in offspring generations (Caballero and Toro, 2000). As shown in Fig. 1B, most of the partial inbreeding coefficients were lower than 0.05, although maximum values reached 0.125 in both Iberian pig varieties. This low inbreeding level was the consequence of the small number of generations elapsed since the foundation of each population, and the implementation of a minimum inbreeding program for mating design.

Variance Components

Table 1 reported posterior means and 95% credibility intervals (95CI) for genetic and environmental random sources of variation. They revealed a very consistent behavior across Iberian pig varieties in terms of environmental and additive genetic variances. Both varieties accumulated the vast majority of variability in the residual term, which was quite anticipatable in a low heritable trait like litter size (Pérez-Enciso and Gianola, 1992; Noguera et al., 2002). On the other hand, permanent environmental contributions (i.e., herd-year-season and environmental sow effects) reached small posterior means (0.12 to 0.26), although their 95CI clearly excluded the null value in all cases. These estimates agreed with previous results reported for other Iberian pig varieties (Pérez-Enciso and Gianola, 1992), and their small contribution to the overall variability may be due to current homogeneity of farm procedures under intensive production systems, even for Iberian pig industry under intensive production systems.

Table 1.

Posterior mean (and 95% credibility interval) for variance components of litter size in Entrepelado and Retinto Iberian pig varieties

Variance component1	Entrepelado variety	Retinto variety
σp12	0.12 (0.05 to 0.20)	0.23 (0.17 to 0.29)
σp22	0.26 (0.09 to 0.46)	0.15 (0.08 to 0.26)
σa2	0.68 (0.38 to 0.94)	0.37 (0.16 to 0.59)
σd2	0.76 (0.15 to 1.31)	0.41 (0.07 to 0.88)
σe2	3.59 (3.41 to 3.77)	3.86 (3.72 to 3.99)

¹Permanent environmental variance for herd-year-season (σ_p1²) and sow (σ_p2²), additive genetic variance (σ_a²), inbreeding depression load variance (σ_d²), and residual variance (σ_e²).

Posterior means were moderate for genetic variances and slightly higher for inbreeding depression than for additive genetic effects. Both Entrepelado (0.76 vs. 0.68 piglets²) and Retinto (0.41 vs. 0.37 piglets²) varieties evidenced the same pattern, although 95CI overlapped in both cases. It is important to highlight that several authors already suggested the relevance of nonadditive sources of variation for fertility-related traits in domestic species (Fuerst and Sölkner, 1994; Nagy et al., 2013; Varona et al., 2018), and our results consistently revealed a remarkable degree of recessive variability for litter size in Iberian pigs. Indeed, 95CI for IDL variance excluded the null estimate in both Iberian pig varieties (Table 1), and the statistical relevance of σ_d² was also corroborated by means of a BF approach. The model including IDL effects was 26.9 times more probable than the alternative model assuming σ_d² = 0 for Entrepelado sows, whereas this BF reduced to 21.7 in the Retinto variety. These BF values provided strong evidence according to Jeffreys’ (1984) scale of evidence. In a similar way, the model including nonzero σ_d² reduced DIC by 17.2 (Entrepelado variety) and 9.7 units (Retinto variety). It is important to highlight that some lethal recessive effects may not be accounted for by d as previously noted by Casellas (2018). This may lead to the underestimation of IDL effects, the same way major genes may bias predicted breeding values if not properly accounted for in the model (Legarra and Vitezica, 2015).

Predicted IDL Effects

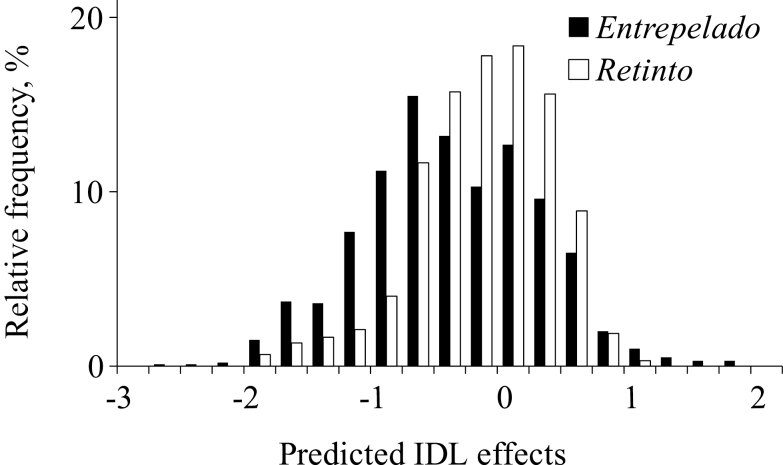
After the original development and implementation of this analytical approach in a small rabbit population (Casellas, 2018), our results were the first genetic evaluation for IDL effects in a livestock population contributing commercial products worldwide. Predicted IDL showed a quasi-symmetrical pattern around 0, although a slight preponderance of the left-hand tail of the distribution can be suggested, at least in the Entrepelado variety (Fig. 2). This may be due to unintended selection or genetic drift after the foundation of this population. Nevertheless, the preponderance of negative IDL effects has been previously reported in rabbits (Casellas, 2018) and is a typical assumption within the context of inbreeding depression (Gulisija et al., 2006; Casellas et al., 2008; Charlesworth and Willis, 2009). Given that available pedigree data traced back less than 10 yr, IDL effects originated along the last few generations. This short-term inbreeding has been typically linked to greater inbreeding depression effects when compared with inbreeding originated far away in the pedigree (Hinrichs et al., 2007).

Figure 2.

Distribution of predicted inbreeding depression load (IDL) effects in Entrepelado and Retinto Iberian pig varieties.

It is important to note that 29.2% and 23.1% of IDL estimates were positive in Entrepelado and Retinto varieties, respectively. Both current variability of IDL effects and the amount of positive values characterized an appealing starting point for new genetic selection endeavors on litter size. Note that predicted IDL effects could be integrated into current selection indexes to take advantage of this additional source of genetic variability. Selection decisions can be taken on the basis of both traditional additive genetic effects and potential (i.e., recessive) genetic contributions from IDL if inbreeding arises in the population. Given the additive inheritance pattern assumed for IDL effects in Materials and Methods section, response to selection in terms of average IDL could be calculated with the same approaches derived for traditional additive breeding values (Dekkers, 1992; Villanueva et al., 1993). Nevertheless, average IDL must not be confounded with realized inbreeding depression, as previously noted. Selection on IDL effects will only affect the phenotype (e.g., litter size) if accompanied by inbreeding. If not, the genetic change in terms of IDL will hide in the genome of the individuals, without contributing benefits or penalties on traits of economic interest for livestock populations. This could be viewed as both a limitation and an advantage at the same time. The birth of some inbred individuals become mandatory to provide relevant data for the genetic analysis of IDL effects. On the other hand, predicted IDL effects identify those ancestors with worse inbreeding-related effects, the ones that should not contribute to inbreeding offspring.

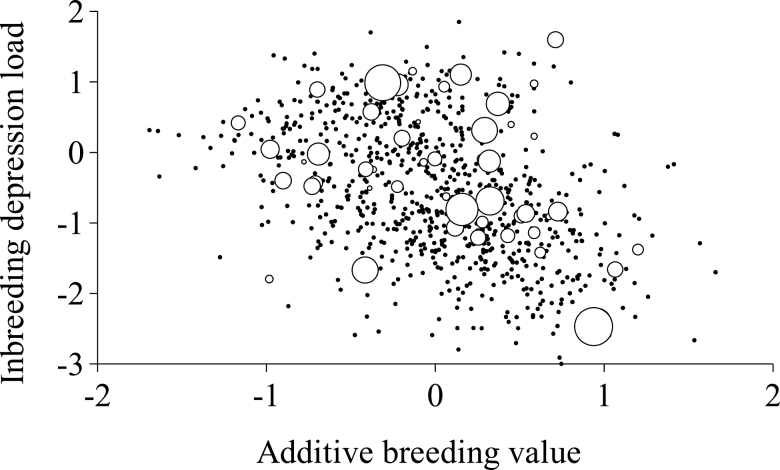
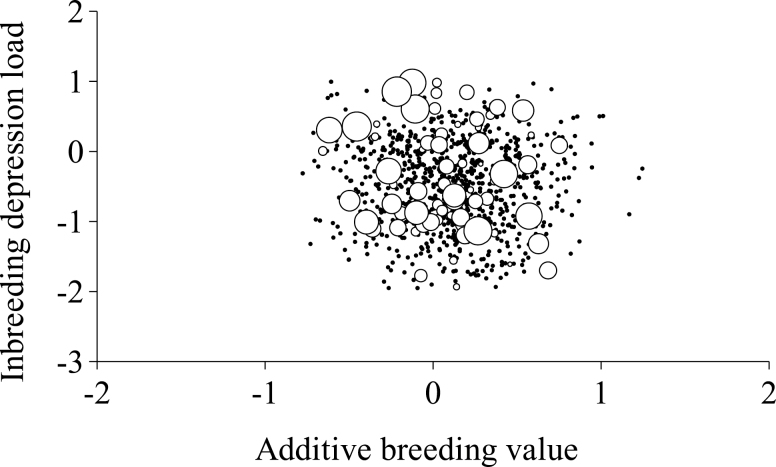
Correlated response due to additive breeding values cannot be completely discarded. The Entrepelado variety suggested a negative genetic correlation between IDL and additive breeding values (Fig. 3), whereas the Retinto variety did not evidence any kind of genetic correlation pattern (Fig. 4). It is important to note that our analytical approach did not assume any kind of genetic correlation between additive (a) and IDL (d) effects, whereas the correlation between posterior means of a and d vectors in the Entrepelado variety reached −0.31. These results agreed with previous estimates obtained for the number of kits at weaning in 3 rabbit populations (Fernández et al., 2017) and dairy traits in cattle (Hoeschele and Vollema, 1993). They highlight potentially negative additive genetic responses if selected for positive IDL (or worse IDLs under traditional selection programs relying on the additive genetic background). Nevertheless, this must be corroborated in future research due to the shortage of results within the context of genetic correlations between additive and dominance effects.

Figure 3.

Plot of predicted inbreeding depression load against additive breeding value for litter size in the Entrepelado Iberian pig variety. White circles correspond to boars and their diameter characterized the number of daughters contributing litter size data (this parameter ranged from 1 to 84), whereas black dots were for sows.

Figure 4.

Plot of predicted inbreeding depression load against additive breeding value for litter size in the Retinto Iberian pig variety. White circles correspond to boars and their diameter characterized the number of daughters contributing litter size data (this parameter ranged from 1 to 52), whereas black dots were for sows.

The other source of correlated responses to selection could be attributable to other phenotypic traits with pleiotropic or linkage disequilibrium dependencies with the one under IDL selection. Selection for those animals with positive and highest IDL estimates for a given trait does not guarantee the same pattern in other traits. Within this context, the inclusion of IDL effects in current selection programs should be accompanied by appropriate evaluations on other traits of economic interest.

Genetic Trend

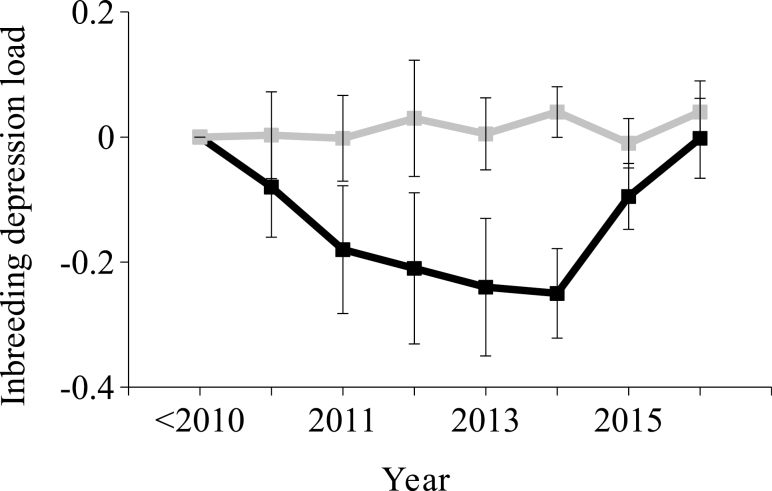
Results shown in Fig. 5 discarded any kind of genetic trend for IDL in the Retinto. This must be seen as an anticipated result because this Iberian pig variety has not been formally selected for IDL, but for the additive genetic background of litter size. On the other hand, the Entrepelado breeding-stock evidenced a progressive and negative tendency until 2014, with 95CI excluding the 0 value since 2011. This reverted in 2015 and 2016, placing the average IDL around 0. This trend in the Entrepelado variety could relate to the negative correlation between additive breeding values and IDL suggested in Fig. 3. As for the Retinto variety, Entrepelado sows have been actively selected on the basis of their additive breeding value, and this may have affected IDL. On the other hand, the small census of these selection nuclei may link any change in the year-by-year average IDL to the stochastic processes inherent to genetic drift. Current data sets are too small to fit multivariate models with non-null genetic covariances to corroborate potential links between additive genetic and IDL in the Entrepelado Iberian pig variety. Future studies will be necessary to test this hypothesis.

Figure 5.

Genetic trend for inbreeding depression load in Entrepelado (black) and Retinto varieties (gray). Squares show the average load of boars and sows born each year, and error bars show the 95% credibility interval. Individuals born before 2010 were grouped in the same category and used as reference (average inbreeding depression load, 0).