Abstract
In the present work, two-dimensional mixed convection Casson fluid flow past an infinite plate in a porous medium is performed under the effects of a uniform magnetic field. Characteristics of heat transfer and mass transfer are analyzed with non-linear thermal radiation, cross-diffusion, chemical reaction, heat generation and, heat absorption. The governing partial differential equations are remodeled into ordinary differential equations using similarity transformation. The homotopy analysis method is implemented to solve the governing dimensionless system of ordinary differential equations. The behavior of different physical parameters is shown graphically. The numerical values of Skin friction, Nusselt number, and Sherwood number are presented in a tabular form. Obtained outcomes are compared with earlier studies in the special case and strong agreement is noted. From graphical representation, it is concluded that velocity and temperature distribution increases with the mixed convection parameter and buoyancy force parameter. An increasing value of Casson fluid parameter, magnetic field parameter, chemical reaction parameter, and diffusion-thermo parameter tends to reduced velocity and temperature profiles. In most of the engineering and real-world problems, skin friction is not desirable, so it can be decreased by decreasing the values of magnetic field parameter, non-linear thermal radiation parameter, heat generation parameter, and temperature ratio parameter.
Keywords: Applied mathematics, Computational mathematics, Condensed matter physics, Electromagnetism, Mechanics, Thermodynamics
1. Introduction
The study of non-Newtonian fluids has attracted the attention of new researchers due to their huge range of practical applications in engineering and science. These fluids show a nonlinear relationship between the stress and the rate of strain which offer much complicated and nonlinear differential systems. Among the non-Newtonian fluids, Casson fluid attracted more attention of researchers due to its applications in the manufacturing of pharmaceutical products, coal in water, china clay, paints, synthetic lubricants, and biological fluids. Casson [1] introduced the first Casson model for the behavior of fluid flow in pigment-oil suspensions. Casson fluid characteristics are different from Newtonian fluids due to the relationships between shear stress and the rate of shear strain. Human blood, Jelly, honey, concentrated fruit juices, and tomato sauce are some examples of Casson fluid. Recently, Khan et al. [2] studied Casson fluid flow with homogeneous-heterogeneous reactions. The collective effects of fluid dynamics, thermodynamics and, electrodynamics give rise to the topic MFD. It is divided into two parts: MHD and MGD. MHD deals with electrically conducting fluids whereas MGD deals with ionized compressible gases. MHD has several applications, namely, fusion research, MHD accelerator, and power generator. Some recent studies concerning the effect of magnetic field on fluid flow can be mentioned through studies [3, 4, 5]. Convection term is arising the mixing of one portion to another portion of the fluid due to gross moments of the bulk of the fluid. There are three types of convection mode which are divided in to free, force and mixed in fluid flow problems. Recently, the free convective MHD flow plays a significant role in the petrochemical industry, heat exchanger design, geophysics and, MHD power generation system. Kataria and Patel [6] discussed unsteady free convective MHD flow of micropolar fluid. Selimefendigil and Öztop [7, 8] studied magnetic field effects on free convective nanofluid flow in a cavity. The concept of Mixed convection in fluid flow problems has attracted many researchers due to its importance in many engineering applications such as food processing, microelectronic devices, cooling of electronic devices and, nuclear reactors. Selimefendigil and. Öztop [9, 10, 11, 12, 13, 14, 15] considered mixed convection MHD flow of nanofluid with different physical conditions. Hayat et al. [16] performed three-dimensional mixed convection MHD flow with variable viscosity whereas, Waqas et al. [17] studied mixed convection MHD flow due to the nonlinear stretched sheet. Currently, many researchers have scrutinized the influence of thermal radiation on the heat transport features of fluids across stretched surfaces. The heat transfer process has many applications in solar power technology, and photochemical reactors, etc. Shah et al. [18] and Sheikholeslami et al. [19] discussed unsteady MHD flow with thermal radiation. Hayat et al. [20] performed solar radiation and Joule heating in the MHD flow of thixotropic nanofluid. Non-linear thermal radiation effects are also important in heat transfer fluid flow problems. The application of heat transfer problems with non-linear thermal radiation is summarized as gas cooled nuclear reactors, counting combustion, furnace design and, nuclear reactor protection. Kumar et al. [21, 22] considered MHD flow over a convective surface with non-linear thermal radiation effects. The porous medium is a hard containing random spaces (pores), joined or separate, distributed within it in either a fixed or random manner. If pores signify a certain portion of the bulk volume, a difficult complex network can be designed which is capable to carry fluids. The porous media play an important role in technology and engineering field. The significant of the MHD flow problems with a porous medium which is done by Kataria and Patel [23]. Research work on MHD Casson fluid flow in a porous medium with radiation can be found in Das [24]. The study of chemical reaction procedures is beneficial for improving a number of chemical technologies, such as food processing, polymer production, and manufacturing of ceramics or glassware. In these procedures, the molecular diffusion via chemical reaction within or at the boundary cannot be determined. Abbas et al. [25] obtained a numerical solution for chemical reaction effects on stagnation point flow of Casson fluid over a stretching/shrinking sheet with thermal radiation. Analytical solution of MHD Casson fluid flow past an oscillating plate in the presence of chemical reaction and thermal radiation obtained by Kataria and Patel [26]. Further, the phenomenon of heat generation/absorption plays a significant role in adjusting the heat transfer rate. The effects of heat generation and heat absorption on MHD flow with different physical situations mentioned in Refs. [27, 28]. Some other relevant studies with thermal radiation, chemical reaction and, heat generation effects on MHD flow with different fluids can be found in Refs. [29, 30]. The Soret and Dufour effect arises when simultaneous heat and mass transfer affecting each other. Due to the concentration gradient, heat transfer process produced which cause the Dufour effect whereas, the mass transfer produced by temperature gradient is called the Soret effect. Kataria and Patel [31] considered Soret effects on free convective Casson fluid flow whereas, Sheikholeslami et al. [32] defined analytical solution for the effect of thermal diffusion and heat-generation on MHD nanofluid flow in a porous medium. The cross diffusion effects are usually of a small order of magnitude. These combine effect shows an important role in the process of solar ponds, biological systems, and, the microstructure of oceans. The cross diffusion effects were used in free or mixed convection MHD flow with heat and mass transfer problems applications. Relevant research work is done in Refs. [33, 34, 35, 36, 37, 38]. Moreover, Kataria and Mittal [39], Kumar et al. [40], Kumaran and Sandeep [41] studied the impact of Brownian motion and thermophoresis on MHD flow with different physical conditions.
The elementary concepts of the homotopy in topology to recommend analytic approximation method, namely the HAM. This technique has been used to solve different types of nonlinear differential equation successfully. The HAM is better compared to numerical methods because it does not include discretization of the variable, hence is free from rounding off errors. The homotopy analysis method was introducing first by Liao [42]. The HAM method can be applied Liao [43, 44] for solving several kinds of a nonlinear system of differential equations problems. The HAM theory is applied effectively to a nonlinear problem arise from the real situation in lots of different fields by researchers, engineers and, scientists. Fallahzadeh and Shakibi [45] to solve the convection-diffusion equation using the homotopy analysis method. Recently, Fagbade et al. [46] obtained an analytical approximation of thermal radiation and heat generation effects on MHD flow of viscoelastic fluid using HAM methods.
The main theme of the present article is to develop the model of cross diffusion effects on MHD Casson fluid flow through a porous medium. A novel aspect of chemical reaction, heat generation and, nonlinear thermal radiation is present. The focal concern of this problem is to investigate the collective effect of cross-diffusion, heat generation, nonlinear radiation and chemical reaction on two-dimensional MHD flow of Casson fluid through a porous medium which is not yet studied. The governing dimensionless systems of ordinary differential equations with imposing initial and boundary conditions are solved using the Homotopy analysis method. The convergence of series solutions is useful for providing the developing linear functions of solutions which is an advantage of the HAM method. Application of these types of research work can be found in fire dynamics in insulations, solar collection systems and, recovery of petroleum products, etc.
2. Model
A graphical explanation of the physical problem of steady two dimensional laminar mixed convective MHD flow of Casson fluid past an infinite plate in a porous medium is depicted in Fig. 1. The uniform ambient temperature and ambient concentration is considered. The values of velocity, temperature and concentration distribution of the sheet to be considered as and respectively. The flow is kept in the region toward a surface according. Coordinate system chosen in such a way that, x-axis along the sheet and the y-axis perpendicular to it. In y-axis direction, the constant strength is applied.
Fig. 1.
Physical sketch of the problem.
The constitutive equation for the Casson fluid can be written as
| (1) |
Where, Deformation rate at component, Yield stress, Dynamic viscosity, Product of the component for deformation rate with itself and, is a critical value of this product based on the non-Newtonian model.
The viscous dissipation and induce magnetic are negligible effects. The governing continuity, momentum, energy and concentration equations under the Boussinesq′s approximation are given below,
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
Here, velocity in the x-direction, velocity in the y-direction, Fluid temperature, Concentration, Specific heat at constant pressure, Radiative heat flux, Concentration susceptibility, Mass diffusion coefficient, thermal diffusion ratio, Electrical conductivity, Fluid density, Porosity of the porous medium, Thermal expansion coefficient, Concentration expansion coefficient, Acceleration due to gravity, Kinematic viscosity coefficient and, Thermal conductivity.
Using Rosseland [48], radiation heat flux can be written as
| (8) |
where, the Stefan–Boltzmann constant and the mean absorption coefficient respectively.
In view to Eqs. (8), Eq. (4) reduced to
| (9) |
Introducing non dimensional variables
where dimensionless stream function, Stretching velocity and Dimensionless coordinator.
Therefore, the dimensionless form of governing equations is expressed as,
| (10) |
| (11) |
| (12) |
Subject to
| (13) |
| (14) |
where, Mixed convection parameter, Buoyancy force parameter, Thermal grashof number, Mass grashof number, Local Reynolds number, Magnetic parameter, Radiation parameter, Prandtl number, Soret number, Dufour number, Schmidt number, permeability of porous medium, chemical reaction parameter, Heat generation/absorption parameter.
Expressions of skin-friction, Nusselt number, and Sherwood number are defined using the relations.
| (15) |
| (16) |
| (17) |
Where is local Reynolds number.
3. Methodology
The HAM is a fundamental idea of topology, proposed by Liao [42]. Homotopy analysis methods is an analytic approximation method with a guarantee of convergence, mainly for nonlinear differential equations. In the application point of view, the HAM has been applied to solve fluid mechanics problems. In this study, the governing equations (10) – (12) are coupled non-linear ordinary differential equations with initial and boundary conditions (13)–(14) whose exact solutions are not possible. Therefore, HAM suggested by Liao [42, 43, 44] is suitable to solve these types of system. Here initial guess and auxiliary linear operators are required for HAM solution which is presented given below:
| (18) |
| (19) |
Satisfying
| (20) |
where are constants.
The deformation of zeroth order can be written as,
| (21) |
| (22) |
| (23) |
Subject to the boundary conditions:
| (24) |
| (25) |
| (26) |
| (27) |
The nonlinear operator is defined as
| (28) |
| (29) |
| (30) |
where and are unknown functions. , and are auxiliary parameters and the nonlinear operators are , and .
Also is an implanting parameter.
For and we have
| (31) |
| (32) |
| (33) |
In other words, when the variation of is taken from 0 to 1 is considered then , and are change from and to and . The series expansion using Taylor′s formula of these functions yields the following,
| (34) |
| (35) |
| (36) |
Where
| (37) |
| (38) |
| (39) |
It is seen that the above series convergence depends upon and . Assuming the nonzero auxiliary parameters so that the convergence of Eqs. (21), (22), and (23) at is appear. Hence it can be obtained the following,
| (40) |
| (41) |
| (42) |
Differentiating Eqs. (21), (22), (23), (24), (25), (26) and (27) m times with respect to , putting , and dividing by , it is obtained the order deformation which can written as,
| (43) |
| (44) |
| (45) |
Subject to the initial and boundary conditions
| (46) |
| (47) |
| (48) |
| (49) |
with
| (50) |
| (51) |
| (52) |
| (53) |
Solving the corresponding mth-order deformation equations,
| (54) |
| (55) |
| (56) |
Here the particular solutions of mth – order equations are . Using boundary conditions, the constants are to be determined.
4. Analysis
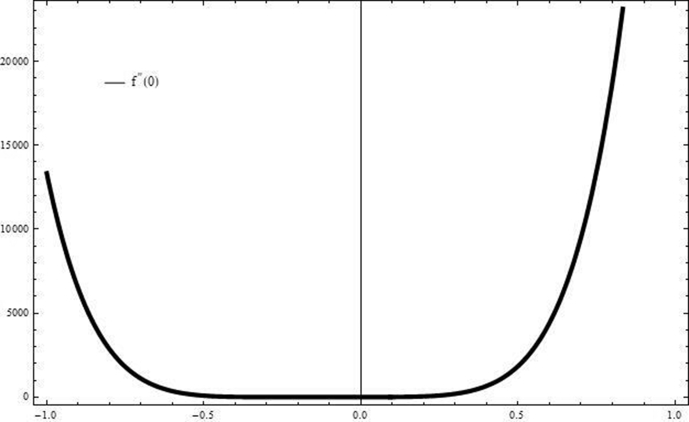
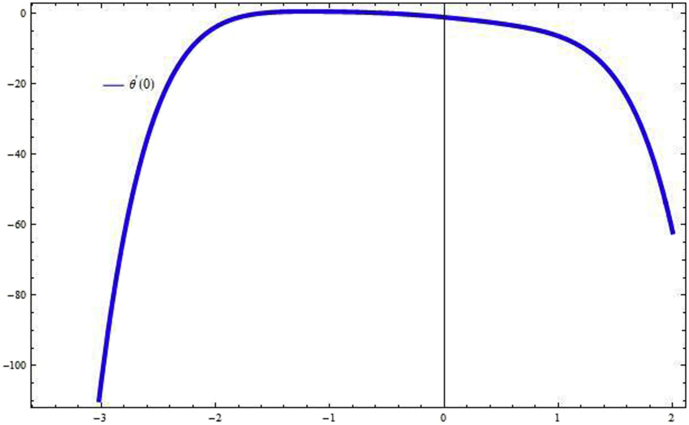
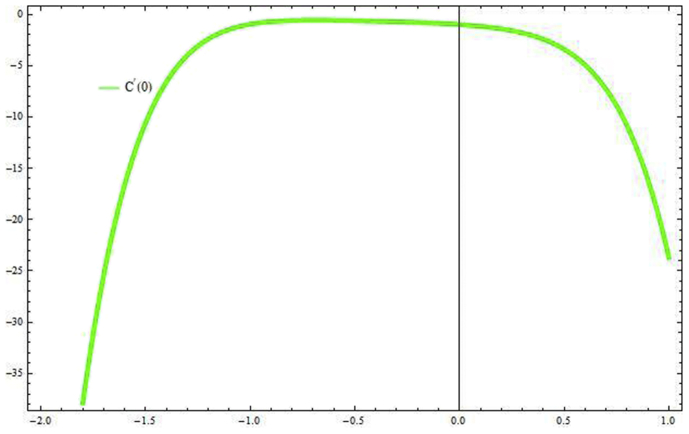
It is well known that convergence of the HAM solutions depends on the auxiliary parameters and . For this concept, the allied h-curves are plotted in Figs. 2, 3, and 4 respectively. These all figures clearly suggest admissible ranges for the auxiliary parameters.
Fig. 2.
h-curve of .
Fig. 3.
h-curve of .
Fig. 4.
h-curve of .
5. Results & discussion
In order to get a rich understanding of the behavior of the problem, a parametric study is completed and the found results are clarified with the support of graphical diagrams. The non-dimensional fluid velocity, fluid temperature, and concentration for several values of the different physical parameter are presented in Figs. 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, and 23.
Fig. 5.
for different values of at
Fig. 6.
for different values of at
Fig. 7.
for different values of at
Fig. 8.
for different values of at
Fig. 9.
for different values of at .
Fig. 10.
for different values of at
Fig. 11.
for different values of at
Fig. 12.
for different values of at
Fig. 13.
for different values of at
Fig. 14.
for different values of at
Fig. 15.
for different values of at
Fig. 16.
for different values of at
Fig. 17.
for different values of at
Fig. 18.
for different values of at
Fig. 19.
for different values of at
Fig. 20.
for different values of at
Fig. 21.
for different values of at
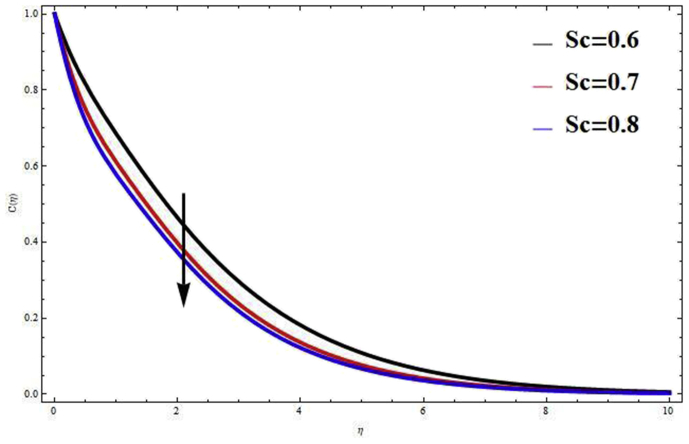
Fig. 22.
for different values of at
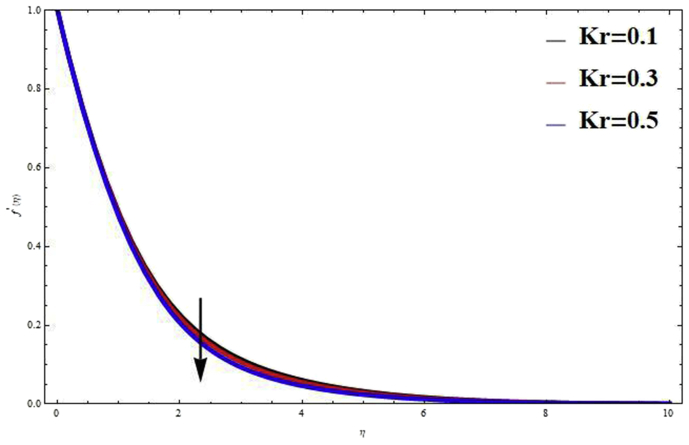
Fig. 23.
for different values of at
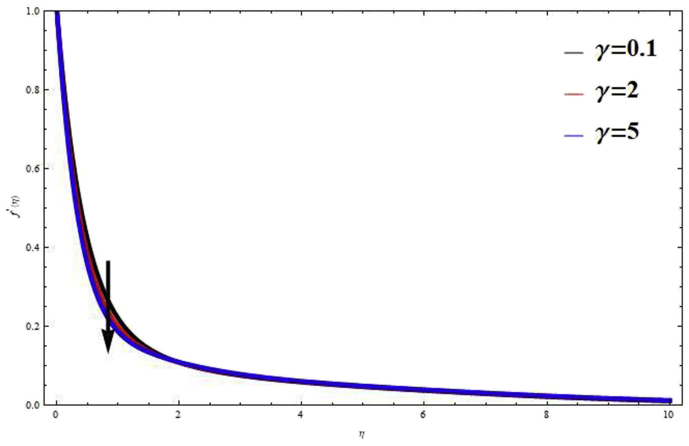
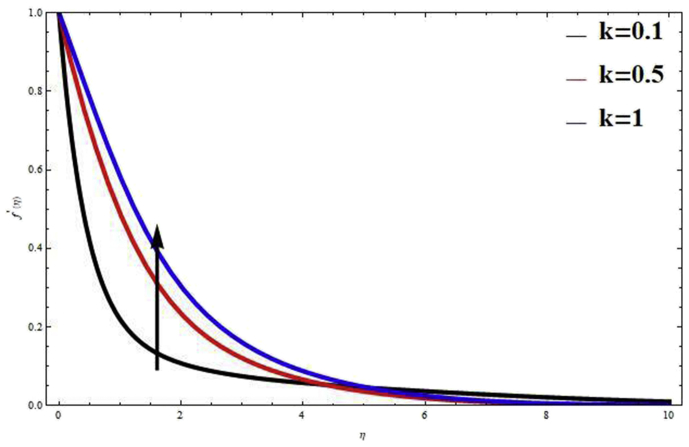
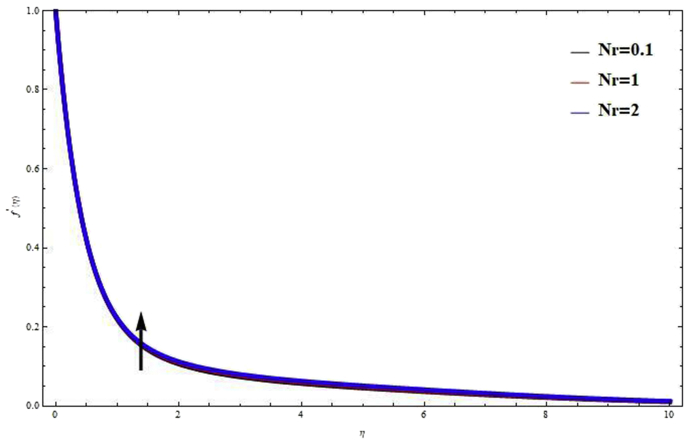
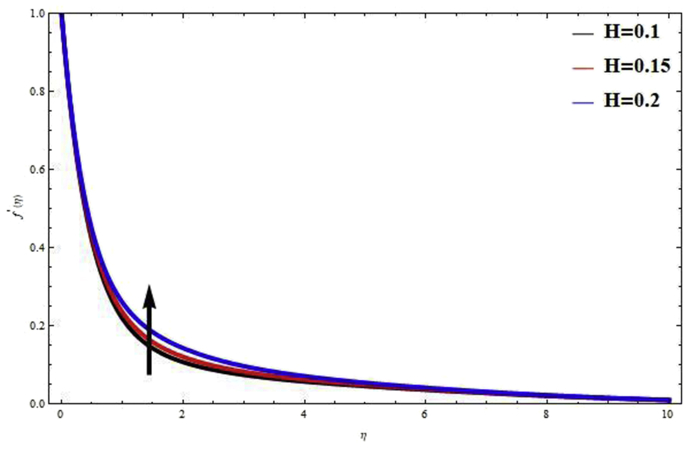
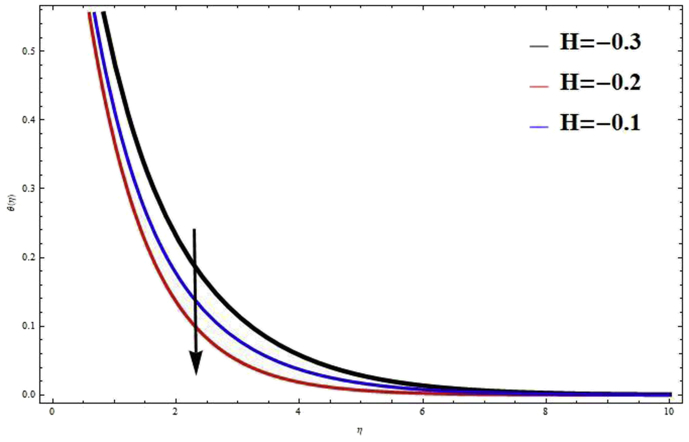
Fig. 5 shows magnetic field parameter effects on velocity profiles. Physically, the Lorentz force becomes stronger with an increase in . Due to this reason, Magnetic parameter tends to the reduced motion of the fluid which is displayed in Fig. 5. Therefore, in fluid flow problems, hydrodynamics situation is better in comparison to the hydromagnetic case. The influence of Casson fluid parameter on velocity profiles are shown in Fig. 6. The yield stress decreases and the thickness of the momentum boundary layer increases, when is increased. Due to this reason velocity distribution decrease with an increase in the values of . Physically, the fluid becomes more viscous with increasing Casson fluid parameter . It is further observed from this graph that when , the fluid behaviours change from non-Newtonian to Newtonian. Fig. 7 shows velocity distribution for several values of permeability parameter . It is seen that velocity distribution increase with increase in . This phenomena is clearly satisfied which is explains the physical situation that as increases. These result are clearly supported with Kataria and Patel [26]. Figs. 8 and 9 shows the effects of thermal radiation parameter on velocity and temperature distribution. It is seen that, thermal radiation parameter tends to improve velocity and temperature distribution. The thermal buoyancy force increase and thickness of the thermal boundary layer decrease, when is increased. Physically, Due to increasing thermal radiation parameter , heat is generated in fluid flow, which leads to improvement in velocity and temperature distribution throughout the fluid flow region. The effects of Heat generation and Heat absorption parameter on temperature and velocity distribution are demonstrated in Figs. 10, 11, 12, and 13. The positive values of indicate the heat is generated whereas negative values means heat is absorption. Above all figures illustrate that velocity and temperature distribution increase with positive values of H (heat source), whereas negative values of H (heat absorbed) have reverse effects on it. These outcomes are strongly supported because the hall of porous is increase due to the effects of heat source which rises the temperature in the flow field.
The influence of Dufour number and Soret number on velocity, temperature and, concentration distribution is shown in Figs. 14, 15, and 16. According to the definition, the values of and to be considered in such a way that their product is constant. From the figure, it is observed that, motion of the fluid elevates with increase in (decrease in ). Physically, the mass buoyancy force increase due to increase the values of , which leads to improve heat transfer process. It is also seen form Fig. 14 that, temperature distribution and its boundary layer thickness heighten with increase in . Figs. 17 and 18 shows effects of reaction parameter on on velocity and concentration profiles. The values of chemical reaction leads to reduce the concentration distribution. This occurrence has a superior agreement with the physical realities because of the weakens the buoyancy effects due to concentration gradients. Finally, it is concluded that chemical reaction tends to reduced velocity and concentration distribution. Effects of buoyancy force parameter N and Mixed convection parameter on velocity distribution are discussed in Figs. 19 and 20 respectively. It is observed that, both parameter tends to improve velocity distribution throughout the flow field. Physically, indicates that heat is converted from the surface. Therefore, velocity of the fluid increases. The buoyancy parameter N performs a ratio of the buoyancy with the inertia of the external forced on the heat and fluid flow. These results indicate that the velocity distribution increase with buoyancy parameter. The impact of temperature ratio parameter on temperature distribution is shown in Fig. 21. From the graph, it is seen that the heat transfer process improve with temperature ratio parameter . The results of Figs. 5, 6, 16, 19, and 20 are in good agreement with the outcomes of work of Kumar et al. [36]. Figs. 22 and 23 shows effects of Prandtl number and Schmidt number on temperature and concentration distribution. It is depict that the temperature and concentration distribution decreases with increase in and respectively. This result is justified because the increase value in , thermal conductivity of the fluid decrease, due to this reason the thermal boundary layer thickness is decreases.
Table 1 shows the HAM convergence analysis for governing dimensionless momentum, energy and concentration equations. It is seen that 10th order of approximation is enough for momentum equation, 15th order approximation is adequate for energy and concentration equations. The variation of the Skin friction, Nusselt number, Sherwood number are shown in Tables 2 and 3 for various values of the governing parameters. It is illustrated that the permeability of porous medium , buoyancy force parameter N and mixed convection parameter tends to improve Skin friction coefficient whereas, Magnetic field M and Casson fluid parameter have reverse effects on it. The local Nusselt number increase with increase in thermal radiation parameter Nr, heat generation H and temperature ratio parameter . Sherwood number decrease with increase in chemical reaction parameter Kr and Dufour number . Thermal-diffusion parameter Sr tends to improved skin friction coefficient, local Nusselt number and Sherwood number. To check the validation of numerical approach, local Nusselt number is computed and compared with previous published work for some special case which is presented in Table 4. It is seen that, the Nusselt number ( at ) is strong agreement with Kumar et al. [36] and Chen [47].
Table 1.
Convergence of the homotopic solutions for different order of approximations at M = 0.5,
| Order of approximation | |||
|---|---|---|---|
| 2 | 1.0516 | 1.6097 | 0.2334 |
| 4 | 1.0534 | 1.6438 | 0.2036 |
| 6 | 1.0538 | 1.6397 | 0.2056 |
| 8 | 1.0539 | 1.6338 | 0.2085 |
| 10 | 1.0538 | 1.6311 | 0.2098 |
| 15 | 1.0538 | 1.6309 | 0.2098 |
| 20 | 1.0538 | 1.6311 | 0.2097 |
| 25 | 1.0538 | 1.6311 | 0.2097 |
| 30 | 1.0538 | 1.6311 | 0.2097 |
Table 2.
Skin friction coefficient, Local Nusselt number and Sherwood number variation at .
| 0.5 | 0.5 | 1 | 0.1 | 1.2 | 15 | −2.848999 | 1.914061 | 0.209640 |
| 0.6 | −2.905504 | 1.915704 | 0.208905 | |||||
| 0.7 | −2.970927 | 1.917595 | 0.208064 | |||||
| 0.6 | −2.670698 | 1.908813 | 0.212005 | |||||
| 0.7 | −2.535931 | 1.904784 | 0.213843 | |||||
| 0.6 | −2.841723 | 1.913831 | 0.209748 | |||||
| 0.7 | −2.834449 | 1.913602 | 0.209856 | |||||
| 0.2 | −2.781439 | 1.912159 | 0.210469 | |||||
| 0.3 | −2.713809 | 1.910258 | 0.211297 | |||||
| 1.3 | −2.849106 | 2.003153 | 0.205647 | |||||
| 1.4 | −2.849227 | 2.108631 | 0.200873 | |||||
| 16 | −2.849104 | 1.903250 | 0.212310 | |||||
| 17 | −2.849136 | 1.890128 | 0.216024 |
Table 3.
Skin friction coefficient, Local Nusselt number and Sherwood number variation at .
| 0.1 | 2 | 1 | 0.22 | 2 | 0.5 | 0.5 | −2.848999 | 1.914061 | 0.209640 |
| 0.2 | −2.849485 | 2.238677 | 0.197827 | ||||||
| 0.3 | −2.849979 | 2.576070 | 0.185602 | ||||||
| 2.1 | −2.848036 | 1.862667 | 0.202047 | ||||||
| 2.2 | −2.847093 | 1.813360 | 0.195549 | ||||||
| 1.1 | −2.849751 | 1.886852 | 0.220177 | ||||||
| 1.2 | −2.850454 | 1.8598425 | 0.2313255 | ||||||
| 0.3 | −2.851298 | 1.818272 | 0.212163 | ||||||
| 0.4 | −2.853238 | 1.702633 | 0.176421 | ||||||
| 2.1 | −2.850023 | 1.947644 | 0.219386 | ||||||
| 2.2 | −2.851018 | 1.9808965 | 0.228800 | ||||||
| 0.6 | −2.850075 | 2.015436 | 0.1753032 | ||||||
| 0.7 | −2.850955 | 2.111142 | 0.142445 | ||||||
| 0.6 | −2.683765 | 1.919038 | 0.207416 | ||||||
| 0.7 | −2.559448 | 1.923065 | 0.205632 |
Table 4.
6. Conclusion
The problem of two-dimensional mixed convection MHD Casson fluid flow in a porous medium is examined by considering cross-diffusion, heat generation, chemical reaction, and nonlinear thermal radiation effects. The numerical solution is obtained by homotopy analysis method. The important results of these research work are listed below:
-
➢
The velocity, temperature and concentration distributions attain maximum value in the neighborhood of the plate and then decreased properly to approach the free stream value.
-
➢
The fluid flow accelerated via mixed convection parameter , buoyancy force parameter , the permeability of porous medium parameter , heat generation parameter H > 0 and thermo-diffusion parameter .
-
➢
A large value of Casson fluid parameter , Magnetic field parameter M, heat absorption parameter H < 0 and chemical reaction parameter have retard effects on velocity distribution.
-
➢
Heat and mass transfer process raise with Dufour number and Soret number respectively.
-
➢
Chemical reaction parameter Kr tends to reduced concentration distribution.
-
➢
The thermal radiation and heat generation tends to increase temperature distribution.
-
➢
In most of the Engineering and real-world problems, skin friction is not desirable, so it can be decreased by decreasing the values of magnetic field parameter M, Casson fluid parameter and chemical reaction parameter .
-
➢
The rate of heat and mass transfer process improved with , and .
Declarations
Author contribution statement
Harshad R Patel: Conceived and designed the analysis; Analyzed and interpreted the data; Contributed analysis tools or data; Wrote the paper.
Funding statement
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Competing interest statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
References
- 1.Casson N. Rheology of Disperse Systems. Pergamon; NewYork: 1959. A flow equation for the pigment oil suspensions of the printing ink type; pp. 84–102. [Google Scholar]
- 2.Khan M.I., Waqas M., Hayat T., Alsaedi A. A comparative study of Casson fluid with homogeneous-heterogeneous reactions. J. Colloid Interface Sci. 2017;498:85–90. doi: 10.1016/j.jcis.2017.03.024. [DOI] [PubMed] [Google Scholar]
- 3.Nagaraju G., Garvandha M. Magnetohydrodynamic viscous fluid flow and heat transfer in a circular pipe under an externally applied constant suction. Heliyon. 2019;5(2) doi: 10.1016/j.heliyon.2019.e01281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sandeep N., Animasaun I.L., Ali M.E. Unsteady liquid film flow of electrically conducting magnetic-nanofluids in the vicinity of a thin elastic sheet. J. Comput. Theor. Nanosci. 2017;14(2):1140–1147. [Google Scholar]
- 5.Sandeep N. Effect of aligned magnetic field on liquid thin film flow of magnetic-nanofluids embedded with graphene nanoparticles. Adv. Powder Technol. 2017;28(3):865–875. [Google Scholar]
- 6.Kataria H.R., Patel H.R. Heat and mass transfer effects on unsteady free convective MHD flow of a micro polar fluid between two vertical walls. Math. Today. 2018;34:42–63. [Google Scholar]
- 7.Selimefendigil F., Öztop H.F. Corrugated conductive partition effects on MHD free convection of CNT-water nanofluid in a cavity. Int. J. Heat Mass Transf. 2019;129:265–277. [Google Scholar]
- 8.Selimefendigil F., Öztop H.F. Role of magnetic field and surface corrugation on natural convection in a nanofluid filled 3D trapezoidal cavity. Int. Commun. Heat Mass Transf. 2018;95:182–196. [Google Scholar]
- 9.Selimefendigil F., Öztop H.F. Modeling and optimization of MHD mixed convection in a lid-driven trapezoidal cavity filled with alumina–water nanofluid: effects of electrical conductivity models. Int. J. Mech. Sci. 2018;136:264–278. [Google Scholar]
- 10.Selimefendigil F., Öztop H.F. Mixed convection in a partially heated triangular cavity filled with nanofluid having a partially flexible wall and internal heat generation. J. Taiwan Inst. Chem. Eng. 2017;70:168–178. [Google Scholar]
- 11.Selimefendigil F., Öztop H.F. MHD mixed convection and entropy generation of power law fluids in a cavity with a partial heater under the effect of a rotating cylinder. Int. J. Heat Mass Transf. 2016;98:40–51. [Google Scholar]
- 12.Selimefendigil F., Öztop H.F. Numerical study of MHD mixed convection in a nanofluid filled lid driven square enclosure with a rotating cylinder. Int. J. Heat Mass Transf. 2014;78:741–754. [Google Scholar]
- 13.Selimefendigil F., Öztop H.F. Mixed convection of nanofluids in a three dimensional cavity with two adiabatic inner rotating cylinders. Int. J. Heat Mass Transf. 2018;117:331–343. [Google Scholar]
- 14.Selimefendigil F., Öztop H.F. Fluid-solid interaction of elastic-step type corrugation effects on the mixed convection of nanofluid in a vented cavity with magnetic field. Int. J. Mech. Sci. 2019;152:185–197. [Google Scholar]
- 15.Selimefendigil F., Öztop H.F., Chamkha A.J. Analysis of mixed convection of nanofluid in a 3D lid-driven trapezoidal cavity with flexible side surfaces and inner cylinder. Int. Commun. Heat Mass Transf. 2017;87:40–51. [Google Scholar]
- 16.Hayat T., Khan M.I., Farooqc M., Gull N., Alsaedi A. Unsteady three-dimensional mixed convection flow with variable viscosity and thermal conductivity. J. Mol. Liq. 2016;223:1297–1310. [Google Scholar]
- 17.Waqas M., Farooq M., Khan M.I., Alsaedi A., Hayat T., Yasmeen T. Magnetohydrodynamic (MHD) mixed convection flow of micropolar liquid due to nonlinear stretched sheet with convective condition. Int. J. Heat Mass Transf. 2016;102:766–772. [Google Scholar]
- 18.Shah Z., Bonyah E., Islam S., Khan W., Ishaq M. Radiative MHD thin film flow of Williamson fluid over an unsteady permeable stretching sheet. Heliyon. 2018;4(10) doi: 10.1016/j.heliyon.2018.e00825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Sheikholeslami M., Kataria H.R., Mittal A.S. Radiation effects on heat transfer of three dimensional nanofluid flow considering thermal interfacial resistance and micro mixing in suspensions. Chin. J. Phys. 2017;55:2254–2272. [Google Scholar]
- 20.Hayat T., Waqas M., Shehzad S.A., Alsaedi A. A model of solar radiation and Joule heating in magnetohydrodynamic (MHD) convective flow of thixotropic nanofluid. J. Mol. Liq. 2016;215:704–710. [Google Scholar]
- 21.Kumar K.A., Sugunamma V., Sandeep N. Impact of non-linear radiation on MHD non-aligned stagnation point flow of micropolar fluid over a convective surface. J. Non Equilib. Thermodyn. 2018;43:327–346. [Google Scholar]
- 22.Kumar K.A., Sugunamma V., Sandeep N., Reddy J.V.R. Numerical examination of MHD nonlinear radiative slip motion of non-Newtonian fluid across a stretching sheet in the presence of porous medium. Heat Transf. Res. 2018 [Google Scholar]
- 23.Kataria H.R., Patel H.R. Heat and mass transfer in magnetohydrodynamic (MHD) Casson fluid flow past over an oscillating vertical plate embedded in porous medium with ramped wall temperature. Propuls. Power Res. 2018;7(3):257–267. [Google Scholar]
- 24.Mabood F., Das K. Outlining the impact of melting on MHD Casson fluid flow past a stretching sheet in a porous medium with radiation. Heliyon. 2019;5(2) doi: 10.1016/j.heliyon.2019.e01216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Abbas Z., Sheikh M., Motsa S.S. Numerical solution of binary chemical reaction on stagnation point flow of Casson fluid over a stretching/shrinking sheet with thermal radiation. Energy. 2016;95:12–20. [Google Scholar]
- 26.Kataria H.R., Patel H.R. Radiation and chemical reaction effects on MHD Casson fluid flow past an oscillating vertical plate embedded in porous medium. Alex. Eng. J. 2016;55:583–595. [Google Scholar]
- 27.Selimefendigil F., Öztop H.F. Natural convection in a flexible sided triangular cavity with internal heat generation under the effect of inclined magnetic field. J. Magn. Magn. Mater. 2016;417:327–337. [Google Scholar]
- 28.Kumar K.A., Reddy J.V.R., Sugunamma V., Sandeep N. Simultaneous solutions for MHD flow of Williamson fluid over a curved sheet with non-uniform heat source/sink. Heat Transf. Res. 2019;50(6):581–603. [Google Scholar]
- 29.Hayat T., Ullah S., Khan M.I., Alsaedi A., Zia Q.M.Z. Non-Darcy flow of water-based carbon nanotubes with nonlinear radiation and heat generation/absorption. Results Phys. 2018;8:473–480. [Google Scholar]
- 30.Kataria H.R., Patel H.R. Effects of chemical reaction and heat generation/absorption on magnetohydrodynamic (MHD) Casson fluid flow over an exponentially accelerated vertical plate embedded in porous medium with ramped wall temperature and ramped surface concentration. Propuls. Power Res. 2019;8(1):35–46. [Google Scholar]
- 31.Kataria H.R., Patel H.R. Soret and heat generation effects on MHD casson fluid flow past an oscillating vertical plate embedded through porous medium. Alex. Eng. J. 2016;55:2125–2137. [Google Scholar]
- 32.Sheikholeslami M., Kataria H.R., Mittal A.S. Effect of thermal diffusion and heat-generation on MHD nanofluid flow past an oscillating vertical plate through porous medium. J. Mol. Liq. 2018;257:12–25. [Google Scholar]
- 33.Raju R.S., Reddy G.J., Rao J.A., Rashidi M.M. Thermal diffusion and diffusion thermo effects on an unsteady heat and mass transfer magnetohydrodynamic natural convection Couette flow using FEM. J. Comput. Des. Eng. 2016;3:349–362. [Google Scholar]
- 34.Kumar A.K., Reddy J.V.R., Sugunamma V., Sandeep N. Impact of cross diffusion on MHD viscoelastic fluid flow past a melting surface with exponential heat source. Multidiscip. Model. Mater. Struct. 2018;14(5):999–1016. [Google Scholar]
- 35.Shah R.A., Khan A., Shuaib M. On the study of flow between unsteady squeezing rotating discs with cross diffusion effects under the influence of variable magnetic field. Heliyon. 2018;4(11) doi: 10.1016/j.heliyon.2018.e00925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kumar K.G., Archana M., Gireesha B.J., Krishanamurthy M.R., Rudraswamy N.G. Cross diffusion effect on MHD mixed convection flow of nonlinear radiative heat and mass transfer of Casson fluid over a vertical plate. Results Phys. 2018;8:694–701. [Google Scholar]
- 37.Ahmed M.A.M., Mohammed M.E., Khidir A.A. The effects of cross-diffusion and radiation on mixed convection from a vertical flat plate embedded in a fluid-saturated porous medium in the presence of viscous dissipation. Propuls. Power Res. 2016;5(2):149–163. [Google Scholar]
- 38.Raju C.S.K., Neeraja G., Dinesh P.A., Vidya K., Rushi Kumar B. MHD Casson fluid in a suspension of convective conditions and cross diffusion across a surface of paraboloid of revolution. Alexandria Eng. J. 2018;57(4):3615–3622. [Google Scholar]
- 39.Kataria H.R., Mittal A.S. Mathematical Analysis of three dimensional nanofluid flow in a rotating system considering thermal interfacial resistance and Brownian motion in suspensions through porous medium. Math. Today. 2018;34:7–24. [Google Scholar]
- 40.Kumar A.K., Sugunamma V., Sandeep N., Reddy J.V.R. Impact of Brownian motion and thermophoresis on bioconvective flow of nanoliquids past a variable thickness surface with slip effects. Multidiscip. Model. Mater. Struct. 2019;15(1):103–132. [Google Scholar]
- 41.Kumaran G., Sandeep N. Thermophoresis and Brownian moment effects on parabolic flow of MHD Casson and Williamson fluids with cross diffusion. J. Mol. Liq. 2017;233:262–269. [Google Scholar]
- 42.Liao S.J. Chapman and Hall/CRC Press; Boca Raton: 2003. Beyond Perturbation: Introduction to Homotopy Analysis Method. [Google Scholar]
- 43.Liao S.J. On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 2004;147:499–513. [Google Scholar]
- 44.Liao S.J. Notes on the homotopy analysis method: some definitions and theorems. Commun. Nonlinear Sci. Numer. Simulat. 2009;14:983–997. [Google Scholar]
- 45.Fallahzadeh A., Shakibi K. A method to solve convection-diffusion equation based on homotopy analysis method. J. Interpolat. Approx. Sci. Comput. 2015;1:1–8. [Google Scholar]
- 46.Fagbade A.I., Falodun B.O., Omowaye A.J. MHD natural convection flow of viscoelastic fluid over an accelerating permeable surface with thermal radiation and heat source or sink: spectral homotopy analysis approach. Ain Shams Eng. J. 2018;9(4):1029–1041. [Google Scholar]
- 47.Chen C.H. Laminar mixed convection adjacent to vertical continuously stretching sheets. Heat Mass Transf. 1998;33:471–476. [Google Scholar]
- 48.Rosseland S. Springer-Verlag; Berlin: 1931. Astrophysik und atom-theoretische Grundlagen. [Google Scholar]