Abstract
Recent studies have shown that quantitative description of gyral shape patterns offers a novel window to examine the relationship between brain structure and function. Along this research line, this paper examines a unique and interesting type of cortical gyral region where 3 different gyral crests meet, termed 3-hinge gyral region. We extracted 3-hinge gyral regions in macaque/chimpanzee/human brains, quantified and compared the relevant DTI-derived fiber densities in 3-hinge and 2-hinge gyral regions. Our observations consistently showed that DTI-derived fiber densities in 3-hinge regions are much higher than those in 2-hinge regions. Therefore, we hypothesize that besides the cortical expansion, denser fiber connections can induce the formation of 3-hinge gyri. To examine the biomechanical basis of this hypothesis, we constructed a series of 3-dimensional finite element soft tissue models based on continuum growth theory to investigate fundamental biomechanical mechanisms of consistent 3-hinge gyri formation. Our computational simulation results consistently showed that during gyrification gyral regions with higher concentrations of growing axonal fibers tend to form 3-hinge gyri. Our integrative approach combining neuroimaging data analysis and computational modeling appears effective in probing a plausible theory of 3-hinge gyri formation and providing new insights into structural and functional cortical architectures and their relationship.
Keywords: cortical folding, DTI, fiber density, primate brains
Introduction
Convoluted cortical folding is a prominent feature of the primate brains (Chen et al. 2012; Li et al. 2016). Convolution may arise at multiple stages, primary, secondary, and tertiary which occurs over a period of several months (Sun and Hevner 2014; Budday et al. 2015c). Primary folding is notably preserved among individuals (Lohmann et al. 2008) while secondary and tertiary foldings vary cross individuals and evolve after primary folding is completed (Gilles et al. 1983), which it is believed that differential growth of the cortex is a possible stimulus for secondary and tertiary folding (Richman et al. 1975; Tallinen et al. 2016). Neuroscientific studies have demonstrated that neural structures of concave sulci and convex gyri emerge from a complex cortical folding process in brain development (Rakic 1988). It has been shown that cortical fold patterns seem to be closely correlated with neurodevelopment (Dubois et al. 2008; Giedd and Rapoport 2010; Li et al. 2014, 2015), cytoarchitecture (Zilles et al. 1997; Fischl et al. 2008), and cognitive functioning (Thompson et al. 2004; Nordahl et al. 2007; Bullmore and Sporns 2009; Honey et al. 2010). Therefore, a quantitative description of complex cortical folding patterns is of fundamental importance to understand the underlying structural (Van Essen 1997; Toro and Burnod 2005; Nie et al. 2012; Bayly et al. 2014) and functional (Schoenemann 2006; Honey et al. 2009; Liu 2011; Deng et al. 2014) mechanisms of the brain. Essentially, the folding pattern of human cerebral cortex is a multi-scale concept, and therefore the research scope of quantitative description of cortical folding can vary from a very small neighborhood on the cortex to the entire cortical surface (Li et al. 2010). In previous studies, descriptors proposed for modeling and analyzing cortical folding patterns can be classified into 2 major categories (Li et al. 2010). The first one was based on the descriptor of curvature and its derivations (Cachia et al. 2001, 2003; Neal et al. 2007). The other one was a global descriptor, the studies of which usually use tools like gyrification index (Zilles et al. 1988; Hardan et al. 2004), spherical wavelets (Yu et al. 2007; Yeo et al. 2008), and intrinsic curvature (Ronan et al. 2014) to quantity the convolution level of the whole cortical surface or a preselected regions of interests (ROIs). In general, both categories of cortical folding descriptors unveiled interesting properties of cerebral cortex and helped understand the regularity and variability of the complex cerebral cortex.
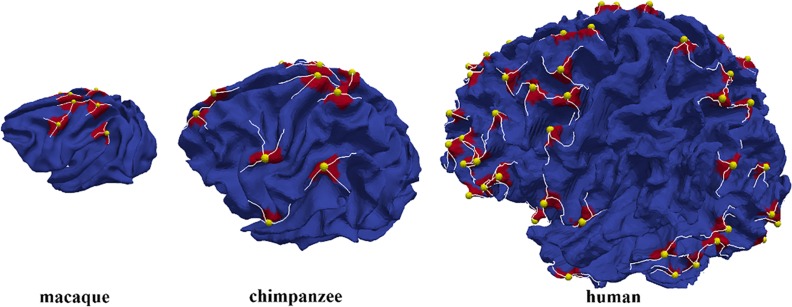
Recently, inspired by the work on folding pattern analysis of rocks in geology, Li et al. proposed a novel way that combined both advantages of parametric method and surface profiling method to analyze cortical folding patterns in terms of gyral hinge numbers (Li et al. 2010). Basically, as illustrated in Figure 1, gyral crests with white curves in Figure 1 are termed 2-hinge gyri while regions where 3 2-hinge gyral crests meet are termed 3-hinge gyri as highlighted by the yellow spheres in Figure 1. It is worth to note (Li et al. 2010) that 4 gyral crests rarely meet to form 4-hinge gyri. Thus, in this paper, we will mainly focus on the discussion of 2-hinge and 3-hinge gyri. Notably, in our recent study (Li et al. 2016), we quantitatively identified and characterized 6 popular and cross-species consistent 3-hinge gyral folds in macaque/chimpanzee/human brains, 2 unique 3 hinges in macaque brains, 6 unique ones in chimpanzee brains and 14 unique ones in human brains. Our quantitative measurements applied to these 3-hinge gyral folds showed the increasing complexity among the primate species we analyzed. However, our prior study (Li et al. 2016) did not explore the possible mechanisms of formation of such cross-species preserved 3-hinge gyri in primate brains which is the main objective of this study.
Figure 1.
Illustration of 2-hinge and 3-hinge gyral folds in macaque, chimpanzee, and human brains.
Specifically, we first extracted the 3-hinge gyral regions in macaque/chimpanzee/human brains by using the automated computational pipeline in Li et al. (2010). Then, based on the 3-hinge gyri on the whole cortical surface, we quantified the densities of diffusion tensor imaging (DTI)-derived fibers connected to these 3-hinge gyral regions, as well as those connected to 2-hinge gyri. Finally, we quantitatively compared the DTI-derived fiber densities in 3-hinge and 2-hinge gyral regions in the entire macaque/chimpanzee/human brains. Our results consistently demonstrated that DTI-derived fiber densities in 3-hinge gyri are much higher than those in 2-hinge gyri. Therefore, we hypothesize that beside the cortical expansion, denser fiber connections can induce the formation of 3-hinge gyri. By constructing a series of 3-dimensional finite element (FE) soft tissue models based on continuum growth theory, we investigated fundamental biomechanical mechanisms of consistent 3-hinge gyri formation and examined the biomechanical basis of this hypothesis.
Methods
Overview of Computational Framework
Basically, there are 4 major computational steps in this work. 1) We modified and employed an automatic computational pipeline to identify 2-hinge and 3-hinge gyral folding patterns across entire primate brain. 2) We quantified the DTI-derived fiber density (Zhang et al. 2014) termed as the number of fibers per unit surface area, over the entire cerebral cortex. 3) We derived the DTI-derived fiber densities on the extracted 2-hinge and 3-hinge gyral regions, and then performed extensive comparisons between them. 4) We designed and constructed a series of computational FE models to investigate the fundamental mechanism of 3-hinge formation. In general, our integrative approach which combines neuroimaging data analysis over macaque/chimpanzee/human brains and computational simulations provides a unique window to understand the deeply rooted regularity of 3-hinge gyri formation and offers a plausible theory that denser growing fiber connections induce 3-hinge gyri formation.
Data Description and Preprocessing
Imaging Data of Human Brains
In this work, DTI images were used to perform the reconstruction of cortical surfaces. In total, 64 human brains from the Q1 release of WU-Minn Human Connectome Project (HCP) consortium (Van Essen et al. 2012) were used in this study, and the age range of these subjects is 22–35 years. For T1-weighted structural MRI, the scan protocol used a TR = 2400 ms, TE = 2.14 ms, flip angle=8°, image matrix = 260 × 311 × 260, and resolution = 0.7 × 0.7 × 0.7 mm3. DTI data collected with spin-echo EPI sequence was acquired using the following parameters: TR = 5520 ms, TE = 89.5 ms, flip angle=78°, FOV = 210 × 180, matrix = 168 × 144, resolution=1.25 × 1.25 × 1.25 mm3, and echo spacing = 0.78 ms. Particularly, a full DTI session includes 6 runs, representing 3 different gradient tables, with each table acquired once with right-to-left and left-to-right phase encoding polarities, respectively. Each gradient table includes approximately 90 diffusion weighting directions plus 6 b = 0 acquisitions interspersed throughout each run. Diffusion weighted data consisted of 3 shells of b = 1000, 2000, and 3000 s/mm2 interspersed with an approximately equal number of acquisitions on each shell within each run. White matter cortical surface reconstructed using DTI data was based on FA maps via the methods in Liu et al. (2008) after performing skull removal, motion correction, eddy current correction and tissue segmentation based on FSL (Jenkinson et al. 2012).
Imaging Data of Chimpanzees
All the 16 chimpanzee subjects (all females, 29.4 ± 12.8 years) used here were members of a colony in the Yerkes National Primate Research Center (YNPRC) at Emory University in Atlanta, GA. All imaging studies were approved by the IACUC of Emory University. Prior to scanning, the subjects were immobilized with ketamine injections (2–6 mg/kg, i.m.) and were subsequently anesthetized with an intravenous propofol drip (10 mg/kg/h) according to standard veterinary procedures used at YNPRC. The subjects remained sedated for the duration of the scans as well as the time needed for transportation between their home cage and the scanner location. After completing scans, chimpanzees were temporarily housed in a single cage for 6–12 h to allow effects of anesthesia to wear off before being returned to their home cage and cage mates. The veterinary staff and research staff assessed the general well-being (i.e., activity, food intake) of the chimpanzees twice daily after the scan for possible distress associated with esthetic accesses.
The anatomical MRI scans were performed on a Siemens 3T Trio scanner with a standard birdcage coil. Foam cushions and elastic straps were used to minimize head motion. T1-weighted MRI images were acquired with a 3D magnetization-prepared rapid gradient echo (MPRAGE) sequence for all participants. For subjects scanned using the MS-EPI (multi-shot double spin-echo echo planar imaging) sequence, the scan protocol, optimized at 3T used a TR = 2400 ms, TE = 4.13 ms, flip angle = 8°, image matrix = 256 × 256 × 192, and resolution = 1.0 × 1.0 × 0.8 mm3, with 2 averages. For subjects scanned using SS-EPI (single-shot double spin-echo echo planar imaging), the scan protocol is similar, despite that the resolution = 0.8 × 0.8 × 0.8 mm3 isotropic. In this study, MRI images from 16 female chimpanzees are used. The preprocessing steps were similar to those used in human data processing and the brains of chimpanzees are scaled to the same size as human brain.
Imaging Data of Macaques
All the 20 macaque subjects (all females, 14 ± 6.7 years) were members of a colony at YNPRC. All MRI scans were approved by IACUC of Emory University. Prior to scanning, the subjects were immobilized with ketamine injections (2–6 mg/kg, i.m.) and were subsequently anesthetized with an intravenous propofol drip (10 mg/kg/h) following standard veterinary procedures used at YNPRC. The macaques remained sedated for the duration of the scans as well as the time needed for transportation between their home cage and the scanner location. After completing scans, macaques were temporarily housed in a single cage for 6–12 h to allow the effects of anesthesia to wear off before being returned to their home cage and cage mates. The veterinary staff and research staff observed the general well-being (i.e., activity, food intake) of the macaques twice daily after the scan for possible distress associated with anesthetic accesses.
The anatomical MRI scans were performed on a Siemens 3T Trio scanner with a standard knee oil. To minimize head motion, foam cushions and elastic straps were used during the scan. Particularly, a specially designed holding device was used to stabilize macaque’s head during scanning with 2 plastic screws anchoring in the macaque’s ear canals tightly. The high resolution T1-weighted MRI images were acquired with a 3D MPRAGE sequence. The scan protocol used a TR = 2500 ms, TE = 3.49 ms, flip angle = 8°, image matrix = 256 × 256 × 192, and resolution = 0.5 × 0.5 × 0.5 mm3, with 3 averages. In this study, MRI images from 20 subjects were used. The preprocessing steps were similar to those used in human data processing and the brains of macaques are scaled to the same size as human brain.
Automatic Pipeline for 2-hinge and 3-hinge Gyri Extraction
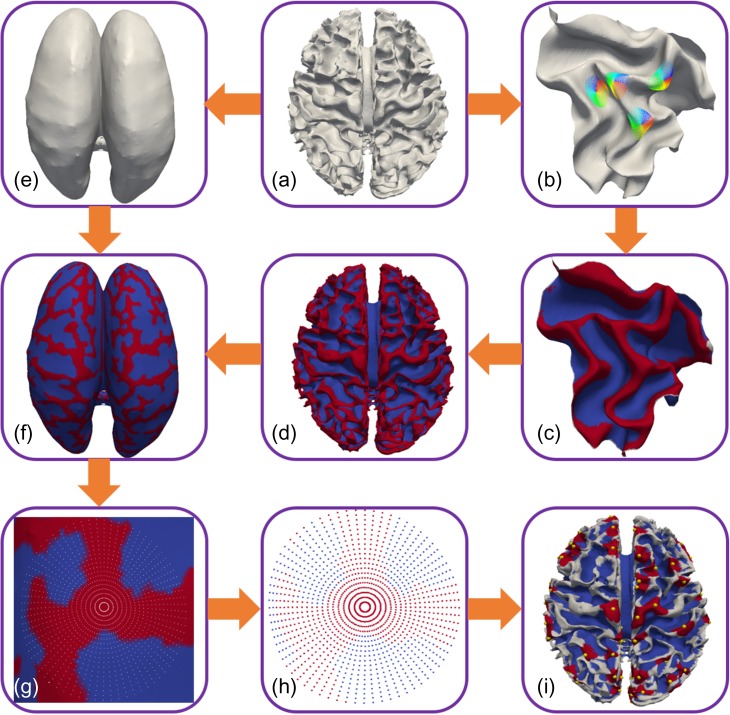
A gyral hinge refers to the region on the top of gyrus with the maximal folding curvature. By following and extending our prior work (Li et al. 2010), we automatically extracted the centers of 3-hinge gyri from these reconstructed cortical surfaces in Section 2.2 (Li et al. 2010). A gyral hinge curve can be traced when hinges are connected along a gyral crest and the number of hinge curves intersecting together at a cross-point can be used to characterize the gyral folding patterns (Li et al. 2010). In order to automatically identify 3-hinge vertices, 2 main steps of surface profiling were proposed and used. Here we take a human brain cortical surface as an example to detail the 2-step process: 1) classifying vertices into 2 groups, gyri and sulci in Figure 2(a)–(d) and 2) finding 3-hinge centers in Figure 2(e)–(i). Firstly, we built a local 3D coordinate system for each vertex on the cortical surface. The normal direction of the vertex was considered as the Z direction and a tangent plane was represented by a 2D polar coordinate system. Then 22 20 mm long spokes were allocated from the vertex along the neighboring surface patch. In total, 20 points were evenly sampled along each spoke. The projections of all spokes on the tangent plane were evenly distributed (5° interval). Then a power function was expressed as follows to fit the model of each spoke:
where is the 2D Cartesian coordinate of a profile based on the 2D polar coordinate system, are parameters of the profile via a least-square fitting method. Then, features of a vertex such as average ratio, average concave, average convex, and sulci-or-gyri can be extracted via mathematical operations (Li et al. 2010). Particularly, the feature, sulci-or-gyri, was used to classify a vertex to be a sulcal vertex or a gyral vertex.
Figure 2.
Illustration of automatic 3-hinge gyral fold extraction on a human brain. (a) A reconstructed white matter (WM) cortical surface; (b) Profiling every voxel on the surface; (c) Cortical features detected after profiling; (d) The cortical surface profiled by sulcus (blue) or gyrus (red); (e) The corresponding inflated surface which has the same number of points as (a); (f) Mapping the sulcus and gyrus feature on the inflated surface; (g) Second profile on a sulcus vertex; (h) Profile spokes labeled by sulcus or gyrus; (i) Cortical surface with the detected centers of 3-hinge (red region, center: yellow dots) and 2-hinge area (gray region).
The second profiling step was only applied on gyral vertices on an inflated surface in order to identify centers of 3-hinge gyri. The inflated surface by FreeSurfer (Fischl 2012) here still retains the original topology information such as the number of vertices and the correspondence between an inflated surface (Fig. 2(g)) and an original surface (Fig. 2(b)). With this set-up, then 72 evenly distributed spokes and 20 evenly sampling points on each spoke were constructed. It is evident that each sampling point with a label indicates whether it is a gyrus or sulcus. Following the construction, we classify each spoke into 2 types—either all sampling points in this spoke are on a gyrus or only part of these points are on a gyrus. For the profile of a vertex, its adjacent all-gyri spokes were clustered into 1 group divided by any part-gyri spoke. If this vertex belongs to 3 all-gyri spoke groups, it is considered as a 3-hinge vertex. Finally, we clustered all adjacent 3-hinge vertices using spatial information and termed the vertex closest to cluster center as a 3-hinge center. In order to compute axonal fiber density of 2-hinge and 3-hinge gyral folds later, we need to define an area for each 3-hinge vertex. Here we consider the surrounding area within a radius r = 6 mm of a 3-hinge center as its corresponding 3-hinge area (Fig. 2(i)). Once the area of 3-hinge vertex is determined, the 2-hinge vertex area can be found by excluding 3-hinge areas.
Fiber Density Calculation on 2-hinge and 3-hinge Gyri
After dividing the gyri vertices into 2-hinge and 3-hinge areas, we then calculate the fiber density on all of the 3 hinges and 2 hinges detected on the cortical surface. Fiber density is defined as the number of DTI-derived streamline fibers per unit surface area (Zhang et al. 2014). Following this definition, we calculated the fiber density of both 3-hinge gyri and 2-hinge gyri by averaging density values of the surrounding area of each vertex within radius r = 2.5 mm of its hinge center, the result of which is then used to represent the fiber density of a certain hinge. Radius of 2.5 mm is chosen to avoid potential overlapping between 2-hinge gyri and 3-hinge gyri when we perform the averaging calculation. Finally, we made comparisons in fiber density between 2-hinge gyri and 3-hinge gyri in macaques, chimpanzees, and human brains. This computational pipeline of measuring fiber densities on 2 hinges and 3 hinges is similar to those used in our prior studies (Chen et al. 2012; Nie et al. 2012).
Computational Model of Biomechanical Simulations
Three-dimensional (3D) FE analyses on a double-layer soft tissue model that mimics a small piece of the cortex are performed to investigate the fundamental mechanism of consistent hinge formation in the cortical folding, as illustrated in Supplementary Figure S1. The top layer represents the developing cortical plate (cortex) and the bottom layer is the core of the brain which is considered as a simple organization of the subplate, intermediate zone and ventricular zone, as we designed and tested in our prior studies (Zhang et al. 2016). The cerebral cortex is a thin (2–4 mm) (Bayly et al. 2014) layer in contrast to the inner core which has a thickness around 50 mm (Tallinen et al. 2014). The dimension of the plate is selected to be large enough (300 × 300 × 50 mm3) in comparison with the wavelength of cortical folds. In Supplementary Figure S1(a), the green area in the middle of the free surface of the cortex layer in the model is an indicator that shows there is a bundle of axonal fibers beneath it. The material properties of the green area are set the same as the cortex, and the main purpose of the green area is to help trace the location of axonal fibers after cortical convolution. Supplementary Figure S1(b) shows the cross-section of the cortex model. The part with blue in the model represents the bundle of axonal fibers which are across the entire core. In this model, we utilize that differential growth in the cortex as the basic driving mechanism for cortical folding, similar to previous simulation studies (Bayly et al. 2013; Razavi , Zhang, Liu, et al. 2015; Zhang et al. 2017).
Growth in this soft tissue model is simulated via thermal expansion (Cao et al. 2012; Razavi and Wang 2015; Razavi et al. 2016). For understanding the detail of analogy between volumetric growth model and thermal stress model please check reference (Cao et al. 2012). The growth rate of bundle of fibers is considered to be variable to conduct different scenarios, so that we can explore how growth rates of axonal fibers can regulate the formation of consistent gyri and hinge patterns for the green area in our model. Material properties of the cortex and core are set as the same in the model since recent study has shown that there is no significant difference in material property between gray and white matter of the brain (Budday et al. 2015a). Our previous studies have shown that morphological patterns of the cortex model after growth are independent of the absolute value of elastic modulus of the cortex and core of the cortex, but they depend on the ratio of their moduli (Razavi , Zhang, Li, et al. 2015; Zhang et al. 2016). The axonal stiffness depends critically on the degree of myelination may change substantially during development (Holland et al. 2015). From other hand, our results showed that stiffness of fibers do not have considerable effect on the gyrification and only their growth ratio show impact. Therefore, in our model, the stiffness of axonal fibers is assumed to be the same as the cortex and core have, and it is set as a constant. All FE simulations are carried out by the popular package of ABAQUS.
Results
Based on the methods described above, we calculated the fiber densities on 2 hinges and 3 hinges in macaque/chimpanzee/human brains. Comparisons were performed across these 3 primate species. Examples of the cortical surfaces color-coded by fiber density values are shown in Supplement Figure S2. We can see that the axonal fibers are much less dense in macaque and chimpanzee brains than that in human brain. Also, the fiber density on gyri is much denser than that on sulci, which is consistent with our previous findings in Chen et al. (2012) and Nie et al. (2012). The quantitative measurements of axonal fiber density in Sections 3.1–3.3 are based on the same computational pipeline.
Fiber Density of 2-hinge Gyri and 3-hinge Gyri in Human Brains
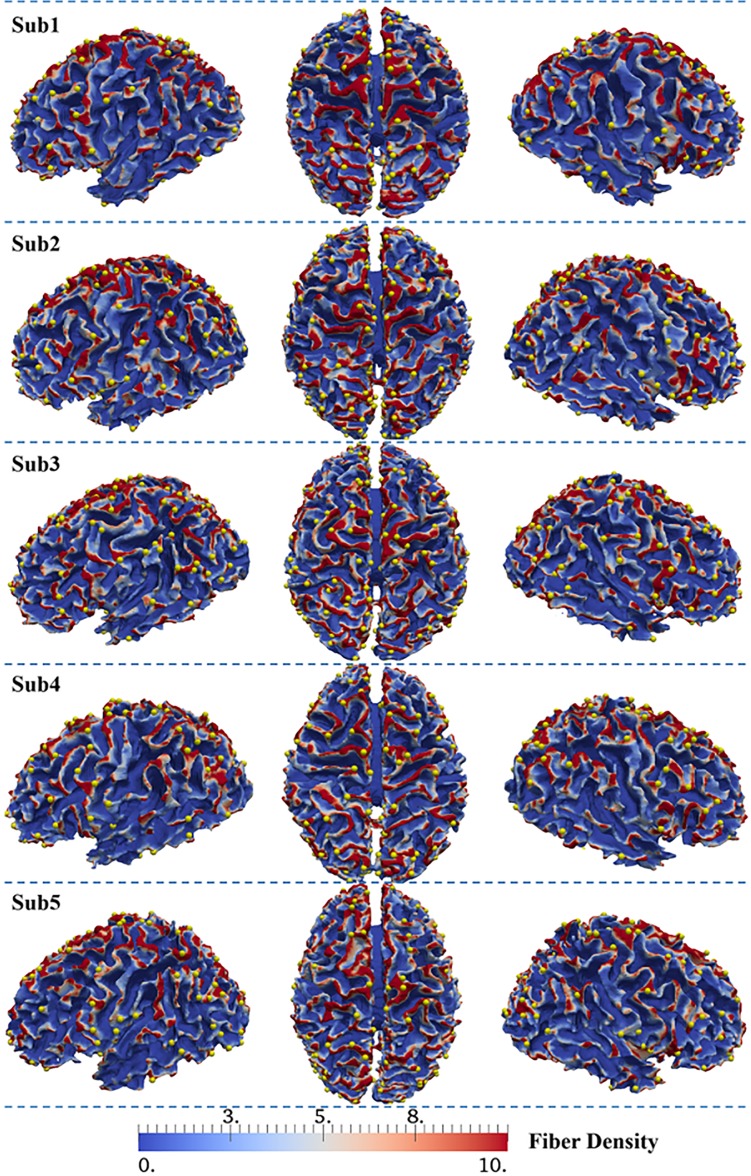
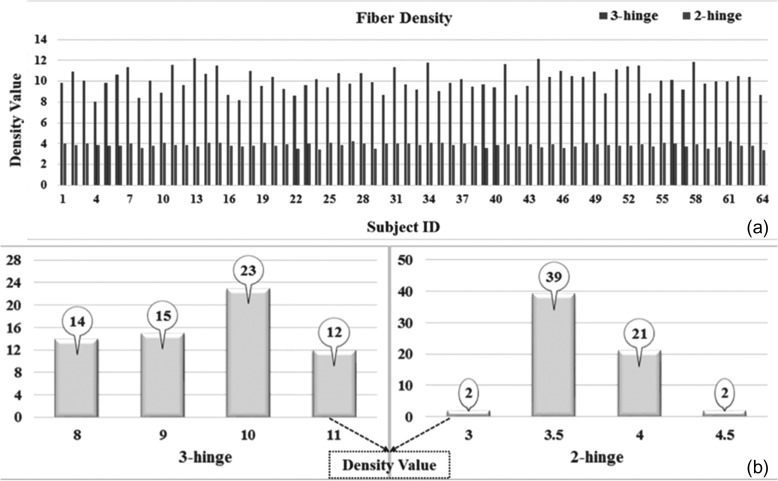
With the approaches described in Section 2.3, 3-hinge gyri were identified on cortical surfaces reconstructed using DTI data from 64 HCP subjects. Among these human brains, the average number of 3 hinges is around 137. Based on the approach in Section 2.4, we obtained the average fiber densities of 3-hinge gyri and 2-hinge gyri which are 10.1 and 3.85, respectively. This result shows a significant difference in the fiber density between 2-hinge and 3-hinge gyral folds, that is, 3-hinge gyral areas have a larger fiber density of more than 2 times than that on 2-hinge gyral areas, in human brains. Figure 3 shows fiber density distribution of 2-hinge gyri and 3-hinge gyri in 5 randomly selected human brains, in which yellow spheres are used to locate the centers of 3-hinge gyral areas. Again, it can be seen that axonal fibers connected to 3-hinge gyri are much denser. In addition, the individually average fiber densities on 2 hinges and 3 hinges in Figure 4(a) suggest a large difference between them. Moreover, Figure 4(b) shows the fiber density distribution of 2-hinge and 3-hinge gyri across 64 human brain subjects. It can be noticed that the fiber density range with the largest number of subjects for 2-hinge gyri is 3–4.5 while the range for 3-hinge gyri is 8–11. Statistical one sample paired t-test (P-value close to 0) also confirms the significance of such difference among these 64 human brains.
Figure 3.
Visualization of the distributions of 2-hinge and 3-hinge fiber densities in 5 randomly selected human brains.
Figure 4.
(a) The average fiber densities on 2 hinges and 3 hinges within the group of 64 human brains; 3 hinges: left bar, 2 hinges: right bar. (b) 2-hinge and 3-hinge fiber density distributions within the group of 64 human brains. The number of subjects in each range is denoted in the circle with an arrow.
Fiber Density of 2-hinge Gyri and 3-hinge Gyri in Chimpanzee and Macaque Brains
In a similar way, fiber densities in 2-hinge gyri and 3-hinge gyri in chimpanzee and macaque brains were quantified and shown in Supplementary Figures S3–6, respectively. Here, the average fiber densities on 2 hinges and 3 hinges in chimpanzee brains are 0.56 and 1.96, respectively; the average fiber densities on 2 hinges and 3 hinges in macaque brains are 0.92 and 4.95, respectively. From Supplementary Figures S4 and S6, we can see an even more significant difference between the fiber densities of 2-hinge and 3-hinge gyral folds, that is, the 3-hinge fiber density is more than 2 times larger than that on 2 hinges in chimpanzee brains and more than 4 times larger than that on 2 hinges in macaque brains. Our results show that the fiber density range with the largest number of subjects for 2-hinge gyri is 0.6–0.8 while the range for 3-hinge gyri is 2–2.5 within the group of 16 chimpanzees. For the group of 20 macaques, the fiber density range with the largest number of subjects for 2-hinge gyri is 1–1.5, while the range for 3-hinge gyri is 4–6. Again, close to 0 P-values can be derived from one sample paired t-test. T-test is performed on the fiber densities on 2 hinges and 3 hinges in the whole brain among all subjects of these 2 species separately, the result of which indicates a very significant difference.
Correlation Between 3-hinge Gyral Morphology Complexity and 3-hinge/2-hinge Gyral Fiber Density Ratio Across 3 Primate Species
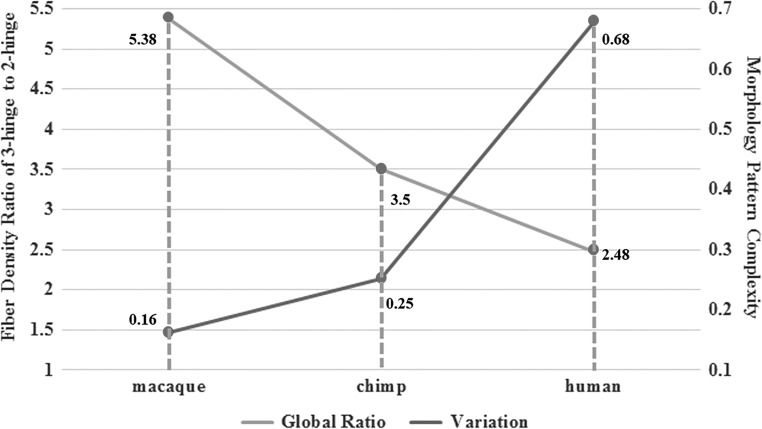
From the results in Sections 3.1 and 3.2, it can be seen that the ratios of the averaged axonal fiber density on 3 hinges to that on 2 hinges across the whole cortical surface are about 5, 3.5, and 2.5 in macaque, chimpanzee, and human brains, respectively. Inspired by this observation, we correlate it with the morphology complexity of 3-hinge gyral folds (Li et al. 2016) and analyzed the relationship between them. Here, the morphology pattern is referred to as morphology feature combination of a 3-hinge gyrus where each hinge-line corresponds to 1 of 5 morphology features: “I,” “V,” “U,” “S,” “O,” detailed in our recent work (Li et al. 2016). Hence, the morphology pattern of each 3 hinge is represented by a combination of 3 morphology features, such as IVO, IUS and so on. Based on the 33 morphology patterns detected among the 3 primate species (Li et al. 2016), we define morphology pattern complexity for each 3-hinge gyrus as a ratio of the number of patterns a 3-hinge gyral fold area has to the total number of patterns 33. Therefore, we can compute morphology pattern complexity of the 3-hinge gyral fold areas for each primate specie and thus derive the mean value for each by averaging them. By analyzing the relationship between 3-hinge morphology pattern complexity and fiber density ratio of 3-hinge to 2-hinge gyri, we noticed that there is an inverse relationship between them across 3 primate species, that is, the more complex the 3-hinge morphology pattern is, the more likely the fiber density ratio of 3-hinge to 2-hinge gyri will be smaller. The illustration of the inverse correlation tendency is shown in Figure 5, in which we can see that from macaque, chimpanzee to human brains, the morphology pattern complexity increase, while the fiber density ratio of 3-hinge to 2-hinge gyri across the whole brain goes down. These interesting observations support our hypothesis that axonal fiber densities might play an important role in regulating the shape formation of 3-hinge gyri, that is, stronger regulations associated with larger fiber density ratios of 3 hinges to 2 hinges induce less 3-hinge morphology complexity and variability.
Figure 5.
Inverse correlation between average fiber density ratio of 3-hinge to 2-hinge gyri and average morphology complexity in macaque, chimpanzee, and human brains. The light gray line is the global fiber density ratio that refers to the vertical axis on the left, and the dark gray line is the morphology complexity that refers to the vertical axis on the right.
Computational Results
Figure 6 shows a dynamic convolution process of a brain model. Both the cortex and axonal fibers in our model are assumed to grow, and after certain growth, our cortex model loses stability and forms the convoluted pattern. As a result, 2-hinge and 3-hinge gyri are observed on the free surface of the cortex. We can also observe that there is a 3-hinge gyrus on top of the axonal fibers in this model. Experimental observations in the literature have revealed that axonal fibers can be either under tension or compression, but the effect of axonal fibers on the formation of consistent gyral hinges remains unanswered (Holland et al. 2015). Therefore, by controlling the growth rate of axonal fibers we are able to tune the force status inside fibers and look into the possible explanations on the formation of consistent gyral hinges in areas with high concentration of fibers. About 2 types of computational models are considered here: 1 without axonal fibers and the other 1 with axonal fibers, as detailed in the following 2 subsections, respectively.
Figure 6.
Initial perturbation and convolution of the model. (a) Different initial perturbations are applied on the free surface of cortex; (b) Instability initiation; (c) Folding after instability; (d) Convolution of the model. The cortex and fibers are growing simultaneously and create a convoluted pattern on the free surface of the cortex. Growth rate of fibers is the same as the cortex growth rate. The dark gray area in the middle is located on a hinge.
Simulation Model without Fiber
In order to determine the effect of axonal fibers on consistent gyral hinge formation, first, we performed a series of computational simulations only with growth in the cortex and considered them as control studies. Since we have performed and published the similar studies (Zhang et al. 2016), here we just summarizes several key findings in brief. The growth in the cortex without any contribution from axonal fibers can produce convoluted patterns with gyri and sulci as we expect, but the sites of gyral hinge formation in the convoluted model look unpredictable and fairly random. In order to confirm this randomness of gyral hinge sites in our simulation models without axonal fibers, we performed a series of computational simulations with the same model specifications (growth rate, geometric parameters, and materials properties) except the initial small perturbations as shown in Figure 6(a). Models with different initial perturbations are hypothesized to mimic the individual brain samples we had in imaging data analyses. These findings suggest that homogeneous growth in the cortex fails to produce consistent gyral hinges on a specific site (Zhang et al. 2016), Combining this simulation result with the imaging data analysis result in Sections 3.1–3.3 that much denser fibers are connected to gyri in comparison with sulci, it is reasonable to hypothesize that denser fiber connections induce or regulate the formation of gyral hinges, including 3-hinge gyri.
Simulation Model with Fibers
Following the control study, we performed another set of simulations to test our hypothesis that the presence of axonal fibers as well as their growth in our cortex model can regulate or determine the sites of gyral hinge formation. By adjusting the growth rate of axonal fibers in our model we can screen through various scenarios to possibly find the right parameters which can produce gyral hinges on top of the axonal fibers. Here, the growth rate of axonal fibers is mimicked by a dimensionless number according to the growth rate of the cortex. Figure 6(d) shows the result of a model with growing axonal fibers. The growth rate of axonal fibers is set the same as the cortex. It can be seen that on top of growing axonal fibers a 3-hinge gyrus is formed. An interesting question arises: how does the presence of the growing axonal fibers influence the sites of gyral hinge formation where all other parameters are kept intact in our model, for example, growth rate of the cortex and mesh size of the computational model?
In order to answer the abovementioned question, we run a considerable amount of FE simulation cases with different growth rates in axonal fibers. We set the growth rate of axonal fibers as 5 different values, all of which are comparable with the growth rate in the cortex. Within models with the same growth rate of axonal fibers, different initial perturbations are hypothesized to mimic the individual brain samples we had in imaging data analyses. Table 1 collects the folding patterns of the middle dark gray area in our model (Fig. 6) after running multiple cases with and without fibers. Results show that there is a very high possibility to form a 3-hinge gyrus in the specific area when the growth rate of axonal fibers is close to the growth rate of the cortex, while the dark gray area in models without axonal fibers could be located on hinge, sulci, or in-between banks.
Table 1.
Statistical results of the numbers of the locations of the special areas on gyral hinges, sulci, and in-between banks
| Model with fibers (growth rate of fibers/growth rate of cortex) | Model without fibers | |||||
|---|---|---|---|---|---|---|
| 0.7 | 0.8 | 0.9 | 1 | 1.1 | ||
| Hinge | 4 | 7 | 9 | 10 | 10 | 14 |
| Sulci | 0 | 0 | 0 | 0 | 0 | 19 |
| Banks | 6 | 3 | 1 | 0 | 0 | 17 |
| Total | 10 | 10 | 10 | 10 | 10 | 50 |
Our results show that a higher growth rate in axonal fibers always leads to 3-hinge gyri formation on top of the axonal fiber bundle. Therefore, our findings imply that the presence of growing axonal fibers could be responsible for forming a consistent gyral hinge in a special area with a higher concentration of axonal fibers. Interestingly, Table 1 also shows that the sites with a high density of growing axonal fibers do not develop any sulci as we observe in experimental results. Supplementary Figure S7 shows 3 different initial perturbations in our model with the presence of growing axonal fibers generally leading to the formation of different hinge patterns, but in all cases the green area always develops a 3-hinge gyrus. These 3-hinge patterns in Supplementary Figure S7 are comparable with experimental 3-hinge patterns like IVO and IUS observed in neuroimaging data. This observation is in good agreement with our experimental observation in individual brain samples and demonstrates the regulating effect of dense growing axonal fibers in the consistent gyral hinges, particularly 3-hinge formation.
Scattered and Different Shapes of Fibers
The main objective of our simplified model was to demonstrate that 3-hinge gyrus can consistently form in a special area with a high density of fibers. We know that in a real brain there are many complex fibers with various types and orientations. Incorporating such complexity into the mechanical kmodel is very challenging at this stage. Therefore, by a simplified model, we are able to incorporate mechanical effect of growing fibers on the formation of 3 hinges. Since we selected a small patch of the entire cortex, therefore it is acceptable to assume that the orientation of fibers is perpendicular to the cortex. In a bigger scale, the type and orientation of fibers can be different across the entire cortex. Here, we focused our study on a single fiber bundle and its counterpart 3 hinges.
In the next step, we increased the number of fiber bundles and placed them randomly in our model. Simulation results, again, confirmed our hypothesis that 3 hinges were always formed at sites where the growing fiber bundles were embedded underneath. Supplementary Figure S8 shows the evolution steps of a FE model with 10 scattered growing fiber bundles.
Figure 7 shows comparison of 2 FE models with a real brain image. Initial location of fibers was set roughly according to the location of 3 hinges from the image data. Initial perturbations were applied on the free surface of FE models. It is clear, after growth and gyrification, that locations of 3 hinges on the free surface of the cortex are the same as the counterparts on the real brain. We speculate the discrepancy between gyri and sulci patterns in the FE models and real brain is due to the effect of 2-hinge fibers which have not been included in the FE models. This issue is not the scope of our study at this stage.
Figure 7.
Contribution of fibers growth on the convolution morphology. (a) FE model # 1; (b) FE model # 2; (c) A small patch of a real brain with 3 hinges. Dark gray dots in 3 figures means 3 hinges.
In order to better represent the realistic fiber growth in brain, we incorporated a gradient growth in a special type of 3 hinges. Since the density of fibers in the junction of 3-hinge lines (spheres in Fig. 7(c)) is higher than those along lines (solid lines in Fig. 7(c)), therefore we constructed a complex FE model to incorporate this growth difference in a fiber bundle. This model allows us to set a high growth ratio in the junction of the 3 hinges and lower the growth ratio along the connecting lines to zero at the tip of lines. In other words, the growth ratio is the highest at the junction of 3 hinges and is zero at the tip of connecting lines, as shown in Supplementary Figure S9. We created several models with and without growing fiber with gradient growth to check the contribution of fibers on the formation of 3 hinges. Results, again, showed that without growth of fibers, 3 hinges might form in random locations (Fig. 8(a)). It is clear, in the bottom row of Figure 8(a), Y-shaped dark gray area can acquire different shapes, since there is no growing fiber beneath them. In contrast, in the top row of Figure 8(a) Y-shaped dark gray area always forms Y-shaped 3 hinges because there are growing fibers beneath these dark gray areas.
Figure 8.
Y-shaped fibers on the formation of 3 hinges: (a) The top row: models with growing fibers; the bottom row: models without growing fibers. (b) Top view of “Y” shape fibers with gradient growth in initial state. (c) Top view of the model after growth and convolution. Growth ratio linearly decreases from the intersection point of hinges lines to the tip of them.
Finally, we added several similar “Y” shape fibers into the computational model. Figure 8(b) shows the initial computational configuration and Figure 8(c) shows the model after growth and cortical convolution. It can be seen that growing fibers are able to control the location and type of the 3 hinges. If other shapes of fibers are implemented in the computational model, different kinds of 3 hinges after convolution are accessible. It is noteworthy to mention that the “Y” shape areas on the cortex, are indicators that show there are the same shape of fiber bundles beneath them. The material properties of the dark gray areas are set the same as the cortex, and the main purpose of the dark gray areas are to help trace the location of axonal fibers after cortical convolution.
Discussion and Conclusion
As far as we know, most of previous major stream descriptors for cortical folding patterns focus on cortical complexity quantification, which are difficult to quantify the variation of folding patterns and infer anatomical correspondence of the cortical landscapes based on exclusively local-scale or global-scale descriptors. However, the descriptor proposed in our work (2 hinges and 3 hinges) took the advantages of both parametric and surface profiling methods to analyze cortical folding patterns in terms of gyral hinge numbers and shapes. Previous works have shown that the axonal fibers connected to gyri are significantly denser than those connected to the sulci in human, chimpanzee, and macaque brains (Nie et al. 2012), which offers a novel explanation into the intrinsic relationship between cortical folding and axonal wiring. In this study, we further quantitatively measured the fiber densities of 2-hinge and 3-hinge gyral areas in macaque, chimpanzee, and human brains and quantitatively compared them within each species, which is a great piece of enhancement compared with the previous ones. Our results overwhelmingly showed that fiber densities in 3-hinge gyri are much higher than those in 2-hinge gyri, and thus we are strongly motivated to hypothesize that besides cortical expansion as the primary mechanism of gyrification, denser fiber connections can also induce the formation of 3-hinge gyri. In order to examine the biomechanical basis of this hypothesis, we designed 3D FE soft tissue models and performed extensive computational simulations with a variety of settings to investigate the fundamental biomechanical mechanism of consistent 3-hinge formation. Our simulation consistently results showed that gyral regions with higher concentrations of growing axonal fibers have much higher probability of forming 3-hinge gyri. Altogether, our integrated studies of neuroimaging data analyses and computational biomechanical simulations offer a plausible theory of 3-hinge gyri formation: denser growing fiber connections induce 3-hinge gyri formation.
The formation of cortical folding, including 3-hinge shape pattern is a result of the interplay of many factors. Cranial constraint and axon maturation, as examples of external and internal causes, can induce cortical folding (Zhang et al. 2016). Heterogeneous growth in cortical regions rather than a global homogeneous differential growth is thought to be as a driving mechanism for cortical folding (Zhang et al. 2016). Even in the schools of axonal theories, 2 divergent ideas—axonal pushing and pulling theory are also proposed to study the mechanism of cortical folding (Van Essen 1997; Nie et al. 2012). In addition, a quite new theory proposed by Budday et al. and Tallinen et al. indicate that the overall geometry of the initial substrate of cerebral cortex may be responsible for folding formation (Budday et al. 2015b; Tallinen et al. 2016). However, in this work, we are only able to discover the positive relationship between axons and 3-hinge patterns based on the data used in the study since high-quality longitudinal in-vivo data and direct mechanical experiments on ex-vivo data, such as indentation on tissues, may be more suitable for causality studies.
Given the strong correlation between brain structure and function, for example, strong structural connectivity predicts functional connectivity (Honey et al., 2009; Deng et al., 2014), complex functional regions locate significantly more on gyral regions than sulcal regions and the most complex ones are usually found in 3-hinge area based on a statistical analysis (Jiang et al. 2015), our future work will explore the functional implications that much stronger axonal fibers are connected to 3-hinge gyri in comparison with 2-hinge gyri. For instance, our prior studies have suggested a functional model of cortical gyri and sulci (Deng et al., 2014), that is, gyri are the functional integration centers while sulci are the local information process units. Following this research line, we will further refine this functional model by differentiating cortical 3-hinge gyri and 2-hinge gyri and strive to characterize the possible different functional roles played by 3-hinge and 2-hinge gyral regions, which also can be extended to investigate a variety of neurodevelopmental diseases. The elucidation of the possible functional role differences of 3-hinge and 2-hinge gyri could potentially fundamentally advance our understanding of the structural and functional brain architectures, as well as their relationships.
Supplementary Material
Supplementary Material
Funding
T.L. was supported by the NIH R01 DA033393, NIH R01 AG-042599, NSF CAREER Award IIS-1149260, NSF CBET-1302089, NSF BCS-1439051, and NSF DBI-1564736.
References
- Bayly P, Okamoto R, Xu G, Shi Y, Taber L. 2013. A cortical folding model incorporating stress-dependent growth explains gyral wavelengths and stress patterns in the developing brain. Phys Biol. 10:016005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bayly P, Taber L, Kroenke C. 2014. Mechanical forces in cerebral cortical folding: a review of measurements and models. J Mech Behav Biomed Mater. 29:568–581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Budday S, Nay R, de Rooij R, Steinmann P, Wyrobek T, Ovaert TC, Kuhl E. 2015. a. Mechanical properties of gray and white matter brain tissue by indentation. J Mech Behav Biomed Mater. 46:318–330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Budday S, Steinmann P, Goriely A, Kuhl E. 2015. b. Size and curvature regulate pattern selection in the mammalian brain. Extr Mech Lett. 4:193–198. [Google Scholar]
- Budday S, Steinmann P, Kuhl E. 2015. c. Secondary instabilities modulate cortical complexity in the mammalian brain. Philos Mag. 95:3244–3256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bullmore E, Sporns O. 2009. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat Rev Neurosci. 10:186–198. [DOI] [PubMed] [Google Scholar]
- Cachia A, Mangin J-F, Rivière D, Boddaert N, Andrade A, Kherif F, Sonigo P, Papadopoulos-Orfanos D, Poline J-B, Bloch Ieditors. 2001. A mean curvature based primal sketch to study the cortical folding process from antenatal to adult brain. International Conference on Medical Image Computing and Computer-Assisted Intervention: 897–904.
- Cachia A, Mangin J-F, Riviere D, Kherif F, Boddaert N, Andrade A, Papadopoulos-Orfanos D, Poline J-B, Bloch I, Zilbovicius M. 2003. A primal sketch of the cortex mean curvature: a morphogenesis based approach to study the variability of the folding patterns. IEEE Trans Med Imaging. 22:754–765. [DOI] [PubMed] [Google Scholar]
- Cao Y, Jiang Y, Li B, Feng X. 2012. Biomechanical modeling of surface wrinkling of soft tissues with growth-dependent mechanical properties. Acta Mech Solida Sinica. 25:483–492. [Google Scholar]
- Chen H, Zhang T, Guo L, Li K, Yu X, Li L, Hu X, Han J, Hu X, Liu T. 2012. Coevolution of gyral folding and structural connection patterns in primate brains. Cereb Cortex. 23:1208–1217. bhs113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deng F, Jiang X, Zhu D, Zhang T, Li K, Guo L, Liu T. 2014. A functional model of cortical gyri and sulci. Brain Struct Funct. 219:1473–1491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dubois J, Benders M, Borradori-Tolsa C, Cachia A, Lazeyras F, Ha-Vinh Leuchter R, Sizonenko SV, Warfield SK, Mangin JF, Hüppi PS. 2008. Primary cortical folding in the human newborn: an early marker of later functional development. Brain. 131:2028–2041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B. 2012. FreeSurfer. Neuroimage. 62:774–781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Rajendran N, Busa E, Augustinack J, Hinds O, Yeo BT, Mohlberg H, Amunts K, Zilles K. 2008. Cortical folding patterns and predicting cytoarchitecture. Cereb Cortex. 18:1973–1980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giedd JN, Rapoport JL. 2010. Structural MRI of pediatric brain development: what have we learned and where are we going? Neuron. 67:728–734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilles FH, Leviton A, Dooling E. 1983. The developing human brain: growth and epidemiologic neuropathology. Boston: John Wright Inc. [Google Scholar]
- Hardan AY, Jou RJ, Keshavan MS, Varma R, Minshew NJ. 2004. Increased frontal cortical folding in autism: a preliminary MRI study. Psychiatry Res. 131:263–268. [DOI] [PubMed] [Google Scholar]
- Holland MA, Miller KE, Kuhl E. 2015. Emerging brain morphologies from axonal elongation. Ann Biomed Eng. 43:1640–1653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Honey C, Sporns O, Cammoun L, Gigandet X, Thiran J-P, Meuli R, Hagmann P. 2009. Predicting human resting-state functional connectivity from structural connectivity. Proc Natl Acad Sci. 106:2035–2040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Honey CJ, Thivierge J-P, Sporns O. 2010. Can structure predict function in the human brain? Neuroimage. 52:766–776. [DOI] [PubMed] [Google Scholar]
- Jenkinson M, Beckmann CF, Behrens TE, Woolrich MW, Smith SM. 2012. Fsl. Neuroimage. 62:782–790. [DOI] [PubMed] [Google Scholar]
- Jiang X, Li X, Lv J, Zhang T, Zhang S, Guo L, Liu T. 2015. Sparse representation of HCP grayordinate data reveals novel functional architecture of cerebral cortex. Hum Brain Mapp. 36:5301–5319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li G, Liu T, Ni D, Lin W, Gilmore JH, Shen D. 2015. Spatiotemporal patterns of cortical fiber density in developing infants, and their relationship with cortical thickness. Hum Brain Mapp. 36:5183–5195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li G, Wang L, Shi F, Lyall AE, Lin W, Gilmore JH, Shen D. 2014. Mapping longitudinal development of local cortical gyrification in infants from birth to 2 years of age. J Neurosci. 34:4228–4238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li K, Guo L, Li G, Nie J, Faraco C, Cui G, Zhao Q, Miller LS, Liu T. 2010. Gyral folding pattern analysis via surface profiling. NeuroImage. 52:1202–1214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X, Chen H, Zhang T, Yu X, Jiang X, Li K, Li L, Razavi MJ, Wang X, Hu X. 2016. Commonly preserved and species-specific gyral folding patterns across primate brains. Brain Struct Funct. 222(5):2127–2141. [DOI] [PubMed] [Google Scholar]
- Liu T. 2011. A few thoughts on brain ROIs. Brain Imaging Behav. 5:189–202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu T, Nie J, Tarokh A, Guo L, Wong ST. 2008. Reconstruction of central cortical surface from brain MRI images: method and application. NeuroImage. 40:991–1002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lohmann G, Von Cramon DY, Colchester AC. 2008. Deep sulcal landmarks provide an organizing framework for human cortical folding. Cereb Cortex. 18:1415–1420. [DOI] [PubMed] [Google Scholar]
- Neal J, Takahashi M, Silva M, Tiao G, Walsh CA, Sheen VL. 2007. Insights into the gyrification of developing ferret brain by magnetic resonance imaging. J Anat. 210:66–77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nie J, Guo L, Li K, Wang Y, Chen G, Li L, Chen H, Deng F, Jiang X, Zhang T. 2012. Axonal fiber terminations concentrate on gyri. Cereb Cortex. 22:2831–2839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nordahl CW, Dierker D, Mostafavi I, Schumann CM, Rivera SM, Amaral DG, Van Essen DC. 2007. Cortical folding abnormalities in autism revealed by surface-based morphometry. J Neurosci. 27:11725–11735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rakic P. 1988. Specification of cerebral cortical areas. Science. 241:170–176. [DOI] [PubMed] [Google Scholar]
- Razavi MJ, Pidaparti R, Wang X. 2016. Surface and interfacial creases in a bilayer tubular soft tissue. Phys Rev E. 94:022405. [DOI] [PubMed] [Google Scholar]
- Razavi MJ, Wang X. 2015. Morphological patterns of a growing biological tube in a confined environment with contacting boundary. RSC Adv. 5:7440–7449. [Google Scholar]
- Razavi MJ, Zhang T, Li X, Liu T, Wang X. 2015. Role of mechanical factors in cortical folding development. Phys Rev E. 92:032701. [DOI] [PubMed] [Google Scholar]
- Razavi MJ, Zhang T, Liu T, Wang X. 2015. Cortical folding pattern and its consistency induced by biological growth. Sci Rep. 5:14477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richman DP, Stewart RM, Hutchinson JW, Caviness VS Jr. 1975. Mechanical model of brain convolutional development. Science. 189(4196):18–21. [DOI] [PubMed] [Google Scholar]
- Ronan L, Voets N, Rua C, Alexander-Bloch A, Hough M, Mackay C, Crow TJ, James A, Giedd JN, Fletcher PC. 2014. Differential tangential expansion as a mechanism for cortical gyrification. Cereb Cortex. 24:2219–2228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schoenemann PT. 2006. Evolution of the size and functional areas of the human brain. Annu Rev Anthropol. 35:379–406. [Google Scholar]
- Sun T, Hevner RF. 2014. Growth and folding of the mammalian cerebral cortex: from molecules to malformations. Nat Rev Neurosci. 15:217–232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tallinen T, Chung JY, Biggins JS, Mahadevan L. 2014. Gyrification from constrained cortical expansion. Proc Natl Acad Sci. 111:12667–12672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tallinen T, Chung JY, Rousseau F, Girard N, Lefèvre J, Mahadevan L. 2016. On the growth and form of cortical convolutions. Nat Phys. 12(6):588–593. [Google Scholar]
- Thompson PM, Hayashi KM, Sowell ER, Gogtay N, Giedd JN, Rapoport JL, de Zubicaray GI, Janke AL, Rose SE, Semple J. 2004. Mapping cortical change in Alzheimer’s disease, brain development, and schizophrenia. Neuroimage. 23:S2–S18. [DOI] [PubMed] [Google Scholar]
- Toro R, Burnod Y. 2005. A morphogenetic model for the development of cortical convolutions. Cereb Cortex. 15:1900–1913. [DOI] [PubMed] [Google Scholar]
- Van Essen DC. 1997. A tension-based theory of morphogenesis and compact wiring in the central nervous system. Nature. 385(6614):313–318. [DOI] [PubMed] [Google Scholar]
- Van Essen DC, Ugurbil K, Auerbach E, Barch D, Behrens T, Bucholz R, Chang A, Chen L, Corbetta M, Curtiss SW. 2012. The Human Connectome Project: a data acquisition perspective. Neuroimage. 62:2222–2231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeo BT, Yu P, Grant PE, Fischl B, Golland Peditors. 2008. Shape analysis with overcomplete spherical wavelets. International Conference on Medical Image Computing and Computer-Assisted Intervention: 468–476. [DOI] [PMC free article] [PubMed]
- Yu P, Yeo BTT, Grant PE, Fischl B, Golland Peditors. 2007. Cortical folding development study based on over-complete spherical wavelets. IEEE 11th International Conference on Computer Vision: 1–8. [DOI] [PMC free article] [PubMed]
- Zhang T, Chen H, Guo L, Li K, Li L, Zhang S, Shen D, Hu X, Liu T. 2014. Characterization of U-shape streamline fibers: methods and applications. Med Image Anal. 18:795–807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang T, Razavi MJ, Chen H, Li Y, Li X, Li L, Guo L, Hu X, Liu T, Wang X. 2017. Mechanisms of circumferential gyral convolution in primate brains. J Comput Neurosci. 42:217–229. [DOI] [PubMed] [Google Scholar]
- Zhang T, Razavi MJ, Li X, Chen H, Liu T, Wang X. 2016. Mechanism of consistent gyrus formation: an experimental and computational study. Sci Rep. 6:37272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zilles K, Armstrong E, Schleicher A, Kretschmann H-J. 1988. The human pattern of gyrification in the cerebral cortex. Anat Embryol (Berl). 179:173–179. [DOI] [PubMed] [Google Scholar]
- Zilles K, Schleicher A, Langemann C, Amunts K, Morosan P, Palomero-Gallagher N, Schormann T, Mohlberg H, Bürgel U, Steinmetz H, et al. 1997. Quantitative analysis of sulci in the human cerebral cortex: development, regional heterogeneity, gender difference, asymmetry, intersubject variability and cortical architecture. Hum Brain Mapp. 5:218–222. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.