Major Feedforward Thalamic Input Into Layer 4C of Primary Visual Cortex in Primate

Abstract

One of the underlying principles of how mammalian circuits are constructed is the relative influence of feedforward to recurrent synaptic drive. It has been dogma in sensory systems that the thalamic feedforward input is relatively weak and that there is a large amplification of the input signal by recurrent feedback. Here we show that in trichromatic primates there is a major feedforward input to layer 4C of primary visual cortex. Using a combination of 3D-electron-microscopy and 3D-confocal imaging of thalamic boutons we found that the average feedforward contribution was about 20% of the total excitatory input in the parvocellular (P) pathway, about 3 times the currently accepted values for primates. In the magnocellular (M) pathway it was around 15%, nearly twice the currently accepted values. New methods showed the total synaptic and cell densities were as much as 150% of currently accepted values. The new estimates of contributions of feedforward synaptic inputs into visual cortex call for a major revision of the design of the canonical cortical circuit.

The quest to identify the canonical features of the cortical circuit has led to a number of important generalizations that can be applied to many neocortical areas across mammalian species (Douglas and Martin 2007a; DaCosta and Martin 2013; Kasthuri et al. 2015). In sensory areas, in particular, a key feature of understanding how the circuits are constructed and how they operate is to determine the relative strength of the thalamocortical (TC) afferent input compared with the recurrent intracortical (IC) synaptic drive (McLaughlin et al. 2000). Prevalent among most of the current theories of cortex is that the direct TC drive is relatively weak and is, by necessity, complemented by a much stronger recurrent IC drive (Douglas and Martin 2007b), leading to the proposal that strong recurrent amplification is essential for generating the signaling properties of the neural population, such as their receptive field characteristics. In primates, the weak TC hypothesis has been supported by reports that there are relatively few synaptic inputs supplied by TC afferents versus inputs supplied by recurrent excitatory axon terminals, ranging from 3.7% to 8.7% for 4Cβ (Peters et al. 1994; Latawiec et al. 2000), which receives 80% of all lateral geniculate nucleus (LGN) afferents. These values are similar to the TC/total excitatory synaptic ratio measured previously in cat area 17 (Ahmed et al. 1994; da Costa and Martin 2009) but lower than the ratios measured in mouse somatosensory cortex (Benshalom and White 1986; Sadaka et al. 2003; Bopp et al. 2017) and squirrel monkey V1 (Tigges and Tigges 1979). Because of the importance of understanding the contributions of different types of inputs to cortex, and because of methodological limitations of the previous studies in primate V1, we have re-evaluated the ratio of TC to total synaptic number using newer methods.

One limitation of the previous measurements of TC and overall synaptic density in V1 (Peters et al. 1994; Latawiec et al. 2000) was that density, a property corresponding to 3D space, was measured from 2D samples. In the current study, we used a novel combination of 3D-electron microscopy (EM) analysis and confocal imaging, also in 3D, of immunolabeled TC terminals to investigate numerical densities of identified thalamic afferent terminals in layers 4Cα, 4Cβ, 4A, and 6 of macaque striate cortex. The confocal imaging technique allowed us to estimate TC densities using large scale automated counting of more than 10⁵ profiles, many orders of magnitude greater than has been possible, even using 3D-EM. The densities were considerably higher than previously reported, especially for the parvocellular division of layer 4C, where densities were 4.3 times earlier estimates (Latawiec et al. 2000).

In the earlier studies, TC inputs were identified either by tracer injection or immunolabeling with parvalbumin (PV); the latter strategy requires a secondary determination that identified PV-immunoreactive (-ir) terminals are also excitatory, to distinguish them from the terminals of PV-expressing interneurons. Recently, another method has been available as it has been established that there is a complementary expression of the vesicular glutamate transporters VGluT1 and VGluT2 in subpopulations of axon terminals of glutamatergic neurons in the central nervous system (CNS). VGluT1 is expressed mainly in the axon terminals of neurons in the telencephalon, whereas VGluT2 has been shown to be expressed in projections from midbrain, thalamus, brainstem, and spinal cord (Fremeau et al. 2001; Fujiyama et al. 2001; Nahmani and Erisir 2005). In particular, Nahmani and Erisir (Nahmani and Erisir 2005) found that only orthogradely labeled LGN terminals in primary visual cortex had vesicles with VGluT2. In primates a number of studies have reported a close correspondence between the cytochrome oxidase (CO) density and VGluT2 bouton distribution in V1 (Bryant et al. 2012; Balaram et al. 2013; Garcia-Marin et al. 2013) and auditory cortex (Hackett and de la Mothe 2009). In the current study, we used VGluT2 as a means of identifying the total population of TC terminals in V1.

A second motivation for reevaluating the proportion of synapses that are TC was that previous reports differed on whether the proportion of TC input to layer 4Cβ was higher or somewhat lower than the input to 4Cα from the magnocellular layers of the LGN (Peters et al. 1994; Latawiec et al. 2000). Our recent qualitative evaluations of the density of VGluT2 in macaque layer 4C (Garcia-Marin et al. 2013) suggested that the density of VGlut2 boutons in layer 4Cβ was higher than in layer 4Cα. Moreover, although the main LGN input to V1 terminates in layer 4C there is also direct thalamic input to layer 4A (Hendrickson et al. 1978; Livingstone and Hubel 1982; Horton 1984) and layer 6 (Hubel and Wiesel 1972; Lund and Boothe 1975; Hendrickson et al. 1978) and sparse input to the CO rich patches in layer 2/3 (Hendrickson et al. 1978; Horton 1984). Previously there have not been any quantitative estimates of TC synapse density in these regions. Therefore, an additional goal of the current study was to make quantitative estimates of synaptic density to layers 4A and 6 and compare their density to the density in layer 4C.

Understanding the efficacy of TC verses IC synaptic strength relies on having reliable estimates of not only the TC synaptic density but also total synaptic density. Recent studies had shown that methods employing 3D reconstruction of postsynaptic densities (PSDs) resulted in higher estimates of total synaptic density than methods using 2D images (Merchan-Perez et al. 2014). It was therefore crucial to determine total synaptic density using 3D methods because if there had been a systematic underestimation of total synaptic density using 2D counting (O’Kusky and Colonnier 1982; Beaulieu et al. 1992; Latawiec et al. 2000) then the estimates of relative density of TC synapses to total density would be artificially high. Our 3D estimates of total synaptic density were higher, by a factor of about 2, than most 2D estimates. By making additional 2D estimates, we confirmed that the discrepancy between 2D and 3D density estimates arose from the counting methods used.

Another important factor in modeling cortex is the ratio of synapses to neurons (Braitenberg and Schüz 1998). Because a recent study applying the optical fractionator method to immunolabeled populations in monkey visual cortex (Giannaris and Rosene 2012) reported neuronal densities that were systematically higher than those reported using older counting procedures (O’Kusky and Colonnier 1982; Beaulieu et al. 1992) we re-evaluated laminar density of neurons in a second series of experiments. We recently implemented a new, automated procedure to count neuronal density in large regions of visual cortex across all cortical layers using 3D counting (Kelly and Hawken 2017); here, we have measured neuronal density in each layer. Within layer 4C the neuronal densities measured using the 3D counting were 1.7–2.2 times the previous estimates (O’Kusky and Colonnier 1982; Beaulieu et al. 1992). Overall, we have obtained new estimates of both synaptic density and neuronal density. We propose that these reflect the underlying neuronal circuits more accurately than previous estimates and will be of central importance in generating realistic models of cortical circuits.

Materials and Methods

Macaque Brain Tissue

Ten macaque monkeys (8 males Macaca fascicularis, ages 2–5.8 years, and 2 females M. nemestrina, ages 7.7 and 18.5 years), previously used for anesthetized electrophysiological recordings, were used in this study. Animals were prepared for recording as described elsewhere (Solomon et al. 2004; Xing et al. 2004). After 4–5 days of recordings, experiments were terminated by intravenous injection of a lethal dose of pentobarbital (60 mg/kg), and brain death was determined by a flat electroencephalogram. Subsequently, animals were transcardially perfused with heparinized 0.01 M phosphate-buffered saline (PBS; pH 7.4) followed by 4 L of 4% paraformaldehyde (PFA) in 0.1 M phosphate buffer (PB; pH 7.4) or followed by 4% PFA + 0.125% Glutaraldehyde (Glu) in 0.1 M PB for the EM studies and the measurements of neuronal density. Some blocks of V1 were removed for track reconstruction of the recording locations of electrophysiologically characterized neurons, and the remaining V1 tissue was cut into small blocks and postfixed in the same fixative for 24–72 h at 4 °C. After fixation, serial 50 μm sagittal sections from the opercular region of V1—representing eccentricities of ~2°–5°—were prepared using a vibratome and batch-processed for VGluT2 or NeuN immunohistochemistry and for the EM study. The remaining sections and blocks were immersed in graded sucrose solutions, and were stored in a cryoprotectant solution at −20 °C.

The layers of area V1 were identified according to Brodmann’s (Brodmann 1909) nomenclature, modified by Lund (1973). This system distinguishes 4 subdivisions of layer 4, namely, 4 A, 4B, 4Cα, and 4Cβ.

All experimental procedures were approved by the New York University Institutional Animal Use and Care Committee and were conducted in strict compliance with the National Institutes of Health (NIH) guidelines for the care and experimental use of animals in research.

Immunofluorescence

Free-floating sections were pretreated using an antigen retrieval (AR) protocol that breaks methylene bridges and exposes antigenic sites to allow antibodies to bind. The AR protocol has been used to enhance VGluT2 immunoreaction in rats (Varoqui et al. 2002), mice (Nakamura et al. 2007), and monkeys (Garcia-Marin et al. 2013). For AR, the buffer solution—0.01 M sodium citrate (pH 8.0)—was heated to 80 °C and individual floating sections were incubated at this temperature for 15 min. Sections were cooled to room temperature for 20 min and were then rinsed 3 times in 0.01 M PBS. Sections were blocked for 1 h in 0.01 M PBS with 0.25% Triton-X and 3% normal goat serum (NGS) and then incubated overnight at 4 °C with mouse anti-VGluT2 antibody (1:4000, MAB5504, Chemicon International, Temecula, CA, USA) in 0.01 M PBS with 0.25% Triton-X and 3% NGS. Sections were rinsed and incubated for 2 h with Alexa biotinylated goat anti-mouse 488 (1:1000, Vector Laboratories, Burlingame, CA). After rinsing in PBS the sections were treated with Autofluorescence Eliminator Reagent (2160, Millipore) to minimize lipofuscin-like autofluorescence. Finally, the sections were washed and mounted with ProLong Gold Antifade Reagent (Invitrogen Corporation, Carlsbad, CA, USA).

For the neuronal quantification, free-floating sections were stained for the pan-neuronal marker NeuN (Mullen et al. 1992; Wolf et al. 1996) using an immunofluorescence protocol described previously (Kelly and Hawken 2017). The total neuronal density in V1 was previously quantified from these samples; here, we have extended the analysis of those data to obtain neuronal density in each layer.

Controls for the secondary antibodies included replacing the primary antibody with preimmune goat serum, omitting the secondary antibody, or replacing the secondary antibody with an incompatible secondary antibody. No significant staining was detected under these control conditions.

The mouse anti-VGluT2 antibody is for a recombinant VGluT2 protein from rat. In Western blot analysis, it appears as an individual band of ~5 kDa. The staining pattern was identical to the data published for macaques in previous studies that used the same monoclonal VGluT2 antibody (Balaram et al. 2013; Garcia-Marin et al. 2013; Marion et al. 2013).

The guinea pig anti-NeuN antibody labels a neuron-specific nuclear protein that is expressed in neurons of nearly all types in vertebrates, although a handful of specific neuronal populations outside the neocortex have been observed to be devoid of the NeuN protein (Mullen et al. 1992; Wolf et al. 1996). Immunocytochemistry using antibodies against NeuN produces immunoreactivity in the nucleus, perikaryon, and sometimes proximal processes, and this provides an objective means of differentiating neurons from glia in the cortex, relative to strategies that rely on expert observation of Nissl-stained nuclei. In the tissue used for this study, the guinea pig polyclonal antibody to NeuN labeled the nuclei and surrounding cytoplasm of neurons throughout all layers of V1. For many neurons, label extended into proximal processes, as described previously (Mullen et al. 1992; Wolf et al. 1996; Gittins and Harrison 2004). Anti-NeuN appeared to label subsets of neurons more intensely than others. For example, the spiny stellate cells in layer 4C were typically more faintly labeled than pyramidal neurons in other layers, and it also appeared to be the case that at least some GABAergic interneurons were relatively faintly labeled. However, these variations in NeuN labeling intensity did not appear to affect the ability to correctly classify cells as neurons.

Estimation of Synaptic Density From 3D-Confocal Stacks

Image stacks consisting of 15–18 image planes (physical size 81.68 μm × 81.68 μm, logical size 1024 × 1024 pixels) were acquired from 4 monkeys in each layer investigated (4 A, 4Cα, 4Cβ, and 6) using a Leica SP5 confocal laser scanning system equipped with an argon/krypton mixed gas laser with excitation peaks at 498 and 594 nm. A ×63 oil-immersion lens was used (numerical aperture, 1.4, working distance, 280 mm, refraction index, 1.45) with a calculated optical zoom factor of 3.0, a pinhole size of 1 airy unit, and z-step of 0.29 μm.

Accurately estimating VGluT2-ir bouton volume is critical to estimating the synaptic density from 3D-confocal stacks. Although confocal microscopy prevents out-of-focus blur by placing a pinhole aperture between the objective and the detector, there is still some light scattering that distorts the visualization of the real object. By applying a deconvolution technique, we could better resolve the objects and more accurately measure bouton volume. We used a blind deconvolution package from Huygens Professional (Scientific Volume Imaging, The Netherlands), in which an adaptive point spread function was used in an iterative process.

After deconvolving the images, a median filter with a radius of 1 pixel was applied to the stack and the distribution of VGluT2-ir boutons across each image stack was estimated using the 3D object counter plugin in FIJI (Schindelin et al. 2012), which identifies each object’s x, y, z position and volume. To avoid the quantification of small speckles in the fluorescence images, we excluded automatically identified “objects” with volumes below a limit that was informed by 3D-EM reconstructions. Our EM results showed that VGluT2-ir boutons typically made multiple synapses and contained mitochondria. The smallest multisynaptic bouton with mitochondria reconstructed at the 3D-EM level measured 0.31 μm³, so we used a cut off lower limit of 50 voxels (0.19 μm³), which by visual inspection effectively removed the nonspecific speckles without being likely to exclude real VGluT2-ir objects.

Because many boutons make multiple synapses, the number of VGluT2-ir puncta is lower than the number of synapses. We determined the relationship between volume and synaptic density from 3D reconstruction of terminal boutons using images from focused ion beam/scanning electron microscopy (FIB/SEM) (see Results for more details) and used this to estimate the synaptic density from the puncta-object volumes.

In the confocal images, we observed systematic variations in puncta counts across regions of the image arising from small undulations in the surface that could be produced by variations in the plane of the vibratome blade as it advanced or in tissue preparation during histological processing. Because antibody penetration was limited, we could not simply set an upper boundary at the level of the troughs of the surface undulations because this left too little tissue for analysis at the peaks of the undulations. Instead, our analysis procedure subdivided each image stack into 18 × 18 μm² subregions, identified the uppermost z plane in each subregion that contained any VGluT2-ir puncta, and selected the z plane immediately deeper into the stack as the upper boundary for that subregion. The number of synapses within each 18 × 18 μm² subregion was then measured from the 4 planes beginning at this upper boundary. The total density for each 72 × 72 μm² image stack was taken to be the sum of the counts from the subregions, divided by the total volume (72 × 72 × 1.2 μm³). Note, each image was 82 × 82 μm², a guard region of 5 μm was used at the xy boundaries so that the analysis region was 72 × 72 μm².

Transmission Electron Microscopy

For EM, we followed the same VGluT2 immunolabeling protocol (antibody, dilution, and AR procedure) as above except that TritonX-100 was excluded from the buffers. After overnight incubation in the primary antibody, the sections were rinsed and incubated for 1 h with a biotinylated horse anti-mouse IgG (1:200, Vector), then for 30 min in a Vectastain ABC immunoperoxidase kit (Vector). Finally, the antibody was visualized with the 3,3′-diaminobenzidine (DAB) tetrahydrochloride chromogen (Sigma-Aldrich, St Louis, MO, USA), which produces a dark, electron-dense precipitate (Fig. 1F). Sections were postfixed in 2% glutaraldehyde in PB for 1 h, treated in 1% osmium tetroxide, dehydrated, and flat embedded in Araldite resin. A correlative light and electron microscopy method (DeFelipe and Fairen 1993) was used to quantify the number of synapses and VGluT2-ir synapses in layer 4Cα and 4Cβ. Sections were photographed under the light microscope and then cut into serial semithin (1 μm thick) sections with an Ultracut (RMC, Inc. MT6000-XL, Wien, Austria) ultramicrotome. The semithin sections were stained with 1% toluidine blue in 1% borax, examined under the light microscope, and photographed to locate the regions of interest, layer 4Cα and 4Cβ, based on neuronal density. Selected semithin sections were further sectioned into serial ultrathin sections (50–70 nm thick) with a diamond knife in the Ultracut. The ultrathin sections were collected on formvar-coated single-slot nickel grids and stained with uranyl acetate and lead citrate before they were examined on a JEOL JEM-1200 EX II (Tokyo, Japan) electron microscope. Photographs were taken in the neuropil (avoiding blood vessels, large myelinated axons and somas) at ×30 000 with a digitalizing image system (Hamamatsu C4742-95 Japan), and at least 25 nonoverlapping micrographs of 22 μm² per monkey were used to estimate the total density of synapses and of VGluT2-ir synapses in layer 4Cα and 4Cβ, as identified in the semithin sections. Although experimenters were not blinded for capturing the images, the sample regions were selected independent of the distribution of VGluT2 label. Previous studies (Granger et al. 1995; Defelipe et al. 1999) had shown that 10 noncontiguous electron micrographs (~sampling area of 350 μm²) were sufficient for estimating the density of any type of synapse found in the neuropil. In the current study, we obtained 25 electron microphotographs (~sampling area 570 μ²) per layer per monkey, exceeding the number determined to be sufficient (Granger et al. 1995; Defelipe et al. 1999).

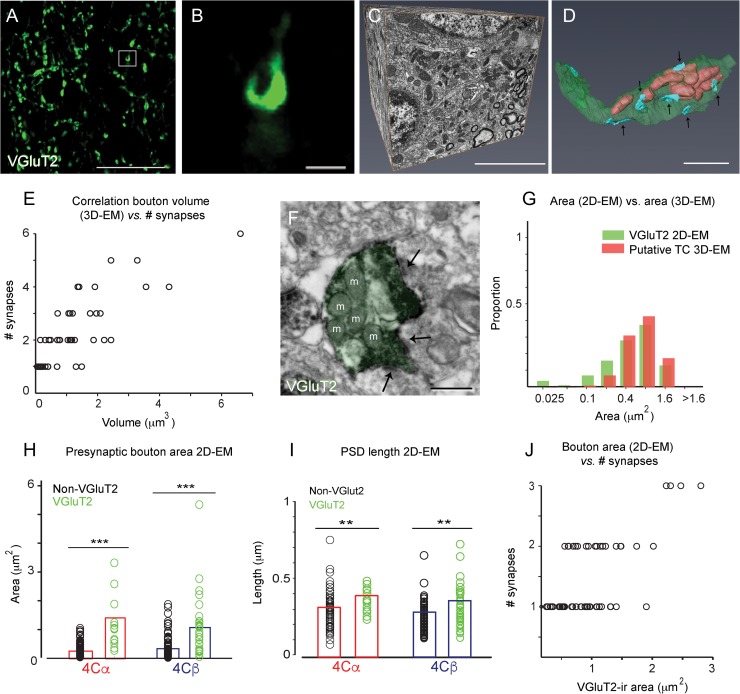
Figure 1.

The experimental approach used to estimate the number of TC synapses from confocal bouton volume. (A) Confocal image showing VGluT2 immunolabeling in layer 4Cβ. (B) Higher magnification of the bouton outlined by the white square in A showing the horseshoe shape that matches the distribution of vesicles in F. (C) Example 3D-EM block, obtained using the FIB/SEM, from a separate sample of tissue than that shown in A, B. (D) 3D reconstruction of a large single bouton in layer 4Cβ with multiple asymmetric synapses (blue, arrows). Mitochondria are observed inside the terminal, appearing as tubular shapes pseudocolored light red within the transparent axon terminal. (E) Positive correlation between bouton volume (excluding the volume occupied by mitochondria) and the number of synapses established by each bouton, determined from 3D reconstruction of 64 boutons in layer 4Cβ from serial EM images (Number synapses = 1.01*Volume + 1.18; r = 0.80). (F) Electron micrograph of a VGluT2-ir bouton (pseudocolored with green) establishing multiple asymmetric synapses (arrows). Mitochondria marked with m. (G) Overlapping distributions of areas of single VGluT2-ir boutons acquired with TEM (green) and areas of cross-sections of “putative TC terminals” selected by their size from 3D-EM blocks (red). (H) Presynaptic areas (bouton areas) of VGluT2-ir (green) and non-VGluT2-ir (black) terminals in both 4Cα and 4Cβ. Difference in area was significant in both 4Cα (P < 0.001) and 4Cβ (P < 0.001), Student’s t-test. (I) PSD lengths established by VGluT2-ir and non-VGluT2-ir terminals in both 4Cα and 4Cβ. PSDs were significantly longer by about 25% for the VGluT2-ir terminals in both 4Cα (P < 0.01) and 4Cβ (P < 0.01), Student’s t-test. (J) Positive correlation between the VGluT2-ir bouton area and the number of synapses measured from 2D-EM single images (Number synapses = 0.74*Area + 0.73; r = 0.66). Data combined from layers 4Cα and 4Cβ. Scale bars: A, 20 μm; B, 1 μm; C, 5 μm; D, 1 μm; F, 500 nm.

To estimate the number of synapses in the neuropil from 2D-EM images, we used the Size–Frequency Method: N_v = N_a/d (Colonnier and Beaulieu 1985), where N_v is the number of synapses per unit volume, N_a is the number of synaptic profiles per unit area, and d is the average length of synaptic junctions (for a detailed description of the procedure used to estimate the synapses see DeFelipe et al. 1999) (shrinkage: 15%). The 2 major morphological types of cortical synapses, denominated type I and type II by Gray (Gray 1959), or asymmetrical and symmetrical types according to Colonnier (Colonnier 1968; for review see Colonnier 1961; Peters et al. 1991; Peters and Palay 1996), were clearly identified in the cortical tissue analyzed. Synapses were classified as asymmetric if they had a PSD, and synapses with a thin PSD were classified as symmetric. Synaptic profiles were identified as terminals only when they met the following criteria: (1) presence of synaptic vesicles, (2) synaptic cleft, and (3) PSD. The synapses in which the synaptic cleft and associated membrane densities could not be visualized clearly (due to the oblique plane of section) were not included in the quantification. The presence of electron-dense peroxidase reaction end product in a presynaptic axonal bouton forming an asymmetric synapse with its postsynaptic target was assumed to identify a bouton from an LGN afferent (VGluT2-ir).

Focused Ion Beam/Scanning Electron Microscope

Three monkeys were selected for the 3D analysis of synapses in layer 4Cα and 4Cβ using the Helios Nanolab DualBeam (FIB/SEM) from FEI (Hillsboro, OR, USA). This microscope utilizes unique DualBeam technology, which combines Focused Ion Beam (FIB) milling and Scanning Electron Microscope (SEM) imaging. The block face is imaged with a scanning electron beam and then the surface is milled; the sequential process of imaging and milling provides serial thin sections of tissue, thereby allowing the visualization and reconstruction of the 3D spatial organization of elements at the ultrastructural level. For the current study we used a thickness of 20 nm, while imaging of the exposed surface was obtained at 1.8 kV acceleration potential using the in-column energy selective backscattered (EsB) electron detector. The aperture size was 30 μm, and the retarding potential of the EsB grid was 1500 V. The imaging and milling processes were repeated in a fully automated way to obtain long series of images that represented a 3D sample of the tissue. Each stack had x,y dimensions of 4096 × 3536 pixels, with an x,y resolution ranging from 2.93 to 3.38 nm/pix, and z dimensions ranging from 160 to 499 images, with a z step size of 20 nm. The original stacks were cropped into nonoverlapping subregions for analysis.

Quantification of Synapses Using ESPina

To select the regions of interest the same correlative light and electron microscopy method was followed as described above. In this way, we unequivocally identified layer 4C by the number and morphology of neurons (high density and small somas, corresponding mainly to the stellate cells of layer 4C). We sampled from the upper and lower parts of layer 4C for layer 4Cα and 4Cβ, respectively, with a minimum of 100 μm between these 2 regions.

To quantify the total density of synapses in the neuropil of layer 4Cα and 4Cβ we used 17 and 21 image stack subregions from 3 monkeys, with a mean total volume sampled of 104.64 μm³ (20.39–186.34 μm³) and 94.89 μm³ (34.91–200.18 μm³) in 4Cα and 4Cβ, respectively (Supplementary Table S1). In each subregion we reconstructed the volume occupied by blood vessels and cells, and these volumes were subtracted from the total volume of each subregion to obtain a synaptic density of the neuropil, in a similar way to Braitenberg and Schüz (1998). To estimate the true density in a tissue volume, which includes not only neuropil but also cell bodies and blood vessels (and which could be compared with our confocal estimates of TC density, which were made from samples of tissue that included space occupied by cell bodies and blood vessels), we had to correct these “neuropil-only” density measures based on the tissue volume occupied by other elements. To do this, we measured all cellular elements (neurons and non-neuronal cells) from image stacks used previously to measure neuronal density. DAPI and NeuN stacks were thresholded, and the ImageJ 3D counting plugin was used to measure areas of foreground regions. Image area measured from NeuN stacks was taken to be the area occupied by neurons; the area occupied by other cell types was estimated as the difference between the areas measured from the DAPI and NeuN image stacks. The relative volume occupied by blood vessels was measured previously (Tsai et al. 2009). The sum of these was used to correct the total volume from which counts were made. See Supplementary Table S1 for density values determined from regions only containing neuropil—we have called these “uncorrected” values—and the corrected values where the volume of blood vessels and cell bodies was factored into the calculation thereby reducing the density estimates.

Synaptic junctions were visualized and manually identified as symmetric or asymmetric (Supplementary Fig. S1) by an expert observer (V.G.M.). Synapses were classified using the same criteria as in the Transmission Electron Microscopy (TEM) study: synapses with a prominent PSD were classified as asymmetric, and synapses with a thin PSD were classified as symmetric. The analysis of synapses in 3D allowed a complete classification of all synapses in a defined volume, regardless of the plane of section. This is an advantage over 2D TEM approach techniques, which leave approximately 40–60% of synapses uncharacterized (DeFelipe et al. 1999; Kubota et al. 2009). With the aid of ESPina software (Morales et al. 2011), the manually identified synapses were automatically segmented and reconstructed in 3D. This segmentation was then confirmed by the expert observer. To quantify the number of synapses per volume, a 3D counting frame was defined within the stack in ESPina. This unbiased “counting brick” was a rectangular prism bounded by 3 acceptance planes and 3 exclusion planes (Howard and Reed 2005; Morales et al. 2011). All objects within the counting brick or intersecting any of the acceptance planes (defined as the front, top, and left sides of the subregion stack) were counted, while any object outside the counting brick or intersecting any of the exclusion planes (back, right, and bottom sides) were not included in the quantification.

3D Reconstruction of Selected Boutons

Using the images from the FIB/SEM, we selected boutons that were fully included in the stack and reconstructed their profiles in 3D using Amira 3D software (FEI, Hillsboro, OR, USA). To calculate the volume occupied by the different compartments we used separate “materials” to identify axonal membrane, mitochondria, and PSDs. We traced the profile of each object in each image plane across the full extent of each bouton and generated a 3D reconstruction for each material. We established the relationship between the bouton volume and the number of synapses for 64 boutons.

Quantification of Neuronal Density

As described previously (Kelly and Hawken 2017), images were acquired from the opercular surface of area V1 in anti-NeuN-labeled sections using a Leica TCS SP5 confocal system and analyzed using an automated method that segments and identifies cells in DAPI-labeled image stacks, then categorizes each cell according to its pattern of immunoreactivity. Laminar boundaries in V1 were identified separately for each sampled image series by visually identifying transitions in cell density and neuronal composition consistent with previous descriptions of these features in V1 (Brodmann 1909; Lund 1973; Valverde 1985).

Calculation of Shrinkage

The degree of tissue shrinkage was measured by comparing sections in x, y, and z dimensions before and after tissue preparation with the aid of Olympus VS120 and confocal Leica SPC5. The average linear shrinkage (S) was calculated by using the following formula: S = (A−0)/A, where A is the absolute value before processing and 0 is the observed valued after processing. This yielded an average linear shrinkage of 18%, 17%, and 30%, in x, y, and z, respectively, for (VGluT2) fluorescence and 3%, 3%, and 9%, in x, y, and z, respectively, for EM.

Statistics

In the EM studies, statistical comparisons between the densities of VGluT2-ir puncta in different layers were performed by using either a parametric (one-way ANOVA and t-test) or a nonparametric test (Kruskal–Wallis or Mann–Whitney) depending on whether the data sets were approximately normally distributed and passed the test for homogeneity of variances, followed by suitable post hoc tests. The data are presented as the mean ± standard error mean (SEM). All statistical comparisons were performed with the aid of the GraphPad Prism 5.1 statistical package (GraphPad, San Diego, CA).

Results

We measured the density of TC synapses using 3D-confocal imaging along with 2D and 3D-EM imaging (Fig. 1). First we used 3D-confocal imaging to estimate VGluT2-ir bouton density and individual bouton volume from large areas of layer 4C—both 4Cα and 4Cβ—from each of 4 animals. The next step was to relate bouton volume (Fig. 1E) to synaptic density because TC boutons often have more than one synaptic apposition (Freund et al. 1989; Nahmani and Erisir 2005; Fig. 1E, J). To do this we turned to a combination of 2D and 3D-EM. Using FIB/SEM image stacks, we reconstructed 64 boutons of different sizes in layer 4C in 3D (Fig. 1C, D) to obtain the relationship between bouton volume and the number of PSDs (Fig. 1E; regression in Fig. 1E legend). In parallel we used immuno-label to identify VGluT2-ir boutons in 2D TEM images of layer 4C neuropil and from these determined the relationship between bouton area and the number of PSDs (Fig. 1J). Using this 3-pronged approach we obtained a comprehensive set of measurements of synaptic density of the TC synapses into layer 4C.

One overall goal of the study was to determine the proportion of feedforward TC synapses to the total synapse density. Because recent studies indicate that prior measures of total synaptic density using 2D images substantially underestimated density (DeFelipe et al. 1999; Kubota et al. 2009) we used our 3D image stacks from the FIB/SEM to estimate total density of asymmetric PSDs and hence excitatory synaptic density. A second overall goal was to determine the synapse/neuron ratio in layer 4C. We used 3D imaging and automated segmentation to reevaluate the neuronal density in layer 4Cα and 4Cβ, finding that long-accepted densities were about half the densities that we measured in the current study. The results of each of these sets of measurements are described in detail below.

Synaptic Density of LGN Afferents in Layer 4C Using 3D-Confocal Imaging of VGluT2-ir Boutons

Although EM provides high-resolution identification of synaptic terminals and their ultrastructural properties, it is a major undertaking to obtain measurements from large areas of tissue. In an effort to accomplish sampling of larger regions across layers 4A, 4C, and 6—the major TC recipient zones of V1—we adopted a quantitative analysis of confocal images where we identified VGluT2-ir boutons in 3D (Fig. 1A, B), measured the volume of each bouton, and then used data from 3D reconstruction of selected terminals from FIB/SEM stacks to predict the synapse density from terminal volume (Fig. 1E). The presynaptic area of VGluT2-ir boutons in 4Cα and 4Cβ was on average 5.4 and 3 times larger, respectively, than non-VGluT2-ir terminal area (Fig. 1H). Furthermore, the length of the PSD was 1.20 times longer in VGluT2-ir boutons than non-VGluT2-ir boutons, both in 4Cα and 4Cβ (Fig. 1I). TC boutons were also observed by Nahmani and Erisir (2005) to have a larger terminal area and a larger synaptic length compared with unlabeled terminals in ferret V1, and TC synapses were shown to have larger PSD area in cat V1 (da Costa and Martin 2011); our results show that TC boutons are also larger and have larger PSD than IC boutons in the monkey. The length of PSDs is proportional to the number of presynaptic vesicles and spine volume (Harris and Stevens 1989), and can reflect the number of postsynaptic AMPA receptors, which in turn contributes to the synaptic strength synapse (Nusser et al. 1998; Matsuzaki et al. 2001). Additionally, bouton area was positively correlated with the number of PSDs per bouton. The majority of the boutons established one synapse (86%), but there was a substantial number of synapses with larger bouton area: 11% made 2 synaptic contacts, and 3% made 3 or more synapses (Fig. 1J). We did not find multisynaptic contacts for the non-VGluT2-ir boutons. Our 3D reconstructions of selected terminals using image stacks from FIB/SEM of layer 4C also showed the same results: the larger the bouton volume, the greater the number of synaptic contacts (Fig. 1E). The relationship between bouton volume (after subtracting mitochondrial volume) and the number of synapses from 3D-EM reconstructions (Fig. 1E) was used to relate bouton volume obtained from 3D-confocal imaging to synaptic density. At the confocal level, VGluT2 did not fill the whole bouton but rather appeared to leave empty spaces (as illustrated in Fig. 1B) that we assumed corresponded to regions occupied by mitochondria. At the EM level, mitochondria are also unlabeled for VGluT2 (Fig. 1F), confirming that they should appear as unlabeled space in the confocal images. Therefore, the mitochondrial volume was subtracted from the total volume in the 3D-EM reconstructed boutons before computing the relationship between volume and synapse number.

Using this approach we determined the distribution of 56 987 VGluT2-ir boutons that had an estimated 105 752 TC synapses (between 22 806 and 29 268 synapses/animal), to obtain the density in different layers of V1 (Fig. 2A, B). In contrast, the total numbers of VGluT2-ir terminals studied with the 2D-EM were only 17 and 30 in 4Cα and 4Cβ, respectively, in 4 animals.

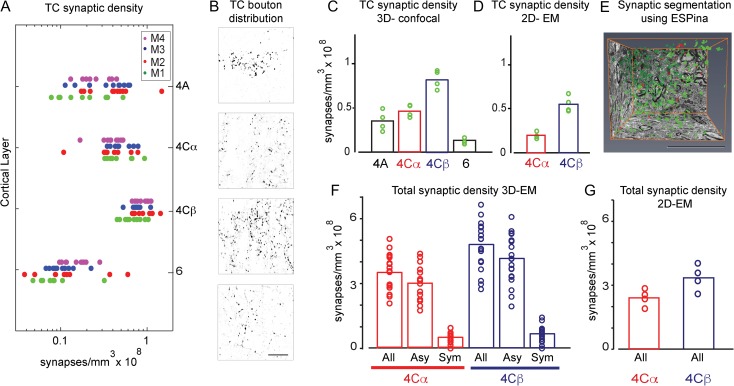
Figure 2.

Distribution of total and TC synaptic density in V1: TC density is considerably greater than currently accepted values. (A) TC synaptic density by layers (4A, 4Cα, 4Cβ, and 6) estimated from confocal images of VGluT2-ir boutons using the relationship between bouton volume and number of synapses (Fig. 1E). Each row shows the data from each of the 4 animals; each point is the density determined for each 72 × 72 μm² region within the confocal image stack. (B) Distribution of VGluT2-ir boutons by layers to illustrate relative density in single confocal images. (C) Mean distribution of the TC synaptic density. Individual animal mean values shown as green circles. Each bar represents the mean across the 4 animals. (D) TC synaptic density obtained from VGluT2-ir terminals determined from 2D-EM images. (E) 3D-EM image segmentation using ESPina to obtain the total synaptic density. (F) Total synaptic density measured using 3D-EM images shown as means (bar height) and measurements from each counting volume (circles; see Supplementary Table S1 for further details). All, Asy, and Sym refer to all, asymmetric and symmetric synapses, respectively. (G) Total synaptic density estimated from 2D-EM images. Bars represent means across 4 animals, and circles are within-animal means. Scale bar in B: 20 μm.

From our 3D-EM data (unpublished results) we found that in almost all axons, when there was a cloud of vesicles there was also a PSD. Recently, Kasthuri et al. (2015) identified 1700 synaptic contacts in a large block of neocortical somatosensory mouse tissue and found that only about 0.5% of vesicle-filled varicosities did not establish classic close synaptic junctions with postynaptic cells. Thus, we consider VGluT2 labeling as a reliable proxy for the presence of a synapse.

The highest density of TC synapses in a 72 × 72 μm² region was found in layer 4Cβ (Fig. 2A, C; Supplementary Table S4). Overall, within 4Cβ the average density across 37 regions from 4 animals was 0.82 × 10⁸ synapses/mm³ (Fig. 2C; Supplementary Table S4). We also determined the variation between regions within each animal (Fig. 2A) using the coefficient of variation (cv = σ/mean); within 4Cβ the cv for all regions in 4 animals was 0.25 (range 0.17–0.28). Therefore, there was relatively little variation between regions within a single animal (low cv’s).

The TC synaptic density in layer 4Cα was 44% lower than in layer 4Cβ. The mean density in layer 4Cα across all regions sampled in 4 animals was 0.46 × 10⁸ synapses/mm³ (Fig. 2C). The within animal ratio between 4Cα and 4Cβ densities ranged from 0.43 to 0.74 (Supplementary Table S4). The difference in density between the 2 recipient zones of layer 4C is somewhat lower than our 2D-EM estimates of the ratio (Fig. 2D) but greater than the most recent measurements from Latawiec et al. (Latawiec et al. 2000), who reported only a slightly higher density in 4Cβ than in 4Cα, with a ratio of 0.84.

To extend the results obtained for upper and lower layer 4C we measured the density for mid layer 4C (Supplementary Table S4). The within animal measurements showed a consistent trend where the sampled 72 × 72 μm² mid region had a TC synaptic density between those in 4Cα and 4Cβ, with an average ratio of 0.91 (4C-mid/4Cβ; Supplementary Table S4). At this point it has not been determined if there is an abrupt transition in TC synaptic density between the 2 recipient zones or if there is a gradual transition in density.

Density estimates from 2D-EM: The only previous study to directly measure the density of LGN axonal synapses at the ultrastructural level in macaque layer 4C (Latawiec et al. 2000) used the observation that excitatory LGN neurons express the calcium binding protein PV, whereas only a subset of inhibitory interneurons and no excitatory neurons in V1 express PV (Van Brederode et al. 1990). Therefore by identifying PV-ir synaptic boutons with asymmetric PSDs, Latawiec et al. (Latawiec et al. 2000) were able to identify the synapses exclusively from the LGN and, using the disector method, estimate their density in 4Cα (0.16 × 10⁸ synapses/mm³) and 4Cβ (0.19 × 10⁸ synapses/mm³).

We measured the synaptic density of VGluT2-ir synapses in 2D images of conventional transmission EM ultrathin sections to compare to the densities obtained with 3D-confocal imaging. Rather than PV (Latawiec et al. 2000) we used VGluT2 immunoreactivity to label TC terminals. In layer 4Cα the density of VGluT2-ir synapses was estimated to be 0.20 ± 0.05 × 10⁸ synapses/mm³ (mean ± SEM) (N = 100; Fig. 2D, Supplementary Table S2). For layer 4Cβ the estimate was more than double: 0.55 ± 0.12 × 10⁸ synapses/mm³ (N = 100; Fig. 2D, Supplementary Table S2). Overall these values using 2D images consistently underestimate densities; they are about half the density obtained with the 3D-confocal method. As we show in the next section this underestimation is consistent with our findings on the total synaptic density as well and can be reconciled with the use of 3D-EM image reconstruction. However, the use of 2D-EM images does not explain the earlier finding that TC synaptic density was similar in layers 4Cα and 4Cβ (Latawiec et al. 2000); our results showed that VGluT2-ir synaptic density was higher in 4Cβ compared with 4Cα regardless of the method used.

3D-Electron-Microscopic Synaptic Quantification Using FIB/SEM

We used 3D-EM to obtain 2 sets of measurements of synapses. In the first we used serial reconstruction of all individual PSDs within a known volume to determine total synaptic density. In the second, we reconstructed individual boutons in 3D to determine total bouton volume and the number of PSDs per bouton. We used data from the 3D set of measurements to determine the conversion from bouton volume to synapse density in our large scale confocal data set.

Total synaptic density: To provide an unbiased estimate of the total synapse density the use of serial ultrathin sections is crucial, because between one-third to one-half of the synapses can be missed in an estimation using single 2D images (DeFelipe et al. 1999; Kubota et al. 2009) due to the difficulty in identifying synapses “en face.” Using the 3D reconstruction of synapses from image stacks obtained using the FIB/SEM (Fig. 2E) we calculated the total number of synapses in 4Cα and 4Cβ from 3 monkeys in which the total volume of tissue was known (Fig. 2F). There was a higher average density of synapses in layer 4Cβ, 4.71 × 10⁸ synapses/mm³ (range 2.73–6.62 × 10⁸ synapses/mm³; N_stacks = 21; N_synapses = 1526; Supplementary Table S1), than in 4Cα where the average density was 3.47 × 10⁸ synapses/mm³ (range 2.05–4.71 × 10⁸ synapses/mm³; N_stacks = 17; N_synapses = 886; Supplementary Table S1). These measurements are for the entire volume and are not confined to the neuropil (see Supplementary Table S1 for uncorrected values).

The ratio of presumptive excitatory to inhibitory synapses (asymmetric:symmetric) for 4Cβ was 6.35 while for 4Cα it was 5.90. Using these values the estimated density of excitatory synapses in 4Cβ was 4.07 × 10⁸ synapses/mm³ and for 4Cα the density was 3.00 × 10⁸ synapses/mm³ (Fig. 2F; Supplementary Table S5).

To compare the 3D estimates with 2D estimates we estimated the total density of synapses from 2D images in 4 monkeys in the 2 sublayers of 4C, 4Cα and 4Cβ, using conventional stereological counting methods, specifically the size–frequency method described previously (Colonnier and Beaulieu 1985). Although the size–frequency method is assumption-based and the disector method is considered to be an unbiased method, similar estimates for the numerical density of synapses are found with both methods (Beaulieu et al. 1992; DeFelipe et al. 1999), and the size–frequency method is more efficient and easier to apply than the disector method (DeFelipe et al. 1999). We found the highest density of synapses in 4Cβ, with an average density of 3.34 ± 0.27 × 10⁸ synapses/mm³ (N = 100; Fig. 2G, Supplementary Table S3), whereas in layer 4Cα the average density was 2.41 ± 0.21 × 10⁸ synapses/mm³ (N = 100; Fig. 2G, Supplementary Table S3) [mean ± SEM]. These values obtained from 2D are similar to those reported in earlier studies that estimated the total synaptic density in macaque layer 4Cα and 4Cβ (O’Kusky and Colonnier 1982; Latawiec et al. 2000). On average we found that layer 4C received 2.88 × 10⁸ synapses/mm³, close to the average reported by O’Kusky and Colonnier (1982) and Latawiec et al. (2000). All of these are lower than the estimate reported by Beaulieu et al. (1992) in layer 4C, 4.51 × 10⁸ synapses/mm³, using both the disector method and the size–frequency distribution.

Estimating TC Contribution to Total Synaptic Density

An important consideration in estimating density is the sampling method and the local variability in density. In the 3D-FIB/SEM study we found more synapses in layer 4Cβ (4.71 × 10⁸ synapses/mm³) than in 4Cα (3.47 × 10⁸ synapses/mm³), but we also showed that in 2D we underestimated, by a factor of about 2, the total number of synapses both in 4Cα and in 4Cβ (comparing 2D-EM total number of synapses vs. 3D-EM uncorrected total number of synapses). Our samples were from regions that contained predominantly neuropil but that also included parts of cell bodies, blood vessels, and myelinated axons. When we estimated the TC density using confocal images it was for large regions that contained all elements of tissue including neurons, glia, and blood vessels. Therefore, to make a reliable estimate of the TC contribution to total density we corrected the 3D-EM estimates of total excitatory density to account for the cortical volume occupied by cell bodies and blood vessels (27% and 37% for 4Cα and 4Cβ, respectively), yielding the density values that would accrue in a relatively large region of cortical tissue within the appropriate layer. First, we measured the volume occupied by cell bodies, blood vessels, and myelinated axons within the sampled blocks and subtracted this from the total volume, thereby estimating the synaptic density in the neuropil (Supplementary Table S1, “Mean, uncorrected”). Then for each sublayer the volume was adjusted to incorporate the average volume occupied by cell bodies and blood vessels, and a new mean value was determined (Supplementary Table S1, “Mean, corrected”). If other studies using comparable methods do not make a similar correction, but instead target their sampling in an attempt to avoid cell bodies or blood vessels, they may overestimate the total synaptic density. Using the values obtained from the 2 3D studies (confocal for TC density and FIB/SEM for total density of excitatory synapses) we found the percentage of TC synapses was 15% for 4Cα and 20% for 4Cβ. The percentages of TC synapses were about 1.8 and 2.9 times the previously reported values in 4Cα and 4Cβ (Latawiec et al. 2000), respectively, and were also larger than the values we obtained using 2D-EM (8% for 4Cα, 16% for 4Cβ).

Other TC Recipient Layers

There have not been any previous estimates of TC synaptic density outside layer 4C in macaque V1. We used the 3D-confocal approach to study the density of TC input to layer 4A and layer 6. Within layer 4 A the TC input pattern is patchy; it has a honeycomb arrangement in tangential view (Carroll and Wong-Riley 1984; Horton 1984; Fitzpatrick et al. 1985; Garcia-Marin et al. 2015). In the analysis we used the same sampling area as for layer 4C, 72 × 72 μm², and for this sampling area the mean density over the 4 animals was 0.35 × 10⁸ synapses/mm³ (Fig. 2A; Supplementary Table S4), but there was considerable local variation within each of the sampling regions. The highest local density (in a 18 × 18 μm² region) was 2.2 × 10⁸ synapses/mm³, and within the local regions that we judged to be part of the dense regions of the honeycomb, density was often seen to be > 1 × 10⁸ synapses/mm³. Thus although the local density in some sampled regions of layer 4A was comparable to densities found in layer 4Cα there were also many regions with considerably lower densities than almost all regions in layer 4Cα of the same animal. There was also considerable interanimal variation in layer 4A density (Fig. 2A). Currently we do not know whether these variations are specific to the region sampled or if they are consistent across the whole of V1. In an earlier study we showed that there was a paucity of VGluT2 immunoreactivity in foveal V1 (Garcia-Marin et al. 2015), and although we did not use tissue from within the foveal representation in the current study we do not know if there is local variation in presumptive TC terminal density across V1, even outside the foveal representation.

The average TC synapse density in layer 6 (Fig. 2A; Supplementary Table S4) was lower than in the other input regions of V1, with an average density of 0.13 × 10⁸ synapses/mm³, about 16% of the density measured in layer 4Cβ. Our earlier qualitative observations (Garcia-Marin et al. 2013) where we observed patches of terminals surrounded by regions that were relatively sparse were confirmed in the quantitative estimates. There were regions of 18 × 18–36 × 36 μm² that had densities of 1.2–0.6 × 10⁸ synapses/mm³ surrounded by regions with very low densities. This suggests a local patchiness and not a uniform cover of TC input. We saw no tendency for a higher density in any particular horizontal strip of the 72 μm deep sampling region.

Neuronal Density in Visual Cortex: Large Scale 3D-Confocal Imaging

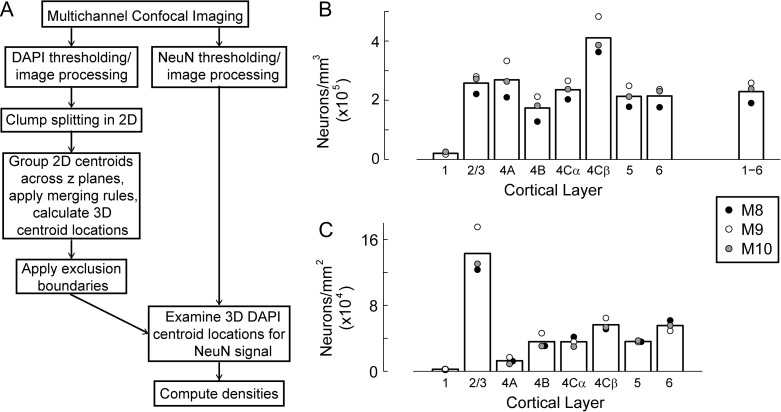
Recent estimates of total neuron number and volume of macaque V1 when converted to density indicate that the overall V1 density is around 2.80 × 10⁵ neurons/mm³ across layers 2–6 (Giannaris and Rosene 2012), more than twice the previously accepted values of neuronal densities in V1 (O’Kusky and Colonnier 1982; Beaulieu et al. 1992) that were determined using methods that may have introduced stereological bias (Mouton et al. 2002). In a recent study, we used an automated procedure (Fig. 3A) to estimate neuronal density throughout the depth of V1 using a combination of DAPI fluorescence to label all cell nuclei and NeuN immunohistochemistry to label neurons, followed by confocal imaging and image segmentation to determine the 3D profile of labeled neurons through the depth of tissue sections (Kelly and Hawken 2017). The neuronal density averaged across all layers of V1 was 2.29 × 10⁵ neurons/mm³ (Fig. 3B, Table 1; Kelly and Hawken 2017), close to the density reported by Giannaris and Rosene (Giannaris and Rosene 2012) but lower than the total neuronal density estimates from some other studies (Algan and Rakic 1997; Kim et al. 1997; Christensen et al. 2007).

Figure 3.

Distribution of neuronal density across cortical layer. (A) The multichannel confocal imaging and 3D image analysis method for automated segmentation and counting of neurons. Confocal image stacks of DAPI and NeuN stained cell nuclei and neurons were acquired. Cell centroid positions in 3D were determined by segmentation of DAPI images followed by grouping of 2D centroids across image planes. DAPI-stained cells were then classified as neuronal or non-neuronal by evaluating thresholded mask images of the NeuN channel for signal at the locations of 3D DAPI centroids. Large numbers of cells (~32 000) and neurons (~22 000) were reliably counted using these automated procedures to provide densities within each cortical layer. (B) Mean neuronal density within each cortical layer (bars in the histogram), with average values obtained from 3 to 5 image series from each of 3 animals (M8, M9, M10) (filled circles). The average value across all layers is shown by the bar labeled 1–6. (C) The total number of neurons under a 1 mm² region within each layer, following the same conventions as in B. For visibility, black points for layers 4A, 4B, and 5 have been offset slightly to the right.

Table 1.

Average cell and neuronal densities within each layer of V1 (mean ± 1 SEM, N = 3)

Layer	Cells (×103) per mm3	Neurons (×103) per mm3	Neurons (×103) per mm2	Neurons (×103) per ODC
1	98.9 ± 3.5	20.7 ± 2.6	2.5 ± 0.07	0.5 ± 0.2
2/3	330.6 ± 24.4	257.8 ± 18.4	143.0 ± 13.3	29.0 ± 3.3
4A	380.2 ± 48.7	268.8 ± 35.6	12.8 ± 1.9	2.6 ± 0.5
4B	285.0 ± 30.9	173.8 ± 24.5	36.0 ± 4.2	7.3 ± 1.1
4Cα	375.6 ± 27.4	235.3 ± 18.2	35.9 ± 2.8	7.3 ± 0.8
4Cβ	538.5 ± 45.3	410.6 ± 36.7	56.5 ± 3.4	11.4 ± 0.8
5	312.6 ± 28.2	213.0 ± 20.5	36.2 ± 0.4	7.3 ± 0.2
6	324.5 ± 21.5	214.5 ± 19.3	55.5 ± 3.0	11.2 ± 1.2
1–6	327.8 ± 25.5	229.1 ± 20.2	378.3 ± 19.7	76.6 ± 4.6

Note: Neurons per ocular dominance column (ODC) was computed assuming a size of 450 × 450 μm² per ODC.

Neuronal density plays a critical role in determining the number of synapses per neuron in the different subregions of layer 4C. Consequently we conducted an additional analysis of our previous data to determine the neuronal density in layers 4Cα and 4Cβ—as well as in other cortical layers—to use in conjunction with synaptic density measures to calculate the average synaptic TC and IC input to layer 4C neurons, the initial defining feature of the circuit architecture. There was considerable difference in density at different depths within V1. In layer 4Cβ average density was 4.11 × 10⁵ neurons/mm³ while in 4Cα the density was 2.35 × 10⁵ neurons/mm³ (Fig. 3B, Table 1). These values are about double those reported in previous studies (O’Kusky and Colonnier 1982; Beaulieu et al. 1992).

Density of Synapses per Neuron

Currently the relative proportion of TC synapses made onto excitatory (spiny stellate) compared with inhibitory interneurons (smooth stellate, PV-ir basket cells) in layer 4C is unknown. As a first approximation we determined the density of TC synapses across the total neuronal population in the different sublayers of 4C. In layer 4Cβ, the previous estimate of average TC synapses per neuron (Latawiec et al. 2000), using neuronal density data from Beaulieu et al. (1992), was 148 synapses per neuron. From the current 3D-confocal studies, the average TC synaptic density within 4Cβ was 0.82 × 10⁸ synapses/mm³ (Fig. 2C) and neuronal density was 4.11 × 10⁵ neurons/mm³ (Fig. 3B, Table 1), indicating 200 TC synapses per neuron (Supplementary Table S5). The total excitatory synaptic density from the 3D-EM study was 4.07 × 10⁸ synapses/mm³, such that the total number of excitatory synapses per neuron was 990 (Supplementary Table S5).

For 4 Cα the number of TC synapses per neuron was 197 (Supplementary Table S5), close to the value of 185 per neuron estimated by Latawiec et al. (2000) using Beaulieu et al. (1992) neuronal density for 4Cα, but 5–11 times the estimates of Peters et al. (1994). Based on our estimate of neuronal density we found 1 276 excitatory synapses per neuron (Supplementary Table S5).

Calculating the total synaptic density per neuron using the values measured in the current study we found there were 1146 synapses per neuron in layer 4Cβ and 1 477 synapses/neuron in 4Cα (Supplementary Table S5). Using 3D-EM the putative TC boutons—those that made multiple synapses—made 82% and 78% of their contacts on spines in 4Cβ and 4Cα, respectively, while the putative IC boutons—those making single synapses per bouton—only made 60% of their synapses on spines in both 4Cβ and 4Cα. Assuming nearly all spines are on excitatory neurons, these percentages, in combination with the numbers of TC and total excitatory synapses per neurons, would predict 717 spines per excitatory neuron in 4Cβ and 923 spines per excitatory neuron in 4Cα. This assumes that the ratio of TC to IC excitatory synapses is similar for excitatory and inhibitory neurons in V1.

Discussion

To obtain an accurate representation of the connectome it is essential to determine the global statistical features of circuits that will provide and define the basis of generating a comprehensive map of connectivity within and between cortical areas (Braitenberg and Schüz 1998; Kleinfeld et al. 2011; Markov et al. 2013; Markram et al. 2015). Although there has been considerable recent work on macrofeatures of the connectivity between cortical regions (Markov et al. 2013; Song et al. 2015) and in the microcircuitry of rodent sensory cortex (Meyer et al. 2010a,b; Oberlaender et al. 2012; Schoonover et al. 2014) there have been fewer advances in our understanding and refinement of specific circuits in primates (daCosta and Martin 2013). Using the tools of immunocytochemistry, large-scale image acquisition, and subsequent image processing, we have re-evaluated the connectivity at the first stage of monkey primary visual cortex.

TC Synaptic Density

Although TC synapses comprise a minority of asymmetric synapses in layer 4C, we found substantially more synaptic connections from the thalamus for the largest visual stream—the parvocellular (P) pathway that contributes around 80% of the input from the eye to the thalamus and onward to V1—than previously reported (Peters et al. 1994; Latawiec et al. 2000). In the current study we determined that the P-pathway contributes around 18% of the total number of synapses in layer 4Cβ and 20% of all excitatory synapses (Supplementary Table 5). This fraction of total asymmetric synaptic density is similar to those reported previously in layer 4 of mouse somatosensory cortex (Benshalom and White 1986; Sadaka et al. 2003; Bopp et al. 2017) and squirrel monkey area 17 (Tigges and Tigges 1979), but is 2–4 times greater than the values most often accepted as the standard for V1 (Douglas and Martin 2007b for review). The density of TC synapses within layer 4Cβ was relatively consistent both within the same animal across sampled regions (Fig. 2A) and between animals (Fig. 2C).

How should these results influence our understanding of the canonical circuit? One of the prevailing views is that the external input is weak (Douglas and Martin 2007b; daCosta and Martin 2013), and consequently models of cortical function need to invoke strong and dominant IC recurrent excitation to amplify the weak TC input signals and generate the receptive field properties observed in input-layer cortical neurons. In this view one of the main roles of inhibition is to stabilize and maintain balanced dynamics within the recurrent circuit (Douglas and Martin 2007b; Binzegger et al. 2009). Part of the support for the “weak” view comes from previous reports of very few TC inputs to layer 4 (<10%) compared with abundant IC inputs. However, our new measurements indicate a substantially greater TC input than was previously indicated, considering synaptic density alone.

If, in addition, the direct LGN excitatory input is more synchronous than the IC recurrent excitatory (Reid and Alonso 1996; Bruno and Simons 2002; Schoonover et al. 2014), then in any model of functional connectivity the direct thalamic feedforward input will play a major role in determining the spiking behavior of the spiny stellate neurons in layer 4Cβ. Functional studies of cat V1 have demonstrated that TC input strongly drives responses in layer 4 cortical neurons and is sufficient to produce orientation tuning, and this functional strength likely reflects not only the absolute number of inputs to layer 4C but also convergence and synchrony of spiking of TC inputs onto individual cortical neurons (Stratford et al. 1996; Chung and Ferster 1998; Usrey et al. 2000). The physiological strength of individual TC versus IC synaptic inputs is also of considerable importance. Some studies (Ferster et al. 1996; Stratford et al. 1996; Chung and Ferster 1998; Tarczy-Hornoch et al. 1999) have reported that TC inputs are stronger than IC inputs, but others have reported no difference in strength between TC and IC inputs (Schoonover et al. 2014). Yet other studies have focused on other features of synapses and their pattern of connections with postsynaptic spiny stellate cells and have also reached differing conclusions (da Costa and Martin 2011; Schoonover et al. 2014). Currently, it is unknown in the monkey cortex whether there are differences between TC and IC inputs in physiological strength, proximity to the soma, or degree of clustering of synapses. Overall, it is important to consider not only the anatomical density of multiple synapse types—as provided in this study—but also other factors that will impact their efficacy.

It may also be the case, as suggested by recent modeling (Chariker et al. 2016), that the TC input is not distributed equally amongst layer 4C neurons. Even in layer 4C there are neurons with quite distinct functional properties: the simple and complex cells of Hubel and Wiesel (Hubel and Wiesel 1962, 1968), which have been described in monkey cortex through multiple studies (Hubel and Wiesel 1968; Dow 1974; Livingstone and Hubel 1984), including our own (Hawken and Parker 1984; Hawken et al. 1988; Ringach et al. 2002). This is best documented for layer 4Cα but is also the case for 4Cβ. According to large scale models, simple and complex cells may have different proportions of TC to IC input, with complex cells receiving few direct TC synapses (Chariker et al. 2016); given that complex cells make up a substantial proportion of the layer 4C population, the remaining population of excitatory simple cells will have an even larger proportion of TC input than the average over the whole population. Therefore the ratio of TC to IC recurrent excitation may vary between neurons within the population of layer 4C neurons, and the TC input may provide a much stronger drive to a subset of cells than envisaged in the canonical circuit.

There is also a substantial IC input from layer 6 to layer 4C (Blasdel et al. 1985; Wiser and Callaway 1996), and we have established that layer 6 is receiving about one-sixth of the direct LGN input that is received by layer 4Cβ. The major output from layer 4Cβ is to layers 2 and 3. It still needs to be determined how much the relative functional contribution of the direct feedforward output from layer 4Cβ will play in determining the drive to layers 2/3 compared with intralaminar drive from within layers 2/3 themselves.

The proportion of excitatory inputs that were TC differed between layers 4Cα and 4Cβ. The magnocellular layers of the LGN dominate the input to layer 4Cα, where we determined the TC synaptic density was 0.46 × 10⁸ synapses/mm³, which accounted for 13% of the total synaptic density and 15% of the excitatory density (Supplementary Table S5). This value is between 1.7 (Latawiec et al. 2000) and 9.6 (Peters et al. 1994) times previous estimates. Because the spiny stellate neurons of upper layer 4C have been shown to have dendritic fields with diameters of 100 μm or more, any neuron with a cell body below the 4C/4B border will have dendrites in the vicinity of the middle region of layer 4C (the region we designated 4Cm) where the density of synapses is higher than in the upper third of 4C (Supplementary Table S4). Consequently it is likely that the percentage of connections from the LGN onto many neurons with cell bodies in 4Cα will be greater than the 13% calculated above. If we use the measured density of 0.74 × 10⁸ TC synapses/mm³ (Supplementary Table S4) for 4Cm and assume a total synaptic density between the values we found for 4Cα and 4Cβ (3.54 × 10⁸ synapses/mm³), then it can be estimated that around 21% of the synaptic connections are from the LGN. For neurons with their cell bodies in layer 4Cα but whose dendrites are in the middle region of layer 4C, it is unknown whether they receive synapses dependent on the proximity of the axonal bouton from P- or M-cell afferents or if there is some degree of specificity for connections from one pathway or the other.

There can be considerable variation in the density of neurons and synapses between individuals. However, the proportions of different classes of synapses (inhibitory/excitatory) remains relatively constant (Hendry et al. 1987). The ratio of TC synapse density in 4Cα/4Cβ ranged from 0.43 to 0.74 with a mean ratio of 0.56 (Supplementary Table S4). This is a relatively small difference between animals, which is reflected in the similarities in absolute densities. We did not determine the neuron density in the same animals used to determine VGluT2-ir in layer 4C, so we cannot calculate the within-animal number of synapses per neuron for each layer to determine if this, like the other ratio values, stays relatively constant between animals. Remarkably, although there are many fewer axons originating from the M layers of the geniculate—at comparable eccentricity, the ratio of magnocellular/parvocellular neurons in the LGN is 0.05–0.1 (Malpeli et al. 1996; Azzopardi et al. 1999)—they contribute about one-third of the TC synapses into layer 4C (Supplementary Table S5).

Neuronal Density

By sampling relatively large regions in 3D and by measuring both synaptic and neuronal densities from comparable regions of V1, we have obtained accurate measurements of both quantities within individual layers that can be related with each other to inform realistic models of cortical processing. A recent extensive study of twenty macaques of various ages reported average neuronal density in V1 of 2.81 × 10⁵ neurons/mm³ (Giannaris and Rosene 2012), more than double the previously reported densities in some studies that reported laminar density distributions (O’Kusky and Colonnier 1982; Beaulieu et al. 1992) and considerably fewer than in other studies (Algan and Rakic 1997); our results were well matched to those of Giannaris and Rosene (2012).

Neuronal densities were higher in all layers (Fig. 3, Table 1) compared with previous results from studies that provided a laminar analysis (O’Kusky and Colonnier 1982; Beaulieu et al. 1992). While the neuronal density varied considerably between layers, the ratio between non-neuronal and neuronal density varied less and was about 0.43 (Table 1), which is in good agreement with other studies (O’Kusky and Colonnier 1982; Christensen et al. 2007; Giannaris and Rosene 2012).

To facilitate the comparison between numbers of neurons in each layer within a single cortical ocular dominance column (ODC), which can be thought of as a processing unit in V1, we have also converted our estimates of neuronal density in each layer (Fig. 3B) to number of neurons per mm² in each layer (Fig. 3C) by multiplying by the radial extent of (cortical depth occupied by) each layer; this can then be converted to the number of neurons in each layer within a single 450 μm × 450 μm ODC (Table 1). Neurons/mm³ (Fig. 3B) is a measure of true density useful for comparative calculations, while neurons/mm² (Fig. 3C) indicates the relative number of neurons in each layer within a columnar/radial processing unit. For example, for layer 2/3 the average vertical extent is 0.68 mm, so the total number of neurons in layer 2/3 under a square mm is ~160 000. In contrast, even though the density of neurons in layer 4A is similar to layer 2/3 (Fig. 3B), the number of neurons in a 1 mm² region in layer 4A is only 20 000 (Fig. 3C) because 4A is only on average ~0.1 mm in vertical extent.

Connectivity in Cortex

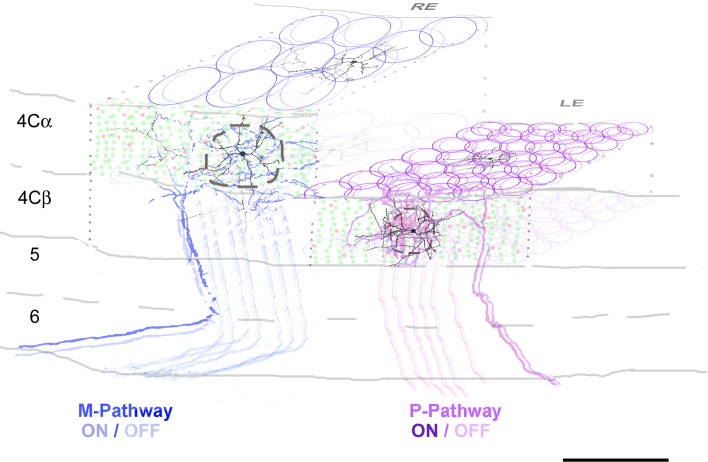
One of the principal goals of determining the synaptic and neuronal densities was to estimate the number of synaptic inputs onto cortical neurons as these numbers are part of the puzzle in determining the strength of synaptic integration from different sources (feedforward and feedback) and hence functional spiking properties of the different neuronal populations (Braitenberg and Schüz 1998; Oberlaender et al. 2012). First, we determined the number of neurons in the subdivisions of layer 4 C within a single ODC measuring 450 μm by 450 μm (Fig. 4; Supplementary Table 5). Given that the total average measured depth of 4C was 344 μm, with each division occupying approximately half the depth (Hendrickson et al. 1978), there were 8185 neurons in 4Cα and 14 315 in 4Cβ within a single ODC. In a separate study we determined the proportion of the total neuronal population that were GABAergic (Kelly et al., in preparation). Within layer 4C, 13% of neurons were GABAergic; therefore, we estimate there to be 1064 and 1575 inhibitory neurons (their distribution is shown as red dots in Fig. 4) and 7121 and 12 740 excitatory neurons (shown in green in Fig. 4) in layers 4Cα and 4Cβ, respectively.

Figure 4.

Schematic representation of the organization of layer 4C in V1. Two ocular dominance columns (ODC’s) are shown as an example (RE and LE: right and left eye, respectively). For clarity only the M-pathway input is shown to the RE ODC and the P-pathway input to the LE ODC. We estimated that 20 and 203 TC fibers are distributed to each ODC within layers 4Cα and 4Cβ, respectively (solid blue and purple circles). We assumed an equal distribution of ON and OFF center afferents, shown as the slightly offset circle pairs. The fine-scale topographic arrangement of neighboring afferents within a column is not known, so the depiction illustrates only the sizes, not the arrangement. Within each ODC we calculated that there were 8 and 7 TC afferents within the dendritic field domain of each spiny stellate cell in 4Cα and 4Cβ, respectively. For each column the spatial extent of the axonal arbor of ON and OFF TC input is shown. The dashed circles indicate the approximate extent of the dendritic domains of spiny stellate neurons. Reconstructions of Golgi stained neurons and horseradish peroxidase-filled TC axons modified from Lund (1973) and from Blasdel and Lund (1983), respectively. Within layer 4Cα and 4Cβ there are 8185 and 14 315 neurons/ODC respectively; 87% are excitatory (green dots) and 13% inhibitory (red dots). Scale bar: 200 μm.

Layer 4Cβ receives input from the P-layers of the LGN. Based on values reported in the literature, we calculated that there were approximately 200 afferents from the P-layers of the LGN terminating in a single cortical ODC (Fig. 4; Supplementary Table S5). The diameter of the axonal spread of each afferent is approximately 100 μm (Blasdel and Lund 1983). Based on these numbers we calculated that there were about 8 afferents with overlapping axonal arbors within each dendritic field of the 4Cβ spiny stellate cells. If each neuron receives, on average, 200 TC synapses, each TC afferent provides 25 synapses to a single neuron (Supplementary Table S5).

The principal LGN input to layer 4Cα is from the M-layers (Fig. 4). The number of M-layer LGN afferents projecting to an ODC is approximately 20 if no branching is taken into account but up to 100 if there is branching (Blasdel et al. 1985) of each afferent into 4 neighboring ODCs (Supplementary Table S5). Assuming no branching, based on the average afferent spread and dendritic fields in 4Cα we calculated that there were 7 afferents in the domain of each spiny stellate (Fig. 4), with each afferent giving rise to approximately 28 synapses on average to an individual neuron.

The above estimates are assuming uniformity of connections. Recent modeling of layer 4Cα has indicated a range of LGN input strengths is needed to account for the functional range of linearity among the 4Cα population. In the functional models the complex cells in 4Cα receive weak direct input from few LGN afferents while linear simple cells with a high linearity index receive from up to 6 afferents (Chariker et al. 2016). The numbers we have estimated are consistent with the conditions necessary to establish the functional characteristics that are found in layer 4Cα and are consistent with predictions that were made previously based on cone density and receptive field subunit size (Hawken and Parker 1991) and based on LGN projection patterns (Angelucci and Sainsbury 2006). The considerably higher ratio of TC/IC synapses than previously assumed and the fine grain of the representation within layer 4Cβ (Fig. 4) has not been addressed in detail in functional receptive field models and remains a considerable challenge.

Our estimate of the number of TC afferents per domain of the spiny stellates—7 and 8 in layer 4Cα and layer 4Cβ, respectively—is considerably lower than earlier estimates (~24, Peters et al. 1994). Studies in other species have not reached a consensus on the number of TC neurons providing input to each cortical neuron in layer 4, with a range from a 10–125 afferents per neuron in cat visual cortex (Tanaka 1983; Peters and Payne 1993; Alonso et al. 2001) and 85–90 in rodent barrel cortex (Bruno and Simons 2002; Bruno and Sakmann 2006). The number of synapses supplied by each TC afferent onto each spiny stellate is also higher in our estimates (25–28) compared with previous estimates (range 1–8) for monkey layer 4Cβ (Peters et al. 1994) and layer 4 of mouse somatosensory cortex (Gil et al. 1999).

When calculating the ratio of synapses/neurons it is important to have accurate estimates of both quantities. In the current study, if values of neuronal density estimated by O’Kusky and Colonnier (1982) or Beaulieu et al. (1992) were used to determine the total number of synapses per neuron in 4Cβ, the outcome would have been 2231–2520 synapses per layer 4Cβ neuron rather than the value of 1146 synapses per neuron (Supplementary Table S5) that was determined based on the neuronal density measurements from the current study (Fig. 3B; Table 1). Similarly, using neuronal densities from Beaulieu et al. (1992) would predict 439 TC synapses per neuron and 2178 excitatory synapses per neuron rather than 200 TC and 990 excitatory synapses per neuron. Had we used previous estimates of synaptic densities (Latawiec et al. 2000) with our new estimates of neuronal density, we would have erroneously estimated there to be 46 TC, 667 excitatory, and 759 total synapses per neuron in layer 4Cβ.

We have estimated the numbers of spines per neuron in layers 4Cα and 4Cβ based on the number of excitatory synapses per neuron and the fractions of TC and IC synapses that are onto spines. Our predictions—923 and 717 spines per neuron in layer 4Cα and 4Cβ, respectively—are similar to values reported for human somatosensory cortex (Jacobs et al. 2001) and only slightly lower than the average spine number in the basal dendritic fields of pyramidal neurons in layers 3–4B of macaque V1 (Oga et al. 2016). However, they are lower than values reported for pyramidal neurons (Mathers 1979; Duan et al. 2003; Young et al. 2014) and spiny stellate cells (Meyer et al. 2010a; Oberlaender et al. 2012; Schoonover et al. 2014) in multiple species and cortical areas. Total spine number is dependent on both spine density and total dendritic length, and all 3 morphological properties (spine number, spine density, total dendritic length) vary between species, cortical areas, and cell types. Because of their small size, the spiny stellate cells of monkey V1 layer 4C might be expected to have fewer total spines than other cell types.

As the detailed connectivity within the local circuit becomes elucidated further, the relative contributions to the total synaptic input from different sources—thalamic feedforward, local recurrent, feedback from other cortical areas, inhibitory (also from different interneuron types), and modulatory—will, in combination, define the functional properties of neuronal firing and be essential for constructing realistic models of the cortical microcircuit. The current study provides new insights into the likely contribution of the thalamic feedforward inputs to layer 4 of cortex, suggesting that the strength of the recurrent amplification needs to be re-evaluated.

Funding

National Institutes of Health (NIH) grants: EY17945, P30 EY013079, T32 EY007136, and NS088906. The 3D-EM stacks were acquired at the Simons Electron Microscopy Center at the New York Structural Biology Center, supported by grants from the Simons Foundation (349247), Empire State Development Division of Science, Technology & Innovation (NYSTAR), and the NIH National Institute of General Medical Sciences (GM103310) with additional support from NIH S10 RR029300-01.