Retinal optical coherence tomography image enhancement via deep learning

Abstract

Optical coherence tomography (OCT) images of the retina are a powerful tool for diagnosing and monitoring eye disease. However, they are plagued by speckle noise, which reduces image quality and reliability of assessment. This paper introduces a novel speckle reduction method inspired by the recent successes of deep learning in medical imaging. We present two versions of the network to reflect the needs and preferences of different end-users. Specifically, we train a convolution neural network to denoise cross-sections from OCT volumes of healthy eyes using either (1) mean-squared error, or (2) a generative adversarial network (GAN) with Wasserstein distance and perceptual similarity. We then interrogate the success of both methods with extensive quantitative and qualitative metrics on cross-sections from both healthy and glaucomatous eyes. The results show that the former approach provides state-of-the-art improvement in quantitative metrics such as PSNR and SSIM, and aids layer segmentation. However, the latter approach, which puts more weight on visual perception, outperformed for qualitative comparisons based on accuracy, clarity, and personal preference. Overall, our results demonstrate the effectiveness and efficiency of a deep learning approach to denoising OCT images, while maintaining subtle details in the images.

1. Introduction

Optical coherence tomography (OCT) has emerged as a powerful imaging modality that allows for non-invasive acquisition of depth-resolved retinal images at microscopic resolution. Measurements performed on OCT images (e.g. layer thickness) have proven themselves to be clinically useful biomarkers for diagnosis and monitoring of diseases such as glaucoma [1,2] and age-related macular degeneration (AMD) [3–6]. However, OCT images are inherently affected by speckle noise, which degrades the image quality, masks image features, and makes it difficult to perform qualitative assessment and quantitative measurements reliably. Therefore, image enhancement is a critical step required in the analysis pipeline to ensure the reliability of disease assessment.

Speckle is the cause of the grainy appearance of OCT images, and is dependent on both the wavelength of the imaging beam and the structural characteristics of the tissue. Therefore, in addition to noise, the speckle also contains information about the textural characteristics and clinical features of the tissue. Separation of these noise and information components is an ongoing challenge, and multiple approaches have been suggested to address it, which can be roughly characterised into frame averaging methods [7], and digital suppression methods [8]. For OCT of the retina, frame averaging operates on the principle that small changes in the subject (such as eye movement) induce changes in the speckle pattern between repeated measurements, which can then be removed through registration of the images and averaging [7]. However, in circumstances where multiple repetitions of the volume are not available, there exists a need to remove speckle noise from single scans without loss of detail. Many digital suppression methods have been proposed (see [8] for a review on speckle suppression specifically in OCT, and [9] for a more recent review of noise suppression in ultrasound images), including spatial domain filtering approaches, where filtering is applied directly to the noisy image [10,11], and transform domain filtering, where images undergo a transformation (such as a wavelet transform or sparse representation) prior to denoising [12–16].

Spatial domain approaches such as variational models can be negatively affected by artefacts like the staircase effect [17]. While the incorporation of total generalised variation regularisation proposed by [11] eliminates this effect, it also serves to remove small structural features in the image. Other approaches, including non-local means filtering [18] require long processing times, particularly for large images, which may be intractable for diagnostic applications. Transform domain filtering approaches have shown much success at denoising, but since they rely on fixed mathematical models they have limited adaptability, have difficulties in distinguishing subtle details from speckle noise, and are prone to artefacts.

In this work, we present a novel deep-learning based algorithm for speckle noise reduction in OCT images. Deep learning approaches are new to the medical image denoising scene, but have already shown promise in enhancing ultrasound [19] and CT [20–22]. Results thus far have shown that deep learning can produce perceptually realistic, enhanced images, that are more convincing, and often faster, than those produced by traditional techniques. The success of such networks arises from their ability to exploit spatial correlations at multiple resolutions using a hierarchical network structure. However, these networks generally require large amounts of high quality data to train their numerous parameters. The additional requirement that both noisy and denoised images are jointly available means that previous studies have relied on introducing artificial perturbations into images to simulate the effects of noise. This is an inherent limitation, since the generated images may not accurately represent the statistical properties of noise in real images, therefore, the trained networks may not perform successfully when applied to real images. To tackle this issue, we encourage our network to remove speckle noise without losing small structural details by training the network to transform noisy OCT images into their enhanced counterparts obtained through frame averaging. Previous studies have suggested that using only mean squared error (MSE) between the input and ground truth images is not a sufficient objective function to produce perceptually convincing enhancements, and have thus implemented generative adversarial network (GAN) architectures and additional objective functions to improve on image quality [21]. However, while perceptual similarity is preferable, it does not convey whether the enhanced image is any more useful to the clinician. Therefore, we implement both a MSE-trained CNN, and a GAN architecture, and introduce several metrics to evaluate both image similarity and enhancement usefulness. The remainder of the paper is structured as follows: In Section 2 we discuss the proposed method for denoising OCT frame data. Section 3 presents a discussion of the datasets, and the evaluation process for gaining quantitative and qualitative results. The results of our method, and a comparison to results using standard algorithms, are presented in Section 4. Our work is summarised in Section 5. Here, conclusions are also drawn and suggestions for future work are given.

2. Method

Let I_R ∈ ℝ^M×N denote a cross section (hereafter called a B-scan) from a raw OCT volume, and I_FA indicate the frame averaged version of the B-scan, created by registering and averaging R consecutively acquired OCT scans (see Section 3 for further details regarding data acquisition and pre-processing). This enhancement process serves to remove speckle noise in the images, and accentuate low contrast structures that are otherwise obscured by noise. However, the denoised images are only available during training. Therefore, our goal is to find a function G that maps I_R to I_FA

$$G:I_R\to I_{FA}.$$ (1)

To achieve this, we train a generator network as a feed-forward convolutional neural network (CNN) G_θG parametrised by θ_G. G_θG maps I_R into a certain distribution I_E. We train the parameters θ_G by minimising an enhancement-specific loss function L, with the aim of making I_E as close as possible to I_FA.

2.1. Network architecture

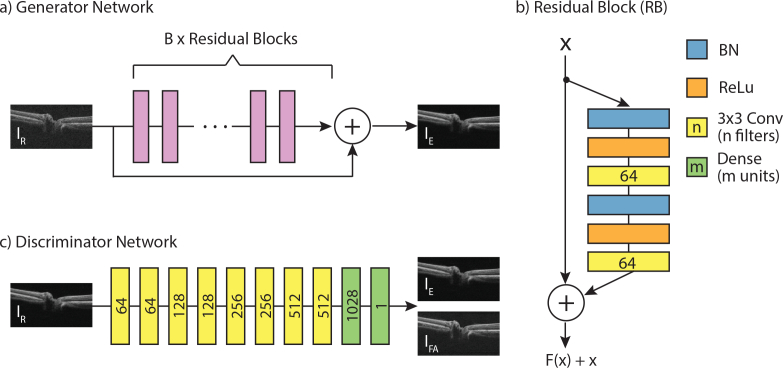
The overall view of the proposed network G_θG is shown in Fig. 1(a). We employ a residual network architecture [23], which is modular in style with multiple connecting blocks of identical structure (shown in Fig. 1(b)). The residual blocks employ pre-activation with batch normalisation (BN) and rectified linear units (ReLU), which improves training and generalisation of the network [23]. Pre-activation precedes two convolutional layers with small 3 × 3 kernels and 64 feature maps. The blocks include a skip link, which combines the signals pre- and post-processing through addition. This helps information to flow through the network, and improves gradient flow during back-propagation. Another skip connection combines the signal prior to the residual blocks with that after processing through addition. This is followed by another pre-activation and convolutional layer, and a final convolutional layer with feature depth of one. The output of this final layer is I_E.

Fig. 1.

Illustration of the proposed networks. The input (I_R) to the generator network (a) is a raw B-scan from the OCT scanner, which undergoes processing by B residual blocks (b) to produce an enhanced image (I_E). The numbers of filters for the convolutional layers, and the number of units for the dense layers, are indicated by numbers on the blocks. The discriminator network (c, described in 2.3) aims to estimate the Wasserstein metric between real (I_FA) and generated (I_E) data distributions.

We train two versions of the generator network G_θG. The first version is trained via a mean-squared error loss, and is referred to as CNN-MSE. The MSE loss favours high peak signal to noise ratio (PSNR), which is a widely-used metric for quantitatively evaluating the quality of OCT images. However, convolutional neural networks trained solely with MSE loss often display overly smooth textures, and lack high-frequency features. Considering the importance of clear layer boundaries in OCT B-scan analysis, this approach alone may not be optimal. Therefore, we trained a second version, referred to as CNN-WGAN, with the aim of creating images which are perceptually indistinguishable from I_FA by formulating the problem in terms of a Wasserstein generative adversarial network (WGAN) [24], and utilising a perceptual loss in addition to the MSE loss. In the next section, we will describe the implementation of these methods.

2.2. Perceptual loss

The perceptual loss is based on high-level features extracted from a pre-trained network [25]. This ensures that the network is trained to replicate image similarities more robustly compared to using per-pixel losses. The perceptual loss is defined as the Euclidean distance between the feature representations of the enhanced image (G_θG (I_R)) and the frame-averaged reference image (I_FA) given by a pre-trained VGG19 network [26].

$$L_{\mathit{VGG}/i.j}=\frac{1}{W_{i,j}{H}_{i,j}}\sum _{x=1}^{W_{i,j}}\sum _{y=1}^{H_{i,j}}{\left({\varphi }_{i,j}{(I_{FA})}_{x,y}-{\varphi }_{i,j}{\left(G_{{\theta }_G}(I_R)\right)}_{x,y}\right)}^2$$ (2)

where, ϕ_i,j indicates the feature map obtained by the j-th convolution, after ReLU activation, prior to the i-th pooling layer, and W_i,j and H_i,j describe the dimensions of the respective feature maps within the VGG network.

2.3. Adversarial loss

Along with the generator network, a generative adversarial network (GAN) involves a discriminator network, D_θD, parametrised by θ_D (shown in Fig. 1). The generator network is trained to produce realistic images, while the discriminator network is trained to identify which images are real versus those that are generated. Here, we implement a WGAN, an improved version of the original GAN, which uses the Earth Mover’s distance [27] to compare two data distributions (that of I_FA and I_E). We optimise both networks in an alternating manner (fixing one and updating the other) to solve the following min-max problem:

$$\begin{array}{ll}\underset{{\theta }_G}{\text{min}}\underset{{\theta }_D}{\text{max}}{L}_{\text{WGAN}}(D,G)=\hfill & -{𝔼}_{I_{FA}}[D(I_{FA})]+{𝔼}_{I_R}[D(G(I_R))]\hfill \\ \hfill & +\lambda {𝔼}_{\widehat{I_{FA}}}[{({\Vert {\mathrm{\Delta }}_{\widehat{I_{FA}}}D(\widehat{I_{FA}})\Vert }_2-1)}^2],\hfill \end{array}$$ (3)

where, the first two terms represent the estimation of the Wasserstein distance, and the final term performs a gradient penalty to enforce the Lipschitz constraint, with penalty coefficient λ. $\widehat{I_E}$ is uniformly sampled along pairs of I_E and I_FA samples. This results in improved stability during training. Additionally, we impose gradient penalty [28], which has been shown to improve convergence of the WGAN compared to gradient clipping. With this approach, our generator can learn to create solutions that are highly similar to real images and thus difficult to classify by D.

Thus, the overall loss of the CNN-WGAN architecture is given by:

$$\underset{{\theta }_G}{\text{min}}\underset{{\theta }_D}{\text{max}}{\lambda }_1{L}_{\text{WGAN}}(D,G)+{\lambda }_2{L}_{VGG}(G)+L_{MSE}(G),$$ (4)

where λ₁ and λ₂ are weighting parameters to control the trade-off between the three components of the loss.

3. Experiments

3.1. Data acquisition and pre-processing

Six OCT volumes were acquired from both eyes of 38 healthy patients on a Cirrus HD-OCT Scanner (Zeiss, Dublin, CA) at a single visit. The scans were centred on the optic nerve head (ONH) and were 200 × 200 ×1024 voxel per cube, acquired from a region 6mm × 6mm × 2mm. These scans were then registered and averaged to create the “ground truth” denoised image. The scan with the highest signal strength (as provided by the scanner software) was chosen as the reference image, and the remaining five volumes were registered to it in two steps. First, a 2-D Elastix registration [29] of the en-face images addressed rotation and translation differences between the consecutive scans (x–y axis registration). Next, individual A-scans from the reference and moving scans were cross-correlated to find the translation that best aligned the scans (Z-axis registration). The resulting volumes were averaged to remove noise. This process produced 76 “denoised” OCT volumes, however 7 volumes were not used for further training or analysis due to inaccurate registration as recognized upon visual inspection, resulting in a cohort of 69 volumes from healthy eyes.

A second set of scans were also acquired from a single eye of 6 glaucoma patients using the same protocol i.e. six ONH-centred scans were acquired on the same visit. The denoised ground truth was generated as described above. Note, however, that this set was not used in the training procedure and was only used to evaluate the method.

3.1.1. Training details

The 69 OCT volumes were split into a training, validation and testing subsets, containing 51, 7 and 11 volumes, respectively. In this way, B-scans from volumes in the hold-out test set were never seen during training. B-scans within 10 voxels of the edge of the volume were not considered during training, since they often contained artefacts from the registration process. Therefore, each denoised volume had 6 corresponding raw volumes, with 180 B-scans, resulting in 55080 B-scan pairs. Patches of size 176 × 176 were extracted from these scans for training, and augmentation was performed by randomising the position of the patch (ensuring that each patch showed a portion of retina), and randomly flipping each patch horizontally. Pairs of patches underwent normalisation prior to training, as such:

$$\tilde{I}=\frac{I-{\mu }_T}{{\sigma }_T},$$ (5)

where I and Ĩ are the original and the normalised B-scans respectively, and μ_T and σ_T are the mean and standard deviation of the training set. This transformation was also applied to validation and hold-out set images. In our experiments, both networks were optimized using Adam algorithm [30], the hyper parameters of which were empirically set as α = e − 5, β₁ = 0.5, β₂ = 0.9. Mini-batch size was 4. The penalty coefficient was set as λ = 10 as suggested in [28], and the loss weighting parameters were empirically set as λ₁ = 1e − 3 and λ₂ = 2e − 6. Training was performed in Tensorflow (https://www.tensorflow.org/) on a NextScale nx360 m4 server with 64 GB of RAM, 800GB SSD, and an NVIDIA Tesla K40 Graphics Processing Unit (GPU) with NVIDIA cuda (v9.0) and cu-dnn (v7.0.5) libraries (http://www.nvidia.com). Training was monitored, and stopped when no further improvement was observed. Training of CNN-MSE and CNN-WGAN took approximately 5 hours and 22 hours respectively. Testing was performed on 1980 B-scans (11 volumes × 180 slices). While the network was trained on patches of images, the fully-convolutional architecture of the network means that images of arbitrary size may be used during testing, therefore entire B-scans where enhanced. Prior to further analytics, the enhanced images were scaled back to their original distribution by:

$$I=\left(\tilde{I}\times {\sigma }_T\right)+{\mu }_T.$$ (6)

3.1.2. Quantitative metrics

We compare the performance of CNN-MSE and CNN-WGAN to two well-known image enhancement techniques: block-matching 3D (BM3D) algorithm [31], implemented using the pyBM3D wrapper in Python, and double-density dual-tree complex wavelet transform (DD-CDWT) [32] (which has shown more recent, promising results on OCT data [33]), implemented using MATLAB (http://eeweb.poly.edu/iselesni/WaveletSoftware/dt2D.html). To fairly compare the speed of the different methods, all were implemented on a MacBook Pro with 2.9 GHz Intel Core i5, 8GB 1867 MHz DDR3. Performance was gauged using standard error metrics such as PSNR, structural similarity index (SSIM), multi-scale structural similarity index (MS-SSIM) metrics, and MSE. SSIM was calculated for pixels considered to be part of the retina. These metrics were computed on a hold-out set of data from the healthy cohort and the entire glaucoma cohort. Statistical significance was determined using paired two-sided Wilcoxon signed-rank tests [34] at p < 0.05.

Additionally, the impact of the proposed enhancement techniques on the visibility of structures of interest was gauged by having multiple independent experts manually annotate five surfaces: the internal limiting membrane (ILM), the posterior border of the retinal nerve fibre layer (RNFL), the ganglion cell and inner plexiform layer (GCIPL), the inner nuclear layer (INL) and Bruch’s membrane (BM) shown in Fig. 4(a). Manual annotations were obtained on 22 slices from the original volumes (2 from each volume of the test set), plus the same images enhanced by CNN-MSE and CNN-WGAN. Half of the slices were chosen from a central section of the volume (containing the cross-section of the ONH), while the other half were chosen at random from a peripheral section (lacking the ONH). The optic nerve head itself was omitted from the annotations. The slices were also repeated in the set and shuffled before being presented to the annotators.

Fig. 4.

a) Portion of a B-scan with surface annotations for five layers. Intra-observer (b) and inter-observer (c) annotation location difference (AAD), averaged over the columns of all annotated B-scans for ILM and GCIPL surfaces (mean ± standard error). Statistical significance at p < 0.001 indicated by *. Results for the remaining layers are shown in Figure 6.

With the assumption that retinal surfaces would be easier to identify with a higher degree of repeatability in clearer images, unsigned variability in the location of the surface location between observers (inter-observer), and for the same observer between multiple repeated scans (intra-observer), titled Average Annotation Difference (AAD) was calculated as follows:

$$\mathit{AAD}=\frac{1}{N\times A}\sum _{n=1}^N\sum _{a=1}^A\left|l_1^{n,a}-l_2^{n,a}\right|$$ (7)

Where l represents the surface location on the a^th column (or A-scan) of the n^th B-scan. The subscript on l indicates the first versus second observer (for inter-observer), or first versus second repeat of the annotation (for intra-observer). A three-way ANOVA was used to compare the effect of the annotator (or annotator pair, for inter-observer AAD), the enhancement technique, and the surface annotated on intra- and inter-observer variability. Statistical significance was then determined using a Tukey-Kramer post-hoc analysis.

3.1.3. Qualitative metrics

We performed a mean opinion score test to quantify the ability of different approaches to reconstruct perceptually convincing images. Given six different representations of a B-scan - unprocessed (“Raw”), enhanced using CNN-WGAN,CNN-MSE, BM3D and DD-CDWT, and frame averaged, three experts were asked to rank the images from best to worst on three metrics:

• 1.Ability to discriminate structures (e.g. retinal layers, blood vessels) (1 = most clear, 6 = least clear)
• 2.Accuracy with which the image represents what you might see at a cellular/microscopic level (1 = most accurate, 6 = least accurate)
• 3.Personal preference for use in clinical practice (1 = most preferred, 6 = least preferred)

The metrics were specifically chosen to understand the differences in perceived clarity (metric 1), accuracy (metric 2), and personal preference (metric 3) between various versions of the same scan. Each observer was simultaneously shown all 6 versions of each of 55 B-scans (5 from each of the 11 test set volumes), in a randomized order, and asked to rank each of the three metrics in turn. Inter-observer agreement was calculated using Cohen’s Kappa Score [35], and statistical significance between observers in their preference for CNN-MSE versus CNN-WGAN was calculated using a Binomial Test (with Bonferroni correction for multiple comparisons).

4. Results

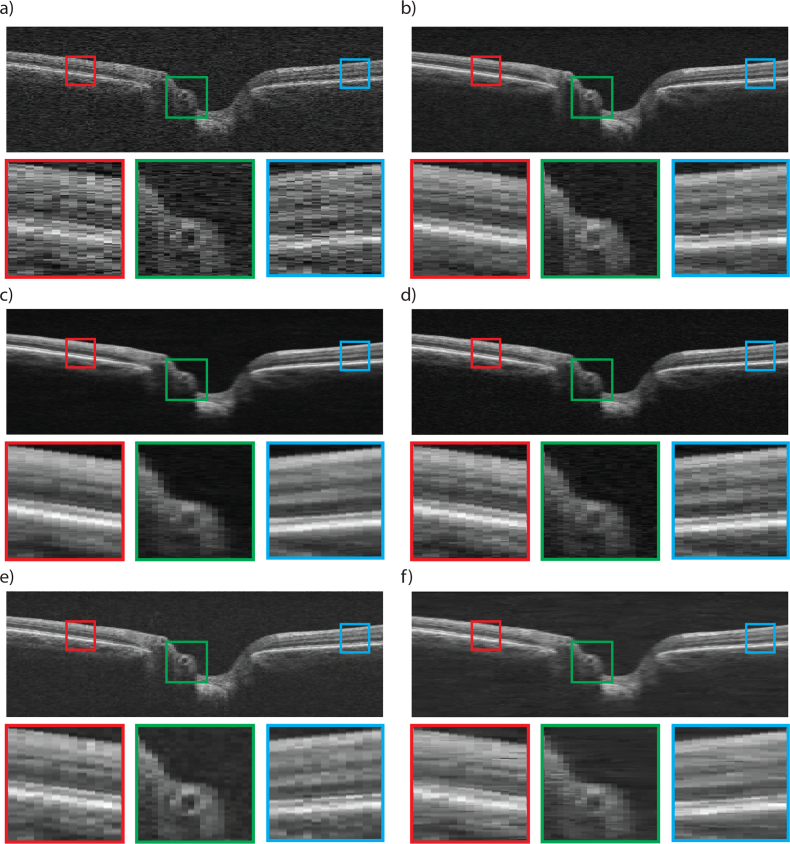
To show the denoising effect of the proposed networks, a representative B-scan from the optic nerve head of a healthy person within the test set is shown in Fig. 2, as it appears in the raw image (a), ground truth achieved through averaging (b), post-processing of the raw scan with CNN-MSE (c), CNN-WGAN (d), BM3D (e), and DD-CDWT (f). The B-scans consisted of 200 A-Scans, each with 1024 pixels. While the scans were kept at this aspect ratio during processing, for display purposes they were resized for better visualisation.

Fig. 2.

OCT Image from a healthy volume captured by Cirrus HD-OCT Scanner (a), and corresponding 6-frame averaged image (b). The result of post-processing of (a) with CNN-MSE (c), CNN-WGAN (d), BM3D (e), and DD-CDWT (f). Three zoomed in, colour coded sections are shown below each B-scan (best viewed in colour).

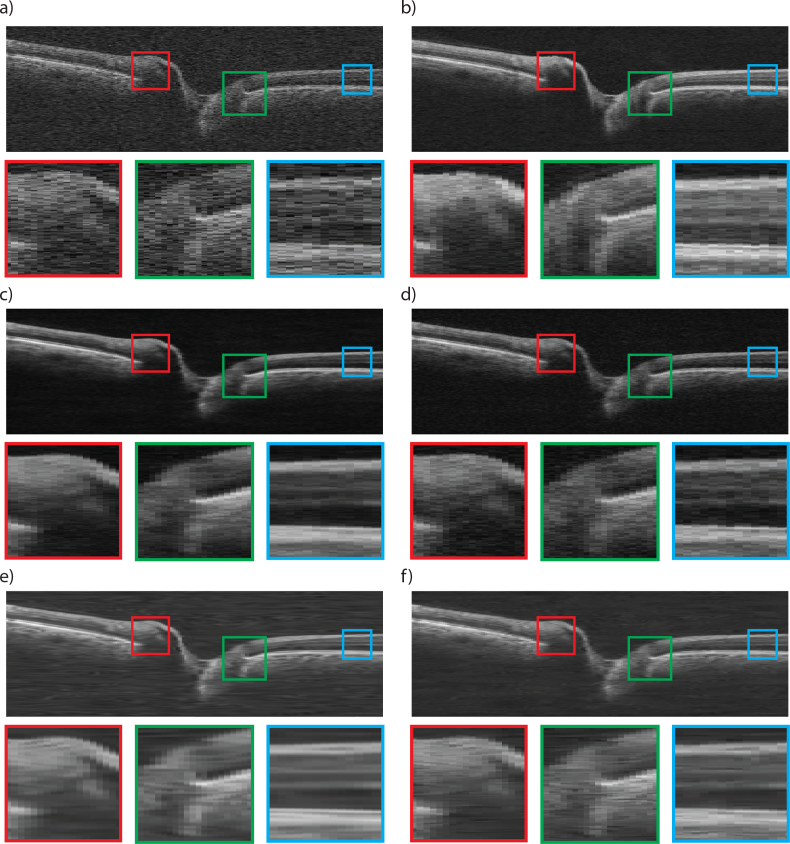
As can be observed, the BM3D method (e) does not over-smooth the image, but still shows some residual noise, and has poor contrast. In comparison, DD-CDWT (f) introduces over smoothing, resulting in loss of layer boundary distinction (particularly evident in the red and blue insets). The images produced by CNN-MSE (c) also show signs of smoothing in that it attains homogeneity within each layer, but does not lose layer separation (as is the case for DD-CDWT), and layers can still be clearly distinguished. CNN-WGAN (d) produces images most similar perceptually to the frame-averaged scans (b), in that it maintains layer texture and boundary clarity without introducing artefacts. Fig. 3 shows a representative scan from a glaucomatous volume. Even though no glaucomatous scans were used during network training, both CNN enhancement methods produce enhanced images with a high degree of accuracy for structural detail. In particular, the border tissue/Bruch’s membrane configuration (green box), which is an important indicator of disc margin in glaucomatous volumes [36] is best preserved in the CNN-WGAN enhancement. Additionally, the two CNN methods do not blur the edges between layers (blue box), as does DD-CDWT. BM3D performs well in the horizontally flat region of the retina indicated by the blue box, but is outperformed by the CNN methods in the other two highlighted regions.

Fig. 3.

OCT Image from a glaucomatous volume captured by Cirrus HD-OCT Scanner (a), and corresponding 6-frame averaged image (b). The result of post-processing of (a) with CNN-MSE (c), CNN-WGAN (d), BM3D (e), and DD-CDWT (f). Three zoomed in, colour coded sections are shown below each B-scan (best viewed in colour).

The average times required to process a B-scan by each method are shown in Table 1. The times reported are averaged over 200 B-scans, with the proposed methods (CNN-MSE and CNN-WGAN) processing all 200 simultaneously.

Table 1.

Time required to process a single B-scan, averaged over 200 B-scans.

Method	Time (seconds)
BM3D	7.84
DD-CDWT	0.72
CNN-WGAN	0.68
CNN-MSE	0.68

The results show that the proposed solutions out-perform existing methods in terms of speed of use. Additionally, the networks are highly parallelizable, and therefore lend themselves to further speed increases on more powerful systems, particularly those with access to a GPU.

4.1. Quantitative results

For quantitative results, we calculated the PSNR, SSIM, MS-SSIM and MSE between six different image types (Raw, BM3D, DD-CDWT, CNN-WGAN and CNN-MSE) and their corresponding frame-averaged scan. The summary data are shown in Table 2. The best performing technique in each metric is shown in bold.

Table 2.

Mean ± standard deviation of the peak signal to noise ratio(PSNR), structural similarity ratio (SSIM), multi-scale structural similarity ratio (MS-SSIM) and mean squared error (MSE) for 1980 healthy B-scans and 1080 B-scans from patients with glaucoma, using the BM3D, DD-CDWT, and the proposed CNN-WGAN and CNN-MSE networks. The best results are shown in bold. All pairwise comparisons (excluding SSIM on glaucoma images processed by BM3D and DD-CDWT) were statistically significant (p < 0.0001).

Healthy	PSNR	SSIM	MS-SSIM	MSE
Raw	26.82±0.67	0.62±0.04	0.79±0.02	136.67±22.43
BM3D	31.17±1.27	0.74±0.04	0.88±0.02	51.53±17.29
DD-CDWT	31.21±1.19	0.75±0.04	0.89±0.02	51.22±15.92
CNN-WGAN	31.83±1.21	0.77±0.03	0.92±0.01	44.52±14.34
CNN-MSE	32.28±1.27	0.78±0.03	0.92±0.01	40.28±13.44

Glaucoma	PSNR	SSIM	MS-SSIM	MSE
Raw	25.46±0.67	0.58±0.04	0.76±0.02	188.32±52.53
BM3D	29.12±1.12	0.74±0.03	0.88±0.03	83.34±44.76
DD-CDWT	29.44±1.18	0.74±0.03	0.89±0.03	77.84±46.15
CNN-WGAN	29.92±1.27	0.76±0.03	0.91±0.02	72.85±46.07
CNN-MSE	30.21±1.12	0.78±0.03	0.92±0.03	70.04±44.91

We observe that the CNN-MSE network delivers the best results on all metrics, with all pairwise comparisons showing statistical significance (p < 0.0001) (excluding the comparison between SSIM on glaucoma images processed by BM3D and DD-CDWT, for which p > 0.05). The CNN-MSE network is also able to greatly improve the quality of glaucomatous volumes, despite having been trained using only healthy volumes. Since visual inspection and quantitative comparison of the enhancement techniques showed that the CNN-based methods were superior to both BM3D and DD-CDWT, these were excluded from further analyses.

While these results show that CNN-MSE is objectively better in terms of image metrics, it has previously been posited that such a network might overly blur images, which in this application might result in reduced layer boundary visibility. Therefore, we define a quantitative assessment based on the effect upon the end user. We asked three experts to annotate five surfaces (ILM, RNFL, GCIPL, INL and BM) in raw images, and those having undergone enhancement with CNN-MSE and CNN-WGAN. Fig. 4(a) shows a section of B-scan, processed by CNN-WGAN, with layer annotations indicated. Each observer annotated each image twice, and the average difference in location of annotations (AAD, defined in Equation 7), both between observers (inter-observer), and for the one observer between repeated scans (intra-observer) was calculated. The intra- and inter-observer AAD for two of the surfaces are shown in Figs. 4(b) and (c).

The results of intra-observer analysis show that compared to raw images, both networks significantly improved the repeatability of layer annotations for all three annotators (p < 0.001, this and all further comparisons in this section were determined via a three-way AVONA with Tukey-Kramer post-hoc analysis). Additionally, this also occurred for all surfaces when controlling for grader (all p < 0.001). Differences between the AAD metric were more pronounced for surfaces that were more difficult to label, as shown in Fig. 4(b) by the difference in AAD between ILM and GCIPL. Controlling for grader, CNN-MSE resulted in significantly smaller AAD values for both GCIPL and BM (both p < 0.001), though there was no significant difference for the other surfaces. Controlling for surface type, AAD for graders 1 and 2 with CNN-MSE was significantly less than that for CNN-WGAN (both p < 0.001), however there was no significant difference for grader 3 (p = 0.850). Overall, grader 3 was more consistent, with significantly smaller AAD for raw images than that for both graders 2 and 3 (both p < 0.001), this was also true for CNN-WGAN images (both p < 0.001).

Results were similar when comparing annotations between graders (Fig. 4(c)). Again, CNN-MSE and CNN-WGAN both resulted in lower AAD than raw (both p < 0.001) for all graders, and this was true for all surfaces when controlling for grader (all p < 0.001). Controlling for surface type, AAD for CNN-MSE was significantly less for two grader pairs (p = 0.003 for 1 vs 2, and p = 0.023 for 1 vs 3), though not significant for the third (p = 0.860). Controlling for grader pairs, CNN-MSE produced significantly improved AAD for RNFL and BM compared to CNN-WGAN (p = 0.030 and p < 0.001, respectively).

Overall, the results show that both enhancement methods drastically improve the reliability and repeatability of manual surface annotations, and that for more difficult surfaces, CNN-MSE sometimes outperforms CNN-WGAN.

4.2. Qualitative results

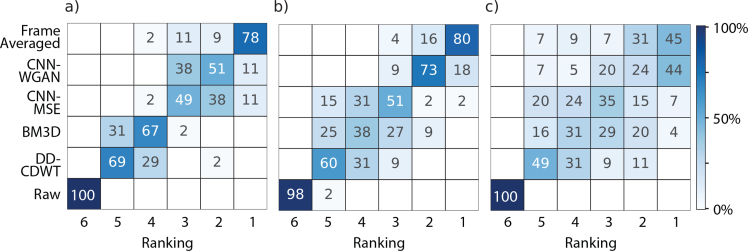
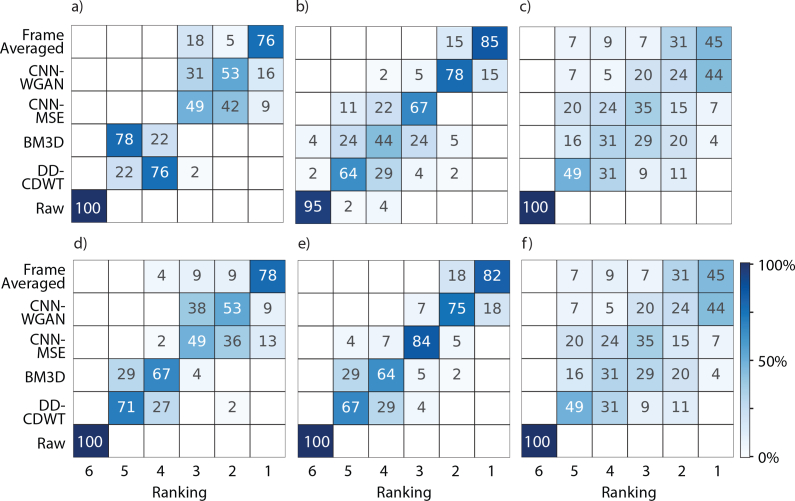
As well as clarifying layer boundary locations, another potential utility for our OCT image enhancement technique is quality improvement for visual inspection of complex anatomic pathologic structures. Therefore, here, we demonstrate the capabilities of the current techniques to improve the perceptual quality of provided images. To sufficiently investigate the qualitative differences between the images we asked three observers to rank the six different versions in three metrics, representative of clarity, accuracy and personal preference (listed in full in section 3.1.3). Observers were shown six versions of the same image: the frame-averaged image, the result of enhancement by CNN-MSE, CNN-WGAN, BM3D and DD-CDWT, and the raw version, which was the input to the four enhancement techniques. The results for clarity are shown in Fig. 5. For the respective results for accuracy and personal preference, see Figure 7 in the Appendix.

Fig. 5.

Qualitative results for perceived clarity for 55 B-scans ranked by observer 1 (a), observer 2 (b) and observer 3 (c) for images acquired by 6-frame averaging (“Ground Truth”), CNN-WGAN, CNN-MSE, BM3D, DD-CDWT and the respective un-processed images (“Raw”). Colour indicates the percentage of images, for the respective image type, in each rank position (where 1=highest rank, 6=lowest rank). Results for accuracy and personal preference are shown in Figure 7.

All three graders ranked the ground truth version the highest in terms of clarity for the majority of images. This is not surprising, given that the frame averaged version represents the ideal scenario, and is what both CNN approaches were trained to reproduce. Impressively, the enhanced scans produced by the two CNN approaches were sometimes ranked higher, with grader 3 rating 44% of the CNN-WGAN scans most clear, almost equal to the percentage of frame-averaged images rated highest (45%). To determine whether different graders shared enhancement preferences for particular images, the inter-observer agreement was measured using Cohen’s Kappa Score (Table 3). A kappa score below 0.2 indicates no agreement, while between 0.21 − 0.39 is considered a minimal level of agreement, and 0.40 − 0.59 indicates weak agreement [35].

Table 3.

Inter-observer agreement as measured by Cohen’s kappa score between the three experts (labelled 1–3) for each of the qualitative metrics.

	1 v 2	1 v 3	2 v 3
Clarity	0.429	0.188	0.250
Accuracy	0.432	0.158	0.174
Preference	0.479	0.191	0.182

These kappa scores reflect weak agreement between graders 1 and 2, and minimal to no agreement between 3 and the others. This is likely due to the inclusion of two enhancement methods (CNN-MSE and CNN-WGAN) that provide similar outcomes, causing the graders to split their preference between the two. A similar effect occurs between BM3D and DD-CDWT, though they are collectively rated lower by all graders. The very low kappa scores for comparisons between grader 3 and the other graders reflects the larger variability grader 3 showed in ratings for all three questions, particularly for CNN-MSE, BM3D and DD-CDWT. While graders 1 and 2 were clear in their prederence for the CNN-based methods. To determine whether graders ranked CNN-MSE or CNN-WGAN higher, the number of times that each was ranked above the other was tallied, and the difference from chance calculated with a binomial test (at a Bonferroni-corrected significance level of p = 0.0056). This showed that all three graders ranked CNN-WGAN images significantly higher than CNN-MSE in all three metrics, however this was only significant for graders 2 and 3 (p < 0.001 for all comparisons).

5. Discussion and future work

In this paper, we demonstrated a novel approach for denoising OCT images using deep learning. We proposed two networks, identical in structure but trained with different objective functions, to remove speckle noise from B-scans. The first network, CNN-MSE, was trained solely to minimise the mean-squared error between the image it produced and one obtained with 6-frame averaging. The second network, CNN-WGAN, was trained using a combination of mean-squared error, perceptual loss, and an adversarial loss. The perceptual loss utilized features representing patterns at multiple pixel scales extracted from a pre-trained network, and therefore is ideal for encouraging edge and texture preservation. The adversarial loss served to push our proposed solution to the natural image manifold using a discriminator network that is trained to differentiate between the enhanced images and image obtained through frame averaging. In contrast to statistical denoising methods, by training the network using averaged images we make no assumptions as to the noise distribution, or presence of artefacts in the images.

Our results show that CNN-MSE quantitatively improves images better than compared methods. Specifically, CNN-MSE showed the highest metrics for PSNR, SSIM, MS-SSIM, and MSE, which were significantly better than the other methods; this was closely followed by CNN-WGAN. Additionally, both CNN-MSE and CNN-WGAN resulted in improved layer annotation by three independent observers, with CNN-MSE showing slightly better results for particularly difficult surfaces. An automated segmentation method using Iowa Reference Algorithms (Retinal Image Analysis Lab, Iowa Institute for Biomedical Imaging, Iowa City, IA [37,38]) was also tested (not shown), but did not provide satisfactory segmentations for any of the enhanced B-scans or for the frame-averaged B-scans. This is likely due to the inclusion of a variety of denoising steps in the method’s pipeline, which merely result in blurring of the layer bourdaries. This will likely be the same in other machine-learning based approaches [39–42] since these techniques also incorporate denoising as well as multi-scale features such as Guassian and Gabor filters.

However, these quantitative improvements were not reflected in the qualitative analysis. This analysis showed that all three graders thought that CNN-WGAN images represented better the details at a microscopic level, and showed structures more clearly than CNN-MSE. This contradiction between the most successful enhancement for quantitative versus qualitative analysis suggests that there exists a dichotomy between the ideal image for the purpose of further analysis, and that for visual inspection. However, given the efficiency of the proposed methods, it is realistic that both methods of enhancement could be used by clinicians for different tasks, based on personal preference.

Since our ground truth images were obtained by averaging only 6 repeated images, they still contained an element of noise (as is evident by observing the background of the images). As such, it is possible that much of the texture that was encouraged by the CNN-WGAN network in its generated images was due to noise. Furthermore, if images without noise had been available, the CNN-WGAN network would likely produce images without noise, but still with accurate textural detail (which the MSE network tends to blur slightly). Without access to ground truth images that have been completely denoised, it is not possible to assess whether this is the case. However, this would be of interest to investigate in the future, possibly by averaging more images. Interestingly, the hint of noise that is shown in the CNN-WGAN likely contributed to these images being ranked most highly in the qualitative assessment, since overly smoothed images (such as those produced by the CNN-MSE network) may suggest that important details have been blurred, thereby reducing confidence in the image.

The frame averaged scans were ranked higher more often by the observers for all metrics, however such an approach requires multiple volumes to be acquired at each visit, followed by registration and frame-averaging. While some devices provide real-time averaging to reduce speckle, this still requires the eye to be kept open and fixated on a target for a longer time, which can be difficult, particularly for elderly patients. Additionally, such systems cannot be used on previously recorded data where multiple scans have not been acquired. Our proposed solution has the advantage of providing a very close approximation of a frame-averaged image, but operates using only a single input image. Therefore, the enhancement can be applied to any existing scans. While training of the network is computationally demanding and can take a long time, particularly for CNN-WGAN, which requires several updates to the discriminator for each generator update, the trained model operates quickly and effectively using only the resources provided by a laptop computer. Additionally, we’ve shown that both CNN methods can generalise to OCT volumes with pathologies that were not part of the training set (as shown by their success at enhancing glaucomatous volumes). It would be of interest in the future to train the network with images containing pathologies, including more dramatic structural pathologies (such as those associated with AMD), since it is likely that this would further improve the performance for unhealthy B-scan enhancement.

6. Conclusion

The proposed deep learning-based enhancement method provides significant improvements in image quality metrics for OCT B-scans, while preserving structural features of the retinal layers. Furthermore, we have shown that by training the same deep neural network in two different ways, perceptually distinct results can be achieved, that may be used interchangeably dependent on the task and personal preference. Despite being trained using only healthy OCT volumes, the two CNN’s presented herein were able to generalise to glaucomatous scans. The fact that such drastic enhancement can be achieved in a short time using only a single scan as input is a testament to effectiveness of deep learning as a viable solution in the clinical setting.

Appendix

Fig. 6.

Intra-observer (a) and inter-observer (b) annotation location difference (AAD), averaged over the columns of all annotated B-scans for BM, INL and RNFL surfaces (mean ± standard error). Statistical significance at p < 0.001 indicated by *.

Fig. 7.

Qualitative results for perceived accuracy (a–c) and personal preference (d–f) for 55 B-scans ranked by observer 1 (a, d), observer 2 (b, e) and observer 3 (c, f) for images acquired by 6-frame averaging (“Ground Truth”), CNN-WGAN, CNN-MSE, BM3D, DD-CDWT and the respective un-processed images (“Raw”). Colour indicates the percentage of images, for the respective image type, in each rank position (where 1=highest rank, 6=lowest rank).

Disclosures

KJH, BJA, MHL, and RG: IBM Research Australia (E).