Differential detection of retinal directionality

Abstract

An adaptive optics fundus camera has been developed that uses simultaneous capture of multiple images via adjacent pupil sectors to provide directional sensitivity. In the chosen realization, a shallow refractive pyramid prism is used to subdivide backscattered light from the retina into four solid angles. Parafoveal fundus images have been captured for the eyes of three healthy subjects and directional scattering has been determined using horizontal and vertical differentials. The results for the photoreceptor cones, blood vessels, and the optic disc are discussed. In the case of cones, the observations are compared with numerical simulations based on a simplistic light-scattering model. Ultimately, the method may have diagnostic potential for diseases that perturb the microscopic structure of the retina.

1. Introduction

Vision is sensitive to the angle of incidence of light on the retina as evidenced by the psychophysical Stiles-Crawford effect of the first kind (SCE-I) [1–5]. Likewise, light which is backscattered by the retina is nonuniform in the pupil in what is commonly referred to as the optical Stiles-Crawford effect (OSCE) [6–12]. For vision, only light in the outer photoreceptor segments matter, whereas for imaging scattering from refractive index inhomogeneities at any location within the eye may contribute to images (albeit confocal detection and/or optical coherence tomography can significantly enhance the depth selectivity). Whereas the SCE-I relies on subjective and time-consuming measurements, the OSCE allows for fast and objective determination of photoreceptor directionality. Thus, exploring the relationship between the SCE-I and the OSCE has diagnostic potential [3,12].

The causes of scattering within photoreceptors remain a topic of debate with likely contributions from inner/outer segment junctions and outer segment terminations [13–16]. One such contribution is the refractive index contrast between densely packed high-index mitochondria organelles and the surrounding cellular matrix in the ellipsoid [17] but also gaps, or lack of membrane invaginations (defects), have been suggested to cause reflections [18]. Backscattered light from the photoreceptors may be guided [2,3] or directional due to the spatial arrangement of the dominant scattering sources and the local variation in refractive index [4]. The OSCE distribution peaks approximately at the same position as the SCE-I in healthy eyes which suggests that cones point predominantly toward a common point [19]. Objective methods to analyze photoreceptor pointing include OSCE pupil imaging [8–11], high-resolution adaptive optics (AO) retinal imaging with fundus cameras using multiple pupil entrance points [20–22] or axial sweeping [23], scanning laser ophthalmoscopy (SLO) [24,25] and optical coherence tomography (OCT) [22,26,27]. The methods allow determination of an effective directionality parameter for light scattering that is similar, though not identical, to the directionality found by psychophysical means [2,4,10].

Annular beams have been used in AO-SLO to reduce the size of the scanning spot [28] and offset-pinhole methodology has facilitated imaging of weakly scattering structures by enhancing the contrast of photoreceptors, ganglion cells, and blood flow [29–32]. Here, we report on a new directional sensitive method that uses a structured pupil in the detection path. This approach differs from the offset-pinhole method by operating in the pupil rather than the image plane. In this way it directly probes the angular distribution of the backscattered imaging light rather than multiply-scattered (indirect imaging) light. Earlier OSCE studies have altered the direction of the incident light by altering the pupil entrance point while capturing individual images of backscattered light in the pupil or retinal image plane [20–22]. Here the light enters near the pupil center (which matters most for vision) and directionality is determined using intensity gradients from simultaneously captured images at different back-scattering angles.

Different structured pupils can be envisioned. In this first realization, we have chosen to use a shallow refractive pyramid prism to subdivide backscattered light from the retina into four adjacent quadrants resulting in four simultaneous retinal images. Pyramid prisms have previously been used to capture multiple images for wavefront sensing in AO [33–35] and to acquire depth information in microscopy [36]. Differential images can provide information about tilt of the scattering sources in a similar way to the quadrant detection used for sensing of cantilever deformations in atomic force microscopy [37]. Here, inclinations of retinal structures are determined using differential imaging to determine effective pointing directions in the horizontal and vertical directions, respectively.

The paper is organized as follows: Section 2 describes the experimental setup and realization. The theoretical model and simulation results are presented in Section 3. Section 4 shows the experimental findings that are discussed in more detail in Section 5. Finally, Section 6 contains the conclusions.

2. Experimental setup and realization

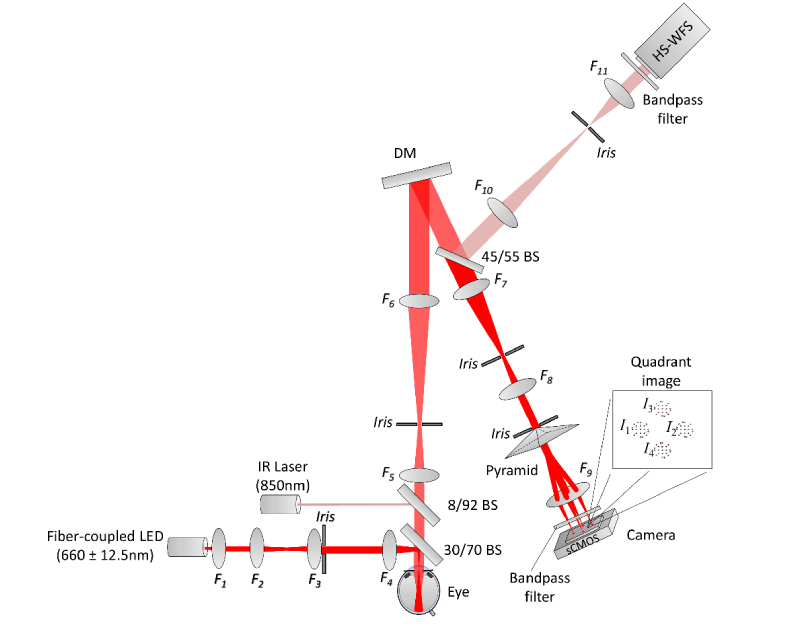
The quadrant pupil has been implemented in an AO fundus camera as shown in Fig. 1. The imaging channel uses a fiber-coupled LED at 660 nm wavelength with 25 nm bandwidth (Thorlabs) for flood illumination of a 2° retinal illumination patch in Maxwellian view.

Fig. 1.

Schematic layout of the flood-illumination fundus camera equipped with the refractive pyramid for quadrant detection of retinal directionality and AO wavefront correction of the eye and system. All lenses are AR-coated achromatic doublets (F₁ to F₁₁) and irises are used to set the beam width and screen against unwanted reflections in the optical path.

Light which is backscattered by the retina is projected from the eye pupil via two 4f telescopes onto the glass pyramid (Eksma) with 170° apex angle mounted in a conjugated plane. Refractive errors induced by the pyramid prism are small due to its large apex angle. It could potentially also operate in reflection (if metal coated) which would eliminate chromatic and refractive errors. The resulting four images are captured simultaneously with a scientific CMOS camera (Neo 5.5 sCMOS Andor) at 33 frames-per-second (fps) with 11-bit resolution. This camera has 6.5 µm pixel size on a 16.6 mm × 14.0 mm sensor and quantum efficiency ∼55% at the imaging wavelength. The image magnification is × 9 from retina to camera (i.e., 775 pixels across the 2° visual degrees). In parallel, a Hartmann-Shack (HS) wavefront sensor (Thorlabs) is used in closed-loop with a deformable mirror (DM) membrane (Mirao-52e Imagine Eyes) and an 850 nm laser diode (Edmund Optics) for real-time aberration correction.

Beam splitters are used to combine and separate the imaging channel from the wavefront sensing. This could potentially be further improved with dichroic mirrors for increased light efficiency. The incident power is 70 µW (imaging channel) and 240 µW (wavefront sensing channel). These values are within the ANSI z136.1 safety standard for continuous light exposure of the eye for both the extended source (imaging) and for the wavefront sensing (focused beam) adding to a total of 37% of the maximum permissible exposure. Bandpass filters are used to block unwanted wavelengths of light from entering the HS-WFS and the sCMOS. The AO system operates continuously throughout the entire imaging session (to keep the root-mean-square wavefront error smaller than ∼0.07 µm) at a variable speed of 33 – 43 Hz and momentarily maintains the DM shape during eye blinks to avoid errors that could otherwise confound the wavefront correction.

Short video sequences (∼3 seconds) were captured for the nasal retina in the right eye of three healthy subjects aged 31-48 years (the authors: SQ, DV, and BV). The study complies with the Declaration of Helsinki for research involving human subjects. AO correction was activated first for all Zernike polynomials up to and including the 5^th radial order for a 6.0 mm pupil to ensure diffraction-limited performance before the video sequence was initiated. The pupil was dilated, and accommodation partially paralyzed, by administrating 2 drops of 1% tropicamide before image acquisition. A distant green spot of light was used for gaze fixation to reduce unwanted eye motion.

3. Differential detection method and numerical scattering model

The four-faceted pyramid is placed in a conjugate pupil plane to provide simultaneous capture of four retinal intensity images ($I_1$,$I_2$,$I_3$,$I_4$) as shown in Fig. 1. When centered, symmetrical backscattering of light through four adjacent pupil sectors produces identical brightness of corresponding structures in all images. Obliqueness in the scattering is revealed by brightness differences between images. Thus, for photoreceptors, this will identify obliqueness with respect to the pyramid apex. For other retinal structures, including blood vessels and the optic disc, it will show preferential scattering directions related to the local topography being imaged.

3.1. Differential detection method

The pointing of individual scattering structures can be determined from the simultaneously-acquired images by calculating a difference vector $\left(\Delta x_{m,n},\Delta y_{m,n}\right)$ at corresponding image pixels $m,n$. The vector components can be written as

$$\Delta x_{m,n}=\frac{I_{2,m,n}-I_{1,m,n}}{I_{2,m,n}+I_{1,m,n}}L;\Delta y_{m,n}=\frac{I_{3,m,n}-I_{4,m,n}}{I_{3,m,n}+I_{4,m,n}}L$$ (1)

where L is a scaling factor that sets the length of all the vectors and the intensity values $I_{\mathrm{1...4},m,n}$ refer to detected brightness of corresponding pixels in the four images. It must be stressed that the value of L can be chosen at will for best visualization of local intensity differences as coordinate vectors. If chosen too short, vectors will appear as dots and if chosen too large vectors will point outside of the image frame. All vectors have components in the range of $-L\le \Delta x_{m,n}\le L$ and $-L\le \Delta y_{m,n}\le L$ where the largest range is found when one pixel equals zero in any of the images.

The implications of Eq. (1) can be appreciated by the vectors in Fig. 2 for a simulated cone mosaic and the intensity differentials used to calculate the obliqueness of each cone. There is no relative tilt of an imaged pixel when both vector components are equal to zero. The absolute tilt is more challenging to determine as it depends on the axial eye length, and the diffraction of light from the retina to the pupil plane. Small structures will backscatter light into a wide angular distribution whereas wide structures will scatter into a smaller angular distribution. This is the approach taken in the numerical model for a schematic eye model (Sec. 3.2).

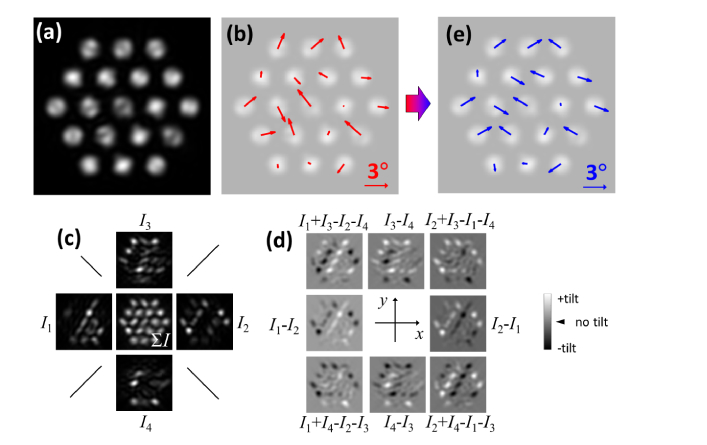
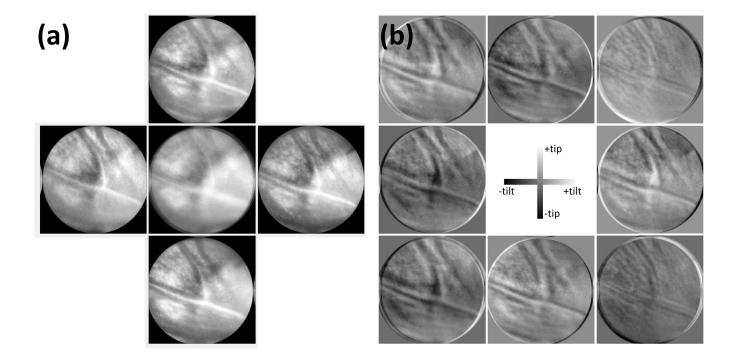
Fig. 2.

Simulated parafoveal cone mosaic imaging and analysis assuming circular reflective scattering layers in the ellipsoid of each photoreceptor. Each reflector is added random tip/tilt with uniform amplitude of up to ± 3°. The resulting intensity image with a full 6.0 mm circular pupil is shown in (a) for a mosaic of 19 cones across a 40 × 40 μm² area. In (b) red arrows show the random tilts of each simulated cone (vectors overlaying the intensity mage). In (c) quadrant retinal images are shown together with the algebraic image sum. In (d) difference images reveal photoreceptor obliqueness mapped onto a grayscale between maximum + 3° (positive, white) and minimum −3° (negative, black) angles. The same grayscale is used both horizontally (tilt) and vertically (tip). Finally, in (e) the reconstructed obliqueness of each simulated cone is shown (blue arrows) as determined from Eq. (1) using only intensity differences at the central pixels of each reflector.

It is of value to introduce a metric, $\sigma$, that can be used locally, and globally, to quantify the relative amount of obliqueness or disarray in captured images. This can be done by averaging over the number of pixels in a square image $N\times N$ as

$$\sigma =\frac{1}{\sqrt{2}{N}^2}{\displaystyle \sum _{n=1}^N{\displaystyle \sum _{m=1}^N\sqrt{{\left(\Delta x_{m,n}/L\right)}^2+{\left(\Delta y_{m,n}/L\right)}^2}}}.$$ (2)

This metric increases when the obliqueness is large and equals zero if there is no obliqueness with respect to the chosen pupil reference point. The normalization with respect to L removes the dependence on the chosen scaling factor used in Eq. (1). Likewise, when only a chosen subset of pixels is used, the obliqueness can be normalized accordingly. This metric falls in the range of $0\le \sigma \le 1$ . Thus, if there is no local obliqueness all corresponding pixels carry equal intensity whereby $\sigma =0$.

Equation (1) and Eq. (2) can be modified to compensate for global tilt by subtracting the average vector $\left(<\Delta x_{m,n}>,<\Delta y_{m,n}>\right)$ from the local values, i.e., $\left(\Delta x_{m,n}-<\Delta x_{m,n}>,\Delta y_{m,n}-<\Delta y_{m,n}>\right)$ and thereby obtain a modified metric $\tilde{\sigma }$ that does not include global tilt. This is the procedure followed for the experimental results shown in Sec. 4. Image normalization of all four retinal images is used before calculation of derivatives. This reduces global obliqueness whereby the two metrics σ and $\tilde{\sigma }$ become almost identical.

It must be stressed that apodization probes the directional light scattering directly by angular resolving the scattered light at the pupil albeit at the cost of spatial resolution. Thus, the method complements but does not replace high-resolution imaging techniques where the unrestricted pupil is used. Pupil apodization differs fundamentally from related techniques, such as the offset-pinhole method used with SLO [29–31], that sample the non-imaging (scattered) light distribution in the image plane at discrete off-axis (and thus non-confocal) points. Pupil apodization targets the directionality of the backscattered imaging light itself. This can also be appreciated from a theoretical description as follows. Differential retinal imaging with pupil apodization using two sectors G_I and G_II that may be quadrants, or adjacent half-pupils, can be expressed as a differential intensity image as

$$I_{differential}={\left|FT\left\{G_I\right\}\ast \overline{O}\right|}^2-{\left|FT\left\{G_{II}\right\}\ast \overline{O}\right|}^2$$ (3)

where $\overline{O}$ is the spatial distribution of light scattered by the retina, FT is the 2-D Fourier transform, and * denotes a convolution. When the scattering is symmetric the differential image determined from Eq. (3) equals zero. Multi-offset and indirect imaging modalities can be used to further enhance the visibility of multiply-scattered light in fundus images [31,32] but without assessing the directionality of the direct imaging light itself as done in the present study and exemplified by Eq. (3).

3.2. Modeled cone mosaic imaged with quadrant pupil detection

A photoreceptor imaging model has been developed to demonstrate the method for a quadrant pupil. An array of parafoveal photoreceptors with 5 μm diameter has been modeled (Matlab) using a circular mirror to represent the dominant scattering layer within each photoreceptor ellipsoid [4,17]. Random variations of scattering microstructures would, on average, be well represented by diffractive micromirrors, which is the approach taken here. A similar approach can be used for more complex scattering domains using dipolar [4] or electromagnetic wave propagation [38,39]. Random tilts of each cone within a uniform distribution of up to ± 3° was assumed. The simulated retinal area represents a 40 × 40 μm² area with 20,000 cones/mm² for a schematic eye with axial length f_eye = 22.2 mm and refractive index n_eye = 1.33. The simulated array of micromirrors was assumed to be illuminated by an axially incident plane wave of light and back-diffracted light, truncated by the eye pupil, has been reimaged using two Fourier transforms. Figure 2(a) shows the resulting intensity images for the cone mosaic with inclinations as shown in Fig. 2(b), corresponding to the vectors expressed by Eq. (1). Some brightness variations that might resemble mode structures can be observed which originate in the diffraction from the oblique micromirrors [4].

Images obtained through the four adjacent pupil sectors are shown in Fig. 2(c) with the algebraic sum of intensities ${\displaystyle \sum I}=I_1\text{+}{I}_2+I_3\text{+}{I}_4$ shown in the middle. The sum resembles the full pupil image in Fig. 2(a) but is not identical since intensities rather than complex fields are added resulting in a lower resolution. Bright dots in the individual images correspond to cones that point mostly into the corresponding quadrant whereas dark areas show cones that point away. The preferential scattering direction, and thus the pointing, is more apparent from differential imaging as seen in Fig. 2(d) that shows pointing left, right, up, down, or along the diagonals with each sub-image scaled to the maximum contrast. Uniform differential images correspond to no obliqueness whereas brightness differences correspond to oblique light scattering as shown in Fig. 2(d). These images directly show the relative inclination of each modeled cone which cannot be deciphered from Fig. 2(a) alone.

To further validate the method, intensity differences at the central pixel of each simulated cone in the quadrant retinal images (Fig. 2(d)) were used with Eq. (1) to calculate the measured obliqueness of each. The resulting vectors are shown in Fig. 2(e). The reconstruction resembles the original although some differences can be seen. These are in part caused by the low central brightness for some of the simulated cones. This difference could potentially be reduced by using the average brightness across the imaged cones, rather than their central brightness only. Evaluation of obliqueness metric for the central pixels of the simulated cones in Fig. 2 results in $\tilde{\sigma }$ = 0.620. In turn, if all cone tilts equal zero (not shown) the intensity reconstruction finds a small value of 0.022.

Differential detection can be applied to photoreceptor cones as modeled above or indeed other retinal structures to reveal preferential directional scattering caused by topography, swelling or refractive-index inhomogeneities. For the experimental results described in Sec. 4 obliqueness vectors were determined at regular intervals which is more valuable and faster when determining a global obliqueness metric.

4. Experimental results

Three examples of relevance have been chosen for analysis: direct imaging of parafoveal cones (Sec. 4.1), retinal blood vessels (Sec. 4.2), and the optic nerve (Sec. 4.3).

4.1. Cone photoreceptors

An example of parafoveal cone mosaic imaging at ∼5° in the upper-nasal region for subject DV is shown in Fig. 3. This shows the combination of images captured with the camera. The accompanying playback visualizations have been reduced to 15 fps for ease of viewing.

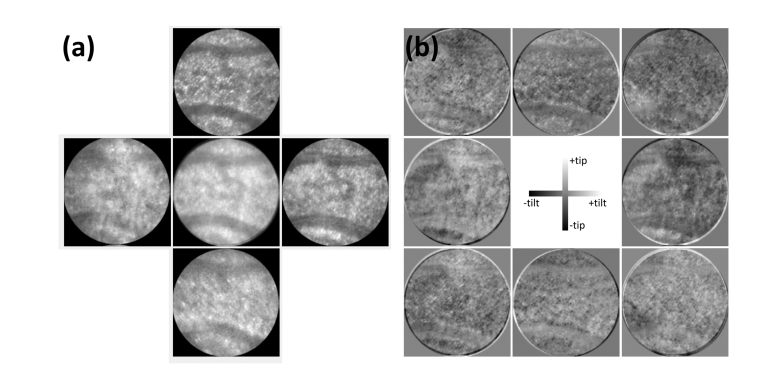
Fig. 3.

Directional light scattering captured for the parafoveal region of subject DV showing (a) four simultaneous images and the sum of the images in the middle (Visualization 1 ^{(6.9MB, mp4)} ) and (b) corresponding difference images (Visualization 2 ^{(12.7MB, mp4)} ). Each image covers 2° visual degrees. The dual scalebar in (b) refers to horizontal tilt (left-to-right) and vertical tilt, or tip (down-to-up).

Colinear registration of the four images is vital to identify directional scattering and minor translations of the individual image positions are needed. Repositioning was achieved by manual identification of a corresponding bright feature in all 4 images corresponding to local cross correlation before the analysis. Bright dots in Fig. 3(b) show cone photoreceptor scattering into the corresponding quadrant whereas dark areas correspond to a lack of scattering into that same quadrant. The range of grayscales show tip and tilts between these limits although unwanted glare light, caused by the lack of confocal detection, complicates the analysis. The obliqueness of scattering for individual photoreceptor cones can be estimated by identifying the same cone in more than one image and calculate its intensity-weighted center-of-mass. This determines the obliqueness as a fraction of the maximum obliqueness in the set of images according to the gray scale in the same way as in Fig. 2(d).

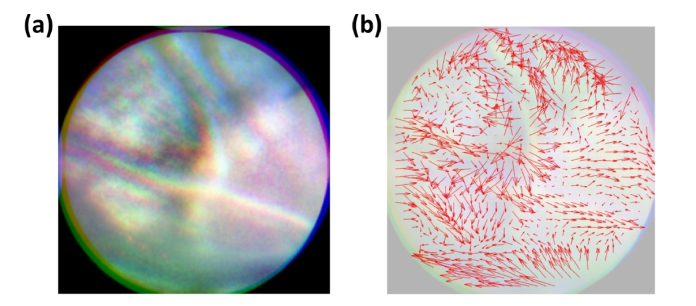
Color coding can be used to aid visualization. This is shown in Fig. 4 for the same data by overlapping the registered images. Downward scattering, i.e., the lower image in Fig. 3(a), has been excluded (to use a tricolor mapping) and the following coding has been used: scattering to the left (blue), scattering upwards (green), and scattering to the right (red). Colors may also be used separately on the horizontal and vertical directions (not shown). A prismatic triangular pyramid could potentially be used to capture just 3 images that could be projected directly onto the RGB colormap. The enlarged view in Fig. 4(b) shows that the cones scatter light in different directions as coded by the color and brightness. To visualize the local inclinations, Fig. 4(c) shows the same image but with obliqueness vectors determined from Eq. (1) superimposed (corrected for the global average tilt). The vectors are plotted at regular intervals, not always coinciding with the cones. Still, careful comparison of Fig. 4(b) and Fig. 4(c) gives added insight into the local preferential scattering directions that is not apparent in a conventional high-resolution AO fundus image.

Fig. 4.

Directional light scattering captured for the parafoveal region of subject DV showing (a) three superimposed simultaneous images left (blue), upper (green) and right (red) and (b) enlarged view of the central region along with the RGB color identification of relative cone pointing directions as determined from three of the four quadrant images. In (c) the inclination vectors have been overlaid to show the local pointing obliqueness calculated using Eq. (1) with all four images thereby removing the ambiguity in the vertical direction. For the chosen section in (c) the disarray parameter equals $\tilde{\sigma }$ = 0.091 and it varies in the range of 0.078 - 0.102 for the duration of the video sequence.

4.2. Blood vessels

An example of blood vessel imaging for subject BV is shown in Fig. 5. The visibility of the vessel walls in difference images is highest in the direction perpendicular to the vessels and the outcome resembles that of phase contrast imaging and offset pinhole SLO [30,31].

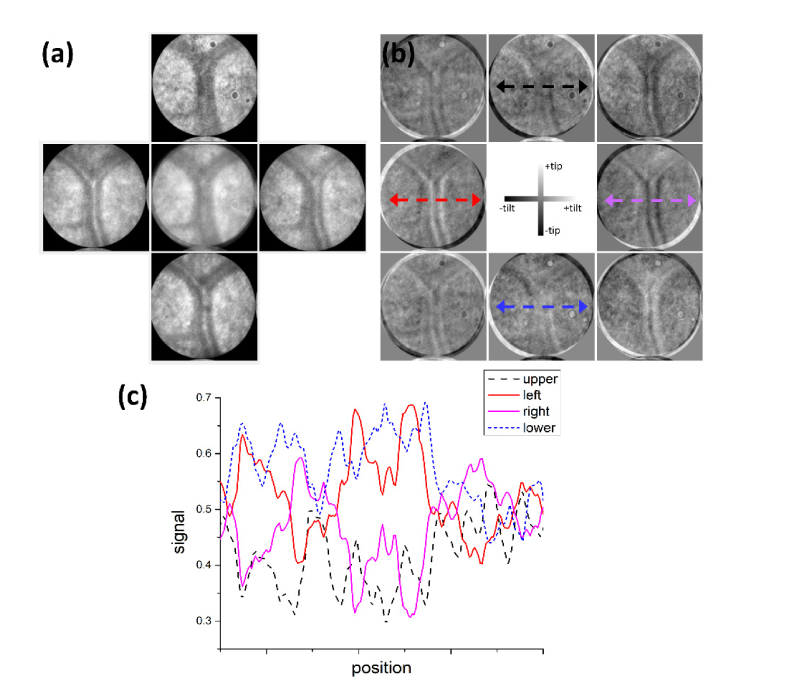
Fig. 5.

Directional light scattering captured for the parafoveal region of subject BV showing the (a) four simultaneous images with the sum of the images in the middle and (b) corresponding difference images. Each image covers 2° visual degrees. In (c) cross-sectional cuts across the central part of the differential images (as indicated by arrows in (b)) are shown.

The oblique light scattering is evident in Fig. 5(b) suggesting a mirror-like reflection off the vessel walls that enhances them in the orthogonal direction. This can be appreciated in the cross-sectional cuts shown in Fig. 5(c). The Michelson contrast of the vessel with respect to its immediate neighborhood equals approximately 8% (upper), 7% (lower), 16% (left) and 22% (right). Color coding can again be used to enhance the visibility of obliqueness. In Fig. 6, the left (blue), upper (green), and right (red) images have been superimposed. A color gradient blue-green-red can be noted across the vertical vessel suggesting a mirrorlike reflection. As a result, the overlaid obliqueness vectors in Fig. 6(c) are largely perpendicular to the vertical vessel.

Fig. 6.

Blood vessel visualization with color coding of scattering to the left (blue), upwards (green) and right (red) producing the (a) RGB color composite image. The magnified region (dashed white square) shows the color gradient across the vessel indicating the changing slope. In (c) the vector pointing has been overlaid to show the local inclinations calculated using Eq. (1). For the chosen section in (c) the disarray parameter equals $\tilde{\sigma }$ = 0.080 and it varies in the range of 0.064 - 0.086 for the duration of the video sequence.

4.3. Optic nerve

Finally, an example of imaging near the optic nerve for subject SQ is shown in Fig. 7. The system magnification was reduced by a factor of 2.7 to capture these larger 5.4° images. Differential detection allows visualization of slopes that may be useful to monitor optic disc or cup changes. The corresponding color-coded image is shown in Fig. 8 where a color gradient can be appreciated in the transition zone at the optic disc as well as across the large vessels although an exact image overlay is complicated by the larger depth variation across the region. The vector plot shows a preferential tilt towards the right in the region of the disc.

Fig. 7.

Example of imaging near the optic nerve (seen in the lower right corner of the images) for subject SQ showing (a) four simultaneous images with the sum of the images in the middle and (b) corresponding difference images. To capture these images the system optics were changed to capture a 5.4° retinal view, rather than the 2° view used in the other examples.

Fig. 8.

Visualization with color coding of scattering to the left (blue), upwards (green) and right (red) producing an RGB color composite image near the optic disc (seen in the lower right part of the image). In (b) the pointing has been overlaid to show the local vectors calculated using Eq. (1). The disarray parameter across the image equals $\tilde{\sigma }$ = 0.090 and it varies in the range of 0.089 - 0.103 for the duration of the video sequence.

The examples demonstrate that a quadrant pupil can be a useful addition for retinal imaging at both high and low magnifications by providing insight into directional scattering. Other bi- or multifaceted configurations can be envisioned that can highlight, possibly dynamically, any direction of relevance. The method may be implemented in other retinal imaging technologies (including SLO, where the differential imaging resembles offset-pinhole technology [29–31], and OCT [16,26,27]) that would better discriminate against straylight as required for accurate quantification of the obliqueness.

5. Discussion

We have presented a method that allows for obliqueness analysis in fundus images acquired through different pupil sectors. This method resolves the angular distribution of light directly in the pupil plane and thus gives additional information not readily available by other means.

Three different scenarios have been reported. The imaging of parafoveal cones, blood vessels, and the optic nerve all for healthy eyes. The results have been discussed in terms of local obliqueness vectors that map out variations in dominant scattering directions across simultaneously-captured images. The determined disarray parameter $\tilde{\sigma }$ is robust across the recorded video sessions varying less than 20%. The frame-to-frame variation, where eye motion is less, is smaller than 3%. In all the cases analyzed here only healthy subjects have been imaged and the obliqueness is small ($\tilde{\sigma }$< 0.103). The simulation of a small cone mosaic with obliqueness of up to 3° resulted in a larger disarray parameter, but cone disarray in healthy eyes is believed to be small.^19,20 If comparing images obtained at different scales it may become relevant to introduce the disarray per unit retinal area or per unit visual angle. In terms of patient imaging, the range of disarray parameters relevant for different retinal diseases remains to be determined but it would be expected to result in larger values when imaging affected regions of similarly-sized structures.

The directional sensitivity is achieved at the cost of a lower resolution. Thus, it would be relevant to capture images first through the full pupil and subsequently, or simultaneously, capture the directional images in a separate imaging channel. The chosen division of the pupil has impact on the achievable resolution and causes a lack of symmetry in the point-spread-function. Moreover, the refraction by the pyramid, though shallow, induces errors that degrade the images. A better approach, though beyond this study, would be to use a full circular apodization pupil centered and off-centered respectively. This would retain the symmetry of the imaging system while still allow calculation of differentials. This could be realized with a spatial light modulator or a digital micromirror device that could sample the pupil at will [40]. This would have increased flexibility without additional image degradation beyond the reduction in sampled pupil size. Ultimately, such methods could be implemented into SLO and OCT systems that offer the best in terms of resolution and discrimination against unwanted components of light.

With further refinement, the method will be used for clinically-relevant imaging of retinal disease. The information acquired may potentially be beneficial in the registration of drusen in macular degeneration or cone dystrophy where the normal arrangement and pointing of photoreceptors may be perturbed via alterations of the retinal topography that would increase the introduced disarray metric. The approach may also prove valuable in the analysis of diabetic retinopathy if combined with polarimetry [41].

6. Conclusions

In this study, we have reported on a new directional sensitive fundus camera that uses a refractive pyramid in the conjugate pupil plane to allow simultaneous capture of four images corresponding to light scattered by the retina into adjacent solid angles in the horizontal and vertical directions. Differential detection reveals differences in the directional scattering. This may possibly be used to monitor progression of diseases that alter the retinal topography [42–47], observe light-induced changes [48,49] or regeneration of photoreceptor outer segments [50]. With further development, a different approach could be implemented for pupil apodization to avoid the refractive errors induced by the refractive pyramid. Options currently being explored in our laboratory include spatial light modulators and digital micromirror devices for adaptive modification of the effective pupil.

The strategy proposed here could with little alteration be implemented in SLO and OCT systems by either sequentially or simultaneously capturing light through different parts of the pupil from which the differential images can be derived. These scanning systems would benefit significantly by their confocal design by eliminating straylight that may otherwise confound the determination of oblique light scattering.

Funding

King Abdullah Scholarship Program; Science Foundation Ireland (08/IN.1/B2053).

Disclosures

The authors declare that there are no conflicts of interest related to this article.