Abstract
Various diseases are relevant to the abnormal blood flow in tissue. Diffuse correlation spectroscopy (DCS) is an emerging technology to extract the blood flow index (BFI) from light electric field temporal autocorrelation data. To account for tissue heterogeneity and irregular geometry, we developed an innovative DCS algorithm (i.e., the Nth order linear algorithm, or simply the NL algorithm) previously, in which the DCS signals are fully utilized through iterative linear regressions. Under the framework of NL algorithm, the BFI to be extracted is significantly influenced by the linear regression approach adopted. In this study, three approaches were proposed and evaluated for performing the iterative linear regressions, in order to understand what are the appropriate regression methods for BFI estimation. The three methods are least-squared minimization (L2 norm), least-absolute minimization (L1 norm) and support vector regression (SVR), where L2 norm is a conventional approach to perform linear regression. L1 norm and SVR are the approaches newly introduced here to process the DCS data. Computer simulations and the autocorrelation data collected from liquid phantom and human tissues are utilized to evaluate the three approaches. The results show that the best performance is achieved by the SVR approach in extracting the BFI values, with an error rate of 2.23% at 3.0 cm source-detector separation. The L1 norm method gives a medium error of 2.81%. In contrast, the L2 norm method leads to the largest error (3.93%) in extracting the BFI values. The outcomes derived from this study will be very helpful for the tissue blood flow measurements, which is critical for translating the DCS technology to the clinic.
1. Introduction
Monitoring tissue hemodynamics is important for early disease diagnosis and treatment evaluation, since many diseases, such as tumors, ischemic stroke and peripheral artery disease, are associated with abnormal blood flow, blood oxygenation or oxygen metabolism. For example, the main cause of ischemic stroke is the deficiency of local cerebral perfusion [1]. Tumors are characterized by the high tissue blood flow and oxygen metabolism as well as low tissue blood oxygen level [2,3]. Sleep apnea leads to large fluctuation in the cerebral blood flow [4]. Although various modalities are available for tissue hemodynamic detection, near-infrared diffuse optical spectroscopy (NIRS) has gained wide applications in numerous physiological and clinical studies, due to portability, low cost and relatively larger penetration depth (up to several centimeters). NIRS utilizes the light intensity collected from the tissue to estimate the oxy- and deoxy-hemoglobin concentrations ([HbO2] and [Hb]), subsequently calculating tissue blood oxygen saturation (StO2) [5,6]. The blood oxygenation only reflects the static balance between oxygen supply and consumption. Blood flow is a dynamic parameter indicating how fast the oxygen is transported to biological tissues, and it is sensitive to many diseases. In recent years, a dynamic NIRS technology, namely, diffuse correlation spectroscopy (DCS), has been rapidly developed [3,7–11]. Unlike the other NIRS technology in which the signals of light intensity are mainly utilized, DCS quantifies the light electric field temporal autocorrelation function at multiple delay times, which is sensitive to the moving scattering, for measurement of blood flow at microvasculature level [9,11]. The tissue blood flow measurement by DCS technology has been validated through comparing with other modalities [12–15]. Additionally, this technology has been applied in clinic for early diagnosis and therapeutic monitoring of various diseases, such as ischemic stroke [1,8,13,16–18], tumor [2,3,7,19–21], obstructive sleep apnea [4], and surgical flap [22]. In some clinical applications, the DCS is combined with NIRS, for the purpose of simultaneously measuring blood flow and oxygenation. The combination of blood flow and oxygenation permits the calculation of the tissue oxygen consumption rate [23,24]. Additionally, the extension of DCS technology to the blood flow imaging, i.e., diffuse correlation tomography (DCT), has been developed over years [25–27].
Conventionally, the blood flow index (BFI) is extracted through fitting the experimental DCS/DCT data with an analytical solution to the diffusion correlation equation (a sort of partial differential equations-PDE), and a semi-infinite or layered slab geometry is often assumed [9,28]. In recent years, several algorithms were proposed, such as the optimal DCS data selection [25], the simultaneously fitting of multiple parameters for DCS curves [29], and the “modified Beer Lambert law” for DCS [30]. These algorithms, however, are all based on the analytical solution, which requires regular geometries.
Most of the biological tissues, however, are heterogeneous and with irregular geometry, particularly for the small tissue with large curvatures. For DCT, a finite element method (FEM) was proposed to reflect the tissue heterogeneity and irregular geometry [26]. Nevertheless, FEM is unable to fully utilize the optical signals and thus susceptible to the data noise. In a word, tissue heterogeneity, irregular geometry, as well as full data utilization cannot be simultaneously taken into consideration by either the analytical solution or FEM method.
To overcome the limitations, we proposed an algorithm, namely, the Nth-order linear (NL) algorithm [31,32]. Unlike the analytical solution or FEM, the NL algorithm does not seek for the solution to PDE. Instead, it combines the integral form of g1(τ) with a N-th order Taylor polynomial. Besides, the tissue heterogeneity and irregular geometry are taken into consideration through the information of photon path lengths. The accuracy of NL algorithm can be validated through computer simulations and experimental animals [31,32]. Very recently, we extended the NL algorithm for use in DCT [27], and the computer simulations on a realistic human head verified its capability in accurate and robust reconstruction of blood flow imaging. For both DCS and DCT, a key step to implement the NL algorithm is the linear regression, from which the autocorrelation data at multiple times are fully utilized.
In practice, all measured data are with noise, and denoising is a critical process in order to extract accurate BFI. Least-squared minimization (L2 norm) is a widely used approach to perform data fitting and linear regression [33], and it was adopted by us and other researchers in previous DCS/DCT data analyses, regardless of the algorithms being adopted (analytical solution, FEM and NL algorithm) [9,26,31,32]. However, the L2 norm is severely affected by the data points with large derivations to the regression line, particularly in low signal intensity and low signal-to-noise ratio (SNR). In recent years, the least-absolute minimization (L1 norm) [34] was adopted frequently as a denoising approach for data analysis. Moreover, an algorithm in field of machine learning, i.e., support vector regression (SVR), is emerging as an advanced approach for data linear regression [35,36]. In this study, for the first time, to the best of our knowledge, we explore the L1 norm and SVR methods to DCS, for data denoising through a linear regression. The denoising outcomes will be compared with the conventional L2 norm approach in the evaluations. All approaches are validated using computer simulation data as well as the experimental data collected from liquid phantom. Additionally, we applied the three approaches to the human subjects in skeletal muscles and brain for evaluation of their potential use in the clinic.
2. Methods
This section starts with an introduction of the DCS instrument and basic principle, followed by the NL algorithm for BFI extraction. Then, we present three approaches to execute the linear regression, i.e., L2 norm, L1 norm and SVR. The procedures for computer simulations, phantom and human experiments, as well as statistical analysis methods, will be described finally.
2.1 DCS instrument and principle
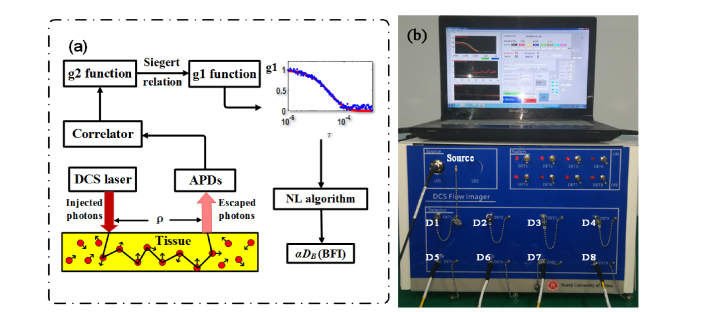
The instrument of DCS flowmetry used in this study is similar to those reported in previous studies [9,13,22]. Briefly, the instrument mainly consists of a continuous-wave laser (785 nm, DL-785-120-SO, Crystalaser, Inc.) at long coherence length (>5m), eight single-photon-counting photodiodes (APDs) (SPCM-780-13-FC, Excelitas Inc., Canada), and an eight-channel correlator (flex05-8ch, Correlator.com, USA), as shown in Fig. 1(b). Through the multi-mode source fiber, long-coherence light from the laser is injected into the tissue. The injected photons experience events of absorption and scattering within the tissue, and a portion of photons eventually escape out the tissue and were collected by single-mode detector fibers placed several centimeters (ρ) away from the source fiber. The collected photons are counted by the APDs and the outputs are taken by an 8-channel correlator board. From the APD outputs (i.e., light intensity), the light intensity temporal autocorrelation function (G2(τ)) is calculated by the correlator board. The normalized G2(τ) function (i.e., g2(τ)) is related to the light electric field temporal autocorrelation (g1(τ)) via the Siegert relation [9]. The decay rate of g1(τ) is closely related to the moving of red blood cells (i.e., blood flow). For instance, a faster decay in g1(τ) curve indicates a larger blood flow value. The value of blood flow can be quantified from the fact that the unnormalized g1(τ) function (i.e., G1(τ)) satisfies the correlation diffusion equation (a form of partial differential equation). Conventionally, with a specific boundary condition (e.g., the semi-infinite), the blood flow index (BFI) value is extracted analytically from the diffusion correlation equation. In this study, the NL algorithm proposed by us (see Section 2.2), which reflects tissue arbitrary geometry and heterogeneity, was used to extract BFI values (Fig. 1(a)).
Fig. 1.
(a) The schematic diagram of DCS components. (b) The instrument of 8-channel DCS flowmetry, wherein the DCS laser (Source) and eight detectors (D1-D8) are labeled on the front panel of the instrument.
2.2 Nth-linear (NL) algorithm for DCS flow extraction
As mentioned earlier, the NL algorithm does not seek for the solution to diffusion correlation equation. Instead, this algorithm is derived from the integral of temporal autocorrelation function g1(τ) over individual photons, in the following expression [31]:
| (1) |
where P(s) is the normalized distribution of detected photon path length s, k0 is the wave vector magnitude of the light in the medium,is the photon random-walk step length, which is equal to(is the reduced scattering coefficient), and τ is the delay time of autocorrelation function. represents the mean-square displacement of the moving scatterers. Because the diffuse model, i.e., <Δr2(τ)> = 6DBτ, has been found to well fit experimental data over a wide range of tissues or organs [9,28], this flow model was adopted in this study. Here, DB is the effective diffusion coefficient. A factor α is added to (i.e.,) to account for the fact that not all scatterers are “moving” in the tissue; α is the ratio of “moving” scatterers to the total number of scatterers. The combined term, αDB, is referred to as BFI in biological tissues.
When combing the Eq. (1) with the N-order Taylor polynomial of g1(τ) function, and performing some mathematical derivations, we reach the following approximations in the case that τ is sufficient small:
| (2) |
| (3) |
where
| (4) |
Equation (2) and (3) are referred to as the first-order and Nth-order linear algorithm respectively. can be determined from the Monte Carlo (MC) simulation of photon migrations in the tissue.
For the first-order approximation (N = 1), the unknown variable αDB only appear in the right-hand side of Eq. (2). Hence, Eq. (2) can be rewritten as follows:
| (5) |
where
| (6) |
The term ZαDB(1) is the slope of linear regression between τ and g1(τ)-1, which is written as:
| (7) |
Once the slope (Sl) is determined from τ and g1(τ)-1 data via linear regression, the unknown(αDB(1)) can be calculated from (7) with NL algorithm.
For the Nth-order approximation (N>1) in Eq. (3), which has unknown αDB on both sides, αDB can be derived iteratively using following equations:
| (8) |
| (9) |
We defined the left sides of Eq. (5) and Eq. (8) as the “modified autocorrelation decays” (MADs). It can be seen from Eq. (5) and Eq. (8) that determination of the slope (Sl) via iterative linear regression is an essential step to extract the BFI (i.e., αDB) from the autocorrelation data.
The mathematical forms of NL algorithm for heterogeneous tissues are similar to those of homogeneous tissues (i.e., Eqs. (2)-(9)), except that multiple slopes (Sl) from different S-D pairs need to be calculated. The slopes (Sl) are used to calculate the BFI values at each tissue type by solving the linear equation system.
To simplify Eq. (5) and Eq. (8), we obtain the expression of linear regression model:
| (10) |
where k is the slope value of linear regression. m is the intercept. Here x represents the delay time τ, and y represents the modified autocorrelation decay (MAD).
2.3 Least-squared (L2 norm minimization) algorithm
As a conventional and easy-implemented approach, L2 norm has been used mostly widely in linear regression.
According to the definition, the loss function of L2 norm is [33]:
| (11) |
where (x1,y1), (x2,y2),…,(xi,yi), xi,yi∈R are the data points collected from DCS measurements.
Since L (y, f(x)) is a differentiable function, its minimization could be reached by solving the following linear equations. i.e.
| (12) |
When using L2 norm, the slope value is largely influenced more severely by the data points far away from the regression line than the data points that are close to or within the regression line. Because the noise more often deviates the true data points from the regression line, those noisy data points have relatively larger squared value of the distance, thus having more weight to determine the slope value than the other points with less noise, and thus the method is not preferred.
2.4 Least-absolute (L1 Norm) minimization algorithm
L1 norm aims to reduce the weight of noise data, and its algorithm loss function is defined as [34]:
| (13) |
From Eq. (13), the weight of noise data would be substantially reduced by decreasing the norm order from 2 to 1. In principle, therefore, the L1 norm could generate more accurate and robust slope estimation. The primary challenge for this approach is how to minimize the L(y, f(x)), since this function is non-differentiable, or in other words, L(y, f(x)) is a non-smooth optimization. In this paper, a linear regression model analysis under the least-absolute deviation criterion is analyzed and transformed into a linear programming problem.
First, we establish a linear regression model in the form of matrix based on DCS data sets:
| (14) |
Here, ‘1’ denotes an n-dimensional column vector at the identical value of 1, and W is the regression coefficient vector, δ ~N (0, σ2I).
The solution to the above model is to solve the following unconstrained non-differentiable optimization problem:
| (15) |
In other words, we aim to derive the minimal solution of the L1 norm of the overdetermined linear equations:
| (16) |
Let A = [1, X], c = y, W can be treated as the difference of two non-negative p + 1dimensional column vectors u, v (i.e., W = u-v). Meanwhile, ξ, η are set as non-negative n dimensional column vectors, then Eq. (16) becomes a compatible linear equation system.
| (17) |
Hence, Eq. (15) becomes the problem of obtaining the minimum of . Let 0p + 1, 1n denotes the column vectors which contains P + 1 zero elements and n elements at value of 1, respectively, this problem is further transformed into a linear programming problem:
| (18) |
Using the algorithm of solving linear programming problems, we can get the optimal solution of the problem (18). Eventually, we obtain the optimal solution W = for the problem (14).
2.5 Linear ε-support vector regression (SVR) algorithm
The SVR, a powerful algorithm in the field of machine learning, was derived from the principle of SVM (support vector machine). The SVM is usually used for classification problems, while the SVR is mainly for regression.
In SVR at a tolerance value of ε, the regression function of linear ε-SVR is written as:
| (19) |
where w is the weight vector; b is a threshold value. Its accuracy is measured by the loss function. Regression estimates can be obtained by minimization of the empirical risk on the DCS data. Unlike the traditional loss functions used for minimization of the empirical risk (e.g., squared error in L2 norm) and absolute value error (e.g., L1 norm), the SVR uses a new type of loss function, namely, ε-insensitive loss function, as depicted below [35,36]:
| (20) |
Note that with the ε-insensitive loss function, when the deviations between the measured value y and the predicted value g(x) do not exceed the tolerance of ε value, the loss function value is zero. In other words, even if the predicted value g(x) and the measured value y are not equal, there is no loss at this point, as long as the difference is less than the tolerance value of ε.
The optimization problem of ε-support vector regression can be expressed as:
| (21) |
where C is a regularization parameter (positive constant). The optimization problem of Eq. (21) can be transformed into a dual problem by the Lagrange's function, and its solution is given by
| (22) |
where the dual variables are subject to constraints. Here we applied the linear ε-SVR algorithm to establish a linear model. The mathematical procedures to perform the ε-linear SVR algorithm are described as follows:
Step1. Establish DCS data sets to perform linear regression:
T = [(x1, y1), (x2, y2), …, (xN, yN)], s.t. (x1, x2, …, xN)T∈X = RN ; yi∈Y = R, i = 1,2,…N.
Step2. Select appropriate values of parameter ε>0 and the penalty parameter C>0.
Step3.Construct and solve the convex quadratic programming problem (CQP)
and its solution is given by.
Step 4. Calculate b: Select the componentorof in interval (0, C). If is selected, then,, Otherwise,.
Step 5. Construct a decision function.
For Step 2, the value selection of parameter ε and penalty parameter C are implemented as follows [37]:
| (23) |
where andare the mean and the standard deviation of the y values of MADs data. Parameter C represents the trade-off between the model complexity and the degree of deviations (i.e., larger than ε) to be tolerated in formula (21).
Recent studies have shown that the value of ε should be proportional to the input noise level, according to the following equation [38].
| (24) |
where n is the size of DCS data.
Once the linear model via linear ε-SVR algorithm was established, we determined the slope of the linear regression by any two pointsin the linear model, as follows:
| (25) |
Finally, regression equation is obtained:
| (26) |
2.6 Tissue model and generation of autocorrelation data
A rectangular-shape geometrical model, at a size of 20 cm × 20 cm × 20 cm was established as the tissue model for computer simulation of blood flow. This size of geometrical model is large enough to cover the optical probe (up to 3 cm source-detector separation) as well as the light penetration depth (up to 2 cm). A package of open-source codes, MCVM (Monte Carlo Modeling of Photon Migration in Voxelized Media) [39], was utilized to perform Monte Carlo (MC) simulation of light propagation within the tissue. A total of 10 million photon packets were injected from laser source to the tissue model. Primary outcomes from MC simulation at 2.5 cm source-detector (S-D) separation were used as inputs to the following equation (i.e., the discrete form of Eq. (1)).
| (27) |
where the optical properties have known parameter values. w(q) is the weight (i.e., the remaining ratio of the escaping photons) of the qth photon packet; and s(q) is path length of the qth photon in tissue. Both the weight and photon path length were derived from light MC simulations.
In actual measurements, noise is unavoidable. To reflect the realistic experiments, appropriate level of noise was added to the autocorrelation function g1(τ) at each delay time (τ). The levels of noise were determined by the photon count rate (i.e., light intensity) which depended on tissue optical properties and S-D separations. A larger separation resulted in a lower light intensity, leading to a larger noise, specified by the following equation [29,40]:
| (28) |
where T is the correlator bin time, Γ is the decay rate, <n> = IT, and I is the detected photon count rate. σ(τ) is the standard deviation of the g1(τ) noise.
The photon count rate (i.e., light intensity) for noise model in computer simulations were set as: 1500 to 30 kcps, corresponding to the four S-D separations (1.5 to 3.0 cm), respectively. Optical properties were set as: μa = 0.05 cm−1 and μs’ = 8.0 cm−1. By combining the optical properties, Monte Carlo simulation outcomes and the assumed BFI (i.e., αDB = 1.2 × 10−8 cm2/s), we performed the repeated computer simulations according to Eq. (27), generating a total of 1000 autocorrelation curves g1(τ) with noise.
2.7 Phantom experiment
Setup of the phantom experiment is to mimic tissue blood flow. The phantom procedures are similar to those reported in previous studies [9,29]. Briefly, the liquid phantom, contained in a rectangular aquarium (Fig. 2(b)), is comprised of distilled water, India ink and intralipid solution. India ink (Chenguang Inc., China) is used to manipulate the absorption coefficient of the phantom,, where λ is the laser wavelength (i.e., 785 nm). India ink is firstly diluted to 1% solution in distilled water. Theof 1% ink solution is measured with a spectrometer (QE-Pro, Ocean Optics Inc., USA). Intralipid (30% solution, Huarui Inc., China), measured with a frequency-domain oximetry instrument (Imagent, ISS Inc., USA), provides the reduced scattering coefficient () of the phantom. The intralipid particles also mimic the motions of red blood cells, i.e., the blood flow at microvasculature level. Appropriate amount of distilled water, as well as the 1% India ink and intralipid solution with known values ofand, were added to the rectangular aquarium, leading to the target values of optical properties ( = 0.05 cm−1 and = 8.0 cm−1). For data acquisitions, the DCS source and detector fibers, both confined in a black foam at different separations (i.e., 1.5 cm, 2.0 cm, 2.5 cm and 3.0 cm), were placed on the phantom surface (Fig. 2(a)). The other end of fibers were connected to the laser and four detectors in instrument of DCS flowmetry respectively, leaving the other four detectors in the DCS instrument unconnected. The autocorrelation data were collected from the liquid phantom for a continuous period of 20 minutes, at a sample time of 1.2 seconds. As such, a total of 1000 autocorrelation curves were obtained from the phantom experiment.
Fig. 2.
(a). A custom-made fiber-optic probe at the S-D separations of 1.5 cm, 2.0 cm, 2.5 cm and 3.0 cm, respectively. (b) Configuration for phantom experiments.
2.8 Manipulation protocol on human subjects
A total of ten healthy volunteers were recruited for the human experiments on leg muscle and brain. The study protocols were approved by the Ethics Committee of the North University of China, the consent forms were signed by all subjects. For human experiments, the emitted light is expanded in diffusive manner, permitting the illuminated area to reach 4 mm diameter over the skin. As thus, the power density delivered to tissue surface is below the safety limit of 4 mW/mm2 [41]. Other fiber configuration for human experiments is the same as for phantom experiments. The optical properties of in vivo tissue were set as: μa = 0.10 cm−1 and μs’ = 8.0 cm−1 respectively, according to the literature [9,42]. At the beginning of leg muscle measurement, the subject lied on a table in supine posture with both legs in relax status. A cuff tourniquet was placed on the upper right leg, and an optical probe (with four S-D separations in range of 1.5 to 3.0 cm) was taped on the surface of calf muscle. A 3-minute DCS data were collected by the DCS device as the baseline value. The cuff tourniquet was then automatically inflated by 230 mmHg air pressure, with the purpose of temporarily blocking the blood into calf muscle. After 3-minute cuff inflation, the cuff tourniquet was deflated, and the DCS blood flow data during a recovery period were collected for another 5 minutes, reaching the end of measurement.
Thereafter, the ten subjects received cerebral blood flow measurement by DCS flowmetry, with optical probe on forehead. For this measurement, the subjects also lied on a table in supine posture. The DCS data were longitudinally collected for 3 minutes, without manipulation of cerebral blood flow. This protocol aims to investigate the robustness of BFI measured in the brain, which represents the tissue with irregular geometry and large curvature.
2.9 Evaluation criteria
For computer simulations, phantom and human experiments, the autocorrelation curves g1(τ) were analyzed with the NL algorithm with the three approaches (L2 norm, L1 norm and SVR), from which the BFIs were extracted. By using the known value of BFI (i.e., αDB,0 = 1.2 × 10−8 cm2/s) preset in computer simulations, the error between the true and reconstructed BFIs was quantified, as follows:
| (29) |
where the RMSE denotes the root-mean squared error; andare the reconstructed and true BFIs, respectively. n is the number of samples. A small RMSE value indicates that the reconstructed BFI value is close to the true one.
In addition to the accuracy, the measurement robustness is defined in below form:
| (30) |
where the ‘σ’ represents the standard deviation of the variable. For computer simulation and phantom experiment wherein no flow changes were manipulated, we used CV values to compare the robustness of the three approaches. A smaller CV value indicates that the reconstructed flow is more stable. In addition, descriptive statistics will be used to summarize the average results, including the mean, standard derivation, minimum and maximum. For human experiments of cuff occlusion wherein the BFI was manipulated to change, we used ANOVA test to compare the response differences produced by the three approaches.
3. Results
In this section, the results from computer simulations, phantom experiments and human subjects were presented. The outcomes of linear regressions by L2 norm, L1 norm and SVR, as well as their derived BFI, were compared. All the computing procedures were performed on a desktop PC (Lenovo ThinkCentre M8600t), with 3.4G Hz CPU and 16G memory.
3.1 Results of computer simulations
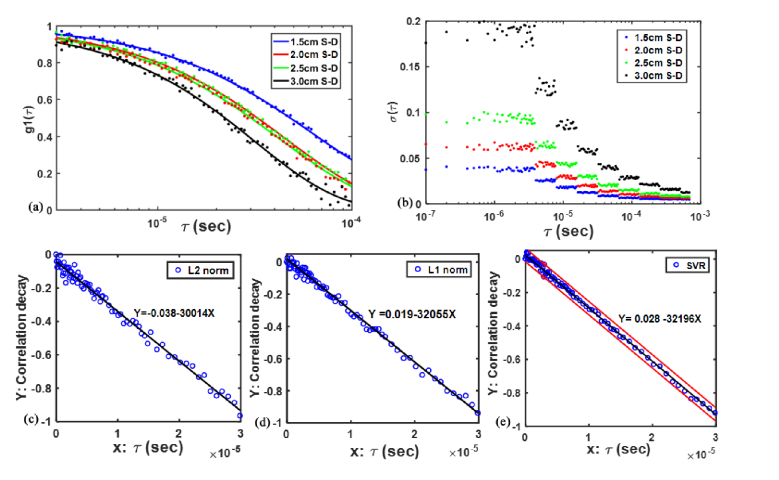
Figure 3(a) shows the autocorrelation functions g1(τ) with noise generated by the computer simulations at four S-D separations, respectively. The g1(τ) noise matches the real data noise determined by the photon count rate (1500 to 30 kcps) [27,29] at four S-D separations (1.5 to 3.0 cm). It is clearly seen that a larger S-D separation leads to more noise in the autocorrelation functions. At the largest S-D separation (i.e., 3.0 cm), the linear regression processed by L2 norm, L1 norm and SVR were presented in Fig. 3(c) through 3(e). The DCS data with the delay time in the range of (79 data points) were used for all linear regressions. As illustrated, the regression line was found to be substantially affected by noisy data points, when L2 norm approach was adopted. This influence was significantly alleviated through using L1 norm approach. With the SVR approach, the data points with large noise appear to be totally excluded in the linear regression, which enhances the accuracy of data analysis.
Fig. 3.
Autocorrelation functions g1(τ) with noise generated by the computer simulations at four S-D separations (a), the g1(τ) noise (b), and the fifth-order linear regression lines ((c)-(e)) by L2 norm, L1 norm and SVR, respectively. The two red lines in Fig. 3(e) denote the decision plane in the SVR approach.
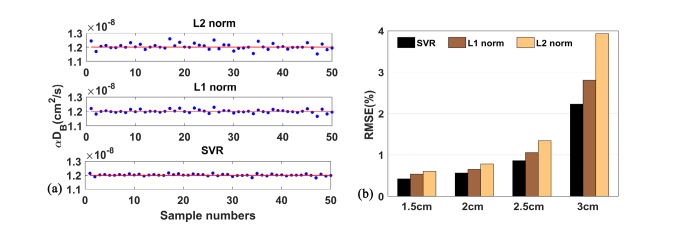
Figure 4(a) shows the time course of BFI values (50 data points) extracted by the fifth-order NL algorithm, in which the L2 norm, L1 norm and SVR are used respectively. As is clearly seen, the L2 norm approach causes a large fluctuation around the BFI baseline. By contrast, the BFI value extracted by the L1 norm is closer to the BFI baseline. The SVR approach can generate the best BFI curve visually, with the minimal inconsistence among different data points.
Fig. 4.
(a) The BFI (i.e., αDB) values of 50 samples reconstructed by L2 norm, L1 norm and SVR approaches respectively in the computer simulations. (b) The RMSE values for 1.5,2.0,2.5 and 3.0 cm S-D separations, when L2 norm, L1 norm and SVR were used, respectively. For any of the three approaches, the NL algorithm was performed at fifth-order.
Moreover, the RMSE values calculated by the L2 norm, L1 norm and SVR are presented in Fig. 4(b). The RMSE was found to be positively influenced by the S-D separation, which is anticipated, because the larger S-D separation leads to a lower signal-to-noise ratio (SNR). At any S-D separations, the SVR performs the best in extracting the BFI values, with the RMSE value in range from 0.42% to 2.23% (i.e., 1.5 cm to 3.0 cm S-D separations). In contrast, the conventional L2 norm method results in the largest RMSE. At the 3.0 cm S-D separation, the RMSE value reached the largest value (3.93%).
Similarly, at the same S-D separations, SVR generated the smallest value of CV. For example, the CV value was 2.66% at 3.0 cm S-D separation when SVR was adopted, while this value was increased to 4.78% when the L2 norm method was adopted.
3.2 Results of phantom experiments
The processing methods for phantom experiment are identical as those for computer simulations, except the optical data were collected from liquid phantom by DCS flowmetry, rather than generated by the computer. The DCS data collected from the phantom experiment match well with the simulated DCS data, in both noise intensity and distribution.
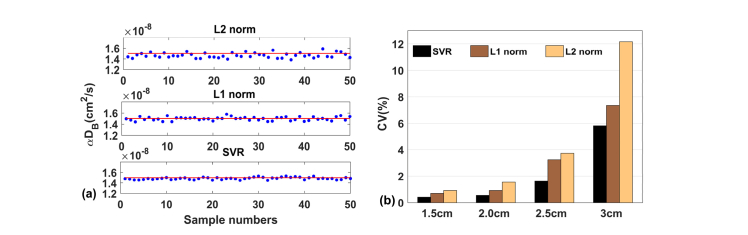
Similar to what we have found in computer simulations, the time course of BFI data points is more scattered by the L2 norm approach, while the data points generated by the L1 norm and SVR approaches are more concentrated (Fig. 5(a)). Among these approaches, the BFI values yielded by the SVR approach appears to be most stable. At the largest S-D separation (i.e.,3.0 cm), average BFI values are 1.47, 1.49 and 1.51 × 10−8 cm2/s by L2 norm, L1 norm and SVR, respectively. These values are in agreement with the reported values (0.4~2.0 × 10−8 cm2/s [29]). Moreover, the CV values generated by L2 norm, L1 norm and SVR are 12.16%, 7.34% and 5.82%, respectively (Fig. 5(b)).
Fig. 5.
(a) The BFI (i.e., αDB) values of 50 samples reconstructed by L2 norm, L1 norm and SVR approaches respectively in the phantom experiments. (b) the CV values for 1.5,2.0,2.5 and 3.0cm S-D separations, when L2 norm, L1 norm and SVR were used, respectively. For any of the three approaches, the NL algorithm was performed at fifth-order.
3.3 Results of experiments on human subjects
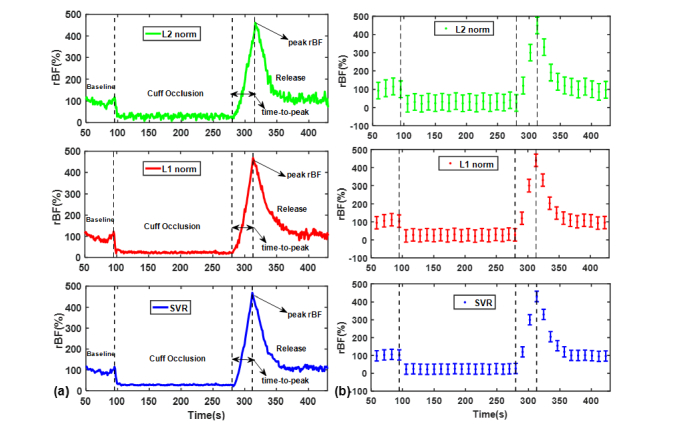
Figure 6 shows the BFI measurements from a representative subject as well as the average changes over all ten subjects during the manipulation protocol of cuff occlusion, wherein the DCS signals collected from the largest S-D separation (i.e., 3.0 cm) were used for data analyses. The blood flow (αDB) data points were normalized to the mean value of the 30-second baseline before the cuff occlusion. With any of the three approaches (L2 norm, L1 norm and SVR), the time course of BFI exhibits typical response to cuff occlusion. Specifically, the occlusion of femoral artery causes immediate reduction in calf blood flow, reaching its minimal value rapidly. There are immediate hyperemic responses following the deflation of cuff tourniquet, causing a rapid increase to its peak value (486%). Thereafter, the BFI is recovered towards its baseline gradually. Nevertheless, SVR yields the smoothest time-course curve of blood flow, when compared to the L2 norm and L1 norm. On average (n = 10), the peak rBF following the cuff deflation was 354 ± 75%, 361 ± 68%, and 359 ± 57%, by the L2 norm, L1 norm and SVR, respectively, when comparing with their baselines (assigning 100%), while their time-to-peak are 35.6 ± 10.7, 36.2 ± 9.3, and 36.9 ± 8.8 seconds, respectively. According to the ANOVA analysis, no significant difference (p>0.05) was found among the three approaches in peak rBF and time-to-peak of the ten subjects. However, the influence of denoising approaches on the individual flow response is still remarkable.
Fig. 6.
(a) Time-course of the relative blood flow (rBF) data points reconstructed by L2 norm, L1 norm and SVR approaches respectively, from a representative subject. (b) The average changes (mean ± standard error) over all ten subjects during the manipulation protocol of cuff occlusion.
For the human brain study, the CV values of BFI measured by L2 norm, L1 norm and SVR approaches were 11.0 ± 1.3%, 6.5 ± 0.6%, 3.8 ± 0.3%, respectively. The order of CV values (i.e., from the largest to smallest) is consistent with those derived from computer simulations and phantom experiments.
4. Discussion and conclusions
As an emerging technology, DCS/DCT has been attracting more attentions in recent years, for the capability to detect microvasculature blood flow with advantages of noninvasiveness, fast and low cost. In addition to the hardware setup (e.g., laser, detector, digital correlator, etc.) and design of the optical probe, the algorithms for data processing are critical, which remarkably influences the quality of blood flow values extracted from the optical signals. In all previous DCS/DCT algorithms, either analytical solution or FEM, it is difficult to account for irregular geometry and tissue heterogeneity, meanwhile utilizing the full autocorrelation data. For the purpose of taking all these factors into consideration, we proposed the NL algorithm and validated its accuracy in extracting the BFI through computer simulations and animal experiments [31,32]. The unique merit of the NL algorithm makes it possible to fully utilize the autocorrelation data through iterative linear regressions, which are considered as a high efficiency denoising approach. In contrast, only the autocorrelation data at single delay time (τ) were used in the previous analytical solution or FEM approach. Although a few denoising methods, such as high-pass filter and data fitting, were adopted in analytical solution and FEM. Those mathematical processes are, in principle, less relevant to the DCS/DCT theory.
Linear regression is a key step to implement the NL algorithm, with the aim to minimize the discrepancy between the theoretical data points (i.e., on the regression line) and the measured data points. This ‘discrepancy’ is often quantified by the least-squared errors of all data (i.e., L2 norm), due to the simple procedure for computer implementations. Therefore, the L2 norm method is solely used at present for DCS/DCT data fitting (analytical solution and FEM) as well as the linear regression (NL algorithm), without exception.
With the advances in calculating technique and computer capacity, more methods to match the discrepancy between the mathematical model and real data were proposed. For example, the L1 norm approach, which was previously assumed hard to implement computationally, has gained popularity in recent years for data fitting. Additionally, the SVR, which is derived from the principle of SVM, has been used widely for a linear or nonlinear regression. Hence, we introduce these advanced methods, for the first time, into DCS data analysis. For a complete evaluation, the L2 norm, L1 norm and SVR are compared in the same data set through computer simulations, liquid phantom and human subject experiments.
The computer simulations were carried out because the BFI can be set as known values (e.g., i.e., αDB = 1.2 × 10−8 cm2/s), allowing for objectively evaluating the accuracy of the three approaches. The liquid phantom, equipped with well-controlled experimental setup, provides stable BFI value, from which the robustness of the three approaches can be evaluated. The short-term cuff occlusion on thigh muscles were selected as human subject manipulation, since this protocol is widely adopted in many physiological studies. Moreover, typical muscle blood flow responses (ischemia and hyperemia) are induced during the cuff inflation and deflation, allowing us to quantify the BFI changes for the three approaches.
The L2 norm and L1 norm have similar mathematical expression in the optimization problems of data fitting, except a different exponential order. With either of the two approaches, all the samples data are included to reconstruct the regression line. For L2 norm, the least-squared requirement pushes the regression line towards the data points with larger deviations, which, however, are often the noise data. The L1 norm method substantially alleviates this problem through decreasing the weight (i.e., from 2 to 1) of data mismatch, thus generating a more accurate linear regression. Both L2 norm and L1 norm have the limit that all data are involved in determining the regression line, including the noise. By introducing the support vector regression or SVR, the noisy data with larger deviations are efficiently excluded, hence promoting the accuracy and robustness of the regression lines.
The outcomes derived from both computer simulations and phantom experiments demonstrate the best performance of SVR approach in extracting the BFI values, with RMSE of 2.23% and CV of 2.66%, respectively, at the largest separation (i.e.,3.0 cm). Likewise, the outcomes derived from all other S-D separations support the conclusion drawn from the largest S-D separation (data were not shown).
In addition to the accuracy and robustness, the cost of computation is also a factor affecting the application of data fitting approach to practical applications, particularly for real-time monitoring. In this study, the computing time to extract a BFI value is 6.48, 28.07 and 52.93 seconds, when using L2 norm, L1 norm and SVR, respectively. With current computational capacity, it is difficult to realize the real-time blood flow measurement with the NL algorithm, when compared with conventional approach of normal fitting. However, in many situations such as physiological research, real-time measurement of blood flow is not mandatory. In those situations, offline data analysis with higher accuracy might work better for the research purpose. Nevertheless, shorten the computation time, especially for the complicated SVR approach, is a future task.
This study investigates the three approaches which are widely representative, and then, for the first time, evaluates them for iterative linear regression in DCS blood flow measurement. In addition to the linear regression that is required by the NL algorithm, data fitting is also critical for other DCS/DCT algorithms, i.e., the analytical solution and FEM. In those algorithms, the L2 norm was exceptionally adopted for data fitting. Hence, the methods proposed in this study (i.e., L1 norm and SVR) have general implication for future DCS/DCT studies. Nowadays, many methods for data processing and classifications (i.e., deep learning) are rapidly developed and would be applicable to DCS/DCT blood flow measurement and imaging, which will be a subject of our future research. Additionally, future research will focus on how to apply the denoising approaches (particularly, the SVR approach) to various physiological and clinical situations, including those with heterogeneous tissues and large curvature.
To conclude, two approaches of data fitting (L1 norm and SVR) for DCS blood flow measurement, have been proposed in this study. Both approaches have been compared with the conventional approach (i.e., the L2 norm) through computer simulations, liquid phantom and human subject experiments. The results have demonstrated the advantages of the proposed approaches over the conventional one in both simulation and human experiment tests. Among the three methods, the SVR performed the best in extracting the blood flow information, with minimal errors and variations. This study promotes the application of an advanced data fitting approach to the clinic, which requires accurate and robust measurements of blood flow by the DCS/DCT technology.
Funding
National Natural Science Foundation of China (61771433, 61671413), National Key Research and Development Program of China (2016YFC0101604); National Key Scientific Instrument and Equipment Development Project of China (2014YQ24044508); Shanxi Scholarship Council of China (2016-087).
Disclosure
The authors declare that there are no conflicts of interest related to this article.
References
- 1.Shang Y., Cheng R., Dong L., Ryan S. J., Saha S. P., Yu G., “Cerebral monitoring during carotid endarterectomy using near-infrared diffuse optical spectroscopies and electroencephalogram,” Phys. Med. Biol. 56(10), 3015–3032 (2011). 10.1088/0031-9155/56/10/008 [DOI] [PubMed] [Google Scholar]
- 2.He L., Lin Y., Huang C., Irwin D., Szabunio M. M., Yu G., “Noncontact diffuse correlation tomography of human breast tumor,” J. Biomed. Opt. 20(8), 086003 (2015). 10.1117/1.JBO.20.8.086003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Choe R., Putt M. E., Carlile P. M., Durduran T., Giammarco J. M., Busch D. R., Jung K. W., Czerniecki B. J., Tchou J., Feldman M. D., Mies C., Rosen M. A., Schnall M. D., DeMichele A., Yodh A. G., “Optically Measured Microvascular Blood Flow Contrast of Malignant Breast Tumors,” PLoS One 9(6), e99683 (2014). 10.1371/journal.pone.0099683 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hou Y., Shang Y., Cheng R., Zhao Y., Qin Y., Kryscio R., Rayapati A., Hayes D., Jr., Yu G., “Obstructive sleep apnea-hypopnea results in significant variations in cerebral hemodynamics detected by diffuse optical spectroscopies,” Physiol. Meas. 35(10), 2135–2148 (2014). 10.1088/0967-3334/35/10/2135 [DOI] [PubMed] [Google Scholar]
- 5.Liu H., Boas D. A., Zhang Y., Yodh A. G., Chance B., “Determination of optical properties and blood oxygenation in tissue using continuous NIR light,” Phys. Med. Biol. 40(11), 1983–1993 (1995). 10.1088/0031-9155/40/11/015 [DOI] [PubMed] [Google Scholar]
- 6.Boas D. A., Gaudette T., Strangman G., Cheng X., Marota J. J. A., Mandeville J. B., “The accuracy of near infrared spectroscopy and imaging during focal changes in cerebral hemodynamics,” Neuroimage 13(1), 76–90 (2001). 10.1006/nimg.2000.0674 [DOI] [PubMed] [Google Scholar]
- 7.Chung S. H., Feldman M. D., Martinez D., Kim H., Putt M. E., Busch D. R., Tchou J., Czerniecki B. J., Schnall M. D., Rosen M. A., DeMichele A., Yodh A. G., Choe R., “Macroscopic optical physiological parameters correlate with microscopic proliferation and vessel area breast cancer signatures,” Breast Cancer Res. 17(1), 72 (2015). 10.1186/s13058-015-0578-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Durduran T., Zhou C., Edlow B. L., Yu G., Choe R., Kim M. N., Cucchiara B. L., Putt M. E., Shah Q., Kasner S. E., Greenberg J. H., Yodh A. G., Detre J. A., “Transcranial optical monitoring of cerebrovascular hemodynamics in acute stroke patients,” Opt. Express 17(5), 3884–3902 (2009). 10.1364/OE.17.003884 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Irwin D., Dong L., Shang Y., Cheng R., Kudrimoti M., Stevens S. D., Yu G., “Influences of tissue absorption and scattering on diffuse correlation spectroscopy blood flow measurements,” Biomed. Opt. Express 2(7), 1969–1985 (2011). 10.1364/BOE.2.001969 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Carp S. A., Dai G. P., Boas D. A., Franceschini M. A., Kim Y. R., “Validation of diffuse correlation spectroscopy measurements of rodent cerebral blood flow with simultaneous arterial spin labeling MRI; towards MRI-optical continuous cerebral metabolic monitoring,” Biomed. Opt. Express 1(2), 553–565 (2010). 10.1364/BOE.1.000553 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Boas D. A., Campbell L. E., Yodh A. G., “Scattering and imaging with diffusing temporal field correlations,” Phys. Rev. Lett. 75(9), 1855–1858 (1995). 10.1103/PhysRevLett.75.1855 [DOI] [PubMed] [Google Scholar]
- 12.Yu G., Floyd T. F., Durduran T., Zhou C., Wang J., Detre J. A., Yodh A. G., “Validation of diffuse correlation spectroscopy for muscle blood flow with concurrent arterial spin labeled perfusion MRI,” Opt. Express 15(3), 1064–1075 (2007). 10.1364/OE.15.001064 [DOI] [PubMed] [Google Scholar]
- 13.Shang Y., Chen L., Toborek M., Yu G., “Diffuse optical monitoring of repeated cerebral ischemia in mice,” Opt. Express 19(21), 20301–20315 (2011). 10.1364/OE.19.020301 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Zhou C., Eucker S. A., Durduran T., Yu G., Ralston J., Friess S. H., Ichord R. N., Margulies S. S., Yodh A. G., “Diffuse optical monitoring of hemodynamic changes in piglet brain with closed head injury,” J. Biomed. Opt. 14(3), 034015 (2009). 10.1117/1.3146814 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Roche-Labarbe N., Carp S. A., Surova A., Patel M., Boas D. A., Grant P. E., Franceschini M. A., “Noninvasive optical measures of CBV, StO(2), CBF index, and rCMRO(2) in human premature neonates’ brains in the first six weeks of life,” Hum. Brain Mapp. 31(3), 341–352 (2010). 10.1002/hbm.20868 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Culver J. P., Durduran T., Furuya D., Cheung C., Greenberg J. H., Yodh A. G., “Diffuse optical tomography of cerebral blood flow, oxygenation, and metabolism in rat during focal ischemia,” J. Cereb. Blood Flow Metab. 23(8), 911–924 (2003). 10.1097/01.WCB.0000076703.71231.BB [DOI] [PubMed] [Google Scholar]
- 17.Favilla C. G., Mesquita R. C., Mullen M., Durduran T., Lu X., Kim M. N., Minkoff D. L., Kasner S. E., Greenberg J. H., Yodh A. G., Detre J. A., “Optical Bedside Monitoring of Cerebral Blood Flow in Acute Ischemic Stroke Patients During Head-of-Bed Manipulation,” Stroke 45(5), 1269–1274 (2014). 10.1161/STROKEAHA.113.004116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhou C., Shimazu T., Durduran T., Luckl J., Kimberg D. Y., Yu G., Chen X. H., Detre J. A., Yodh A. G., Greenberg J. H., “Acute functional recovery of cerebral blood flow after forebrain ischemia in rat,” J. Cereb. Blood Flow Metab. 28(7), 1275–1284 (2008). 10.1038/jcbfm.2008.21 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Durduran T., Choe R., Yu G., Zhou C., Tchou J. C., Czerniecki B. J., Yodh A. G., “Diffuse optical measurement of blood flow in breast tumors,” Opt. Lett. 30(21), 2915–2917 (2005). 10.1364/OL.30.002915 [DOI] [PubMed] [Google Scholar]
- 20.Sunar U., Makonnen S., Zhou C., Durduran T., Yu G., Wang H. W., Lee W. M. F., Yodh A. G., “Hemodynamic responses to antivascular therapy and ionizing radiation assessed by diffuse optical spectroscopies,” Opt. Express 15(23), 15507–15516 (2007). 10.1364/OE.15.015507 [DOI] [PubMed] [Google Scholar]
- 21.Sunar U., Quon H., Durduran T., Zhang J., Du J., Zhou C., Yu G., Choe R., Kilger A., Lustig R., Loevner L., Nioka S., Chance B., Yodh A. G., “Noninvasive diffuse optical measurement of blood flow and blood oxygenation for monitoring radiation therapy in patients with head and neck tumors: a pilot study,” J. Biomed. Opt. 11(6), 064021 (2006). 10.1117/1.2397548 [DOI] [PubMed] [Google Scholar]
- 22.Huang C., Radabaugh J. P., Aouad R. K., Lin Y., Gal T. J., Patel A. B., Valentino J., Shang Y., Yu G., “Noncontact diffuse optical assessment of blood flow changes in head and neck free tissue transfer flaps,” J. Biomed. Opt. 20(7), 075008 (2015). 10.1117/1.JBO.20.7.075008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Shang Y., Gurley K., Symons B., Long D., Srikuea R., Crofford L. J., Peterson C. A., Yu G., “Noninvasive optical characterization of muscle blood flow, oxygenation, and metabolism in women with fibromyalgia,” Arthritis Res. Ther. 14(6), R236 (2012). 10.1186/ar4079 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Durduran T., Yu G., Burnett M. G., Detre J. A., Greenberg J. H., Wang J., Zhou C., Yodh A. G., “Diffuse optical measurement of blood flow, blood oxygenation, and metabolism in a human brain during sensorimotor cortex activation,” Opt. Lett. 29(15), 1766–1768 (2004). 10.1364/OL.29.001766 [DOI] [PubMed] [Google Scholar]
- 25.Zhou C., Yu G., Furuya D., Greenberg J., Yodh A., Durduran T., “Diffuse optical correlation tomography of cerebral blood flow during cortical spreading depression in rat brain,” Opt. Express 14(3), 1125–1144 (2006). 10.1364/OE.14.001125 [DOI] [PubMed] [Google Scholar]
- 26.Lin Y., Huang C., Irwin D., He L., Shang Y., Yu G., “Three-dimensional flow contrast imaging of deep tissue using noncontact diffuse correlation tomography,” Appl. Phys. Lett. 104(12), 121103 (2014). 10.1063/1.4869469 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Zhang X., Gui Z., Qiao Z., Liu Y., Shang Y., “Nth-order linear algorithm for diffuse correlation tomography,” Biomed. Opt. Express 9(5), 2365–2382 (2018). 10.1364/BOE.9.002365 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Cheung C., Culver J. P., Takahashi K., Greenberg J. H., Yodh A. G., “In vivo cerebrovascular measurement combining diffuse near-infrared absorption and correlation spectroscopies,” Phys. Med. Biol. 46(8), 2053–2065 (2001). 10.1088/0031-9155/46/8/302 [DOI] [PubMed] [Google Scholar]
- 29.Dong L., He L., Lin Y., Shang Y., Yu G., “Simultaneously extracting multiple parameters via fitting one single autocorrelation function curve in diffuse correlation spectroscopy,” IEEE Trans. Biomed. Eng. 60(2), 361–368 (2013). 10.1109/TBME.2012.2226885 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Baker W. B., Parthasarathy A. B., Busch D. R., Mesquita R. C., Greenberg J. H., Yodh A. G., “Modified Beer-Lambert law for blood flow,” Biomed. Opt. Express 5(11), 4053–4075 (2014). 10.1364/BOE.5.004053 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Shang Y., Li T., Chen L., Lin Y., Toborek M., Yu G., “Extraction of diffuse correlation spectroscopy flow index by integration of Nth-order linear model with Monte Carlo simulation,” Appl. Phys. Lett. 104(19), 193703 (2014). 10.1063/1.4876216 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Shang Y., Yu G., “A Nth-order linear algorithm for extracting diffuse correlation spectroscopy blood flow indices in heterogeneous tissues,” Appl. Phys. Lett. 105(13), 133702 (2014). 10.1063/1.4896992 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Molins A., Stufflebeam S. M., Brown E. N., Hämäläinen M. S., “Quantification of the benefit from integrating MEG and EEG data in minimum l2-norm estimation,” Neuroimage 42(3), 1069–1077 (2008). 10.1016/j.neuroimage.2008.05.064 [DOI] [PubMed] [Google Scholar]
- 34.Donoho D. L., “For most large underdetermined systems of linear equations the minimal l(1)-norm solution is also the sparsest solution,” Commun. Pure Appl. Math. 59(6), 797–829 (2006). 10.1002/cpa.20132 [DOI] [Google Scholar]
- 35.Vapnik V., Statistical Learning Theory (Wiley, New York, 1998). [Google Scholar]
- 36.Vapnik V., The Nature of Statistical Learning Theory (Springer, Berlin, 1999). [Google Scholar]
- 37.Cherkassky V., Ma Y., “Practical selection of SVM parameters and noise estimation for SVM regression,” Neural Netw. 17(1), 113–126 (2004). 10.1016/S0893-6080(03)00169-2 [DOI] [PubMed] [Google Scholar]
- 38.Nong J., “Parameters Selection and Noise Estimation of SVM Regression,” in Fifth International Joint Conference on Computational Sciences and Optimization(IEEE, 2012), pp. 118–122. 10.1109/CSO.2012.33 [DOI] [Google Scholar]
- 39.Li T., Gong H., Luo Q. M., “Mcvm: Monte Carlo Modeling of Photon Migration in Voxelized Media,” J. Innov. Opt. Health Sci. 3(02), 91–102 (2010). 10.1142/S1793545810000927 [DOI] [Google Scholar]
- 40.Koppel D. E., “Statistical Accuracy in Fluorescence Correlation Spectroscopy,” Phys. Rev. A 10(6), 1938–1945 (1974). 10.1103/PhysRevA.10.1938 [DOI] [Google Scholar]
- 41.Dietsche G., Ninck M., Ortolf C., Li J., Jaillon F., Gisler T., “Fiber-based multispeckle detection for time-resolved diffusing-wave spectroscopy: characterization and application to blood flow detection in deep tissue,” Appl. Opt. 46(35), 8506–8514 (2007). 10.1364/AO.46.008506 [DOI] [PubMed] [Google Scholar]
- 42.Li T., Lin Y., Shang Y., He L., Huang C., Szabunio M., Yu G., “Simultaneous measurement of deep tissue blood flow and oxygenation using noncontact diffuse correlation spectroscopy flow-oximeter,” Sci. Rep. 3(1), 1358 (2013). 10.1038/srep01358 [DOI] [PMC free article] [PubMed] [Google Scholar]