Quantitative real-time pulse oximetry with ultrafast frequency-domain diffuse optics and deep neural network processing

Abstract

Pulse oximetry is a ubiquitous optical technology, widely used for diagnosis and treatment guidance. Current pulse oximeters provide indications of arterial oxygen saturation. We present here a new quantitative methodology that extends the capability of pulse oximetry and provides real-time molar concentrations of oxy- and deoxy-hemoglobin at rates of up to 27 Hz by using advanced digital hardware, real-time firmware processing, and ultra-fast optical property calculations with a deep neural network (DNN). The technique utilizes a high-speed frequency domain spectroscopy system with five frequency-multiplexed wavelengths. High-speed demultiplexing and data reduction were performed in firmware. The DNN inversion algorithm was benchmarked as five orders of magnitude faster than conventional iterative methods for optical property extractions. The DNN provided unbiased optical property extractions, with an average error of 0 ± 5.6% in absorption and 0 ± 1.4% in reduced scattering. Together, these improvements enabled the measurement, calculation, and real-time continuous display of hemoglobin concentrations. A proof-of-concept cuff occlusion measurement was performed to demonstrate the ability of the device to track oxy- and deoxy-hemoglobin, and measure quantitative photoplethysmographic changes during the cardiac cycle. This technique substantially extends the capability of pulse oximetry and provides unprecedented real-time non-invasive functional information with broad applicability for cardiopulmonary applications.

1. Introduction

Pulse oximetry is a ubiquitous optical technology used for the measurement of arterial oxygen saturation and pulse rate in hospital and out-patient settings. First utilized as early as the 1940s [1], pulse oximetry is a critical tool for monitoring oxygen transport in the body. This information is essential for patient care in a variety of clinical situations, including anesthesia monitoring [2], post-operative evaluation [3], triage [4], and for monitoring patients with reduced lung function due to asthma [5] or chronic obstructive pulmonary disorder [6]. Arterial oxygen saturation measured by pulse oximetry has been proposed as the “fifth vital sign”, with some suggesting that it be viewed with the same level of importance as blood pressure and pulse rate [7,8]. Conventional pulse oximeters use ratiometric multi-wavelength transmission or reflectance measurements in superficial tissue to calculate arterial oxygen saturation. Measurements are collected with at least two illumination wavelengths in the near-infrared (NIR) to provide differential contrast to oxy and deoxy-hemoglobin. The measurement of the time-varying optical changes that occur during the cardiac cycle allows pulse oximetry to isolate the arterial vascular compartment, which, unlike the venous compartment, undergoes volume changes with each beat of the heart [9]. Additionally, the utilization of the ratiometric optical signal avoids the confounding effects of optical scattering, which would otherwise limit the ability to quantify absorption-related metrics including hemoglobin concentrations. In practice, ratiometric measurements are typically calibrated using a precomputed correction factor (determined using invasive co-oximetry), and reported as an absolute value of oxygen saturation [10].

While there is no question about the clinical importance of arterial oxygen saturation, current pulse oximeters generally focus on this single parameter, and lack the ability to provide more comprehensive hemodynamic information, including independent and quantitative measurements of oxyhemoglobin, deoxyhemoglobin, and total hemoglobin. These additional parameters have the potential to increase the diagnostic and prognostic potential of pulse oximetry, and real-time, non-invasive hemodynamic monitoring more generally, but require more advanced optical measurements and analysis techniques that have not been yet been integrated into real-time methodologies. To date, both hardware and software bottlenecks severely limit the ability of relevant technologies to extract quantitative hemodynamic parameters at a sufficient measurement rate to capture the cardiac cycle in real-time [11,12]. For example, the two most common quantitative oximetry techniques, time-domain diffuse optical spectroscopy (TD-DOS) and frequency-domain diffuse optical spectroscopy (FD-DOS), which have the unique capability of disentangling the effects of optical scattering from absorption-based hemoglobin measurements, are typically used to monitor relatively slow changes in tissue hemoglobin concentrations, with measurements often taking several seconds or longer [13]. Additionally, the extraction of molar concentrations of oxy- and deoxy-hemoglobin using TD-DOS and FD-DOS requires significant data processing, including the use of light transport models and data fitting, resulting in substantial post-acquisition bottlenecks [14,15]. In this work we overcome these limitations to develop a new technique that is capable of noninvasively quantifying and displaying absolute concentrations of oxy- and deoxy-hemoglobin in real-time. To accomplish this, we have leveraged our recent work in the development of ultrafast FD-DOS hardware [16], together with new developments in real-time firmware data processing, as well as an unprecedented improvement in the speed of optical property extractions through a new deep neural network (DNN) inversion algorithm. In the following sections, we will show that the integration of these advances enables the calculation and display of quantitative hemoglobin concentrations at a rate of up to 27 Hz.

2. Methods

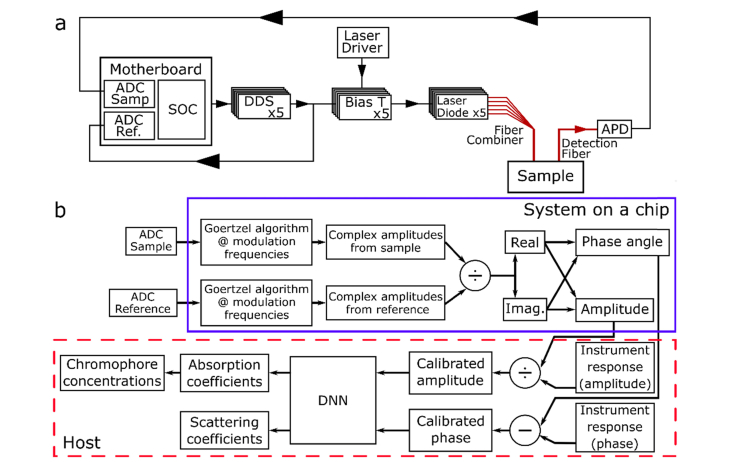
A schematic diagram of the custom hardware used in this study is shown in Fig. 1(a). This hardware is described in detail in our previous publication [16]. Briefly, five near infrared lasers (690, 785, 808, 830, and 850 nm) were modulated at different radio frequencies using five direct digital synthesis boards (DDS) controlled by a single board computer (MircoZed Zynq-7010 SOC). The light from each laser was coupled into separate 400 µm optical fibers and then combined into a single ferrule and placed in contact with the sample surface. Remitted light was collected by a 3 mm diameter optical fiber bundle in a reflectance geometry. A source-detector separation of 10 mm was used for all measurements. A 3 mm active area avalanche photodiode (Hamamatsu, S11519-30) was used as an optical detector, and the resulting analog signal was digitized with a 2-channel, 12 bit, 250 MHz analog to digital converter (ADC). A reference signal taken directly from the DDS boards was recorded on the second channel of the ADC and used to remove the modulation frequency dependent instrument response.

Fig. 1.

(a) Schematic diagram of the system. A system on a chip (SOC) drives 5 direct digital synthesis boards (DDS) to modulate 5 lasers which were combined and passed through a sample. An optical fiber collected the multiply scattered light, which was detected by an avalanche photo diode (APD). The APD signal was digitized by one channel of an analog to digital converter (ADC). The second channel of the ADC digitized a reference signal from the DDS boards. Each time the system was restarted, a measurement was taken on a calibration phantom (not shown) to calculate the instrument response. (b) Schematic diagram of the signal processing pathway. Items inside the blue box (solid line) were performed on the SOC. Items in the red box (dashed line) were performed on the host computer.

For each acquisition, the amplitude and phase of the light passing through the sample was measured at 35 modulation frequencies between 50 and 288 MHz in steps of 7 MHz. Collected signals were aliased by the ADC at modulation frequencies above 125 MHz due to the sampling rate of the ADC. Aliasing did not lead to any loss of information in this case because the laser modulation frequencies always mapped to unique and non-overlapping frequencies in the baseband. Since the modulated signals are narrow-band with known frequencies, the amplitude and phase could be extracted from the undersampled signals [16]. While theoretically only one modulation frequency is necessary to separate absorption from scattering [17], other groups have found that using multiple frequencies resulted in measurements that were less susceptible to noise [15,18]. The choice of 35 frequencies represented a compromise between data quality and acquisition speed. The five lasers were frequency multiplexed and offset from each other in 7 MHz increments. For each frequency, 4096 samples were collected and stored on the SOC for demultiplexing.

System calibration was performed using a tissue-simulating phantom with known optical properties (i.e. absorption (µ_a) and reduced scattering (µ_s′)). Measurements of this optical phantom were used to determine the instrument response of the system, which was removed from subsequent measurements. A phantom fabricated and characterized for a previous multi-center clinical study of FD-DOS was used for calibration [14]. Following calibration, the amplitude and phase measurements collected from a sample were used as input to a deep neural network (DNN) inversion algorithm, which mapped amplitude and phase to optical properties (described in Section 2.2). Least squares fitting was used to determine hemoglobin concentrations from the resulting µ_a values based on published molar extinction coefficients for each chromophore at each wavelength [19].

2.1 Demultiplexing

A C++ implementation of the Goertzel algorithm was used to demultiplex the detected signal using the known modulation frequency of each laser. The Goertzel algorithm is a computationally efficient method for calculating an individual term of a discrete Fourier transform. This algorithm has been utilized previously for frequency-domain diffuse optics and many other applications, and details on the algorithm are readily available in literature [20,21]. In this work, the Goertzel algorithm was run by the SOC for each frequency step, for each laser, for both the sample and the reference channels to obtain the amplitude and phase of each signal. For a typical acquisition consisting of measurements from 5 lasers at 35 modulation frequencies from 2 channels (i.e. sample and reference), the Goertzel algorithm was run by the SOC 350 times per acquisition, resulting in a total of 70, 32 bit floating point values describing the amplitude and phase of each laser being transferred to the host computer at a repetition rate of approximately 27 times per second. The implementation of the Goertzel algorithm on the SOC reduced data transfer to the host computer by a factor of 3,500 × , removing a major barrier to real-time visualization.

2.2 Optical property extraction

Following the transfer of multi-wavelength amplitude and phase data to the host computer, an inversion algorithm was used to extract tissue optical properties. In prior comparable FD-DOS systems, an iterative algorithm (e.g. Levenberg–Marquardt) was used to fit the calibrated amplitude and phase values to an analytical forward model of photon transport in diffuse media [22]. This method is commonly utilized in the field, but is time-consuming due to its iterative nature, significantly limiting the achievable display rate.

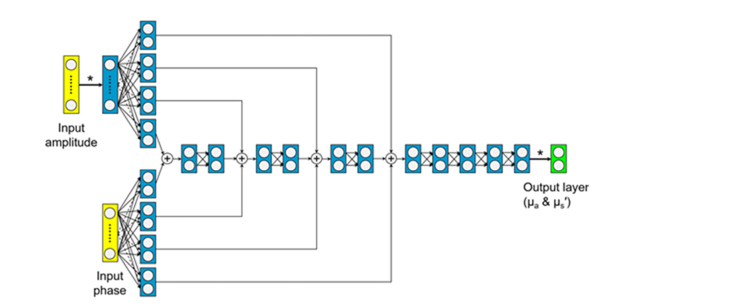
To overcome this limitation, we designed, trained, and tested a DNN as a new ultra-fast FD-DOS inversion algorithm. The DNN structure utilized for this work is a densely connected convolutional network (Fig. 2) based on ResNet and DenseNet. This network structure tends to have fewer free parameters than other DNN structures, and is faster to train without loss of accuracy [23,24]. Calibrated amplitude and phase data from 35 modulation frequencies was used as input to the DNN. The phase and amplitude were processed by four layers, each with two neurons. The output of those layers were added, and the result was used as the input to four fully-connected layers, each with two neurons. The final output of the DNN was an estimate of the optical properties of the sample.

Fig. 2.

Diagram of the structure of the deep neural network used to estimate absorption and scattering from calibrated amplitude and phase. Input nodes are shown in yellow, open circles indicate neurons, solid lines represent connections between layers, and the output layer is shown in green. Asterisks denote scaling of the input amplitude at the beginning and descaling at the end. The structure was chosen to have relatively few free parameters to decrease training time and reduce the likelihood of overfitting.

The DNN was trained using a data set generated by the analytical model described above. To generate the training data, a wide range of optical properties were sampled on a grid, with µ_a sampled from 0.001 mm⁻¹ to 0.05 mm⁻¹ in increments of 0.001 mm⁻¹, and µ_s′ sampled from 0.5 mm⁻¹ to 1.5 mm⁻¹ in increments of 0.01 mm⁻¹. These values of absorption and scattering were chosen to cover the range of typical optical properties of tissue at the near-infrared wavelengths utilized in this system. This resulted in 5050 optical property pairs with amplitude and phase values at each of the 35 modulation frequencies. The training was performed using TensorFlow with Keras as a high-level API. The training used Adam optimization with an initial learning rate of 0.001 and batch size of 128 [25]. The activation function for each neuron was a hyperbolic tangent sigmoid transfer function, which is nonlinear and maps data from (-∞, + ∞) to (−1, 1). The mean squared error was minimized as the loss function. Training of the DNN took about one hour on a GPU-equipped desktop with Intel i7-7700K CPU and NVIDIA Geforce 1060 6GB GPU. Once trained, the final model was implemented as a MATLAB function to interface with the instrument front-end.

2.3 DNN accuracy and speed

The accuracy of optical property extractions with the DNN were evaluated using simulated data with and without noise. 10,000 random optical property pairs were generated, and the theoretical amplitude and phase values were calculated using the analytical model. Gaussian noise with standard deviations of 1%, 5%, 10%, and 20% was added to the theoretical values of amplitude and phase, and the noisy data were processed using both the iterative method and the DNN. New optical property pairs were generated for each noise level. The accuracy of each method was assessed by comparing the extracted optical properties with the known optical properties.

To compare the speed of the DNN with the iterative method, first amplitude and phase values for 10, 100, 1,000, and 10,000 randomly generated optical property pairs were calculated. 2% Gaussian noise was added to the amplitude values and 8% noise was added to the phase values. The distribution of noise was derived from measuring the noise characteristics of the instrument itself. The optical property extraction computation time was measured on a desktop PC with an Intel i7-6700 CPU. Timing from 10 sets of random optical property values were used to calculate the mean and standard deviation of execution time. For DNN processing, the measured time approached the resolution of the Matlab timing functions. To account for this, each optical property set was calculated by the DNN 500 times to allow a measurable amount of time to pass. The values reported are the measured time divided by 500. Similarly, each set of optical properties calculated with the iterative method was performed twice and the final reported value is the time elapsed divided by 2.

2.4 Human measurement

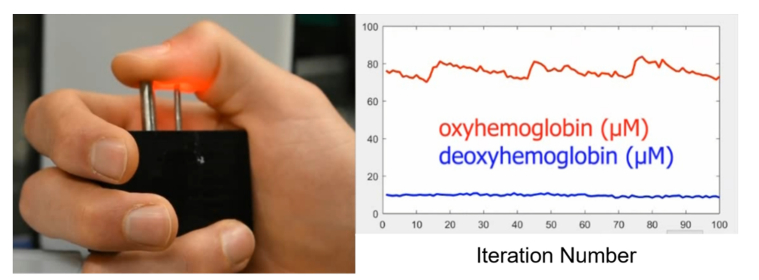
To test the utility of this device in an in vivo setting, oxy- and deoxy-hemoglobin concentrations (µM) were measured on the thumb of a healthy volunteer before, during, and after an arterial occlusion on the upper arm. All procedures were approved by the Boston University Institutional Review Board. Following informed consent, the volunteer placed his thumb on the source and detector fibers of the device (Fig. 3). The thumb was chosen for ease of measurement and because it consistently yielded a strong pulsatile signal when using a source-detector separation of 10 mm. The source-detector separation was chosen to maximize the signal-to-noise ratio, and to match the depth of penetration of photons to the large arteries in the thumb located 1.5 to 2.5 mm below the skin surface [26]. Forward models of photon propagation in tissue show a mean photon depth of ~2 mm when a 10 mm source-detector separation is used [27]. A real-time “pulse finder” was implemented by continuously displaying the measured amplitude of the 850 nm laser. This enabled placement of the probe in a location with a strong pulsatile signal. We and others, have observed that variations in probe-tissue contact pressure can induce artefactual changes in measured hemoglobin concentrations [28]. To minimize this effect, a pressure sensor (Interlink Electronics, FSR 400) was used to provide continuous feedback to the subject, which helped to maintain constant probe pressure. In total, 12,500 measurements were calculated from the subject at a rate of 27 Hz over approximately 8 minutes, and the data was displayed in real-time. For the first 2.5 minutes the subject was asked to sit quietly. Following this baseline measurement, the subject inflated a blood-pressure cuff to 200 mmHg. The pressure was maintained for 2.5 minutes and then released. The remainder of the time was used to observe the recovery.

Fig. 3.

A still image from Visualization 1 ^{(7.5MB, avi)} depicting the instrument front-end showing real-time traces of oxy- and deoxy-hemoglobin during the measurement procedure. Inset: synchronized video of the subject’s hand during acquisition. Light from the source-fiber (right silver ferrule) passes through the thumb and is collected by the detector fiber (left silver ferrule).

3. Results

3.1 Accuracy and speed

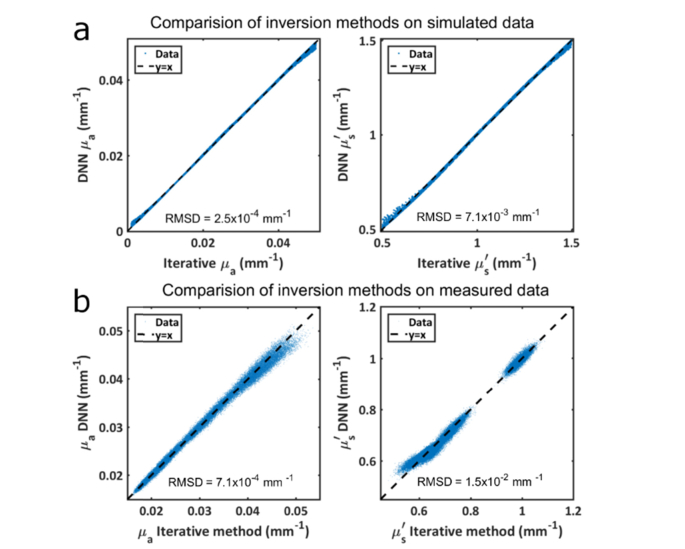
Table 1 shows a summary of accuracy results comparing the iterative and DNN methods. In general, the DNN was found to be highly accurate when tested using simulated data. The DNN provided unbiased optical properties estimates when tested without noise, with a mean error of 0 mm⁻¹. The standard deviation of the errors was less than 5% in absorption, and less than 1% in scattering. Under the same conditions, the iterative model yielded no errors, which is unsurprising as the same model was used for data generation and fitting. When 5% Gaussian noise was added to both amplitude and phase, both the DNN and the iterative method were again unbiased (a mean error of 0%). In this case, the iterative method yielded errors with a standard deviation of 2.1% and 1.3% for µ_a and µ_s′ respectively. The DNN had slightly worse performance, yielding errors with a standard deviation of 5.6% and 1.4%. A comparison between the two methods is shown graphically in Fig. 4 for the case of no noise (panel a) and for in vivo data (panel b). The root mean squared difference (RMSD) between the two methods using simulated data was 0.0003 mm⁻¹ for µ_a and 0.007 mm⁻¹ for µ_s′. Using experimental data, the RMSD was 0.0007 mm⁻¹ for µ_a and 0.002 mm⁻¹ for µ_s′.

Table 1. Average ± standard deviation percent error in optical property extraction based on 10,000 randomly generated optical property pairs for the iterative and deep neural network (DNN) methods. Gaussian noise with the noted standard deviation was added to both amplitude and phase.

	Percent Error
	Iterative		DNN
	µa	µs′	µa	µs′
No noise	0.0 ± 0.0%	0.0 ± 0.0%	0 ± 4.8%	0.0 ± 0.88%
1% noise	0.0 ± 0.42%	0.0 ± 0.26%	0 ± 5.2%	0.0 ± 0.90%
5% noise	0 ± 2.1%	0 ± 1.3%	0 ± 5.6%	0 ± 1.4%
10% noise	0 ± 4.3%	0 ± 2.6%	1 ± 7.2%	0 ± 2.5%
20% noise	2 ± 9.0%	1 ± 5.2%	1 ± 11%	0 ± 1.8%

Fig. 4.

(a) Comparison of optical property values between the iterative and DNN methods using simulated data without adding noise. The root mean squared difference between the two methods is noted in each plot along with the black dashed identity line. (b) The same comparison using experimental data from a human subject. The gap in scattering values from ~0.8 to ~0.9 mm⁻¹ is due to the wavelength dependent nature of scattering. Scattering coefficients clustered around 1 mm⁻¹ are from 690 nm photons which experience significantly more scattering than the longer wavelengths used.

The DNN was substantially faster at extracting optical properties than the iterative method. Execution times for both methods are tabulated in Table 2. On average, a single optical property extraction using the iterative method took approximately 20 ms and only 9 µs using the DNN. Five optical property inversions are required for each chromophore extraction (i.e. one inversion per wavelength). Overall, the DNN was 3-5 orders of magnitude faster than the iterative method under comparable conditions.

Table 2. Average ± standard deviation of execution times for the indicated number of optical property extractions. Measurement was repeated 10 times. 2% and 8% Gaussian noise was added to amplitude and phase respectively to simulate an experimental measurement.

	Run Time
# of Inversions	Iterative (s)	DNN (µs)
10	0.20 ± 0.011	93 ± 6
100	2.02 ± 0.050	140 ± 7
1,000	20.1 ± 0.24	680 ± 97
10,000	220 ± 21	5000 ± 1400

3.2 In vivo testing

When improvements in hardware, firmware, inversion algorithm, and visualization were integrated into a single system and data stream, optical properties and tissue chromophores were visualized at 27 Hz.

Molar concentrations of oxyhemoglobin and deoxyhemoglobin from a normal volunteer undergoing an arterial occlusion was collected, processed, and displayed in real-time. Figure 5 shows traces of the tissue oxy- and deoxy-hemoglobin concentrations derived from the µ_a values output by the DNN. A video captured during the measurement demonstrating the real-time capability of the system is shown in Visualization 1 ^{(7.5MB, avi)} . Following the acquisition, the same data was saved and processed using the iterative method. A comparison of the optical property extractions obtained by the two methods is shown in Fig. 4(b), which are in good agreement.

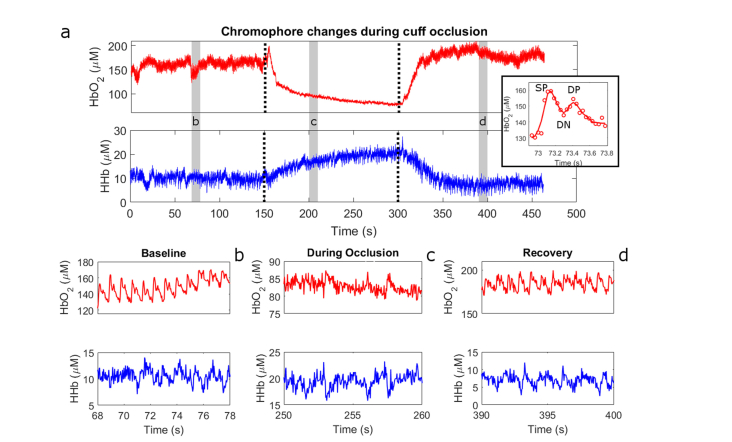
Fig. 5.

(a) Tissue oxyhemoglobin (top) and deoxyhemoglobin (bottom) traces from the thumb of a human subject. Dotted lines indicate the start and end of an arterial occlusion on the upper arm. Gray boxes indicate the regions that are zoomed in in panels (b)-(d). Note the disappearance of the pulsatile signal during the occlusion in panel (c). Inset: Oxyhemoglobin changes over a single pulse. Data points are indicated with circles and the line is a 7-point loess fit to those points. Features of the pulse such as the systolic peak (SP), dicrotic notch (DN), and diastolic peak (DP) are readily appreciated.

The overall trends observed during the cuff occlusion here are similar to those reported in literature [29,30]. For example, the values of oxy- and deoxy-hemoglobin are relatively stable during the 2.5-minute baseline acquisition. There is a substantial drop in oxyhemoglobin and a concomitant rise in deoxyhemoglobin during the occlusion as oxygen is consumed by metabolically active tissue. There is a sharp rebound in oxyhemoglobin above the baseline after the occlusion, followed by a settling towards the baseline value. Deoxyhemoglobin shows a steady decline towards the baseline level of approximately 10 µM after the occlusion. Previous measurements using this system on the forearm [16], showed hemoglobin saturation levels close to 50%. The saturation values we observe here are greater than 90%, which likely indicates probing of the superficial arterial compartment.

Unlike prior reports, pulsatile changes in oxyhemoglobin concentration are also clearly observable during the baseline and recovery stages when viewed over a smaller timescale (Fig. 5(b) and 5(d)). The period of these changes is approximately 0.9 s, matching a normal adult pulse rate. Oxyhemoglobin pulsations are attributed to the cardiac cycle, and result from the expansion of vessels in the highly-oxygenated arterial vascular compartment following systole, ultimately increasing the total amount of oxygenated blood in the probed volume. The systolic peak, diastolic peak, and dicrotic notch are clearly visible in each pulse (see inset of Fig. 5(a)). These features are commonly observable with photoplethysmography (PPG), but our system is the first to report these values in quantitative (i.e. µM) fashion without the use of simplifying assumptions such as time-invariant optical scattering or guesses about the initial tissue chromophore concentrations. No pulsatile changes were observed during the occlusion (Fig. 5(c)) as blood flow from the heart was mechanically obstructed during this phase of the study.

4. Discussion

In this work we have demonstrated that the combination of recently developed ultrafast frequency-domain diffuse optics with improvements in firmware and deep neural network processing can provide real-time and accurate extractions of optical properties and chromophore concentrations. Combined, these advances enable a powerful tissue oxygenation monitor that is capable of acquiring, processing, and displaying absolute concentrations of hemoglobin at rates sufficient to capture the cardiac cycle.

This work has several important implications. For example, the clinical measurement of total hemoglobin currently requires invasive blood draws followed by blood-gas analysis, a procedure that requires relatively long intervals between repeated measures due to labor and cost constraints. Additionally, invasive blood sampling can sometimes exacerbate conditions such as bleeding or anemia [31]. The non-invasive and real-time display of total hemoglobin can potentially address these limitations for a number of clinical scenarios. For example, this method could be used to speed the diagnosis of anemia (abnormally low concentrations of hemoglobin), or polycythemia (abnormally high concentrations of hemoglobin). Additionally, this method may assist in tracking changes in tissue hemoglobin concentrations that can result from hemorrhage (i.e. hypovolemia) or the administration of fluids [32]. In these circumstances, careful monitoring and management of hemoglobin levels has been shown to be essential for recovery [33]. Similarly, during blood transfusion the maintenance of total hemoglobin levels within a normal range has been shown to be crucial for reducing the risk of mortality [34]. In both cases, the real-time continuous assessment of hemoglobin concentrations could have a significant impact on the ability to respond to changes in the clinical setting. Independent measurements of oxy and deoxyhemoglobin has been less explored for their diagnostic and prognostic potential, but may provide additional clinical opportunities.

The ability to extract hemoglobin concentrations at a sufficient rate to capture the cardiac cycle is also potentially enabling for a number of applications. The pulsatile changes measured in this study are similar to photoplethysmography (PPG) waves provided by some conventional pulse oximetry devices and dedicated PPG devices, and the shape of these PPG signals has been shown to aid in the diagnosis of shock, peripheral artery disease, and arrhythmias [35]. This method extends beyond traditional PPG however, in that it provides absolute changes in µ_a (mm⁻¹) and oxy and deoxyhemoglobin (µM) during each cardiac cycle. This information could be used to determine new quantitative and disease specific thresholds for diagnosis, potentially improving the diagnostic potential beyond current PPG.

There are several prior reports of quantitative pulse oximetry methods. For example, Franceschini et al. reported a system that utilized multi-distance frequency-domain measurements to extract arterial and total tissue saturation from tissue [36]. In that work, the authors utilized a single modulation frequency of 110 MHz, and updated µ_s′ estimates every 10 seconds. Additionally, their total measurement repetition rate was approximately 4.5 Hz. This method was advanced in later work and applied to the extraction of venous oxygen saturation [37]. More recently, Farzam et al. utilized a similar frequency-domain technique to quantify optical property changes in bone, capturing approximately 8 measurements during each cardiac cycle [38]. Our method is different from these prior examples in a number of key ways. First, the current system utilizes a single source-detector separation, and a sweep of modulation frequencies, which has been shown to improve optical property extractions [15,18]. Second, these prior methods utilized either a hybrid frequency-domain and continuous wave technique in which frequency domain data was used to update and correct for photon pathlengths at regular intervals [36,37], or a relatively slow frequency-domain approach [38]. In contrast, the current system acquires and processes frequency-domain data in real-time, providing µ_a and µ_s′ at a rate of up to 27 Hz, approximately 4x faster than prior works. This allows the probe position to be moved on tissue without re-calibration of pathlength correction. It also allows for finer detail of the PPG signal to be obtained using only frequency-domain measurements, including the identification of features such as the dicrotic notch. Additionally, it provides this information, along with chromophore extractions, in real-time for immediate clinical feedback.

In this work acquisition speed is limited by the demultiplexing currently performed on the SOC. Going forward, further improvements in acquisition speed and signal-to-noise ratio (SNR) are possible through the implementation of the Goertzel algorithm in a field programmable gate array, which would enable in-line demultiplexing of the signal, potentially increasing the acquisition rate up to several kilohertz. While few biological changes happen at these speeds, this advance would enable more samples per frequency to be collected, or multiple samples to be averaged to increase the SNR.

Finally, we note that although this work represents the first use of a DNN to provide real-time optical property extractions from frequency-domain diffuse optical measurements, other neural network structures may further improve accuracy and speed of optical property inversions. In this work, we used a multilayer structure with cross-layer connections, an architecture inspired by DenseNet and ResNet [23,24]. Alternatively, convolutional neural network layers could be used to encode phase and amplitude measurements at multiple modulation frequencies. A fully-connected layer could then be added to invert optical properties. It is possible that such a convolutional structure may lead to fewer trainable parameters and improved training efficiency while potentially maintaining comparable accuracy.

In conclusion, this work demonstrated a substantial advance towards “quantitative pulse oximetry”, by demonstrating that tissue optical properties and hemoglobin concentrations can be extracted and visualized in real-time at an unpresented repetition rate. The additional information provided by this technique is likely to provide significant diagnostic and prognostic value for a wide range of clinical applications.

Funding

Department of Defense (Award No. W81XWH-15-1-0070), The Coulter Foundation, Boston University’s Office of Technology Transfer, and American Cancer Society (Grant No. RSG14-014-01-CCE).

Disclosures

The authors declare that there are no conflicts of interest related to this article