Three Dimensional Ultrashort Echo Time Imaging with Tri-component Analysis for Human Cortical Bone

Abstract

Purpose:

To investigate tri-component analysis of human cortical bone using a multi-peak fat signal model with 3D ultrashort echo time (UTE) Cones sequences on a clinical 3T scanner.

Methods:

Tri-component fitting of bound water, pore water, and fat content using a multi-peak fat spectra model was proposed for 3D UTE imaging of cortical bone. 3D UTE Cones acquisitions combined with tri-component analysis were used to investigate bound and pore water T2*s and fractions, as well as fat T2* and fraction in cortical bone. Feasibility studies were performed on nine human cortical bone (HCB) specimens with regions of interests (ROIs) selected from the endosteum to the periosteum in four circumferential regions. Microcomputed tomography (μCT) studies were performed to measure bone porosity and bone mineral density (BMD) for comparison and validation of the bound and pore water analyses.

Results:

The oscillation of the signal decay was well-fitted with proposed tri-component model. The sum of the pore water and fat fractions from tri-component analysis showed a high correlation with μCT porosity (R=0.74, P<0.01). Estimated bound water fraction also demonstrated a high correlation with BMD (R= 0.70, P<0.01).

Conclusion:

Tri-component analysis significantly improves the estimation of bound and pore water fractions in human cortical bone.

Introduction

Bone fracture is a widespread problem that affects over 75 million people worldwide and that results in more than 2.3 million osteoporotic fractures per year globally [1]. Historically, investigations into factors which underlie bone fracture risk have focused on evaluation of areal bone mineral density (aBMD) [2, 3]. However, numerous studies have pointed to other more complex factors at multiple scale lengths as contributors to bone fragility [4], including bone geometry and microarchitecture [5,6], and, of increasing focus, water content. Most water in cortical bone exists in the ‘bound’ form, either loosely bound to the organic matrix or tightly bound to mineral [7,8]. A smaller fraction of water exists in the ‘free’, or ‘pore’, form, residing within the pores of the Haversian canals, as well as within the lacunae and canaliculi systems [9]. The loosely bound water (BW) provides information on bone organic matrix density, whereas the pore water (PW) provides information on cortical porosity [10]. It is of critical importance to separate these two water components during analysis, as they provide complementary information about bone biomechanics [11].

In recent years, based on both two-dimensional (2D) and 3D ultrashort echo time (UTE) sequences, bi-component exponential T2* fitting has been extensively studied as a method to separate bound and pore water in order to quantify matrix density and porosity [12–14]. T2* of BW is about 10 times shorter than that of PW, and can therefore be separated using UTE acquisitions combined with bi-component analysis [9]. Bae et al. reported a moderate correlation between human bone PW fraction and micro-computed tomography (μCT) porosity (R²= 0.31) [15]. More recently, Seifert et al. reported a good correlation between the long T2* fraction and μCT porosity (R²= 0.70 at 1.5 T and R²= 0.50 at 3 T), as well as between short T2* fraction and organic matrix density (R²= 0.63 at 1.5 T and R²= 0.44 at 3 T) [16]. Other UTE-based biomarkers have also been reported to correlate well with μCT based results, such as effective T2* [17], dual UTE magnitude ratio [18], magnetization transfer ratio [19], and macromolecular proton fraction [20].

In addition to the bound and pore water components, human cortical bone may possess a considerable amount of fat that contributes to the total MRI signal. Several studies have observed oscillation of the multi-echo MRI signals during the bi-component fitting procedure [21,22]. Li reported observing oscillation of the signal when using bi-component fitting for human cortical bone, a phenomenon most likely due to the chemical shift caused by the fat in human cortical bone (HCB) [23]. Therefore, to improve the accuracy of bound and pore water quantification and evaluation in cortical bone, we propose a tri-component fitting method that incorporates a multi-peak spectral modeling of fat content.

In this study, the effects of fat on the quantifications of bound and pore water were first simulated using bi- and tri-component models. Then, HCB specimens were scanned using UTE MRI technique, and the results were analyzed by bi-component and tri-component fittings. The bi- and tri-component results were compared, then statistical correlations were calculated between MRI results and μCT-based porosity, and between MRI results and bone mineral density (BMD).

Methods

Pulse sequence

MRI of the specimens was performed on a 3T MR750 scanner (GE Healthcare, Waukesha, Wisconsin, USA) using a previously reported 3D UTE Cones sequence [24,25]. An eight-channel transmit/receive knee coil was used for signal excitation and reception. Scanning parameters included: field of view (FOV)=12 cm, sampling bandwidth=125 kHz, sampling window=1504 μs, flip angle=10°, TR=50 ms, voxel size= 0.5×0.5×2.0 mm³. UTE images were acquired with a series of 18 TE delays (9 sets of dual echo UTE acquisitions with 18 TEs of 0.032, 0.2, 0.4, 0.6, 0.8, 1.2, 1.6, 2.4, 3.0, 3.6, 4.4, 5.2, 6.0, 6.8, 7.6, 15, 20, 25 ms). Scan time was 108 minutes for all sequences.

Multi-component signal model

T2* can be measured through exponential fitting of UTE images acquired at progressively increased TEs. For bi-component fitting, two components, namely a short T2* component and a longer T2* component, were assumed. With this model, the UTE MR signal is given by equation (1),

$$S^{*}\left(t\right)=F_s\times e^{-\frac{t}{T_{2S}^{*}}}+F_L\times e^{-\frac{t}{T_{2L}^{*}}}+noise$$ (1)

where S*(t) is the normalized UTE MR signal, F_S and F_L are the fractions of the short and long T2* components, respectively (F_S + F_L = 1), and noise is white Gaussian noise. To better describe the component fractions, R_SL is defined in equation (2) as the ratio between short and long component fractions.

$$R_{SL}=\raisebox{1ex}{$F_S$}\!\left/ \!\raisebox{-1ex}{$F_L$}\right.$$ (2)

However, for HCBs, equation (1) is not correct for most cases since it does not consider fat in the model. Therefore, in our study, we proposed a new tri-component fitting model, which includes a fat component in addition to the water component. Specifically, multi-spectral lipid peaks in bone were considered in the tri-component model, as shown in equation (3),

$$S^{*}\left(t\right)=F_s\times e^{-\frac{t}{T_{2S}^{*}}}+F_L\times e^{-\frac{t}{T_{2L}^{*}}}+F_F\times e^{-\frac{t}{T_{2F}^{*}}}\sum _n{\alpha }_n{e}^{-i2\pi f_{n}t}+noise$$ (3)

where α_n is the relative amplitude of the n^th spectral peak of fat, f_n is the corresponding multi-spectral peak frequency shift, and F_F is fat fraction, such that F_S + F_L + F_F = 1. In this study, we assumed that there was no significant difference between the fat in bone marrow and fat present in other adipose tissue models based on Ren’s study [26]; therefore, we adopted a 9-peak fat model [27].

Simulation

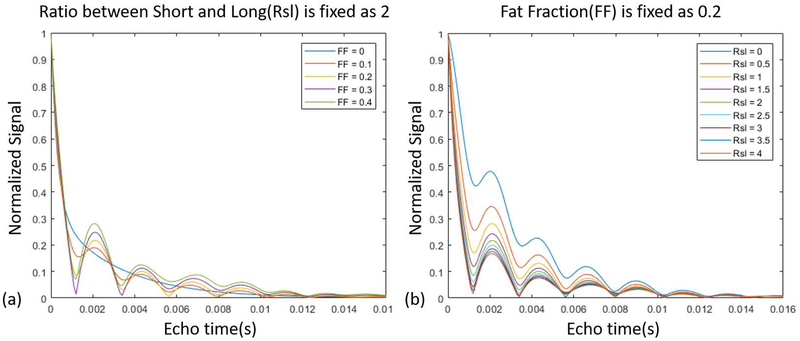
Many factors may affect the final results of bi-component or tri-component fitting, such as the signal-to-noise ratio (SNR) and the number of fitting components [28]. To observe the effects of fat on different components proportions, free induction decay signals for different R_SL and F_F values were simulated, as shown in Figure 1. Numerical simulation studies were also performed on both the bi-component and tri-component models and compared together, as presented in Supporting Information Figures S1 and S2.

Figure 1.

Signal simulation based on a tri-component model (without noise). (a) shows how the signal changes for different fat fractions (F_F), while the ratio between the short T2* (bound water) and long T2* (pore water) components (R_SL) is fixed as 2. (b) shows how the signal changes for different R_SL values, while F_F is fixed as 0.2.

In vitro study

Nine cortical bone specimens were harvested from fresh-frozen human tibial midshafts (n=9, 63±19 years old, 5 females and 4 males) provided by a nonprofit whole-body donation company (United Tissue Network, Phoenix, AZ). Bone specimens were cut to 25 mm in length using a Delta Shop Master band saw (Delta Machinery, Tennessee, USA). Bone specimens were stored in phosphate buffered saline (PBS) solution for 2 hours prior to imaging.

Data Fitting Analysis

The bi- and tri-component analysis algorithms were written in MATLAB (The Mathworks Inc., Natick, MA, USA) and executed offline on the DICOM images (only containing MRI magnitude signals). Bi-exponential and tri-exponential signal decay fittings, described above, were performed for T2* and fraction measurements of shorter and longer T2* water components, with additional fat fraction and fat T2* measurements obtained for tri-exponential fitting. For both the simulation and in vitro datasets, the initial F_F, F_S, and F_L values were equal to 0.33, while initial $T_{2F}^{*}$, $T_{2S}^{*}$, and $T_{2L}^{*}$ values were 5, 0.3, and 10 ms, respectively. The program allowed manual placement of regions of interest (ROIs) on the first image of the series. ROIs were then copied to each subsequent image. The mean intensity within each of the ROIs was used for subsequent curve fitting. The fitting was based on a least square curve fitting algorithm (lsqcurvefit in MATLAB).

μCT image analysis

A 5-mm thick section was cut from each of nine bone specimens at their middle length using a precise low speed saw (Isomet 1000, Buehler, USA). The short specimens were scanned all together using a Skyscan 1076 μCT scanner (Kontich, Belgium) at 8.78 μm isotropic voxel size. Other scanning parameters were as follows: 0.05 mm aluminum plus 0.038 mm copper filter, 100 kV, 100 mA, 0.4° rotation step, 4 frame averaging, 6 hours total scan time.

MRI results from one 2-mm slice were compared with the average calculated from 222 slices of μCT data (8.87 μm thick). Twelve ROIs were selected at three cortical bone bands (from the endosteum to the periosteum) and at four anatomical sites (anterior, mid-medial, mid-lateral, and posterior). For each bone specimen, the MRI image was registered to the μCT-based porosity map by deriving the affine transform using four manually selected matched points in both datasets.

All data analyses were performed using MATLAB. The μCT data were processed to calculate the average porosity map for an axial 2-mm slice of the bone samples. A single gray level threshold was used for image segmentation to distinguish between bone and pores. This threshold was selected for each dataset using the peaks of gray level histograms and visual inspection of the raw images. The porosity pixel maps were generated by superimposing all 222 binary images. BMD was calculated for each voxel by comparing its gray level with the average gray level of the scanned hydroxyapatite phantom with known density (0.25 and 0.5 gr/cm³).

Statistical analysis

For all 100 ROIs from 9 bones (4 ROIs from 1 bone sample, 12 ROIs from other 8 bone samples), the following comparisons were made: (1) fraction of the longer T2* component from bi-component analysis (F_L_2com) with μCT porosity, (2) fraction of the longer T2* component from tri-component analysis (F_L_3com) with μCT porosity, (3) the sum of fat fraction and fraction of the longer T2* component from tri-component analysis (F_F+F_L_3com) with μCT porosity, (4) fraction of the shorter T2* component from bi-component analysis (F_S_2com) with μCT-based BMD, and (5) fraction of the shorter T2* component from tri-component analysis (F_S_3com) with μCT-based BMD. For more detailed investigations, the Pearson’s correlations coefficients between all bi-component and tri-component parameters against the μCT-based results were calculated within the four studied tibial regions (anterior, mid-medial, mid-lateral, and posterior).

Results

Comparisons between bi- and tri-component simulation results are shown in Figure 1. The simulations in Figure 1 (a) illustrate the fat fraction impact on the signal decay pattern, such that increasing the fat fraction enhances the oscillation levels. Figure 1 (b) shows the impact of R_SL on the signal decay pattern. Figure S1 presents a comparison between the estimated fractions and T2* values obtained from bi- and tri-component fittings on the simulated signals.

Figure 2 shows typical mapping results for a representative bone specimen. Figures 2 (b), (e), and (j) demonstrate the porosity maps from μCT, F_L_2com, and F_L_3com, respectively. Local maxima in both F_L_2com (e) and F_L_3com (f), as shown by red arrows, correspond to void regions in the porosity map (b), indicating that PBS resided in the pores of bone during MRI scanning. Figures 2 (c), (f), and (k) show the μCT-based BMD mapping, F_S_2com, and F_S_3com, respectively. F_S_3com clearly demonstrates more similarity to BMD mapping compared with F_S_2com.

Figure 2.

Typical mapping results for one bone specimen (73-year-old male). (a) is the μCT image. (b) and (c) are the porosity maps and BMD maps obtained from the μCT results. (d) is the magnitude of the corresponding UTE image with echo time of 0.032ms. (e) and (f) are the short and long T2* component fraction maps obtained from bi-component fitting analysis. (i), (j), and (k) are fat, short, and long T2* component fraction maps obtained from tri-component fitting analysis. Red arrows in (a) and (b) indicate pores in bone, while arrows in (d), (e), and(j) indicate residual PBS in the pores, which resulted in high MRI signal, as well as high fraction of long T2* component.

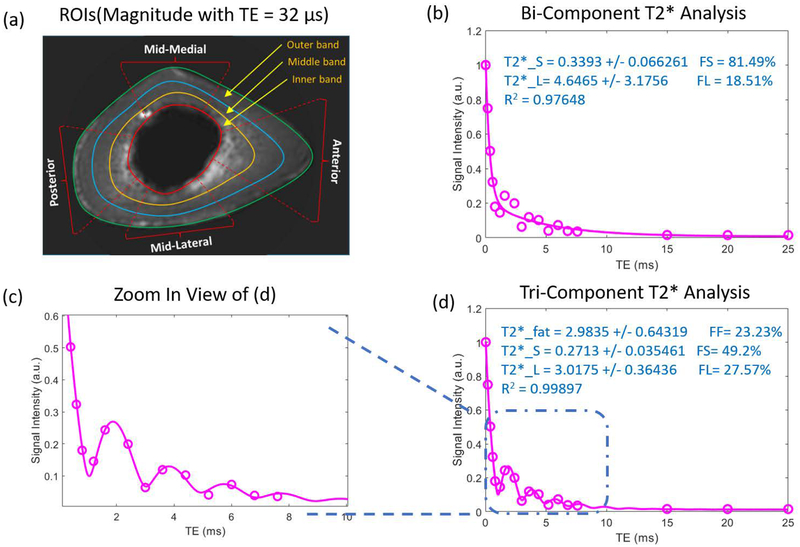
A selection of typical ROIs for one bone specimen is shown in Figure 3 (a), where the bone is divided into four zones: anterior, posterior, mid-medial, and mid-lateral. Each zone is also separated into three bands: inner, middle, and outer band. Figures 3 (b, d) show bi-component and tri-component fitting results for the ROI at the middle band of the anterior zone. Additionally, the zoom-in fitting curve shows that the tri-component model fit the actual data points better than the bi-component model did. The UTE image SNR (mean signal in ROI divided by signal standard deviation in background) at four representative ROIs selected in the bone middle band were 65.5, 36.3, 37.5, and 34.5, respectively.

Figure 3.

ROI selection for one human cortical bone specimen MRI image at echo time of 0.032ms (a) and typical fitting results of both bi-component and tri-component analyses for anterior middle band (b, d). (c) is the enlarged view of the fitted results of the oscillation area.

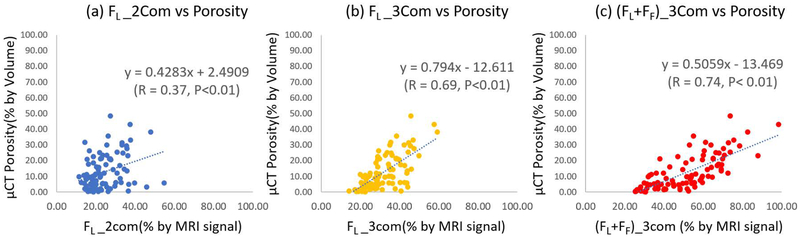
Figures 4 (a)–(c) show the correlations of F_L_2com, F_L_3com, and (F_L + F_F)_3com with μCT porosity for all analyzed ROIs, respectively. The Pearson correlation coefficient between (F_L + F_F)_3com and μCT porosity (R=0.74) was much higher than F_L_2com and F_L_3com correlation coefficients with porosity (R=0.37 and R=0.69, respectively).

Figure 4.

Scatter plots and linear regressions of μCT porosity on pore water fractions estimated with bi-component and tri-component fittings. (a) shows μCT porosity versus pore water fraction estimated with bi-component fitting (F_L_2com), (b) shows μCT porosity versus pore water fraction estimated with tri-component fitting (F_L_3com), and (c) shows μCT porosity versus the sum of pore water fraction and fat fraction estimated with tri-component fitting ((F_L+F_F)_3com).

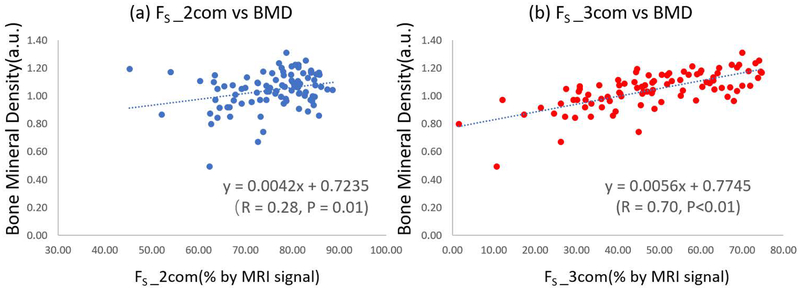
Figures 5 (a) and (b) show the regression analyses of F_S_2com and F_S_3com versus μCT-based BMD, with correlation coefficients equal to 0.28 and 0.70, respectively.

Figure 5.

Scatter plot and linear regression analyses of μCT-based BMD on bound water fractions estimated with bi-component and tri-component fitting. (a) shows μCT BMD versus bound water fraction estimated with bi-component fitting (F_S_2com), while (b) shows μCT BMD versus bound water fraction estimated with tri-component fitting (F_S_3com).

Table S1 presents the Pearson’s correlations between bi-component and tri-component parameters against the μCT results. Considering all studied ROIs, the correlations coefficients between μCT results and tri-component fractions were higher compared with those between μCT and bi-component fractions. Figure S3 shows how the average F_F+F_L_3com correlated with average μCT based porosity where both demonstrated decreasing patterns from inner band towards outer band. However, the average F_L_2com did not decrease progressively from inner band towards outer band.

Discussion

In this study, a tri-component model for T2* analyses in human cortical bone was proposed to include consideration of the chemical shift from fat. Oscillation of the MRI signal was well-fitted using the proposed tri-component model, with improved correlation coefficients over conventional bi-component fitting. As Biswas et al. and Li et al. [13, 23] have both shown, signal oscillation caused by fat in human cortical bone is inevitable. Although the fat content in bone marrow has been extensively studied, the effect of fat in the middle and outer layers of the cortical bone is still unclear. As highlighted in this study with 3D UTE Cones sequence, the fat content in all cortical bone layers must be considered when analyzing the bone water fractions.

MRI correlations with μCT-based porosity suggested that the tri-component model provides a more accurate estimation of the pore water (F_L) and bound water (F_S) fractions compared with bi-component model. A large number of ROIs (i.e., 100) from nine human cortical bone specimens were analyzed with both MRI and μCT. MRI data with 18 different TEs using 3D UTE cones sequences were fitted with both bi-component and tri-component models. The (F_L + F_F)_3com revealed the highest correlation with porosity measured by μCT (R=0.74), which suggests that the bone pores not only contain a pore water component, but also a fat component.

Ex vivo experiments of human cortical bones showed that short T2* component fraction (F_S) estimated from tri_component fitting was much lower than that of bi-component fitting, especially in the inner and middle bands of the bone (Figures 2 (f) and (k)). This phenomenon is well explained in the simulation study results. As seen in Figure 1, the signal from a tri-component fitting model drops sharply at ultrashort echo times (0–8 ms). In bi-component fitting models, much of the contributions from fat are counted as bound water, resulting in a higher BW fraction and, consequently, a higher estimate of R_SL. This overestimation of bound water (F_S) in bi-component fitting is inevitable even with optimized TE selection.

The large offset and change in slope between μCT and MR measures of porosity, as shown in Figure 4, were mainly due to the huge difference in spatial resolution, or voxel size, in μCT and MR imaging. In μCT, the porosity is calculated as the ratio of pore volume and total bone volume, whereas in MR imaging, the porosity is calculated as the pore water fraction. Our μCT imaging system had a limited spatial resolution with a voxel size of 9 μm. Therefore, small pores (e.g., lacunae and canaliculi, smaller than 9 μm in diameter) could not be detected by μCT. However, by using UTE MRI, pore water in both large and small pores could be estimated by separating pore water and bound water signal via bi-component or tri-component fitting. Consequently, although the small pores themselves did not contribute to μCT porosity, pore water which was present in those small pores contributed to UTE MRI porosity. As a result, pore water fraction measured by MRI was always higher than μCT porosity. Similar offset between μCT volume-based porosity and MRI signal-based porosity can be seen in the literature [29].

This study had several limitations. Firstly, UTE images with 18 different TEs required 108 minutes. Reduced echo numbers and optimized TE selection for tri-component fitting will be needed for future clinical studies. Secondly, intra-voxel dephasing caused by background gradients, which can bias T2* quantification, was not considered in this study, since the main focus was to investigate the tri-component model and its advantages over the bi-component model. In the next stage, we will explore how spatial resolution affects T2*s and relative fractions in bi-component and tri-component analyses and will explore potential techniques to correct for intra-voxel dephasing [30]. Thirdly, a relatively small number of human cortical bone samples (n = 9) were investigated, although a relatively large number of ROIs (n = 100) were analyzed in this study. More human cortical bone samples from different donors are likely to further increase the statistical significance of this study. Fourthly, the multi-peak fat spectra model was adopted from the fat model in liver, with reference to the fat model in marrow at 7T, based on an assumption that the fat in the cortical bone has no significant difference from other adipose tissue. The literature lacks a comprehensive report on fat peak modelling in cortical bone.

Conclusion

The 3D cones UTE tri-component T2* fitting method proposed in this study was based on a multi-peak spectroscopy fat model. The presented tri-component model was able to accurately quantify T2* and fractions of bound and pore water in cortical bone. The increased accuracy of tri-component analysis over bi-component analysis was demonstrated using μCT-based porosity and BMD measurements in 9 human tibial bone samples. The oscillation of the signal decay for selected ROIs was well-fitted with the proposed tri-component model. The sum of pore water and fat fractions from tri-component fitting resulted in the highest correlation with porosity measured, suggesting a new potential biomarker for evaluation of bone quality for future clinical practice.

Supplementary Material

Supp info

Supporting Information Table S1. Pearson's correlation coefficients between bi-component and tri-component analyses against μCT-based results.

Supporting Information Figure S1. Simulation study for the T2* value estimation of both short T2* (bound water) and long T2* (pore water) components with the bi-component and tri-component fitting models. When fat fraction is almost zero (0.01), as shown in (a) and (b), both bi-component and tri-component obtain correct T2* of short and long T2* component. When fat fraction is 0.2, as shown in (c) and (d), T2* of long T2* component is overestimated with bi-component analysis and a large standard deviation is found; meanwhile, T2* of long T2* component is still correct with tri-component analysis.

Supporting Information Figure S2. Simulation study for the fractions of both short T2* (bound water) and long T2* (pore water) components with the bi-component and tri-component fitting models. When fat fraction is as low as 0.01, as shown in (a) and (b), both bi-component and tri-component obtain correct fraction of short and long T2* component. When fat fraction is 0.1, as shown in (c) and (d), fraction of short T2* component is overestimated and fraction of long T2* component is underestimated with bi-component analysis, while fractions of both short and long T2* component are still correct with tri-component analysis.

Supporting Information Figure S3. Statistical results for the three ROI regions (inner band, middle band, outer band). Pore water fraction estimated from bi-component fitting (FL_2com) shows no trend for the three bands, while the sum of pore water fraction and fat fraction estimated with tri-component fitting (FL + FF)_3com shows progressive decrease from inner to outer bands; this trend correlates very well with μCT porosity.