Spatial Analysis of Multichannel Surface EMG in Hemiplegic Stroke

Abstract

We investigated spatial activation patterns of upper extremity muscles during isometric force generation in both intact persons and in hemispheric stroke survivors. We used a 128-channel surface electromyogram (EMG) grid to record the electrical activity of biceps brachii muscles during these contractions. EMG data were processed to develop 2-dimensional root mean square (RMS) maps of muscle activity. Our objective was to determine whether motor impairments following stroke were associated with changes in the muscle activity maps and in the spatial distribution of muscular activation.

We found that, for a given subject, spatial patterns in muscle activity maps were consistent across all measured contraction levels differing only the RMS EMG. However, the maps from opposite arms (stroke-affected vs. non-affected) of stroke survivors were significantly different from each other, especially when compared to the differences observed intact participants.

Our analyses revealed that chronic stroke altered the size and the location of the active region in these maps. The former is potentially related to disruption of fiber and tissue structure, possibly linked to factors such as extracellular fat accumulation, connective tissue infiltration, muscle fiber atrophy, fiber shortening and fiber loss. Changes in spatial patterns in muscle activity maps may also be linked to a shift in the location of the innervation zone or the endplate region of muscles. Furthermore, the textural analysis of EMG activity maps showed a larger pixel-to-pixel variability in stroke-affected muscles.

Alterations in the muscle activity maps were also related to functional impairment (estimated using Fugl-Meyer score, FM) and to the degree of spasticity (estimated using the modified Ashworth scale, MAS). Overall, our investigation revealed that the muscle architecture and morphology were significantly altered in chronic stroke.

I. INTRODUCTION

STROKE is one of the leading causes of long-term disability in the United States, with an annual incidence of approximately 800,000 [1]. Motor deficits following stroke are most evident in the contralesional (opposite of the lesion side of the brain) limbs, and may involve muscle weakness, fatigue, abnormal muscle tone, and joint and muscle contracture [2–4]. Stroke may also lead to alterations in the overall morphology, micro-architecture, and functionality of skeletal muscles [5–13]. Possible mechanisms for these morphological changes include fiber atrophy [4, 5], connective tissue infiltration [4, 9, 14–16], shifts in fiber type (from type II to type I) [4, 8–10], shortening of muscle fibers by virtue of sarcomere loss [3, 11, 17–20], increased variability in muscle fiber size [21], changes in mechanical stiffness [11, 22–25], fiber and motor unit loss [26, 27] and fiber re-innervation [6, 10]. The muscle morphological changes can, in turn, affect individual muscle functionality as well as inter-muscular coordination and lead to degradation of motor functions.

Recently, it has been shown that multichannel surface EMG grid electrodes may help us gather information about neural inputs to muscle as well as structural data about a given muscle [28–30]. Apart from the conventional time-domain and spectral analysis of EMG signals leading to information about motor neurons, estimation of the muscle fiber conduction velocity, and identification of innervation zones, the multichannel EMG data can be used to develop 2-dimensional root mean square (RMS) maps, usually referred to as the muscle activity maps [31, 32]. These maps are a graphical representation of the EMG amplitude (RMS) across the muscle surface, and provide activation information in a novel spatial form [31]. The muscle activity maps can be used to examine spatial distributions of muscle activity under various conditions, and can provide descriptions of motor unit recruitment and firing rate properties [33–35]. These maps have also been analyzed to investigate spatial distribution of muscle activity in intact participants for various applications including ergonomics, exercise, and sports [31, 33]. Analogous spatial patterns in EMG maps have even been analyzed as potential signals for robotic arm control [36].

The objective of our study was to use spatial muscle activity maps to characterize potential alterations in the muscle architecture and function following stroke. Our hypothesis is that if muscle fiber loss or atrophy is fiber-type dependent, we might expect to see regional variations in activation, linked to the uneven distribution of fiber types throughout the muscle [4, 37–39]. Alternatively, if there is an extensive infiltration of collagenous tissue, we might expect to see more diffused muscle activity map with a higher pixel-to-pixel variation at all contraction levels [4, 16]. Finally, if motor unit loss prevailed, we might expect to see patchy activation, with evidence for altered innervation zones (IZ) [26, 27].

In line with our hypothesis, we found that the muscle activity maps were substantially altered following stroke; specifically, we observed changes in size the activity region, the location of IZ (endplate region) and in pixel-to-pixel variability.

II. METHODS

We recorded multichannel surface EMG and force data from biceps brachii muscles in both arms of hemispheric stroke survivors and intact participants. The institutional review board of the Northwestern University approved the protocol, and all volunteers provided informed consent before the experiment. A total of sixteen hemiplegic chronic stroke survivors and nine intact volunteers participated in the study. The median age of stroke survivors was 58 years with a range of 39 to 70 years, and the median of ‘time since stroke’ was 6.6 years with a range of 2 to 26 years. Stroke survivors’ clinical data in presented in Table 1. Three stroke survivors were unable to complete the study for the reasons mentioned in Table 1. The intact participants consisted of five male and four female volunteers with the age ranging from 22 to 78 years. All intact participants were right-hand dominant. A 128-channel surface EMG electrode grid in a 16×8 arrangement and w-EMG amplifier (developed at LISiN, Turin, Italy) was used to record monopolar (MP) EMG data at a sampling rate of 2441.4 Hz. The multichannel EMG grid had an inter-electrode distance of 10 mm in both horizontal and vertical directions, with a recording surface diameter of 3 mm for each electrode. The length and width of the EMG grid were approximately 16 cm and 8 cm that was sufficient to cover the biceps muscle.

Table 1.

Clinical information of stroke survivors

ID	Gender	Time since stroke (months)	Dominant / affected arm	FM (Fugl- Meyer)	MAS (Modified Ashworth score)
1	F	55	R/R	18	1
2	F	The participant was feeling fatigued.
3	F	The participant was feeling fatigued.
4	M	318	R/L	19	2
5	M	135	L/R	52
6	F	29	R/R	24	1+
7	F	134	R/R	16	2
8	F	44	R/R	36	1+
9	F	79	R/R	51	0
10	M	48	R/R	53	1
11	F	270	R/L	9	1+
12	F	The participant was unable to visit for the second session.
13	M	144	R/L	17	2
14	M	22	L/L	18	3
15	M	73	R/L	21	1+
16	F	109	R/R	49	1

A. EMG Data Recording.

Each participant was seated comfortably in a Biodex chair, with the elbow in approximately 120° flexion, shoulder in 10° flexion and 45° abduction, and the forearm pronated to 45°. To ensure isolation of the biceps brachii and thereby reduce contamination of force production from other muscles, we cast the forearm from elbow to fingers and secured the casted forearm in a custom-built fixture centered approximately at the wrist. The fixture was also attached to a six degree-of-freedom load cell (Delta SI-660–60 ATI, NC USA) to record force/torques generated at the wrist. The elbow was supported with rubber pads from bottom to keep the forearm parallel to the ground. Various key parameters were logged, including the length of the upper arm (from acromion to superior border of cubital fossa), the circumference of the biceps at the middle muscle belly, height of the Biodex chair, and moment-arm from lateral epicondyle to the load cell. A double-adhesive tape/foam was used to attach the multichannel surface EMG grid to muscle. The individual electrodes made contact with the skin through electrically conductive gel. To ensure consistent placement of grids on both arms of a person, we considered the line joining the acromion and the distal biceps tendon insertion to be the mediolateral center of the grid. We also marked muscle boundaries over the skin by palpation. The grid was placed over the muscle using the mediolateral center line and boundary markings; ensuring that the whole muscle was covered symmetrically by the grid [31]. The reference electrode was placed on the elbow (olecranon). The stroke-affected arm was tested in the first session and non-affected another session on a different day. Data from intact participants was recorded on the same day in two consecutive sessions. In Fig. 1A and B, we present our EMG data recording setup that included forearm casting, custom-built fixture, load cell and EMG grid.

Fig. 1:

Experimental setup for the surface EMG recording. (A) The arm cast, a custom-built fixture with a load cell, and 128-channel EMG grid electrode placed on the biceps of a stroke participant are shown. (B) A closer view of the EMG grid (16cm × 8 cm in size) covering the whole biceps muscle is shown. (C) The force profile of a representative participant is shown. Two repetitions of the same contraction with a rest of 75 secs were performed.

After securing the arm and placing the EMG grid over the biceps, we began by recording the maximum voluntary contraction (MVC) force at the elbow joint. Participants were required to generate their maximum elbow flexion force and hold for approximately 3 to 5 seconds. Two repetitions of the MVC were recorded. In case the force variability exceeded approximately 10% in the recorded MVC data, additional repetitions of MVC were performed. We allowed sufficient time between repetitions to avoid fatigue and discomfort. For the stroke participants, we used MVC of the affected arm to calculate different contraction levels for the experiment; we refer to this as the force-matching protocol [29, 40]. For intact participants, the MVCs of respective arms were recorded and used subsequently. After recording the MVC, each participant was required to perform two contractions at each of the five force levels, i.e., 20%, 30%, 40%, 50%, and 60% of the (affected) MVC in a randomized fashion. The EMG signals from the long head were recorded first and later from the short head of biceps brachii under similar conditions and without changing any hardware/software configurations. This practice was essential due to the limited capacity of the EMG amplifier hardware. We followed a trapezoidal force generation paradigm, where the participants were required to increase the force production slowly, maintain a constant force level for approximately ten seconds and then slowly decrease the force to the resting level. With a break of 1 to 2 minutes, the same force generation paradigm was repeated for the second trial. The force output from a representative participant is shown in Fig. 1C. The force and the EMG data were later processed using Spike2 (CED, Cambridge, England) and Matlab (Natick, MA, USA).

B. EMG Data Processing

The raw EMG signals were bandpass filtered (10–500 Hz) with an 8^th order Butterworth zero lag filter [41]. Later, five seconds of isometric EMG data from each trial was extracted discarding transitional parts of the EMG signal present at the start and end of each contraction. We visually analyzed frequency contents of the isometric EMG signal and did not observe significant powerline interference at 60 Hz and, therefore, no powerline filtering was performed. Isometric EMG data from both trials was combined that resulted in 10 secs long, 128-channel isometric MP EMG data stream.

1). Muscle activity maps (RMS EMG)

The EMG data was segmented into 250 milliseconds long analysis windows and RMS values in each window (40 windows) for all 128 channels were calculated using:

$${\text{RMS}}_k=\sqrt{\frac{1}{N}}{\sum }_i{x}_i^2,$$ (1)

where, N represents total samples of the raw signal for k^th EMG channel. We arranged the resulting 128-channel data in the form of 16×8 map reproducing the same spatial arrangement that was used to record the surface EMG data from the biceps muscle (long and short head). To remove the effect of contraction level and highlight spatial pattern in these maps, we normalized each map by dividing all RMS values (from 64 channels) with the maximum RMS value. The resulting normalized maps had a maximum value of one and a minimum value equal to any positive number less than one.

2). Support Vector Machine (SVM) classification

The SVM classifier was used to quantify whether the spatial pattern of muscle activation observed in normalized EMG RMS maps were consistent 1) across various contraction levels (20% to 60% MVC), and 2) between opposite arms (left vs. right in intact participants and stroke-affected vs. non-affected in stroke survivors). For this purpose, we used SVM classifier in one class classification (OCC) scheme which is specifically used to identify outliers in single-class data [42]. For the former analysis, normalized maps from all contraction levels of muscle were pooled and ten-fold cross-validation was performed. The pooled data was randomly divided into ten equal sized subsamples. Nine out of ten subsamples were used for training and the tenth one for validation and the procedure was repeated for ten times so that every subsample is used as testing data once. Finally, the ten-fold cross-validation scheme was repeated thirty times. For the later analysis, normalized maps from a biceps muscle (right for intact and non-affected for stroke) was used to train the SVM and maps from other biceps were used for testing the classifier.

3). Correlation and Euclidean distances

The correlation and similarity (or distance) between normalized maps of opposite arms were quantified considering each map representing a vector in a multidimensional space and calculating correlation and Euclidean distances as defined in Appendix I between these vectors. A significantly higher distance (correlation or Euclidean) value highlighted that two maps were widely different from each other and vice versa.

4). Muscle activity region – size and location

We defined a measure called the muscle activity region size, in units of the number of pixels, to quantify the active muscle region in a normalized EMG map [43]. In the EMG literature, various algorithms have been proposed to identify the active region automatically in muscle activity maps; however, we found that a simple thresholding at 70% of the maximum RMS EMG was sufficient [43]. Therefore, all EMG channels having normalized RMS amplitude value above 0.7 were considered active and counted to find the size of the active region. To find the center of the location of the muscle activity region, we found the EMG channel that had maximum RMS value. The location was specified in units of number pixels along the muscle fibers starting from the most distal row of EMG grid. Each pixel in the map represented a distance of 10 mm on the muscle. Later, we normalized the calculated location value by the number of EMG channels along muscle fibers (16). As the maximum MP EMG signal is observed around the endplate region or IZ [32], we consider this location as the IZ.

5). Monopolar (MP) to Single Differential (SD) ratio

There are numerous spatial filters available in the literature that can be used to improve spatial selectivity or remove non-propagating and common components from the surface EMG signals, e.g., single differential (SD), double differential (DD), or the Laplacian filter [44]. Extending the same concept of spatial selectivity and non-propagating/common signal components, we calculated the ratio of the EMG signal in MP and SD configurations. The MP and SD RMS values were used to calculate the MP to SD ratios (referred to as MP/SD) for all EMG channels using:

$$\text{MP}/{\text{SD}}_i=\frac{\text{RMS}\left[{\text{EMG}}_{\text{i}}\right]}{\text{RMS}\left[EM{G}_{i+1}-{\text{EMG}}_{\text{i}}\right]},$$ (2)

where EMG_i; represents raw MP EMG signal recorded from the i^th channel. The channel i and i + 1 are located along muscle fibers.

$$\text{Normalized}\text{MP}/\text{SD}=\frac{\text{MP}/\text{SDmap}\left(\text{Affected}\text{Biceps}\right)}{\text{MP}/\text{SDmap}(\text{Non\_Affected}\text{Biceps})},$$ (3)

where MP/SD_map represents spatial average of all MP/SD ratios in a map.

The proposed ratio quantifies the amount of non-propagating and common components of the EMG signal. A larger MP/SD ratio is an indication of increased common signal possibly linked to 1) an increased distance between the EMG source (i.e., the muscle fibers) and surface electrode, 2) muscle cross-talk, or 3) the end of fiber non-propagating components [45, 46]. The normalized MP/SD ratio represented relative (affected vs. non-affected) amount of non-propagating/common components in the EMG signal.

C. Textural Analysis

The pixel-to-pixel variability of muscle activity maps was quantified using the textural analysis techniques [47]. Each map was converted into grayscale image and gray level co-occurrence matrix (GLCM) was calculated. The GLCM is a histogram of co-occurring gray scale values at a specified offset and captures textural variations of an image [48, 49]. From the GLCM, we calculated two statistics, i.e., homogeneity and correlation (defined in Appendix III). The homogeneity is a measure of closeness of distribution of elements in the GLCM and ranges from 0 to 1. A less homogeneous map results in a lower value of the homogeneity. Similarly, the correlation is the measure of how correlated a pixel is to its neighbors over the whole image and ranges in value between −1 and 1. Both statistics are used to quantify textural variation or the pixel-to-pixel variability of images [47].

D. Statistical Analysis

All data were tested for normality separately using the Kolmogorov–Smirnov test, where the null hypothesis was that standardized data were following a standard normal distribution. We were unable to reject the null hypothesis at the 95% significance. Therefore, for all later analysis, parametric statistics were used to compare and analyze data considering the probability of type-I error α = 0.05. The statistical tests were performed in Matlab and IBM SPSS 21 (IBM, Armonk, NY).

The correlation/Euclidean distance data were analyzed using a linear model and mixed effect model to study the relationship between group type (i.e., intact or stroke referred to as the independent variable) and the correlation/Euclidean distance (dependent variable). We hypothesized that the correlation/Euclidean distance are a function of the group type (stroke or intact). In the linear model, we consider group type as fixed effect. While, in the mixed effects model, we considered group type as the fixed effect and subject as the random effect. P-values were obtained by simulated likelihood ratio tests of the full model with the random effect and the model without the random effect of subjects. We report F test results of the mixed model for the fixed effect of group type where the Satterthwaite approximation was used to estimate degrees of freedom.

III. RESULTS

The muscle activity maps are a representation of temporal as well as spatial muscular activation recorded from the surface of the muscle. Here, we present these maps and spatial patterns emerging from these maps in both intact participants and stroke survivors. We compare maps of opposite arms to show the effect of stroke. We note that maps from opposite arms of stroke survivors were considerably different from each other at all contraction levels as compared to intact participants.

A. Muscle Activity (RMS EMG) Maps

In Fig. 2A, we present monopolar EMG muscle activity maps from both arms of a representative intact participant. The maps show muscle activity in long and short heads of biceps muscle at five contraction levels (20% to 60% MVC). A gradual increase in EMG activity (dark pixels colors) is evident with increasing contraction. The maps show a unique muscle activation pattern, i.e., high EMG activity around muscle belly (over the IZ) that smoothly decreases towards both proximal and distal tendons [32, 50]. The spatial activity pattern conforms to the fusiform shape of the biceps muscle. In Fig. 2B, we present normalized (performed using maximum RMS EMG in a map) muscle activity maps of the same participant. The normalization accentuated the spatial activation pattern within each map and removed the effect of contraction level; and would thus allow comparison of spatial pattern across contraction levels. In Fig. 2B, the consistency of activation pattern between opposite arms (top and bottom maps with each column) is also evident.

Fig. 2 :

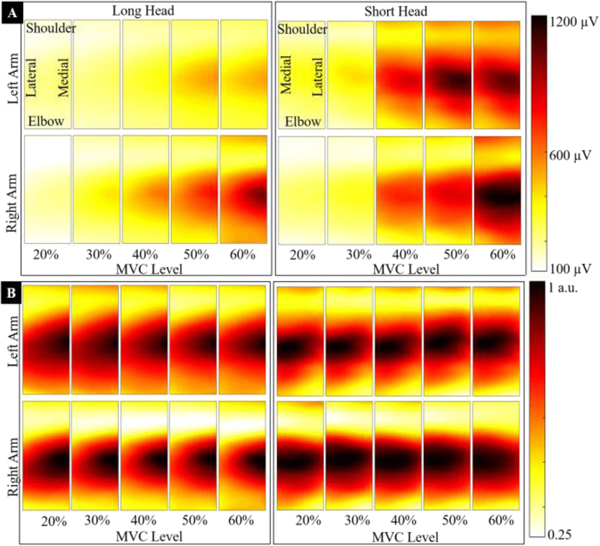
Muscle activity maps of a representative (non-normalized and normalized) intact participant are presented. (A) The maps show activation in the long and short heads (left and right of the fig. respectively) of biceps muscle at five contraction levels (20%, to 60% MVC). The top row of maps refers to the left arm and bottom to the right arm. Each column presents maps from opposite arms for the same contraction level. The anatomical orientation is marked on maps. The color scale for all maps varies between 100 μV (light yellow) to 1200 μV MP RMS EMG (dark red) and is shown on the right. A gradual increase in the RMS EMG with increasing contraction is evident. The muscle activity maps show a unique spatial pattern, i.e., a high MP EMG activity around muscle belly, i.e., over IZ that decreases smoothly towards the proximal and distal tendons. (B) The normalized maps (performed using the maximum RMS EMG value from each map) from the same participant are presented. A consistent spatial activation pattern is visually identifiable in all maps after normalization.

However, in case of stroke survivors we observed significant alterations in normalized maps as shown in Fig. 3. In one stroke survivor (Fig. 3A), we observed an enlargement (diffusion) of the muscle activity region, while in another (Fig. 3B), we observed contraction (shrinkage) of the activity region on the stroke-affected side. It is important to note that changes in the size of the activity region (diffusion or shrinkage) are consistent across all contraction levels.

Fig. 3:

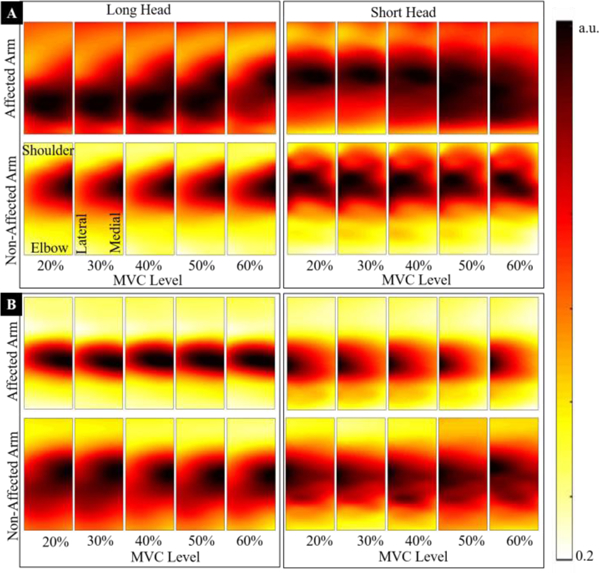
Normalized (performed with maximum RMS EMG of each map) muscle activity maps from biceps muscles of both arms of two representative stroke survivor are presented. The maps show activation in the long and short heads (left and right of the fig. respectively) of the biceps brachii at five contraction levels (20% to 60% MVC). The top row of maps refers to stroke-affected arm and bottom to the non-affected arm. Each column presents maps from opposite arms at same contraction. The consistency of spatial patterns across contraction levels in each muscle (head of the biceps) is also obvious. We observed two distinctly different patterns of muscle activation in the stroke-affected muscle. In (A), the activity region was increased, i.e., a diffused activity pattern was evident in stroke-affected muscles, while in another stroke participant (B), the activity region of the stroke-affected muscle was significantly reduced (shrunken).

B. Consistency of Spatial Patterns in Normalized Maps

The SVM classifier was used to quantify consistency of spatial activity pattern in maps 1) across contraction levels as well as, 2) of opposite arms. For the first case, using normalized maps from all different contraction levels, the estimated average misclassification or outlier rate across all participants is presented in Fig. 4A. The SVM algorithm was able to correctly classify more than 95% maps in each muscle (p<.05), i.e., less than 5% maps were classified as outliers. For later case, the normalized maps from right/non-affected limb were used to train the classifier and maps from left/stroke-affected arm were used for testing. The results are present in Fig. 4B, and we note significantly higher misclassification rate for stroke survivors (p<.05). Furthermore, the differences between maps of opposite arms were quantified using the normalized correlation and Euclidean distances calculated between maps of opposite arms and are shown in Fig. 5. The normalization was performed using the maxim value to scale y-axis between zero and one. We note that at each contraction level, the corresponding maps of stroke survivors showed higher Euclidean and correlation distances. Both linear fixed effect and mixed effect models were fitted to the data. A visual inspection of residual plots did not reveal any obvious deviations from homoscedasticity or normality. The mixed effect model performed significantly better than the linear model (p<.0001) for both dependent variables. The differences between both groups (stroke and intact) were significant, i.e., F(1, 37.15) = 40.51 and p <.001 for the correlation distance and F(1, 50.8) = 40.51 p < .001 for the Euclidean distance.

Fig. 4:

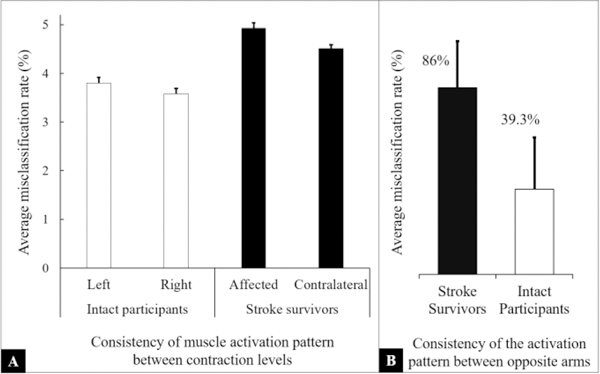
Quantification of consistency of spatial muscle activation patterns within a muscle (between contraction levels) and between muscles (opposite arms, left vs. right and stroke-affected vs. non-affected) is presented. (A) Average misclassification rate quantifying consistency of spatial muscle activation pattern between contraction levels for intact participants and stroke survivors is shown. The normalized muscle activity maps were used as the only feature for the SVM classifier. It is evident that the muscle activation patterns across all force levels were consistent, i.e., misclassification rate below 5%. (B) Average misclassification rate showing the consistency of muscle activity pattern between muscles of opposite arms are presented. The SVM classifier was trained using normalized muscle activity maps from right/non-affected biceps and tested using maps of left/affected maps. The classification errors increased for both intact as well as stroke participants. A substantial rise in the misclassification for stroke survivors was resulting from the fact that the muscle activity maps from opposite arms of stroke survivors were vastly different from each other.

Fig. 5:

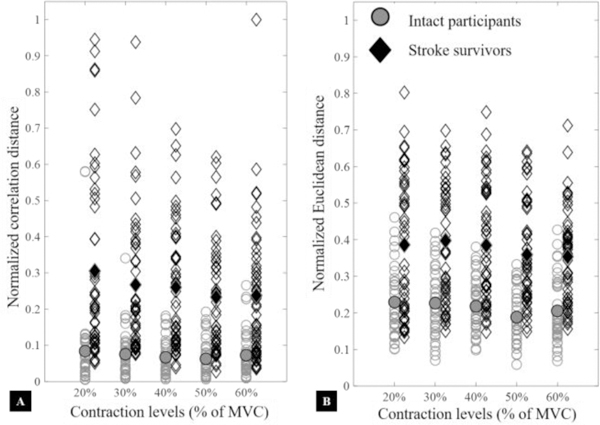
Normalized Euclidean and correlation distances between corresponding maps of stroke survivors and intact participants. Normalization was using the highest value to scale the y-axes from zero to unity. Empty shapes present distances between normalized muscle activity maps of opposite arms while the filled ones represent median values. Red and diamond shapes show distances (between opposite arms) for stroke survivors, and blue and circular shapes show the same for intact participants. We observed that corresponding maps of stroke survivors from opposite arms were less correlated and more distant from each other as compared to intact participants (p<.05).

C. Muscle Activity Regions in Stroke and Intact Participants

The size and the location of the center of the active region in muscle activity maps were calculated and analyzed for all stroke survivors and intact participants to quantify changes attributable to stroke. The percentage difference in the size of active regions between opposite arms of intact and stroke participants (left vs. right and stroke-affected vs. non-affected) was calculated and shown in Fig. 6A. We note that all intact participants showed a difference of 20% or less in the size of activity region between opposite arms. Furthermore, we observe that 56% (5 out of 9) showed a difference of less than 10%. However, in stroke survivors, we noted an opposite trend, i.e., substantial differences in the size of the active region (> 20%) were observed for more than half of the tested participants (54%). Similarly, we calculated the differences in the location of the IZ between opposite arms in intact and stroke participants in units of map pixels (EMG electrodes). Later, we calculated the number of participants for each value and present results in Fig. 6B. The bars in fig. represent the number of participants (intact or stroke) for each of the three categories, i.e., no difference in the location of IZ, a difference of one pixel, and a difference of two or more pixels between opposite arms. We noted that all intact participants showed a difference of one or fewer pixels. Moreover, 67% intact participants showed no difference in the location of the endplate region. However, for stroke survivors we observed that more than 50% participants showed differences of more than 2 pixels (20mm or more) between affected and non-affected muscles.

Fig. 6:

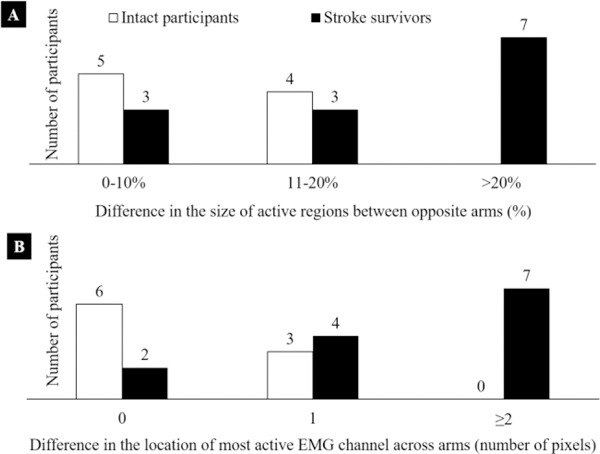
Number of participants, (stroke survivors and intact) falling into each of the three categories of differences in the size of the activity region between opposite arms. The first group represents a smaller difference in the size of activity regions in the range of 10% or less. Five intact and three stroke survivors fall into this category. The last category represents a considerable difference in the range of 20% or more. There are seven stroke survivors in this category and no intact participants. It is evident that stroke survivors showed significant differences in the size of active muscle region between their arms. However, such strong differences were not observed in intact participants. Number of participants, (stroke survivors and intact) falling into each of the three categories of differences in the location of the maximum activity channel between opposite arms. The location of the maximum activity channel represents the endplate region or the IZ. The first category represents no difference in the location between opposite arms while the last group represents a large difference of two pixels (20 mm) or more. There are seven stroke survivors in this category and no intact participants. It is evident that stroke survivors showed significant differences in the location of the IZ between their opposite arms. However, such strong differences were not observed in intact participants.

In Fig. 7, we present the normalized size of the active region (normalized using the size of the map, i.e., 64 pixels) and normalized location of IZ (normalized using the number of EMG channels along muscle fascicles, i.e., 16) for all stroke participants. In Fig. 7A, we note that the data are divided into three groups, i.e., no change, diffusion of the activity regions, and shrinkage of the activity region. We found two stroke participants (15%) in the first group, four (31%) in the second group and seven stroke participants (54%) in the third group. In Fig. 7B, the location data is divided into three groups, namely, no significant shift (< 10mm), a medium change (>10 mm but < 20 mm), and a large shift (> 20 mm). We found no significant shift in the location of three stroke survivors (23%), medium shift in three (23%) and a substantial shift in rest of the tested stroke participants (54%). In Table 2, we present a summary of stroke survivors’ muscle activity maps using the shift in the location of endplate region (no change, medium and large) and the spatial activity pattern (no change, diffusion, and shrinkage). The values in the table cells are the total number of stroke survivors falling in each category and their mean clinical data, i.e., Fugl-Meyer (FM) score and modified Ashworth Scale. We observed those stroke survivors who showed changes in both location of endplate region and in activation patterns were functionally more impaired (low FM) and more spastic (high MAS). The stroke survivors with shrunken patterns and medium to a large shift in the endplate region had the lowest FM scores. We further note that changes in the size of the activity region had a relatively higher correlation with functional impairment and spasticity as compared to shift in the location of IZ.

Fig. 7:

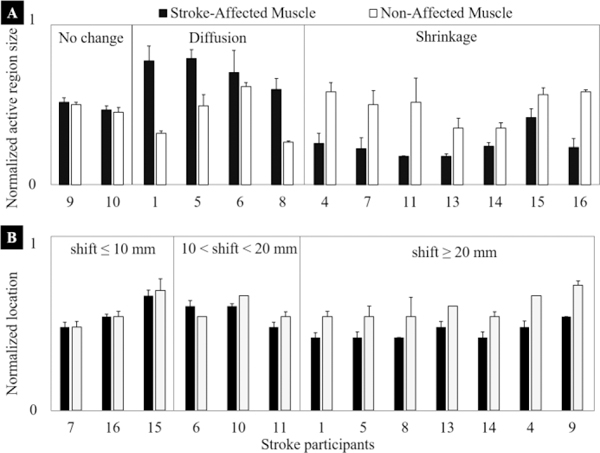
The normalized size of the active region in muscle activity maps of opposite arms in stroke survivors. Two stroke survivors (15%) showed no significant differences in the size of the active region, four (31%) showed an increase (diffused) while remaining seven (54%) showed reduced active region size (shrinkage). Normalized location of the activity region (most active channel) in muscle activity maps of opposite arms in stroke survivors. The location was measured as the row number and was normalized to the maximum rows, i.e., 16. This location represents the IZ of the biceps muscle. Three stroke survivors (23%) showed no significant differences in the location of the active region, another three (23%) showed a medium shift in the range of 10mm to 20mm while remaining seven (54%) showed a large shift of 20mm or more.

Table 2:

The table presents partition of stroke survivors with respect to their spatial muscle activity patterns and shift in the location of innervation zone.

Muscle activity region size	Location of innervation zone Number of stroke survivors, [average FM score, median modified Ashworth]
	No significant shift (≤10 mm)	Medium shift (10 to 20 mm)	Large shift (> 20 mm)
No change		1 [53,1]	1 [51,0]
Diffused patterns (increase in size)		1 [24,1+]	3 [27,1+]
Shrunk patterns (decrease in size)	3 [29, 1+]	1 [9,1+]	3 [18,2]

D. MP/SD Ratio

In Fig. 8, we present normalized active region size plotted against the normalized MP/SD ratios for all stroke participants. The normalization of the active region size was performed using data of the non-affected biceps. The fig. provides a quantitative relationship between muscle activity patterns (no change, diffused, and shrunk) and the amount of nonpropagating/common signal components in the EMG signal. We observed a linear relationship between the MP/SD ratios and the activity region size, i.e., the stroke survivors who showed a diffused EMG pattern also exhibited relatively a large amount of non-propagating signals and vice versa.

Fig. 8:

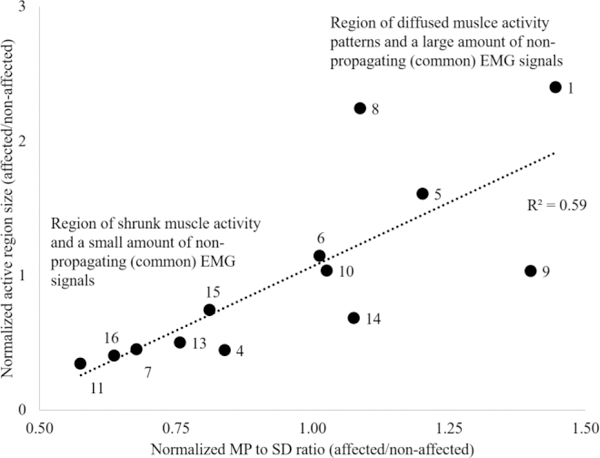
The normalized active region size is plotted against the normalized MP/SD ratio for all stroke participants. The bottom left area represents participants that showed shrunk (reduced size of) muscle activity patterns and relatively a small quantity of non-propagating (common) EMG signals. The top right region represents participants that showed diffused EMG patterns and a large amount of no-propagating components. A linear relation between two parameters (active region size and MP/SD ratio) is evident.

E. Textural Analysis

The textural analysis of normalized muscle activity maps was performed to estimate pixel-to-pixel (or channel-to-channel) variability. The GLCM statistics, i.e., homogeneity and correlation were calculated for maps of all contraction levels and both arms, and average values are presented in Fig. 9. We note that frequently the stroke-affected muscles exhibited less homogeneity and correlation, thus higher pixel-to-pixel variability.

Fig. 9:

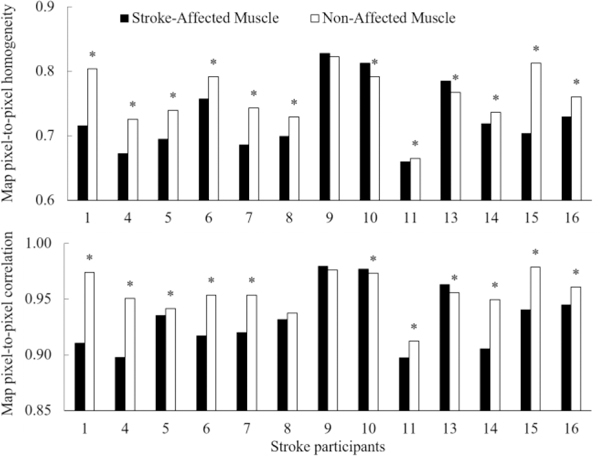
The textual analysis of muscle activity maps in stroke survivors. The pixel-to-pixel homogeneity and correlation are presented for affected vs. non-affected muscle in all stroke survivors. The bars present average values over maps of all contraction levels and ^‘*’ shows the statistically significant difference at 95%. We note that 77% (10 out of 13) of the tested stroke survivors showed less pixel-to-pixel homogeneity in the affected muscle, while 69% (9 out of 10) showed lower pixel-to-pixel correlation. Both GLCM statistics, i.e., pixel-pixel correlation and homogeneity show that normalized muscle activity maps of stroke-affected biceps exhibited relatively higher pixel-to-pixel variability.

IV. DISCUSSION

Stroke is a cerebrovascular event that routinely results in abnormal motor control characteristics, as well as may lead to alterations in both skeletal muscle structure and functions. Using multichannel surface EMG, we developed muscle activity maps of a heterogeneous chronic stroke population with varying degrees of functional impairment and spasticity, i.e., FM ranging from 9 to 53 and modified Ashworth Scale ranging from zero to 3.

We observed the highest intensity of MP EMG around the endplate region (belly of the muscle), and this level declined smoothly in all directions, following a fusiform or shape of the biceps muscle (Fig. 2 and Fig. 3) [32, 50]. Similarly, all channels showed a monotonic increase in the amplitude (RMS EMG) with increasing contraction level that appears to coincide with the muscle thickness, at least in a subjective way. We demonstrated that a unique muscle activation pattern existed for each subject and that the spatial pattern was consistent across all measured effort levels with an average misclassification rate of less than 5% for all tested participants (Fig. 4A). We also noted that muscle activation patterns were not entirely consistent between opposite arms, even in intact participants (Fig. 4B), i.e., a misclassification rate of 39% existed for intact participants. A major contributing factor may have been differences in the location of EMG electrode grid on the biceps muscle between opposite arms. Nevertheless, the misclassification rate for stroke survivors was much higher, i.e. more than 86% and, therefore, we believe that there were other, more substantial modifications in the muscle activity maps of stroke survivors, presumably arising from alterations in muscle morphology following stroke. We made similar observations using the Euclidean and correlation distances analyses (Fig. 5) and found that between arms (non-affected vs. affected) the activity maps of stroke survivors had larger Euclidean distances and were less correlated as compared to intact participants (left vs. right).

Our analysis of muscle activity maps revealed that both the size of the activity region and location of the IZ in each map were significantly altered following stroke (Fig. 6). For the size of the activity region, we found significant differences between opposite arms in 11 out of 13 stroke survivors (85%, Fig. 7A). We noted that changes in the size of the activity region were also related to the level of functional impairment in stroke survivors. Two mildly impaired stroke survivors (ID-9 and 10) with FM scores of 51 and 53 respectively did not show significant differences in the size of their muscle activity regions. The other two groups that showed either diffusion or shrinkage of spatial patterns had a varied degree of functional impairment and spasticity and we did not find a strong correlation between their clinical measures (FM and MAS) and changes in the spatial patterns. For the IZ, stroke survivors showed a notable degree of variability between affected and non-affected arms (Fig. 7B). We found that 77% of the tested stroke participants showed a shift of 10mm or more in the location of IZ while 54% showed a change of 20mm or more. Following stroke, the loss of motor units and consequently the process of de/re-innervation may have caused the IZ to shift significantly, although the origins of this hypothetical sequence remain unclear [6, 10, 32].

We observed a linear relationship between the intensity of non-propagating components (i.e., parts of the MP EMG signal that are present across multiple channels along muscle fascicles) and the muscle activity patterns. The shrunken activity pattern was related to a relatively smaller amount of non-propagating components in stroke-affected muscles, while a large amount of non-propagating components was linked to a diffused activity pattern. The absence of non-propagating components argues against a contribution from excessive fat over the muscle, and connective tissue infiltration, and may potentially be linked to the muscle fiber de/re-innervation, i.e., the process of de/re-innervation may have resulted in a considerable amount of non-propagating components. The increase in non-propagating components might also be linked to the dispersion of the IZ in re-innervated motor units.

We are not entirely sure what all mechanisms may be at play after stroke; however, we can speculate about some possible explanations for the observations. For the shrunken EMG patterns, the major contributors to the abnormal changes in the muscle architecture may include muscle fiber shortening (i.e. contracture), fiber atrophy [4, 5], and increased variation in the muscle fiber size [21]. Muscle contracture and reduction in the length of fibers may have been caused by a significant decrease in the number of sarcomeres inside muscle fibers [3, 11, 17–19]. The compound effect of these alterations may have resulted in the shrinkage of muscle activation patterns. On the other hand, for the diffused muscle activity patterns, the major contributors to the muscle architectural changes may include connective tissue infiltration [4, 9, 14–16, 51] and increased fat content [14–16]. These two mechanisms would potentially modify the traveling action potentials with a low-pass filter effect before detection by the surface EMG electrodes [52], resulting in a flatter EMG signal without peaks and with a larger amount of non-propagating signal components, i.e., high MP/SD ratio and diffused EMG patterns. However, as is evident from Table 2, multiple mechanisms may be at work in stroke-affected muscles. The increased variability in the texture of the stroke survivors’ maps may result from regional variations in activation, linked to the uneven distribution of fiber types, and/or patchy infiltration of connective tissue in the muscle.

One important factor, which is hard to address accurately, is the relationship between the spatial resolution of the EMG grids to the spatial properties of the underlying muscle pathology that we are trying to track. The spatial resolution of the grids is limited by the inter-electrode spacing, and by recording electrode dimensions (area of the recording surface in contact with the skin). The former is the primary determinant of the spatial resolution. It is very likely that the underlying pathology (extracellular matrix increase or connective tissue infiltration) has a spatial distribution of the order of fractions of millimeters or even microns. By this, we mean that the matrix accumulation will likely develop around individual muscle fibers or groups of muscle fibers with sub-millimeter spacing, indicating that our grid resolution is probably much too coarse to capture this spacing. It follows that our grid recordings are providing a more global and probabilistic analysis of muscle tissue architecture, rather than a detailed map. Even if we were to reduce both the inter-electrode distance and the size of the electrode recording surface, we might still be an order of magnitude too large to capture the detailed pathology. Also, the low-pass filtering provided by the skin and subcutaneous fats also limits the resolution of the grid. To adequately capture the spatial properties of the tissue, we may need different electrode designs, coupled with novel techniques such as high-resolution ultrasound and measurements of tissue mechanical properties derived using acoustic shear wave ultrasound techniques.

One methodological limitation of this study was related to the triceps brachii activity, which was not recorded. The abnormal co-contraction of the triceps muscle during elbow flexion tasks is reported in the literature [2]. However, as already discussed, the spatial muscle activity patterns emerging in normalized EMG maps are not strongly affected by the levels of activity of the muscle.

V. CONCLUSION

The multichannel surface EMG data from stroke-affected upper-extremity muscles was used to develop RMS maps at various contraction levels. These maps represented muscle activity in the spatial domain and were aimed to investigate post-stroke alterations in muscle structure and functions. Previously, multichannel EMG studies focused on motor unit information extraction, estimation of conduction velocity, or identification of the end-plate region. However, in this study, we focused on the spatial analysis that provided novel information about muscle functions after a brain injury. We found that the muscle activation patterns were consistent across measured contraction levels; however, the spatial patterns of stroke-affected muscles were substantially different from those recorded from non-affected muscles in the same person. In particular, the size of the active region and the location of the IZ were altered with an increased amount of pixel-to-pixel variability. We believe that the changed spatial patterns following stroke are indicative of underlying architectural and morphological changes, and these may contribute to major functional changes as well.

VI. APPENDICES

A. Appendix I

The Euclidean and correlation distances are defined as:

$$\begin{gathered} d_{\mathit{\text{Eulidean}}}=\sqrt{\frac{1}{N}{\sum }_{ij}(a_{ij}-b_{ij}{)}^2,} \\ {d}_{Correlation}=1-\frac{\left(a_{ij}-\overline{a}\right){\left(b_{ij}-\overline{b}\right)}^t}{\sqrt{\left(a_{ij}-\overline{a}\right){\left(a_{ij}-\overline{a}\right)}^t}\sqrt{\left(b_{ij}-\overline{b}\right){\left(b_{ij}-\overline{b}\right)}^t}}, \end{gathered}$$

where a_ij and b_ij represent pixels from affected/right and non-affected/left arm maps respectively for stroke survivors/intact participants, N represents the total number of pixels in a map, superscript t represents transpose and $\overline{x}=\frac{1}{N}{\sum }_{ij}{x}_{ij}$.

B. Appendix II

We estimated following GLCM statistics:

$$\text{Correlaiton}={\sum }_{ij}\frac{\left(i-{\mu }_i\right)\left(j-{\mu }_j\right)p(i,j)}{{\sigma }_i{\sigma }_j},$$

$$\text{Homogeneity}={\sum }_{ij}\left[p(i,j)/1+|i-j|\right],$$

where, p(i,j) is the value of pixel at location i and j, $\mu =\frac{{\sum }_i{x}_i}{n},$ where n is the total number of pixels x and

$$\sigma =\sqrt{\frac{1}{n}{\sum }_i{\left(x_i-\mu \right)}^2}.$$