Abstract
Purpose
We present a computationally feasible and iterative multi-voxel spatially regularized algorithm for myelin water fraction (MWF) reconstruction. This method utilizes 3D spatial correlations present in anatomical / pathological tissues and underlying B1+-inhomogeneity or flip angle inhomogeneity to enhance the noise robustness of the reconstruction while intrinsically accounting for stimulated echo contributions using T2-distribution data alone.
Methods
Simulated data and in vivo data acquired using 3D non-selective multi-echo spin echo (3DNS-MESE) were used to compare the reconstruction quality of the proposed approach against those of the popular algorithm (the method by Prasloski et al.) and previously proposed 2D multi-slice spatial regularization spatial regularization approach. We also investigated whether the inter-sequence correlations and agreements improved as a result of the proposed approach. MWF-quantifications from two sequences, 3DNS-MESE vs 3DNS-gradient and spin echo (3DNS-GRASE), were compared for both reconstruction approaches to assess correlations and agreements between inter-sequence MWF-value pairs. MWF values from whole-brain data of six volunteers and two multiple sclerosis patients are being reported as well.
Results
In comparison with competing approaches such as Prasloski’s method or our previously proposed 2D multi-slice spatial regularization spatial regularization method, the proposed method showed better agreements with simulated truths using regression analyses and Bland-Altman analyses. For 3DNS-MESE data, MWF-maps reconstructed using the proposed algorithm provided better depictions of white matter structures in subcortical areas adjoining gray matter which agreed more closely with corresponding contrasts on T2-weighted images than MWF-maps reconstructed with the method by Prasloski et al. We also achieved a higher level of correlations and agreements between inter-sequence (3DNS-MESE vs 3DNS-GRASE) MWF-value pairs.
Conclusion
The proposed algorithm provides more noise-robust fits to T2-decay data and improves MWF-quantifications in white matter structures especially in the sub-cortical white matter and major white matter tract regions.
Keywords: T2 relaxometry, Demyelination, Myelin water fraction, Extended phase graph, Multi-exponential, Spatial Regularization, EPG, Inverse Laplacian Transform, Damped exponential
INTRODUCTION
The role of Myelin water fraction (MWF), extracted using multi-echo spin echo (MESE) T2-decay data, as a in vivo bio-marker for demyelination in the brain has already been well established in multiple sclerosis (MS) patients (1) and animal models (2–5). Further, MWF-mapping has been used for investigating various neurological disorders/deficits, such as MS (6–8), ischemic stroke (9), repeated mild traumatic brain injury (10), normal aging (11) etc.
Accurate MWF quantification requires high initial signal-to-noise ratio (iSNR or SNR of 1st echo) of 500–1000 (12), along with a sufficiently accurate accounting of contributions from stimulated echo pathways (SEPs) (13–16). Traditionally, the most commonly used sequence for multi-echo T2 (MET2) mapping used to be the single-slice multi-echo-spin-echo (MESE) sequence. The sequence consisted of a slice-selective 90° pulse, followed by a series of nonselective composite RF pulses for spin refocusing. On either side of each 180° pulse, slice-select crusher gradient pulses of alternating sign and decreasing amplitude were applied for eliminating contributions from stimulated echoes and contributions from outside the selected slice (17). Ignoring any contribution from stimulated echo pathways (SEPs), multi-exponential models were fitted to T2-decay data (18, 19). Conventionally, the Tikhonov regularization was implemented in the temporal domain (6, 18, 20, 21). To further improve the noise robustness, some approaches (19, 22–24) also utilized spatial regularization. However, the gradient crushing scheme is far from perfect (25) and so, the effect of stimulated echo pathways (SEPs) are never truly eliminated. It was only somewhat recently (13) that MWF imaging included crusher scheme such that acquired signals included contributions from SEPs. In recent years, many processing approaches, within both nonlinear (14, 15) and linear (13, 16) frameworks, have been proposed to account for SEPs while inverting quantitative T2 relaxometry (QT2R) data. Nonlinear post-processing approaches (14, 15) model underlying T2 distribution using representation requiring fewer number of parameters. Whereas Layton et al. (15) employed the discrete three pool model in Bayesian formulation framework; Akhondi-Asl et al. (14) modeled underlying T2-distributions as the continuous distribution in form of the sum of Wald distributions. Both these approaches require assumptions about the shape of the underlying T2 distribution and number of pools. Some of these assumptions may easily get violated in diseases such as multiple sclerosis (MS), where several competing pathological processes co-exist. Even for the case of a healthy volunteer, Fig 2 of Akhondi-Asl (14) showed very high MWF-values (~0.2) for grey matter (GM) structures such as putamen and globus pallidus, whereas MWF-values in many areas of major white matter (WM) tracts were less than <0.1). This trend is unrealistic as grey matter regions of interest (ROIs), with cell bodies as a major component, cannot have higher MWF value than white matter, with myelinated myelin being a major component. In contrast, the method proposed by Prasloski et al. (13) and our previous 2D multi-slice spatial regularization analysis approach (16) do not require any explicit prior assumption about the number of underlying pools or their shapes, other than requiring the distributions to be continuous. Here, the choice of the T2-scale may affect MWF-quantification as well (also see the discussion section). Both methods account for contributions from SEPs within nonnegative least square (NNLS) formulation. Though the implementation of Tikhonov regularization in the temporal domain by Prasloski et al. (13) did improve the noise robustness of solutions, many regions of interest (ROIs) still suffered from noise instability showing salt-pepper like appearances (Fig. 7 of (13)). The 2D multi-slice spatial regularization analysis method previously proposed by us (16) resulted in better noise robustness due to the imposition of similarity constraints in 2D local neighborhood basis.
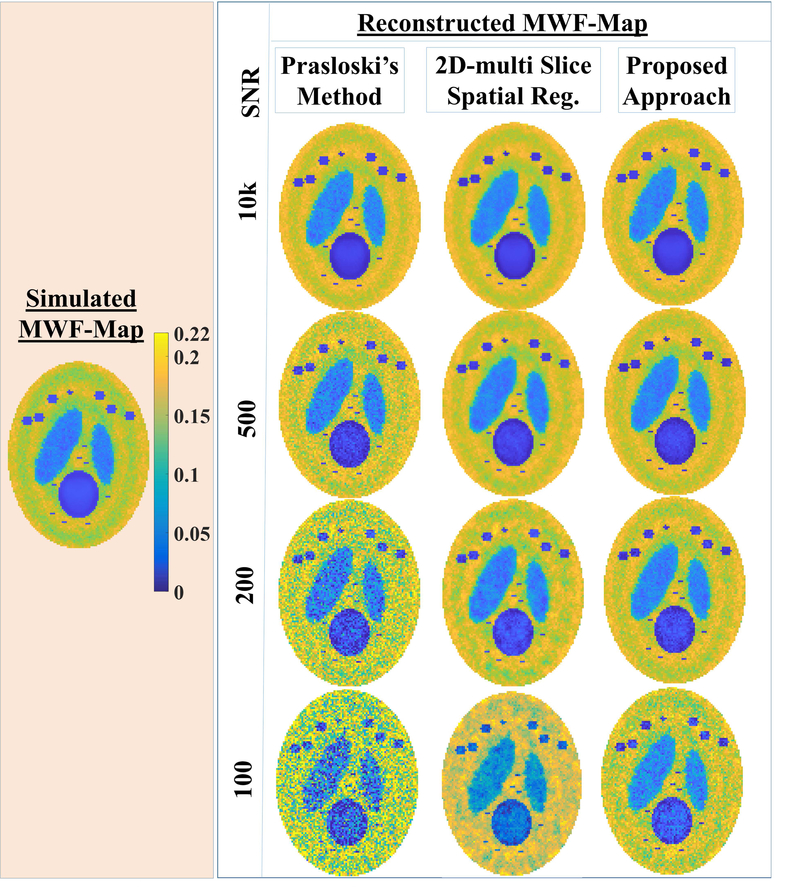
Fig. 2.A.
The reconstructed MWF-maps (right panel) are compared for competing processing approaches, namely: the PM approach, our 2D multi-slice spatial regularization approach, the current approach for simulated MWF-map (left panel) at different SNR (10000, 500, 200, 100). At high SNR of 10000, MWF-map reconstructed using either of methods were very close to the simulated truth. At lower SNR (200, 100), the Prasloski’s method (PM) led to large intra-structural variabilities. At SNR ≤ 200, the current approach reconstruct more faithfully than our earlier 2D- multi slice approach. Also, notice that MWF-reconstructions using the proposed approach are closer to the simulated truth.
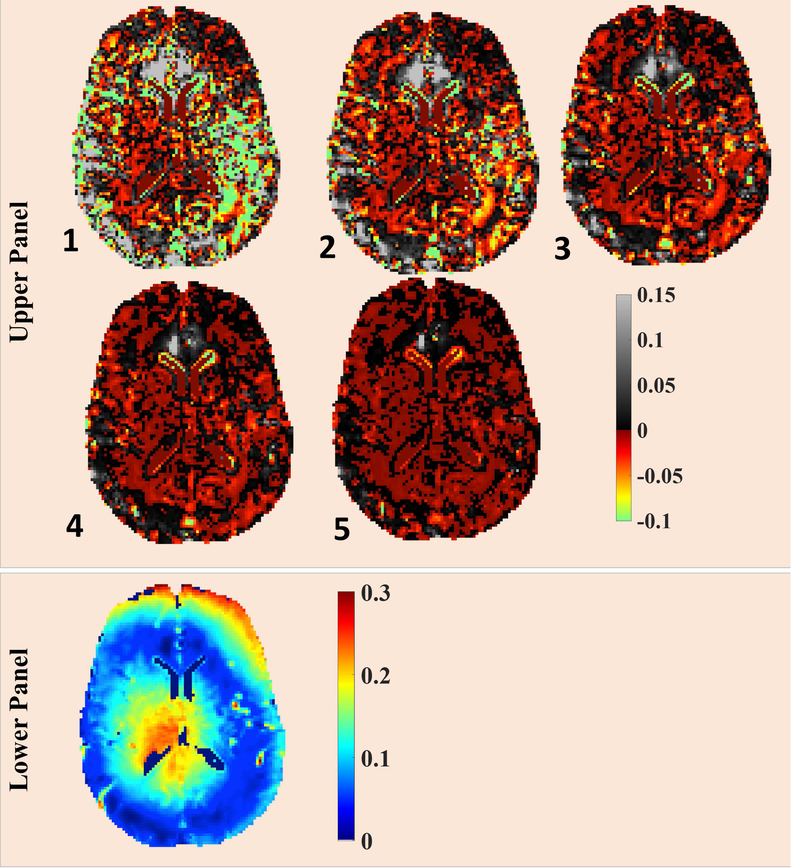
Fig. 7.
Upper Panel: The convergence pattern of FAI-map for the proposed method is being presented. The FAI-map from 6th iteration was taken as reference image and the plotted images corresponds to fractional difference of FAI-map at particular iteration with respect to 6th iteration, normalized w.r.t. FAI-map from 6th iteration. Lower Panel: FAI-map at 6th iteration is presented.
On the upper panel, the iteration numbers of subsequent iterations are reported on left-bottom corners of respective figures.
The current work can be considered an extension of our previously proposed 2D multi-slice spatial regularization analysis method (16) to 3D multi-echo data with many major improvements. Current objective function includes an additional term which imposes spatial smoothness constraints with respect to (w.r.t.) flip angle in-homogeneity (FAI)-maps (definition: FAI = absolute (1-B1+)). The proposed data-inversion procedure iteratively refines over the FAI-map and the T2-distribution map (or voxel-wise T2 distribution). Our solver requires initial guesses of FAI-map and μT, introduced later, to start. The conventionally regularized approach provides good starting point; none the less, we show empirically that the solver tends to converge to the same solution for randomly perturbed initial guesses of FAI-map. The implementation of 3D first order first difference (FOFD) for the refinement of T2-distribution map was made feasible by the use of the L-BFGS-B solver (limited memory Broyden–Fletcher–Goldfarb–Shanno solver with bound) (26). Additionally, the spatially regularized approach for the FAI-refinement has been implemented in nonlinear optimization framework. The function: lsqnonlin of Matlab requires values of system matrices and Jacobians at various FAI-values, whose explicit calculations using EPG model are very time consuming. To speed up, system matrices and Jacobians, at intermediate FAI-values, were estimated by utilizing the approximation involving their pre-calculated values at regular grid points (500 linearly spaced FAI-values between 0–0.4).
In this manuscript, we demonstrate the improved performance of the proposed algorithm against the popular algorithm by Prasloski et al. (13) (abbreviation: PM) and our previously proposed 2D multi-slice spatial regularization analysis method (16) using simulated data. For in vivo data, only the comparisons between the proposed approach and the PM approach have been presented to avoid overcrowdings on relevant figures. We also compare MWF quantifications from two sequences: 3DNS-GRASE (20), a sequence fast enough to be clinically feasible, and the gold standard 3DNS-MESE sequence and show that better correlations and agreements between inter-sequence MWF-value pairs are achievable using the proposed algorithm. This also indirectly supports our claim of the superior performance of the proposed algorithm over competing NNLS solvers.
THEORY
In our previous 2D multi-slice spatial regularization analysis method (16), in-plane spatial correlations present in 2D multi slice MESE data were used to improve the noise robustness, while simultaneously accounting for contributions from SEPs:
| [1] |
where column vectors and are multi-voxel T2-distributions and multi-voxel multi-echo data respectively. The superscript “EPG” stands for the extended phase graph model and the subscript “MV” stands for “multi voxel”. is the block diagonal matrix, with dense matrices AEPG’s as its block units. Further, = intensity at echo time-point TE(i) due to unit water fraction at T2 value T2(j) for a known/pre-determined flip angle error (FAI): δ. MT is the diagonal matrix with the square root of voxel-wise temporal regularization constant, √μT, along its diagonal and μS is the spatial regularization parameter. DS is the 2D first order first difference (FOFD) operator.
The data fidelity is accounted by the first term of Eqn. [1]; while the second term i.e. the conventional regularization term penalizes large contributions from isolated T2-points in inferred T2-distributions. The third term imposes spatial smoothness constraints on underlying T2-distribution solutions.
To capture the underlying tissue similarity present in 3D anatomical/pathological structures, we propose to minimize the following objective function consisting of both types of variables ,:
| [2] |
Here, is the multi-voxel FAI column vector and DV is the 3D FOFD operator.
We would like to point out three differences between Eqn. [1] and Eqn. [2]. First, an additional term (the 4th term) was included which imposes spatial smoothness constraints w.r.t. FAI-maps. Second, the matrix DS, the 2D FOFD operator in Eqn. [1], has been replaced by DV, the 3D FOFD operator. Third, since the resolution along the slice encoding direction could be different from in-plane resolution, different elements of DV are weighted by corresponding inverse distance of nearest neighbors. Technical innovations to make minimization of Eqn. [2] have already been briefly described in the introduction section and would be discussed in detail later.
ALGORITHMIC IMPLEMENTATION
Proposed Processing Algorithm
The proposed data-inversion procedure iteratively refines both the FAI-map and the T2-distribution map (or voxel-wise T2 distribution). The alternative minimization approach was used to solve Eqn. [2]. Please refer to the Appendix-A for the processing algorithm and for the discussion about its convergence.
The pre-spatial regularization step requires estimating the μT-map, along with the initial estimate of FAI-map. In our previous approach (16), the FAI-map (called flip angle error map in that version) was jointly estimated along with the μT–map as the part of the conventional regularization step. That computation was a time consuming process (~6 hours for full brain). In contrast, our current approach does not involve any regularization for the initial estimates of FAI-map, similar to the approach by Prasloski et al. (13). This modification itself has resulted in appreciably reduced (initial FAI estimate ~2 hours for full brain) processing time. Also, unlike our previous approach (16), the current algorithm allows FAI-map to evolve during the spatial regularization step.
The voxel-wise estimation of underlying FAIs or would not be sufficiently accurate due to the presence of the experimental noise. The iterative nature of the proposed algorithm allows both the T2-distribution map and the FAI-map to converge to more accurate estimations. It has been shown empirically that the solver tends to converge to the same solution for randomly perturbed initial guesses. In contrast, there is no convergence guarantee for our previous approach (16) as the objective function in Eqn. [1] depends on the latent variables , which were not allowed to evolve beyond initial estimates. This is equally true for the approach by Prasloski et al. (13).
A naïve implementation of “lsqnonlin” to minimize the part of objective function (refer Eqn. [3B] of appendix A) would take ~day for matrix of size (128×128×50) as each intermediate step of “lsqnonlin” requires the calculation of the system matrix and its Jacobian at candidate FAI-value using extended phase graph (EPG) model. Since it was possible to separate FAI-dependence of the objective function from T2-distribution dependence, the system matrix and corresponding Jacobians were pre-calculated for 500 linearly spaced FAI-values between 0–0.4 and their values at intermediate FAI-values were approximated using these pre-calculated values during lsqnonlin optimization.
The desktop-workstation implementation of DV as the 3D FOFD operator (Eqn. [3C] of appendix A) would not have been feasible using sparse non-negative least square (SNNLS) solver due to the computationally intensive nature for such assignment (processing time for single iteration ~1 weeks for data set of size 128×128×60). This implementation has been made feasible through the use of the L-BFGS-B solver (limited memory Broyden–Fletcher–Goldfarb–Shanno solver with bound) (26) (refer Appendix E).
Processing an entire data set at once was not feasible due to limited computational resources available on a typical desktop workstation. Therefore, the algorithm was performed on successive data selecting windows (DSWs) of 16×16×16 voxels with a 4-voxel overlap to eliminate tiling and edge effects. The tiling and edge effect was visually evident in form of periodic rectangular discontinuities. While stitching these successive DSWs, 2-voxel wide regions across DSW-edges were discarded. The choice of smaller overlap size was insufficient to eliminate the tiling and the edge effects completely. Given the overlap size, selecting smaller DSWs led to increase in the processing time as, effectively, only a few voxels were selected in each processing step.
Prasloski’s method (abbreviation: PM)
We made following changes to Prasloski’s approach (13) in our implementation of their method: (i) Sixty-five T2 values were chosen between 5 ms to 2000 ms. In comparison, Prasloski et al. (13) used forty T2 points on logarithmic scale between 15–2000 ms. (ii) Forty-one linearly spaced points were chosen between 0 to 0.4 as candidate values for FAI. (iii) The pseudocode described in (16) was used to calculated the system matrix AEPG as a function of FAI-values.
METHODS
For MWF reconstruction, contributions from short T2 (5 ms < T2 < 40 ms) were assumed to be due to water trapped inside the myelin bilayers.
Simulation
Single-voxel T2-decay
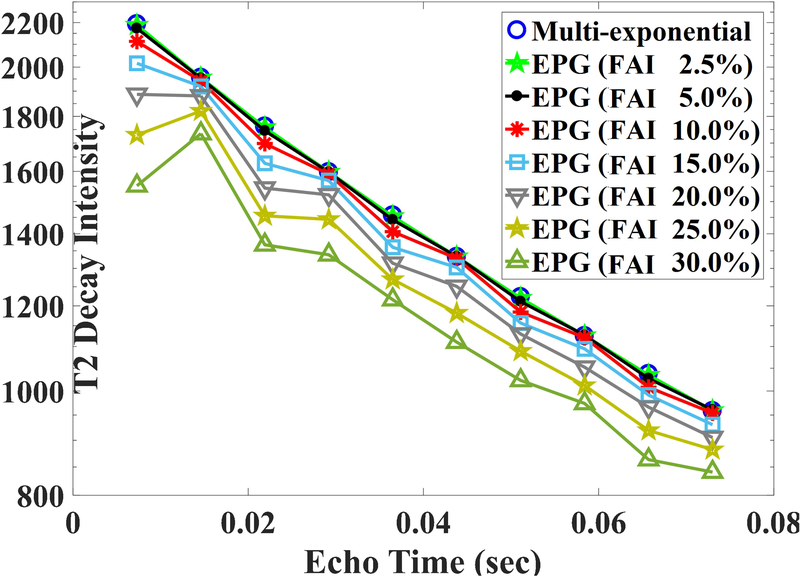
The T2-distribution was assumed to be the sum of three normal distributions (means: 20 ms, 85 ms, 400 ms; standard deviations: 7 ms, 15 ms, 50 ms) and with a fixed MWF value = 0.15. T2-decay curves (Fig. 1) at various FAI-values (in percentages: 2.5,5.0,10,15,20,25,30) were generated using the extended phase graph (EPG) model (27), with no noise being added.
Fig 1.
The simulated T2-decay curve (First 10 points) from underlying three pool distributions using multi-exponential model (ignoring effect of FAI) and using EPG model with different extent of FAIs. Y-axis is on the logarithmic scale. For small FAI (say < 5%), there were very little divergences between multi-exponential decay curve and EPG based T2-decay curves. Also, even-echoes-compensation scheme of CPMG sequence was imperfect for higher FAI > 15%.
Multi-voxel data
To assess the accuracy and the noise robustness of the proposed algorithm, 3D QT2R data were simulated using 3D equivalent of the Shepp Logan phantom with matrix size 128×128×16. The phantom consisted of four distinct regions (Supplementary Fig. 1). Underlying voxels consisted of three pools, simulated using the sum of three normal distributions (means: 20 ms, 85 ms, 400 ms; standard deviations: 7 ms, 15 ms, 50 ms). By adjusting the heights of distributions for short and intermediate T2 pools, we assigned different MWF-values to four regions. Two big regions of interest (ROIs) (Supplementary Fig. 1) corresponded to gray matter like and normal appearing WM like structures with respective MWF-values of ~0.06, ~0.1695. To assess the performance of the reconstruction algorithm in lesion quantifications under typical MWF-imaging protocol, two different types of ROIs were simulated; namely: lesion type-1, lesion type-2 (Supplementary Fig. 1). Structures inside lesion type-2 are much smaller in size (2–8 voxels wide), whereas the structures inside lesion type-1 is much wider in size (~25 voxels wide). We allowed for patch-wise smoothly varying intra-structural variabilities in all regions. The lesion type-1 simulated a large demyelinating areas with MWF-values ranging from 0.036 at the center to 0.022 at the periphery. For structures inside lesion type-2, MWF-values were kept constant ~0.028–0.034.Various iSNR-levels, between 100 and 10000, were simulated with the addition of Rician noise.
In vivo Experiments at 3T
The imaging study involving human subjects was approved by the local Institutional Review Board (University Medical Center, Hamburg-Eppendorf, Germany). Six volunteers (5 males, 23–36 years; 1 female; 21 years) and two primary progressive MS patients (both males; ages 23, 29 years), diagnosed based on the 2010 revisions of the McDonald criteria (28), were scanned on a 3T MRI scanner (Ingenia, Philips Healthcare, The Netherlands). Written informed consents were obtained from all subjects prior to scanning. A 32 channel head and neck coil was used for all in vivo imaging. T2-weighted images were also acquired (TE = 80 ms) with a resolution of 1×1×2.5 mm3.
For the purpose of measuring SNR, a selected heathy volunteer was scanned twice with identical sequence parameters and the difference image was calculated. Finally, SNR was calculated in white matter regions as: √2×(mean signal/ standard deviation of the difference image).
Data with partial brain coverage are used to compare the performance of the proposed algorithm against the method by Prasloski et al. (13) and to compare inter-sequence (3DNSMESE and 3DNS-GRASE) region of interest (ROI) averaged MWF-pairs. The lower resolution was chosen for full brain data to keep the 3DNS-GRASE scan time < 20 minutes.
For all MET2 experiments (3DNS-MESE and 3DNS-GRASE), the constant gradient crusher scheme was used. So, signals from stimulated echoes are not avoided, but instead contribute to the signal.
3DNS-MESE and 3DNS-GRASE Experiments (partial brain coverage)
T2 relaxometry data (magnitude only) from two healthy volunteers were acquired using both sequences with following common sequence parameters: echo spacing = 7.2ms, number of echoes = 32; TR 2000 ms; axial FOV 230×190 mm, resolution 2×2×2.5 mm3, 16 slices; SENSE reduction factor 2×1.5; Oversampling in slice encoding 1.8; readout BW 225 Hz/pixel; averages (NEX) 2; acquisition time for 3DNS-GRASE ~11 minutes; acquisition time for 3DNS-MESE ~32 minutes. 3DNS-GRASE sequence was implemented with all scan parameters being identical to 3DNS-MESE, except: EPI factor =3. Two averages were acquired to ensure that a typical WM voxel had iSNR of more than ~200.
3DNS-GRASE Experiment (full brain coverage)
Six healthy volunteers and two MS patients were scanned using the 3DNS-GRASE sequence with all scan parameters being identical to 3DNS-GRASE with partial brain data, except: Oversampling in slice encoding 1.0; NEX = 1; Resolution 3×3×3 mm3; It took ~16 minutes to acquire whole brain (~60 slices) data.
Two volunteers were also scanned twice for scan-rescan reproducibility, with more than a week between successive scans.
SNR
For finer resolution data sets, the iSNR of voxels in major WM area were 200–250; while SNRs of the last (32th) echo were 13–18. For the coarse resolution QT2R data sets, iSNRs of WM voxels were even higher (~400). Given these SNR values, no Rician noise correction was needed.
T1, T2-scale, μT, μS, μδ and FAI
Rather than measuring the T1-map, we used constant value of T1 = 1000 ms. Sixty-five points were chosen in the range of 5–2000 ms for the T2 on a logarithmic scale.
The range of μT was kept between 10−5 to 10−1. The optimized value of μS has been assumed to be spatially invariant: where is the median of voxel-wise μT-map and αS is a suitable scalar in the range of 10–10000, chosen as described in Appendix-B, C.
Forty-one candidates for FAI were selected from 0 to 0.40 at a regular interval of 0.01. We allowed small penalties to non-smooth FAI-solutions and the optimal value of μδ was chosen as described in Appendix-B, C.
Evaluation criteria
For both simulated and experimental data, we used the root mean square (rms) of the fitting error (RMS-FE) as a metric. Additionally, reconstructions were assessed both at the level of generated MWF-map and FAI-map in case of simulation and were compared against ground truths.
Fractional change as a measure for the stopping criteria
The fractional change (FC) of voxel-wise T2-distribution (X) was calculated for successive iteration as:
Finally, the rms of the fractional change (RMS-FC) was calculated over entire 3D FC-map.
Normalized Fitting error (NFE) for T2-decay and its rms value (RMS-NFE)
The fitting error was calculated for both experimental and simulated T2 decay data on voxel-wise basis as:
Where YExperiment and YFit (= AEPGX) are column vectors representing single-voxel experimental data and fitted T2-decay respectively. Finally, the rms of the fitting error (RMSFE) was calculated over the entire 3D FE-map.
Normalized reconstruction error (NRE) and its rms value (RMS-NRE)
For simulated data, the NRE for the scalar metric of interest “p” was calculated for each voxel as:
Such NRE-map was generated for MWF-maps and FAI-maps in case of simulated data. Finally, the rms of the reconstruction error (RMS-NREp) for the metric of interest “p” was calculated over entire 3D NREp map.
Contribution of temporal prior (CTPT2D) to T2 distribution
The contribution of temporal prior term was calculated on multi-voxel basis as:
Where and are multi-voxel T2-distribution and multi-voxel data as column vectors. Finally their RMS value was calculated.
Contribution of spatial prior (CSPT2D) to T2 distribution
To assess the extent of the spatial smoothness enforced by the proposed algorithm, the contribution of spatial prior term, equivalent to 3rd term of Eqn. [3] with μS = 1, was calculated on multi-voxel basis as:
Where DV is the 3D FOFD operator and and are multi-voxel T2-distribution and multi-voxel data as column vectors.
Contribution of spatial prior (CSPFAI) to flip angle error
To assess the extent of the spatial smoothness enforced by the proposed algorithm, the contribution of spatial prior term, equivalent to 4th term of Eqn. [3] with μδ = 1, was calculated on multi-voxel basis as:
Where and are multi-voxel FAI-map and multi-voxel data as column vectors. Regions of interest (ROIs) for selected WM structures were manually drawn by T.F.
Statistical Analysis
Linear regression analyses and Bland Altman plots were performed for following evaluations: (i) To provide performance comparison between proposed approach and competing NNLS based approaches by assessing correlations and agreements between simulated and reconstruction voxel-wise MWF-pairs. (ii) To assess correlations and agreements between inter-sequence (3DNS-MESE vs 3DNS-GRASE) ROI averaged MWF-pairs; (iii) To assess correlations and agreements between scan-rescan ROI averaged MWF-pairs. In case of linear regression analyses, slopes and intercepts of regression line and R2 values were calculated. In case of Bland Altman plots, mean differences and confidence intervals (CIs) were calculated.
For scan-rescan reproducibility, intra-class correlation coefficients (ICCs) were also calculated.
An unpaired T-test was performed to test differences of the mean MWF in the normal appearing WM (NAWM) of MS-patients and healthy volunteers. Mean MWF-values from the selected ROIs of each patient were compared to the corresponding averaged mean MWF-values of all healthy volunteers. Due to the small sample size, p-values should be considered descriptively.
RESULTS
Using Matlab 2014b (utilizing 5 of 6 cores processor Intel-Xeon-E5670 running at 2.4 GHz with 32 GB RAM), the proposed processing took ~15–16 hours to invert full brain QT2R data (size 80×80×64; 6 iterations). The reconstruction using the PM approach took ~2.25 hours.
By the 6th iteration of our algorithm, the rms of the fractional change of voxel-wise T2-distribution map (voxel-wise T2-distribution) was much less than 1.0% and so the algorithm were terminated at 6th iteration.
Simulation
Single-voxel T2-decay
Fig. 1 depicts the simulated results, showing the FAI-dependence of T2-decay curves for a typical WM voxel. For better visualization, only ten echo time points are being displayed and the log-scale is used along y-axis (Fig. 1). For small FAIs (≤ 5%), divergences between the EPG model based T2-decay curves and ideal multi-exponential T2-decay curve were not appreciable. For intermediate FAIs (5–10%), even-echoes compensation scheme of Carl Purcell Meiboom Gill (CPMG) sequence was very efficient, with respective even-echo intensities matching well with corresponding multi-exponential T2-decay intensities. However, the even-echoes compensation scheme of the CPMG sequence seemed to be less effective for FAIs ~15% and appeared to fail completely from FAIs ~20–30% or greater.
Multi-voxel data
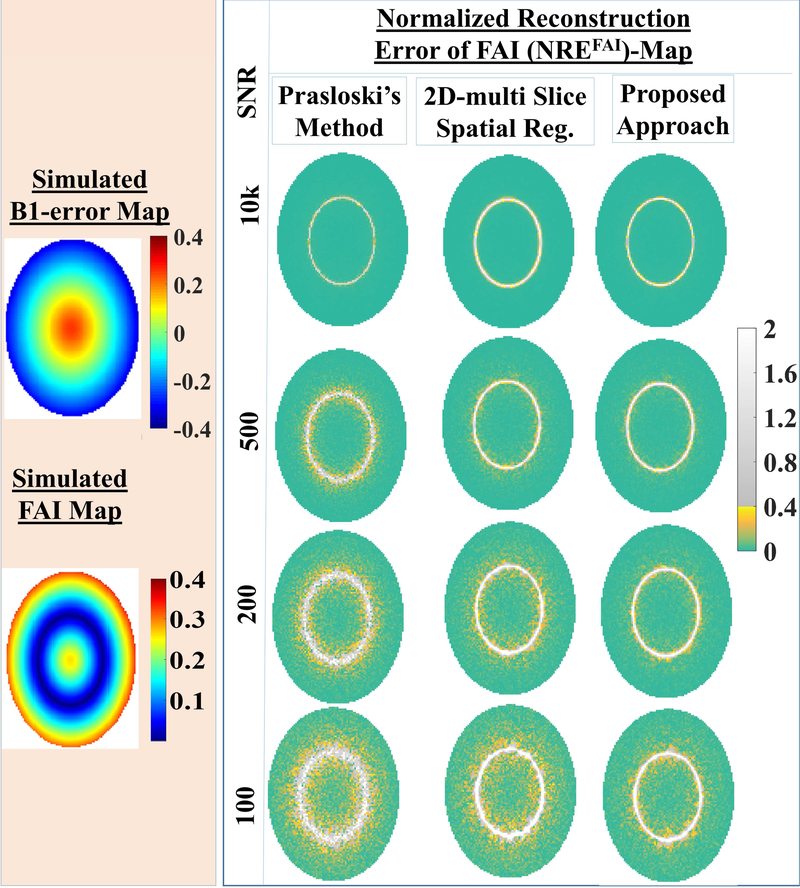
Using the simulated data with different SNR levels (10000, 500, 200, 100), the performance of the proposed approach is compared against the competing NNLS based approaches: the PM approach and our previously proposed 2D multi slice spatial regularization approach for both MWF-reconstructions (Fig 2.A.) and FAI-reconstructions (Fig 2.B.). At high SNR of 10000, MWF-maps reconstructed using either of methods were very close to the simulated truth (Fig 2.A.). At lower SNRs (200, 100), the PM method led to large intra-structural variabilities. At SNR ≤ 200, the current approach reconstruct more faithfully than our earlier 2D- multi slice spatial regularization approach. Also, notice that MWF-reconstructions using the proposed approach are closer to the simulated truth. In the case of the FAI-reconstruction, corresponding normalized residual error (NREFAI)-maps are shown (Fig. 2, B) to bring out performance differences. At high SNR of 10000, FAI-map reconstructed using either of methods were very close to the ground truth. Even at this simulated case of very high SNR, NREFAI–maps for all approaches showed a elliptical ring where NREFAI-values were appreciably higher. Voxels inside this ring corresponded to low “simulated” FAIs (≤5%), which did not have appreciable SEP signatures to begin with (Fig. 1) and did not require the correction. At lower SNR (≤ 200), the proposed approach is the best performer among all competing approaches even when it comes to FAI-reconstructions. Further, voxel-wise regression analyses and Bland-Altman analyses were performed between simulated MWF-maps and reconstructions for three approaches, namely: Prasloski’s approach, our 2D multi-slice spatial regularization approach and the proposed reconstruction at different SNRs. With respect to regression analyses, the proposed reconstruction showed better regression fit (Tab. 1) in terms of R2. With respect to Bland-Altman analyses (Tab. 2), the proposed reconstruction showed narrower confidence intervals. It should be noticed that reconstructed MWF-values were more biased when simulated MWF-values were lower (Tabs. 1,2). For instance, all approaches showed poorer regression fits and wider confidence intervals for Bland-Altman analyses for the simulated lesion of type-2 with lowest simulated MWF-values among all simulated ROIs. None the less, the proposed algorithm showed superior performance for even such cases.
Fig. 2.B.
The reconstructed FAI-maps are compared for competing processing approaches, namely: the PM approach, our 2D multi-slice spatial regularization approach, the current approach for simulated FAI-map (left panel) at different SNR (10000, 500, 200, 100). To better assess reconstruction performances, normalized reconstruction error of FAI-map w.r.t. simulated FAI-map are displayed (right panel). At high SNR of 10000, FAI-map reconstructed using either of methods were very close to the truth. At lower SNR (≤ 200), proposed approach is the best performer among all competing approaches.
Tab. 1.
The regression analyses were performed between simulated data and reconstructions for three approaches, namely: Prasloski’s approach, our 2D multi-slice spatial regularization approach and the proposed reconstruction at different SNRs.
| SNR | Prasloski’s approach | Our multi-slice spatial regularization approach | Proposed Reconstruction | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 10000 | Slope | Intercept (x 10−2) | R2 (x10−2) | Slope | Intercept (x 10−2) | R2 (x10−2) | Slope | Intercept (x 10−2) | R2 (x10−2) | |
| NAWM-like | 0.961 | 1.46 | 98.0 | 0.852 | 3.14 | 92.3 | 0.966 | 1.38 | 98.5 | |
| GM-like | 1.208 | −0.59 | 97.8 | 1.061 | 0.38 | 88.9 | 1.114 | −0.03 | 98.8 | |
| Lesion-1 | 1.067 | −1.23 | 99.6 | 0.926 | −0.91 | 94.1 | 1.024 | −1.11 | 99.7 | |
| Lesion-2 | 0.878 | −0.60 | 53.9 | 0.355 | 0.73 | 43.0 | 1.213 | −1.73 | 74.2 | |
| 500 | NAWM-like | 0.983 | 1.02 | 35.6 | 0.863 | 2.89 | 76.9 | 0.938 | 1.73 | 83.2 |
| GM-like | 1.160 | −0.73 | 48.8 | 1.093 | −0.21 | 80.2 | 1.074 | 0.03 | 86.5 | |
| Lesion-1 | 1.112 | −1.05 | 60.0 | 0.923 | −0.63 | 83.7 | 0.906 | −0.66 | 79.7 | |
| Lesion-2 | 1.156 | −1.07 | 1.70 | 0.429 | 0.93 | 15.9 | 1.981 | −4.57 | 21.7 | |
| 200 | NAWM-like | 0.976 | 0.99 | 10.8 | 0.868 | 2.68 | 44.5 | 0.907 | 2.10 | 53.1 |
| GM-like | 1.087 | −0.42 | 15.1 | 1.041 | −0.040 | 53.5 | 1.043 | 0.26 | 62.4 | |
| Lesion-1 | 1.006 | −0.07 | 19.7 | 0.842 | 0.24 | 51.0 | 0.800 | 0.12 | 47.3 | |
| Lesion-2 | 2.740 | −5.46 | 1.9 | 2.183 | −4.15 | 6.5 | 2.180 | −4.93 | 9.1 | |
| 100 | NAWM-like | 0.997 | 0.70 | 3.7 | 0.857 | 2.81 | 18.12 | 0.916 | 2.04 | 20.1 |
| GM-like | 0.965 | 0.98 | 4.9 | 0.926 | 1.19 | 24.79 | 0.992 | 0.98 | 26.9 | |
| Lesion-1 | 0.938 | 1.13 | 7.2 | 0.759 | 1.42 | 21.8 | 0.750 | 1.24 | 16.6 | |
| Lesion-2 | 1.927 | −1.90 | 3.4 | 1.068 | 0.21 | 0.6 | 3.156 | −7.32 | 4.4 | |
Tab. 2.
The Bland-Altman analyses were performed between simulated data and reconstructions for three approaches, namely: Prasloski’s approach, our 2D multi-slice spatial regularization approach and the proposed reconstruction at different SNRs.
| SNR | Prasloski’s approach | our 2D multi-slice spatially regularized approach | Proposed approach | ||||
|---|---|---|---|---|---|---|---|
| 10000 | Mean (x10−2) | Confidence Interval (x 10−2) | Mean (x 10−2) | Confidence Interval (x 10−2) | Mean (x 10−2) | Confidence Interval (x 10−2) | |
| NAWM-like | 16.49 | [ −1.14, 0.55] | 16.45 | [ −1.36, − 0.17] | 16.49 | [ −1.09, −0.59] | |
| GM-like | 6.94 | [ −1.41, 0.13] | 6.94 | [ −1.55, 0.11] | 6.91 | [ −1.11, −0.33] | |
| Lesion-1 | 2.55 | [ 0.81, 1.24] | 2.50 | [ 0.59, 1.68] | 2.55 | [ 0.90, 1.18] | |
| Lesion-2 | 2.64 | [ 0.80, 1.18] | 2.49 | [ 0.04, 2.55] | 2.60 | [ 0.89, 1.23] | |
| 500 | NAWM-like | 16.44 | [ −3.47, 1.98] | 16.41 | [ −1.70, 0.32] | 16.44 | [ −1.61, 0.14] |
| GM-like | 06.71 | [ −3.12, 2.49] | 6.76 | [ −1.69, 0.88] | 6.82 | [ −1.53, 0.48] | |
| Lesion-1 | 02.71 | [ −1.35, 2.76] | 2.63 | [ −0.06, 1.80] | 2.59 | [ −0.11, 1.99] | |
| Lesion-2 | 02.84 | [ −1.44, 2.61] | 2.70 | [ −0.43, 2.16] | 2.39 | [ 0.60, 2.39] | |
| 200 | NAWM-like | 16.37 | [−6.37, 5.17] | 16.35 | [ −2.57, 1.46] | 16.38 | [ −2.38, 1.15] |
| GM-like | 6.63 | [−6.17, 5.86] | 6.67 | [ −2.50, 2.04] | 6.83 | [ −2.45, 1.37] | |
| Lesion-1 | 3.04 | [−4.52, 4.61] | 2.95 | [−1.65, 2.13] | 2.82 | [ −1.46, 2.45] | |
| Lesion-2 | 3.13 | [−4.59, 4.60] | 2.91 | [ −1.48, 2.37] | 2.52 | [ −0.38, 2.84] | |
| 100 | NAWM-like | 16.40 | [−11.20, 9.88] | 16.33 | [ −4.29, 3.25] | 16.41 | [ −4.45, 3.08] |
| GM-like | 6.93 | [−10.69, 9.18] | 6.91 | [−4.47, 3.07] | 7.02 | [ −4.74, 2.90] | |
| Lesion-1 | 3.54 | [−8.54, 6.66] | 3.41 | [−3.96, 2.60] | 3.31 | [ −4.30, 3.35] | |
| Lesion-2 | 3.63 | [−8.57, 6.58] | 3.34 | [−3.65, 2.81] | 2.85 | [ 2.87, 3.99] | |
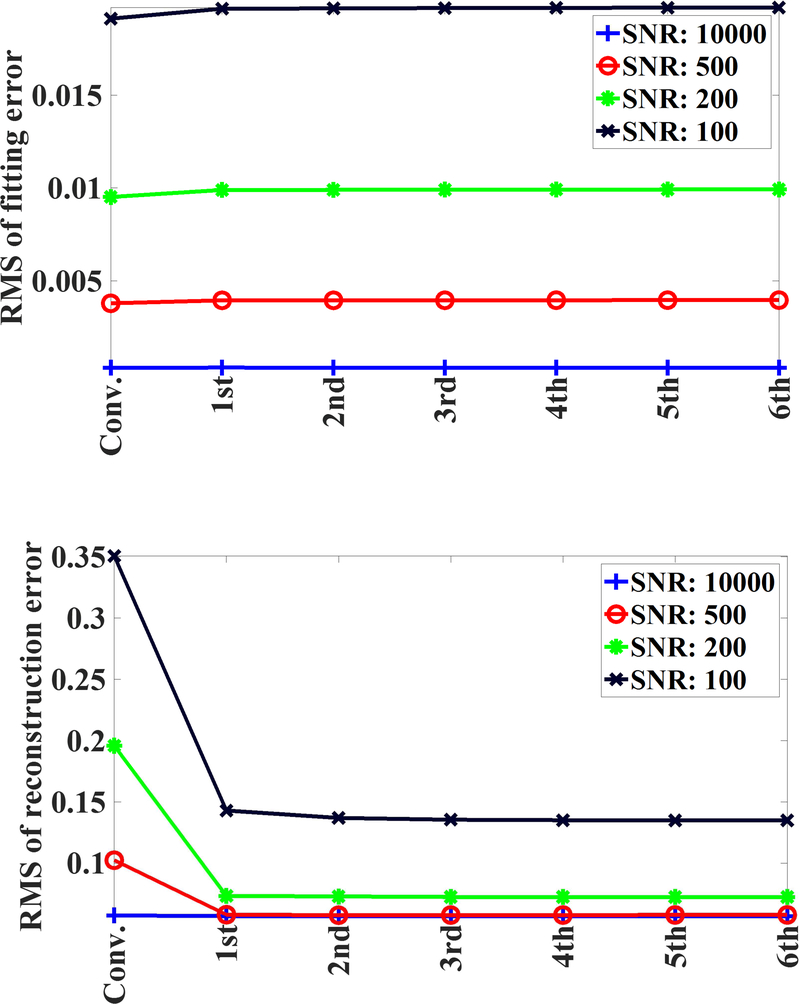
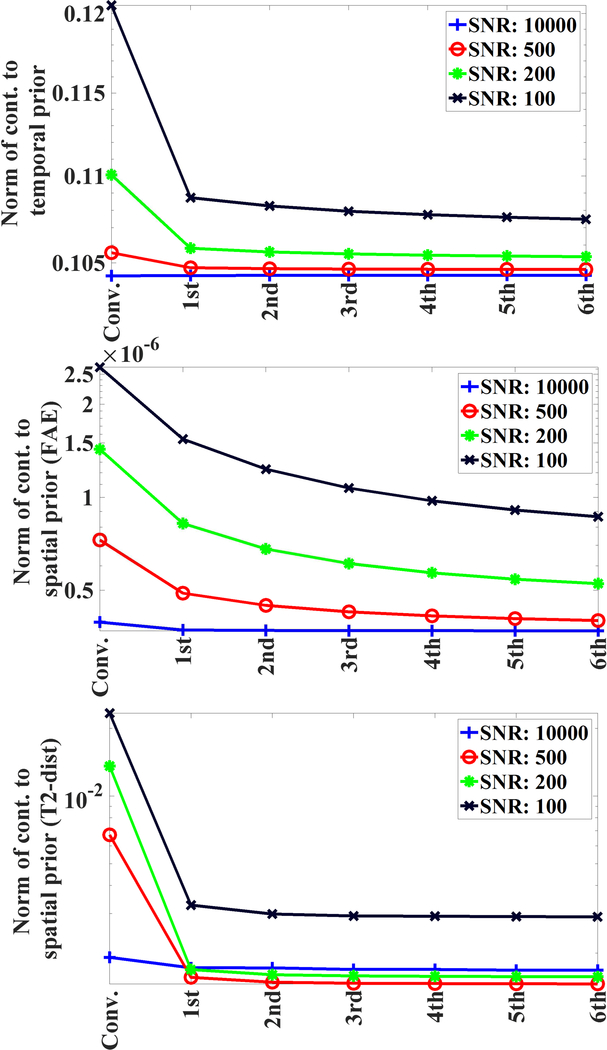
As depicted in Fig. 3, the implementation of our algorithm resulted in slight increase (1–3%) in rms-values of normalized fitting error across all SNRs; whereas rms-values of normalized reconstruction error decreased substantially for the proposed algorithm. Further, the contribution of temporal prior decreased only by small percentage as a result of the implementation of our algorithm (Fig 4). Some changes was expected as 4D T2 distribution maps were getting refined over various iterations. With respect to the contribution of spatial prior for both FAI-map and T2-distribution map (Fig 4), the proposed algorithm resulted in appreciable decrease in those values for simulated data at different SNR levels.
Fig. 3.
RMS of fitting errors and rms of the reconstruction errors plotted for the conventionally regularized solution and various iterations of the proposed solver.
Fig. 4.
Contribution to temporal prior (CTP), contribution to spatial prior (CSP) for T2 distribution and CSP of FAI plotted for the conventionally regularized solution and various iterations of proposed solver. Y-axes are on log scales.
Further, intra/extra-cellular water fraction (IEWF) or long T2-water fraction (LTWF) maps were also reconstructed for simulated data and it was found that accurate reconstructions of these two pools are not feasible for maximum echo time TEmax ~200–300 ms (supplementary Fig. 2). This is true for most of published MWF-studies as well.
Experiments at 3T Scanner
For the justification of using constant value of T1=1000 ms in the MWF-reconstruction, please refer to the appendix D.
3DNS-MESE and 3DNS-GRASE Experiments (partial brain coverage)
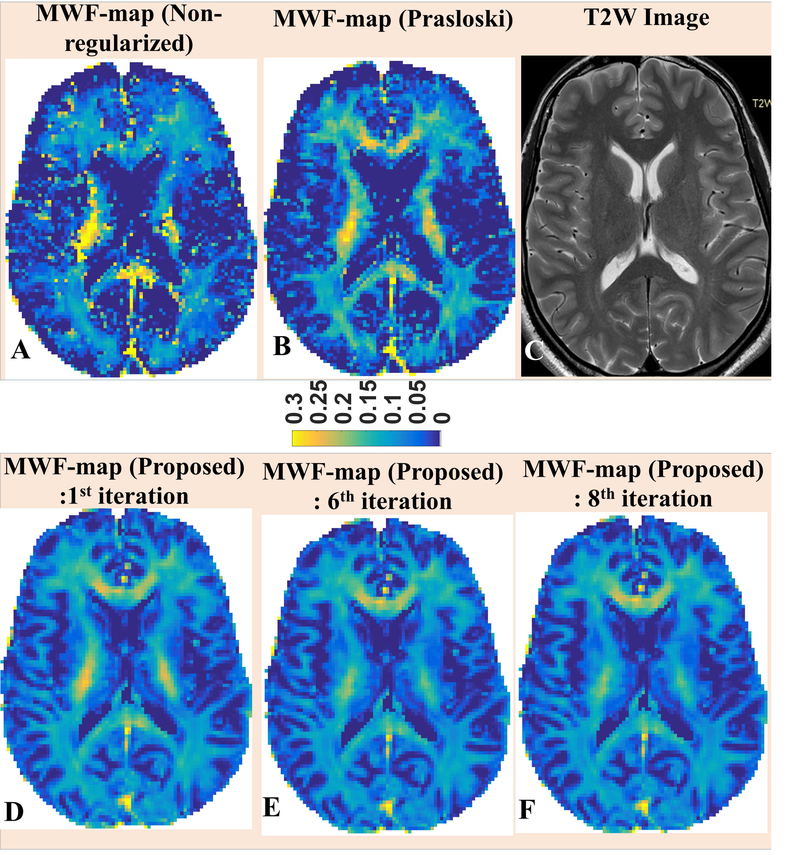
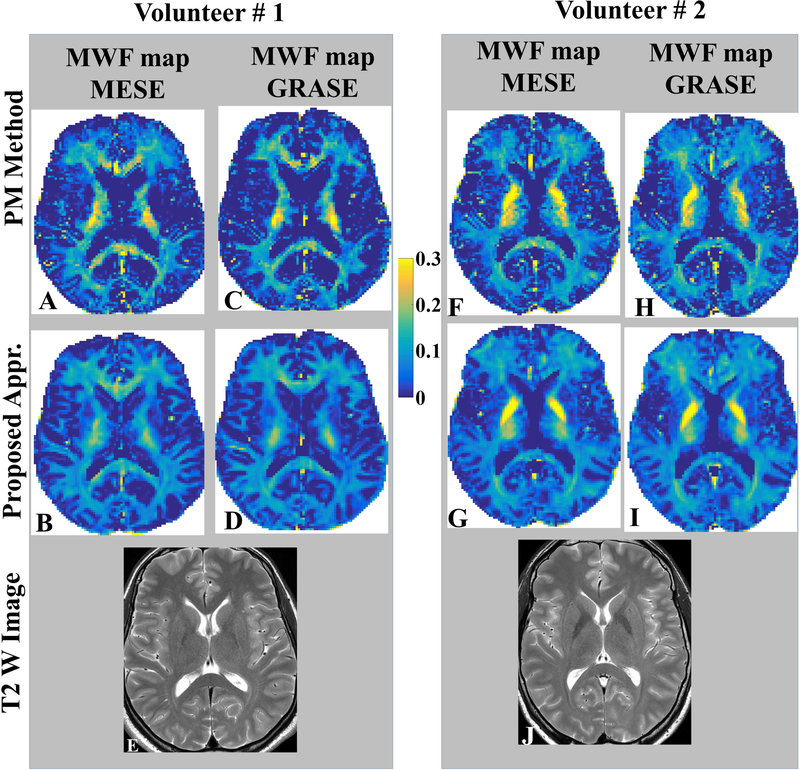
MWF-maps were reconstructed using both approaches (the PM approach and the proposed approach) for two 3DNS-MESE data sets. For comparison, corresponding MWF-reconstructions are presented for single slice of a healthy volunteer (Fig. 5, upper panel, B & E). In addition, MWF-map using non-regularized approach is also presented (Fig. 5, upper panel, A). Since the in-vivo ground truth was unknown, the contrast present in T2W images acquired at TE = 80 ms was used (Fig. 5, upper panel, C) as an independent metric. It should be noticed that since both non-regularized solution (Fig. 5A) and conventionally regularized solution (Fig. 5B) shared the same estimate of FAI-map, differences in their respective MWF-reconstructions could only be attributed to different extents of over-fitting to the noisy data being employed in both methods. As evident from the visual comparison to corresponding T2 weighted image (Fig. 5C), non-regularized MWF-map appeared to over fit noisy data more severely and resultant MWF-map could not capture the WM integrity faithfully. In comparison with conventionally regularized counterpart, MWF-values from the non-regularized MWF-map appeared overestimated in certain ROIs, such as in central portion of WM seen in presented slice (Fig. 5A), and under-estimated in genu and splenium of corpus callosum giving illusions of the loss of WM integrity in those ROIs. MWF-map from the conventionally regularized approach, with appreciably reduced degree of over-fitting owing to the additional penalty term, depicted the WM-integrity more faithfully. However, the hyper-intensity visible in central region of presented slice still did not match with corresponding contrast on T2W image. Also, MWF-reconstruction using the PM method still appeared to be noisier and did not delineate GM-WM interfaces accurately. On the other hand, the spatially regularized approach aims to avoid over fitting by employing the similarity constraint on local neighborhood basis. The resultant MWF-map had better depictions of WM structures in subcortical areas adjoining GM and matched more closely to the WM-integrity evident in Fig. 5C. Compared to the proposed approach, MWF-values using the PM method were over-expressed in the central portion of WM in the presented slice and under-expressed in other ROIs such as putamen and globus pallidus (Figs. 6, 7); however, corresponding FAI-values were under-expressed for the PM approach in all of aforementioned ROIs (Fig. 7). It should also be noticed that these ROIs fall into regions where FOI-values were higher (Fig 7, lower panel) and it’s evident that initial FAI-determination procedure has the tendency to underestimate stimulated echo contributions in higher FAI-regions. Based on these observation, we infer that the FAI-uncertainty add an additional degree of uncertainty to overfitting in QT2R inversion. This over-fitting has a general tendency to over-estimate higher MWF-values, such as in WM, and under-estimate lower MWF-values; though the behavior could be contrary in certain ROIs (refer to genu and splenium of first image in Fig. 6). Further, though more apparent in cortical regions, improvements were also noticeable in central brain region as well (supplementary Fig. 3). Such improvements were noticed across both in vivo 3DNS-MESE QT2R data sets.
Fig. 5.
Top-row: MWF maps reconstructed using: A) the non-regularized method; B) the Prasloski’s method. The T2-weighted image is shown for reference (C). Bottom-row: MWF-reconstructions from selected iterations of the proposed algorithm are also being presented.
The final reconstruction using the proposed method correspond to the 6th iteration.
Notice that our algorithm produces MWF-maps with better WM-GM contrasts and better depiction of the WM structures adjoining GM (top-row). Also, notice that the hyper-intensities on central WM regions the MWF-map using the PM approach are similar to MWF-reconstruction from the first iteration. However, the hyper-intensities gets suppressed in subsequent iterations.
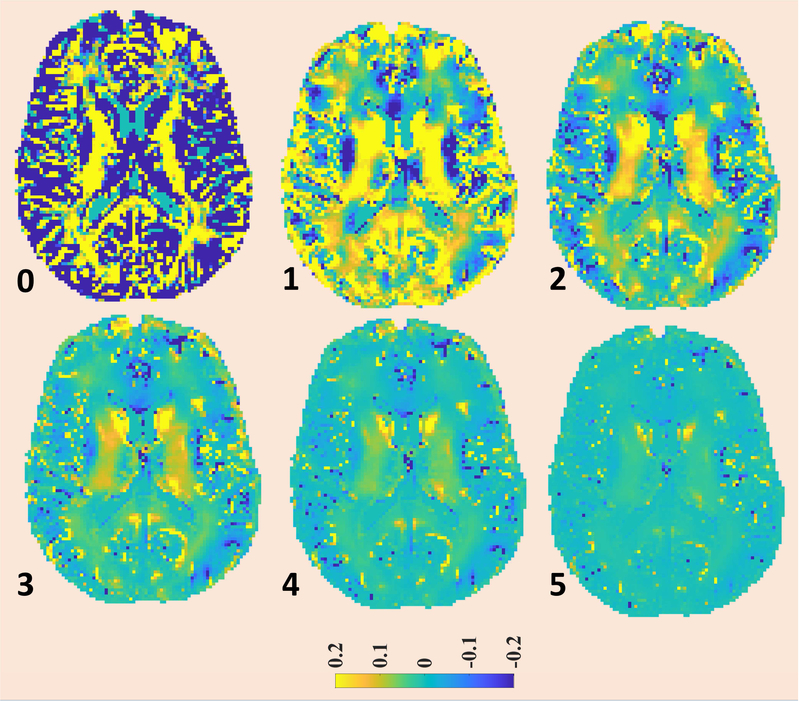
Fig. 6.
The convergence pattern of MWF-map for the proposed method is being presented. The MWF-map from 6th iteration was taken as reference image and the plotted images corresponds to fractional difference of MWF-map at the particular iteration to corresponding map at 6th iteration, normalized w.r.t. MWF-map from 6th iteration.
The first image corresponds to conventional regularization (0th iteration). The iteration numbers of subsequent iterations are reported on left-bottom corners of respective figures.
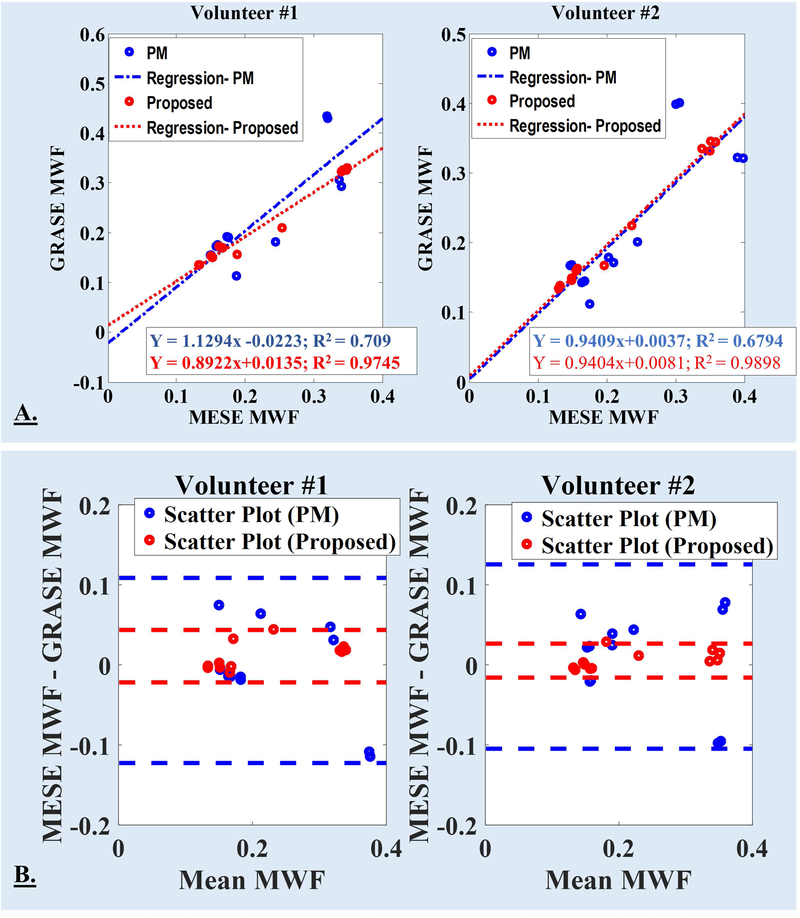
It should be noticed that QT2R data using both 3DNS-MESE and 3DNS-GRASE sequences were acquired for only two volunteers and MWF-maps were reconstructed using two approaches, namely: Prasloski’s approach and our proposed approach. Based on visual assessment, the voxel-wise inter-sequence (3DNS-MESE vs. 3DNS-GRASE) MWF-maps reconstructed using the proposed method appeared more consistent with each other (Fig. 8) and matched more closely with contrasts on corresponding T2w images. Voxel-wise comparison between MESE and GRASE based quantification was not feasible due to voxels shifts in GRASE based acquisition with respect to MESE acquisition; hence, mean MWF value-pairs over ten distinct white matter ROIs were compared in two healthy volunteers for both reconstruction approaches and inter-sequence (3DNS-MESE vs. 3DNS-GRASE) correlations and agreements were assessed. Linear regression analyses showed better correlations between inter-sequence MWF-value-pairs for the proposed algorithm (volunteer #1: R2 = 0.9745; volunteer #2: R2 = 0.9898) against the PM approach (volunteer #1: R2 = 0.709; volunteer #2: R2 = 0.6794) (also refer Fig. 9.A.). Bland Altman analyses showed a better agreements between inter-sequence MWF-value-pairs for the proposed algorithm (volunteer #1: mean difference = 0.0109, CI = [0.0437, −0.0219]; volunteer #2: mean difference = 0.0053, CI = [0.0265, −0.0159]) against the PM approach (volunteer #1: mean difference = −0.0070, CI = [0.1086, −0.1227]; volunteer #2: mean difference = 0.0104, CI = [0.1256, −0.1048]) (Fig. 9.B.) with narrower confidence intervals.
Fig. 8.
Comparison of MWF-quantifications between MESE and GRASE sequences for both algorithms, namely 1) Algorithm of Prasloski et al.; and 2) The AM (alternating minimization) based Multi voxel spatial regularization approach with stimulated echo correction (MVSR-STEC) are being presented for two volunteers. Common color bar for MWF-map is shown in the middle. Bottom row shows T2W TSE images acquired at TE 80 ms. A better correspondence between both sequences should be noticed for the proposed algorithm.
Fig. 9.
A. For both volunteers, linear regression analysis between inter-sequence (MESE and GRASE) mean MWF values were performed for both reconstruction approaches: the PM approach and the proposed approach. The eqn. for linear fits and R2 are included with each plots in panel-A (PM: blue text; proposed: red text). B. For each volunteer, Bland Altman plot comparing the difference in MWF as a function of the inter-sequence mean value are being plotted for both reconstruction approaches. Solid lines represent confidence intervals, defined as [mean difference + (−1.96, +1.96) × standard deviation], for both reconstruction methods (PM: blue dashed lines; proposed: red dashed lines).
Full brain 3DNS-GRASE
ROI-averaged MWF-values showed a very good reproducibility for scan-rescan criteria with intra-class coefficients (ICC) of >0.94 (ICC of 0.94 for volunteer 1 and 0.95 for volunteer 2). Linear regression analyses showed an excellent correlations between scan-rescan MWF-value-pairs (volunteer #1: slope = 1.021, intercept = −0.0005, R2 = 0.9976; volunteer #2: slope = 0.0098, intercept = 0.0015, R2 = 0.9983). Bland Altman analyses also showed an excellent agreement between scan-rescan MWF-value-pairs with small mean differences and narrow confidence intervals (CI) (volunteer #1: mean difference = −0.0031, CI = [0.0038 −0.0099]; volunteer #2: mean difference = −0.0015, CI = [0.0031 −0.0060]).
The mean MWF-values in all normal appearing WM ROIs (i.e. frontal, parietal, occipital) of the MS patients were found to be significantly reduced compared to mean MWF-values in the corresponding normal WM ROIs of healthy volunteers (typical WM mask shown in supplementary Fig. 4). Furthermore, we observed a significant reduction of mean MWF measurements in the genu of corpus callosum (CC) and the splenium of CC of both patients (p<0.001) compared to corresponding values in their healthy counterparts. No significant differences of the mean MWF measurements were found in the CST (cortical spinal tract) between patients and healthy controls. Details on the ROI-averaged MWF-values measured in healthy volunteers and MS patients are listed in Tabs. 3 and 4 respectively and corresponding range of Intra-volunteer MWF variabilities across major white matter regions are listed in Supplementary Tab. 1. Mean MWF-values inside specific lesions are reported in Tab. 5.
Tab. 3.
MWF values for major WM structures obtained using the proposed algorithm (MVSR-STEC), reported for six volunteers.
| Brain structures | Vol# 1 | Vol# 2 | Vol# 3 | Vol# 4 | Vol# 5 | Vol# 6 | Mean ± standard deviation over six volunteers |
|---|---|---|---|---|---|---|---|
| Right frontal | 0.145 | 0.1472 | 0.142 | 0.1299 | 0.1569 | 0.1493 | 0.1451±0.0090 |
| Left frontal | 0.1484 | 0.1473 | 0.1462 | 0.1228 | 0.1541 | 0.1417 | 0.1434±0.0109 |
| Right parietal | 0.1984 | 0.1899 | 0.153 | 0.1694 | 0.1682 | 0.1766 | 0.1759±0.0163 |
| Left parietal | 0.1955 | 0.1842 | 0.1504 | 0.1662 | 0.1677 | 0.1741 | 0.1730±0.0156 |
| Right occipital | 0.1007 | 0.0969 | 0.1121 | 0.1051 | 0.1113 | 0.1148 | 0.1068±0.0071 |
| Left occipital | 0.1061 | 0.0902 | 0.1153 | 0.1093 | 0.1108 | 0.1194 | 0.1085±0.0101 |
| Right CST# | 0.2785 | 0.2194 | 0.3304 | 0.2569 | 0.2822 | 0.2658 | 0.2722±0.0363 |
| Left CST# | 0.2729 | 0.2195 | 0.3358 | 0.2502 | 0.2846 | 0.2682 | 0.2719±0.0387 |
| Splenium of CC* | 0.1226 | 0.1215 | 0.1959 | 0.1457 | 0.1616 | 0.1723 | 0.1533±0.0292 |
| Genu of CC* | 0.1113 | 0.1227 | 0.1336 | 0.1071 | 0.1078 | 0.1098 | 0.1154±0.0106 |
CST stands for Cortical spinal tract. CST ROIs were defined in the posterior limb of internal capsule.
CC stands for the Corpus Callosum.
Tab. 4.
MWF values for major WM structures obtained using the proposed algorithm (MVSR-STEC), reported for two multiple sclerosis patients.
| Brain structures | MS patient 1 | MS patient 2 | ||||
|---|---|---|---|---|---|---|
| ROI averaged MWF | Mean relative difference wrt to mean MWF across healthy volunteers | p-value | ROI averaged MWF | Mean relative difference wrt to mean MWF across healthy volunteers | p-value | |
| Right frontal | 0.0740 | −48.98% | <0.001 | 0.0688 | −52.57% | <0.001 |
| Left frontal | 0.0757 | −47.22% | <0.001 | 0.0711 | −50.42% | <0.001 |
| Right parietal | 0.1497 | −14.90% | <0.001 | 0.0992 | −43.61% | <0.001 |
| Left parietal | 0.1402 | 18.97% | <0.001 | 0.0928 | −46.36% | <0.001 |
| Right occipital | 0.0830 | −22.30% | <0.001 | 0.0707 | −33.81% | <0.001 |
| Left occipital | 0.0838 | −22.78% | <0.001 | 0.0685 | −36.88% | <0.001 |
| Right CST# | 0.3083 | +13.26% | ≥0.05 | 0.2555 | −6.13% | ≥0.05 |
| Left CST# | 0.2996 | +10.20% | ≥0.05 | 0.2546 | −6.35% | ≥0.05 |
| Splenium of CC* | 0.1082 | −29.40% | <0.001 | 0.0984 | −35.80% | <0.001 |
| Genu of CC* | 0.0858 | −25.64% | <0.001 | 0.0748 | −35.17% | <0.001 |
CST stands for Cortical spinal tract. CST ROIs were defined in the posterior limb of internal capsule.
CC stands for the Corpus Callosum.
Tab. 5.
Mean MWFs in specific MS-lesions, depicted in supplementary Fig. 5, of two multiple sclerosis patients.
| Patients | Lesion location | MWF |
|---|---|---|
| 1 | frontal lesion | 0.024± 0.029 |
| 1 | occipital lesion | 0.068 ± 0.030 |
| 2 | left-in-image | 0.040 ± 0.032 |
| 2 | right-in-image | 0.038 ± 0.022 |
DISCUSSION
For simulated data, the proposed algorithm resulted in better quantification accuracy over both approaches: the approach of Prasloski et al.(13) and our previously proposed 2D multi-slice spatial regularization approach (16). For in vivo 3DNS-MESE data analyses, MWF-maps reconstructed using the proposed method showed better WM-GM delineation and matched more closely to corresponding contrasts on T2W images than the PM method achieved. Further, the proposed reconstruction resulted in better correlations and agreements between inter-sequence ROI-averaged MWF-pairs (3DNS-MESE vs 3DNS-GRASE). It should be noticed that Prasloski et al. (29) reported a higher R2-value (≈ 0.99) for similar correlation analyses between intersequence ROI-averaged MWF-value-pairs against R2-value (≈ 0.68–0.71) reported for our implementation of their (PM) approach. Based on a comparative visual assessment of voxel-wise MWF-maps reported in their paper (Fig. 2 of (29) vs Fig. 6 of the current manuscript), we believe that the better R2-value can be attributed to differences in ROI localizations and their sizes. Further, the following general trend was observed across all healthy volunteers: MWFPosterior-internal-capsule > MWFSplenium-CC > MWFGenu-CC, which is consistent with previously reported values (13, 21, 29).
The choice of the T2-scale is known to affect the NNLS-based MWF quantifications (13, 16). As a standard practice, NNLS based approaches choose T2-scale on the logarithmic basis as it can probe different time scales involved in neurological tissues with sufficient T2-time-point density while still keeping total sampling points manageable (nT2<100). Ideally, one would like to keep nT2 as small as possible to reduce the computational cost and make the underlying inverse problem better conditioned. However, it cannot be set arbitrary small as the resultant sample density would be insufficient to capture the characteristics of underlying T2-dsitributions. Myelin quantifications are independent of the choice of nT2, if nT2 is sufficiently large. Accordingly, Prasloski et al (13) choose nT2 = 40; while we choose nT2 = 50 in our previous work (16). We would also like to clarify that we only investigated nT2 ~ 25, 50, 100, 150, 200 in our previous work, while looking at the stability of MWF-calculation as a function of nT2. In our current work, we have chosen 65 points (vs 50 points in our earlier approach) to allow for additional T2-scale (current 5–2000 ms vs 5–600 ms in our earlier approach).
Even in recent years, many researchers (30, 31) have been resorting to simple strategies to limit the effects of stimulated echoes, such as skipping the first echo in the train; however, this would turn out to be inefficient in most part of imaging volumes. Though the even echoes compensation scheme of the CPMG sequence is efficient for small and intermediate FAI (10–15%), this is not the case with the odd echoes. Further, for higher FAIs, even echoes compensation scheme is also not effective either. Therefore, throwing away the first echo or all odd echoes would be a suboptimal strategy as stimulated echo pathways must be accounted for. On the other hand, many MR physicists avoid using regularization based data processing approaches due to their concerns about solutions getting biased by inclusion of additional penalty/prior term to the underlying data fidelity model. However, their approaches, of relying on the data fidelity term alone, would be particularly unsuitable for ill-conditioned problems, which are known to be very sensitive to the noise. The variability in data analysis comes from two sources: (i) the noise present in data (ii) the inherent tissue variability. By relying on the data fidelity term alone, one allows the noise present in data to affect the analysis, which usually overshadows the inherent tissue variability. By optimally choosing regularization strengths, the proposed approach suppresses fluctuations due to noise while still allowing for inherent tissue variability. As in conventionally regularized approach, though the implementation of the Tikhonov regularization in the temporal domain does improve the noise robustness of solutions, significant number of voxels still suffered from noise instability, leading to salt-pepper like appearances even in normal white matter on MWF-maps. We have relied on temporal and spatial regularization for the de-noising and the improved depiction of cortical structures matching the T2W contrast. Further, the solutions depend on the regularization constants: μT and μS. By optimally choosing regularization strengths using L-curve, the proposed processing approach suppresses fluctuations due to the noise while still allowing for the inherent tissue variability. However, that can still introduce slight spatial smoothing and possible contrast bias. We would like to point out that it’s not possible to estimate the bias in vivo as the ground truth is unknown. As shown with the simulated data, the reconstructed MWF-values were more biased when simulated MWF-values were lower (Tabs. 1,2). In our understanding, a major component of the bias seen in myelin deficient region could be attributed to the experimental limitation on the achievable shortest echo time and would be common across various myelin water processing approaches. The pre-factors to multi-exponential corresponding to short T2 components would be very small for severely myelin deficient regions, leaving very little signal contribution from short T2 even by second echo and that would lead to appreciable uncertainty about short T2 component. This may bias the results towards longer T2 values.
Over-fitting to noisy multi echo data used to be an issue, even when multi exponential model was utilized(19). The uncertainty about FAI-values add additional degree of complexity to over-fitting issue in the non-regularized method and the PM method. The FAI-map determination in the PM approach utilized the 1-dimensional grid over possible FAI-values: δ followed by the interpolations. The residual norms, , were minimized at all grid-points using non-regularized xNR; and δgrid-point corresponding to minimum residual norm was chosen as the optimum FAI-value for that voxel. In such an non-regularized setting, the presence of the noise can lead to the over-fitting with the following condition:. In other words, (δgrid-point, xNR) can fit better than the solution pair (δtrue, xtrue) closer to the ground truth. Since the conventionally regularized solution uses the same FAI-map, corresponding solutions (δgrid-point, xconv) can still satisfy the following condition for many ROIs:. In our current approach, though initial approximation of FAI-map followed similar strategy, (δspatial, xspatial) were refined in subsequently steps. In those subsequent steps, our data fitting procedure avoided overfitting as it got good estimate of voxel wise noise through use of spatial smoothness constraint in that local neighborhood. As we have seen in Figs. 6 & 7, over-estimation or under-estimation of FAI-values cannot be directly mapped to either underestimations or over-estimations of MWF-maps and it rather adds up to the complexity of over-fitting issue.
We did not elaborate on some other interesting spatial regularization approaches (22–24) to multi echo data analysis in the introduction section, as those works did not involve the correction for the contributions from SEPs. The priors utilized by multi-echo approaches of Du et al. (22) and Yoo et al. (24) involved the divergence between voxel wise T2 distribution “xSpatial” and T2 distribution prior “xPrior” or the term ||xSpatial-xPrior||2, though “xPrior” was calculated differently in both approaches. A common drawback of their approaches is that the candidate distribution prior “xPrior” was calculated using solutions post conventional regularization “xConventional” and was not allowed to evolve during spatial regularization step. Though, “xPrior” is not calculated directly in our approach, it does get calculated implicitly as we impose spatial smoothness constraints locally. In our framework, that implicitly calculated “xPrior” and spatial regularized solution “xSpatial” are coupled together and hence, “xPrior” evolves even during the numerical optimization step of Eqn. [3C]. Thus, the weak prior utilized by our solver is better equipped to get the sense of spatial similarity present in a local neighborhood and thus, avoids over-fitting. The multi-component analysis by Labadie et al. (23) utilizes longitudinal data with different underlying physics (fast exchange, inversion, inversion efficiency etc.). However, the spatial regularization approach is quite similar to our earlier works (16, 19). Here, we would also like to point out that the inversion of multi echo T2-decay can be mapped to inverse Laplacian transform of “modulated” exponentially restricted real function. As such, our data inversion approach may have applications in other MRI modalities such as diffusion weighted imaging, T1 relaxometry etc.
We would like to point out that direct measurement of multi-exponential T1 in brain has been reported by Labadie et al. (23) and it would be relevant to talk about the impact of such findings on the MWF quantification in MET2 experiments. As a pre-requisite for observing the multi-exponential nature of T1, their post-processing (23) required modeling of the inversion efficiency on voxel wise basis. Otherwise, the longitudinal relaxation would still be seen as a mono-exponential recovery for other experiments and this would be valid for our experiment as well, which does not involve any inversion RF pulse. We would like to point out that our protocol was not designed to accurately map long T2- components (cerebrospinal fluid or CSF, edema etc.), which would require acquiring maximum TE (or TEmax) ~800 ms (32). We have further shown that the accuracy of MWF-map itself does not get appreciably compromised, even if data for long TEs are not acquired. This result is not surprising as the accurate quantification of MWF-values does not require allocation of non-myelin contribution to intermediate (intra-/extra-cellular pool) components and long T2-components. We have also shown that even accurate mapping of intermediate T2 pool (intra-/extra-cellular or IE-pool) would require acquisition of long echo times as one still need to separate non-myelin components into intermediate and long T2 pools. So, making inference about IE-pool or corresponding geometric mean T2-value with maximum TE (~200–300 ms), as was done in (11, 33, 34), may be unreliable.
We would also like to justify the use of incorporating stimulated echo correction intrinsically i.e. without any additional acquisition of B1+-map, even though low resolution B1+-map can be acquired pretty fast. However, using B1+-map would be a suboptimal strategy due to the limitation of extended phase graph (EPG) model that we implemented. Whereas the width of each configuration state is assumed to be a delta peak in spatial frequency space as per the “ideal” EPG model (12); it has a finite approximate width given by δk = 1/ (resolution in the frequency space). This finite width can be attributed to tissue microstructures, susceptibility effects and different diffusion coefficients of multiple pools in voxel of interest. Also, the crusher pair has to be sufficiently high to minimize the contamination coming from secondary echoes of finite width. Additionally, a more accurate EPG model should account for the diffusion effect. In the presence of these unaccounted confounding sources, the effective B1+-map experienced by T2-decay would be significantly perturbed over experimentally measured B1+-map.
For the coil used in our experiment, the iSNR did not drop appreciably along slice encoding direction, supporting our decision to keep αS invariant over entire imaging volumes. However, the iSNR may drop rapidly across the slice encoding direction when using a surface coil. In those cases, αS should be allowed to vary from slice to slice.
The present study is a “proof of concept” study performed in order to test the proposed algorithm and not a clinical study. As only six healthy volunteers and two MS patients were enrolled, this study lacks statistical power to make valid clinical inferences. We have also ignored the effect of CSF on our analyses. The role of CSF on MWF quantification can be quite multi-facet. The simulated result showed that though our protocol was not equipped to accurately reconstruct either intermediate or/and long T2 pool due to maximum TE being used ~ 220 ms, it did not have appreciable effect on MWF quantifications (supplementary Fig. 2). However, the role of CSF goes beyond its role as a high T2 pool and two possible factors may contribute: its pulsation effect and the enhanced inter-compartmental exchange due to its presence. First, due to the pulsation effect of CSF in non-gated sequence, the T2 decay curve in CSF-areas may not fit simple damped exponential model (supplementary Fig. 6). We expect the pulsation of CSF to have relatively minor effect in cortical areas. Second, possible contributions can come from inter-compartmental exchanges, which have been conventionally assumed to negligible for T2-decay (35). Recent pathology-influenced simulations by Levesque et al. (36) have suggested that MWFs may be significantly affected by water exchange. In this context, CSF may bias MWF-quantifications in cortical structures more significantly than other inner WM structures as one can expect higher inter-compartmental exchanges in those regions. This exchange may effect MWF-values in other area as well. This topic warrants further investigation and is beyond the scope of the current work.
On the processing side, the proposed approach is significantly more time consuming that widely used algorithm by Prasloski et al. (13). In favor of the current approach, we would like to point out that either Prasloski approach or our previous 2D multi-slice spatial regularization approach (16) may be terminating the optimization procedure prematurely, leading to suboptimal solutions in some parts of brain. None the less, the proposed algorithm is still fast enough to analyse full brain QT2R data (matrix ~128×128×50) within 14–15 hours on a desktop computer running on 8 years old Intel Xeon X5670 processor (launch date: quarter 1st, 2010). Further, L-BFGS-B solver is the most time consuming part of the algorithm, accounting for 80–85% of the computational time due to its repeated calls. Given that Fei et al. (37) has already shown that L-BFGS-B algorithm on large size problem could run faster by a factor >20× with GPU (graphical processing unit) optimization, a significant reduction in processing time is feasible in future. Unfortunately, DK was unable to implement it due to the lack of access to a workstation with CUDA-enabled NVIDIA GPUs.
Measuring T2 distribution exactly is not feasible, given the experimental constraints with echo spacing. Since minimum echo spacing is usually 7–10 ms, even by the second echo the contributions of small T2 components decay by ~e−1. This issue cannot be side-stepped by any prior about data or modelling. Fortunately, the definition of MWF as formulated by Whittall and MacKay (18), makes it possible to extract meaningful parameter in spite of these experimental limitations. As discussed in appendix F, the estimated value of MWF depends on three factors: (i) T2 distribution segment in myelin range:; (ii) T2 distribution segment in non-myelin range: and (iii) Stimulated echo contribution. The signature of stimulated echo lasts only few echoes before they damp out by 50–60 ms and XNon-myelin are least affected by this. In that respect, one can ignore the effect of stimulated echo contribution on . Please notice that while most of myelin water imaging protocols utilized in literatures, including the current study, are not even equipped to measure XNon-myelin correctly, given TEmax < 250–300 ms; these can calculate sufficiently accurately. On the other hand, XMyelin and “Stimulated echo contribution” seems to be coupled in the problem. However, this “artificial” coupling appears because the numerical function for EPG model needs T2 distribution as inputs; otherwise, the damping in T2-decay should only depend on the ideal (or noise free) multi-exponential decay and underlying “effective” B1 inhomogeneity. The presented algorithm does a more reasonable job of estimating MWF compared to the competing algorithms because all three aforementioned parameters are calculated more accurately due to the utilization of 3D spatial constraints.
In conclusion, the proposed algorithm provides solutions with better convergence properties, along with a more robust fit to T2-decay data compared with competing NNLS based approaches. The reconstructed MWF-maps showed visual improvements in the depiction of subcortical structures and also in other parts of normal white matter. Further, the proposed algorithm tends to converge to the same solution for randomly perturbed initial guesses and is fast enough to analyse full brain QT2R data (matrix ~128×128×50) within 14–15 hours on a desktop workstation.
Supplementary Material
Supplementary Fig. 10. A cartoon depiction of T2 decay, showing the T2 contributions of myelin and non-myelin contributions projected to TE ➔ 0 ms.
Supplementary Tab. 1. Range of Intra-volunteer MWF variability across major white matter regions.
Supplementary Fig. 1: Masks for four different type of regions: namely, gray matter, normal appearing white matter, lesion type-1, lesion type-2.
Supplementary Fig. 2: Water fraction reconstructions for three pools using simulated data (SNR 200). Evidence shows that the current protocol (TEmax ~ 200 ms) is insufficient to accurately reconstruct either intra/extra-cellular water fraction (IEWF) or long T2-water fraction (LTWF).
Supplementary Fig. 3: Top-row: MWF maps reconstructed using: A) Prasloski’s method; B) the proposed approach are being compared. The T2-weighted image is shown for reference (C). Images are cropped to depict only the central portion of imaging slices and then zoomed.
Supplementary Fig. 4: Example of typical Masks that were used to generate white matter ROIs used in Tabs. 3, 4.
Supplementary Fig. 5: T2W images from both multiple sclerosis patients showing locations of lesions.
Supplementary Fig. 6: Typical T2 decays (B) from four chosen points inside CSF areas. Those points are shown in A.
Supplementary Fig. 7. The L2-norm of the data term and it’s first two derivatives as function of voxel wise FAI: δvoxel. It should be noticed that the objective function has only one minimum, where dfvoxel/dδvoxel = 0 and d2fvoxel/dδ2voxel > 0. In other words, fvoxel is a unimodal function.
Supplementary Fig. 8. MWF-maps, FAI-maps and their respective normalized reconstruction error (NRE)-maps at three selected iterations for the randomized perturbed initial guess of FAE-map.
Please notice that current spatially regularized procedure requires an estimate of the flip angle error map to start with. NRE-maps, shown in the figure, were calculated w.r.t. reconstructions, where the initial estimate of FAI-map was taken from the conventional approach.
Supplementary Fig. 9: (A) The fitting error map and the contribution of spatial prior (CSP) map as a function of different extent of spatial regularization strengths, αs for simulated data. As αs increases, the CSP-values across all voxels decrease at the cost of increase in respective voxel wise fitting errors. Not all reconstructions are shown due to limited space. (B) Typical L-curve approach used to decide the optimum regularization strength. The root mean squares (RMSs) of fitting errors and CSP were calculated for entire data set and correspondingly, logarithm of RMS-FE vs logarithm of RMS-CSP were plotted. That resulted in L-shaped curve and the value of αS closest to the origin was chosen as the optimal value.
Tab. 7.
For non-regularized solutions of multi voxel simulated data, five metrics to judge the quality of solutions is presented here for various SNRs.
For conventionally regularized and proposed approaches, same information are presented in Figs. 3, 4. Plotting corresponding values for non-regularized solution was avoided as those are usually of different orders.
| SNR | ||||
|---|---|---|---|---|
| 10k | 500 | 200 | 100 | |
| RMS of NFE | 1.93×10−3 | 3.73×10−3 | 9.45×10−3 | 19.0×10−3 |
| RMS of NRE | 0.4106 | 0.5094 | 0.5992 | 0.728 |
| CTPT2d | 0.2725 | 0.3140 | 0.3254 | 0.3365 |
| CSPT2d | 540 | 563 | 586 | 608 |
| CSPFAE | 3.95×10−7 | 7.28×10−7 | 14.3×10−7 | 26.3×10−7 |
NFE stands for normalized fitting error
NRE stands for normalized reconstruction error
CTPT2D stands for contribution of temporal prior for T2 distribution
CSPT2D stands for contribution of spatial prior for T2 distribution
CSPFAE stands for contribution of spatial prior for T2 FAE map.
Highlights.
An accurate determination of T2 distribution in short T2 pool regime is not feasible, given the shortest achievable echo time in multi echo T2 relaxometry experiment is ~ 7–10 milliseconds.
The voxel wise estimation of myelin water fraction value depends on three scalar values rather than entire T2 distributions (refer to appendix F): (i) Sum of signal contribution from short T2 pools; (ii) sum of contributions from non-myelin pools and (iii) accounting for the stimulated echo contributions.
By utilizing 3D spatial correlations present in anatomical / pathological tissues and underlying B1+-inhomogeneity or flip angle inhomogeneity map, the proposed approach estimates aforementioned scalar values more accurately than the competing algorithms, leading to the enhanced noise robustness of the reconstruction.
Using measured B1+-map to correct for the stimulated echo contributions would be suboptimal for reasons mentioned in the discussion section.
ACKNOLEDGEMENT
All authors would like to thank Dr. Hendrik Kooijman, Philips Healthcare, Hamburg, Germany for providing valuable support and guidance regarding sequence optimization. DK would like to acknowledge the valuable guidance from Dr. Matthew Jacobson, Dana Farber Cancer Institute, Harvard Medical School, USA, regarding establishing the convergence of proposed algorithm empirically. DK will also like to thank Prof. Stephen Becker, Dept. of Applied Mathematics, University of Colorado Boulder, USA for informative discussions regarding the convergence property of Alternate Minimization algorithms.
APPENDICES
Appendix A. Proposed Processing Algorithm and Its Convergence
Initialization step
We first set μS=0, μδ=0, then the single-voxel equivalent of Eqn. [2] becomes:
| [3A] |
Initial estimate of FAI-map was performed by additionally setting μT=0 and minimizing the first term only(13). Once the FAI-map was known, the voxel-wise optimum μT was determined by solving Eqn. [3A] using the L-curve method with the generalized cross-validation approach (38) and corresponding temporally regularized T2-distribution was then determined.
Alternating Minimization (AM) Approach
We generated a sequence of variables:, , estimates of respective variables at nth iteration, until convergence:
| [3B] |
| [3C] |
Where and is obtained from y after sufficiently padding it with zeros along its column to ensure its length is the same as the number of rows of is the misfit function defined later.
Eqn. [3B]
The misfit function in Eqn. [3B] only depends on , and does not require the exact knowledge of and even corresponding any degenerate solution would serve fine for this purpose. To elaborate, if two distributions were to satisfy , then it would also satisfy and the value of would be the same in either case. In our algorithm, most appropriate solution for X is being determined using Eqn. [3C] only.
We assumed temporally/spatially regularized T2-distributions, estimated in previous step/iteration, to be true distributions and estimated spatially smooth solutions for FAI-map. Further, the nonlinear minimization in [3B] was achieved using “lsqnonlin” function of Matlab, employing trust-region-reflective algorithm. As the B1+-inhomogenities at 3T scanner is known to be ±30%, all components of were bounded between 0–0.4. To speed up the calculation, AEPG’s and corresponding Jacobians were pre-calculated for 500 linearly spaced δ-values between 0–0.4 and values at intermediate δ-values, needed during lsqnonlin optimization, were approximated using these pre-calculated values. Without this trick, this step alone would take ~day of processing time.
Eqn. [3C]
Using the FAI-map derived in the previous step, matrices AEPG’s for each voxel are constructed using the EPG model (refer (16) for the pseudo code). The block diagonal matrix is then constructed using AEPG from relevant voxels along its diagonal blocks. μS was chosen as described later. With known , MT and μS, Eqn. [3C] can be minimized using the L-BFGS-B solver (26).
The Matlab implementation of our processing approach will be shared with readers on request.
Convergence
From physics point of view, T2-decay damping, resulting from B1+-inhomogeneities, should depend on underlying “pure” multi exponential decay, i.e. T2 decay in the absence of B1+inhomogeneities, and not on underlying T2 distribution. In that ideal scenerio, the sub-problem in Eqn. [3B] would get uncoupled from Eqn. [3C]. Hence for this “idealized” formulation, it would be sufficient to show that both sub-problems converge to their respective global minima. The expression in Eqn. [3C] is a L2-norm of a linear function in x, which is convex in nature. Given it’s convex nature, it’s guaranteed to converge to its global minima. On the other hand, one would expect the expression in Eqn. [3B] to converge locally as the first term involves a L2-norm of a nonlinear function of . However, if we consider single-voxel equivalent of first term i.e., then its first derivative changes sign only once and the second derivative is positive at that point (Supplementary Fig. 7). Correspondingly, the function fvoxel is unimodal as there is only one minima near δ0 (solution for no noise case). With unimodal functions, any extreme (minimum/maximum) is guaranteed to be the global extreme. Since the block diagonal matrix consists of AEPG(δVoxel) from individual voxels along its diagonal with no off-diagonal term, the corresponding multi-voxel equivalent i.e. is a multi-variate unimodal function with only one minimum w.r.t.. Hence, Eqn. [B] will converge to global minima for this multivariate function as well.
Unfortunately, the EPG model for the MET2 experiment requires T2 distribution as one of inputs and that makes Eqn. [3B] dependent on T2 distribution. Also, L-BFGS-B solver, used for minimizing Eqn. [3C], is known to depend on initial guesses. In the presence of these confounding issues, it’s non-trivial to investigate or establish global convergence mathematically for multi voxel problem and is beyond the scope of this work. We are rather establishing that our formulation satisfy more general first-derivative based optimality condition. We have already shown the effect of SNR on the convergence of reconstruction (Figs. 3, 4). Additionally, we are showing that solutions tend to convergence empirically for randomly perturbed initial guesses.
First-derivative based optimality condition
Alternating minimization of a function f(p,q) where p and q are vectors is known to “converge” if f is continuously differentiable and f(p,q) is unimodal in p for fixed q and unimodal in q for fixed p (39). Since aforementioned condition is satisfied for our objective, the convergence is guaranteed. The “convergence” here means the gradient will be zero (in the absence of constraints), or will satisfy more general first-derivative based optimality conditions (if there are constraints).
Showing the global convergence empirically
To provide the empirical evidence in the support of the global convergence of the solver, we have used the multi voxel simulated data with SNR = 200, described before. To show the empirical robustness of the solver, numerical optimizations were performed for randomly perturbed initial guesses. Our spatially regularized procedure requires an estimate of the flip angle error map to start with. As an empirical evidence, we compared two cases of initial guesses of flip angle error maps:
Case-1: The initial estimate of FAI-map was taken from the conventional approach. We allowed the solver to run till 6th iterations. The convergence was measured with respect to 6th iteration reconstructions (MWF-map, FAI-map) from this case.
Case-2: The initial estimate of FAI-map, taken from the conventional approach, was perturbed randomly between 0–50% of original voxel wise FAI-values.
NRE-maps at various iterations, shown in supplementary Fig. 8, corresponds to case-2 and were calculated w.r.t. 6th iteration reconstructions from case-1. Evidently, the solver tended to reach the same solution irrespective of initial guesses.
Appendix B: Importance of multiplicative scalars for prior terms
Usually, prior terms are an order of magnitude different than the data penalty term. As the combined cost function involves data penalty term along with the temporal and spatial prior terms, it’s very crucial that all prior terms should have same order of magnitude as the data penalty term; otherwise, the optimization routine would have no impact on prior terms.
i). Conventional regularization constant
The chosen range of μT ensures the aforementioned requirement is met for conventional regularization term without any additional multiplicative factor.
ii). Spatial regularization constant for T2-distribution mapping
Consistent with our previously published approach, median(μT-map) is being used as the multiplicative term. In other words, μS is being used as:
Where αS1 is the appropriate spatial regularization strength.
Alternatively, the multiplicative term can be calculated as described for the case of FAI-mapping.
iii). Spatial regularization constant for flip angle mapping
After setting μS = 0 and μδ = 0, we solve the Eqn. [2]. For the calculated voxel-wise T2-distribution, we calculated rms of residuals and rms of contributions of desired spatial prior terms. The multiplicative term is then the ratio of residuals to contribution of 4th term calculated for the aforementioned solution. In other words, μδ is being used as:
Where αS2 is the appropriate spatial regularization strength.
Appendix C. Strategy for optimizing spatial regularization strength, αS
The optimum value of both spatial regularization constants: μS and μδ depends on respective spatial regularization strengths: αS1, αS2. Since optimizing αS for all possible values would be time consuming, following strategy was used:
Step-0: Calculating multiplicative scalar term for spatial prior terms, as described previously.
Step-1: Reconstructions at pre-selected αS-points : The QT2R reconstructions with single iteration was performed for following initial values: αS = [10, 50, 100, 200, 1000, 1500, 2000, 2500, 3000, 5000, 10000]. Correspondingly, RMS-CSP-values and RMS-FE-values at these points are calculated.
Step-2: Plotting of L-curve and evaluation of exit condition: L-curve was plotted between RMS-CSP-values and RMS-FE-values. Three αS-points, at distances closest to the origin, were detected and the exit condition, as described later, was evaluated. The optimization is terminated at this step, if the exit condition is satisfied.
Step-3: Generating additional αS-points on L-curve: Say three αS–points of interest were α1, α2, α3, with α2 having shortest distance to the origin. Following that, we searched for optimum αS in two ranges: α1 to α2, α3 to α3. At mid-points of each range, reconstructions were performed. Correspondingly, RMS-CSP-values and RMS-FE-values at these two new points were recalculated.
We repeated step-2 and step-3 until the exit condition was satisfied.
To speed up the optimization process, only small imaging volume (say, size 40×40×16 or 64×64×16), instead of the entire data set (size 80×80×64 or 128×128×16), was used for this purpose.
Exit condition
Two points on L-curve at the shortest distance to the origin is chosen and the αS-optimization was terminated if the relative difference between RMS-CSP-values at these two points is less than 0.1%.
L-curve used for αS optimization
For each reconstruction, the voxel-wise FE and CSP term were calculated (simulated data case: Supplementary Fig. 9, Panel-A). Solutions corresponding to small αS’s were found to be under-regularized, with high CSP-values. As the value of αS increased, the contribution of CSP term decreased at the cost of the increase in the fitting error and solutions becomes over-regularized for very high αS. Further, the plot between the rms of CSP (RMSCSP) and the rms of fitting error (RMSFE) (Supplementary Fig. 7, Panel-B) appears to be L-shaped and the value of αS, at the shortest distance to the origin, is taken as the optimum value.
Appendix D. Justifying assumed T1 for experimental data
We used a constant value for T1 (= 1000 ms). T1-value could have affected our calculation in these two possible ways: i) by affecting the equilibrium magnetization; and ii) by altering the calculating for the stimulated echo contribution. At 3T, the average T1-values for WM and the cerebral GM have been reported as ~850–1100 ms and ~1350 ms respectively (40). With the “effective TR” of 1.77s. (i.e. TR ~1.6T1–2T1), the equilibrium magnetizations were expected to be ~0.79–0.86Mo in different WM voxels, where Mo is the equilibrium magnetization. As we were not in the Rician noise regime (SNR of last echo 13–18 in WM regions), incomplete T1-recovery would have only caused the overall downward shift of T2-decay and its effect on QT2R analysis were ignored. To test the effect of assumed T1 on the stimulated echo pathways, we processed a single data set for two additional values of assumed T1 = 850 ms, 1100 ms and the normalized difference of these MWF-maps were calculated with respect to our original analysis (with assumed T1 = 1000 ms). The 90th percentiles were found to be 0.0806 and 0.0817 for assumed T1 = 850 ms, and 1100 ms respectively (Tab. 6). This justifies our selection. However, for the smaller TR (1000–1500 ms), a prior determination of T1-values would be required.
Tab. 6.
A single multi-echo experimental data set was processed and MWF-maps were reconstructed for two additional values of assumed T1 = 850 ms and 1100 ms, apart from our original choice of T1=1000 ms. Relative voxel-wise difference-map were calculated between MWF-map calculated using T1=1000 ms and either of MWF-maps calculated using other additional values of T1. The relative difference at various percentiles are being reported here.
| Relative divergence of voxel wise MWF-maps | ||
|---|---|---|
| Assumed T1 = 850 ms | Assumed T1 = 1100 ms | |
| Percentile 50 | 0.0174 | 0.0168 |
| Percentile 90 | 0.0816 | 0.0807 |
| Percentile 97 | 0.1525 | 0.1526 |
| Percentile 99 | 0.2368 | 0.2440 |
Appendix E. Comments about Limited Memory Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm with Box Constraints (L-BFGS-B) (26)
L-BFGS-B solver (26), a limited-memory variant of Broyden–Fletcher–Goldfarb–Shanno (BFGS) quasi-Newton method with bound, made it feasible to implement 3D operator even on a work desktop computer. Whereas the original BFGS stores a dense n×n approximation to the inverse Hessian (n = number of variables), L-BFGS stores a history of the past m updates (often m<10) of the position x and gradient ∇f(x) and these updates are used to perform operations requiring the inverse Hessian (Hk)-vector product. Due to its resulting linear memory requirement, the L-BFGS method is particularly well suited for optimization problems with a large number of variables.
The L-BFGS-B algorithm extends L-BFGS to handle simple box constraints (form li ≤ xi ≤ ui where li and ui are per-variable constant lower and upper bounds, respectively). The method works by identifying fixed and free variables at every step (using a simple gradient method), and then using the L-BFGS method on the free variables only to get higher accuracy, and then repeating the process.
The solutions of L-BFGS-B algorithm are known to be sensitive to initial guesses. However, the temporally regularized solution, from step 1 of our algorithm, serves as good guess for the spatially regularized problem. Being a variant of quasi-Newton method, the solution is refined over multiple iterations/runs before L-BFGS-B solver outputs the optimum value. We are using the term “inner iteration” to denote these runs to distinguish it from “outer iteration” over which the presented approach refines T2-distribution and stimulated echo contributions successively.
Appendix F. Geometric Interpretation of the Definition of MWF
The MWF has defined as the ratio of the signal contribution from short T2 range to over-all T2 contribution:
Where the geometric interpretation of OA, OB are depicted in the supplementary fig. 10. Please notice that pre-factors of these multi exponentials are nothing but the corresponding mono exponential T2 decay curves projected to TE ➔ 0 ms.
There are three possible sources of quantification error in MWF-estimations:
T2 distribution segment in myelin range:
T2 distribution segment in non-myelin range:
Stimulated echo contribution
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
BIBILIOGRAPHY
- 1.Laule C, Leung E, Li DKB, Troboulsee AL, Paty DW, MacKay AL, et al. Myelin water imaging in multiple sclerosis: quantitative correlations with histopathology. Multiple Sclerosis. 2006;12(6):747–53. [DOI] [PubMed] [Google Scholar]
- 2.Moore GR, Leung E, MacKay AL, Vavasour IM, Whittall KP, Cover KS, et al. A pathology-MRI study of the short-T2 component in formalin-fixed multiple sclerosis brain. Neurology. 2000;55(10):1506–10. [DOI] [PubMed] [Google Scholar]
- 3.Kozlowski P, Liu J, Yung AC, Tetzlaff W. High-resolution myelin water measurements in rat spinal cord. Magn Reson Med. 2008;59(4):796–802. [DOI] [PubMed] [Google Scholar]
- 4.Stanisz GJ, Webb S, Munro CA, Pun T, Midha R. MR properties of excised neural tissue following experimentally induced inflammation. Magn Reson Med. 2004;51(3):473–9. [DOI] [PubMed] [Google Scholar]
- 5.Pun TW, Odrobina E, Xu QG, Lam TY, Munro CA, Midha R, et al. Histological and magnetic resonance analysis of sciatic nerves in the tellurium model of neuropathy. J Peripher Nerv Syst. 2005;10(1):38–46. [DOI] [PubMed] [Google Scholar]
- 6.Laule C, Vavasour IM, Moore GR, Oger J, Li DK, Paty DW, et al. Water content and myelin water fraction in multiple sclerosis. A T2 relaxation study. J Neurol. 2004;251(3):284–93. [DOI] [PubMed] [Google Scholar]
- 7.Neema M, Goldberg-Zimring D, Guss ZD, Healy BC, Guttmann CR, Houtchens MK, et al. 3 T MRI relaxometry detects T2 prolongation in the cerebral normal-appearing white matter in multiple sclerosis. Neuroimage. 2009;46(3):633–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Faizy TD, Thaler C, Kumar D, Sedlacik J, Broocks G, Grosser M, et al. Heterogeneity of Multiple Sclerosis Lesions in Multislice Myelin Water Imaging. PLoS One. 2016;11(3):e0151496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kumar D, Ludewig P, Raj A, Magnus T, Fiehler J, Heesen C, et al. Preclinical Study of Stroke using T2relaxometry and Diffusion Weighted Imaging. In: Proceedings of ISMRM, Salt Lake City, USA 2013:2923. [Google Scholar]
- 10.Wright AD, Jarrett M, Vavasour I, Shahinfard E, Kolind S, van Donkelaar P, et al. Myelin Water Fraction Is Transiently Reduced after a Single Mild Traumatic Brain Injury - A Prospective Cohort Study in Collegiate Hockey Players. Plos One. 2016;11(2). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Billiet T, Vandenbulcke M, Madler B, Peeters R, Dhollander T, Zhang H, et al. Age-related microstructural differences quantified using myelin water imaging and advanced diffusion MRI. Neurobiol Aging. 2015;36(6):2107–21. [DOI] [PubMed] [Google Scholar]
- 12.Graham SJ, Stanchev PL, Bronskill MJ. Criteria for analysis of multicomponent tissue T2 relaxation data. Magn Reson Med. 1996;35(3):370–8. [DOI] [PubMed] [Google Scholar]
- 13.Prasloski T, Madler B, Xiang QS, MacKay A, Jones C. Applications of stimulated echo correction to multicomponent T2 analysis. Magn Reson Med. 2012;67(6):1803–14. [DOI] [PubMed] [Google Scholar]
- 14.Akhondi-Asl A, Afacan O, Mulkern RV, Warfield SK. T2-relaxometry for myelin water fraction xtraction using wald distribution and extended phase graph. Med Image Comput Comput Assist Interv. 2014;17(Pt 3):145–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Layton KJ, Morelande M, Wright D, Farrell PM, Moran B, Johnston LA. Modelling and estimation of multicomponent T(2) distributions. IEEE Trans Med Imaging. 2013;32(8):1423–34. [DOI] [PubMed] [Google Scholar]
- 16.Kumar D, Siemonsen S, Heesen C, Fiehler J, Sedlacik J. Noise robust spatially regularized myelin water fraction mapping with the intrinsic B1 -error correction based on the linearized version of the extended phase graph model. J Magn Reson Imaging. 2016;43(4):80017. [DOI] [PubMed] [Google Scholar]
- 17.Poon CS, Henkelman RM. Practical T2 quantitation for clinical applications. J Magn Reson Imaging. 1992;2(5):541–53. [DOI] [PubMed] [Google Scholar]
- 18.Whittall K, Mackay A. Quantitative interpretation of NMR relaxation data. J Magn Reson. 1989;84:134–52. [Google Scholar]
- 19.Kumar D, Nguyen TD, Gauthier SA, Raj A. Bayesian Algorithm Using Spatial Priors for Multiexponential T2 Relaxometry From Multiecho Spin Echo MRI. Magnetic Resonance in Medicine. 2012;68(5):1536–43. [DOI] [PubMed] [Google Scholar]
- 20.Madler B, MacKay AL. In-vivo 3D Mutli-component T2-Relaxation Measurements for Quantitative Myelin Imaging at 3T. Proc ISMRM. 2006(13):2112. [Google Scholar]
- 21.Meyers SM, Laule C, Vavasour IM, Kolind SH, Madler B, Tam R, et al. Reproducibility of myelin water fraction analysis: a comparison of region of interest and voxel-based analysis methods. Magn Reson Imaging. 2009;27(8):1096–103. [DOI] [PubMed] [Google Scholar]
- 22.Hwang D, Du YP. Improved myelin water quantification using spatially regularized nonnegative least squares algorithm. J Magn Reson Imaging. 2009;30(1):203–8. [DOI] [PubMed] [Google Scholar]
- 23.Labadie C, Lee JH, Rooney WD, Jarchow S, Aubert-Frecon M, Springer CS, et al. Myelin Water Mapping by Spatially Regularized Longitudinal Relaxographic Imaging at High Magnetic Fields. Magnetic Resonance in Medicine. 2014;71(1):375–87. [DOI] [PubMed] [Google Scholar]
- 24.Yoo Y, Tam R. Non-local spatial regularization of MRI T2 relaxation images for myelin water quantification. Med Image Comput Comput Assist Interv. 2013;16(Pt 1):614–21. [DOI] [PubMed] [Google Scholar]
- 25.Bernstein MA, King KF, Zhou XJ. Handbook of MRI Pulse Sequences. 1 ed. San Diego, CA, USA: Academic Press; 2004. [Google Scholar]
- 26.Zhu CY, Byrd RH, Lu PH, Nocedal J. Algorithm 778: L-BFGS-B: Fortran subroutines for large-scale bound-constrained optimization. Acm T Math Software. 1997;23(4):550–60. [Google Scholar]
- 27.Hennig J, Weigel M, Scheffler K. Calculation of flip angles for echo trains with predefined amplitudes with the extended phase graph (EPG)-algorithm: principles and applications to hyperecho and TRAPS sequences. Magn Reson Med. 2004;51(1):68–80. [DOI] [PubMed] [Google Scholar]
- 28.Polman CH, Reingold SC, Banwell B, Clanet M, Cohen JA, Filippi M, et al. Diagnostic criteria for multiple sclerosis: 2010 revisions to the McDonald criteria. Ann Neurol. 2011;69(2):292–302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Prasloski T, Rauscher A, MacKay AL, Hodgson M, Vavasour IM, Laule C, et al. Rapid whole cerebrum myelin water imaging using a 3D GRASE sequence. Neuroimage. 2012;63(1):533–9. [DOI] [PubMed] [Google Scholar]
- 30.Biasiolli L, Lindsay AC, Chai JT, Choudhury RP, Robson MD. In-vivo quantitative T2 mapping of carotid arteries in atherosclerotic patients: segmentation and T2 measurement of plaque components. J Cardiovasc Magn Reson. 2013;15:69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wagnerova D, Herynek V, Dezortova M, Marusic P, Krsek P, Zamecnik J, et al. The relationships between quantitative MR parameters in hippocampus in healthy subjects and patients with temporal lobe epilepsy. Physiol Res. 2015;64(3):407–17. [DOI] [PubMed] [Google Scholar]
- 32.Laule C, Vavasour IM, Madler B, Kolind SH, Sirrs SM, Brief EE, et al. MR evidence of long T2 water in pathological white matter. J Magn Reson Imaging. 2007;26(4):1117–21. [DOI] [PubMed] [Google Scholar]
- 33.Kavroulakis E, Simos PG, Kalaitzakis G, Maris TG, Karageorgou D, Zaganas I, et al. Myelin content changes in probable Alzheimer’s disease and mild cognitive impairment: Associations with age and severity of neuropsychiatric impairment. J Magn Reson Imaging. 2017. [DOI] [PubMed] [Google Scholar]
- 34.Dayan M, Hurtado Rua SM, Monohan E, Fujimoto K, Pandya S, LoCastro EM, et al. MRI Analysis of White Matter Myelin Water Content in Multiple Sclerosis: A Novel Approach Applied to Finding Correlates of Cortical Thinning. Front Neurosci. 2017;11:284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kalantari S, Laule C, Bjarnason TA, Vavasour IM, MacKay AL. Insight into In Vivo Magnetization Exchange in Human White Matter Regions. Magnetic Resonance in Medicine. 2011;66(4):1142–51. [DOI] [PubMed] [Google Scholar]
- 36.Levesque IR, Pike GB. Characterizing Healthy and Diseased White Matter Using Quantitative Magnetization Transfer and Multicomponent T-2 Relaxometry: A Unified View via a Four-Pool Model. Magnetic Resonance in Medicine. 2009;62(6):1487–96. [DOI] [PubMed] [Google Scholar]
- 37.Fei Y, Rong G, Wang B, Wang W. Parallel L-BFGS-B algorithm on GPU. Computers & Graphics 2014;40(1):1–9. [Google Scholar]
- 38.Hansen PC. Analysis of Discrete Ill-Posed Problems by Means of the L-Curve. SIAM Review. 1992;34:561–81. [Google Scholar]
- 39.Bertsekas DP. Nonlinear programming. 2 ed. Belmont, Mass: Athena Scientific; 1995. x, 646 p. p. [Google Scholar]
- 40.Wansapura JP, Holland SK, Dunn RS, Ball WS. NMR relaxation times in the human brain at 3.0 tesla. Jmri-Journal of Magnetic Resonance Imaging. 1999;9(4):531–8. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Fig. 10. A cartoon depiction of T2 decay, showing the T2 contributions of myelin and non-myelin contributions projected to TE ➔ 0 ms.
Supplementary Tab. 1. Range of Intra-volunteer MWF variability across major white matter regions.
Supplementary Fig. 1: Masks for four different type of regions: namely, gray matter, normal appearing white matter, lesion type-1, lesion type-2.
Supplementary Fig. 2: Water fraction reconstructions for three pools using simulated data (SNR 200). Evidence shows that the current protocol (TEmax ~ 200 ms) is insufficient to accurately reconstruct either intra/extra-cellular water fraction (IEWF) or long T2-water fraction (LTWF).
Supplementary Fig. 3: Top-row: MWF maps reconstructed using: A) Prasloski’s method; B) the proposed approach are being compared. The T2-weighted image is shown for reference (C). Images are cropped to depict only the central portion of imaging slices and then zoomed.
Supplementary Fig. 4: Example of typical Masks that were used to generate white matter ROIs used in Tabs. 3, 4.
Supplementary Fig. 5: T2W images from both multiple sclerosis patients showing locations of lesions.
Supplementary Fig. 6: Typical T2 decays (B) from four chosen points inside CSF areas. Those points are shown in A.
Supplementary Fig. 7. The L2-norm of the data term and it’s first two derivatives as function of voxel wise FAI: δvoxel. It should be noticed that the objective function has only one minimum, where dfvoxel/dδvoxel = 0 and d2fvoxel/dδ2voxel > 0. In other words, fvoxel is a unimodal function.
Supplementary Fig. 8. MWF-maps, FAI-maps and their respective normalized reconstruction error (NRE)-maps at three selected iterations for the randomized perturbed initial guess of FAE-map.
Please notice that current spatially regularized procedure requires an estimate of the flip angle error map to start with. NRE-maps, shown in the figure, were calculated w.r.t. reconstructions, where the initial estimate of FAI-map was taken from the conventional approach.
Supplementary Fig. 9: (A) The fitting error map and the contribution of spatial prior (CSP) map as a function of different extent of spatial regularization strengths, αs for simulated data. As αs increases, the CSP-values across all voxels decrease at the cost of increase in respective voxel wise fitting errors. Not all reconstructions are shown due to limited space. (B) Typical L-curve approach used to decide the optimum regularization strength. The root mean squares (RMSs) of fitting errors and CSP were calculated for entire data set and correspondingly, logarithm of RMS-FE vs logarithm of RMS-CSP were plotted. That resulted in L-shaped curve and the value of αS closest to the origin was chosen as the optimal value.