Exploring the conformations of nitric oxide synthase with fluorescence

Abstract

Multi-domain oxidoreductases are a family of enzymes that catalyze oxidation-reduction reactions through a series of electron transfers. Efficient electron transfer requires a sequence of protein conformations that position electron donor and acceptor domains in close proximity to each other so that electron transfer can occur efficiently. An example is mammalian nitric oxide synthase (NOS), which consists of an N-terminal oxygenase domain containing heme and a C-terminal reductase domain containing NADPH/FAD and FMN subdomains. We describe the use of time-resolved and single-molecule fluorescence to detect and characterize the conformations and conformational dynamics of the neuronal and endothelial isoforms of NOS. Fluorescence signals are provided by a fluorescent dye attached to the Ca²⁺-signaling protein calmodulin (CaM), which regulates NOS activity. Time-resolved fluorescence decays reveal the presence of at least four underlying conformational states that are differentiated by the extent of fluorescence quenching. Single-molecule fluorescence displays transitions between conformational states on the time scales of milliseconds to seconds. This review describes the type of information available by analysis of time-resolved and single-molecule fluorescence experiments.

2. INTRODUCTION

2.1. Nitric oxide synthase and electron transfer

Nitric Oxide Synthase (NOS) enzymes are multi-domain proteins in the cytochrome P450 family that produce nitric oxide, a signaling molecule important for vasodilation, neurotransmission, and the innate immune response (1, 2). NOS catalyzes the synthesis of NO through two sequential oxidations of arginine bound at the heme cofactor to form citrulline and nitric oxide (NO) (3). During catalysis NOS facilitates an intricate sequence of electron transfers to shuttle electrons from a C-terminal reductase domain to an N-terminal oxygenase domain. NOS monomers dimerize at the oxygenase domain to form a functional dimer. The reductase and oxygenase domains are connected by a linker that incorporates a binding site for the Ca²⁺-signaling protein calmodulin (CaM). The reductase domain itself consists of an NADPH/FAD subdomain and an FMN subdomain. Electron transfer in NOS is initiated by hydride transfer from NADPH to FAD (Figure 1). In CaM-activated NOS single electrons are then transferred from FAD to FMN and finally to the heme cofactor in the oxygenase domain of the opposite monomer.

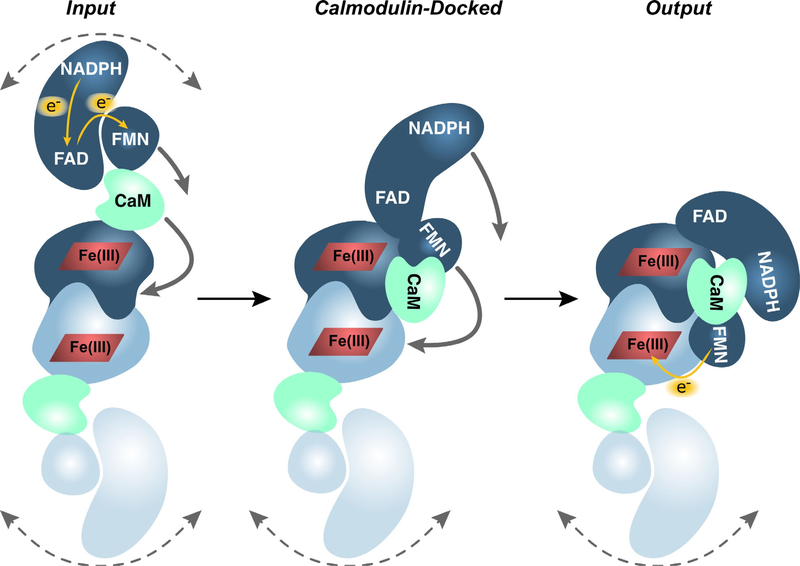
Figure 1.

NOS homodimer subdomain structure and electron transfer sequence. Hydride transfer from NADPH to FAD is followed by electron transfer to the FMN subdomain and then to the heme in the oxygenase domain of the partner NOS monomer. Electron transfer from FAD to FMN and from FMN to heme is activated by binding of calmodulin. NOS conformational changes based on electron microscopy structures showing the Input, Calmodulin-Docked, and Output conformations. (Figure adapted with permission from ref. (9))

There are two classes of mammalian NOS enzymes: constitutive NOS and inducible NOS (iNOS). The constitutive class consists of endothelial NOS (eNOS) and neuronal NOS (nNOS), which are the subject of this review. There are some structural differences among the three isoforms but the main difference is that eNOS and nNOS bind CaM reversibly so that their activity depends on the concentration of calcium (Ca²⁺) in the environment. They are constitutively expressed and hence constantly available for activation by Ca²⁺-CaM. On the other hand, CaM when complexed with iNOS binds Ca²⁺ with such high affinity that Ca²⁺-CaM remains essentially irreversibly bound to iNOS, and its activity does not appear to depend on the concentration of Ca²⁺ in the environment.

While partial crystal structures of NOS exist (for example (4–6)), a complete crystal structure has not been obtained, presumably because of conformational mobility of the enzyme. Structural studies of NOS by single-particle electron microscopy (7–10), hydrogen-deuterium exchange mass spectrometry (11), and electron paramagnetic resonance (12–14) are reviewed elsewhere in this volume.

2.2. Conformational gating

The rates of biological electron transfer characteristically depend exponentially on the edge-to-edge distance between electron donor and acceptor, k ~ exp(−βr) where typically β ≈ 1.4. Å⁻¹ (15). Most biological electron transfers occur at edge-to-edge distances less than ~14 Å (15, 16). Electron transfer rates between donor-acceptor partners are likely exceedingly slow unless the enzyme attains a conformation where donor and acceptor interact closely. This suggests that the FMN subdomain in particular must undergo conformational motions of tens of Ångströms (2), interacting first with the FAD domain to accept an electron and then with the oxygenase domain of the opposite monomer to donate an electron to the heme cofactor. This leads to the hypothesis that electron transfer rates in NOS are controlled primarily by conformational dynamics rather than the intrinsic electron-transfer rate. NOS activity is therefore expected to depend on the formation of a sequence of conformations that place successive electron donor and acceptor pairs in close proximity for efficient electron transfer (Figure 1). A number of authors have proposed that this phenomenon, termed “conformational gating” or “conformational sampling,” controls NOS activity (17, 18).

These requirements suggest that conformational gating occurs primarily via the FMN subdomain. Electron-transfer rates from FMN to heme have been determined from flash photolysis experiments (19, 20). The measured FMN to heme electron-transfer rate constant with CaM is 262 s⁻¹ in an nNOS construct lacking the NADPH/FAD subdomain (19), setting a lower limit on the intrinsic electron-transfer rate in the “output” state of the enzyme, the state where catalysis occurs at the heme. The fact that the actual electron-transfer rate in the nNOS holoenzyme with bound CaM is 36 s⁻¹ (21), an order of magnitude slower, implicates conformational gating as the rate-limiting factor in NOS activity. CaM-activated NO synthase activity occurs at maximal rates of 0.1. s⁻¹ to 0.2. s⁻¹ in eNOS and ~0.9. s⁻¹ in nNOS (22, 23), differing by almost an order of magnitude, even though the catalyzed reaction is the same and the reduction potentials for electron-transfer pairs are similar in the two isoforms (24). As electron transfer to the heme cofactor is rate limiting for catalysis (25), these observations again suggest that conformational dynamics regulate NOS activity. If this hypothesis is correct, differences in conformational dynamics could also explain the different activities of nNOS and eNOS.

NOS activity is dependent on CaM. Thus CaM binding to constitutive NOS (eNOS or nNOS) modulates the conformational landscape of the enzyme. Several researchers have proposed that CaM regulates NOS enzymatic activity by docking to the oxygenase domain, thereby constraining and regulating the accessible conformations of the CaM-NOS complex to control the rates of electron transfer between the reductase and oxygenase domains (7, 9, 11, 26).

3. NOS CONFORMATIONS DETECTED BY FLUORESCENCE

3.1. Conformational signatures in fluorescence

In many cases changes in protein conformations can be detected by fluorescence. Although information about protein conformations can sometimes be deduced from steady-state fluorescence measurements, more specific information can usually be achieved by time resolution of fluorescence decays. For example, multiple fluorescence decay components can often be interpreted in terms of multiple conformational populations characterized by different degrees of fluorescence quenching. Quenching may occur by photoinduced electron transfer or other photochemical reactions, by interaction with quenchers present in the solvent or protein, or by Förster resonance energy transfer (FRET) (27). Indeed, FRET is one of the most versatile techniques for detecting protein conformations and conformational changes is (28, 29).

3.2. Fluorescence of flavin cofactors

There are two general approaches to studying protein conformation by fluorescence, and both have been applied to NOS. One approach relies on the native fluorescence of intrinsic fluorophores in the protein such as the aromatic amino acids tryptophan and tyrosine or cofactors such as flavins. Fluorescence decays from the intrinsic flavin fluorescence of nNOS reported by Kungl and co-workers were sensitive to CaM binding (30). Further analysis by Salerno and co-workers of flavin fluorescence decays in both iNOS (31) and nNOS (26) showed that flavin fluorescence appeared to be quenched by interaction between the flavins FAD and FMN in the input state. Their results on nNOS further demonstrated the critical role of CaM on the available conformations, particularly in the formation of a state that they interpreted as the output state with FMN apparently in close proximity to heme. Lifetime analysis revealed a third component with a fluorescence lifetime close to that of FMN in solution. This population was attributed to “open” conformations where the FMN domain is not associated with either the FAD or the oxygenase domains and is therefore more accessible to the surrounding solution.

3.3. NOS and fluorescent labels

The second approach involves labeling proteins with artificial fluorophores. Although this requires the extra steps of labeling specific sites in the protein and then verifying that protein function is not thereby impaired, it allows the use of fluorophores with high absorption coefficients and high fluorescence quantum yields. The resulting high brightness allows sensitivity down to the single-molecule level.

If one wishes to attach an extrinsic fluorophore to a protein such as NOS, one faces the challenge of labeling the protein with a single fluorophore at a specific location in the protein. Most proteins have multiple potential labeling sites (typically amines or the sulfhydryl groups of Cys residues), complicating the desired labeling with a single fluorophore at a specific site. CaM is an exception, as native mammalian CaM contains no Cys residues, and a non-native Cys can be inserted wherever desired by site-directed mutagenesis for labeling with a fluorophore derivatized with maleimide, iodoacetamide, or other thiol-reactive group (32–34). This approach solves the problem of multiple labeling sites on NOS by attachment of the label to the activating protein CaM instead of directly to NOS (33, 35, 36) and was used to characterize conformational changes of CaM upon binding to NOS (33, 35, 36). Using labeled CaM, Guillemette and co-workers showed that visible fluorophores are quenched upon binding to NOS and attributed the quenching to FRET between the fluorophore and the oxygenase heme groups (35).

Lu and co-workers implemented another approach to specific fluorescence labeling (37). Starting with the NOS reductase domain, they mutated accessible Cys residues to form a “Cys-lite” construct into which they inserted two Cys residues, one on the FAD domain and one on the FMN domain. This construct has the advantage of allowing experiments to probe the effect of CaM binding on conformational dynamics. Single-molecule measurements characterized conformational dynamics in the absence and presence of CaM. The results suggested that CaM narrows the range of available conformational states. Of course, as the construct lacks the oxygenase domain, it cannot form the rate-limiting output state of the enzyme, and the transfer of electrons from the reductase to the oxygenase domain could not be probed.

3.4. Time-resolved fluorescence of labeled CaM bound to NOS

In our research group we used fluorescence-labeled CaM to probe the conformations of NOS-CaM complexes by time-resolved and single-molecule fluorescence spectroscopy. We describe below how bringing in the dimension of time, either in bulk solution (fluorescence decay measurements) or single-molecule detection (fluorescence time sequences) adds information not available in steady-state measurements.

We recorded fluorescence decays of CaM labeled with Alexa Fluor 488 (CaM-AF488) and with Alexa Fluor 594 (CaM-AF594) bound to eNOS or nNOS by time-correlated single-photon counting (TCSPC). A question often faced in the analysis of complex fluorescence decays is how many exponential components are warranted in the fit. Our expectation is that each exponential component corresponds to a conformation (or set of conformations) of the enzyme, and further that the amplitude of each component reports the relative population of that conformation. If the number of exponentials included in the fit is too low, a given exponential component could represent an average over two unresolved populations with different lifetimes. A reliable statistical procedure is needed to determine the number of exponentials warranted by the data rather than assuming that number a priori. Unlike conventional nonlinear least-squares fitting procedures, in the maximum entropy method (MEM) it is not necessary to specify in advance the number of exponential components (38). In MEM an “entropy” constraint minimizes variation in the amplitudes of a sequence of lifetime components (in our case 200 logarithmically spaced components spanning from ~0.0.1 ns to 10 ns). We analyzed the decays with Pulse5, a Bayesian implementation of MEM (39), to yield the distribution of fluorescence lifetimes (40). The result is a fit with the minimum number of fluorescence decay components warranted by the data. (Fits by nonlinear regression to multiple exponentials gave similar results with lifetimes corresponding to the peaks of the MEM lifetime distributions.) Widths of the peaks in the distribution most likely reflect noise in the data rather than inhomogeneity in the underlying populations.

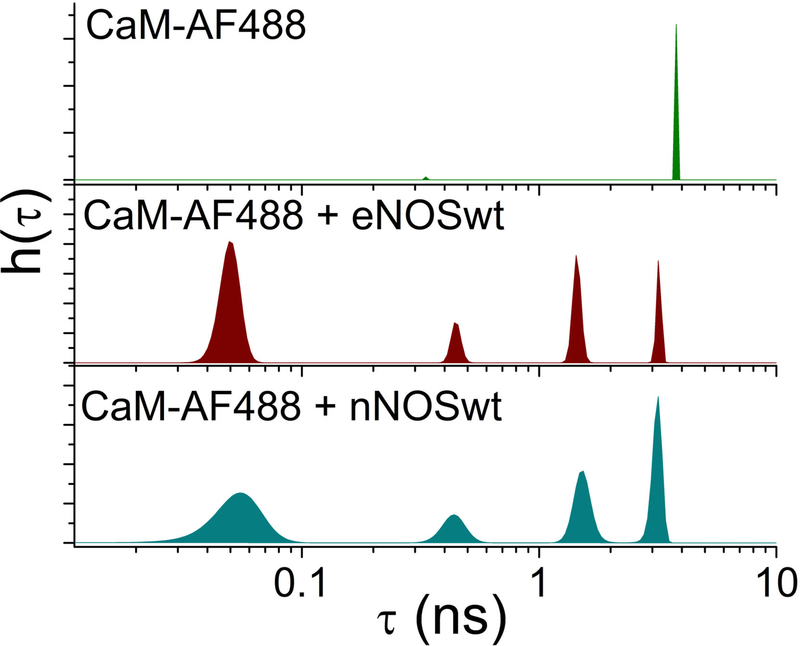
Figure 2 shows recovered lifetime distributions for CaM labeled with the fluorophore CaM-AF488. In the absence of NOS, a single lifetime of 4 ns was observed for CaM-AF488. This is equal to the fluorescence lifetime of AF488 alone, as expected. In contrast, in the presence of eNOS or nNOS four populations with lifetimes from 0.1 ns to 4 ns were detected for CaM-AF488 at Ca²⁺ concentrations sufficient to saturate the Ca²⁺ binding sites of CaM. This result suggests the existence of at least four conformations of CaM-eNOS complexes with distinct quenching efficiencies.

Figure 2.

Fluorescence lifetime distributions for CaM-AF488 in the absence of NOS (top) or in the presence of wild-type eNOS (middle) or nNOS (bottom). Plots show lifetime distributions h(τ) recovered by MEM fitting to fluorescence decays.

We conclude that different quenching states signify different conformations with different FRET efficiencies. The extent of quenching is most likely related to the distance of the fluorophore from the heme groups. Energy transfer to FMN and/or FAD is also a possibility, but the calculated Förster radii (40) and measurements (36) suggest that the contribution of flavin to quenching is minor. We estimated the Förster radius for energy transfer from Alexa Fluor 488 to heme to be 51 Å, compared to 25 Å for energy transfer to FMN (40), so energy transfer to heme is likely to dominate the fluorescence quenching. NOS dimers contain two heme groups, increasing the expected FRET rate. Uncertainty in the FRET orientational factor (κ²) is likely not a significant issue because the planar nature of the heme Q-band spectroscopic transition. This transition consists of two perpendicular in-plane degenerate transition moments (41). The result is that any direction within the heme plane can serve as the accepting dipole, providing intrinsic orientational averaging (42).

Whatever the source of quenching, different quenching states can be taken to signify different conformational states. For CaM-AF488 complexed with either eNOS or nNOS four lifetime peaks were resolved. Two conformations are highly quenched, one with a lifetime of 0.1–0.2 ns and one with lifetime ~0.7 ns. Given that FRET from AF488 to the two heme cofactors in the oxygenase domain homodimer is the dominant source of quenching (36), these highly-quenched states are consistent with a close juxtaposition of the fluorescence label with heme. Two other populations with lifetimes of ~2 ns and ~4 ns correspond to conformations where CaM is not in close proximity to the oxygenase domain.

3.5. Calcium dependence of formation of conformations

Clues into the nature of the conformational states of NOS observed in fluorescence decays can be obtained from the Ca²⁺ dependence of the populations of each conformational state. NOS is activated by CaM, a calcium signaling protein, which binds up to four Ca²⁺ ions, two each in its N-terminal and C-terminal lobes (43). As a result, the activity of NOS is sensitive to the Ca²⁺ concentration. Resting cytosolic concentrations of free Ca²⁺ are typically ca. 100 nM or less in both endothelial (22, 44) and neuronal (45) cells. During Ca²⁺ transients the free Ca²⁺ concentration can reach 5–10 μM in neuronal cells (46, 47). Endothelial cells are activated by an increase in intracellular free Ca²⁺ to ca. 1 μM (44, 48).

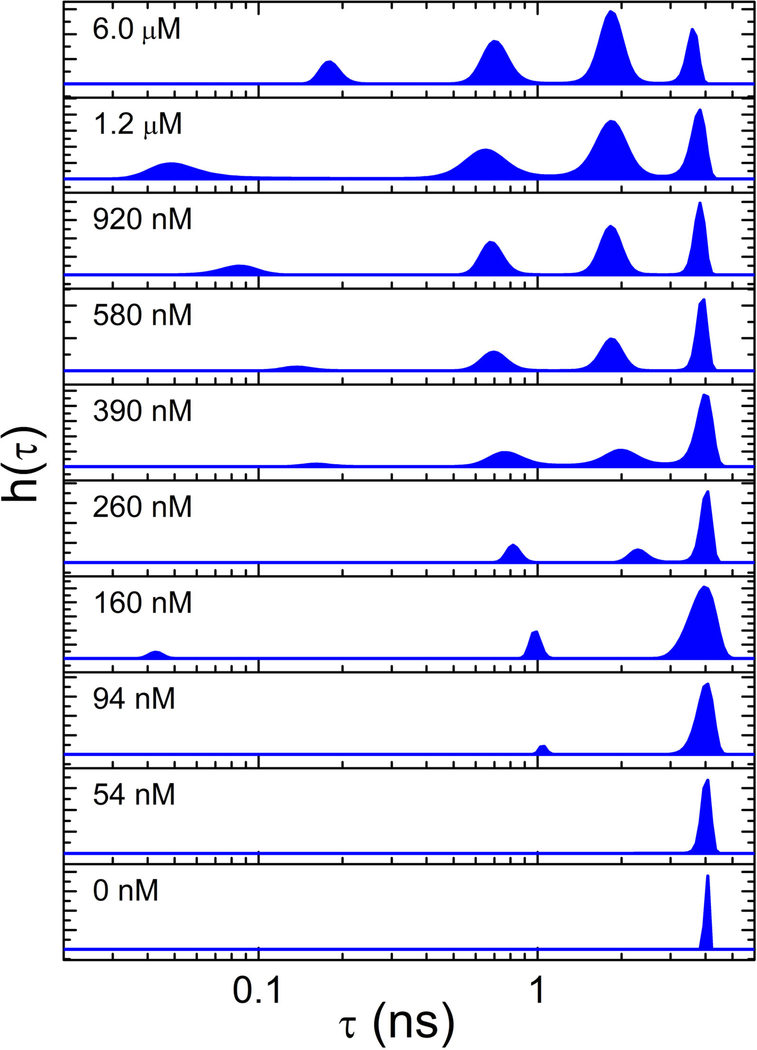
Both steady-state and time-resolved fluorescence of labeled CaM bound to eNOS are sensitive to Ca²⁺ concentrations (40). Figure 3 shows the Ca²⁺ dependence of the lifetime distributions for CaM in the presence of eNOS. (The phosphomimetic S1179D mutant of eNOS was used for these experiments because of its higher NO synthase activity (49).) At low Ca²⁺ concentration, the only population present has a lifetime of ~4 ns, corresponding to the fluorescence lifetime of AF488. As the Ca²⁺ concentration was increased, quenched lifetimes appeared indicating binding of CaM to NOS. Figure 4 shows plots of the amplitude of each fluorescence lifetime component as well as the steady-state fluorescence intensity distributions as a function of Ca²⁺ concentration. Ca²⁺ binding within each lobe of CaM is highly cooperative (50). The Ca²⁺ dependence of both the steady-state and lifetime-resolved fluorescence measurements was fit to a sequential Ca²⁺-binding scheme (22) in which cooperative binding of two Ca²⁺ ions to the CaM C-lobe drives formation of an initial (Ca²⁺)₂-CaM-eNOS complex. Binding of two additional Ca²⁺ ions to the N-lobe yields the complex (Ca²⁺)₄-CaM-eNOS:

$$\text{CaM}+\text{eNOS}\stackrel{{}^{2{\text{Ca}}^{2+}}}{\rightleftharpoons }{\left({\text{Ca}}^{2+}\right)}_2\text{CaM}\cdot \text{eNOS}\stackrel{{}^{2{\text{Ca}}^{2+}}}{\rightleftharpoons }{\left({\text{Ca}}^{2+}\right)}_4\text{CaM}\cdot \text{eNOS}$$ (Scheme 1)

Figure 3.

MEM lifetime distributions for CaM-AF488-S1179D-eNOS at the Ca2+ concentrations listed in each panel. Excitation was at 488 nm and emission was detected at 515 nm. Quenching increases with decreasing lifetime from right to left. Note that variation in the lifetime of the shortest-lifetime population is magnified by the log scale. Figure used with permission from ref. (40)

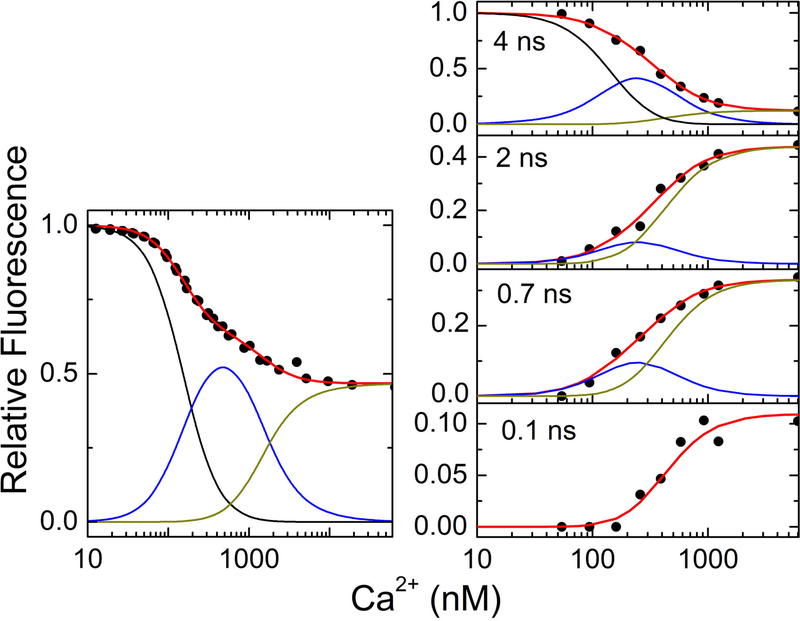
Figure 4.

(Left) Steady-state fluorescence of CaM-T34C-AF594 with eNOS-WT vs. Ca2+ concentration. Fluorescence of AF594 (λex = 594 nm, λem = 615 nm) and Fluo-4 (λex = 494 nm, λem = 515 nm) was detected following additions of buffered Ca2+, and Ca2+ concentrations were calculated from Fluo-4 fluorescence. (Right) Amplitudes of time-resolved fluorescence populations as a percentage of total population for CaM-T34C-AF488 (200 nM) with eNOS- S1179D (800 nM) vs. Ca2+ concentration. The Ca2+ concentration was determined in similarly prepared solutions containing the Ca2+ indicator Quin-2. Red lines show fits to the steady-state (left) and time-resolved (right) data of a sequential binding model including contributions from free CaM (black), Ca2CaM-eNOS (blue), and Ca4CaM-eNOS (dark yellow). Fits show that the 0.1.-ns component (bottom panel) forms only with four Ca2+ bound to CaM. Data in right panel were replotted from ref (40).

This analysis shows that the conformations represented by lifetimes of ~4 ns, ~2 ns, and ~0.7. ns initially form upon binding of two Ca²⁺ ions (see blue curves in Figure 4). However, the highly quenched state with lifetime ~0.1. ns forms only after four Ca²⁺ ions are bound to CaM. This result is consistent with studies of the Ca²⁺ dependence of eNOS activity by Persechini and co-workers (22, 49), who found that CaM can bind to eNOS upon binding two Ca²⁺ ions, but synthase activity requires binding of four Ca²⁺ ions to CaM. This result suggests, therefore, that the highly quenched state is required for synthase activity, and we tentatively assigned it to the output state of the enzyme (40).

Although analysis of fluorescence decays of NOS in bulk solution gives information about the population of conformational states, it tells us nothing about the dynamics of conformational interchange. For that we turn to single-molecule methods.

4. DYNAMICS

Tracking conformational dynamics in proteins presents a formidable challenge. Conventional structural methods do not have sufficient time resolution to resolve conformational dynamics. Stopped-flow and other bulk kinetic methods, while bringing in the element of time, may not report conformational state. In traditional kinetic studies, the rate of product formation is measured (e.g. reduction of cytochrome c (51)). Such observations are ensemble measurements, yielding rates that are convolutions of individual steps, and an attempt is made to deduce conformational kinetics indirectly in the context of a kinetic model. In contrast, single-molecule fluorescence measurements can directly track both conformational states and dynamics. Single-molecule approaches can thus serve as a valuable complement to conventional kinetic measurements.

4.1. Single-molecule fluorescence trajectories

Single-molecule fluorescence measurements were carried out on an inverted fluorescence microscope (40). To track single-molecule fluorescence over periods of seconds, the molecule must be tethered to a surface so that fluorescence from a single molecule can be detected for sufficiently long time periods. A single-molecule time sequence (termed a “fluorescence trajectory”) can then be recorded until the fluorophore permanently photobleaches, allowing trajectory lengths of tens of seconds or longer.

To record fluorescence trajectories, CaM-AF488 or CaM-AF594 was incubated with eNOS and the solution was placed on a coverslip with surface derivatized with poly(L-lysine)-poly(ethylene glycol) functionalized with Ni²⁺ or Cu²⁺. CaM-NOS complexes could then be tethered by binding of its His₆-tag to the surface. Trajectories were recorded in 20-ms steps at saturating Ca²⁺ concentration so that CaM-NOS could access all fully active conformations.

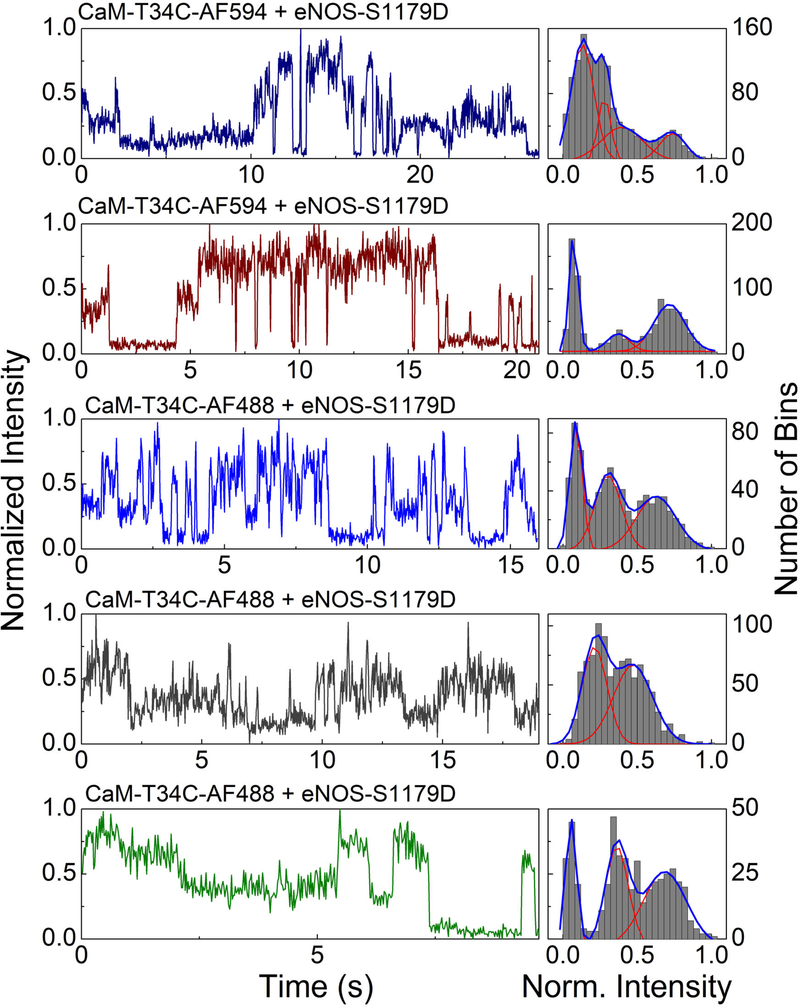
Examples of trajectories are shown in Figure 5. Single CaM-AF488-eNOS complexes were observed to access multiple fluorescence states with transitions between states on time scales from ~100 ms to several seconds. Histograms of the intensities recorded in each trajectory suggest distinct underlying FRET states. For most trajectories Gaussian fits to the histograms suggest two to four distinct fluorescence states, broadened by photon-counting noise (shot noise) (Figure 5). Noteworthy again is the presence of a highly quenched state. In these trajectories, the highly quenched state has the longest average time duration in the trajectories, suggesting that this state may correspond to the highly quenched state detected in fluorescence decays (Figure 2) and the rate-limiting output state of the enzyme.

Figure 5.

Single molecule trajectories (left) and histograms (right) for immobilized eNOS-S1179D; top two panels, on Cu2+ surface with CaM-T34C-AF594; middle panel, in agarose gel with CaM- AF488; bottom two panels, on Cu2+ surface with CaMAF488. Trajectories were recorded in 20-ms time bins. The right column for each trajectory shows a histogram of the normalized fluorescence intensity per time bin over the course of the trajectory with fits to sums of Gaussian distributions. Intensities were normalized to the range between the minimum and maximum intensity. The left axis label applies to the fluorescence trajectories and the right axis label to the intensity histograms. Figure adapted with permission from ref. (40).

The most basic model of conformational dynamics of NOS (Scheme 2) contains three states: one in which the FMN domain is docked to the FAD domain (the “input” state), one where the FMN domain is dissociated (“open” state), and one in which the FMN domain is docked to the oxygenase domain (the “output” state). (In this scheme, “•” denotes interacting domains, and “-” denotes non-interacting domains.)

$$\underset{\text{input}}{\text{FAD}•\text{FMN-oxy}}\underset{{\mathrm{k}}_{-1}}{\overset{{\mathrm{k}}_1}{\rightleftharpoons }}\underset{\text{open}}{\text{FAD-FMN-oxy}}\underset{{\mathrm{k}}_{-2}}{\overset{{\mathrm{k}}_2}{\rightleftharpoons }}\underset{\text{output}}{\text{FAD-FMN}•\text{oxy}}$$ (Scheme 2)

Note that this scheme represents conformational changes, in accordance with the conformational-gating hypothesis, rather than, say, product formation. Fluorescence lifetime populations such as those in Figures 2 and 3 indicate the presence of more than three states, and structural studies reveal a CaM-docked conformation (Figure 1). The challenge is to extract rate constants for conformational change by analysis of fluorescence trajectories such as those in Figure 5.

4.2. Analysis of correlation functions

One method of characterizing the dynamics in single-molecule trajectories is calculation of the correlation function

$$C(\tau )=\frac{\langle \mathrm{\Delta }I(t+\tau )\mathrm{\Delta }I(t)\rangle }{\langle \mathrm{\Delta }{I}^2\rangle }$$

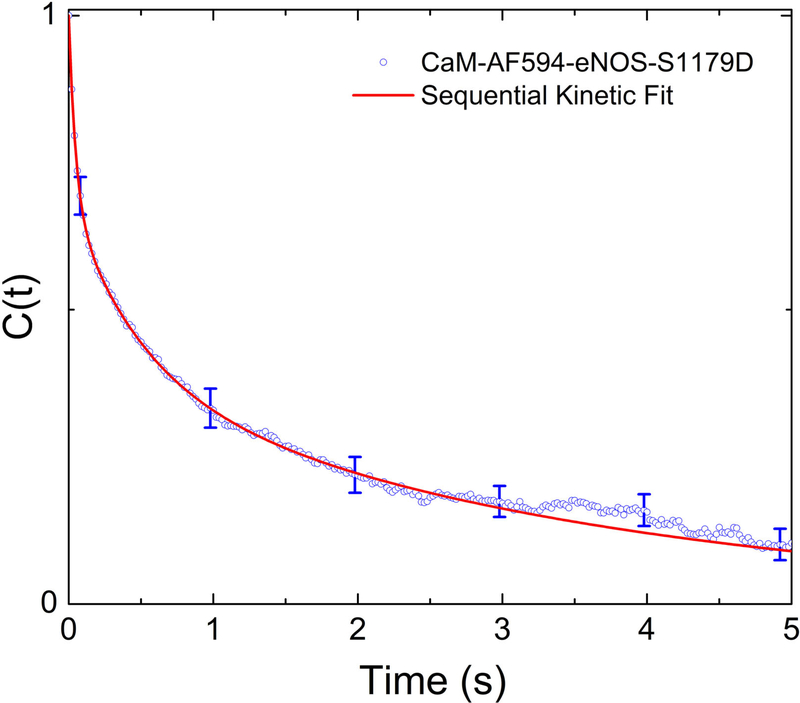
where I(t) is the fluorescence intensity, ΔI(t) = I(t)− ⟨I(t)⟩, and ⟨x(t)⟩ represents the time average of x. Figure 6 shows the average of the correlation function from multiple trajectories for CaM-AF594. The correlation function C(τ) describes how similar the fluorescence intensity is, on average, at a time t+τ compared to the intensity at time t. It can be thought of as describing the loss of “memory” of an initial state of the protein. The correlation function C(τ) calculated from our single-molecule fluorescence signals clearly decays on multiple time scales, reflecting conformational dynamics on time scales from milliseconds to seconds.

Figure 6.

Correlation function calculated single-molecule fluorescence trajectories of CaM-AF594 bound to eNOS-S1179D. Correlation functions were calculated from individual trajectories and then averaged together. Error bars show 95% confidence limits. The red line shows a fit to a sequential kinetic model discussed in Section 4.2 (Scheme 4). Data were replotted from ref. (40).

Schenter et al. (52) developed a method for calculating a correlation function directly from a kinetic model. In general, any kinetic scheme can be modeled, provided that the postulated kinetic states have different fluorescent signatures. In the formalism of Schenter et al., the correlation function C(t) is given by (52):

$$C(\tau )=\sum _{j,i}\frac{\langle \mathrm{\Delta }{I}_j{G}_{ji}(t,t+\tau )\mathrm{\Delta }{I}_i{P}_i^{eq}\rangle }{\langle \mathrm{\Delta }{I}^2\rangle }$$

In this equation, I_i represents the fluorescence of state i, $P_i^{eq}$ is the equilibrium population of state i, and G_ji(t₁,t₂) is the conditional probability of finding the system in state j at time t₂ given that it is in state i at time t₁. The transition probability G_ji can be derived from a transition matrix representing the kinetic scheme with appropriate rate constants. The correlation function can then be calculated by summing over all possible starting (i) and ending (j) states. The populations, fluorescence levels, and rate constants must all be either supplied or determined by fitting data. For analysis of eNOS-CaM single-molecule trajectories these variables were constrained to the fullest extent possible utilizing the information obtained from the fluorescence lifetime experiments. This fixes the fluorescence levels, equilibrium populations, and half of the necessary rate constants. Consequently, the forward rate constants were the only adjustable variables for fitting to the experimental correlation function.

The validity of the correlation function calculation and subsequent kinetic analysis routines was tested by generating and analyzing simulated trajectories. In the simplest case, the simulated data was generated by collecting a series of on and off times from two exponential distributions. This mimics a two-state process (A ⇌ B) and yields a single exponential correlation function with a rate constant given by the sum of the forward and reverse rate constants, as expected. After applying appropriate constraints to the equilibrium populations and fluorescence levels, the corresponding kinetic analysis returns the forward rate constant, provided that the simulated trajectory had a sufficient number of turnovers.

It is not yet apparent how the states observed in eNOS-CaM single-molecule fluorescence relate to the three states present in previous models. Furthermore, since we cannot identify with certainty the particular states contributing to any individual trajectory, it is not yet possible to construct a mechanism by other methods of trajectory analysis (e.g. hidden Markov methods (53, 54)). For these reasons, we attempted to model the data by considering all possible transitions between four quenching levels in a fit to the experimental correlation function. The transition matrix for the Schenter formalism was generated for a series of transitions:

$$(i)\underset{k_{ij}=k_{ji}\left(\frac{P_i^{eq}}{P_j^{eq}}\right)}{\overset{k_{ji}}{\rightleftharpoons }}(j)i,j=1\dots 4\mathrm{and}j>i$$ (Scheme 3)

Here, state 1 is essentially unquenched while states 2, 3, and 4 are quenched to increasing degrees. Incorporating all possible transitions yields a six-variable fitting function that can be optimized via non-linear fitting. The optimized results were insensitive to starting conditions and returned the same mechanism (i.e. the same set of non-zero rate constants) for CaM labeled with two different fluorophores (Alexa Fluor 488 and Alexa Fluor 594). The resulting non-zero rate constants for CaM-AF594 are given below. (Similar rate constants were obtained with CaM-AF488.)

$$(2)\underset{13.8{\mathrm{s}}^{-1}}{\overset{8.4{\mathrm{s}}^{-1}}{\rightleftharpoons }}(1)\underset{0.79{\mathrm{s}}^{-1}}{\overset{0.98{\mathrm{s}}^{-1}}{\rightleftharpoons }}(3)\underset{0.16{\mathrm{s}}^{-1}}{\overset{0.06{\mathrm{s}}^{-1}}{\rightleftharpoons }}(4)$$ (Scheme 4)

The rate constants for other possible transitions (e.g. (1) ⇌ (4)) were negligible. Hence, this analysis argues for a sequential kinetic mechanism, where each state is kinetically interconnected with (at most) two other states. The two least-quenched rapidly, whereas the two most quenched states (3 and 4) interchange more slowly. State (3) appears to be a “gateway” state to the formation of the most highly quenched state, state (4). Formation of state (4) is slow, but once formed, this state is likely to persist for several seconds, as observed by inspection of single-molecule trajectories.

5. PERSPECTIVES: RELATING STRUCTURE AND DYNAMICS

Multi-domain redox-active enzymes in the NAD(P)H-dependent FMN reductase superfamily, which includes NOS enzymes, facilitate a sequence of electron transfer events that direct electron flow. The challenge is to understand how multidomain oxidoreductases like NOS enzymes activate and control electron transfer both spatially and temporally. In mammalian NOS, the oxygenase domain is fused with a dedicated reductase domain to ensure close proximity to a supply of electrons. The picture of NOS dynamics proposed here and elsewhere (17, 18) is one of conformational gating, where electron transfer is regulated by conformational changes rather than by the intrinsic electron transfer rates once electron donor and acceptor are in place.

Understanding how conformational dynamics regulate NOS activity requires an approach that can directly relate dynamics to conformations. The sequence and timing of conformational changes and their responses to CaM or substrate binding must be elucidated to understand the activity and regulation in NOS. Single-molecule fluorescence provides a way to track them in real time. Sensitivity to conformation is provided by different extents of fluorescence quenching for different conformations.

The time scales of conformational interchange can be determined from single-molecule fluorescence trajectories, as illustrated by fitting to the intensity correlation function described above. However, more detailed information is contained in fluorescence trajectories such as those in Figure 5. Analysis by hidden Markov methods (53, 54), for example, will allow lag times in each fluorescence state to be tabulated to determine state lifetimes. State-to-state transition probabilities can then be extracted to determine kinetic connectivity (which states can interchange with which other states). The results will test the model proposed in Section 4.2. Relating these rates to the activity of the enzyme will require modeling and comparison to experimental results.

With this approach, a method is available to answer central questions about NOS functions. Outstanding questions include the following: (1) What are the time scales of conformational interchange, and what is the kinetic connectivity of each conformational state? (2) How does the sequence and dynamics of conformational states determine the activity of the enzyme? (3) Can conformational dynamics explain differences in activity between nNOS and eNOS isoforms? Work along these lines is underway.