Test–Retest Reliability of Graph Metrics in High‐resolution Functional Connectomics: A Resting‐State Functional MRI Study

Summary

Background

The combination of resting‐state functional MRI (R‐fMRI) technique and graph theoretical approaches has emerged as a promising tool for characterizing the topological organization of brain networks, that is, functional connectomics. In particular, the construction and analysis of high‐resolution brain connectomics at a voxel scale are important because they do not require prior regional parcellations and provide finer spatial information about brain connectivity. However, the test–retest reliability of voxel‐based functional connectomics remains largely unclear.

Aims

This study tended to investigate both short‐term (∼20 min apart) and long‐term (6 weeks apart) test–retest (TRT) reliability of graph metrics of voxel‐based brain networks.

Methods

Based on graph theoretical approaches, we analyzed R‐fMRI data from 53 young healthy adults who completed two scanning sessions (session 1 included two scans 20 min apart; session 2 included one scan that was performed after an interval of ∼6 weeks).

Results

The high‐resolution networks exhibited prominent small‐world and modular properties and included functional hubs mainly located at the default‐mode, salience, and executive control systems. Further analysis revealed that test‐retest reliabilities of network metrics were sensitive to the scanning orders and intervals, with fair to excellent long‐term reliability between Scan 1 and Scan 3 and lower reliability involving Scan 2. In the long‐term case (Scan 1 and Scan 3), most network metrics were generally test–retest reliable, with the highest reliability in global metrics in the clustering coefficient and in the nodal metrics in nodal degree and efficiency.

Conclusion

We showed high test–retest reliability for graph properties in the high‐resolution functional connectomics, which provides important guidance for choosing reliable network metrics and analysis strategies in future studies.

Introduction

In the past several years, increasing attention has been focused on studies of functional connectivity patterns of the human brain networks, that is, the functional connectomics 1, 2, 3. With the assistance of noninvasive imaging techniques such as resting‐state functional MRI (R‐fMRI) and graph theoretical approaches, researchers have found many important topological characteristics in the functional networks of the human brain, including small‐worldness, modularity, and highly connected hubs (for reviews, see 4, 5, 6). There is also evidence that these network characteristics undergo remarkable changes during normal development 7, 8, aging 9, 10, and neuropsychiatric disorders 11, 12, 13. These studies have provided crucial insights into the topological organization of the human brain in health and disease.

In the brain network construction, the definition of nodes is of fundamental importance and can profoundly affect the graph‐based parameters (e.g., clustering coefficient, characteristic path length, and small‐worldness) of the brain networks 14, 15, 16 and the associated test–retest (TRT) reliability 17. Network nodes can be defined by either regions of interest (ROIs) or imaging voxels 18, 19. Currently, most brain network studies have been confined to the ROI‐defined nodes due to the limitation of the available computational power. For the ROI‐based network analysis, there are various different anatomically and/or functionally defined parcellation schemes and the selection between them is still controversial. In addition, the functional activity within a given ROI is usually considered as homogeneous, ignoring the possible spatial inhomogeneity within large ROIs 20. In contrast, voxel‐based brain networks possess more naturally defined nodes (i.e., imaging voxels) in a higher spatial resolution without prior parcellations, which may unveil more detailed connectivity information especially for regions that contain multiple subdivisions 16. Recently, graph analyses of voxel‐based brain networks have been performed in R‐fMRI studies 16, 21, 22; however, the TRT reliability of these network metrics remains to be further investigated.

Reliable measures with both low intrasubject and high intersubject variability are essential to infer convincing conclusions and to serve as potential clinical biomarkers. Previous research has suggested that the functional brain networks derived from R‐fMRI data can be modulated by various confounding factors including emotional states 23, consciousness levels 24, 25, scan conditions 26, cognitive states before scanning 27, and diverse data analysis/preprocessing strategies such as global signal regression (GSR) and head motion 28, 29. These factors are likely to contribute to the temporal changes in functional networks and increase the intrasubject variability of the network metrics, thereby affecting their TRT reliability. A few R‐fMRI studies 17, 29, 30, 31, 32 have investigated the TRT reliability of ROI‐based network metrics and have shown their dependences on several confounding factors, including the definition of nodes and edges and strategies for nuisance regression (e.g., with/without GSR). Recent studies in voxelwise R‐fMRI networks have mainly focused on the TRT reliability of nodal centrality metrics (e.g., degree and eigenvector) 33, 34, 35 and have revealed moderate to good TRT reliability in most hub regions. A previous task fMRI study 36 reported that several global metrics (e.g., clustering coefficient and characteristic path length) of voxel‐based brain networks are highly reproducible, but restricts the TRT analysis to healthy elderly adults during an executive task. Thus, the TRT reliability of multiple graph metrics (e.g., small‐worldness, modularity, and nodal centrality analysis) in voxel‐based whole‐brain functional networks during resting‐state remains to be systematically elucidated, especially for healthy young adults.

Using an R‐fMRI TRT dataset of 53 healthy young adults with a narrow age range (19–30 years), in this study, we constructed individual whole‐brain functional networks at a voxel level with 25K nodes and systematically investigated both short‐term (approximately 20 min apart) and long‐term (6 weeks apart) TRT reliability of network metrics, including various global and nodal properties. The voxel‐based network construction and analysis were performed based on a CPU‐GPU hybrid platform 37. Intraclass coefficient (ICC) was used to measure the TRT reliability of the network metrics, as suggested by prior works 17, 29, 30. Finally, we examined the impacts of different connectivity thresholds and preprocessing strategies, such as global signal removal and head motion correction, on the TRT reliability of voxel‐based brain networks.

Materials and Methods

Participants

The R‐fMRI TRT data are a subset of the Connectivity‐based Brain Imaging Research Database (C‐BIRD) at the Beijing Normal University (http://fcon_1000.projects.nitrc.org/indi/CoRR/html/bnu_1.html). In brief, the dataset consists of R‐fMRI scans (~ 6.5 min) that were acquired from 57 healthy young adults (male/female: 30/27; age: 19–30 years) who completed two MRI scanning sessions within an interval of ~ 6 weeks (40.94 ± 4.51 days). All participants are right‐handed and have no history of neurological and psychiatric disorders. Data of four subjects were excluded from the analysis because three of them had excess head motion (translation > 2 mm or rotation >2°; ID: N0006, N0016, and N0027) and one subject (ID: N0044) had missing slices in R‐fMRI data. All analyses were performed based on the data of the remaining 53 healthy adults (male/female: 28/25; age: 19–30 years). Written informed consent was obtained from each participant, and this study was approved by the Institutional Review Board of the State Key Laboratory of Cognitive Neuroscience and Learning at the Beijing Normal University.

Data Acquisition and Preprocessing

All MRI data were obtained using a Siemens Trio Tim 3.0T scanner (Siemens, Erlangen, Germany) with a 12‐channel phased‐array head coil in the Imaging Center for Brain Research, Beijing Normal University. All participants underwent two scanning sessions as follows. The first session included two R‐fMRI scans, T1, T2, and diffusion MRI. The two R‐fMRI scans (Scan 1 and Scan 2) were at the beginning and the end of the session (~20 min apart), respectively. The second session included R‐fMRI (Scan 3), T1, and diffusion MRI. Participants were instructed to rest and relax with their eyes closed and not fall asleep, and none of the participants fell asleep during the MRI scans according to a simple questionnaire after the MRI scan. R‐fMRI data were obtained using an echo‐planar imaging (EPI) sequence with the following parameters: TR/TE = 2000 ms/30 ms, FA = 90°, FOV = 200 × 200 mm, matrix = 64 × 64, slices = 33, thickness = 3.5 mm, voxel size = 3.1 × 3.1 × 3.5 mm³, gap = 0.7 mm, and 200 volumes. 3D high‐resolution brain structural images were acquired using a T1‐weighted, sagittal 3D magnetization‐prepared rapid gradient echo (MP‐RAGE) sequences. The sequence parameters were TR/TE = 2530 ms/3.39 ms, FA = 7°, FOV = 256 mm×256 mm, matrix = 256 × 256, slices = 144, slice thickness = 1.33 mm, and voxel size = 1.3 × 1×1 mm³. Diffusion imaging data were not used in this study.

All R‐fMRI images were preprocessed using DPARSF 38 and SPM8 (www.fil.ion.ucl.ac.uk/spm/). The first five time points were first discarded from each of three scans for magnetic field stabilization and allowing participants to adapt to the scanning environment. The subsequent preprocessing steps included slice time correction and head motion correction. During the head motion correction, three subjects (subject ID: N0006, N0016, and N0027) were excluded from subsequent analysis due to large head motion in at least one scan with a criterion of 2 mm or 2. Next, the corrected functional images were normalized to the MNI space using T1 image unified segmentation, resampled to 4 mm isotropic voxels, and further smoothed via a Gaussian kernel with a 4 mm full width at half maximum. Then, linear detrending and a temporal band‐pass filtering (0.01–0.08 Hz) were performed. Finally, six head motion parameters and three other confounding signals, including white matter, cerebrospinal fluid, and global signals, were removed from BOLD time series for all voxels.

Network Construction

The functional network construction was constrained within a gray matter mask of 25,218 voxels, which was generated by thresholding a prior gray matter probability map (>0.2) provided by SPM8. We computed Pearson's correlations between all pairs of nodes (i.e., brain voxels), resulting in three 25,218 × 25,218 correlation matrices for each subject (one matrix for one R‐fMRI scan). All negative correlations were removed, considering their ambiguous biological interpretation 31. Then, we binarized these individual correlation matrices at a range of connectivity density thresholds and obtained a set of binary networks. The lower bound of density was set at S₁ = 0.1% to maintain estimable small‐world properties and high network connectedness, and the upper bound of density was set at S ₂ = 10.0% to ensure the sparsity nature of the brain networks and simultaneously remove the weak correlations as possible. Within the range of 0.1% to 10.0%, seven connectivity densities (i.e., 0.1%, 0.4%, 0.7%, 1%, 4%, 7%, and 10%) were selected to construct the voxelwise functional networks and further to investigate the TRT reliability of network metrics. This range of density ensured that most voxels were connected to the largest component of the network, reducing the bias from the isolated nodes on the computation of global metrics.

Network Analysis

Network Metrics

To describe the basic characteristics of the voxelwise brain networks at each connectivity density, we first computed the mean functional connectivity strength, the size of the largest component, and the number of isolated voxels. The mean functional connectivity strength of a network was evaluated by averaging the functional connectivity (i.e., Pearson's correlation) across all existing edges in the network at a specific density. The size of the largest component was estimated by counting the number of node voxels within the largest connected cluster. The isolated voxels were referred to those voxels without any connections in the network.

We further examined the topological attributes of the brain networks, which can be categorized into two levels: global and nodal metrics (Table S1). The former included the network clustering coefficient, Cp; the characteristic shortest path length, Lp; the normalized clustering coefficient, γ (i.e., Cp/Cp_rand); the normalized characteristic path length, λ (i.e., Lp/Lp_rand); the small‐worldness, σ (i.e., γ/λ); and the modularity, Q. Notably, Cp and γ quantify the extent of local integrity of the brain networks, but Lp and λ quantify the extent of global integrity of the brain networks. Specifically, Cp_rand and Lp_rand refer to the average of Cp and Lp obtained from 10 surrogate random networks, respectively, that possess the same number of nodes, edges, and identical degree distribution with the original brain networks. For modular detection, we utilized the Louvain algorithm 39, which is fast and efficient for large networks. Notably, to reduce the potential effects of isolated voxels, the characteristic shortest path length, Lp, was calculated as the “harmonic mean” distance among all possible pairs of nodes. At the nodal level, we calculated the following four metrics for a given voxel, i: nodal degree, k_i; nodal efficiency, e_i; nodal betweenness, b_i; and participation coefficient, p_i. For each nodal metric, a group‐level map was generated by averaging individual metrics across subjects for each scan and then converted into z‐scores. Functional hubs were identified with a criterion of one standard deviation above the average value across the brain (i.e., z‐score > 1). The computation of all the above network metrics was carried out on a CPU‐GPU hybrid platform proposed by Wang et al. 37. More details of the GPU implementation can be found 37.

Test–retest Reliability

To evaluate the TRT reliability of the graph metrics between any two scans, we employed a common index of intraclass correlation coefficient (ICC) 40, 41. Given we used the same scanner and acquisition settings for all three R‐fMRI scans, we preferred a one‐way analysis of variation (ANOVA) model with random subject effects between every pair of scans as follows:

$$\text{ICC}=\frac{\text{BMS}-\text{WMS}}{\text{BMS}+(\mathrm{k}-1)\text{WMS}},$$ (1)

where BMS is the between‐subjects mean square, WMS is the within‐subject mean square, and k is the number of repeated observations per subject (here, k = 2). This form of ICC has been used to measure the TRT reliability of graph metrics in previous R‐fMRI studies 17, 31. In this study, we calculated both short‐term and long‐term TRT reliability for network metrics of interest at each density: The short‐term reliability was estimated based on the data in Scan 1 and Scan 2, and two forms of the long‐term reliability, long‐term I based on the data between Scan 1 and Scan 3, and long‐term II based on the data between Scan 2 and Scan 3. According to the criteria adopted from Winer 42 and Sampat et al. 43, TRT reliability was categorized as excellent (ICC > 0.75), good (ICC 0.6–0.75), moderate or fair (ICC 0.4–0.6), low (ICC 0.25–0.4), and poor (ICC < 0.25), respectively.

Statistical Analysis

We performed the following statistical analysis at each connectivity density. For each global metric, we first calculated Pearson's correlation coefficient across subjects to elucidate the consistency of the intersubject variation between every pair of scans. Then, a repeated‐measures analysis of variation (ANOVA) was used to examine differences in the network metric of interest among scans, followed by post hoc paired t‐tests on each possible combination of scans to find out which scan was responsible for the difference. For each nodal metric, the spatial similarity of the group‐level functional maps between different scans was assessed with an across‐voxel correlation analysis. Next, a repeated‐measures ANOVA and post hoc paired t‐tests were performed in a voxelwise manner to show the spatial maps of the interscan differences. All statistical maps were corrected for multiple comparisons using a Monte Carlo simulation [AlphaSim by Ledberg et al. 44] with a criterion of P < 0.05. Specifically, the resulting F‐maps were corrected within the gray matter mask (uncorrected P < 0.05 with a cluster size > 16). Post hoc paired t‐maps were corrected within the masks showing significant main effects on scans for each nodal metric (uncorrected P < 0.05 with the minimal cluster sizes of 11, 12, 6, and 8 for degree, efficiency, betweenness, and PC, respectively).

Effects of Global Signals on TRT Reliability

Several prior R‐fMRI studies have demonstrated the positive impacts of regressing out signals of white matter and cerebrospinal fluid on the TRT reliability of ROI‐based networks 29, 30. The effects and the necessity of the GSR, however, remain controversial as the physiological basis of the global signals is still ambiguous 45, 46. The removal of global signals has complicated effects on the TRT reliability of both ROI‐defined 29, 31 and voxelwise 33 functional networks. To further investigate the effects of global signals on the TRT reliability of multiple topological metrics in the voxelwise networks, we also performed a network analysis without GSR. Additionally, we calculated the power spectrum and the amplitude of the low‐frequency fluctuation (ALFF) of individual global signals, followed by a TRT analysis between scans.

Effects of Head Motion on TRT Reliability

Head motion has been regarded primarily as a nuisance in the analysis of functional connectivity, and several methods have recently been proposed to reduce the effects of subject motion 28, 47, 48, 49. To evaluate the effects of transient head motion, we used a scrubbing approach 47 to eliminate the volumes with large instantaneous head motion [frame displacement (FD) > 0.5 mm] and their neighboring volumes (one back and two forward). After the elimination, subjects for whom we retained more than 90% of the original data in all three scans were included in the subsequent analysis. Then, we reconstructed the functional networks in the same way and recalculated the TRT reliability for both global and nodal metrics as a validation of our results.

Results

TRT Reliability of Mean Functional Connectivity Strength and Connected Network Size

The mean correlation coefficients of the functional connectivity matrices without thresholding were 0.081 ± 0.0065, 0.083 ± 0.0061, and 0.080 ± 0.0052 across subjects for Scan 1, Scan 2, and Scan 3, respectively. Among the three scans, higher cross‐subject correlation and TRT reliability were found between Scan 1 and Scan 3 (r = 0.59, P < 0.00001; ICC = 0.55), while Scan 2 showed lower correlation and TRT reliability with the other two scans (r = 0.26, P = 0.055, ICC = 0.023 between Scan 1 and Scan 2; r = 0.14, P = 0.32, ICC = 0.03 between Scan 2 and Scan 3). For each scan, we further measured the mean functional connectivity strength, the largest component size, and the number of isolated voxels in the whole‐brain networks across seven different connection densities. As shown in Figure 1A, we observed that the distributions of each metric across densities almost coincided across the different scans. Notably, when the connectivity density value exceeded 1%, most individual brain networks were fully connected without isolated nodes and possessed the same size as the largest components (Figure 1A). For each metric, further analysis revealed a higher cross‐subject correlation between Scan 1 and Scan 3 (red lines) at each density (r > 0.37, P < 0.01) (Figure 1B) and moderate to excellent TRT reliability (all ICCs > 0.4 at a density larger than 1%, Figure 1C) between the two scans (i.e., long term I). At a density value of < 1% in which the brain networks were not fully connected, it was not surprising that both the largest component size and the number of isolated voxels showed low or poor TRT reliability (ICC < 0.4) (Figure 1C), especially between Scan 1 and Scan 2 (i.e., short term) and between Scan 2 and Scan 3 (i.e., long term II).

Figure 1.

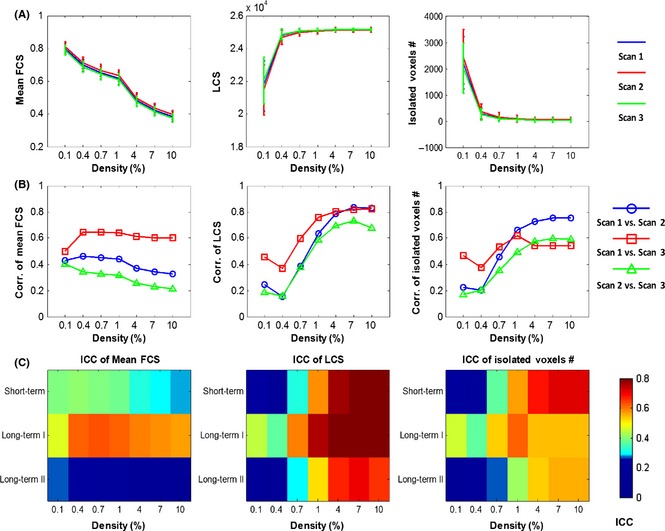
Functional connectivity networks at different connectivity densities. For each scan and each individual, three essential properties of the voxel‐based functional networks were calculated at different connectivity densities, including the mean functional connectivity strength (FCS), the largest component size (LCS), and the number of isolated nodes. (A) Both the mean FCS and number of isolated voxels decreased with an increase in network density, while the LCS increased when the network density rose. (B) The Pearson correlation coefficients between any pairs of the scans across subjects on each metric. (C) Three terms of TRT reliability for each metric. For these metrics, higher correlation and reliability were found between Scan 1 and Scan 3 (long‐term I). ICC, intraclass correlation coefficient.

TRT Reliability of Global Network Metrics

Global Network Metrics

Across all seven density levels, individual brain networks showed prominent small‐world characteristics as characterized by σ > 1, except one subject in the first scan at the density of 0.1% (σ = 0.95). For different scans, four metrics including γ, Lp, λ, and σ exhibited similarly decreasing profiles across increasing densities, accompanied by decreased intersubject variation (Figure 2A). The modularity index, Q, also decreased with increasing densities in the three scans, but kept a relatively stable intersubject variation (Figure 2A). In contrast to other metrics, Cp increased sharply from 0.1% to 0.4% density and fluctuated within a narrow range at the higher density levels (Figure 2A).

Figure 2.

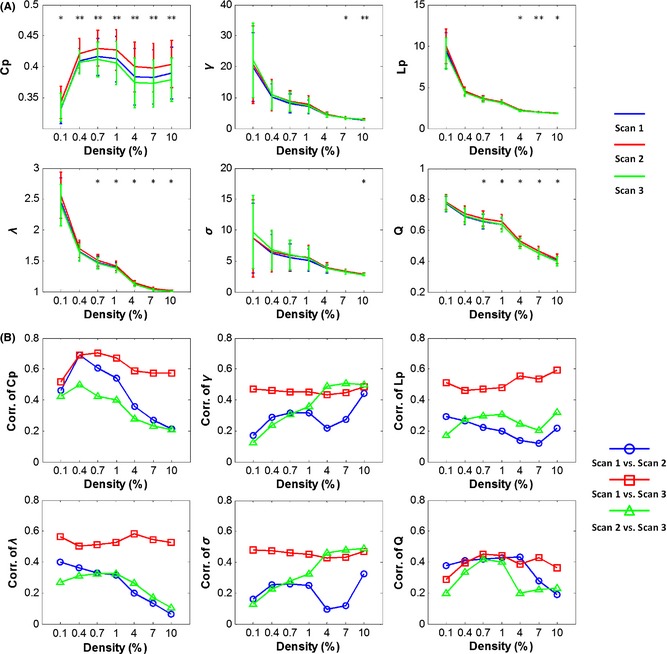
Global metrics and intersubject correlation among different scans at different connectivity densities. (A) Mean values across subjects decreased with an increase in network density for all global metrics except Cp. (B) Correlations of global metrics across subjects between each pair of the three scans. In (A), “*”and “**”denote that at the specific density, a significant difference was found among the three scans at the level of P = 0.01 and the level of P = 0.001, respectively, from a repeated‐measures ANOVA. Cp, clustering coefficient; γ, gamma; σ, sigma; Lp, characteristic path length; λ, lambda; Q, modularity.

Interscan Differences in Global Network Metrics

A one‐way repeated‐measures ANOVA showed significant differences in Cp among the three scans across all seven densities (F _(2,52) > 5.25, P < 0.007, Figure 2A). For other global metrics (γ, Lp, λ, σ, and Q), significant differences were also observed on higher density levels above 1.0% (P < 0.01, Figure 2A). Post hoc paired t‐tests revealed that these differences mainly resulted from the dissimilarity of Scan 2 with the other two scans (Table S2). Further correlation analysis also exhibited relatively higher consistencies across subjects between Scan 1 and Scan 3 (red lines, r > 0.43, P < 0.005) than between Scan 1 and Scan 2 (blue lines) and between Scan 2 and Scan 3 (green lines) for all global metrics examined (Figure 2B).

TRT Reliability in Global Network Metrics

Figure 3 shows the TRT reliability of six global metrics between every pair of scans over the density range examined. Generally, most global metrics showed moderate to good TRT reliability between Scan 1 and Scan 3 (long‐term I). For example, Cp was found to be most reliable as the ICC values ranged from 0.52 to 0.69 across different densities, whereas Q exhibited moderate ICC values ranging from 0.29 to 0.45. In contrast with the long‐term I (Scan 1 and Scan 3), both the short‐term (Scan 1 and Scan 2) and long‐term II (Scan 2 and Scan 3) scans exhibited poor to fair ICC values for most metrics.

Figure 3.

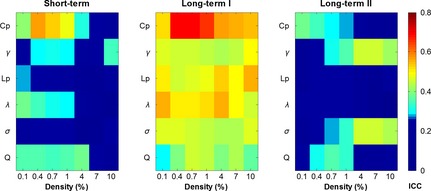
TRT reliability of global network metrics. Higher long‐term I reliability than short‐term and long‐term II reliability was found for all six global metrics. ICC values less than 0.25 are displayed with the same dark blue color indicating poor reliability. Cp, clustering coefficient; γ, gamma; σ, sigma; Lp, characteristic path length; λ, lambda; Q, modularity.

Functional Hubs and Their TRT Reliability

Functional Hubs

Four nodal metrics (i.e., nodal degree, nodal efficiency, nodal betweenness, and participation coefficient) were calculated to estimate the topological roles of nodes in the whole‐brain networks in a voxelwise manner at different densities. For each nodal metric, the spatial patterns between scans were highly similar, regardless of the density considered (Figures S1 and S2), as indicated by significantly positive correlations across different density levels (r > 0.7, P < 0.00001, Figure 4A). We displayed the group‐level voxelwise nodal centrality maps at a density of 4.0%, which exhibited the highest interscan consistency for all nodal metrics between Scan 1 and Scan 3 (r > 0.79, P < 0.00001). As shown in Figure 4B, the spatial distribution of functional hubs exhibited similar patterns for the three nodal centrality metrics (nodal degree, efficiency, and betweenness). The functional hubs identified by these three metrics (called global hubs) were mainly located at regions in the default‐mode network (DMN) [e.g., the bilateral precuneus/posterior cingulate cortex (PCu/PCC), the medial prefrontal cortex (MPFC), and the inferior parietal lobule (IPL)], the salience network [e.g., the anterior insula and dorsal anterior cingulate cortex (dACC)], and the executive control network (ECN) [e.g., the dorsolateral prefrontal cortex (dlPFC) and superior parietal cortex]. Similar hub regions were also identified by these three nodal metrics at other densities (Figures S1 and S2). Notably, brain regions with high participation coefficients (called connector hubs) were mainly located in several subcortical regions (e.g., caudate nucleus, putamen, and thalamus), the medial temporal lobe (e.g., hippocampus and parahippocampal gyrus), and the precentral gyrus. No conjunction of hub regions was detected for all four nodal metrics (Figure 4B). Regions with high overlap level across nodal metrics were mostly (>99%) attributable to their higher degree, efficiency, and betweenness values (Figure 4B). Interestingly, at the lowest density (e.g., 0.1%), the spatial patterns of connector hubs identified by the participation coefficient were approximately similar to those derived from the nodal degree and efficiency metrics (Figures S1 and S3), with an overlap in several DMN regions (e.g., PCu/PCC and IPL). As the density increased, the connector hubs shifted from the DMN regions to several subcortical regions and the medial temporal lobe (Figure S3), suggesting that the identification of connector hubs is sensitive to the selection of network thresholds.

Figure 4.

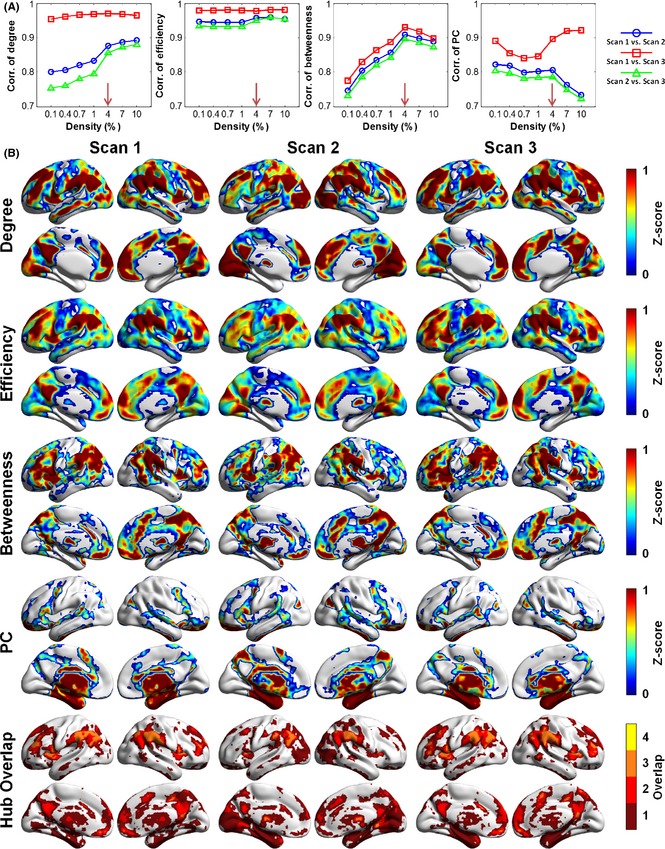
Voxelwise hub maps and their interscan correlations. (A) The interscan consistency of spatial patterns of functional hubs was the highest at 4.0% density for the four nodal metrics examined. (B) Group‐level voxelwise maps of functional hubs and the overlap of hub regions identified by different metrics at 4.0% density. For each metric, regions with z‐scores above 1 were defined as hubs indicated by the color of dark red. In the last row, colors indicate the number of different types of functional hubs overlapping in an area. The global hubs identified by degree, efficiency, and betweenness showed similar spatial patterns, while the PC detected different connector hub regions at this density. All surface‐based figures are drawn with BrainNet Viewer 70. PC, participation coefficient.

Interscan Differences in Brain Hubs

Although the spatial patterns of functional hubs were similar in all three scans, some differences in the nodal centrality maps can be found among the scans (Figure 4B). For example, a visual examination indicated that both the visual cortex and thalamus in Scan 2 exhibited higher values in the degree and efficiency metrics than in Scan 1 or Scan 3. These interscan differences were further confirmed by the repeated‐measures ANOVA among the three scans for each nodal metric (Figure S4A). Again, post hoc paired t‐tests illustrated that these differences mainly originated from Scan 2 (Figure S4B): There were very few significant differences in the nodal centrality values between Scan 1 and Scan 3, but many significant differences either between Scan 1 and Scan 2 or between Scan 2 and Scan 3.

TRT Reliability of Functional Hubs

For each nodal metric, the TRT reliability of each voxel was quantified by an ICC value under different interscan intervals. The mean TRT reliability values of nodal degree and efficiency metrics were higher than those of nodal betweenness and participation coefficients in the whole‐brain networks, regardless of connectivity densities (Figure 5A). Further, the mean TRT reliability values between Scan 1 and Scan 3 (i.e., the long‐term I, red bars) were the highest, regardless of different connectivity densities and nodal metrics (Figure 5A). Regionally, in the long‐term I, many brain regions, including the major components of the DMN, the salience, and ECN networks, showed fair to good TRT reliability (ICC > 0.4) for the degree and efficiency metrics (Figure 5B). In the short‐term and long‐term II, only a few regions showed high TRT reliability for the two metrics (Figure 5B). In contrast to the nodal degree and efficiency metrics, nodal betweenness and the participation coefficient were found to be less reliable regardless of connectivity densities and scanning intervals (Figure 5B), with a large proportion (>88%) of regions exhibiting poor to low reliability (ICC < 0.4).

Figure 5.

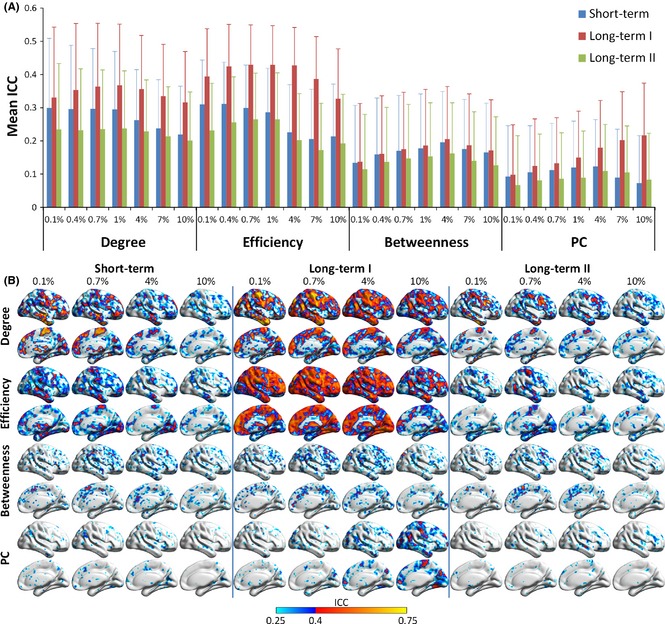
TRT reliability of nodal metrics. (A) Mean ICC values and their standard deviations across the brain for four nodal metrics (i.e., degree, efficiency, betweenness, and PC). (B) Voxelwise maps of ICC values for different nodal metrics at four densities (i.e., 0.1%, 0.7%, 4.0%, and 10.0%). In (B), ICC values are displayed within the right brain. Only voxels with ICC values above 0.25 are displayed, with a blue color indicating low reliability (ICC 0.25–0.4) and red to yellow for larger ICC values (above 0.4). Degree and efficiency were observed to be more reliable in the long‐term I, while betweenness and PC showed overall low ICC values in all three terms. PC, participation coefficient; ICC, intraclass correlation coefficient.

Influence of Global Signals on TRT Reliability

To investigate the influence of global signals on the TRT reliability of network metrics, we also constructed the voxel‐based whole‐brain functional networks without GSR in the preprocessing stage. The cross‐subject correlation analysis for each global metric revealed a higher consistency of intersubject variation between Scan 1 and Scan 3 across all density levels (r > 0.28, P < 0.05). The TRT reliability analysis revealed that most global metrics exhibited moderate to good reliability (ICC > 0.4) between Scan 1 and Scan 3 (i.e., the long‐term I), and poor or low reliability in either the short‐term or long‐term II, without GSR (Figure 6A). Compared with the results in Figure 3, the reliability of short‐term and long‐term II was decreased without GSR.

Figure 6.

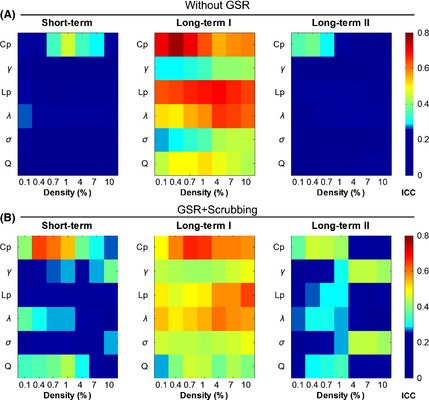
TRT reliability of the global network metrics derived without GSR (A) and with head motion scrubbing after GSR (B). All global metrics exhibited higher ICC values in the long‐term I than the short‐term and the long‐term II. GSR, global signal removal; ICC, intraclass correlation coefficient.

Figure 7 illustrates the nodal centrality maps (Scan 1) and their long‐term I TRT reliability without GSR at a density of 4%. The spatial patterns of both global hubs and connector hubs (Figure 7) were approximately consistent with those identified with GSR (Figure 4B): Most regions in the DMN and ECN networks exhibited higher degree, efficiency, and betweenness values, whereas several subcortical regions and the medial temporal lobe exhibited higher participation coefficient values. For all nodal metrics, the TRT reliability results (Figure 7 and Figure S5) were largely consistent with those with GSR. However, there were still slight differences compared to those with GSR: The posterior visual cortex and postcentral gyrus became more conspicuous hubs in the brain networks without GSR for both degree and efficiency measures, whereas the insula, dlPFC, and anterior DMN regions became inconspicuous.

Figure 7.

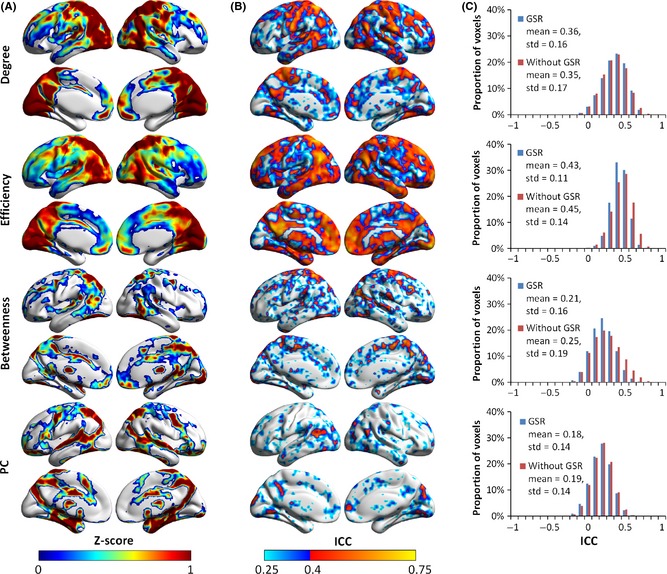
Group‐level voxelwise functional hub maps and TRT reliability of the nodal metrics based on R‐fMRI data without GSR at the density of 4.0%. (A) Spatial patterns of the four nodal metrics (i.e., degree, efficiency, betweenness, and PC) for Scan 1. (B) Spatial maps of long‐term I reliability of the nodal metrics in the case without GSR. (C) Normalized histograms of ICC values across the brain showed similar results for degree and PC in two cases (i.e., with GSR and without GSR), while the distribution profile of ICC values shifted slightly to the right for efficiency and betweenness. Although the spatial configuration of hub regions and reliability, compared with Figures 4 and 5, showed slight differences for all nodal metrics in (A) and (B), degree and efficiency were also more reliable than betweenness and PC, and most hub regions showed moderate to good reliability for these two metrics, which is compatible with previous results with GSR. GSR, global signal removal; ICC, intraclass correlation coefficient; PC, participation coefficient.

To further explore the effect of global signal on our results, we charted the power spectrum of individual global signals under each scan and found a higher amplitude value in the low‐frequency range in Scan 2 than in either Scan 1 or Scan 3 (Figure 8A). A repeated‐measures one‐way ANOVA revealed significant differences in ALFF of the global signals among scans [Greenhouse–Geisser corrected F _{(1.580,82.148)}  = 21.2, P < 0.00001]. Further post hoc paired t‐tests indicated nonsignificant differences in ALFF between Scan 1 and Scan 3 (P = 0.32), but a significant difference either between Scan 1 and Scan 2 or between Scan 2 and Scan 3 (P < 0.0001).

Figure 8.

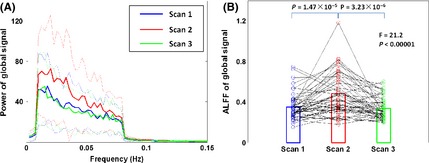
The power spectrum and amplitude of the low‐frequency fluctuation (ALFF) of global signals. (A) The power spectrums of global signals of the three scans are represented as mean value (solid lines) with standard deviation (dotted lines) across subjects. The Scan 2 showed higher amplitude value in the low‐frequency range than Scan 1 and Scan 3. (B) The changing curve of the ALFF for each subject was illustrated, and the circle represents each scan of each subject. Subsequent statistical analysis revealed significantly higher ALFF of global signals in Scan 2 than the other two scans (P < 0.0001). ALFF, amplitude of low‐frequency fluctuation.

Influence of Head Motion on TRT Reliability

A repeated‐measures ANOVA with post hoc analysis was performed on the mean FD 47 across three scans to reveal the differences in head motion between different scans. Significant differences were observed across three scans (Greenhouse–Geisser corrected F _{(1.674, 87.074)} = 5.12, P = 0.012). Further post hoc analysis revealed that the head motion in Scan 2 was significantly larger than in Scan 1 (T₍₅₂₎ = 2.93, P = 0.005) and marginally larger than in Scan 3 (T₍₅₂₎ = 1.72, P = 0.09), indicating that the subjects moved more in Scan 2 than in other two scans. The potential influence of head motion on TRT reliability was investigated with the operation of data scrubbing. After the operation of head motion scrubbing, the data from five subjects (two subjects, N0005 and N0060, in Scan 1; three subjects, N0003, N0017, and N0050, in Scan 2; none in Scan 3) were excluded from further analysis because more than 10% of the original data were removed in at least one scan. Then, we re‐analyzed the TRT reliability of the global and nodal metrics in the functional brain networks that were constructed from the scrubbed data. All the results involving the global (Figure 6B) and nodal (Figure S6) TRT analysis showed comparable results to the main findings (Figures 3, 4, 5), while the ICC of some network metrics was higher under a few network densities after the performing the scrubbing procedure (e.g., Cp in 0.4% for short‐term, Lp in 10% for long‐term I, and Lp and λ in 0.4%, 0.7%, and 1% for long‐term II. Figures 3 and 6).

Discussion

Using R‐fMRI data from 57 young healthy participants, we systematically investigated the TRT reliability of graph metrics in the voxelwise human brain functional networks. The main results are threefold: First, small‐world and modular properties were consistently observed in the voxel‐based functional brain networks even when different methodologies were used, and the functional hub regions were mainly located in several DMN, salience, and ECN networks. These results are largely compatible with previous voxel‐based brain network studies 16, 22, 33. Second, both global and nodal metrics were generally more reliable in the long‐term I than short‐term, with the highest reliability in global metrics in Cp, in nodal metrics, and in nodal degree and efficiency. Thirdly, validation analyses without GSR and with head motion scrubbing did not affect our main findings.

TRT Reliability of Global Network Metrics

For six global metrics (Cp, Lp, γ, λ, σ, and Q), we observed that the TRT reliability was higher for the long‐term I than the short‐term, consistent with our previous findings based on ROI‐based network analyses using another independent TRT R‐fMRI dataset 17, 32. However, the present study showed moderate to good long‐term I reliabilities for most global metrics (e.g., Cp, Lp, γ, λ, and σ), which were much higher than the results in previous studies showing poor TRT reliability for most global network metrics 17, 32. This discrepancy may be explained by two factors. First, the definition of long‐term I reliability used here was different from that in the two previous studies. The present study assessed long‐term TRT reliability by comparing Scan 1 and Scan 3, whereas Wang et al. 17 and Liang et al. (2011) assessed reliability by averaging the functional connectivity matrices of two short‐term scans and then comparing them with a long‐term scan. Given that Scan 2 exhibited a significantly different pattern than the other scans (Table S2), averaging the two short‐term scans may reduce the TRT reliability 17, 32. This hypothesis can be further supported by our findings demonstrating the overall low TRT reliability in short‐term (Scan 1 and Scan 2) and long‐term II (Scan 2 and Scan 3). Secondly, the present study examined the finer‐grained parcellation at a voxelwise level, which may enhance the TRT reliability. In ROI‐based network analyses, the spatial inhomogeneity within ROIs could lead to poor specificities of BOLD signals, thereby reducing TRT reliability. Notably, unlike our findings here, a previous voxelwise fMRI study 36 reported good to excellent short‐term TRT reliability for several global network metrics (e.g., Cp and Lp) in healthy elder adults. However, their data are collected during an executive task, not resting‐state, which may lead to the higher TRT reliability of network metrics. In addition, the topological organization of functional networks may undergo remarkable changes during aging 50, and the different age range considered in Telesford et al. 36 may also have potential influence on the TRT reliability.

TRT Reliability of Nodal Metrics

Recently, researchers have paid more attention to the exploration of hub regions characterized by different nodal centrality measures 6, 34, 51. Using nodal degree, efficiency, and betweenness measures, we identified global hubs in the voxel‐based brain networks, which were mostly located at the regions belonging to the DMN and ECN, consistent with previous R‐fMRI studies 33, 34, 37, 51, 52, 53. These global hubs have been considered to play an essential role in the global information communications across regions 53. Using a participation coefficient measure, we identified connector hubs, but the spatial patterns were sensitive to the selection of network density thresholds: The connectors were similar to those global hubs at a low density threshold (0.1%), but were different at increasing thresholds, primarily distributed in the thalamus, medial temporal lobe, supplemental motor area, insula, superior temporal gyrus, and superior parietal cortex. These connectors are important for the information integration and exchanges across different functional modules or systems. Such a pattern has been observed in several previous R‐fMRI studies 54, 55.

The studies on nodal centrality in voxel‐based brain networks have potential benefits for researches associated with development, aging, and diseases (for review, see 6), and longitudinal studies on drug effects 56, suggesting the necessity of TRT reliability analysis for these nodal metrics prior to basic and clinical study 30, 57. In our study, we found that degree and nodal efficiency exhibited moderate to good long‐term I reliability in most hub regions (e.g., the major components of the DMN, salience, and ECN networks), which is in accordance with the previous studies 17, 33. However, betweenness and participation coefficient showed overall low reliability regardless of the spatial location and interscan intervals. Lower TRT reliability of these two metrics could be attributed to their strong dependence on the connection patterns. The estimation of betweenness largely depends on the specific path in a network. Slightly changing the connection pattern by adding or removing a few edges may change the shortest path between nodes and thus have a large effect on nodal betweenness. The calculation of the participation coefficient is influenced by the modular architecture of a network, which may undergo changes in short time 58 and can be modulated by mental states during the scan 59. Slight modifications of the modular architectures between scans may result in profound changes in participation coefficients. Therefore, these two metrics may be more sensitive to noise than degree and efficiency. The application of these two nodal metrics in longitudinal studies should be used with caution due to their distinct TRT reliability.

Effects of InterScan Time Intervals

We found that the TRT reliabilities of global and nodal metrics were both sensitive to time intervals between scans. All network metrics showed poor to low short‐term reliability across the whole density range. Using another independent dataset at NITRC (http://www.nitrc.org/projects/trt), Wang et al. 17 also reported low reliability of ROI‐based network metrics between scans within the same session (45 min apart). This observation may result from the alteration of Scan 2 which exhibited significant differences from the other two scans in several network metrics (e.g., Cp, and Q, as seen in Table S2). Scan 2 and Scan 1 were obtained in the same session separated by several other MRI sequences with low requirements for subject compliance, via a fixed scanning order, and all subjects kept awake during the MRI scans according to a simple questionnaire after the MRI scans. Therefore, the network difference may be largely attributed to the scanning‐order effects due to continuous scanning, such as the alteration of subjects’ mental states (e.g., increased drowsiness and reduced patience). The potential changes in brain states between different scans can be further supported by the significantly different global signals observed in Scan 2 and the other two scans (Figure 8). In contrast, Telesford et al. 36 reported a very high short‐term reliability for several graph metrics in voxelwise networks. One important cause is that these networks were constructed under the executive task condition, which might highly constrain the topological pattern of the functional brain networks. Our finding here suggests that the scanning scheme may affect the intrinsic functional network topology, which should be considered in the experimental design for future R‐fMRI studies.

Effects of Global Signal and Head Motion

Effects of Global Signal

The effect and necessity of GSR in the research of intrinsic functional networks are currently hot issues 29, 31, 46, 60. Similar to a previous study of voxelwise functional hubs 33, we found that the spatial configuration of functional hubs exhibited a slight alteration without GSR. This finding may result from the shift of the correlation distributions across the brain without global signal removal 31, 45. Nevertheless, in contrast to the results of Liao et al. 33 and Guo et al. 30, we found the overall level of TRT reliability was not improved for either global or nodal metrics without GSR. This discrepancy may be due to the different thresholding strategies used for network construction. In the work by Liao et al. 33, a fixed correlation threshold was employed to construct networks, which largely raises network densities without GSR in comparison with those with GSR. Higher densities may reduce the sensitivity of network organization to noise and thus improve the TRT reliability. In the current study, we instead utilized a fixed density threshold to keep the network connectedness at the same level with/without GSR, explaining why no significant enhancement in TRT reliability was observed in case of without GSR.

Moreover, we found that the TRT reliability of global metrics, without GSR, seemed to be more sensitive to time intervals between scans. Specifically, lower short‐term reliability and long‐term II reliability were observed in case of without GSR (Figure 6), comparing with those obtained with GSR (Figure 3). This phenomenon may be explained by the alteration of the global signal in Scan 2, indicated by the altered spectrum and ALFF of global signals (Figure 8). Thus, the regression of global signals reduced this scanning‐order effect on network topologies and enhanced the short‐term and long‐term II reliability. This change in global signal may result from the possible changes in subjects’ mental states during the continuous scanning. Previous studies have shown that global signals were tightly linked to neural activity 61 and exhibited a higher variability in schizophrenia 62. Our results could provide circumstantial evidence supporting the links between global signals and neural activity 61, 62. Together, GSR could be related to the brain states of subjects, and their effects could be varied due to the different data acquisition and processing strategies employed in experiments and should be cautiously considered.

Additionally, in Figure 8, we found a subject (ID: N0017) with extremely high ALFF (three standards above the average value across subjects) of global signals in Scan 2. We cautiously validated the main results by removing this subject as an outlier, and we found that the TRT reliability still remained a poor to low level for all global metrics between Scan 2 and the other two scans (Figure S7).

Effects of Head Motion

The statistical analyses on the mean FD indicated that subjects exhibited large head motion in Scan 2, which may be an evidence of the increased drowsiness and reduced patience during the continuous scanning that we mentioned before. Therefore, the larger head motion along with the worse mental state (e.g., tension, anxiety, and fatigue) in Scan 2 than in Scan 1 and Scan 3 may be the potential factors to cause the relatively low short‐term and long‐term II reliability. Further researches would be valuable to study the effects of head motion on network metrics, investigate the relationship between head motion and mental state, and propose innovative methods to better reduce the effects of head motion.

Methodological Considerations

Several issues need to be further addressed. First of all, we used a traditional sampling rate (TR = 2s) for data acquisition in our study. The results may be confounded by the aliasing of high‐frequency respiratory (~ 0.3 Hz) and cardiac (~ 1 Hz) noises, despite being processed with a band‐pass filtering (0.01~0.1 Hz) 63, 64. Recently, the development of imaging techniques, including multiband echo‐planar imaging 65, 66 and MR‐encephalography 67, has enabled whole‐brain image acquisition at a higher temporal resolution (<1 s), which can diminish the effects of respiratory and cardiac noises 64. Therefore, further studies of functional network topologies based on multiband data can be considered to enhance the TRT reliability in future work. Second, our results showed that the functional connectivity patterns have been largely changed in Scan 2 after several MRI sequences, which may be due to the alteration of individual mental states. In other words, the decrease in TRT reliability for the network metrics may be a reflection of underlying physiological changes. Thus, an investigation of the physiological basis of network metrics is an important topic for future work. In addition, aside from the functional networks studied here, the TRT reliability of structural networks at a high resolution is another essential issue for future neuroimaging studies and should be systematically studied. Furthermore, the coupling between high‐resolution functional and structural networks and its reliability are interesting topics for the future. Finally, we investigated the R‐fMRI data of young healthy subjects without considering the aging issue. As indicated in previous studies 8, 68, 69, the network metrics undergo changes during the development and aging process. This aging effect may influence the TRT reliability of the network metrics for subjects in different age ranges, which may be partly responsible for some of the different results between the present study and in Telesford et al. 36. Exploring the TRT reliability of functional networks at different age stages could be informative for the subsequent basic and clinical applications.

Supporting information

Table S1 Network metrics for binary networks examined in the current study.

Table S2 Results of inter‐scan comparison analysis on global network metrics.

Figure S1 Group‐level functional hub maps at the density of 0.1%.

Figure S2 Group‐level functional hub maps at the density of 10.0%.

Figure S2 Group‐level functional hub maps at the density of 10.0%.

Figure S3 Voxel‐wise connector hub maps across seven density levels.

Figure S4 Results of voxel‐wise statistical analysis on four nodal metrics at the density of 4.0%.

Figure S5 TRT reliability of nodal metrics without GSR.

Figure S6 Group‐level functional hubs maps and TRT reliability maps of nodal metrics based on R‐fMRI data with head‐motion scrubbing and GSR.

Figure S7 Short‐term and long‐term II TRT reliability of global metrics after removing an outlier in Scan 2.