Sex-Specific Longitudinal Modeling of Short-Term Power in 11- to 18-Year-Olds

ABSTRACT

Purpose

To investigate, longitudinally, short-term power output in relation to sex and concurrent changes in age, body mass, fat-free mass (FFM), and maturity status.

Methods

Multiplicative multilevel modeling which enables the effects of variables to be partitioned concurrently within an allometric framework was used to analyze the peak power (PP) and mean power (MP) of 388 11- to 18-yr-olds. Multilevel models were founded on 763 (405 from boys; 358 from girls) determinations of PP and MP from Wingate anaerobic tests, supported by anthropometric measures and maturity status.

Results

In both sexes, PP and MP were significantly (P < 0.001) correlated with age, body mass, and FFM. After controlling for body mass, initial models showed positive effects for age on PP and MP, with negative effects for sex and a sex by age interaction. Sex-specific models showed maturity status to have no additional effect on either PP or MP once age and body mass had been controlled for. Skinfold thicknesses in addition to body mass to provide a surrogate for FFM, yielded a significantly (P < 0.05) better statistical fit in all models compared with those based on either body mass or FFM estimated from youth-specific skinfold equations. Models founded on estimated FFM provided a significantly (P < 0.05) better fit than those based on body mass.

Conclusions

With body mass controlled for boys’ PP and MP are higher than those of girls and sex differences increase with age from 11 to 18 yr. A multilevel modeling approach has showed that in both sexes the most powerful influences on short-term power output are concurrent changes in age and FFM as reflected by the combination of body mass and skinfold thicknesses.

The assessment and interpretation of young people’s aerobic power is well documented but maximal-intensity exercise, principally reliant on anaerobic metabolism, is less extensively researched and poorly understood. Ethical and technological constraints restrict direct measurement of the intramuscular rate of energy production, and current knowledge is largely based on analyses of performance outcomes. Numerous performance tests have been developed but pediatric research has primarily focused on the assessment of power output during the Wingate anaerobic test (WAnT) (1).

During the WAnT, power output is calculated from maximal pedaling cadence against a fixed braking force with peak power (PP) output recorded within a few seconds of exercise onset and total power output averaged over the 30-s test period and expressed as mean power (MP) output. An age-related range of different body mass-related braking forces has been recommended (2) but WAnT determined PP and MP do not appear to be affected by moderate variations in braking force (3) and within individual studies, it has been shown to be a robust and reliable test (1). In practice, some studies have addressed the issue of a common body mass-related braking force by identifying the individual optimal braking force for PP through a series of short sprints performed against a range of randomly introduced constant braking forces, usually centered around the conventional WAnT braking force of 0.74 N·kg⁻¹ (4). Determined in this manner, PP is referred to as optimized peak power (OPP). In addition, pediatric exercise scientists have adopted a plethora of different WAnT protocols. These include use of a standardized pretest warm-up (5), a rolling start (6), the use of toe clips (7), alterations of cycle crank length in relation to leg length (8), differences in the time (e.g., 1, 3, or 5 s) over which PP is recorded (9), and estimations of the work done to overcome the inertia of the flywheel and the internal resistance of the cycle ergometer (10).

The use of a range of methodologies has precluded confident comparisons of cross-sectional PP and MP data across studies and resulted in wide variations in reported “typical” values in relation to age. There are insufficient MP data to draw secure conclusions but cross-sectional data consistently indicate that PP increases with age until ~13 yr with no discernible sex difference. In fact, in several studies which do not monitor maturity status, girls outscore similar age boys. From ~13 yr of age, boys experience a marked increase in PP, which continues into young adulthood, with girls exhibiting a smaller increase with age (9).

Recognizing that during the growth period PP and MP are highly correlated with both body mass and fat-free mass (FFM), most cross-sectional studies have opted to control for this through ratio scaling (i.e., by dividing PP or MP by body mass or FFM and expressing it in watts per kilogram). Using this technique, boys’ PP and MP have been demonstrated to be significantly higher than those of girls by ~13 yr of age and the sex difference to increase with age. Girls’ PP and MP ratio-scaled with body mass generally level-off from ~14 to 15 yr of age, whereas boys’ values increase until ~17 yr when PP and MP in watts per kilogram begin to plateau or even decrease with age. The pattern with PP ratio-scaled with FFM is similar although the sex differences are much reduced (9,11). It is well documented, however, that ratio scaling is a flawed methodology which clouds understanding of exercise performance during youth. It does not have a rigorous scientific rationale, is not statistically justified, favors lighter individuals (e.g., later-maturing youth), and penalizes heavier (e.g., overweight or more mature youth) individuals (12,13).

In the most comprehensive and rigorously analyzed cross-sectional studies of PP in youth, the OPP of 189 9- to 18-yr-old girls and 506 7- to 18-yr-old boys were determined (14,15). No consideration was given to maturity status in these studies, but the relationships between OPP and age, body mass, FFM estimated from youth-specific equations (16), and lean leg volume (LLV) estimated anthropometrically (17) were analyzed with log-linear regression. The relative contribution of anthropometric variables to the total variance in OPP was investigated using an allometric model. Optimized peak power was reported to be correlated with body mass but more strongly related to FFM and LLV. In both boys and girls, OPP was reported to be at least as well related to FFM as to LLV and the authors recommended the use of FFM as an appropriate scaling variable in large-scale investigations (14,15).

It seems logical in body mass-supported exercise, such as cycling, to standardize performance to LLV. On the other hand, FFM might be more appropriate because it includes other muscles (e.g., gluteus maximus, arm muscles, and trunk muscles) which contribute to cycling performance in addition to muscles included in LLV. In practice, FFM has been consistently supported as the most appropriate anthropometric scaling variable of short-term cycling power during growth and maturation (11,14,15). In conjunction with body mass, the youth-specific equations to predict percent body fat from skinfolds derived by Slaughter et al. (16) are the most commonly used to estimate FFM. Validation studies of the methodology have, however, revealed wide limits of agreement and a tendency to under-predict body fat in girls and overpredict body fat in boys (18). It has been demonstrated that skinfold thicknesses and body mass together provide a surrogate for FFM which, in studies of the development of youth aerobic power, explain more of the variance in peak oxygen uptake (peak V˙O₂) than the estimation of FFM from youth-specific skinfolds equations (19). This has not been explored with PP and MP data.

Longitudinal studies, with at least three measures separated by time (20), provide a more rigorous interpretation of developmental exercise physiology but before the present study, there are, to our knowledge, no longitudinal studies of the PP and MP of both boys and girls. The longitudinal data available are limited to three short duration studies with small numbers of participants. The first published study only reported data in ratio with body mass and contributed little to our understanding (21). The second study reported boys’ PP and MP to increase with age. Pubic hair (PH) development was assessed but the experimental design precluded analysis of the effects of maturity status on performance (22). The only study to include girls determined the OPP of 12-yr-olds and then repeated the process on three subsequent occasions each 6 months apart. MP was not determined. With body mass appropriately controlled for OPP was reported to increase with age with no significant (P > 0.05) sex differences but the data are limited by the study’s 18 month duration, small age range, and nonconsideration of maturity status (23).

Collectively the experimental designs, methodology, statistical analyses, and data interpretation in the extant literature have revealed few insights into PP and MP in relation to sex, age, body mass, FFM, and maturity status. The emergence (24) and regular refinement (25) of multilevel regression modeling has, however, opened up new analytical approaches to developmental exercise physiology. Multilevel modeling enables the effects of variables such as age, body mass, FFM, and maturity status to be partitioned concurrently within an allometric framework to provide a flexible and sensitive interpretation of exercise performance variables. Moreover, in contrast to traditional methods that require a complete longitudinal data set both the number of observations per individual and the temporal spacing of the observations may vary within a multilevel model.

In an innovative re-analysis of previously published data, Nevill et al. (26) introduced multiplicative, allometric modeling to pediatric sport science and with the present authors applied it to interpreting growth and maturation changes in the peak oxygen uptake of 11- to 13-yr-olds (27). Multilevel allometric modeling has subsequently been used in, for example, longitudinal studies of 11- to 13-yr-olds’ physical activity (28) and 12- to 14-yr-olds’ muscle strength (29) but the development of 11- to 18-yr-olds’ PP and MP using a multiplicative, allometric modeling approach had not been explored before the present study.

The purpose of this study was therefore to use a multiplicative, allometric modeling approach to enhance understanding of the development of PP and MP from 11 to 18 yr of age in relation to sex, age, maturity status, body mass, and FFM. A subsidiary objective was to compare sex-specific and age-related models of the development of PP and MP founded on body mass and sum of skinfold thicknesses as a surrogate of FFM with those based on FFM estimated from youth-specific skinfold equations.

METHODS

Participants

Two hundred and fifty (124 girls; 126 boys) 11- to 12-yr-olds from local state schools volunteered to participate in a series of studies involving three annual assessments of aerobic power and short-term power output. The project was subsequently extended to cover the age range 11 to 18 yr with an additional 138 (66 girls, 72 boys) 11- to 14-yr-olds volunteering for annual assessments. The project received ethical approval from the Exeter District Health Authority Ethical Committee, and all participants provided written informed consent signed by themselves and their guardian. Some of the initial PP and MP data have been reported as the project progressed (30) but the complete data set has not previously been brought together for analysis, sex-specific models have not been developed, and FFM has not been explored. The aerobic power data have been reported elsewhere (19).

Experimental procedures

Participants visited the Research Center annually and were well-habituated to the laboratory environment, to the laboratory personnel, and to the experimental procedures. Anthropometric measures were taken as described by the International Biological Programme (31), and apparatus was calibrated according to the manufacturer’s instructions. Body mass was determined using Avery balance scales (Avery, Birmingham, UK). Skinfold thicknesses over the triceps and subscapular regions were measured using Holtain skinfold calipers (Holtain Ltd, Crosswell, UK). Percentage body fat was predicted from skinfolds using youth-specific equations (16) and FFM was subsequently estimated from body mass and predicted percent body fat. Maturity status was visually assessed by the Research Center nurse using the indices for PH development described by Tanner (32).

Peak power and MP were determined using the WAnT. All tests were conducted on a friction-loaded cycle ergometer (Monark 814E; Monark-Crescent AB, Varberg, Sweden) interfaced with a microcomputer and calibrated according to the manufacturer’s instructions. The seat height and handlebars were adjusted for each participant and, in accord with the extant literature, the test braking force was set in relation to body mass at 0.74 N·kg⁻¹ (9). After a standardized 3-min warm-up involving pedaling at 60 rpm interspersed with three all-out sprints lasting 2–3 s, the WAnT commenced from a rolling start pedaling with toe clips fixed to the pedals at 60 rpm against a minimal resistance (i.e., with the weight basket supported). When a constant pedal rate was attained a countdown of “3–2-1-Go” was given, the test resistance was applied, and the computer activated. On the signal “Go” participants, with strong verbal encouragement, cycled as fast as possible and power output, corrected for inertia and load (10) was calculated each second for the 30-s duration of the test. The highest power output achieved in 1 s was recorded as PP and MP was calculated as the average power output over the 30-s duration of the test.

Data analysis

Descriptive statistics were determined using SPSS v25 (IBM SPSS Statistics). Factors associated with the development of PP and MP were analyzed using multilevel regression modeling (MLWin v3.02, Center for Multilevel Modeling, University of Bristol, UK) based upon the multiplicative, allometric approach originally described by Nevill et al. (26) for the analysis of strength development (equation 1):

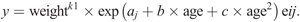
Log transformation linearizes the model as follows (equation 2) forming the starting point for analyses:

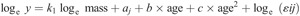
Initial (baseline) models investigated sex differences across the age range 11 to 18 yr with age and body mass controlled for. All investigated parameters were fixed with the exception of the constant (intercept term) which was allowed to vary randomly at level 2 (allowing individuals to have their own intercept term) and the multiplicative error term ɛ which also varied randomly at level 1 (within individuals). The subscripts i and j in equation 1 denote this random variation at levels 1 and 2, respectively. Age was centered on the group mean. From the baseline model of age, age², and body mass, sex differences were investigated using the indicator variable boys = 0, girls = 1 which sets the boys’ constant as the baseline from which the girls’ parameter is allowed to deviate. The interaction term age by sex which describes differential development of PP and MP between girls and boys and the age² term which indicates changes in the size of the age effect as the rate of change in growth decreases were also entered. In subsequent sex-specific analyses, additional explanatory variables were introduced including sum of triceps and subscapular skinfold thicknesses and indicator variables for maturity status of PH stages 2, 3, 4, and 5 compared with stage 1. Finally, maturity status was introduced to baseline models of FFM, age and age².

Parameter estimates were considered significant (P < 0.05) where their value exceeded twice the SE. A comparison of the goodness of fit of the different models was obtained from the change in the deviance statistic (−2× log-likelihood) with reference to the number of fitted parameters. In a comparison of two models with the same number of fitted parameters, the model with the smallest −2× log-likelihood reflects that with the best fit. Additional parameters contribute to improved fit from the change in −2× log-likelihood according to a χ² statistic for additional degrees of freedom added.

RESULTS

The timing and number of measures per individual are allowed to vary within a multilevel analysis. In the present study test occasions were scheduled annually and there were no significant differences (P > 0.05) between those who were unable to attend an annual test occasion and the rest of their sex-specific group in age, body mass, skinfold thicknesses, or short-term power output. The analyses were founded on 763 (405 from boys and 358 from girls) measurements of age, body mass, skinfold thicknesses, PP, and MP supported by 696 (376 from boys and 320 from girls) assessments of maturity status.

In boys, PP (W) and MP (W) were significantly (P < 0.001) correlated with age (PP, r = 0.76; MP, r = 0.78), body mass (PP, r = 0.83; MP, r = 0.85), and estimated FFM (PP, r = 0.87; MP, r = 0.91). These relationships are illustrated in Figure 1. In girls, PP (W) and MP (W) data were significantly (P < 0.001) correlated with age (PP, r = 0.71; MP, r = 0.67), body mass (PP, r = 0.71; MP, r = 0.72), and estimated FFM (PP, r = 0.76; MP, r = 0.78). These relationships are illustrated in Figure 2.

FIGURE 1.

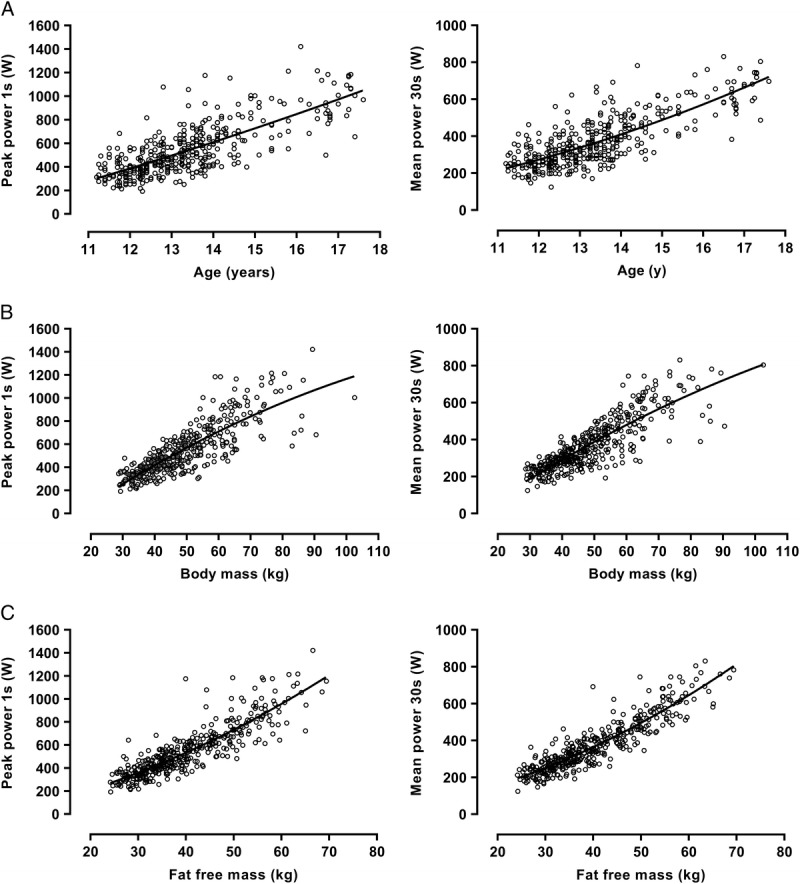
Peak power and MP in boys in relation to age (A), body mass (B), and estimated FFM (C), Data are from 405 WAnT determinations of 11- to 18-yr-old boys’ peak power and MP. FFM is estimated from youth-specific equations (16).

FIGURE 2.

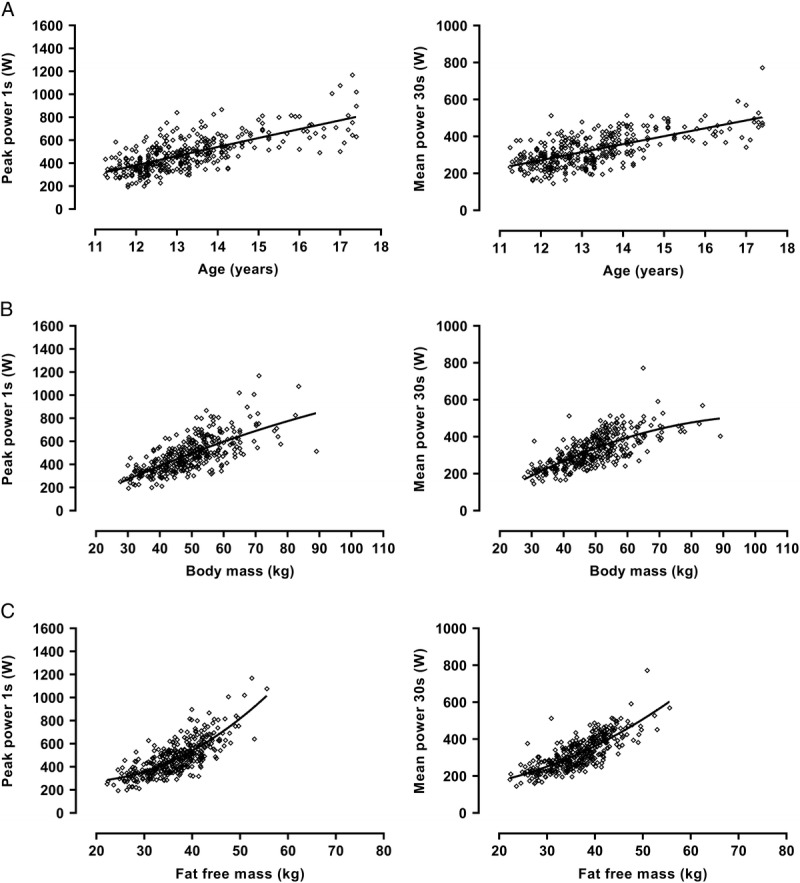
Peak power and MP in girls in relation to age (A), body mass (B), and estimated FFM (C), Data are from 358 WAnT determinations of 11- to 18-yr-old girls’ peak power and MP. FFM is estimated from youth-specific equations (16).

Multilevel models for the whole data set

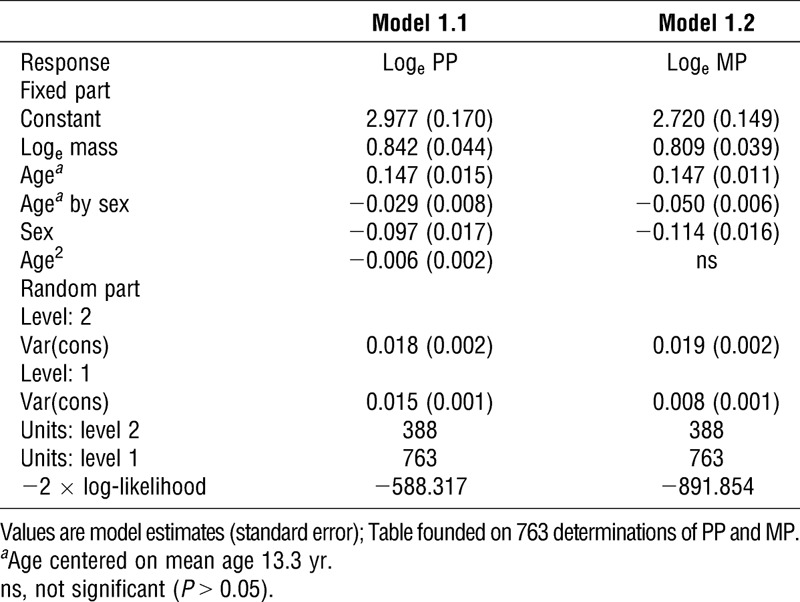
The results of modeling PP and MP from the whole data set with age are summarized in Table 1. In model 1.1 with body mass controlled for, a significant, positive age effect on PP was observed with negative sex and age by sex terms plus a small but significant negative effect for age². Model 1.2 shows the baseline model for MP with body mass as the sole anthropometric covariate. With body mass controlled for, significant increases in MP with age were observed with significant, negative sex and age by sex interaction terms.

TABLE 1.

Multilevel models for PP and MP in 11- to 18-yr-olds.

Multilevel models for boys

Multilevel models for PP and MP for boys are summarized in Table 2. In model 2.1, with body mass controlled for, an independent, additional positive effect of age and a negative effect of age² on PP were identified. Model 2.2 includes the additional covariate of sum of triceps and subscapular skinfold thicknesses providing, with body mass, a surrogate for FFM. The entry of skinfolds into the model yielded a significant negative term and an increased contribution from body mass. Having controlled for body mass and skinfold thicknesses an additional, significant, positive effect of age was observed although this was considerably reduced compared to model 2.1 and the age² term became nonsignificant (P > 0.05). Model 2.3 describes the results of modeling PP with estimated FFM replacing body mass. A significant, positive exponent for estimated FFM was obtained with an additional, positive age effect. The difference in the −2 × log-likelihood showed model 2.2 to be a better statistical fit for the data than both model 2.1 and model 2.3 despite the one additional fitted parameter.

TABLE 2.

Multilevel models for PP and MP in 11- to 18-yr-old boys.

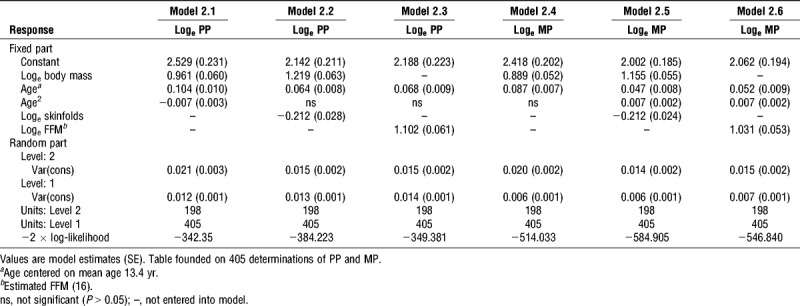
In model 2.4, with body mass controlled for, an additional, significant, positive effect of age on MP was noted. Model 2.5, with body mass and skinfolds controlled for and additional significant, positive age and age² effects, proved to offer a better statistical fit for the data than both model 2.4 and model 2.6, which were based on body mass and estimated FFM, respectively. Model 2.6 was a better statistical fit than model 2.4. The effects of maturity status were investigated but did not contribute significantly to any of the boys’ PP or MP models.

Multilevel models for girls

Multilevel models for PP and MP for girls are summarized in Table 3. In model 3.1 for PP with body mass controlled for, an independent, additional positive effect of age and a negative effect of age² were identified. The addition of sum of two skinfold thicknesses in model 3.2 yielded significant positive and negative terms for body mass and sum of skinfolds, respectively, with a significant, positive effect of age remaining. Model 3.3 illustrates modeling PP with estimated FFM replacing body mass. A significant, positive exponent for estimated FFM was obtained with a comparable additional age effect but model 3.2 provided a better statistical fit for the data than both model 3.1 and model 3.3 despite the one additional fitted parameter. Model 3.3 provided a better statistical fit than model 3.1.

TABLE 3.

Multilevel models for PP and MP in 11- to 18-yr-old girls.

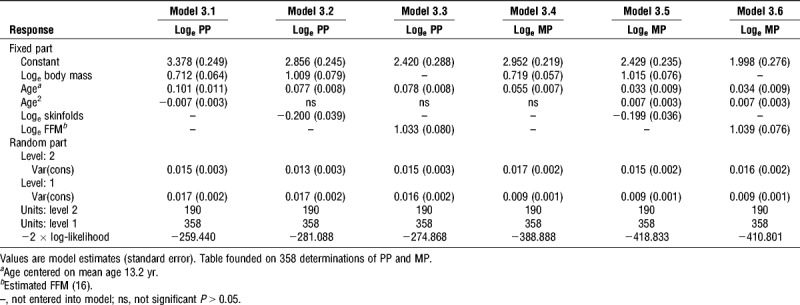
In model 3.4 for MP with body mass controlled for, an independent, additional positive effect of age was identified confirming an increase of MP over and above that due to increases with body mass. In model 3.5, sum of two skinfold thicknesses was entered in addition to body mass. This model yielded significant, negative and positive exponents for skinfold thicknesses and body mass, respectively, with additional, significant, positive age and age² terms. Model 3.6 identified a significant, positive exponent for estimated FFM plus comparable positive age and age² effects to model 3.5. Model 3.5 with body mass and sum of skinfolds proved to offer a better statistical fit for MP data than models 3.4 and 3.6 based on body mass and estimated FFM, respectively, with model 3.6 providing a better fit than model 3.4. The effects of maturity status were investigated but did not contribute significantly to any of the multilevel models of girls’ PP or MP.

DISCUSSION

Descriptive data describing PP and MP in relation to age, body mass, and estimated FFM, respectively, are presented for boys in Figure 1 and the corresponding girls’ data are presented in Figure 2. The data describing PP and MP in relation to age are in accord with those reported in cross-sectional studies with similar values for girls and boys until ~13 yr but sex differences increasing with age thereafter to ~30% in favor of boys by ~17 yr of age (9,11). There are no comparative longitudinal data but the present data show increases in PP and MP in relation to age to be near-linear in both sexes. The positive age, negative sex, and negative age by sex terms in models 1.1 and 1.2 show that even with body mass controlled for PP and MP are higher in boys than in girls and that they increase with age in both sexes although the age effect is smaller in girls. The small negative age² term in model 1.1 indicates that the size of the age effect on PP is reduced as the rate of growth decreases.

Correlations between PP and MP with anthropometric variables are highly significant but in both sexes, in agreement with the sparse literature (14,15), correlations with estimated FFM are higher than those with body mass. PP and MP data begin to level-off at higher body masses, particularly in girls of ~50 to 55 kg and above, probably due to the maturity status-driven increase in fat mass. In contrast, girls’ PP and MP increase at a greater rate in relation to estimated FFM from ~35 to 40 kg. Boys’ PP and MP data indicate similar but less marked trends from ~45 to 50 kg estimated FFM.

Girls normally enter puberty before similarly age boys and the magnitude of changes observed in anthropometric and performance-related variables are sex-specific. It is therefore appropriate to analyze the development of girls’ and boys’ PP and MP in sex-specific models rather than combining data as in Table 1. However, the sex-specific models of the pattern of development of PP and MP are remarkably similar. With body mass controlled for, age exerts a significant additional effect on PP and MP in both sexes accompanied by a small negative age² term in PP models and a small positive age² term in the MP models. In all models the introduction of maturity status (i.e., PH development) had no significant effect. This is in direct contrast to the development of aerobic power in the same young people. In a parallel study, the present participants had their peak V˙O₂ measured annually within 24 h of their PP and MP and, with age and body mass controlled for PH stages 2 to 5 each made a significant positive contribution to explaining the development of peakV˙O₂(19).

In both sexes, models founded on estimated FFM are superior to those with body mass as the sole anthropometric covariate but the models with the best statistical fit are those based on body mass and sum of skinfold thicknesses. It is likely that the effects of maturity status on PP and MP are expressed within the FFM contribution to the models as changes in FFM are driven by the timing and tempo of maturation (33,34). A similar outcome was noted in the development of aerobic power where the models including body mass and skinfold thicknesses or estimated FFM negated the independent effects of maturity status. From a methodological perspective it is also noteworthy that in models of aerobic power the use of body mass and sum of skinfolds as a surrogate for FFM provided in all models a superior statistical fit to the data than FFM estimated from youth-specific equations (19).

The models show that changes in PP and MP with age are associated with sex-specific and maturity status-driven increases in FFM. FFM increases by ~90% and ~40% in boys and girls, respectively, from 11 to 16 yr. The influence of sex-specific maturity status on FFM is evidenced by % changes in FFM being at their peak around the time of peak height velocity (PHV). Boys’ FFM increases by ~83% over the period 2 yr pre-PHV to 2 yr post-PHV. The greatest increase in girls’ FFM (~31%) occurs over a shorter 2-yr period centered on PHV and then levels-off. Boys’ muscle mass reaches ~54% of body mass at 18 yr, whereas, in girls, muscle mass is ~45% of body mass at 13 yr and then, in relative (but not absolute) terms, declines because of fat accumulation in puberty (33,34).

Short-term cycling power is primarily developed from the leg muscles and sex differences in PP can, at least partially, be attributed to girls having ~70% of the leg muscle mass of boys by the end of adolescence (34). The maximum force exerted by a muscle is reliant on the number of sarcomeres arranged in parallel and is proportional to the cross-sectional area of the muscle or the square of the linear dimensions (l²). Power is the product of force (l²) and velocity. The velocity of muscle shortening depends on the number of sarcomeres in series and is directly proportional to the length (l) of the muscle. Power is therefore related to l³ and is likely to be best represented by the active muscle volume. In two multilevel modeling investigations the thigh muscle volume of 10- to 12-yr-olds and 12- to 14-yr-olds, respectively, was determined using magnetic resonance imaging, on two occasions 1 yr apart. One study used the WAnT to determine PP and MP and the other determined OPP. The multilevel models demonstrated that in both boys and girls thigh muscle volume made a significant, additional contribution to explaining sex differences and changes in OPP, PP, and MP with age over and above those attributed to body mass (23,35).

Within the models small but significant age effects for PP and MP, independent of, and additional to, changes due to FFM were observed for both boys and girls. In combination with the increases in FFM it is likely that these reflect not only increases in total muscle volume but also changes in maturity status–related factors such as muscle activation (i.e., the decline in activation deficit) (36), muscle structure (34), muscle fiber type (37), and muscle metabolism (37) which were not investigated herein. These factors have been comprehensively reviewed elsewhere in relation to the ethical and methodological challenges of exploring their influence on maximal-intensity exercise in youth but there is a paucity of empirical evidence on their relative contributions to short-term power output in 11- to 18-yr-olds (9,36,37).

Limitations of the WAnT

A strong case can be made to relate the braking force in the WAnT to LLV. However, the use of anthropometric equations developed with adults (17) to estimate LLV in youth has been demonstrated to be untenable (38) and the use of resource-intensive techniques, such as magnetic resonance imaging to determine LLV is not currently feasible in large-scale studies. Several studies have investigated the effects of different body mass–related braking forces on PP with inconsistent results. For example, the conventional WAnT braking force of 0.74 N·kg⁻¹ has been reported to be appropriate in 10- to 12-yr-old boys and girls and 15-yr-old boys but too high for 14-yr-old girls to obtain OPP (14,15). On the other hand, the mean difference between PP and OPP, determined from significantly (P < 0.05) different braking forces centered around 0.74 N·kg⁻¹, has been reported to be ~2% and ~6% in 14-yr-old girls and boys, respectively, and not significantly (P > 0.05) different in either sex (4). On balance, it appears that in the age group studied herein the WAnT-determined PP in youth is generally resilient to moderate variations in body mass–related braking force and appropriate for large-scale studies although there are likely to be individual exceptions (e.g., overweight youth).

The determination of MP is less secure than PP and is not necessarily optimal if the braking force is set to optimize PP. If the braking force is set too high for optimal MP determination, as the WAnT progresses fatigue causes a reduction in the pedaling rate thus affecting the power to velocity ratio and resulting in a fall in power output. In addition, as both boys and girls reach ~60% to 70% of their peak V˙O₂ during the WAnT (39), MP represents an interplay between aerobic and anaerobic metabolism which, partially due to variations in mechanical efficiency, is difficult to unravel and has been estimated to lie within the range of 16% to 45% (10). The V˙O₂ kinetics response at the onset of very heavy-intensity exercise slows as young people move through their teens so an age-related increase in the anaerobic contribution to MP would be expected but is yet to be quantified (40). Nevertheless, MP remains an important physiological variable with applications in many sports (33) and regardless of the balance of anaerobic or aerobic metabolism involved, the development of FFM has been shown herein to strongly influence MP.

To obtain true maximal power output on a cycle ergometer, the braking force should be matched to muscle capability so that the test can be performed at optimal pedal cadence. In a longitudinal study, this would ideally require the optimal braking force to be determined specifically for each of PP and MP on each test occasion. The WAnT, however, remains the most practical and robust laboratory or field test with which to investigate the PP and MP of large numbers of young people. Within the present data, although FFM indicated by body mass and skinfolds provided the best statistical fit for determining longitudinal changes in PP and MP, the models based on estimated FFM identified almost identical age effects and gave rise to significantly better models than with body mass as the sole anthropometric covariate. Therefore, as previously recommended from cross-sectional data (15) and supported by the present longitudinal data, a braking force based on estimated FFM is likely to be superior to one based on body mass, and more practicable than one related to LLV and should be prioritized in future large-scale studies.

CONCLUSIONS

The present study is the first to investigate the performance of 11- to 18-yr-olds on the WAnT using a multiplicative allometric approach which has enabled a sex-specific, concurrent analysis of variables contributing to the development of PP and MP. It has been demonstrated that even during body mass-supported exercise such as cycling, PP and MP are strongly related to anthropometric variables. With body mass controlled for, PP and MP are higher in boys than in girls from 11 to 18 yr with the sex difference increasing with age. In both sexes, it is FFM, as best reflected herein by a combination of body mass and skinfolds, which is the dominant influence on the development of PP and MP. Additional independent effects of maturity status were not significant and are likely to be expressed within the FFM contribution to the models as changes in FFM are associated with the timing and tempo of maturation.

CONFLICTS OF INTEREST

The authors have no conflicts of interest to disclose. The results of the present study do not constitute endorsement by the American College of Sports Medicine.

The results of the study are presented clearly, honestly, and without fabrication, falsification, or inappropriate data manipulation.