Abstract
Paracrine PDGF signaling is involved in many processes in the body, both normal and pathological, including embryonic development, angiogenesis, and wound healing as well as liver fibrosis, atherosclerosis, and cancers. We explored this seemingly dual (normal and pathological) role of PDGF mathematically by modeling the release of PDGF in brain tissue and then varying the dynamics of this release. Resulting simulations show that by varying the dynamics of a PDGF source, our model predicts three possible outcomes for PDGF–driven cellular recruitment and lesion growth: (1) localized, short duration of growth, (2) localized, chronic growth, and (3) widespread chronic growth. Further, our model predicts that the type of response is much more sensitive to the duration of PDGF exposure than the maximum level of that exposure. This suggests that extended duration of paracrine PDGF signal during otherwise normal processes could potentially lead to lesions having a phenotype consistent with pathologic conditions.
Keywords: platelet-derived growth factor, scarring, gliosis, oligodendroglial progenitors
1. Introduction
Platelet-derived growth factor (PDGF) ligands and receptors are expressed by many cell types and are implicated in many processes in the human body—both beneficial and harmful. The cells that can produce PDGF are widespread and include vascular endothelial cells, smooth muscle cells, macrophages, and astrocytes [16,25,33,49]. Cells that express the receptors for these cells include a number of mesenchymal stem cells and stromal cells such as fibroblasts and oligodendroglial progenitor cells [2,3,24,25,50]. Because they are frequently found near each other, these two groups of cells, those producing PDGFs and those that express PDGF receptors (PDGFRs), can thus communicate with each other in paracrine signaling loops, wherein one cell communicates to another nearby cell. This PDGF signal causes the receptive cells to divide, move, and sometimes differentiate [16,20,25]. Through these paracrine loops, PDGF plays a pivotal role in development [8, 28], contributes to angiogenesis and maintenance repair of blood vessels [21, 38], and in the central nervous system stimulates axonal remyelination through the proliferation, migration, and differentiation of oligodendroglial progenitor cells [1, 47]. In addition to these beneficial roles, paracrine PDGF signaling is associated with many harmful pathologic conditions. For example, it is involved in the formation of scar tissue, being active in the processes of gliosis [56], liver fibrosis and steatosis [13], atherosclerosis [12, 50], renal diseases [11], and even Alzheimer’s disease [40]. Overexpression of PDGF or PDGF receptors has been found in many cancers, as well, including glioblastoma [26,37,39,60,61], prostate carcinoma [59], chronic myelomonocytic leukemia [4], colorectal cancer [36,44], and hepatocellular carcinoma [13,62]. With many studies uncovering stromal involvement in a wide number of cancers [15, 23, 35], it is clear that paracrine signaling has broad importantance for cancer. PDGF is one contributor which we have sought to understand better in the context of cancer, but studying its normal role more fully can arguably give us an even greater picture of how paracrine PDGF signaling contributes to pathologies such as cancer.
Previously, we have explored some of the effects of paracrine PDGF-BB in the brain by creating a mathematical model of PDGF-driven brain tumors, wherein paracrine PDGF drives the recruitment of oligodendroglial progenitor cells (OPCs) to form large, fast-growing tumors [42]. This mathematical model was based on the experimental results of Assanah, et. al. [5], where retrovirally transduced cells secreted PDGF-BB, stimulating the proliferation and migration of oligodendroglial progenitor cells (OPCs), thereby recruiting them to the tumors, which closely resembled human glioblastoma. This is consistent with findings that OPCs express PDGFRa (PDGFR type alpha), since PDGF-BB can can bind to PDGFRa and all other types of PDGF receptor [27, 46]. We modeled the transduced cell population dynamics, as well as that of the responding OPCs and unbound PDGF-BB, and observed that levels of PDGF signal could affect the growth of the tumor, both in terms of size and the steepness of the density profile of invading cells [42, 43]. This led us to question the role of PDGF signaling in a broader context. Since PDGF signaling is involved in the stroma of tumors as well as other diseased and normal tissue, we wanted to explore the threshold between these. Specifically, what defines the boundary between a healed wound versus a fibrotic scar or even neoplasia? When does a good thing become bad?
To help answer these questions, we set out to mathematically investigate the dynamics of PDGF secretion and responding cells using a minimal modeling approach that focuses exclusively on the interplay between PDGF and a general target cell population, restricting ourselves to the brain. Our present model is an adaptation of our previous PDGF-driven glioma growth model, wherein the source of PDGF is changed to be nonspecific. PDGFs can be released by a number of cell types in response to a stimulus, such as an injury event, and this release is further modified by signals including proinflammatory cytokines that are released by still other cells, making the modeling of the contibutors to a PDGF source complex [29]. Further, there are at least five isoforms of PDGF and these have different binding preferences among the three known PDGFR isoforms. For the purpose of this present investigation, it is useful to reduce this complexity and vary the PDGF dynamics directly to allow us to focus on the consequences of that PDGF once secreted, using PDGF-BB since it uniquely binds to all PDGFR types. In particular, we set out to understand the relative contributions of the maximum exogenous PDGF level and duration of PDGF signaling, making these explicit parameters in our model. By varying these two parameters within biologically relevant domains, we observe a wide array of possible outcomes in terms of the recruitment of cells, from small localized responses that stop growing in a matter of days, to extensive growth responses that continue for weeks. Furthermore, we found that the duration of PDGF signal is more influential in driving these outcomes than the peak release amount.
2. Methods
To model the general process of PDGF signaling in the brain, we started with two equations from our prior PDGF-driven tumor model [42, 43]—those describing the dynamics of PDGF and of recruited untransduced OPCs—and generalized them with a few modifications. Arguably the most critical change is that in this model we have a nonspecific localized PDGF source in the equation for PDGF concentration, with a secrection rate that decays over time. The decay of this secretion activity is indicated by a rate parameter, λ, and through another parameter, Smax, we set the maximum value that the PDGF source may secrete. Another notable change is that we do not model any autocrine signaling, only paracrine signaling.
2.1. Model Equations
Our model is composed of two coupled PDEs. The first of our model reaction–diffusion equations (1) describes the change in PDGF concentration, represented by variable p, as a function of both the diffusion and consumption of PDGF. The second (2) describes the change in cell density, represented by variable r, over time and space as a function of PDGF–dependent migration and proliferation.
| (1) |
| (2) |
The first term in the right–hand side of equation (1) describes the diffusion of PDGF at rate Dp. The second term describes the loss of PDGF due to consumption by the PDGF–responsive cells at rate qr. This loss is also modified by a scaling term, β(p) which is defined in equation (5) and described in the text that follows the equation. Finally, the third term describes the secretion of PDGF at rate Smax exp{−λt}, where Smax is the maximum secretion rate. This secretion rate decays over time at rate λ. This whole term is scaled by the ratio of recruited cells to the carrying capacity. In this way, we indirectly capture the effects of other PDGF–secreting cells recruited to the site (by other signaling molecules) which may result in further release of PDGF. Mathematically, this is also useful in moving the source spatially away from its initial point source (see Section 2.3 for details about the initial conditions).
In equation (2), and are the diffusion and proliferation rates of the PDGF–responsive cells, respectively, which depend on the local concentration of PDGF, p, and the density of PDGF–responsive cells, r, as follows:
| (3) |
| (4) |
where
| (5) |
The parameters Dr and ρr are the maximum values that can be attained by the diffusion rate and proliferation rate, respectively, when the density is low and the PDGF concentration is high. The scaling terms that implement the dependence on p and r are valued between zero and one, and act to reduce the rates of diffusion and proliferation when there is little PDGF present to stimulate these effects and/or limited space due to high cell density. In the latter, we use a logistic growth term, 1 − r/K, where K is the carrying capacity. The PDGF–dependent scaling term is derived in part from Michaelis–Menten binding kinetics, which gives us β(p) (5). β(p) is a direct application of Michaelis–Menten kinetics, where parameter km is the concentration of PDGF at which half maximal receptor binding occurs. We also wanted to capture the downstream effect of this bound PDGF on cellular proliferation and movement (downstream in terms of biochemical pathways). This is traditionally done with a pharmacodynamic model and an EC50 parameter— that is, the half maximal effective concentration—in place of km. To incorporate both the binding of PDGF and the downstream effect of bound PDGF on behavior together in one term, we devised a term that utilized both parameters and fit the dose response data from [46]. (See Figure 1, which shows the curve generated by our downstream PDGF response term in relation to this data, as well as other data that we used for finding our initial condition, which is described in Section 2.3.1.) Note that we chose to model cellular movement as a diffusion process, as in our prior work [42,43]. This choice was based on our analysis of tracks from cells moving in acute tissue slice assays, which showed that cells move in directed random walks along white matter tracks [30, 42]. Since our domain is 1D with spherical symmetry, we do not differentiate between the impacts of different tissue types on cell movement.
Fig. 1: Control and Experimental PDGF concentrations in relation to model dose response curve.
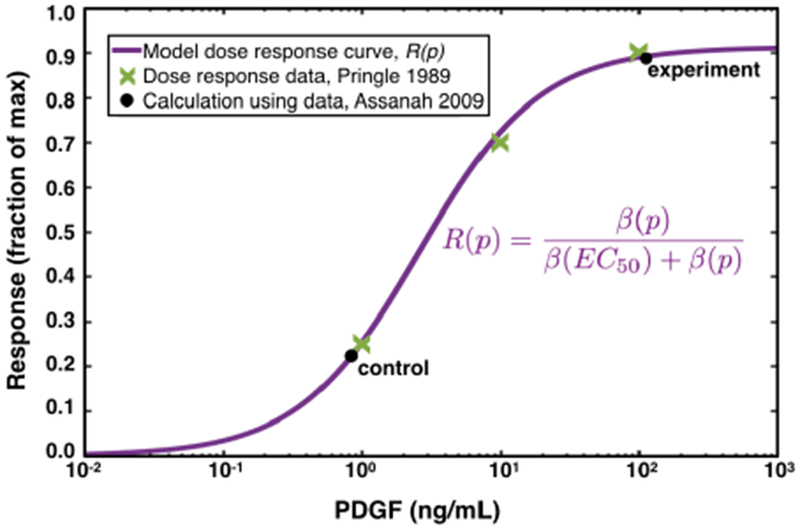
The model dose response curve is shown by the solid purple line, which fits the experimental dose response data from [46] shown by the green Xs. The PDGF concentration due to wounding (10) (which is computed in section 2.3.1), as well as that for the experiment with 100 ng/mL added exogenous PDGF is indicated by the black dots. Notice that the response level of the experiment is four-fold higher than that of the control, as found in [6].
2.2. Parameters
Most parameter values are kept the same as those from the PDGF-driven tumor model (detailed derivation of these may be found in [42] and the associated supplement). As a result, many are OPC–specific; however, since we lack experimental data on the other cell types and are grouping OPCs together with other PDGF–responsive cells, we take these values as an approximation for the features of the combined pool of PDGF–responsive cells in our model. Additionally, we have two new parameters—those describing the dynamics of the PDGF source term, λ and Smax. There are many interacting components that may affect the secretion of PDGF, which we have not attempted to capture. Rather than describing the process exactly, we sought a simple term with as few parameters as possible that still allow us to capture the varied outcomes corresponding to different PDGF secretion dynamics. Because we have not connected these with distinct biological processes and because we wanted to examine the possibilities of a variety of PDGF signal dynamics, we first varied the two parameters over three orders of magnitude. This then allowed us to hone in on a parameter regime that yielded the most physiological results (i.e., PDGF levels remained within experimentally observed levels), which we explore in section 3. Parameters and their values are listed in Table 1.
Table 1: Model Parameters and their Values.
Most of these parameters are derived in [42] and its supplemental material, as noted in the Source column.
| Symbol | Definition | Value | Units | Source |
|---|---|---|---|---|
| Dr | max diffusion rate of recruited cells | 5.8 × 10−5 | [42] | |
| Dp | diffusion rate of PDGF | 5 × 10−4 | [42,57] | |
| ρr | max proliferation rate of recruited cells | [42] | ||
| qr | max rate of PDGF uptake by recruited cells | 10−5.15 | [42] | |
| K | cellular carrying capacity | 2.3 × 108 | [42] | |
| km | [PDGF] at which half max binding occurs | 30 | [42,46] | |
| EC50 | [PDGF] achieving half max dose response | 101/2 | [42] | |
| O2a | baseline population of OPCs in gray matter | 2.2 × 106 | [42] | |
| Smax | maximum PDGF secretion | 10 to 100 | * | |
| λ | decay of PDGF secretion | 0.01 to 0.1 | * |
Indicated parameters were varied across a range of values to explore their effect on simulation outcomes, as discussed in the results (Section 3).
2.3. Initial and Boundary Conditions
For this model, we assume some arbitrary inciting event, such as an injury, sets everything in motion, causing an initial release of PDGF. We start our simulations shortly after PDGF has started to be released, thus avoiding the complexity of simulating the event itself, and use a nonzero initial condition for the PDGF.
2.3.1. Initial PDGF concentration, p0
To estimate the value for p0, we made use of available data on the proliferation rates of cells in brain tissue, with and without added PDGF from an experiment performed by Assanah, et al. [6]. Briefly, this experiment compares cellular proliferation of cells in rat brain tissue in acute slice culture with added exogenous PDGF (experimental condition), and without (control condition). The harvested tissue itself has some level of PDGF due to the injury involved in removing it from the animal. Thus, by comparing the control and experimental conditions, we can estimate the PDGF released by the response to the injury. Specifically, it was observed that adding 100 ng/mL of PDGF to the experimental condition caused an approximately four-fold increase in proliferation rate of OPCs as compared to the control condition.
Interpreting this mathematically, they both start with some baseline amount, which we designate as p0. Then the experimental case is given additional PDGF, so that the control has p0 ng/mL PDGF, and the experimental condition has p0 + 100 ng/mL PDGF. Response is measured in proliferation, a downstream effect of PDGF, so we can use our downstream PDGF effect ratio from equations (3) and (4), which we write here as
| (6) |
where β(p) and β(EC50) are given in equation (5), and we use the parameter values km = 30 ng/mL and (as given in Table 1).
Using this response term in conjunction with the experimental result, we have the relationship
| (7) |
which means “the response to PDGF observed in the experimental case is equal to four times the response observed in the control case.” Note that we could alternatively use the entire proliferation term given in equation (4), but then ρr(1 − r/K) would divide out from both sides, giving the same result. Expanding this relationship using the definition of R(p) in (6), we have:
| (8) |
Through algebraic manipulations (see A for details), we arrive at a quadratic polynomial in p0 with the following roots:
| (9) |
Since the latter of these is non physiologic, we adopt the first root to two decimal places as our approximate value for p0 (accounting for potential measurement error in the experimental data), localized to within 0.03 cm of the site of injury:
| (10) |
This computed value for the PDGF concentration in the control condition, and correspondingly the experimental condition, from the experiment in [6] are plotted against the model dose response curve R(p) in Figure 1.
2.3.2. Initial PDGF-responsive cell density, r0
Given that we are pooling a number of different cell populations together for our PDGF–responsive cells, it is a bit difficult to determine the total number of all the cells that are normally present, particularly those in blood vessel walls. However, OPCs have a widespread presence throughout the normal adult brain. In adult humans, glial progenitors have been estimated to have a relative abundance of about 3–4% [45, 51, 52] of total cells, or 5–8% of all glial cells [34]. If we assume that 3% of estimated normal cellularity of the brain—which is about 80 million cells/mL averaged across all regions in humans [10]—represent glial progenitors, we arrive at approximately 2 × 106. In rat brain tissue, approximately 250 immunofluorescently labeled OPCs were counted in a spherical volume of radius 300 μm = 0.03 cm. This gives us cells/cm3. Evaluating this, and noting that 1 cm3= 1 mL, we get approximately 2.21 × 106 cells/mL. While this is a bit higher than the other estimate for human tissue, it is in the same general order of magnitude, and is likely closer to the total number of PDGF-responsive cells which include more than just OPCs. Thus, we take 2.21 × 106 cells/mL as a reasonable estimate for the average baseline density of PDGF–responsive cells throughout the brain:
| (11) |
2.3.3. Boundary
We take the whole brain as our domain, and the skull as the boundary, as this best matches the actual biological setting. For simplicity, we simulate the model in one dimension, assuming spherical symmetry. Generalizing the volume of the rat brain to a sphere, we find that it is approximately 1 cm in radius. Thus, our domain is x ∊ [0, 1], where we assume that the injury takes place in the center, at x = 0.
Further, we assume that the boundary representing the skull at x = 1 allows neither PDGF nor OPCs to leave the brain, giving us a no-flux boundary condition:
| (12) |
where n denotes the normal vector on the boundary.
2.4. Numerical solution.
We solved the model numerically using the pdepe function in Matlab® (MATLAB Release 2015a, The MathWorks, Inc., Natick, Massachusetts, United States), in one dimension on a spherically symmetric domain, using the boundary conditions and initial conditions given in section 2.3. The pdepe function uses ode15s for time integration, enabling it to handle any stiffness from the diffusion terms by adjusting the time step appropriately. In our simulations, we specified solutions to be recorded at time intervals of half days up to tf = 250 days, and our spatial steps were 1/375 = 0.0027 cm, which is equivalent to 27 μm—slightly more than the diameter of an oligodendroglial progenitor cell. Our codes may be found here: https://github.com/scmassey/varied_paracrine_PDGF_dynamics.
2.5. Thresholding to look at growth.
In order to measure changes in the growth of lesions comprised of recruited PDGF–responsive cells, we defined a threshold for each simulation to help us identify the “leading edge” of the lesion in a way that would accommodate the wide variation in maximum cell densities attained by the lesions across our simulations. To do this, for each simulation, we first found the maximum cell density at any of the spatial locations of our domain at a later time point (after the cells have had some time to build up):
| (13) |
Then, we set our threshold to be 50% of the difference between this maximum and the baseline number of cells above the baseline number of the cells:
| (14) |
Using this threshold we found the outer most location (recalling that our x domain is a radius) where this value was attained or exceeded at all time points for each simulation, and used this information to make growth comparisons.
3. Simulation Results
To explore the effects of varied magnitude and duration of PDGF signaling, we performed simulations across a range of parameter values for the PDGF source term. We varied Smax, the maximum level of PDGF secretion, from 10 to 100 ng/mL/day in increments of 10, and varied λ, the decay rate of PDGF secretion activity, from 0.01 to 0.1 days−1 in increments of 0.01. The output of these 100 simulations are compared in terms of the growth dynamics of the lesions created by cells responding to the PDGF signal, which were most easily visualized in heatmaps. We also looked at the individual simulations from different regions of the heatmaps to better resolve the indicated differences in these dynamics.
3.1. Smaller PDGF secretion activity decay rate, λ, and larger maximum PDGF secretion level, Smax, parameters in PDGF source term cause extensive and chronic growth.
For each simulation, we used the technique described in section 2.5 to determine the outer edge of the lesion at each time point. We then used this to determine the duration of growth for each simulation until either: (a) the lesion reached a fatal size, defined as 0.5 cm radius (inside the black outline in Figures 2A and B), or (b) the growth rate fell below one cell diameter per five days (i.e., 10 μm/ 5 days or 4 × 10−5 cm/day, outside the black outline in Figures 2A and B). Note that due to these different criteria, shorter times inside the black outline in Figure 2A correspond to simulated lesions that achieved a lethal size sooner due to a faster growth rate, while shorter times outside of this black outlined region correspond to simulated lesions whose growth rate slowed to near zero earlier. Looking at the heatmap in Figure 2A, we observe that for smaller decay rates, λ, in combination with higher maximum values for the source concentration, Smax, the resulting higher and persistent PDGF signal causes stimulation of cells for upwards of 40 days. Similar trends are seen in the size of lesions in Figure 2B, with the larger lesions corresponding to smaller values of the decay rate of secretion activity, λ, and larger values of the maximum PDGF secretion level, Smax. It is notable when comparing these two heatmaps that the transition from short growth times to long growth times is more gradual (Figure 2A), while that from small radii to large radii is more sharp Figure 2B).
Fig. 2: Time elapsed until lesion expansion slows to less than one cell diameter in five days or lethal size reached and corresponding lesion sizes at those times.
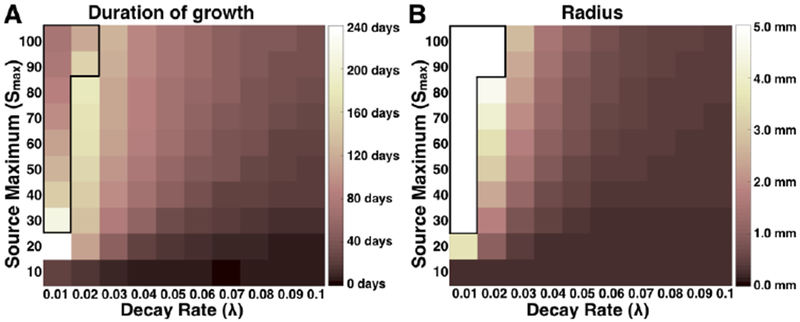
Simulations were run across a range of maximum PDGF source (Smax) and decay rate (λ) parameters until lethal size is reached (defined as 5 mm radius), or until the outward expansion of the 50% cell density region slows to less than one cell diameter in five days (outside of the black outline). The length of time until either criterion has been reached for each simulation is given in (A), and the radii of simulated lesions’ regions of 50% cell density at these times is shown in (B). Higher values correspond with lighter shades, as indicated by the color axes. Values in (A) that are greater than 40 days indicate chronic lesions, and values in (B) that are greater than 1 mm indicate large lesions.
3.2. PDGF secretion activity decay rate, λ, has a more pronounced effect than the maximum PDGF secretion level, Smax.
While both the decay rate and maximum level of PDGF source must work in concert to get very large lesions to form, we see that decay rate is more influential on both the overall size of the lesions of PDGF–responsive cells and the length of time for which that distribution expands radially. This can be seen most clearly from the left-most columns of the heat maps, which correspond to smaller decay rates, λ. The lighter shades indicate greater time duration in Figure 2A and bigger radius in Figure 2B. These appear to cluster in the three left-most columns for all but the smallest value of Smax.
3.3. Paracrine PDGF signaling dynamics lead to three possible growth outcomes.
Combining our results together into one picture, we see three growth regimes caused by the PDGF secretion (Figure 3). Since experimental models of brain injury response have shown reactive OPCs distributed within 0.3 to 2 mm of the site of injury, with rapid OPC division continuing for seven to 14 days [22, 48], we consider active growth continuing beyond 40 days to be “chronic.” We also consider lesions larger than 1 mm in radius to be “large,” since that is 10% of the rat brain radius. The lower right corners of the heatmaps in Figure 2, which are overlaid in Figure 3A as a visual aid, thus correspond to simulated lesions that are small and acute (dark tones). In the middle of these heatmaps, simulated lesions are small but chronic (mid-tones in the overlaid image). The lighter shades in the upper left corner/left–most columns correpond to simulated lesions that are both large and chronic. To see examples of these, we focused on three simulations, one from each of these regions, labeled 1–3 in Figure 3A to indicate the corresponding values of parameters λ and Smax. We plotted the location of the lesion “edge” (the 50% maximum cell density as computed in section 2.5) versus time for three different simulations (Figure 3B). These curves are labeled 1–3 to correspond with simulations indicated in panel A. From these curves, we see that the growth dynamics of simulations in the middle region (labeled 2) yield a small lesion—not much bigger than that from the lower right region (labeled 1)—yet that growth persists for a longer period before lesions stop expanding. The curve labeled 3 is much larger, highlighting the sharp transition from small to large lesions indicated by the heat map in Figure 2B.
Fig. 3: Growth regimes from combined heatmaps and corresponding PDGF concentrations.
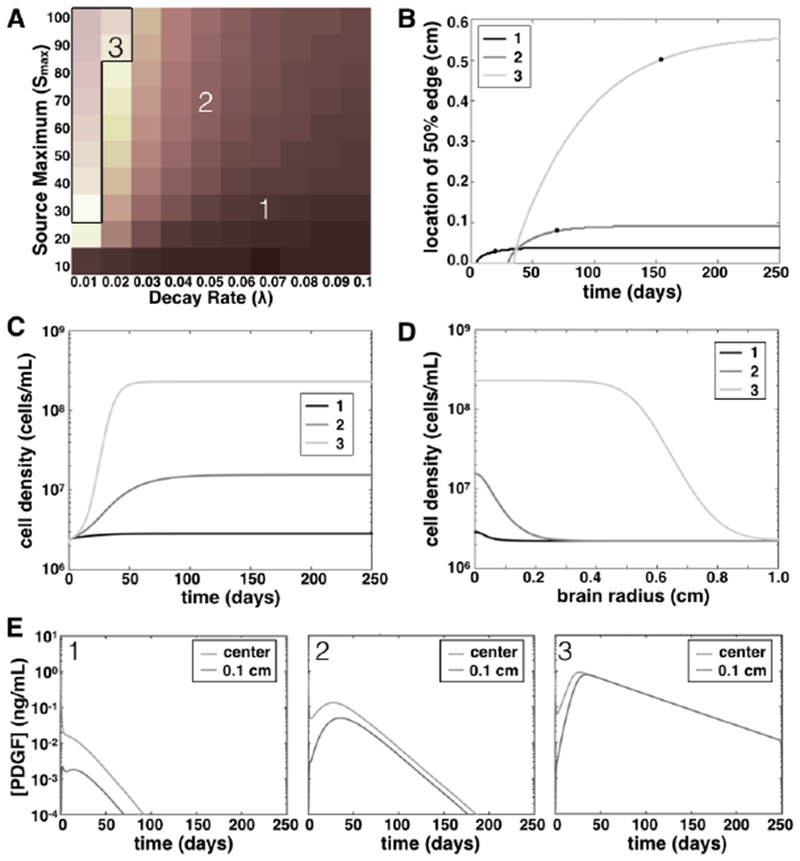
A. Overlaying the heatmaps of Figure 2 create a picture of three growth regimes in our simulations, depending on the PDGF growth parameters: (1) limited growth, short duration; (2) limited growth, long duration; and (3) extensive growth, long duration. The numbered squares correspond to the simulations plotted in panels B–D, as well as the numbered plots in E. B. Curves show the growth of the edge of the 50% cell density region of simulated lesions versus time for three simulations indicated in (A). Black dots show when and what size the simulation was when its growth rate was less than 4 × 10−5 cm/day, or in the case of (3), fatal size was reached. C. Cell density at the center of the lesion (near the inciting event location) versus time, for simulations from the three different growth regimes as indicated in A. D. Cell density at the end of simulation time (250 days) vs radius of the rat brain, our spatial domain, for three simulations as indicated in A. E. Curves show PDGF levels as they change over time at both the center of the domain and at 0.1 cm radius for three different simulations, corresponding with the growth regimes of the same number.
To further illustrate the differences in growth between these three different growth types, we plotted the density of PDGF–responsive cells vs time at the center of the lesion (Figure 3C) and vs the radius of our domain at the end of simulation time (tf = 250 days, Figure 3D). Thus we see that not only is the spatial extent of the lesions of PDGF–responsive cells larger for the small λ values, but also the density of these lesions is larger. The PDGF levels that result from the specified parameter values for these three simulations are plotted in Figure 3E. Note that in these plots of PDGF concentration vs time, the smaller decay rate keeps PDGF levels higher at the end of simulations, but in all cases the PDGF level is maintained below km and EC50. Thus, the large lesions are attained not due to extraordinarily high levels of PDGF, but rather a persistent moderate amount of PDGF.
4. Discussion
Overall, our results suggest that variations in paracrine PDGF secretion can create very dramatic effects in brain tissue. Modulating this paracrine PDGF signal in simulations, we observed three growth regimes, as detailed in results section 3.3. In the first, PDGF is released in response to some signal, causing a short burst of growth for PDGF–receptive cells. This growth is limited both in time and in spatial extent. The second involves a longer duration of elevated PDGF signal, causing a corresponding increase in duration of the PDGF–stimulation of cell growth. However, the spatial extent of this effect in terms of lesion growth is still limited. Finally, in the third regime, there is sustained PDGF secretion at high levels, causing both long time duration and large spatial extent of lesion growth. These various cellular responses to paracrine PDGF that we observe for the different parameter values suggest possible connections with physiological processes. For example, the first type of PDGF signal and response, with small size and short duration, is similar to what we might see in the healing of a small wound, such as a small brain stab injury. The second, with limited size, but longer duration, is perhaps what we might see with an injury healing process that leaves a scar (localized fibrosis or gliosis). The third regime with its more extreme size and time duration might correspond to PDGF signaling in neoplastic processes.
Notably, there are some findings that support these suggested connections. One study looked at brain stab wounds in rodents and found that measurable PDGF-B was noted around days 3 and 4 post injury and that the spatial distribution of the PDGF matched that of the resulting glial scar [56]. Another recent study found that vascular insufficiency led to chronic gliosis in an animal model of brain tissue transplantation [7]. It is quite likely that the sustained levels of angiogenic factors released in response to the insufficiency, including PDGF, caused the recruitment of more than just vascular endothelial and smooth muscle cells, but also oligodendroglial progenitor cells and fibroblasts, which in turn gave rise to the chronic gliosis. Finally, animal studies have shown that increased paracrine PDGF signaling can lead to the formation of tumors that resemble glioblastoma [5,19], and PDGF signaling has been shown to play a role in human glioblastoma [26, 37, 39, 60, 61].
Our model further predicts that the duration of elevated PDGF signal may be generally more impactful than the maximum level of that signal in contributing to tissue pathologies. As a result, this may suggest that incomplete inhibition of PDGF signaling could greatly diminish the efficacy of PDGF–inhibitor therapies against stromal recruitment in tumors, for example, rather than merely a slight reduction in benefit. It also suggests that limiting the duration of PDGF secretion or exposure could be key to reducing the formation of scar tissues. Note that in our model, we did not include an explicit term for PDGF decay, as the consumption rate of PDGF assumed to be much faster given the high abundance of PDGFR+ cells in the brain. However, in models incorporating PDGF–inhibitors, or where there are fewer PDGFR+ cells, it may be important to add a PDGF decay term. Additionally, we modeled PDGFR+ cell movement as a diffusion process since our prior work analyzing PDGF-driven movement of oligodendroglial progenitor cells (perhaps the most abundant PDGFR+ cells in the brain) in acute slice culture showed movement that was most consistent with a directed random walk along white matter tracts [30, 31, 41, 42]. Models that focus on other types of PDGFR+ cells or that seek to account for the precise location of an injury or inflammatory response may require the implementation of chemotactic effects and/or gray vs white matter effects (if in brain) to account for anisotropic movement of cells, which has been implemented for brain tumors in [54, 55]. Future models seeking to incorporate the complex determinants of PDGF secretion would do well to focus on the temporal aspects of those upstream processes in order to have the maximal impact on patient outcomes. As noted in the methods, we took a more “downstream” approach and parameterized our initial value of PDGF due to an insult by relying on available data from an acute slice culture experiment reported in Assanah, et al. [6] (the acute slice culture technique has also been used in [18, 32, 53], primarily to study cellular migration in tissue). This particular experiment was originally done to demonstrate the effect of applied PDGF-BB in greatly increasing cellular proliferation, but it was also useful for our purposes due to the injury process of tissue harvest and the nature of the experiment, which kept the tissue alive in culture. Others may find similar utility in repurposing data from previously conducted experiments, as it is not always practical or even possible to create bespoke experiments to parameterize mathematical models.
Since PDGF recruits oligodendroglial progenitors, fibroblasts, and vascular endothelial cells in the brain, there could be implications for angiogenesis and fibrotic changes—i.e., not just the extent of response and its chronicity, but also the “badness” of the resulting affected tissue. Further, it seems likely that similar results may be found for other tissues as well as for other growth factors. Recent studies have shown that stromal changes such as fibrosis can drive tumor invasion [15], and there have even been case reports of patients with traumatic brain injuries that years later become sites of glioblastoma, most recently in Tyagi, et al. [58]. These highlight the need to better understand normal stromal function in tissues, and mathematical models further exploring this interplay between a variety of growth factors and stromal cell types could be especially useful for the medical community moving forward. Antiangiogenic therapies (which inhibit growth factor receptors) given to cancer patients have sometimes caused severe side effects, including hypertension, skin lesions, intestinal perforations, hemorrhaging, and even heart failure [14, 17]. On the other hand PDGF and other growth factors given to surgical patients to facilitate healing [3,9,63] could potentially lead to scarring or worse. PDGF and other growth factors are already being manipulated in human patients in the clinic, without fully understanding how to balance its effects—more research is needed to ensure that future growth factor–modulating therapies are optimized for patients’ needs.
Acknowledgments
This material is based upon work supported by the National Science Foundation Graduate Research Fellowship Program under Grant No. DGE-0781824, the James S. McDonnell Foundation Collaborative Activity Award #220020264, the National Institutes of Health (U01CA220378, U54CA210180, U54CA143970, U54CA193489, R01NS060752, R01CA16437, P01CA42045), the Ben and Catherine Ivy Foundation, the University of Washington Academic Pathology Fund, the James D. Murray Endowed Chair in the Nancy and Buster Alvord Brain Tumor Center at the University of Washington. The content is solely the responsibility of the authors. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation or any other supporting agencies. As always, KRS is eternally grateful to the unwavering support of Dr. E. C. “Buster” Alvord, Jr (1923—2010); may this manuscript continue to honor his memory and foster his scientific legacy.
A. Details of derivation of p0
Recall from Section 2.3 that we have the following relationship:
| (15) |
which describes the increased activity of one condition of cells that has added exogenous PDGF relative to others that lack this added PDGF. Given that they are still active, and have been injured during tissue removal, we assume that there is a shared baseline amount of PDGF, p0.
Expanding this relationship using the definition of R(p) in (6), we have:
| (16) |
| (17) |
Since β(EC50) is a constant, for notational simplicity we set γ = β(EC50) throughout the following algebra. This lets us write
| (18) |
Then we can cross multiply the denominators and expand the β terms:
| (19) |
| (20) |
| (21) |
Move all terms to one side for simplicity:
| (22) |
Now, multiply both sides by km + p0 and km + p0 + 100:
| (23) |
Expanding and then collecting by powers of p0:
| (24) |
| (25) |
| (26) |
Now we can use the quadratic formula to find the roots of this equation, letting
| (27) |
| (28) |
| (29) |
for the formula
Recalling that we use parameter values km = 30 ng/mL and , such that , this computes to (in decimal approximation):
| (30) |
The latter of these does not make sense as a physical quantity, so we adopt the first as our approximate value for p0:
| (31) |
Footnotes
Publisher's Disclaimer: This Author Accepted Manuscript is a PDF file of an unedited peer-reviewed manuscript that has been accepted for publication but has not been copyedited or corrected. The official version of record that is published in the journal is kept up to date and so may therefore differ from this version.
Contributor Information
Susan Christine Massey, Precision Neurotherapeutics Innovation Program, Mayo Clinic, 5777 E Mayo Blvd, Phoenix, AZ 85054, tel:480-342-3930, massey.susan@mayo.edu.
Andrea Hawkins-Daarud, Precision Neurotherapeutics Innovation Program, Mayo Clinic, Phoenix, AZ.
Jill Gallaher, Integrative Mathematical Oncology, Moffitt Cancer Center, Tampa, FL.
Alexander R. A. Anderson, Integrative Mathematical Oncology, Moffitt Cancer Center, Tampa, FL
Peter Canoll, Division of Neuropathology, Department of Pathology and Cell Biology, Columbia University School of Medicine, New York, NY.
Kristin R. Swanson, Precision Neurotherapeutics Innovation Program, Mayo Clinic, Phoenix, AZ
References
- 1.Allamargot C, Pouplard-Barthelaix A, Fressinaud C: A single intracerebral microinjection of platelet-derived growth factor (pdgf) accelerates the rate of remyelination in vivo. Brain research 918(1), 28–39 (2001). DOI 10.1016/S0006-8993(01)02761-5 [DOI] [PubMed] [Google Scholar]
- 2.Andrae J, Gallini R, Betsholtz C: Role of platelet-derived growth factors in physiology and medicine. Genes & development 22(10), 1276–1312 (2008). DOI 10.1101/gad.1653708 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Andrew J, Hoyland J, Freemont A, Marsh D: Platelet-derived growth factor expression in normally healing human fractures. Bone 16(4), 455–460 (1995). DOI 10.1016/8756-3282(95)90191-4 [DOI] [PubMed] [Google Scholar]
- 4.Apperley JF, Gardembas M, Melo JV, Russell-Jones R, Bain BJ, Baxter EJ, Chase A, Chessells JM, Colombat M, Dearden CE, Dimitrijevic S, Mahon FX, Marin D, Nikolova Z, Olavarria E, Silberman S, Schultheis B, Cross NC, Goldman JM: Response to imatinib mesylate in patients with chronic myeloproliferative diseases with rearrangements of the platelet-derived growth factor receptor beta. New England Journal of Medicine 347(7), 481–487 (2002). DOI 10.1056/NEJMoa020150 PMID: [DOI] [PubMed] [Google Scholar]
- 5.Assanah M, Lochhead R, Ogden A, Bruce J, Goldman J, Canoll P: Glial progenitors in adult white matter are driven to form malignant gliomas by platelet-derived growth factor-expressing retroviruses. J Neurosci 26(25), 6781–90 (2006). DOI 10.1523/jneurosci.0514-06.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Assanah MC, Bruce JN, Suzuki SO, Chen A, Goldman JE, Canoll P: Pdgf stimulates the massive expansion of glial progenitors in the neonatal forebrain. Glia (2009). DOI 10.1002/glia.20895 [DOI] [PubMed] [Google Scholar]
- 7.Bates KA, Drummond ES, Cozens GS, Harvey AR: Vascular insufficiency, not inflammation, contributes to chronic gliosis in a rat cns transplantation model. Restorative neurology and neuroscience 34(2), 313–323 (2016). DOI 10.3233/RNN-150591 [DOI] [PubMed] [Google Scholar]
- 8.Betsholtz C: Biology of platelet-derived growth factors in development. Birth Defects Research Part C: Embryo Today: Reviews 69(4), 272–285 (2003). DOI 10.1002/bdrc.10030 [DOI] [PubMed] [Google Scholar]
- 9.Bissell L, Tibrewal S, Sahni V, S Khan W: Growth factors and platelet rich plasma in anterior cruciate ligament reconstruction. Current stem cell research & therapy 10(1), 19–25 (2015) [DOI] [PubMed] [Google Scholar]
- 10.Blinkov SM, Glezer II: The human brain in figures and tables: a quantitative handbook. Basic Books; (1968) [Google Scholar]
- 11.Boor P, Ostendorf T, Floege J: Pdgf and the progression of renal disease. Nephrology Dialysis Transplantation 29(suppl 1), i45–i54 (2014). DOI 10.1093/ndt/gft273 [DOI] [PubMed] [Google Scholar]
- 12.Boucher P, Gotthardt M: Lrp and pdgf signaling: a pathway to atherosclerosis. Trends in cardiovascular medicine 14(2), 55–60 (2004). DOI 10.1016/j.tcm.2003.12.001 [DOI] [PubMed] [Google Scholar]
- 13.Campbell JS, Hughes SD, Gilbertson DG, Palmer TE, Holdren MS, Haran AC, Odell MM, Bauer RL, Ren HP, Haugen HS, Yeh MM, Fausto N: Platelet-derived growth factor c induces liver fibrosis, steatosis, and hepatocellular carcinoma. Proceedings of the National Academy of Sciences of the United States of America 102(9), 3389–3394 (2005). DOI 10.1073/pnas.0409722102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chintalgattu V, Ai D, Langley RR, Zhang J, Bankson JA, Shih TL, Reddy AK, Coombes KR, Daher IN, Pati S, Patel SS, Pocius JS, Taffet GE, Buja LM, Entman ML, Khakoo AY: Cardiomyocyte pdgfr-signaling is an essential component of the mouse cardiac response to load-induced stress. The Journal of Clinical Investigation 120(2), 472–484 (2010). DOI 10.1172/JCI39434 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.De Wever O, Demetter P, Mareel M, Bracke M: Stromal myofibroblasts are drivers of invasive cancer growth. International journal of cancer 123(10), 2229–2238 (2008). DOI 10.1002/ijc.23925 [DOI] [PubMed] [Google Scholar]
- 16.Demoulin JB, Essaghir A: Pdgf receptor signaling networks in normal and cancer cells. Cytokine & growth factor reviews 25(3), 273–283 (2014). DOI 10.1016/j.cytogfr.2014.03.003 [DOI] [PubMed] [Google Scholar]
- 17.Eschenhagen T, Force T, Ewer MS, de Keulenaer GW, Suter TM, Anker SD, Avkiran M, de Azambuja E, Balligand JL, Brutsaert DL, Condorelli G, Hansen A, Heymans S, Hill JA, Hirsch E, Hilfiker-Kleiner D, Janssens S, de Jong S, Neubauer G, Pieske B, Ponikowski P, Pirmohamed M, Rauchhaus M, Sawyer D, Sugden PH, Wojta J, Zannad F, Shah AM: Cardiovascular side effects of cancer therapies: a position statement from the heart failure association of the european society of cardiology. European Journal of Heart Failure 13(1), 1–10 (2011). DOI 10.1093/eurjhf/hfq213 [DOI] [PubMed] [Google Scholar]
- 18.Farin A, Suzuki SO, Weiker M, Goldman JE, Bruce JN, Canoll P: Transplanted glioma cells migrate and proliferate on host brain vasculature: a dynamic analysis. Glia 53(8), 799–808 (2006). DOI 10.1002/glia.20334 [DOI] [PubMed] [Google Scholar]
- 19.Fomchenko EI, Holland EC: Platelet-derived growth factor-mediated gliomagenesis and brain tumor recruitment. Neurosurg Clin N Am 18(1), 39–58, viii (2007). DOI 10.1016/j.nec.2006.10.006 [DOI] [PubMed] [Google Scholar]
- 20.Frost EE, Zhou Z, Krasnesky K, Armstrong RC: Initiation of oligodendrocyte progenitor cell migration by a pdgf-a activated extracellular regulated kinase (erk) signaling pathway. Neurochem Res 34(1), 169–181 (2009). DOI 10.1007/s11064-008-9748-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gerhardt H, Betsholtz C: Endothelial-pericyte interactions in angiogenesis. Cell and tissue research 314(1), 15–23 (2003). DOI 10.1007/s00441-003-0745-x [DOI] [PubMed] [Google Scholar]
- 22.Hampton D, Rhodes K, Zhao C, Franklin R, Fawcett J: The responses of oligodendrocyte precursor cells, astrocytes and microglia to a cortical stab injury, in the brain. Neuroscience 127(4), 813–820 (2004). DOI 10.1016/j.neuroscience.2004.05.028 [DOI] [PubMed] [Google Scholar]
- 23.Hanahan D, Coussens LM: Accessories to the crime: functions of cells recruited to the tumor microenvironment. Cancer cell 21(3), 309–322 (2012). DOI 10.1016/j.ccr.2012.02.022 [DOI] [PubMed] [Google Scholar]
- 24.Hayes BJ, Riehle KJ, Shimizu-Albergine M, Bauer RL, Hudkins KL, Johansson F, Yeh MM, Mahoney WM Jr, Yeung RS, Campbell JS: Activation of platelet-derived growth factor receptor alpha contributes to liver fibrosis. PloS one 9(3), e92, 925 (2014). DOI 10.1371/journal.pone.0092925 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Heldin CH, Westermark B: Mechanism of action and in vivo role of platelet-derived growth factor. Physiological Reviews 79(4), 1283–1316 (1999). DOI 10.1152/physrev.1999.79.4.1283 [DOI] [PubMed] [Google Scholar]
- 26.Hermanson M, Funa K, Hartman M, Claesson-Welsh L, Heldin CH, Westermark B, Nistér M: Platelet-derived growth factor and its receptors in human glioma tissue: Expression of messenger rna and protein suggests the presence of autocrine and paracrine loops. Cancer Research 52(11), 3213–3219 (1992). URL http://cancerres.aacrjournals.org/content/52/11/3213 [PubMed] [Google Scholar]
- 27.van Heyningen P, Calver AR, Richardson WD: Control of progenitor cell number by mitogen supply and demand. Current Biology 11, 232–241 (2001). DOI 10.1016/S0960-9822(01)00075-6 [DOI] [PubMed] [Google Scholar]
- 28.Hoch RV, Soriano P: Roles of pdgf in animal development. Development 130(20), 4769–4784 (2003). DOI 10.1242/dev.00721 [DOI] [PubMed] [Google Scholar]
- 29.Ingram JL, Rice AB, Geisenhoffer K, Madtes DK, Bonner JC: Il-13 and il-1β promote lung fibroblast growth through coordinated up-regulation of pdgf-aa and pdgf-rα. The FASEB journal 18(10), 1132–1134 (2004). DOI 10.1096/fj.03-1492fje [DOI] [PubMed] [Google Scholar]
- 30.Ivkovic S, Beadle C, Noticewala S, Massey SC, Swanson KR, Toro LN, Bresnick AR, Canoll P, Rosenfeld SS: Direct inhibition of myosin II effectively blocks glioma invasion in the presence of multiple motogens. Molecular Biology of the Cell 23(4), 533–542 (2012). DOI 10.1091/mbc.e11-01-0039 URL [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Juliano J, Gil O, Hawkins-Daarud A, Noticewala S, Rockne RC, Gallaher J, Massey SC, Sims PA, Anderson AR, Swanson KR, et al. : Comparative dynamics of microglial and glioma cell motility at the infiltrative margin of brain tumours. Journal of The Royal Society Interface 15(139), 20170, 582 (2018). DOI 10.1098/rsif.2017.0582 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kakita A, Goldman JE: Patterns and dynamics of svz cell migration in the postnatal forebrain: monitoring living progenitors in slice preparations. Neuron 23(3), 461–472 (1999). DOI 10.1016/S0896-6273(00)80800-4 [DOI] [PubMed] [Google Scholar]
- 33.Kohler N, Lipton A: Platelets as a source of fibroblast growth-promoting activity. Experimental cell research 87(2), 297–301 (1974). DOI 10.1016/0014-4827(74)90484-4 [DOI] [PubMed] [Google Scholar]
- 34.Levine JM, Reynolds R, Fawcett JW: The oligodendrocyte precursor cell in health and disease. Trends in Neurosciences 24(1), 39–47 (2001). DOI 10.1016/S0166-2236(00)01691-X [DOI] [PubMed] [Google Scholar]
- 35.Li H, Fan X, Houghton J: Tumor microenvironment: the role of the tumor stroma in cancer. Journal of cellular biochemistry 101(4), 805–815 (2007). DOI 10.1002/jcb.21159 [DOI] [PubMed] [Google Scholar]
- 36.Lindmark G, Sundberg C, Glimelius B, Påhlman L, Rubin K, Gerdin B: Stromal expression of platelet-derived growth factor beta-receptor and platelet-derived growth factor b-chain in colorectal cancer. Laboratory investigation; a journal of technical methods and pathology 69(6), 682–689 (1993). URL http://europepmc.org/abstract/MED/8264231 [PubMed] [Google Scholar]
- 37.Lopez K, Assanah M, Waziri A, Fusco D, Tannenbaum A, Linskey K, McKhann GM, Sisti MB, Bruce J, Canoll P: Human glioma cells recruit and expand adult glial progenitors via paracrine platelet-derived growth factor signaling. Neurosurgery 62(6), 1424–1425 (2008). DOI 10.1227/01.neu.0000333529.85150.cf [DOI] [Google Scholar]
- 38.Majesky MW, Reidy MA, Bowen-Pope DF, Hart CE, Wilcox JN, Schwartz SM: Pdgf ligand and receptor gene expression during repair of arterial injury. The Journal of Cell Biology 111(5), 2149–2158 (1990). DOI 10.1083/jcb.111.5.2149 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Majumdar K, Radotra BD, Vasishta RK, Pathak A: Platelet-derived growth factor expression correlates with tumor grade and proliferative activity in human oligodendrogliomas. Surgical neurology 72(1), 54–60 (2009). DOI 10.1016/j.surneu.2008.10.001 [DOI] [PubMed] [Google Scholar]
- 40.Masliah E, Mallory M, Alford M, Deteresa R, Saitoh T: Pdgf is associated with neuronal and glial alterations of alzheimer’s disease. Neurobiology of aging 16(4), 549–556 (1995). DOI 10.1016/0197-4580(95)00050-O [DOI] [PubMed] [Google Scholar]
- 41.Massey SC: Multi-scale modeling of paracrine pdgf-driven glioma growth and invasion. Ph.D. thesis (2017). URLhttps://digital.lib.washington.edu/researchworks/handle/1773/38058 [Google Scholar]
- 42.Massey SC, Assanah MC, Lopez KA, Canoll P, Swanson KR: Glial progenitor cell recruitment drives aggressive glioma growth: mathematical and experimental modelling. Journal of The Royal Society Interface 9(73), 1757–1766 (2012). DOI 10.1098/rsif.2012.0030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Massey SC, Rockne RC, Hawkins-Daarud A, Gallaher J, Anderson ARA, Canoll P, Swanson KR: Simulating pdgf-driven glioma growth and invasion in an anatomically accurate brain domain. Bulletin of Mathematical Biology 80(5), 1292–1309 (2018). DOI 10.1007/s11538-017-0312-3 [DOI] [PubMed] [Google Scholar]
- 44.Nakamura Y, Tanaka F, Yoshikawa Y, Mimori K, Inoue H, Yanaga K, Mori M: Pdgf-bb is a novel prognostic factor in colorectal cancer. Annals of surgical oncology 15(8), 2129–2136 (2008). DOI 10.1245/s10434-008-9943-9 [DOI] [PubMed] [Google Scholar]
- 45.Nunes MC, Roy NS, Keyoung HM, Goodman RR, McKhann G, Jiang L, Kang J, Nedergaard M, Goldman SA: Identification and isolation of multipotential neural progenitor cells from the subcortical white matter of the adult human brain. Nature Medicine 9(4), 439–447 (2003). DOI 10.1038/nm837 [DOI] [PubMed] [Google Scholar]
- 46.Pringle N, Collarini EJ, Mosley MJ, Heldin CH, Westermark B, Richardson WD: Pdgf a chain homodimers drive proliferation of bipotential (o-2a) glial progenitor cells in the developing rat optic nerve. The EMBO journal 8(4), 1049 (1989). DOI 10.1002/j.1460-2075.1989.tb03472.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Redwine JM, Armstrong RC: In vivo proliferation of oligodendrocyte progenitors expressing pdgfar during early remyelination. Journal of neurobiology 37(3), 413–428 (1998). DOI 10.1002/(SICI)1097-4695(19981115)37:3(413::AID-NEU7)3.0.CO;2-8 [DOI] [PubMed] [Google Scholar]
- 48.Rhodes K, Raivich G, Fawcett J: The injury response of oligodendrocyte precursor cells is induced by platelets, macrophages and inflammation-associated cytokines. Neuroscience 140(1), 87–100 (2006). DOI 10.1016/j.neuroscience.2006.01.055 [DOI] [PubMed] [Google Scholar]
- 49.Ross R, Glomset J, Kariya B, Harker L: A platelet-dependent serum factor that stimulates the proliferation of arterial smooth muscle cells in vitro. Proceedings of the National Academy of Sciences 71(4), 1207–1210 (1974). DOI 10.1073/pnas.71.4.1207 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Ross R, Raines EW, Bowen-Pope DF: The biology of platelet-derived growth factor. Cell 46(2), 155–169 (1986). DOI 10.1016/0092-8674(86)90733-6 [DOI] [PubMed] [Google Scholar]
- 51.Roy NS, Wang S, Harrison-Restelli C, Benraiss A, Fraser RAR, Gravel M, Braun PE, Goldman SA: Identification, isolation, and promoter-defined separation of mitotic oligodendrocyte progenitor cells from the adult human subcortical white matter. The Journal of Neuroscience 19(22), 9986–9995 (1999). DOI 10.1523/JNEUROSCI.19-22-09986.1999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Scolding N, Franklin R, Stevens S, Heldin CH, Compston A, Newcombe J: Oligodendrocyte progenitors are present in the normal adult human cns and the lesions of multiple sclerosis. Brain 121(12), 2221–2228 (1998). DOI 10.1093/brain/121.12.2221 [DOI] [PubMed] [Google Scholar]
- 53.Suzuki SO, Goldman JE: Multiple cell populations in the early postnatal subventricular zone take distinct migratory pathways: a dynamic study of glial and neuronal progenitor migration. Journal of Neuroscience 23(10), 4240–4250 (2003). DOI 10.1523/JNEUROSCI.23-10-04240.2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Swan A, Hillen T, Bowman JC, Murtha AD: A patient-specific anisotropic diffusion model for brain tumour spread. Bulletin of mathematical biology 80(5), 1259–1291 (2018). DOI 10.1007/s11538-017-0271-8 [DOI] [PubMed] [Google Scholar]
- 55.Swanson KR, Alvord EC Jr, Murray J: A quantitative model for differential motility of gliomas in grey and white matter. Cell proliferation 33(5), 317–329 (2000). DOI 10.1046/j.1365-2184.2000.00177.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Takayama S, Sasahara M, Iihara K, Handa J, Hazama F: Platelet-derived growth factor b-chain-like immunoreactivity in injured rat brain. Brain research 653(1), 131–140 (1994). DOI 10.1016/0006-8993(94)90381-6 [DOI] [PubMed] [Google Scholar]
- 57.Thorne RG, Hrabètovä S, Nicholson C: Diffusion of epidermal growth factor in rat brain extracellular space measured by integrative optical imaging. Journal of Neurophysiology 92(6), 3471–3481 (2004). DOI 10.1152/jn.00352.2004 [DOI] [PubMed] [Google Scholar]
- 58.Tyagi V, Theobald J, Barger J, Bustoros M, Bayin NS, Modrek AS, Kader M, Anderer EG, Donahue B, Fatterpekar G, et al. : Traumatic brain injury and subsequent glioblastoma development: Review of the literature and case reports. Surgical Neurology International 7 (2016). DOI 10.4103/2152-7806.189296 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Ustach CV, Huang W, Conley-LaComb MK, Lin CY, Che M, Abrams J, Kim HRC: A novel signaling axis of matriptase/pdgf-d/-pdgfr in human prostate cancer. Cancer Research 70(23), 9631–9640 (2010). DOI 10.1158/0008-5472.CAN-10-0511 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.van der Valk P, Lindeman J, Kamphorst W: Growth factor profiles of human gliomas: Do non-tumour cells contribute to tumour growth in glioma? Annals of Oncology 8(10), 1023–1029 (1997). DOI 10.1023/A:1008265905505 [DOI] [PubMed] [Google Scholar]
- 61.Westermark B, Heldin CH, Nister M: Platelet-derived growth factor in human glioma. Glia 15(3), 257–63 (1995). DOI 10.1002/glia.440150307 [DOI] [PubMed] [Google Scholar]
- 62.Wright JH, Johnson MM, Shimizu-Albergine M, Bauer RL, Hayes BJ, Surapisitchat J, Hudkins KL, Riehle KJ, Johnson SC, Yeh MM, et al. : Paracrine activation of hepatic stellate cells in platelet-derived growth factor c transgenic mice: Evidence for stromal induction of hepatocellular carcinoma. International Journal of Cancer 134(4), 778–788 (2014). DOI 10.1002/ijc.28421 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Younger A, Wing K, Penner M, Cresswell M: A study to evaluate the safety of platelet-derived growth factor for treatment of osteochondral defects of the talus. Knee Surgery, Sports Traumatology, Arthroscopy 24(4), 1250–1258 (2016). DOI 10.1007/s0016 [DOI] [PMC free article] [PubMed] [Google Scholar]


