Estimation for an Accelerated Failure Time Model with Intermediate States as Auxiliary Information

Abstract

The accelerated failure time (AFT) model is a common method for estimating the effect of a covariate directly on a patient’s survival time. In some cases, death is the final (absorbing) state of a progressive multi-state process, however when the survival time for a subject is censored, traditional AFT models ignore the intermediate information from the subject’s most recent disease state despite its relevance to the mortality process. We propose a method to estimate an AFT model for survival time to the absorbing state that uses the additional data on intermediate state transition times as auxiliary information when a patient is right censored. The method extends the Gehan AFT estimating equation by conditioning on each patient’s censoring time and their disease state at their censoring time. With simulation studies, we demonstrate that the estimator is empirically unbiased, and can improve efficiency over commonly used estimators that ignore the intermediate states.

1. Introduction

In many chronic diseases, patients move through a series of progressively worsening disease states until a primary failure such as death. Further, in clinical studies of progressive diseases, we often will not know every subject’s failure time because many are lost to follow-up or do not fail within the time period of the study. We may, however, also have information on their disease course recorded up to their last follow-up time. For a clinical study of a progressive disease, we will provide an estimator for the effect on survival time that incorporates the information from these intermediate disease states as auxiliary information in a manner relevant to the primary failure. When there are relatively few observed primary failures in the study, it can be challenging to precisely estimate this effect. The goal of this paper is to utilize the intermediate states to get a more precise and holistic estimate of the treatment effect.

The proportional hazards model has been used to obtain estimates of a survival treatment effect with auxiliary information, for example in Lu and Tsiatis (2008). While the PH model is useful for testing and hazard ratio estimation, the estimate does not have a direct interpretation in terms of the survival time for a subject. Alternatively, the estimate for an accelerated failure time (AFT) model has the straightforward interpretation of the treatment accelerating (or decelerating) the average time to failure. This makes it an appealing alternative to the proportional hazards model.

The standard semiparametric AFT model relates the covariates to the logarithm of the survival time through the following regression model:

$$log\left(T_i\right)={\beta }_0^{\prime }{X}_i+{\epsilon }_i$$ (1)

where T_i is the failure time for subject i, ε_i are i.i.d. with unspecified distribution function F, β₀ is a vector of parameters, and X_i is a vector of covariates.

Several methods for estimating parameters of the semiparametric AFT model arose from treating the censored data linear rank tests as estimating equations (Prentice 1978; Tsiatis 1990). These linear rank tests include the popular log-rank (Mantel 1966; Cox 1972), Peto-Peto (Peto and Peto 1972), and Gehan (1965) tests. The weighted-log rank test with the Gehan weight has become a particularly attractive estimating function due to properties that make it more practical for model fitting than other methods. Fygenson and Ritov (1994) showed that this estimating equation is monotone in each component of β, and Jin et al. (2003) developed an algorithm using linear programming to reliably estimate the parameters in multidimensional settings. Further, the Gehan function is amenable to smooth approximations, which allows for computationally simpler parameter and variance estimation (Brown and Wang 2007; Heller 2007).

These estimators for AFT models are based on univariate failure times, so they need to be modified to incorporate the intermediate states. Under the same premise of using linear rank tests as estimating equations, we propose estimating the AFT parameters based on a recent extension of the Gehan test statistic proposed by Ramchandani et al. (2015) that accounts for the observation of intermediate events, such as disease progression, among censored subjects. The test statistic modifies the Gehan test by estimating probabilities for each subject surviving longer than each of the other subjects conditional on their follow-up times and their last observed disease states. These probabilities are estimated using multi-state models, and allow us to compute the expected Wilcoxon ranks of survival for each subject conditional on what we observe. The idea is to obtain more precise parameter estimates by using intermediate disease status as additional information to the usual death and censoring times. This allows us to meaningfully include the intermediate transitions into parameter estimation while not allowing them to dominate the estimator. The key assumption that we have to make in order to obtain interpretable parameter estimates is that each transition of the process, in addition to the total time from origin to the absorbing failure, follows an accelerated failure time model. The AFT model is a natural one to use in this case because of its straightforward interpretation in terms of linearly accelerating or decelerating a disease process.

In section 2, we will describe the model under which we are operating, and provide a formulation of the proposed estimating equation under the assumption that the probabilities were known. We will then describe the Aalen-Johansen estimator, which we use to estimate the probabilities. We follow by proposing a method for estimating the variance of the parameters based on a Monte Carlo smoothing method given by Jin et al. (2014). In section 3, we describe the simulation studies. We illustrate the method on a clinical trial for Amyotrophic Lateral Sclerosis (ALS) in section 4, and conclude with a discussion in section 5.

2. Methods

Suppose T_i is a failure time, and C_i the independent right censoring time for subject i; let Y_i=min(T_i,C_i), $e_i^{\beta }=log\left(Y_i\right)-{\beta }^{\prime }{X}_i$ (the observed residual), and δ_i =I(T_i≤C_i),i=1, …,n. The Fygenson-Ritov (Gehan) estimating equation for fitting the semiparametric accelerated failure time model is given by:

$$U_G\left(\beta \right)=\frac{1}{n^2}\sum _{i=1}^n\sum _{j=1}^n{\delta }_i\left(X_i-X_j\right)I\left(e_i^{\beta }<e_j^{\beta }\right)=0$$ (2)

With a binary covariate, this equation is simply the Gehan-Wilcoxon test applied to the observed residuals, and counts all the pairs for which we know that $log\left(T_i\right)-{\beta }^{\prime }{X}_i<log\left(T_j\right)-{\beta }^{\prime }{X}_j$, i.e. that the failure time residual for one individual is less than the failure time residual for another. However, we can possibly get better precision if all pairs of residuals, whether uncensored or censored, contribute to the statistic in a meaningful way. The idea is to base an estimating equation on the expected scores of U_G(β) conditional on what we observe. Let ${\tilde{e}}_i^{\beta }=log\left(T_i\right)-X_i^{\prime }\beta$ denote the possibly unobserved failure time residual for individual i. A straightforward modification to the above estimating equation (2) would be:

$$U_E\left(\beta \right)=\frac{1}{n^2}\sum _{i=1}^n\sum _{j=1}^n\left(X_i-X_j\right)P\left({\tilde{e}}_i^{\beta }<{\tilde{e}}_j^{\beta }|e_i^{\beta },e_j^{\beta },{\delta }_i,{\delta }_j\right)=0$$ (3)

where $P\left({\tilde{e}}_i^{\beta }<{\tilde{e}}_j^{\beta }|e_i^{\beta },e_j^{\beta },{\delta }_i,{\delta }_j\right)$ represents the probability that the failure time residual for subject i is less than that of subject j, conditional on each of their residual follow-up times and their failure status. This estimating equation is related to Efron’s modification of the Gehan-Wilcoxon test (1967). Another way to think of the conditional probabilities in (3) is in terms of disease states. In the above setting, we are in the simple case of two disease states: alive and dead, with δ_i the indicator for the latter. However, if we are in the setting of a chronic disease where individuals pass through multiple states on the way to failure, we can condition the above probabilities on the disease states of the individuals at each of their last observed times to get a more precise estimate of the model parameters. Examples of this type of intermediate data include cancer stage progression, neurodegeneration from ALS, and Alzheimer’s disease transitioning from mild to severe. This can be an especially useful extension for studies with relatively low failure rates over long periods of time.

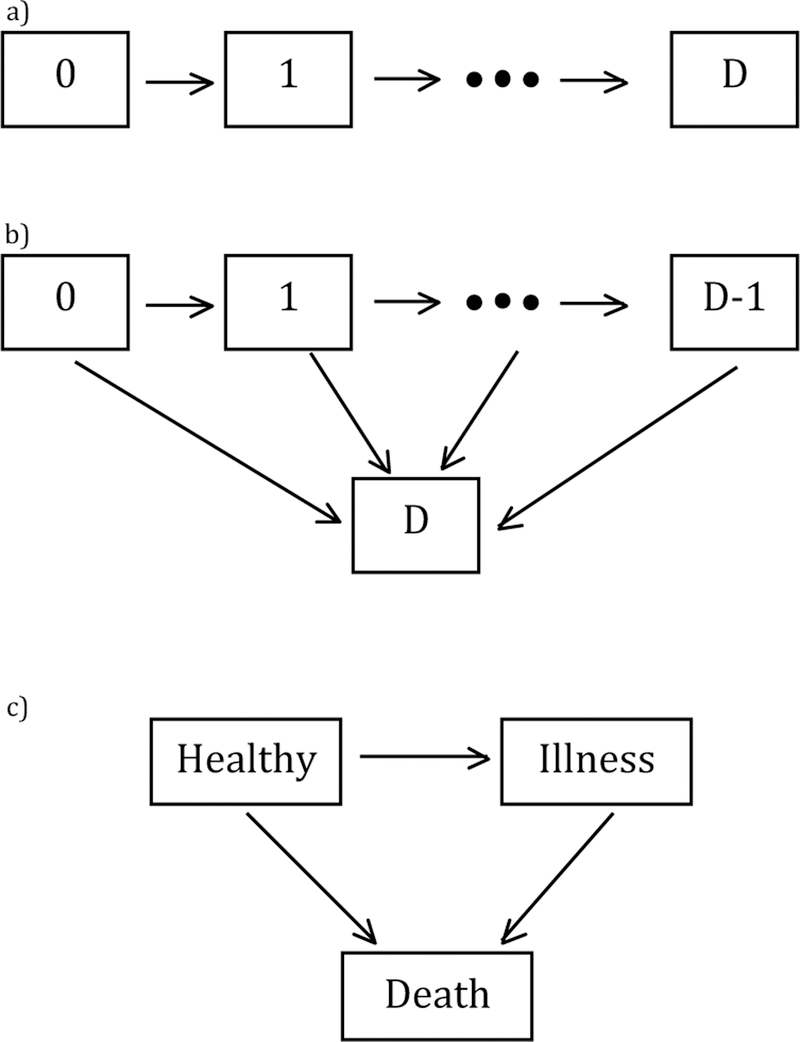
To develop this idea more precisely, suppose individuals move through a finite set of states S ={0,1,2,…,D} governed by a progressive multi-state process, where 0 is the initial state, D represents the single absorbing state, and that transitions to each state are observed exactly. We will consider progressive models of the forms given in Figure 1, and assume that the structure of the model is known and correctly specified. Let S_i(t) denote the state of individual i at time t, let T_i,gh denote the random variable for the transition time for individual i from state g to state h, where g ϵ {0,1,…,D-1}, h ϵ {1,2,…D}, and h > g. Let T_i be the absorbing failure time for individual i (i.e the time from origin to the absorbing state) We will assume that each transition from one state to another follows an AFT model, i.e. $log\left(T_{i,gh}\right)={\beta }_{gh}^{\prime }{X}_i+{\epsilon }_{i,gh}$, where the ε_i,gh are i.i.d. with unspecified distribution function and independent of X_i. If the absorbing failure time from origin (time 0) follows the AFT model $log\left(T_i\right)={\beta }_0^{\prime }{X}_i+{\epsilon }_i$, where ε_i are i.i.d. with unspecified distribution function and independent of X_i, it follows that β_gh=β₀ for models of the forms given in Figure 1 (proof in Appendix A.1).

Fig. 1.

a) Progressive multi-state model; b) Progressive multi-state model where absorbing state can be reached from any state; c) Illness-death model without recovery from illness

Additionally, we let C_i be a censoring random variable independent of the multistate process, Y_i = min(T_i,C_i), and δ_i = I(T_i ≤ C_i). Let $e_i^{\beta }=log\left(Y_i\right)-{\beta }^{\prime }{X}_i$, and ${\tilde{e}}_i{}^{\beta }=log\left(T_i\right)-{\beta }^{\prime }{X}_i$. Under the model described, a reasonable estimating equation for β is:

$$U_P\left(\beta \right)=\frac{1}{n^2}\sum _{i=1}^n\sum _{j=1}^n\left(X_i-X_j\right)P\left({\tilde{e}}_i^{\beta }<{\tilde{e}}_j^{\beta }|S_i\left(e_i^{\beta }\right),S_j\left(e_j^{\beta }\right)\right)=0$$ (4)

where $P\left({\tilde{e}}_i{}^{\beta }<{\tilde{e}}_j{}^{\beta }|S_i\left(e_i^{\beta }\right),S_j\left(e_j^{\beta }\right)\right)$ represents the probability that the failure time residual for individual i will be less than the failure time residual for individual j conditional on each of their observed disease states at their observed follow-up time residual. This extension of the Gehan estimating equation is based on the extension of Gehan’s test statistic proposed by Ramchandani et al. (2015) to account for intermediate disease state information. At β = β₀,this equation is centered around 0 under the true, unknown, probability measure. (See Appendix A.2). The estimating equation in (4) can also be written as:

$$U_P\left(\beta \right)=\frac{1}{n^2}\sum _i\sum _{j<i}\left(X_i-X_j\right)\left[P\left({\tilde{e}}_i{}^{\beta }<{\tilde{e}}_j{}^{\beta }|S_i\left(e_i^{\beta }\right),S_j\left(e_j^{\beta }\right)\right)-P\left({\tilde{e}}_i{}^{\beta }>{\tilde{e}}_j{}^{\beta }|S_i\left(e_i^{\beta }\right),S_j\left(e_j^{\beta }\right)\right)\right]=0$$ (5)

This formulation of U_P(β) can be identified as an order 2 U-statistic, thus giving us asymptotic normality of the score function at a fixed β, and providing a way of computing the covariance matrix of $\sqrt{n}{U}_P\left(\beta \right)$. Let D(β) denote the asymptotic covariance matrix of $\sqrt{n}{U}_P\left(\beta \right)$ From standard U-statistics theory, D(β) has elements that can be estimated with:

$$D_{l,m}\left(\beta \right)=\frac{1}{n^3}\sum _i\sum _j\sum _{k\ne j}\left(X_{il}-X_{jl}\right)\left(X_{im}-X_{km}\right){\varphi }_{ij}^{\beta }{\varphi }_{ik}^{\beta },$$ (6)

where ${\varphi }_{ij}^{\beta }=P\left({\tilde{e}}_i{}^{\beta }<{\tilde{e}}_j{}^{\beta }|S_i\left(e_j^{\beta }\right),S_j\left(e_j^{\beta }\right)\right)-P\left({\tilde{e}}_i{}^{\beta }>{\tilde{e}}_j{}^{\beta }|S_i\left(e_i^{\beta }\right),S_j\left(e_j^{\beta }\right)\right)$ (Van der Vaart 2000).

When we know that $log\left(T_i\right)-{\beta }^{\prime }{X}_i<log\left(T_j\right)-{\beta }^{\prime }{X}_j$ _,the conditional probability in the summand of (4) is known and equal to 1, just as in the Gehan estimating equation, U_G(β). This would happen in the scenario where both subjects i and j had reached the absorbing state, or if subject i reached the absorbing state and their residual time to the absorbing state was less than the residual time of subject j. It follows that we can rewrite U_P(β) as the sum of U_G(β) and an additional term of probabilities for censored subjects:

$$\begin{gathered} U_P\left(\beta \right)=\sum _i\sum _j\left(X_i-X_j\right)I\left(e_i^{\beta }<e_j^{\beta }\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left\{{\delta }_i+\left(1-{\delta }_i\right)\left[P\left({\tilde{e}}_i{}^{\beta }<{\tilde{e}}_j{}^{\beta }|S_i\left(e_i^{\beta }\right),S_j\left(e_j^{\beta }\right)\right)-P\left({\tilde{e}}_i{}^{\beta }>{\tilde{e}}_j{}^{\beta }|S_i\left(e_i^{\beta }\right),S_j\left(e_j^{\beta }\right)\right)\right]\right\}=0 \end{gathered}$$ (7)

The summand of the estimating equation U_P(β) is based on the true probabilities, but in practice we have to estimate the probabilities. This can be done in a number of ways using event history models that account for incomplete observation. In this paper, we will estimate the probabilities nonparametrically using the Aalen-Johansen estimator.

2.1. The Aalen-Johansen Estimator

To estimate the failure probabilities, we propose using the empirical transition matrix developed by Aalen and Johansen (1978), fit on the residuals of each transition time. The Aalen-Johansen estimator is a natural generalization of the Kaplan-Meier estimator for non-homogeneous Markov chains with a finite number of states (Aalen et al 2008). Suppose we have a finite number of states S ={0,1,…,D}. Let α_g,h(t) denote the transition intensity from state g to state h, where g ≠ h. This describes the instantaneous risk, or the hazard, of transitioning from state g to state h at time t. Now, let P_g,h(s,t) denote the probability of a subject being in state h at time t given that the subject was in state g at time s. This is called a transition probability, and it is the g,h entry of the d x d transition probability matrix P(s,t). The transition probability matrix can be written as a function of the transition intensities through the product integral:

$$\mathbf{P}\left(s,t\right)=\mathbf{\prod }_{\left(s,t\right]}\left[\mathbf{I}+d\mathbf{A}\left(u\right)\right]$$

where I is the identity matrix, and A(u) is the cumulative transition intensity matrix with elements $A_{gh}\left(t\right)={\int }_0^t{\alpha }_{gh}\left(u\right)du$. Let N_gh(t) be the number of individuals observed to experience a transition from state g to h between time 0 and time t, and let Y_g(t) be the number of individuals in state g just before time t. For g ≠ h, we can use the Nelson-Aalen estimator to estimate the cumulative hazard A_gh(t), yielding ${\widehat{{\rm A}}}_{gh}\left(t\right)={\int }_0^t\frac{d{N}_{gh}\left(u\right)}{Y_g\left(u\right)}$, which can also be written as ${\sum }_{u\le t}\frac{\Delta N_{gh}\left(u\right)}{Y_g\left(u\right)}$, where ∆N_gh(u) represents the number of transitions from state g to state h at time u. Also, we let ${\widehat{{\rm A}}}_{gg}\left(t\right)=-{\sum }_{h\ne g}{\widehat{{\rm A}}}_{gh}\left(t\right)$, so that the rows of the d × d matrix $\widehat{\mathbf{A}}\left(t\right)$ sum to 0. Suppose u₁ < u₂ < … are the exact times when a transition between any two states are observed. Then the estimate for P(s,t) is given by the matrix product:

$$\widehat{\mathbf{P}}\left(s,t\right)=\prod _{s<u_j\le t}\left[I+d\widehat{A}\left(u_j\right)\right].$$

where $d\widehat{A}\left(u_j\right)=\widehat{A}\left(u_j\right)-\widehat{A}\left(u_{j-1}\right)$, and we define u₀ = 0. For example, in a progressive three state model, this expression written out in full using the counting process notation described above would be:

$$\widehat{\mathbf{P}}\left(s,t\right)=\prod _{s<u_j\le t}\left(\begin{array}{ccc}1-\frac{\Delta {{\rm N}}_{01}\left(u_j\right)}{Y_0\left(u_j\right)}& \frac{\Delta {{\rm N}}_{01}\left(u_j\right)}{Y_0\left(u_j\right)}& 0\\ 0& 1-\frac{\Delta {{\rm N}}_{12}\left(u\right)}{Y_1\left(u_j\right)}& \frac{\Delta {{\rm N}}_{12}\left(u\right)}{Y_1\left(u_j\right)}\\ 0& 0& 1\end{array}\right)$$

In the presence of censoring, these transition probabilities will be used to estimate the probability of an individual’s lifetime being less than another individual’s, on the scale of the failure time residual, ${\tilde{e}}^{\beta }=log\left(T\right)-{\beta }^{\prime }X$. The rationale for estimating the transition probabilities based on the residuals is that, under our assumed model, the trajectory of each patient based on their residual transition times is identically distributed at the true β₀. There are several statistical packages that allow for the computation of the Aalen-Johansen estimator. One excellent option is the etm package in R (Allignol et al 2011; R Core Team 2014).

2.2. The Estimating Equation

For the estimating equation U_P(β), when comparing two subjects, we have two scenarios where we would need to estimate a probability: when subject i is censored and j is uncensored, and when both are censored. In the first case, suppose subject i is censored in state k and j is uncensored. Then we can estimate $\left[P\left({\tilde{e}}_i^{\beta }<{\tilde{e}}_j^{\beta }|S_i\left(e_i^{\beta }\right)=k,S_j\left(e_j^{\beta }\right)=d\right)-P\left({\tilde{e}}_i^{\beta }>{\tilde{e}}_j^{\beta }|S_i\left(e_i^{\beta }\right)=k,S_j\left(e_j^{\beta }\right)=d\right)\right]$ with $\left[{\widehat{P}}_{kd}\left(e_i^{\beta },e_j^{\beta }-\right)+{\widehat{P}}_{kd}\left(e_i^{\beta },e_j^{\beta }\right)-1\right]$ where t− indicates a time just before time t. Now suppose that subject i is censored in state k, subject j is censored in state k′ and $e_i^{\beta }<e_j^{\beta }$. Then $P\left({\tilde{e}}_i{}^{\beta }<{\tilde{e}}_j{}^{\beta }|S_i\left(e_i^{\beta }\right)=k,S_j\left(e_j^{\beta }\right)=k^{\prime }\right)-P\left({\tilde{e}}_i{}^{\beta }>{\tilde{e}}_j{}^{\beta }|S_i\left(e_i^{\beta }\right)=k,S_j\left(e_j^{\beta }\right)=k^{\prime }\right)$ can be estimated with:

$${\int }_{e_i^{\beta }}^{\infty }\left[1-{\widehat{P}}_{k^{\prime },d}\left(e_j^{\beta },t\right)\right]d{\widehat{P}}_{k,d}\left(e_i^{\beta },t\right)-{\int }_{e_j^{\beta }}^{\infty }\left[1-{\widehat{P}}_{k,d}\left(e_i^{\beta },t\right)\right]d{\widehat{P}}_{k^{\prime },d}\left(e_j^{\beta },t\right)$$ (8)

where by convention we define $\widehat{P}\left(e_i,t\right)=0$ for t≤e_i. Note that these expressions are general in the sense that we can use them for any multi-state models where we estimate transition probabilities. In the case of the Aalen-Johansen estimator, the probabilities are step-functions, so in practice equation (8) is computed with sums. Denote the maximum follow-up residual time as $e_{max}^{\beta }$ and let t₁,t₂, … be the jumps in $\widehat{P}\left(s,t\right)$ for any fixed s. We can compute (8) as:

$$\begin{gathered} \sum _{l\hspace{0.17em}:\hspace{0.33em}{e}_i^{\beta }<t_l\le e_{max}^{\beta }}\left[1-{\widehat{P}}_{k^{\prime },d}\left(e_j,t_l\right)\right]\left[{\widehat{P}}_{k,d}\left(e_i,t_l\right)-{\widehat{P}}_{k,d}\left(e_i,t_{l-1}\right)\right] \\ -\sum _{l\hspace{0.17em}:\hspace{0.33em}{e}_j^{\beta }<t_l\le e_{max}^{\beta }}\left[1-{\widehat{P}}_{k,d}\left(e_i,t_l\right)\right]\left[{\widehat{P}}_{k^{\prime },d}\left(e_j,t_l\right)-{\widehat{P}}_{k^{\prime },d}\left(e_j,t_{l-1}\right)\right] \end{gathered}$$

We now denote the estimating equation U_P(β) as $U_P\left(\beta ;\widehat{\mathbf{A}}\right)$ to indicate that the equation depends on the estimated cumulative transition hazard matrices $\widehat{\mathbf{A}}\left(\cdot \right)$. The estimating equation can now be written as:

$$\begin{gathered} U_P\left(\beta ;\widehat{\mathbf{A}}\right)=\frac{1}{n^2}\sum _i\sum _j\left(X_i-X_j\right)I\left(e_i^{\beta }<e_j^{\beta }\right)\left\{{\delta }_i+\left(1-{\delta }_i\right){\delta }_j\left[{\widehat{P}}_{S_i\left(e_i^{\beta }\right),d}\left(e_i^{\beta },e_j^{\beta }-\right)+{\widehat{P}}_{S_i\left(e_i^{\beta }\right),d}\left(e_i^{\beta },e_j^{\beta }\right)-1\right]\right. \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}+\left(1-{\delta }_i\right)\left(1-{\delta }_j\right)\left[{\int }_{e_i^{\beta }}^{\infty }\left[1-{\widehat{P}}_{S_j\left(e_j^{\beta }\right),d}\left(e_j^{\beta },t\right)\right]d{\widehat{P}}_{S_i\left(e_i^{\beta }\right),d}\left(e_i^{\beta },t\right)\right. \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}-{\int }_{e_j^{\beta }}^{\infty }\left[1-{\widehat{P}}_{S_i\left(e_i^{\beta }\right),d}\left(e_i^{\beta },t\right)\right]\left.\left.d{\widehat{P}}_{S_j\left(e_j^{\beta }\right),d}\left(e_j^{\beta },t\right)\right]\right\} \end{gathered}$$ (9)

The estimate $\widehat{\beta }$ is the value of β where $U_P\left(\beta ;\widehat{A}\right)$ crosses 0.

In the simple two-state model, this estimator is similar to the Peto-Prentice version of the weighted log-rank estimator. Note that by using the Aalen-Johansen estimator for the probabilities, we are additionally making the assumption that the error terms for the multi-state process arise from a non-homogeneous Markov process. However, the method is more general as the probabilities can be estimated in other ways as well, including parametrically. Alternative estimates for the probabilities may be used if one wants to relax the Markov assumption, such as those proposed by de Uña-Álvarez and Meira-Machado (2015), and Meira-Machado et al. (2006). Nevertheless, simulations suggest that the proposed estimator works well in some non-Markov settings as well.

2.3. Remark on estimation and asymptotic properties

As described in Section 2, the estimating function U_P(β) is a U-statistic when we know the true conditional probabilities in the summand of the statistic of equation (5). Those conditional probabilities are based on the true cumulative hazard process A(·) described in section 2.1. In practice we do not know the true hazard process, and we propose estimating it to obtain the necessary transition probabilities. By estimating this process, the estimating equation is no longer strictly a U-statistic, so the usual properties of U-statistics do not directly apply. While this may have implications on the convergence and asymptotic variance of the estimator, our simulation studies suggest that the estimator as presented is unbiased and that the variance estimator described in the next section is close to the empirical variance.

Additionally, it is clear that the proposed estimating equation is neither continuous nor monotone in β. This is not a major problem when there is a single covariate, but for multidimensional settings, it can make estimation of β difficult and admits the possibility of multiple solutions. In these settings, we could first find a consistent auxiliary estimator, such as the Gehan estimator that is obtained with linear programming as described by Jin et al. (2003). We would then solve for β as the minimizer of the norm $\parallel U_P\left(\beta ;\widehat{A}\right)\parallel$ using a derivative-free optimization algorithm, such as Nelder-Mead (1965), with the consistent auxiliary estimator as an initial value to arrive at a solution in the correct neighborhood of β₀. We encourage use of various starting values to ensure that the estimate obtained is the global minimizer.

While it is not ensured that a solution will exist in finite samples, at least one solution should exist provided that the following conditions apply:

1. If there are p covariates, there are at least p + 1 failures to the absorbing state.

2. The distribution of covariates among those who have had an absorbing failure are not concentrated on a hyperplane of the dimension of the parameter space; i.e. if the covariate vectors among subjects who had an absorbing failure are linearly dependent, a p-dimensional solution may not exist.

3. Covariates are bounded and have finite variance.

4. Densities of the sojourn and absorbing failure times are bounded and have finite variance.

2.4. Inference Procedure for $\widehat{\beta }$

It is well known that variance estimation for the parameters of the ordinary semiparametric accelerated failure time model is difficult. This is because the estimating equations are non-smooth, and the usual sandwich variance estimate involves the derivative of the unknown hazard function of the error terms. For the general weightedlog rank estimating functions, it has been established that the covariance matrix for $\sqrt{n}\left(\widehat{\beta }-{\beta }_0\right)$ is given by V=B⁻¹DB^−1T, where B is the non-singular slope matrix of the estimating function U(β) and D is the variance of the score function, each evaluated at β₀ (Kalbfleisch and Prentice 2011). Estimation of D is straightforward, but the discontinuities of the estimating equation do not allow for direct computation of B using derivatives; further, direct numerical differentiation can be unstable in practice. This will similarly be the case for our estimating function, where we may estimate D using the asymptotic variance formula for the U-statistic with the resubstituted probability estimates, but where an estimate of B is difficult to obtain due to the discontinuity of the estimating equation in finite samples.

In light of these issues, some authors have pursued a smooth approximation of the Gehan estimating equation to allow for straightforward parameter and variance estimation (Brown and Wang 2007; Heller 2007). While this approach works well for the Gehan estimating equation, it is not straightforward to obtain smooth versions for other AFT estimators. To accommodate other types of estimators, Jin et al. (2014) proposed a Monte Carlo smoothing method based on the approach of Brown and Wang (2007) for estimating standard errors.

The idea is that in large samples, the distribution of $\widehat{\beta }-{\beta }_0$ is approximately equal to n^−1/2V^1/2Z, where Z is a standard normal random vector and V is the covariance matrix of $\sqrt{n}\left(\widehat{\beta }-{\beta }_0\right)$. This induces the smooth estimating function $\tilde{U}\left(V,\beta \right)=E_Z\left[U\left(\beta +n^{-1/2}{V}^{1/2}Z\right)\right]$, where the expectation is taken with respect to the vector Z. They then argue that the derivative of the smooth function $\tilde{U}\left(V,\beta \right)$ is given by:

$$B\left(\Gamma ;\beta \right)=E_Z\left[U\left(\beta +\Gamma Z\right)Z^T{\Gamma }^{-1}\right]$$ (10)

where Г=n^−1/2V^1/2. They propose an iterative method where they numerically approximate the integral in (10), update Г(the current estimate for the standard error for $\widehat{\beta }$) and iterate through until convergence of Г. One approach is a Monte Carlo method (MCM), with which perturbed score equations must be evaluated a very large number of times. This is an intuitive and simple way to estimate B, but it requires a very large number of function evaluations at each step of the algorithm. The other approach is a Gaussian Quadrature Method (GQM), which we choose to implement here because it can be far more computationally efficient while giving similar results to the MCM. The idea is to choose a p-dimensional grid of nodes based on onedimensional Gauss-Hermite quadrature, obtain their corresponding weights, and use those to approximate the integral in (10). We describe the algorithm in Appendix A.3. Confidence intervals for $\widehat{\beta }$ can be obtained by the Wald method.

An alternative to this method would be to use a bootstrap approach for estimating the variance of $\widehat{\beta }$. The classical bootstrap would entail resampling subjects’ entire trajectory with replacement, reestimating the requisite probabilities using the Aalen-Johansen estimator, and obtaining an estimate of ${\widehat{\beta }}^{\ast }$ that solves the estimating equation based on the new sample. This process would be repeated a large number of times M, with standard errors computed from the empirical distribution of ${\widehat{\beta }}^{\ast }={\left({\widehat{\beta }}_1^{\ast },\dots ,{\widehat{\beta }}_M^{\ast }\right)}^T$. Confidence intervals for β₀ can be obtained either with the Wald method, or directly from the empirical distribution of ${\widehat{\beta }}^{\ast }$.

3. Simulations

To test the performance of our estimator, we simulated data from a 3-state progressive multi-state model of the form 0→ 1 →2 (where 2 is the absorbing state), such that the acceleration parameter acts on the entire process. Let T_ik represent the time taken to transition from state k-1 to state k. We generated the sojourn times $log\left(T_{ik}\right)=2+{\beta }_0{X}_i+{\epsilon }_{ik}$, for k=1,2, i=1,….,n Clearly, the absorbing state failure time $T_i=T_{i1}+T_{i2}$ satisfies $log\left(T_i\right)=2+{\beta }_0{X}_i+{\epsilon }_i$. We set β₀= 0.7, which corresponds approximately to a 2-fold acceleration of the failure time for a unit difference in the covariate X. This was done for various choices of ε_ik, including distributions for which the Markov assumption does not hold. In one setting, the ε_ik were independent of each other, and had either standard extreme-value (log-Weibull), standard normal, standard logistic distributions. In another setting we allowed the ε_ik to be correlated, with standard multivariate normal distributions with either correlation ρ = 0.5 and ρ= 0.9. It should be noted that these are the distributions of the state sojourn times and not the distributions of the absorbing failure times. The covariate X_i was normally distributed with mean 0 and standard deviation 0.5 in all settings. Censoring values were generated from a Uniform(0,τ), with τ chosen to yield a desired level of censoring. In each setting, we also allowed censoring to depend on the covariate, with C_i distributed as exp(1.5X_i)·Uniform(0,τ).

We computed the bias, empirical standard error, and empirical MSE for the Fygenson-Ritov (Gehan), the Peto-Prentice, the Log-rank, and the Proposed estimators. For the proposed estimator, we also computed standard error estimates, 95% coverage probabilities based on Wald confidence intervals, and relative efficiencies of the proposed estimator compared to the Gehan, Peto-Prentice, and Log-rank estimators. The variance of the score equation was obtained using equation (6) with the resubstituted probability estimates. Standard error estimates for the proposed estimator were obtained using the GQM method with 16 Gauss-Hermite quadrature nodes, and a tolerance level of 10⁻⁴ for convergence of Г. 1000 simulations were used in each setting, with sample sizes of 100 and 200.

Recall that the Gehan estimating function is given in equation (2). The Log-rank and Peto-Prentice estimating functions are given by:

$$\sum _i{w}_i{\delta }_i\left(x_i-\frac{{\sum }_j{x}_{j}I\left(e_i^{\beta }\le e_j^{\beta }\right)}{{\sum }_{j}I\left(e_i^{\beta }\le e_j^{\beta }\right)}\right)$$

where for the Log-rank estimator w_i = 1, and for the Peto-Prentice estimator $\widehat{F}\left(e_i^{\beta }\right)$, where $\widehat{F}\left(\cdot \right)$ denotes the left-continuous Kaplan-Meier estimator based on the observed residuals.

The results are given in Tables 1 and 2. Table 1 refers to the setting where the censoring distributions are independent of the covariate, while Table 2 refers to the unequal censoring case. Observe that in all settings, the proposed estimator is essentially unbiased, the average of the standard error estimator is close to the empirical standard error, and the coverage probabilities are close to the nominal level of 0.95. In addition, the proposed estimator is more efficient than the Gehan, Peto-Prentice, and Log-rank estimators in each of these settings, with the most efficiency gains coming in cases of high censoring. It is not expected that in finite samples the proposed estimator will always be more efficient, but these simulations demonstrate the potential efficiency gains we can get when the intermediate states are taken into account as auxiliary information.

Table 1.

Equal Censoring. Dist: Sojourn Time Distributions; PC: Percent Censoring; SE: empirical standard error; SEE: mean of standard error estimator; CP: 95% coverage probability; RE: Relative efficiency of Proposed estimator compared to Gehan/P-P estimator = MSE(Gehan/P-P)/MSE(Proposed);. EV: Extreme-Value (log-Weibull); L: Logistic; N: Normal; CN1: Correlated Normal (ρ = 0.5); CN2: Correlated Normal(ρ=0.9).

			Proposed				Gehan			Peto-Prentice			Log-Rank
N	Dist.	PC	Bias	SE	SEE	CP	Bias	SE	RE	Bias	SE	RE	Bias	SE	RE
100	EV	50	0.012	0.196	0.198	0.935	0.016	0.216	1.213	0.016	0.206	1.101	0.012	0.200	1.034
		75	0.013	0.263	0.261	0.947	0.024	0.321	1.496	0.026	0.306	1.356	0.026	0.306	1.358
	L	50	0.012	0.303	0.295	0.938	0.014	0.314	1.073	0.013	0.318	1.101	0.013	0.335	1.219
		75	0.008	0.351	0.348	0.946	0.009	0.390	1.239	0.013	0.388	1.222	0.012	0.395	1.268
	N	50	−0.005	0.180	0.179	0.943	0.002	0.191	1.133	0.000	0.190	1.117	0.005	0.201	1.257
		75	−0.007	0.221	0.221	0.936	−0.000	0.253	1.314	−0.001	0.255	1.330	0.003	0.265	1.447
	CN1	50	0.005	0.211	0.205	0.941	0.005	0.225	1.144	0.007	0.226	1.153	0.003	0.241	1.308
		75	0.011	0.245	0.243	0.931	0.012	0.284	1.340	0.013	0.282	1.318	0.014	0.296	1.455
	CN2	50	−0.004	0.223	0.220	0.940	−0.005	0.238	1.136	−0.006	0.240	1.160	−0.003	0.252	1.282
		75	0.004	0.259	0.264	0.946	0.014	0.307	1.410	0.010	0.305	1.389	0.010	0.315	1.481
200	EV	50	0.004	0.145	0.139	0.939	0.006	0.161	1.229	0.005	0.153	1.122	0.010	0.151	1.092
		75	−0.010	0.174	0.184	0.951	−0.004	0.214	1.504	−0.005	0.201	1.334	−0.004	0.206	1.401
	L	50	0.005	0.212	0.210	0.943	0.007	0.218	1.058	0.008	0.219	1.069	0.005	0.233	1.202
		75	−0.012	0.236	0.241	0.951	−0.002	0.268	1.291	−0.002	0.264	1.247	−0.000	0.268	1.286
	N	50	−0.000	0.130	0.127	0.944	−0.001	0.135	1.081	0.000	0.136	1.100	−0.002	0.145	1.244
		75	0.003	0.145	0.156	0.953	0.010	0.166	1.316	0.009	0.166	1.307	0.012	0.174	1.435
	CN1	50	−0.006	0.143	0.146	0.959	−0.007	0.155	1.173	−0.006	0.154	1.151	−0.007	0.163	1.296
		75	0.001	0.173	0.172	0.943	0.007	0.203	1.384	0.007	0.205	1.405	0.009	0.213	1.517
	CN2	50	0.000	0.155	0.156	0.949	−0.001	0.168	1.181	−0.000	0.167	1.169	0.003	0.175	1.279
		75	−0.002	0.180	0.186	0.955	−0.005	0.212	1.394	−0.005	0.210	1.361	−0.005	0.217	1.459

Table 2.

Unequal Censoring. Dist: Sojourn Time Distributions; PC: Percent Censoring; SE: empirical standard error; SEE: mean of standard error estimator; CP: 95% coverage probability; RE: Relative efficiency of Proposed estimator compared to Gehan/P-P/LR estimator = MSE(Gehan/P-P/LR)/MSE(Proposed);. EV: Extreme-Value (log-Weibull); L: Logistic; N: Normal; CN1: Correlated Normal (ρ = 0.5); CN2: Correlated Normal(ρ=0.9).

			Proposed				Gehan			Peto-Prentice			Log-Rank
N	Dist.	PC	Bias	SE	SEE	CP	Bias	SE	RE	Bias	SE	RE	Bias	SE	RE
100	EV	50	−0.013	0.214	0.200	0.928	−0.018	0.234	1.193	−0.017	0.225	1.109	−0.018	0.218	1.040
		75	−0.018	0.257	0.273	0.953	−0.033	0.323	1.592	−0.029	0.302	1.390	−0.025	0.298	1.351
	L	50	−0.016	0.308	0.297	0.933	−0.017	0.311	1.016	−0.016	0.315	1.043	−0.013	0.331	1.155
		75	−0.026	0.337	0.352	0.950	−0.031	0.379	1.261	−0.032	0.377	1.251	−0.026	0.387	1.316
	N	50	0.001	0.179	0.180	0.946	−0.002	0.189	1.112	−0.003	0.189	1.120	0.002	0.206	1.320
		75	−0.000	0.216	0.223	0.940	−0.002	0.241	1.247	−0.004	0.246	1.298	−0.006	0.253	1.378
	CN1	50	−0.007	0.212	0.205	0.932	−0.013	0.229	1.162	−0.011	0.229	1.167	−0.014	0.241	1.292
		75	−0.010	0.243	0.249	0.943	−0.022	0.279	1.322	−0.018	0.283	1.361	−0.025	0.286	1.392
	CN2	50	−0.004	0.233	0.223	0.934	−0.004	0.249	1.138	−0.004	0.248	1.125	−0.003	0.259	1.229
		75	−0.005	0.262	0.267	0.949	−0.012	0.313	1.435	−0.007	0.316	1.462	−0.009	0.325	1.549
200	EV	50	−0.003	0.145	0.142	0.950	−0.007	0.161	1.232	−0.006	0.154	1.134	−0.010	0.151	1.089
		75	−0.001	0.182	0.190	0.951	−0.016	0.226	1.561	−0.012	0.209	1.333	−0.012	0.211	1.355
	L	50	0.012	0.213	0.208	0.943	0.009	0.214	1.007	0.009	0.217	1.041	0.012	0.232	1.189
		75	−0.002	0.232	0.246	0.955	−0.001	0.261	1.265	−0.002	0.265	1.307	−0.003	0.272	1.378
	N	50	−0.003	0.127	0.129	0.949	−0.005	0.133	1.094	−0.005	0.132	1.084	−0.005	0.142	1.253
		75	0.000	0.149	0.160	0.962	−0.006	0.169	1.288	−0.006	0.170	1.303	−0.005	0.177	1.421
	CN1	50	0.001	0.146	0.146	0.945	−0.001	0.156	1.151	−0.001	0.157	1.155	−0.002	0.165	1.285
		75	−0.010	0.165	0.177	0.959	−0.011	0.193	1.375	−0.014	0.192	1.368	−0.016	0.201	1.490
	CN2	50	−0.011	0.161	0.158	0.937	−0.015	0.173	1.158	−0.015	0.173	1.157	−0.017	0.179	1.256
		75	−0.009	0.179	0.191	0.963	−0.017	0.212	1.399	−0.015	0.210	1.369	−0.016	0.215	1.441

4. Example

We will illustrate the proposed method on data from a clinical trial of patients with ALS (Berry et al 2013). Subjects in the trial were monitored for survival, and rate of decline in neurological function as measured by their ALSFRS-R scores. The ALSFRS-R is a functional rating scale by which physicians estimate the degree of functional impairment in ALS patients (Cedarbaum et al 1999). The scale ranges from 0–48, with a higher score indicating better function. We are interested in estimating the effect of treatment on survival, using ALSFRS-R score as the intermediate information. ALSFRS-R was measured periodically in patients until death, drop-out, or the end of the study. We discretized this score into 3 states: 33–48 (state 1), 17–32 (2), 0–16 (3). We assume the transition time occurs when a transition is observed, and we allowed all forward transitions that were seen in the data, but no backward transitions. This means that even if someone actually moved from state 2 to 1 for example, that they were kept in state 2 for the analysis. There were a total of 513 subjects in the analysis, an average follow-up time of 1.5 years, a maximum follow up time of 5.5 years, and 43% of all subjects were censored. It is known that site of disease onset is associated with survival, so we choose to include this covariate in the model.

We estimated coefficients for the model $log\hspace{0.33em}{T}_i={\beta }_{trt}\times treatment+{\beta }_{site}\times site+{\epsilon }_i$, where treatment = 1 for “active” and 0 for “placebo”, and site indicates site of disease onset (1 for bulbar-onset, 0 for limb-onset). We first estimated the coefficients using the Gehan estimating equations. The Gehan estimators were (.217, −.350) for treatment and site of onset, respectively. We then estimated the coefficients using the proposed estimating equation given in (9). This was done using the optim function in R, with the Nelder-Mead method and using the Gehan estimates as initial values. The coefficients for the proposed estimator were (.210, −.383). This implies that average progression and survival time among the treated group, adjusted for site of onset, was estimated to be exp(.21) = 1.23 times that of the placebo group. Similarly, adjusting for treatment, average progression and survival time in the bulbar-onset group was 0.68 times that in the limb-onset group.

Standard errors were estimated using the GQM method described in section 2.3 and Appendix A.3, and the bootstrap. Using the formula in (6), the covariance matrix of the score equation, D, was estimated to be:

$$\left(\begin{array}{cc}.063& .001\\ .001& .046\end{array}\right).$$

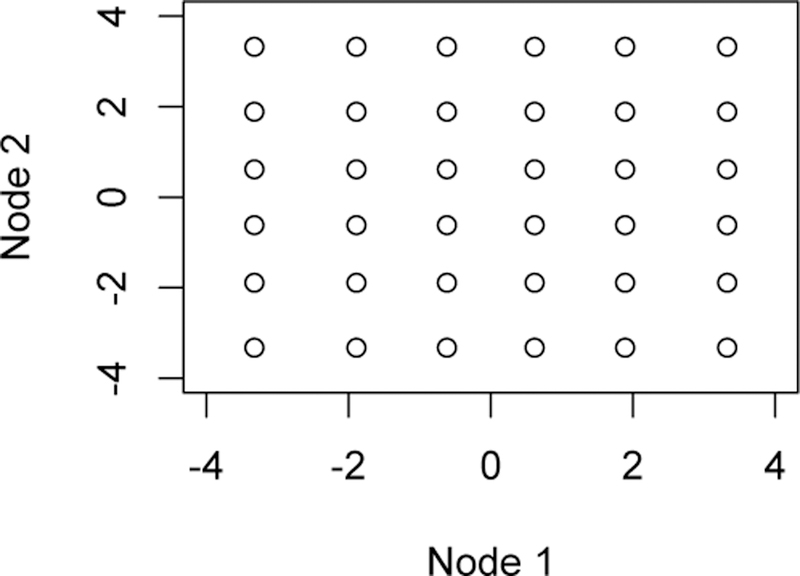
For the GQM, we used 6 Gauss-Hermite quadrature nodes, given by the values z = ±(2.35, 1.33, 0.436), with requisite weights w = (.0045, .157, .725). The transformed nodes $z^{\ast }=\sqrt{2}z$ were used in order to approximate the desired integral in equation (10). An illustration of the grid of points over which we approximate the integral is given in Figure 2.

Fig. 2.

Points $z_j^{\ast }$ used to evaluate the double integral in (10)

The algorithm converged in 4 iterations within a .0001 tolerance level for each entry of the estimated covariance matrix G. Standard error estimates of the coefficients for treatment and site of onset were .144 and .173, and p-values based on Wald test statistics were .145 and .026, respectively. We also estimated standard errors using the bootstrap, yielding standard error estimates of .145 and .159, with Wald p-values given by .148 and .016, respectively. We conclude that treatment, adjusted for site of onset, is not significantly associated with progression and survival when adjusted for disease site of onset, but that bulbar site of onset of is associated with earlier progression and failure, resulting in almost two-thirds the average survival time of patients whose site of onset was in a limb. These results were not unexpected given the difficulty of treating ALS, and that site of onset is established as prognostic of survival.

5. Discussion

While the asymptotic properties are not fully developed, simulations have demonstrated that the proposed estimator and the corresponding standard error estimator have good finite-sample properties in several settings. The estimators are close to their empirical values under semi-Markov sojourn time distributions, correlated sojourn time distributions (non-Markov), and when the censoring distribution depends on the covariates.

In most settings, the proposed estimator was more efficient than those obtained with the Gehan and Peto-Prentice estimators that ignore intermediate events. The improvement in efficiency will depend on the sojourn time distributions and the censoring distributions, with the most improvement in settings where there is very high censoring. Thus, the method of estimation can be particularly useful for shorter studies where the main event of interest is rarely observed, but subjects are monitored frequently for intermediate “benchmarks” as well. An example of this would be any relatively short clinical trial of a chronic disease such as ALS.

A key assumption for the proposed estimator is that the acceleration parameters act on every transition of the process. This is a stronger assumption than the ordinary accelerated failure time model for two states, but a necessary one to ensure that the AFT parameters we estimate are interpretable as such. Thus, it would be useful to devise a procedure to check if the AFT model holds in the manner specified. One potential way would be to treat the time from origin to state k as a failure time, and use the Gehan estimating equation to estimate β_k, for each non-initial state k = 1, …, D. We could then construct a test for H₀ : β_j = β_k, j ≠ k, using the method proposed by Lin and Wei (1992). If one was instead interested in estimating AFT parameters for each particular state’s sojourn time, Huang’s accelerated sojourn times model (2002) is the appropriate choice.

Additionally, under our assumed model, there may be other more efficient ways of estimating the desired parameters, such as in the framework of clustered or multivariate failure times (Johnson and Strawderman 2009; Chiou et al 2014). Other estimators could be proposed where each transition time for every participant contributes to the estimation, however, methods that may directly incorporate all intermediate transition times into estimation are somewhat different than what we are proposing. We are essentially treating the intermediate failures as auxiliary information that informs the primary failure of interest, the absorbing state. The absorbing failures still drive the proposed estimator, with some additional information gleaned from the intermediate disease states. Under the assumed model, more emphasis on the intermediate transitions can certainly make more efficient use of all of the observed data, but it was our desire to have an estimator driven primarily by survival that also incorporated the intermediate information in a manner directly relevant to the survival outcome. This also makes the proposed estimator more robust to intermediate transitions departing from the assumed AFT model.

To give more weight to the intermediate transitions, we can possibly estimate parameters from Huang’s (2002) accelerated sojourn times model, and use a weighted combination of those model estimates and the ordinary semiparametric AFT estimate based on the survival time. For example, suppose we have a four-state progressive model with an absorbing state and two intermediate states. The weighted estimator could be given by w₁β_H1 + w₂β_H2 + (1−w₁−w₂)β_G where w1 + w2≤1, β_H,k represents Huang’s model estimates for the k^th sojourn time, and β_G represents the Gehan estimator for overall survival. The weights could be specified based on some combination of clinical input, standard error of the estimates, and a measure of model fit. Huang’s proposed goodness of fit test restricts the amount of follow-up data used by creating an artificial censoring time at various points of follow-up. Then new estimates for the parameter can be computed and compared with the estimate based on the entire follow-up time. Weights may be based on the relative level of variation between the restricted follow-up estimates and the original. Estimating the standard error for such an estimator will involve estimating the covariance between the components and could prove difficult, but a resampling procedure may be viable. Studying this weighted approach and the GEE approach proposed by Chiou (2014) in the multi-state context may be an avenue of further research.

The proposed estimating equation does not have the same desirable property of monotonicity as the Gehan estimating equation, but its close relationship with the Gehan function can make parameter estimation feasible in practical settings with sufficient sample size. In order to simplify parameter and standard error estimation, an induced smoothing approach may also work well with the proposed estimator, but such an approach would involve smoothing both the indicator functions and the transition probability estimates of the estimating function. Aalen and Johansen (1978) provide an asymptotically equivalent smooth version of their estimator that could be used for this purpose.

The asymptotic properties of the estimator need to be explored in greater detail. As with the traditional censored linear rank estimators, the key result is to establish asymptotic linearity of the score function in a neighborhood of β₀, from which consistency and asymptotic normality of the estimate $\widehat{\beta }$ typically follow. Our simulation studies suggest this to be the case under certain assumptions, but it remains to be formally established.

A Appendix

A.1. Proof that β parameters for each transition are equal when individual transitions and overall survival time follow an AFT model

Consider a progressive model of D + 1 states as in Figure 1a. Let T_gh indicate a continuous random variable for time to transition from state g to state h. Let $T=T_{01}+T_{12}+\dots +T_{D-1,D}$. Further, suppose $T=exp\left({\beta }_{0}X+\epsilon \right)$, where ε is independent of X. Let $T_{g-1,g}=exp\left({\beta }_{g}X+{\epsilon }_g\right)$ for g = 1,…, D, where ε_g is also independent of X. Then we have:

$$\begin{gathered} T=exp\left({\beta }_{0}X+\epsilon \right)=exp\left({\beta }_{1}X+{\epsilon }_1\right)+\dots +exp\left({\beta }_{D}X+{\epsilon }_D\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}=exp\left({\beta }_{0}X\right)\frac{exp\left({\beta }_{1}X\right)}{exp\left({\beta }_{0}X\right)}exp\left({\epsilon }_1\right)+\dots +exp\left({\beta }_{0}X\right)\frac{exp\left({\beta }_{D}X\right)}{exp\left({\beta }_{0}X\right)}exp\left({\epsilon }_D\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}=exp\left({\beta }_{0}X\right)\left\{exp\left[\left({\beta }_1-{\beta }_0\right)X+{\epsilon }_1\right]+\dots +exp\left[\left({\beta }_D-{\beta }_0\right)X+{\epsilon }_D\right]\right\} \end{gathered}$$

Since $T=exp\left({\beta }_{0}X\right)exp\left(\epsilon \right)$, It follows that $\epsilon =log\left\{exp\left[\left({\beta }_1-{\beta }_0\right)X+{\epsilon }_1\right]+\dots +exp\left[\left({\beta }_D-{\beta }_0\right)X+{\epsilon }_D\right]\right\}$. Without loss of generality, suppose that β₁ ≠ β₀. Then we have that $\epsilon =log\left\{exp\left[cX+{\epsilon }_1\right]+\dots +exp\left[\left({\beta }_D-{\beta }_0\right)X+{\epsilon }_D\right]\right\}$.where c is a non-zero constant. In this case, ε is not independent of X and cannot be independent of X unless ε₁ is not independent of X. But by our model assumptions, ε and ε_g are independent of X for g = 1,…, D, so it must be the case that β₁ = 0. Similarly, we will have that ${\beta }_2=\dots ={\beta }_D={\beta }_0$.

A similar argument can be used for progressive models that have the form in Figure 1b. We will show the case of the progressive illness-death model (Figure 1c), but the proof is analogous for models with a larger state space. Suppose we have a 3-state model where subjects can transition from state 0→1, 1→2, and 0→2, with state 2 as the absorbing state. As before, let T_gh denote the random variable for the direct transition from state g to state h, let T denote the absorbing failure time from origin, and assume $T=exp\left({\beta }_{0}X+\epsilon \right)$, where ε is independent of X. Let $T_{gh}=exp\left({\beta }_{gh}X+{\epsilon }_{gh}\right)$ for g = 0, 1, h = 1, 2, and h > g, where ε_gh is also independent of X. We have that

$$\begin{gathered} T=1\left[exp\left({\beta }_{01}X+{\epsilon }_{01}\right)\le exp\left({\beta }_{02}X+{\epsilon }_{02}\right)\right]\left[exp\left({\beta }_{01}X+{\epsilon }_{01}\right)+exp\left({\beta }_{12}X+{\epsilon }_{12}\right)\right] \\ \hspace{1em}+I\left[exp\left({\beta }_{01}X+{\epsilon }_{01}\right)>exp\left({\beta }_{02}X+{\epsilon }_{02}\right)\right]\left[exp\left({\beta }_{02}X+{\epsilon }_{02}\right)\right] \\ \hspace{1em}=exp\left({\beta }_{0}X\right)I\left[exp\left({\beta }_{01}X+{\epsilon }_{01}\right)\le exp\left({\beta }_{02}X+{\epsilon }_{02}\right)\right]\left\{exp\left[\left({\beta }_{01}-{\beta }_0\right)X+{\epsilon }_{01}\right]\left({\beta }_{12}-{\beta }_0\right)X+{\epsilon }_{12}\right\} \\ \hspace{1em}+exp\left({\beta }_{0}X\right)I\left[exp\left({\beta }_{01}X+{\epsilon }_{01}\right)>exp\left({\beta }_{02}X+{\epsilon }_{02}\right)\right]\left\{exp\left[\left({\beta }_{02}-{\beta }_0\right)X+{\epsilon }_{02}\right]\right\} \end{gathered}$$ (11)

Since $T=exp\left({\beta }_{01}X+\epsilon \right)$, it follows that $\epsilon =log\left\{I\left[exp\left({\beta }_{01}X+{\epsilon }_{01}\right)<exp\left({\beta }_{02}X+{\epsilon }_{02}\right)\right]\left\{exp\left[\left({\beta }_{01}-{\beta }_0\right)X+{\epsilon }_{01}\right]+exp\left[\left({\beta }_{12}-{\beta }_0\right)X+{\epsilon }_{12}\right]\right\}+I\left[exp\left({\beta }_{01}X+{\epsilon }_{01}\right)\right]>exp\left({\beta }_{02}X+{\epsilon }_{02}\right)\left\{exp\left[\left({\beta }_{02}+{\beta }_0\right)X+{\epsilon }_{02}\right]\right\}\right\}$. In order for the indicator functions to be independent of X, we would need β₀₁ = β₀₂, and in order for the non-indicator terms to be independent of X, we need β₀₁ = β₁₂ = β₀₂ = β₀. If at least one of β₀₁, β₁₂, β₀₂ are not equal to β₀, then ε is not independent of X, which contradicts our model assumption.

A.2. Justification for Estimating Equation

Consider the formulation of the estimating equation given in (5):

$$U_P\left(\beta \right)=\frac{1}{n^2}\sum _i\sum _{j<i}\left(X_i-X_j\right)\left[P\left({\tilde{e}}_i{}^{\beta }<{\tilde{e}}_j{}^{\beta }|S_i\left(e_j^{\beta }\right),S_j\left(e_j^{\beta }\right)\right)-P\left({\tilde{e}}_i{}^{\beta }>{\tilde{e}}_j{}^{\beta }|S_i\left(e_i^{\beta }\right),S_j\left(e_j^{\beta }\right)\right)\right]$$

We can think of the probabilities as expectations of an indicator function conditional on what we observe:

$$\frac{1}{n^2}\sum _i\sum _{j<i}\left(X_i-X_j\right)E\left[I\left({\tilde{e}}_i{}^{\beta }<{\tilde{e}}_j{}^{\beta }|S_i\left(e_j^{\beta }\right),S_j\left(e_j^{\beta }\right)\right)-I\left({\tilde{e}}_i{}^{\beta }>{\tilde{e}}_j{}^{\beta }|S_i\left(e_i^{\beta }\right),S_j\left(e_j^{\beta }\right)\right)\right]$$

where the expectation is taken with respect to the distribution of the residual failure times conditional on the disease states at the residual follow-up times. This function can be seen to be centered at 0 when β = β₀, as its expectation is:

$$\left(X_i-X_j\right)E\left\{E\left[I\left({\tilde{e}}_i{}^{\beta }<{\tilde{e}}_j{}^{\beta }|S_i\left(e_i^{\beta }\right),S_j\left(e_j^{\beta }\right)\right)-I\left({\tilde{e}}_i{}^{\beta }>{\tilde{e}}_j{}^{\beta }|S_i\left(e_i^{\beta }\right),S_j\left(e_j^{\beta }\right)\right)\right]\right\}$$

where the outside expectation is taken with respect to the distribution of the observed states at the residual follow-up times. By the law of iterated expectations, this is simply equal to:

$$\left(X_i-X_j\right)\left[P\left({\tilde{e}}_i{}^{\beta }<{\tilde{e}}_j{}^{\beta }\right)-P\left({\tilde{e}}_i{}^{\beta }>{\tilde{e}}_j{}^{\beta }\right)\right]$$

Since ${\tilde{e}}_i{}^{\beta }$ and ${\tilde{e}}_j{}^{\beta }$ are i.i.d. and independent of X_i and X_j when β = β₀, it follows that the expectation is 0 under boundedness of the residual failure time and log censoring time densities, and the covariates.

A.3. Variance estimation for $\widehat{\beta }$: Gaussian Quadrature Method

First, we give the assumptions in Jin et al. for validity of their Monte Carlo Method and Gaussian Quadrature Method of variance estimation (Jin et al 2014). Suppose we denote the estimating equation as U (β ), and β₀ is the true parameter vector:

Assumption 1: $\sqrt{n}U\left({\beta }_0\right)$ is asymptotically normal with mean 0 and covariance matrix D.

Assumption 2: The estimator $\widehat{\beta }$ is root-n consistent, and $\sqrt{n}\left(\widehat{\beta }-{\beta }_0\right)$ is asymptotically normal with mean 0 and covariance matrix V.

Assumption 3: U (β ) is locally asymptotically linear in a neighborhood of β₀.

Let B be the limiting slope matrix of U (β₀). B is difficult to estimate because the estimating function U is not smooth in β. First, we define Г = n^−1/2V ^1/2, where V = B⁻¹DB⁻¹, i.e. the variance of $\sqrt{n}\left(\widehat{\beta }-{\beta }_0\right)$. We are ultimately interested in estimating Г, which depends on B. Jin et al. show that the derivative B of a smoothed version of the estimating equation satisfies the following expression:

$$B\left(\Gamma ;\beta \right)=E_Z\left[U\left(\beta +\Gamma {\rm Z}\right)Z^T{\Gamma }^{-1}\right].$$ (12)

We can use Gaussian quadrature or Monte Carlo methods to approximate B(Г; β ) and evaluate Г, but notice that B(Г; β ) also depends on Г, resulting in an iterative algorithm. We describe our implementation of the algorithm for the Gaussian Quadrature Method below:

1. Calculate an estimate $\widehat{D}$ for D, the covariance matrix of $\sqrt{n}U\left(\beta \right)$. This can be done using the formula in (6), or a bootstrap procedure. Set Г₀ = n^−1/2I.

2. Suppose the dimension of β is p. Choose m nodes x _j, j = 1,…, m, based on one-dimensional Gauss- Hermite quadrature, and let z₁, z₂,…, z_mp each be a p×1 vector for a unique single combination of the m nodes among p points. For example, if we choose 5 1-D Gauss-Hermite quadrature nodes, and we had 2 βʹ_s to estimate, we would have 5² unique vectors z _j of 2-dimensional nodes for estimating the (double) integral of interest; these two dimensional nodes would be (x₁, x₁), (x₁, x₂),…, (x₂, x₁),…, (x₅, x₅) (see Figure 2). Let w_j be the p×1 vector of Gaussian quadrature weights corresponding to the nodes in z _j. Thus, we will have a grid of points over which we approximate the p-dimensional integral B(Г; β). We are interested in computing the integral, ${{\int }_{-\infty }^{\infty }\left(\frac{1}{\sqrt{2\pi }}\right)}^p{e}^{-x_p^2/2}\dots e^{-x_1^2/2}\left[U\left(\beta +\Gamma x\right)x^T{\Gamma }^{-1}\right]d{x}_1\dots d{x}_p$. Since Gauss-Hermite quadrature computes integrals of the form ${\int }_{-\infty }^{\infty }{e}^{-x^2}f\left(x\right)dx$, we use a change of variable on x so that we can write the integral in this form. Set $x^{\ast }=\sqrt{2}x$ = then the integral becomes ${{\int }_{-\infty }^{\infty }\left(\frac{1}{\sqrt{\pi }}\right)}^p{e}^{-x_1^{{}^{\ast }2}}\dots e^{-x_p^{{}^{\ast }2}}\left[U\left(\beta +\Gamma x^{\ast }\right)x^{\ast T}{\Gamma }^{-1}\right]d{x}_1^{\ast }\dots d{x}_p^{\ast }$ Thus, let $z_j^{\ast }=\sqrt{2}{z}_j$ for all j, and proceed.

3. Compute at the k^th step:

   $$B_k=B\left({\Gamma }_{k-1};\widehat{\beta }\right)=\frac{1}{{\sqrt{\pi }}^p}\sum _{j=1}^{m}U\left(\widehat{\beta }+{\Gamma }_{k-1}{z}_j^{\ast }\right)z_j^{\ast }{\Gamma }_{k-1}^{-1}\prod _{l=1}^p{w}_{jl}$$ (13)

   where w_jl is the l^th element of the weight vector w_j.

4. Calculate $G_k=B_k^{-1}\widehat{D}{B}_k^{-1}$ and let ${\Gamma }_k=G_k^{1/2}{n}_k^{-1/2}$.

5. Repeat steps 3 and 4 until Г_k converges within a specified tolerance level.

The diagonal of the matrix Г_k at the last iteration yields the standard error estimates for the vector $\widehat{\beta }$. The MCM is the same as the above method, except that in step 2 the z _j vectors are randomly generated from a standard multivariate normal distribution, and in step 3 B_k is estimated as $B\left({\Gamma }_{k-1};\widehat{\beta }\right)=\frac{1}{m}{\sum }_{j=1}^{m}U\left(\widehat{\beta }+{\Gamma }_{k-1}{z}_j\right)z_j^T{\Gamma }_{k-1}^{-1}$. In simulations, we found that as few as 8–10 Gauss-Hermite nodes worked reasonably well for the variance estimation when there is a single covariate.