Abstract
Incomplete multi-view clustering optimally integrates a group of pre-specified incomplete views to improve clustering performance. Among various excellent solutions, multiple kernel k-means with incomplete kernels forms a benchmark, which redefines the incomplete multi-view clustering as a joint optimization problem where the imputation and clustering are alternatively performed until convergence. However, the comparatively intensive computational and storage complexities preclude it from practical applications. To address these issues, we propose Late Fusion Incomplete Multi-view Clustering (LF-IMVC) which effectively and efficiently integrates the incomplete clustering matrices generated by incomplete views. Specifically, our algorithm jointly learns a consensus clustering matrix, imputes each incomplete base matrix, and optimizes the corresponding permutation matrices. We develop a three-step iterative algorithm to solve the resultant optimization problem with linear computational complexity and theoretically prove its convergence. Further, we conduct comprehensive experiments to study the proposed LF-IMVC in terms of clustering accuracy, running time, advantages of late fusion multi-view clustering, evolution of the learned consensus clustering matrix, parameter sensitivity and convergence. As indicated, our algorithm significantly and consistently outperforms some state-of-the-art algorithms with much less running time and memory.
Index Terms: multiple kernel clustering, multiple view learning, incomplete kernel learning
1. Introduction
Multi-view clustering (MVC) optimally integrates features from different views to improve clustering performance [1]. It has been intensively studied during the last few decade [2], [3], [4], [5], [6], [7], [8], [9], [10], [11], [12], [13], [14] and widely used in various applications, including object segmentation [15], [16], object pose estimation [17], image re-ranking [18], saliency detection [19], information retrieval [20], Cancer Biology [21], to name just a few.
A common assumption adopted by the aforementioned MVC algorithms is that all the views are complete. However, it is not uncommon to see that some views of a sample are absent in some practical applications such as Alzheimer’s disease prediction [22] and cardiac disease discrimination [23]. The research along this line is termed as incomplete multi-view clustering (IMVC), which can be roughly grouped into two categories. The first category firstly fills the incomplete views with an imputation algorithm and then applies a standard MVC algorithm to these imputed views, which is termed “two-stage” algorithm. The widely used imputation algorithms include zero-filling, mean value filling, k-nearest-neighbor filling and expectation-maximization (EM) filling [24]. Some advanced algorithms have recently been proposed to perform matrix imputation [25], [26], [27], [28]. For example, the work in [25] constructs a full kernel matrix for the other incomplete view with the help of one complete view. The work in [26] proposes an algorithm to accomplish multi-view learning with incomplete views by exploiting the connections of multiple views, where different views are assumed to be generated from a shared subspace. A multi-incomplete-view clustering (MIC) algorithm and its online variant are proposed in [27], [29]. It first fills the missing instances in each incomplete view with average feature values, and adopts a joint weighted NMF algorithm to learn not only a latent feature matrix for each view but also minimize the disagreement between the latent feature matrices and the consensus matrix. By giving missing instances from each view lower weights, MIC minimizes the negative influences from the missing instances. In addition, the approach in [28] proposes to predict missing rows and columns of a base kernel by modelling both within-view and between-view relationships among kernel values. By observing that the above-mentioned “two-stage” algorithms disconnect the processes of imputation and clustering, the other category, termed as “one-stage”, puts forward to unify imputation and clustering into a single optimization procedure and instantiate a clustering-oriented algorithm termed as multiple kernel k-means with incomplete kernels (MKKM-IK) algorithm [30]. Specifically, the clustering result at the last iteration guides the imputation of absent kernel elements, and the latter is used in turn to conduct the subsequent clustering. By this way, these two procedures are seamlessly connected, with the aim to achieve better clustering performance.
Of the above-mentioned IMVC algorithms, the “one-stage” methods form a benchmark, where the incomplete views are optimized to best serve clustering. The main contribution of these methods is the unification of imputation and clustering, so that the imputation would be meaningful and beneficial for clustering. It has been well known that the “one-stage” methods can achieve excellent clustering performance [30], but they also suffer from some non-ignorable drawbacks. Firstly, the high time and space complexities prevent them from being applied to large-scale clustering tasks. Secondly, existing “one-stage” methods directly impute multiple incomplete similarity matrices, in which the number of variables increases quadratically with the number of samples for each view. This could make the whole optimization over-complicated and also considerably increase the risk of falling into a low-quality local minimum. Thirdly, note that a clustering result is determined by a whole similarity matrix in [30]. As a result, the imputation to an incomplete similarity matrix has impact to the clustering of all samples, no matter whether a sample is complete or not. When an imputation is not of high quality, it could adversely affect the clustering result of all samples, especially for those with complete views.
All of the above issues signal that directly imputing the incomplete similarity matrices seems to be problematic and that a more efficient and effective approach shall be taken. We argue that multiple view clustering is essentially a task of information fusion. It is known that information fusion can be performed at different levels. From bottom to up, they are raw data level, feature level and decision level, respectively. Although performing at lower levels could lead to promising result, working at higher levels has the advantage of reduced computational complexity and less interference to the individual decision made from each information channel.
In light of this, we propose to impute each incomplete base clustering matrix which is a partition matrix generated by performing clustering on each individual incomplete similarity matrix, instead of itself. This algorithm is termed as Late Fusion Incomplete Multi-view Clustering (LF-IMVC) in this paper. These base clustering matrices are then optimally utilized to learn a common clustering partition matrix, termed consensus clustering matrix. It is then employed to impute each incomplete base clustering matrix. These two steps are alternatively performed until convergence. Specifically, we maximize the alignment between the consensus clustering matrix and an uniformly weighted base clustering matrices with an optimal permutation, together with an extra term which constraints each base clustering matrix not far from its incomplete one. We design a simple and efficient algorithm to solve the resultant optimization problem by three singular value decomposition (SVD) per iteration, and analyze its computational and storage complexities and theoretically prove its convergence. After that, we conduct comprehensive experiments on eleven benchmark datasets to study the properties of the proposed algorithm, including the clustering accuracy with the various missing ratios, the running time with the various number of samples, the evolution of the learned consensus matrix with iterations, the clustering accuracy with the variation of hyper-parameter and the objective value with iterations. As demonstrated, LF-IMVC significantly and consistently outperforms the state-of-the-art methods in terms of clustering accuracy with much less running time.
We end up this section by clarifying the difference between the proposed LF-IMVC and some recent late fusion MVC [14], [31]. The work in [31] proposes a multi-view clustering ensemble algorithm based on multi-view clustering and clustering ensembles. Specifically, a Gaussian kernel with a pre-specified parameter σ is applied into each view data to construct multiple kernel matrices. They are taken as the input of multiple kernel k-means algorithms to generate a clustering partition, which is a partition of given samples. By this way, one can obtain more clustering partitions by taking different σ, which are integrated by a clustering ensemble algorithm. The difference between this work and ours is that it cannot be able to handle clustering ensembles with incomplete clustering partitions. A Multi-View Ensemble Clustering (MVEC) framework is proposed in [14] to solve multi-view clustering (MVC) in an ensemble clustering way. It generates basic partitions (BPs) for each view individually and seeks for a consensus partition among all the BPs. The low-rank and sparse decomposition are employed to explicitly consider the connection between different views and detect the noises in each view. Moreover, the spectral ensemble clustering task is also involved to achieve the final consensus partition. As seen, MVEC [14] and the proposed LF-IMVC clearly differ from the motivation, formulation, computational complexity and ability in handling incomplete views.
2. Related Work
Multiple kernel k-means (MKKM) provides an elegant framework for multi-view clustering. In this section, we briefly review MKKM and its variants of handling incomplete multi-view clustering.
2.1. Multiple Kernel k-means (MKKM)
Let be a collection of n samples, and be the p-th feature mapping that maps × onto a reproducing kernel Hilbert space . In multiple kernel setting, each sample is represented as ϕβ(x) = [β1 ϕ1 (x(1))⊤, ⋯, βm ϕm (x(m))⊤]⊤, where x(p) denotes the p-th (1 ≤ p ≤ m) view of x, β = [β1, ⋯, βm]⊤ consists of the coefficients of the m base kernels . These coefficients will be optimized during learning.
Based on the definition of ϕβ(x), a kernel function can be expressed as
| (1) |
A kernel matrix Kβ is then calculated by applying the kernel function κβ (⋅,⋅) into Based on the kernel matrix Kβ, the objective of MKKM can be written as
| (2) |
where Ik is an identity matrix with size k × k.
The optimization problem in Eq.(2) can be solved by alternatively updating H and β:
i) Optimizing H given β. With the kernel coefficients β fixed, H can be obtained by solving a kernel k-means clustering optimization problem shown in Eq.(3);
| (3) |
The optimal H for Eq.(3) can be obtained by taking the k eigenvectors having the larger eigenvalues of Kβ [32].
ii) Optimizing β given H. With H fixed, β can be optimized via solving the following quadratic programming with linear constraints,
| (4) |
2.2. MKKM with Incomplete Kernels (MKKM-IK)
The recent work in [30] has extended the existing MKKM to enable it to handle incomplete multi-view clustering. In specific, it unifies the imputation and clustering procedure into a single optimization objective and alternatively optimizes each of them. That is, i) imputing the absent kernels under the guidance of clustering; and ii) updating the clustering with the imputed kernels. The above idea is mathematically fulfilled as follows,
| (5) |
where sp (1 ≤ p ≤ m) denote the sample indices for which the p-th view is present and be used to denote the kernel sub-matrix computed with these samples. The constraint is imposed to ensure that Kp maintains the known entries during the course. As seen, the ultimate goal of Eq.(5) is clustering, while the imputation of incomplete kernels can be treated as a by-product of learning.
A three-step alternative algorithm is then developed to solve the optimization problem in Eq.(5):
i) Optimizing H with fixed β and . Given β and , the optimization in Eq.(5) for H reduces to a standard kernel k-means problem, which can be efficiently solved as Eq.(3);
ii) Optimizing with fixed β and H. Given β and H, the optimization in Eq.(5) with respect to each Kp is equivalent to the following optimization problem,
| (6) |
It is shown that the optimal Kp in Eq.(6) has the closed-form expression as in Eq.(7), where U = In – HH⊤ and U(cm) is obtained by taking the entries of U corresponding to the complete and incomplete sample indices. Interested readers are referred to [30].
iii) Optimizing β with fixed H and . Given H and , the optimization in Eq.(5) for β is a quadratic programming with linear constraints, which can be efficiently solved as in Eq.(4).
| (7) |
Although the recently proposed MKKM-IK demonstrates excellent clustering performance in various applications [30], it also suffers from the following non-ignorable drawbacks. Firstly, from the above optimization procedure, we observe that its computational complexity is per iteration, where n, np (np ≤ n) and m are the number of all samples, observed samples of p-th view and views. During the learning procedure, it requires to store m base kernel matrices with size n. Therefore, its storage complexity is . The relatively high computational and storage complexities preclude it from being applied to large-scale clustering tasks. Furthermore, as seen from Eq.(7), there are elements to be imputed for the p-th incomplete base kernel matrix Kp(1 ≤ p ≤ m). It unnecessarily increases the complexity of the optimization and the risk of being trapped into a low-quality local minimum. In addition, the imputation on would affect the clustering of all samples, no matter whether they are complete. This improperly increases the impact of imputation on all samples, especially for those with complete views. As a result, instead of imputing incomplete similarity matrices , we propose to impute the incomplete base clustering matrices to address the aforementioned issues. Moreover, we argue that this way of imputation could be more natural and reasonable since all of them reside in the space of clustering partition, which would produce better imputation and finally boost the clustering.
3. Late Fusion Incomplete Multi-view Clustering (LF-IMVC)
3.1. The Proposed Formulation
According to the above discussion, we turn to fill incomplete base clustering matrices with , which can be obtained by solving kernel k-means in Eq.(5) with m incomplete base kernel matrices . Note that other similarity based clustering algorithms such as spectral clustering can also be used to generate .
LF-IMVC proposes to simultaneously perform clustering and the imputation of missing elements among base clustering matrices with . Specifically, it firstly finds a consensus clustering matrix H from , and then imputes the incomplete parts of them with the learned consensus matrix. By this way, the above two learning processes can be seamlessly coupled and they are allowed to negotiate with each other to achieve better clustering. The above idea can be fulfilled as follows,
| (8) |
where H and Hp are the consensus clustering matrix and the p-th base clustering matrix, respectively, and Wp is the p-th permutation matrix in order to optimally match Hp and H. The constraint is imposed to ensure that Hp maintains the known entries during the course. The orthogonal constraints are imposed on H, Hp and Wp since they are clustering matrices and permutation matrix, respectively.
Compared with MKKM-IK [30], the objective function of LF-IMVC in Eq.(8) has the following nice properties: (1) Less imputation variables: The number of elements needs to be filled for the p-th view is (n − np) × k, which is much less than required by MKKM IK because in practice. This could dramatically simplify the model and usually reduce the risk of being trapped into a local minimum. As a result, our optimization would be more robust to the initialization during optimization. (2) Less vulnerable to low-quality imputation: In LF-IMVC, clustering on samples with complete views will not be affected by the imputation. However, it is not this case for MKKM-IK because it needs to fill all incomplete elements and conduct eign-decomposition on the whole imputed similarity for clustering. This is helpful to make the proposed model be more robust in the whole course of optimization.
Although the objective in Eq.(8) is not difficult to understand, the equality and orthogonal constraints on Hp make the optimization intractable. To address this issue, we remove the equality constraint on Hp and instead require it to maximally align with . This leads to the follow optimization problem in Eq.(9).
| (9) |
where with other elements being zeros and λ is a regularization parameter to trade of clustering and imputation.
Though the model in Eq.(9) is simple, it admits the following advantages: 1) our objective function is more direct and well targets the ultimate goal, i.e., clustering, by integrating imputation and clustering into one unified learning framework, where the imputation is treated as a byproduct; 2) our formulation utilizes H to complete each incomplete base clustering matrix rather than the incomplete base kernels matrices as in [30], which is more natural since both H and reside in clustering partition space; 3) our algorithm is able to naturally deal with a large number of base clustering matrices and adaptively combine them for clustering; 4) our algorithm does not require any views to be completely observed, which is however necessary for some of the existing imputation algorithms such as [25].
3.2. Alternative Optimization
Simultaneously optimizing H, and in Eq.(9) is difficult. In the following, we design a simple and computationally efficient three-step algorithm to solve it alternatively. At each step, the resultant optimization is reduced to a SVD, which can be efficiently solved by off the-shelf packages.
3.2.1. Solving H with fixed and
Given and , the optimization w.r.t H in Eq.(9) is equivalent to
| (10) |
where . It is a singular value decomposition (SVD) problem and can be efficiently solved with computational complexity , where k is the number of clusters.
3.2.2. Solving with fixed and H
Given and H, the optimization w.r.t permutation matrix Wp in Eq.(9) equivalently reduces to the following one,
| (11) |
where . Again, it is a SVD optimization problem with computational complexity .
3.2.3. Solving with fixed H and
Given H and , the optimization w.r.t Hp in Eq.(9) is equivalent to
| (12) |
where . Once again, it is a SVD problem and can be efficiently solved with computational complexity .
Algorithm 1.
The Proposed LF-IMVC
In sum, our algorithm for solving Eq.(9) is outlined in Algorithm 1, where the absent entries of are initially imputed with zeros and obj(t) denotes the objective value at the t-th iteration. The following Theorem 1 shows Algorithm 1 is guaranteed to converge.
Theorem 1. Algorithm 1 is guaranteed to converge to a local optimum.
Proof. Note that for . Based on this inequality, we derive the upper bound of the objective in Eq.(9). Note that . Also, . Therefore, the objective in Eq.(9) is upper bounded. Meanwhile, it is worth pointing out that the optimization with one variable while keeping the other two is a SVD, which is a strictly convex optimization and the optimum can be achieved. Therefore, the objective of Algorithm 1 is guaranteed to be monotonically increased when optimizing one variable with others fixed at each iteration. At the same time, the objective is upper-bounded by . As a result, our algorithm is guaranteed to converge to a local minimum.
3.3. Discussion and Extension
We end up this section by firstly analyzing the computational and storage complexities, initialization of , and then discussing some potential extensions of LF-IMVC.
Computational complexity:
As seen from Algorithm 1, the computational complexity of LF-IMVC is per iteration, where n, m and k are the number of samples, views and clusters, respectively. Therefore, LFIMVC has a linear computational complexity with number of samples, which enables it more efficiently to handle large scale clustering tasks when compared with MKKM-IK [30].
Storage complexity:
During the learning procedure, Algorithm 1 needs to store H and . Its storage complexity is , which is much less than that of MKKM-IK with since n ≫ k.
Initialization of :
In our implementation, each p is generated by solving a conventional kernel k-means with K (sp, sp), where is a kernel matrix calculated with np observed samples of the p-view. Its computational complexity is . Note that this procedure is required to perform only once. O As a result, the computational cost in this initialization can be treated as a constant. Note that any technique that can boost the scalability of kernel k-means (or spectral clustering) such as [33] can be directly applied to ours to shorten this initialization. We simply initialize the incomplete part of as zeros, and as identity matrix. This initialization has well demonstrated superior clustering performance of LFIMVC in our experiments.
Extentions:
LF-IMVC inherits the advantage of MKKMIK [30] which unifies the imputation and clustering into a single procedure. Instead of completing kernel matrices, LF-IMVC imputes the incomplete base clustering matrices which are generated by performing kernel k-means with incomplete base kernel matrices. The algorithm in this work can be extended from the following aspects. Firstly, LFIMVC could be further improved by sufficiently considering the correlation among . For example, we may build this correlation by other criteria such as Kullback-Leibler (KL) divergence [34], maximum mean discrepancy [35], Hilbert-Schmidt independence criteria (HSIC), to name just a few. This prior knowledge could provide a good regularization on mutual base clustering matrix completion, and would be helpful to improve the clustering performance. Secondly, the weights of base clustering matrices could be adaptively adjusted in order to find the better consensus clustering matrix H, making it better serve for clustering. Thirdly, the way in generating could be readily extendable to other similarity based clustering algorithms, such us spectral clustering [36], [37]. It could further improve the clustering performance. Last but not least, the idea of joint imputation and clustering is so natural that can be generalized to other learning task such as classification, feature selection/extraction, etc.
4. Experiments
4.1. Experimental settings
The proposed algorithm is experimentally evaluated on eleven widely used multiple kernel benchmarkdata sets shown in Table 4, where each kernel matrix corresponds to one view. They are Oxford Flower17 and Flower1021, Caltech1022, UCI-Digital3, Protein Fold Prediction4 and Columbia Consumer Video (CCV)5. For these datasets, all kernel matrices are pre-computed and can be publicly downloaded from the above websites. Meanwhile, Caltech102–5 means the number of samples belonging to each cluster is 5, and so on.
TABLE 4:
Datasets used in our experiments.
| Dataset | #Samples | #Kernels | #Classes |
|---|---|---|---|
| Flower17 | 1360 | 7 | 17 |
| Flower102 | 8189 | 4 | 102 |
| Caltech102–5 | 510 | 48 | 102 |
| Caltech102–10 | 1020 | 48 | 102 |
| Caltech102–15 | 1530 | 48 | 102 |
| Caltech102–20 | 2040 | 48 | 102 |
| Caltech102–25 | 2550 | 48 | 102 |
| Caltech102–30 | 3060 | 48 | 102 |
| UCI-Digital | 2000 | 3 | 10 |
| ProteinFold | 694 | 12 | 27 |
| CCV | 6773 | 6 | 20 |
We compare the proposed algorithm with several commonly used imputation methods, including zero filling (ZF), mean filling (MF), k-nearest-neighbor filling (KNN) and the alignment-maximization filling (AF) proposed in [25]. The widely used MKKM [21] is applied with these imputed base kernels. These two-stage methods are termed MKKM+ZF, MKKM+MF, MKKM+KNN and MKKM+AF, respectively. In addition, some recently proposed MKKM based method MKKM-IK [30], late fusion method [14] and NMF based method [27] are also incorporated into comparison.
For all data sets, it is assumed that the true number of clusters k is known and it is set as the true number of classes. We follow the approach in [30] to generate the missing vectors as follows. We first randomly select round(ε * n) samples, where round(·) denotes a rounding function. For each selected sample, a random vector v = (υ1, ⋯ , υm) ∊ [0, 1]m and a scalar υ0 (υ0 ∊ [0, 1]) are then generated, respectively. The p-th view will be present for this sample if υp ≥ υ0 is satisfied. In case none of υ1, ⋯ , υm can satisfy this condition, we will generate a new v to ensure that at least one view is available for a sample. Note that this does not mean that we require a complete view across all the samples. After the above step, we will be able to obtain the index vector sp listing the samples whose p-th view is present. The parameter ε, termed missing ratio in this experiment, controls the percentage of samples that have absent views, and it affects the performance of the algorithms in comparison. In order to show this point in depth, we compare these algorithms with respect to ε. Specifically, ε on all the datasets is set as [0.1 : 0.1 : 0.9].
The widely used clustering accuracy (ACC), normalized mutual information (NMI) and purity are applied to evaluate the clustering performance. Specifically, ACC is defined as follows,
| (13) |
where ci and yi represent the obtained cluster label and the provided ground-truth label of xi (1 ≤ i ≤ n), n is the number of samples, δ(u, υ) is the delta function that equals one if u = υ and equals zero otherwise, and map(ci) is the permutation mapping function that maps each cluster label ci to the equivalent label from data. The best mapping can be found by using the Kuhn-Munkres algorithm [38]. Similarly, NMI is defined as follows. Let y and c denote the set of clusters obtained from the ground truth and a clustering algorithm, respectively. Their mutual information metric MI(y, c) is defined as follows:
| (14) |
where p(yi) and p(cj) are the probabilities that a sample arbitrarily selected from data belongs to the clusters yi and cj, respectively, and p(yi, cj) is the joint probability that the arbitrarily selected samples belongs to the clusters yi and cj at the same time. The normalized mutual information (NMI) is then defined as follows:
| (15) |
where H(y) and H(c) are the entropies of y and c, respectively.
For all algorithms, we repeat each experiment for 50 times with random initialization to reduce the affect of randomness caused by k-means, and report the best result. Meanwhile, we randomly generate the “incomplete” patterns for 30 times in the above-mentioned way and report the statistical results. The aggregated ACC, NMI and purity are used to evaluate the goodness of the algorithms in comparison. Taking the aggregated ACC for example, it is obtained by averaging the averaged ACC achieved by an algorithm over different ε.
In the following parts, we conduct comprehensive experiments to study the properties of LF-IMVC from six aspects: clustering performance, running time, the advantage of joint imputation and clustering in a late fusion manner, the evolution of the learned consensus clustering matrix, parameter sensitivity and convergence.
4.2. Clustering Performance
4.2.1. Experimental Results on Flower17 and Flower102
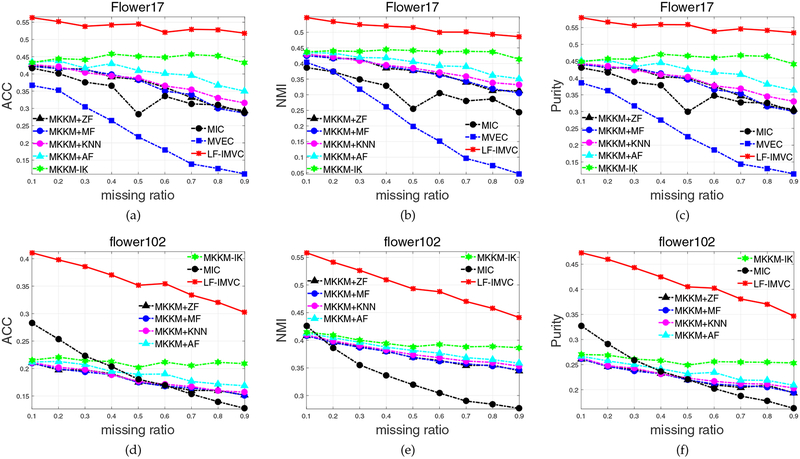
Figure 1 presents the ACC, NMI and purity comparison of the above algorithms with different missing ratios on the Flower17 and Flower102 datasets. We have the following observations: 1) The recently proposed MKKMIK [30] (in green) significantly outperforms existing two-stage imputation methods. For example, it exceeds the best two-stage imputation method (AF+MKKM) by 0.1%, 0.6%, 2.5%, 2.8%, 4.1%, 4.7%, 6.0%, 8.5%, 8.2% in terms of clustering accuracy, with the variation of missing ratios in [0.1, ⋯, 0.9] on Flower17. These results verify the effectiveness of its joint optimization on imputation and clustering. 2) The proposed LFIMVC significantly and consistently outperforms MKKM-IK. Specifically, it improves the latter by 13.0%, 10.7%, 9.7%, 8.5%, 9.4%, 7.3%, 7.3%, 7.6%, 8.6% with the variation of missing ratios in [0.1⋯, 0.9] on Flower17. These results verify the effectiveness of imputing base clustering matrices rather than kernel matrices. 3) The superiority of LF-IMVC is more significant when the missing ratio is relatively small. For example, LF-IMVC improves the second best algorithm (MKKM-IK) by 13% on Flower17 in terms of clustering accuracy when the missing ratio is 0.1 (see Figure 1a).
Fig. 1:
Clustering accuracy, NMI and purity comparison with various missing ratios on Flower17 and Flower102. The results of MVEC [14] on Flower102 are not reported due to the “out of memory” error.
We also report the aggregated ACC, NMI and purity, and the standard deviation in Table 1, where the one with the highest performance is shown in bold. Again, we observe that the proposed algorithm significantly outperforms MKKM+ZF, MKKM+MF, MKKM+KNN, MKKM+AF and MKKM-IK. For example, LF-IMVC exceeds the second best one (MKKM-IK) by 9.1% and 14.8% in terms of clustering accuracy on Flower17 and Flower102, respectively. These results are consistent with our observations in Figure 1.
TABLE 1:
Aggregated ACC, NMI and purity comparison (mean±std) of different clustering algorithms on Flower17 and Flower102.
| Datasets | MKKM+ZF | MKKM+MF | MKKM+KNN | MKKM+AF | MKKM-IK | MIC | MVEC | LF-IMVC |
|---|---|---|---|---|---|---|---|---|
| [25] | [30] | [27] | [14] | Proposed | ||||
| ACC | ||||||||
| Flower17 | 36.90 ± 0.77 | 36.75 ± 0.57 | 37.78 ± 0.61 | 40.48 ± 0.73 | 44.63 ± 0.57 | 34.33 ± 2.19 | 22.89 ± 0.39 | 53.75 ± 0.46 |
| Flower102 | 17.98 ± 0.15 | 18.01 ± 0.17 | 18.23 ± 0.13 | 19.22 ± 0.14 | 21.09 ± 0.16 | 19.26 ± 0.22 | – | 35.93 ± 0.22 |
| NMI | ||||||||
| Flower17 | 37.31 ± 0.41 | 37.28 ± 0.45 | 38.22 ± 0.48 | 40.07 ± 0.44 | 43.67 ± 0.29 | 31.22 ± 2.27 | 21.36 ± 0.34 | 51.34 ± 0.31 |
| Flower102 | 37.38 ± 0.13 | 37.39 ± 0.14 | 37.80 ± 0.09 | 38.38 ± 0.13 | 39.56 ± 0.12 | 33.10 ± 0.24 | – | 49.90 ± 0.11 |
| Purity | ||||||||
| Flower17 | 38.36 ± 0.63 | 38.30 ± 0.60 | 39.30 ± 0.57 | 41.99 ± 0.60 | 45.89 ± 0.48 | 35.71 ± 2.17 | 23.77 ± 0.39 | 55.35 ± 0.26 |
| Flower102 | 22.45 ± 0.11 | 22.43 ± 0.12 | 22.80 ± 0.12 | 23.73 ± 0.18 | 25.76 ± 0.18 | 22.95 ± 0.25 | – | 41.22 ± 0.19 |
4.2.2. Experimental Results on Caltech102
Caltech102 has been widely used as a benchmark dataset to evaluate the performance of multi-view clustering [6]. Here we also compare all the above-mentioned algorithms on this data set where the number of samples for each cluster varies in the range of 5, 10, ⋯, 30. The clustering results of different algorithms with the variation of missing ratio are reported in Figure 2. The results on Caltech102–5 dataset are omitted due to space limit.
Fig. 2:
Clustering accuracy, NMI and purity comparison with various missing ratios on Caltech102. The results of MVEC [14] on Caltech102–20, Caltech102–25 and Caltech102–30 are not reported due to the “out of memory” error.
As can be seen, compared with existing two-stage imputation algorithms, the curve with green color corresponding to the recently proposed MKKM-IK [30] is on the top when the missing ratio varies from 0.1 to 0.9 in terms of ACC, NMI and purity, indicating its superior clustering performance. Meanwhile, the proposed LF-IMVC further significantly improves the performance of MKKM-IK. Taking the results in Figure 2 for example. MKKM-IK demonstrates the overall satisfying performance. However, LF-IMVC further significantly and consistently improves its performance. Moreover, from the sub-figures 2a-2m, we clearly see that the improvement of LF-IMVC over the compared ones is more significant with the increase of number of samples. The aggregated ACC, NMI and purity are also reported in Table 2. We again clearly see the advantages of our algorithms over the other ones in terms of ACC, NMI and purity. These results have well demonstrated the effectiveness and advantages of incorporating base clustering matrix reconstruction in clustering.
TABLE 2:
Aggregated ACC, NMI and purity comparison (mean±std) of different clustering algorithms on Caltech102.
| Datasets | MKKM+ZF | MKKM+MF | MKKM+KNN | MKKM+AF | MKKM-IK | MIC | MVEC | LF-IMVC |
|---|---|---|---|---|---|---|---|---|
| [25] | [30] | [27] | [14] | Proposed | ||||
| ACC | ||||||||
| Caltech102–5 | 26.07 ± 0.34 | 25.65 ± 0.26 | 27.30 ± 0.28 | 29.00 ± 0.29 | 28.88 ± 0.32 | 32.92 ± 0.44 | 28.11 ± 0.31 | 38.28 ± 0.29 |
| Caltech102–10 | 19.73 ± 0.19 | 19.68 ± 0.24 | 21.51 ± 0.20 | 22.56 ± 0.20 | 22.74 ± 0.17 | 31.37 ± 0.44 | 24.05 ± 0.19 | 35.12 ± 0.16 |
| Caltech102–15 | 17.12 ± 0.23 | 17.08 ± 0.17 | 18.89 ± 0.13 | 20.32 ± 0.19 | 20.79 ± 0.24 | 29.74 ± 0.37 | 16.87 ± 0.15 | 34.46 ± 0.22 |
| Caltech102–20 | 15.67 ± 0.12 | 15.65 ± 0.22 | 17.29 ± 0.16 | 18.89 ± 0.20 | 19.47 ± 0.14 | 28.57 ± 0.20 | – | 34.14 ± 0.25 |
| Caltech102–25 | 14.65 ± 0.18 | 14.58 ± 0.13 | 16.24 ± 0.13 | 17.71 ± 0.20 | 18.26 ± 0.18 | 27.36 ± 0.37 | – | 33.16 ± 0.19 |
| Caltech102–30 | 14.15 ± 0.12 | 14.05 ± 0.14 | 15.51 ± 0.16 | 17.11 ± 0.18 | 17.80 ± 0.22 | 26.69 ± 0.48 | – | 32.93 ± 0.20 |
| NMI | ||||||||
| Caltech102–5 | 64.33 ± 0.18 | 63.93 ± 0.14 | 65.87 ± 0.19 | 66.55 ± 0.11 | 66.48 ± 0.16 | 68.45 ± 0.16 | 63.12 ± 0.41 | 71.20 ± 0.18 |
| Caltech102–10 | 53.62 ± 0.12 | 53.65 ± 0.09 | 55.24 ± 0.11 | 55.72 ± 0.19 | 55.83 ± 0.14 | 61.05 ± 0.10 | 51.8 ± 0.24 | 63.60 ± 0.11 |
| Caltech102–15 | 47.40 ± 0.13 | 47.39 ± 0.11 | 48.82 ± 0.11 | 49.69 ± 0.13 | 50.06 ± 0.11 | 56.29 ± 0.19 | 45.12 ± 0.17 | 59.74 ± 0.10 |
| Caltech102–20 | 43.11 ± 0.10 | 43.08 ± 0.17 | 44.54 ± 0.12 | 45.58 ± 0.15 | 46.03 ± 0.07 | 53.12 ± 0.15 | – | 57.17 ± 0.17 |
| Caltech102–25 | 39.98 ± 0.10 | 39.88 ± 0.11 | 41.47 ± 0.09 | 42.45 ± 0.15 | 42.96 ± 0.18 | 50.40 ± 0.30 | – | 54.86 ± 0.06 |
| Caltech102–30 | 37.78 ± 0.08 | 37.66 ± 0.12 | 39.15 ± 0.13 | 40.29 ± 0.12 | 40.92 ± 0.14 | 48.34 ± 0.39 | – | 53.37 ± 0.11 |
| Purity | ||||||||
| Caltech102–5 | 26.73 ± 0.37 | 26.37 ± 0.31 | 27.90 ± 0.29 | 29.75 ± 0.34 | 29.59 ± 0.34 | 34.05 ± 0.47 | 29.1 ± 0.28 | 39.93 ± 0.29 |
| Caltech102–10 | 20.99 ± 0.15 | 20.97 ± 0.22 | 22.90 ± 0.22 | 23.96 ± 0.26 | 24.16 ± 0.23 | 32.80 ± 0.39 | 25.67 ± 0.22 | 37.06 ± 0.14 |
| Caltech102–15 | 18.52 ± 0.20 | 18.45 ± 0.16 | 20.39 ± 0.17 | 21.62 ± 0.18 | 22.16 ± 0.23 | 31.15 ± 0.40 | 17.68 ± 0.18 | 36.35 ± 0.16 |
| Caltech102–20 | 17.05 ± 0.11 | 17.02 ± 0.19 | 18.81 ± 0.22 | 20.17 ± 0.19 | 20.89 ± 0.14 | 30.00 ± 0.25 | – | 36.17 ± 0.23 |
| Caltech102–25 | 16.02 ± 0.22 | 15.99 ± 0.15 | 17.74 ± 0.15 | 19.12 ± 0.15 | 19.71 ± 0.14 | 28.89 ± 0.28 | – | 35.46 ± 0.23 |
| Caltech102–30 | 15.41 ± 0.10 | 15.36 ± 0.12 | 17.01 ± 0.14 | 18.39 ± 0.20 | 19.13 ± 0.22 | 28.12 ± 0.57 | – | 35.04 ± 0.16 |
4.2.3. Experimental Results on UCI-Digital
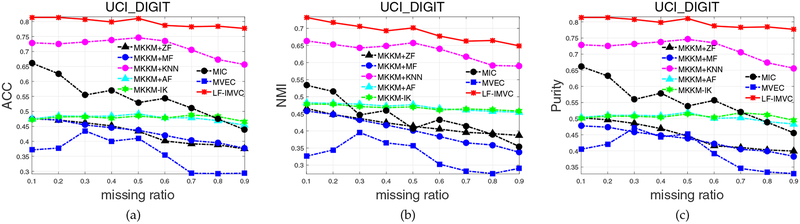
UCI-Digital dataset has been widely used as a benchmark in multi-view clustering. We also compare the clustering performance of the aforementioned algorithms on this dataset. The clustering accuracy, NMI and purity of these algorithms with the variation of missing ratio are plotted in Figure 3. From Figure 3a, we observe that the newly proposed MKKM-IK gives poor performance on this dataset, which is clearly inferior to the MKKM+KNN. The proposed LF-IMVC significantly improves this situation, demonstrating superior clustering performance. For example, it exceeds the second best one (MKKM+KNN) by 7.9%, 8.4%, 8.2%, 5.9%, 6.2%, 5.6%, 8.0%, 12.4%, 13.6% in terms of ACC. Similar results can be observed by aggregated clustering results in Table 3.
Fig. 3:
Clustering accuracy, NMI and purity comparison with various missing ratios on UCI-Digital.
TABLE 3:
Aggregated ACC, NMI and purity comparison (mean±std) of different clustering algorithms on UCI-Digital.
| Datasets | MKKM+ZF | MKKM+MF | MKKM+KNN | MKKM+AF | MKKM-IK | MIC | MVEC | LF-IMVC |
|---|---|---|---|---|---|---|---|---|
| [25] | [30] | [27] | [14] | Proposed | ||||
| ACC | ||||||||
| UCI-Digital | 42.74 ± 0.42 | 43.06 ± 0.29 | 71.32 ± 0.97 | 47.91 ± 0.46 | 48.02 ± 0.43 | 54.55 ± 1.12 | 35.88 ± 0.36 | 79.80 ± 0.55 |
| NMI | ||||||||
| UCI-Digital | 41.77 ± 0.19 | 40.01 ± 0.21 | 63.27 ± 0.52 | 46.98 ± 0.23 | 46.87 ± 0.24 | 43.93 ± 0.51 | 32.65 ± 1.09 | 68.99 ± 0.48 |
| Purity | ||||||||
| UCI-Digital | 44.64 ± 0.46 | 43.36 ± 0.26 | 71.44 ± 0.70 | 50.39 ± 0.33 | 50.75 ± 0.38 | 55.47 ± 0.82 | 39.94 ± 0.66 | 79.80 ± 0.55 |
4.2.4. Experimental Results on Protein Fold
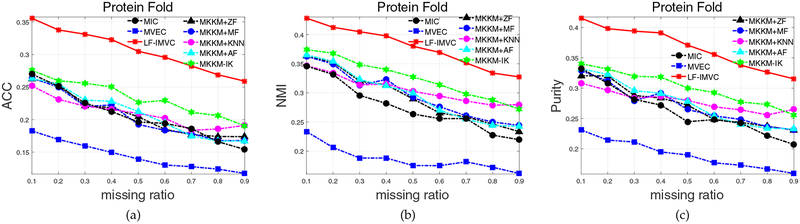
We have evaluated the aforementioned algorithms on Protein Fold dataset, which is a benchmark with 12 views. The clustering performance of these algorithms with the variation of missing is plotted in Figure 4 and the corresponding aggregated clustering accuracy, NMI and purity are reported in Table 5. From Table 4, we again see that the proposed LF-IMVC significantly and consistently outperforms the compared ones with the variation of missing ratio. This superiority coincides with the results in Table 5.
Fig. 4:
Clustering accuracy, NMI and purity comparison with various missing ratios on Protein Fold.
TABLE 5:
Aggregated ACC, NMI and purity comparison (mean±std) of different clustering algorithms on Protein Fold.
| Datasets | MKKM+ZF | MKKM+MF | MKKM+KNN | MKKM+AF | MKKM-IK | MIC | MVEC | LF-IMVC |
|---|---|---|---|---|---|---|---|---|
| [25] | [30] | [27] | [14] | Proposed | ||||
| ACC | ||||||||
| ProteinFold | 20.80 ± 0.20 | 20.49 ± 0.32 | 21.13 ± 0.51 | 20.97 ± 0.21 | 23.22 ± 0.56 | 20.62 ± 0.42 | 14.44 ± 0.44 | 30.69 ± 0.37 |
| NMI | ||||||||
| ProteinFold | 29.33 ± 0.35 | 29.52 ± 0.45 | 30.51 ± 0.40 | 29.54 ± 0.27 | 32.29 ± 0.56 | 27.53 ± 0.49 | 18.68 ± 0.40 | 37.93 ± 0.26 |
| Purity | ||||||||
| ProteinFold | 27.22 ± 0.39 | 27.16 ± 0.35 | 27.85 ± 0.51 | 27.52 ± 0.44 | 29.82 ± 0.67 | 26.20 ± 0.52 | 19.08 ± 0.39 | 36.70 ± 0.29 |
4.2.5. Experimental Results on CCV
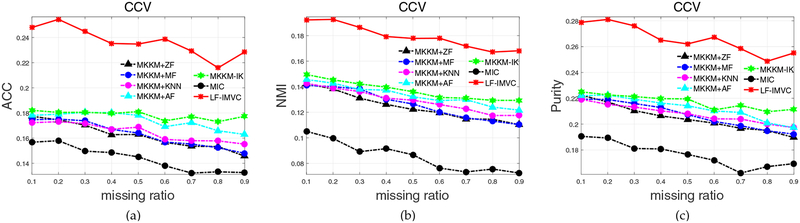
We finally evaluate the performance of LF-IMVC on CCV dataset, and report the results in Figure 5 and Table 6. We once again observe that the proposed LF-IMVC significantly outperforms the compared ones in terms of ACC, NMI and purity. These results further verify the effectiveness of LFIMVC.
Fig. 5:
Clustering accuracy, NMI and purity comparison with various missing ratios on CCV. The results of MVEC [14] on CCV are not reported due to the “out of memory” error.
TABLE 6:
Aggregated ACC, NMI and purity comparison (mean±std) of different clustering algorithms on CCV.
| Datasets | MKKM+ZF | MKKM+MF | MKKM+KNN | MKKM+AF | MKKM-IK | MIC | LF-IMVC |
|---|---|---|---|---|---|---|---|
| [25] | [30] | [27] | Proposed | ||||
| ACC | |||||||
| CCV | 16.23 ± 0.15 | 16.33 ± 0.19 | 16.55 ± 0.23 | 17.39 ± 0.26 | 17.90 ± 0.21 | 14.38 ± 0.22 | 23.65 ± 0.23 |
| NMI | |||||||
| CCV | 12.46 ± 0.08 | 12.63 ± 0.12 | 12.90 ± 0.10 | 13.33 ± 0.13 | 13.76 ± 0.17 | 8.55 ± 0.27 | 17.96 ± 0.10 |
| Purity | |||||||
| CCV | 20.46 ± 0.12 | 20.68 ± 0.12 | 20.81 ± 0.12 | 21.28 ± 0.21 | 21.74 ± 0.18 | 17.66 ± 0.23 | 26.63 ± 0.24 |
The above experimental results on Flower17, Flower102, Caltech102, Protein Fold, UCI-Digital and CCV have well demonstrated that LF-IMVC is superior to some state-of the-art in terms of clustering accuracy, NMI and purity. We attribute the superiority of LF-IMVC as two aspects: i) The joint optimization on imputation and clustering. On one hand, the imputation is guided by the clustering results, which makes the imputation more directly targeted at the ultimate goal. On the other hand, this meaningful imputation is beneficial to refine the clustering results. These two learning processes negotiate with each other, leading to improved clustering performance. In contrast, MKKM+ZF, MKKM+MF, MKKM+KNN, MKKM+AF and MIC [27] do not fully take advantage of the connection between the imputation and clustering procedures. This could produce imputation that does not well serve the subsequent clustering as originally expected, affecting the clustering performance. ii) Completing the incomplete base clustering matrices with the consensus one. Different from MKKM-IK where the consensus clustering matrix H is utilized to fill incomplete base kernels, LF-IMVC imputes each incomplete base clustering matrix with H. The latter is more natural and reasonable since both H and incomplete base clustering matrices reside in the same clustering space, leading to more suitable imputation. These factors bring forth the significant improvements on clustering performance.
4.3. Running Time
To compare the computational complexity of the abovementioned algorithms, we record the running time of these algorithms on these benchmark datasets and report them in Table 7. As can be seen, LF-IMVC has the shortest running time on all datasets except Caltech102–5 and Caltech102–10, demonstrating the high computational efficiency. In particular, LF-IMVC is much more computationally efficient than the recently proposed MKKM-IK [30], both of which work in the “one-stage” style to jointly optimize clustering and imputation. Meanwhile, we observe that the running time of LF-IMVC on Caltech102–5 and Caltech102–10 is slightly longer than that of MKKM. This is because the two datasets have relatively small number of samples and large number of clusters. In such case, the computational complexity of LF-IMVC and MKKM is comparable.
TABLE 7:
Aggregated running time comparison (mean±std) of different clustering algorithms on benchmark datasets (in seconds). All experiments are conducted on a PC machine with an Intel(R) Core(TM)-i7–5820, 3.3 GHz CPU and 16G RAM in MATLAB environment. The results of MVEC [14] on CCV, Flower102, Caltech102–20, Caltech102–25 and Caltech102–30 are not reported due to the “out of memory” error.
| Datasets | MKKM+ZF | MKKM+MF | MKKM+KNN | MKKM+AF | MKKM-IK | MIC | MVEC | LF-IMVC |
|---|---|---|---|---|---|---|---|---|
| [25] | [30] | [27] | [14] | Proposed | ||||
| ProteinFold | 1.6 ± 0.2 | 1.5 ± 0.1 | 2.3 ± 0.2 | 1.8 ± 0.2 | 4.1 ± 0.6 | 192.1 ± 2.8 | 163.0 ± 1.4 | 1.1 ± 0.1 |
| CCV | 83.7 ± 10.8 | 85.9 ± 10.7 | 124.1 ± 14.5 | 106.4 ± 11.3 | 130.8 ± 5.2 | 2070.8 ± 15.1 | – | 23.0 ± 4.8 |
| Flower17 | 2.8 ± 0.3 | 2.8 ± 0.3 | 3.9 ± 0.5 | 3.5 ± 0.4 | 5.4 ± 0.6 | 186.4 ± 6.5 | 603.3 ± 13.1 | 1.5 ± 0.2 |
| Flower102 | 230.0 ± 17.4 | 239.3 ± 27.9 | 340.7 ± 17.1 | 279.4 ± 28.1 | 322.1 ± 31.0 | 5161.9 ± 94.1 | – | 117.2 ± 10.0 |
| UCI-Digital | 4.3 ± 0.4 | 4.2 ± 0.5 | 4.4 ± 0.5 | 5.0 ± 0.6 | 7.8 ± 0.9 | 153.4 ± 3.6 | 906.1 ± 30.0 | 1.3 ± 0.2 |
| Caltech102–5 | 4.4 ± 0.2 | 4.4 ± 0.1 | 6.8 ± 0.2 | 4.8 ± 0.2 | 31.6 ± 3.3 | 1204.3 ± 330.4 | 187.4 ± 1.0 | 16.6 ± 0.4 |
| Caltech102–10 | 17.3 ± 0.7 | 17.2 ± 0.7 | 29.5 ± 0.7 | 18.9 ± 0.6 | 74.3 ± 17.0 | 2211.3 ± 668.1 | 809.7 ± 14.0 | 25.8 ± 0.6 |
| Caltech102–15 | 55.6 ± 0.7 | 55.8 ± 0.7 | 84.1 ± 2.3 | 58.1 ± 2.1 | 197.1 ± 28.4 | 3379.8 ± 867.8 | 2226.4 ± 46.1 | 44.9 ± 0.6 |
| Caltech102–20 | 111.0 ± 4.7 | 111.3 ± 4.6 | 199.7 ± 25.3 | 120.6 ± 4.8 | 320.3 ± 37.6 | 5370.2 ± 1753.1 | – | 75.5 ± 0.7 |
| Caltech102–25 | 207.3 ± 14.8 | 209.2 ± 19.7 | 362.7 ± 18.7 | 200.6 ± 4.6 | 566.1 ± 71.0 | 9265.5 ± 1465.2 | – | 32.4 ± 2.4 |
| Caltech102–30 | 357.2 ± 21.5 | 364.5 ± 24.4 | 616.4 ± 36.9 | 360.2 ± 16.8 | 828.2 ± 33.4 | 11896.0 ± 1875.8 | – | 139.2 ± 0.8 |
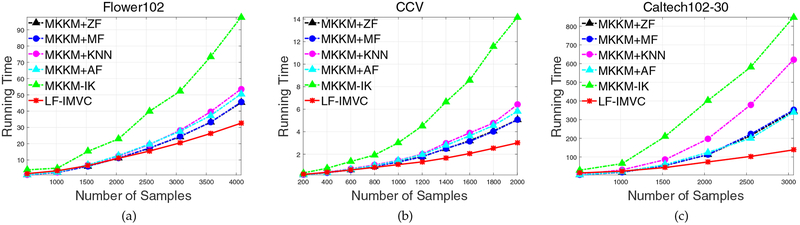
We then design an extra experiment to study the relationship between running time and the number of samples. To see this point in depth, we randomly select samples from three largest datasets, i.e., Flower102, CCV and Caltech102–30, run the aforementioned algorithms and then record their running time. The running time of these algorithms with the number of selected samples are plotted in Figure 6. We have the following observations from these figures: 1) The running time of LF-IMVC is nearly linear with the number of samples. 2) The superiority of LF-IMVC is more significant with the increase of samples, indicating its computational efficiency in handling large-scale clustering tasks.
Fig. 6:
Running time comparison of different algorithms with various number of samples on Flower102, CCV and Caltech102–30 datasets.
In sum, the experimental results in Table 7 and Figure 6 have well demonstrated the computational advantage of LF-IMVC.
4.4. Advantages of Late Fusion MVC
Though both MKKM-IK [30] and the proposed LF-IMVC unify the imputation and clustering into a single optimization, they are different in the manner of imputation: the former is early fusion (or kernel-level imputation), while the latter is a kind of late fusion (or decision-level imputation). Specifically, MKKM-IK [30] initializes the incomplete parts of each Kp with zeros, and jointly performs MKKM clustering and imputation until convergence. Differently, late fusion MVC with zero-filling (LF-MVC+ZF)6 firstly imputes the incomplete parts of each Hp with zeros, and learns a consensus clustering matrix H from . As seen, H obtained by MKKM-IK and LF-MVC+ZF are significantly different. This difference would lead to dramatic difference in clustering performance.
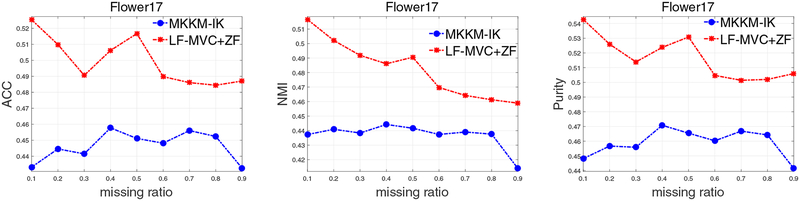
To clearly demonstrate the advantages of late fusion MVC, we conduct an extra experiment to empirically compare MKKM-IK and LF-MVC+ZF on Flower17, as reported in Figure 10. As observed, the clustering performance of LF-MVC+ZF is much better than that of MKKM-IK. This clearly demonstrates the advantages and effectiveness of the proposed late fusion MVC.
Fig. 10:
Clustering accuracy, NMI and purity comparison of MKKM-IK [30] and LF-MVC+ZF with various missing ratios on Flower17.
4.5. Evolution of the Learned Consensus Clustering Matrix
In this section, we conduct experiments to show the evolution of the learned consensus clustering matrix H during the learning procedure. Specifically, we evaluate the NMI of LF-IMVC based on the H learned at each iteration on all datasets and plot the curves in Figure 7. From these figures, we observe that the NMI on all datasets gradually increases to a maximum and generally maintains it up to slight variation. Other curves in terms of clustering accuracy and purity have similar trend and are omitted due to space limit. These experiments have clearly demonstrated the effectiveness of learned consensus clustering matrix, indicating the advantage of imputing incomplete base clustering matrices.
Fig. 7:
The clustering results by the learned H of LF-IMVC with iterations, where λ is set as 2−3 on Flower17, Flower102, CCV, UCI-digtal and Caltech102–30 datasets in this experiment. The results in terms of ACC and purity with other missing ratios are similar and omitted due to space limit.
4.6. Parameter Sensitivity Analysis
As can be seen in Eq. (9), LF-IMVC introduces the regularization parameter λ to trade off the clustering and imputation. In the following, we conduct experiments to show the effect of this parameter on the clustering performance on all datasets. Figure 8 presents the NMI of LF-IMVC by varying λ from 2−15 to 215, where the MKKM-IK is also provided as a baseline. From these figures, we observe that the NMI first increases to a high value and generally maintains it up to slight variation with the increasing value of λ. LF-IMVC demonstrates stable performance across a wide range of λ. These experiments have well shown that LF-IMVC is not very sensitive to the variation of the parameter.
Fig. 8:
The sensitivity of LF-IMVC with the variation of λ on Flower17, Flower102, CCV, UCI-digtal and Caltech102–30 datasets. The results in terms of ACC and purity with other missing ratios are similar and omitted due to space limit.
4.7. Convergence
Our algorithms are theoretically guaranteed to converge according to Theorem 1. We record the objective values of LF-IMVC with iterations on all datasets and plot them in Figure 9. As observed, the objective value of LF-IMVC does monotonically increase at each iteration and that it usually converges in less than 200 iterations.
Fig. 9:
The objective value of LF-IMVC with iterations on Flower17, Flower102, CCV, UCI-digtal and Caltech102–30 datasets. The curves with other missing ratios are similar and omitted due to space limit.
5. Conclusion
While the recently proposed MKKM-IK [30] is able to handle incomplete multi-view clustering, the relatively high computational and space complexities prevent it from large scale clustering tasks. This paper proposes a late fusion approach to simultaneously clustering and imputing the incomplete base clustering matrices. The proposed algorithm effectively and efficiently solves the resultant optimization problem, and demonstrates well improved clustering performance via extensive experiments on benchmark datasets. In the future, instead of uniformly integrating each base clustering matrix, we plan to further improve the clustering performance by automatically updating them during the learning course. Moreover, we are going to explore the correlation among base clustering matrices and use it to further improve the imputation.
Acknowledgements
This work was supported by the Natural Science Foundation of China (project no. 61773392, 61672528 and 61701451).
Biographies

Xinwang Liu received his PhD degree from National University of Defense Technology (NUDT), China. He is now Assistant Researcher of School of Computer, NUDT. His current research interests include kernel learning and unsupervised feature learning. Dr. Liu has published 40+ peer-reviewed papers, including those in highly regarded journals and conferences such as IEEE T-IP, IEEE T-NNLS, IEEE T-IFS, ICCV, AAAI, IJCAI, etc. He served on the Technical Program Committees of IJCAI 2016–2018 and AAAI 2016–2018.

Xinzhong Zhu is a professor at College of Mathematics, Physics and Information Engineering, Zhejiang Normal University, PR China. He received his Ph.D. degree at XIDIAN University, China. His research interests include machine learning, computer vision, manufacturing informatization, robotics and system integration, and intelligent manufacturing. He is a member of the ACM.

Miaomiao Li is in pursuit of her PhD degree at National University of Defense Technology, China. She is now Lecture of Changsha College, Changsha, China. Her current research interests include kernel learning and multi-view clustering. Miaomiao Li has published several peer-reviewed papers such as AAAI, IJCAI, Neurocomputing, etc. She serves on the Technical Program Committees of IJCAI 2017.

Lei Wang received his PhD degree from Nanyang Technological University, Singapore. He is now Associate Professor at School of Computing and Information Technology of University of Wollongong, Australia. His research interests include machine learning, pattern recognition, and computer vision. Dr. Wang has published 120+ peer-reviewed papers, including those in highly regarded journals and conferences such as IEEE T-PAMI, IJCV, CVPR, ICCV and ECCV, etc. He was awarded the Early Career Researcher Award by Australian Academy of Science and Australian Research Council. He served as the General Co-Chair of DICTA 2014 and on the Technical Program Committees of 20+ international conferences and workshops. Lei Wang is senior member of IEEE.

Chang Tang received his Ph.D. degree from Tianjin University, Tianjin, China in 2016. He joined the AMRL Lab of the University of Wollongong between Sep. 2014 and Sep. 2015. He is currently an associate professor at the School of Computer Science, China University of Geosciences, Wuhan, China. His current research interests include machine learning and data mining. Dr. Tang served on the Technical Program Committees of IJCAI 2018 and ICME 2018.

Jianping Yin received his PhD degree from National University of Defense Technology (NUDT), China. He is now the distinguished Professor at Dongguan University of Technology. His research interests include pattern recognition and machine learning. Dr. Yin has published 100+ peer-reviewed papers, including IEEE TCSVT, IEEE T-NNLS, PR, AAAI, IJCAI, etc. He was awarded China National Excellence Doctoral Dissertation’ Supervisor and National Excellence Teacher. He served on the Technical Program Committees of 30+ international conferences and workshops.

Dinggang Shen is Jeffrey Houpt Distinguished Investigator, and a Professor of Radiology, Biomedical Research Imaging Center (BRIC), Computer Science, and Biomedical Engineering in the University of North Carolina at Chapel Hill (UNC-CH). He is currently directing the Center for Image Analysis and Informatics, the Image Display, Enhancement, and Analysis (IDEA) Lab in the Department of Radiology, and also the medical image analysis core in the BRIC. He was a tenure-track assistant professor in the University of Pennsylvanian (UPenn), and a faculty member in the Johns Hopkins University. Dr. Shens research interests include medical image analysis, computer vision, and pattern recognition. He has published more than 800 papers in the international journals and conference proceedings. He serves as an editorial board member for eight international journals. He has also served in the Board of Directors, The Medical Image Computing and Computer Assisted Intervention (MICCAI) Society, in 2012–2015, and will be General Chair for MICCAI 2019. He is Fellow of IEEE, Fellow of The American Institute for Medical and Biological Engineering (AIMBE), and also Fellow of The International Association for Pattern Recognition (IAPR).

Huaimin Wang received the Ph.D. degree in computer science from NUDT, China in 1992. He is now a professor in the State Key Laboratory of High Performance Computing, NUDT. He has been awarded the Chang Jiang Scholars by Ministry of Education of China, and the Distinct Young Scholar by the National Natural Science Foundation of China (NSFC). He has worked as the director of several grand research projects and has published more than 100 research papers in international conferences and journals. His current research interests include middleware, software agent and trust-worthy computing.

Wen Gao received his PhD degree from University of Tokyo, Japan. He is now Boya Chair Professor and the Director of Faculty of Information and Engineering Sciences at Peking University, and the founding director of National Engineering Lab. for Video Technology (NELVT) at Peking University. Prof. Gao works in the areas of multimedia and computer vision, topics including video coding, video analysis, multimedia retrieval, face recognition, multimodal interfaces, and virtual reality. He published seven books, over 220 papers in refereed journals, and over 600 papers in selected international conferences. His publications have been cited for over 28,000 times, and his H-index is 75, according to Google Scholar. He served or serves on the editorial board for several journals, such as IEEE T-IP, IEEE T-CSVT, IEEE Trans. on Multimedia, IEEE T-AMD. He chaired a number of prestigious international conferences on multimedia and video signal processing, such as IEEE ICME 2007, ACM Multimedia 2009, IEEE ISCAS 2013, and also served on the advisory and technical committees of numerous professional organizations. Prof. Gao has been featured by IEEE Spectrum in June 2005 as one of the “Ten To Watch” among China’s leading technologists. He is a fellow of IEEE, a fellow of ACM, and a member of Chinese Academy of Engineering.
Footnotes
Note that the proposed LF-IMVC reduces to LF-MVC+ZF when λ in Eq. (9) approaches +∞.
Contributor Information
Xinwang Liu, Email: xinwangliu@nudt.edu.cn, School of Computer, National University of Defense Technology, Changsha, China, 410073..
Xinzhong Zhu, Email: zxz@zjnu.edu.cn, College of Mathematics, Physics and Information Engineering, Zhejiang Normal University, Jinhua, Zhengjiang, China, 321004..
Miaomiao Li, Email: miaomiaolinudt@gmail.com, Department of Computer, Changsha College, Changsha, China, 410073..
Lei Wang, Email: leiw@uow.edu.au, School of Computing and Information Technology, University of Wollongong, NSW, Australia, 2522..
Chang Tang, Email: tangchang@cug.edu.cn, School of Computer Science, China University of Geo-sciences, 430074..
Jianping Yin, Email: jpyin@dgut.edu.cn, Dongguan University of Technology, Guangdong, China..
Ding-gang Shen, Email: dgshen@med.unc.edu, Department of Radiology and BRIC, University of North Carolina at Chapel Hill, North Carolina 27599, USA, and also with Department of Brain and Cognitive Engineering, Korea University, Seoul 02841, Republic of Korea..
Huaimin Wang, Email: whm_2@163.com, School of Computer, National University of Defense Technology, Changsha, China, 410073..
Wen Gao, Email: wgao@pku.edu.cn, School of Electronics Engineering and Computer Science, Peking University, Beijing, China, 100871..
References
- [1].Bickel S and Scheffer T, “Multi-view clustering,” in Proceedings of the 4th IEEE International Conference on Data Mining (ICDM 2004), 2004, pp. 19–26. [Google Scholar]
- [2].Zhao B, Kwok JT, and Zhang C, “Multiple kernel clustering,” in SDM, 2009, pp. 638–649. [Google Scholar]
- [3].Yu S, Tranchevent L-C, Liu X, Glänzel W, Suykens JAK, Moor BD, and Moreau Y, “Optimized data fusion for kernel k-means clustering,” IEEE TPAMI, vol. 34, no. 5, pp. 1031–1039, 2012. [DOI] [PubMed] [Google Scholar]
- [4].Li S, Jiang Y, and Zhou Z, “Partial multi-view clustering,” in AAAI, 2014, pp. 1968–1974. [Google Scholar]
- [5].Du L, Zhou P, Shi L, Wang H, Fan M, Wang W, and Shen Y-D, “Robust multiple kernel k-means clustering using l21-norm.” in IJCAI, 2015, pp. 3476–3482. [Google Scholar]
- [6].Liu X, Dou Y, Yin J, Wang L, and Zhu E, “Multiple kernel k-means clustering with matrix-induced regularization,” in AAAI, 2016, pp. 1888–1894. [Google Scholar]
- [7].Li M, Liu X, Wang L, Dou Y, Yin J, and Zhu E, “Multiple kernel clustering with local kernel alignment maximization,” in IJCAI, 2016, pp. 1704–1710. [Google Scholar]
- [8].Liu X, Zhou S, Wang Y, Li M, Dou Y, Zhu E, and Yin J, “Optimal neighborhood kernel clustering with multiple kernels,” in AAAI, 2017, pp. 2266–2272. [Google Scholar]
- [9].Li Y, Nie F, Huang H, and Huang J, “Large-scale multi-view spectral clustering via bipartite graph,” in AAAI, 2015, pp. 2750–2756. [Google Scholar]
- [10].Cai X, Nie F, and Huang H, “Multi-view k-means clustering on big data,” in IJCAI, 2013, pp. 2598–2604. [Google Scholar]
- [11].Tao Z, Liu H, and Fu Y, “Simultaneous clustering and ensemble,” in AAAI, 2017, pp. 1546–1552. [Google Scholar]
- [12].Liu J, Wang C, Danilevsky M, and Han J, “Large-scale spectral clustering on graphs,” in IJCAI, 2013, pp. 1486–1492. [Google Scholar]
- [13].Zhang R, Li S, Fang T, Zhu S, and Quan L, “Joint camera clustering and surface segmentation for large-scale multi-view stereo,” in ICCV, 2015, pp. 2084–2092. [Google Scholar]
- [14].Tao Z, Liu H, Li S, Ding Z, and Fu Y, “From ensemble clustering to multi-view clustering,” in IJCAI, 2017, pp. 2843–2849. [Google Scholar]
- [15].Djelouah A, Franco J, Boyer E, Clerc FL, and Pérez P, “Sparse multi-view consistency for object segmentation,” IEEE Trans. Pattern Anal. Mach. Intell, vol. 37, no. 9, pp. 1890–1903, 2015. [DOI] [PubMed] [Google Scholar]
- [16].Djelouah A, Franco J, Boyer E, Clerc FL, and Pérez P, “Multi-view object segmentation in space and time,” in ICCV, 2013, pp. 2640–2647. [Google Scholar]
- [17].Li C, Bai J, and Hager GD, “A Unified Framework for Multi-View Multi-Class Object Pose Estimation,” ArXiv e-prints, March 2018. [Google Scholar]
- [18].Li J, Xu C, Yang W, Sun C, and Tao D, “Discriminative multi-view interactive image re-ranking,” IEEE Trans. Image Processing, vol. 26, no. 7, pp. 3113–3127, 2017. [DOI] [PubMed] [Google Scholar]
- [19].Yao X, Han J, Zhang D, and Nie F, “Revisiting co-saliency detection: A novel approach based on two-stage multi-view spectral rotation co-clustering,” IEEE Trans. Image Processing, vol. 26, no. 7, pp. 3196–3209, 2017. [DOI] [PubMed] [Google Scholar]
- [20].Bruno E and Marchand-Maillet S, “Multiview clustering: a late fusion approach using latent models,” in ACM SIGIR, 2009, pp. 736–737. [Google Scholar]
- [21].Gönen M and Margolin AA, “Localized data fusion for kernel k-means clustering with application to cancer biology,” in NIPS, 2014, pp. 1305–1313. [Google Scholar]
- [22].Xiang S, Yuan L, Fan W, Wang Y, Thompson PM, and Ye J, “Multi-source learning with block-wise missing data for alzheimer’s disease prediction,” in ACM SIGKDD, 2013, pp. 185–193. [Google Scholar]
- [23].Kumar R, Chen T, Hardt M, Beymer D, Brannon K, and Syeda-Mahmood TF, “Multiple kernel completion and its application to cardiac disease discrimination,” in ISBI, 2013, pp. 764–767. [Google Scholar]
- [24].Ghahramani Z and Jordan MI, “Supervised learning from incomplete data via an EM approach,” in NIPS, 1993, pp. 120–127. [Google Scholar]
- [25].Trivedi A, Rai P, Daumé III H, and DuVall SL, “Multiview clustering with incomplete views,” in NIPS 2010: Machine Learning for Social Computing Workshop, Whistler, Canada, 2010. [Google Scholar]
- [26].Xu C, Tao D, and Xu C, “Multi-view learning with incomplete views,” IEEE Trans. Image Processing, vol. 24, no. 12, pp. 5812–5825, 2015. [DOI] [PubMed] [Google Scholar]
- [27].Shao W, He L, and Yu PS, “Multiple incomplete views clustering via weighted nonnegative matrix factorization with l2,1 regularization,” in ECML PKDD, 2015, pp. 318–334. [Google Scholar]
- [28].Bhadra S, Kaski S, and Rousu J, “Multi-view kernel completion,” in arXiv:1602.02518, 2016. [Google Scholar]
- [29].Shao W, He L, Lu C, and Yu PS, “Online multi-view clustering with incomplete views,” in IEEE International Conference on Big Data, 2016, pp. 1012–1017. [Google Scholar]
- [30].Liu X, Li M, Wang L, Dou Y, Yin J, and Zhu E, “Multiple kernel k-means with incomplete kernels,” in AAAI, 2017, pp. 2259–2265. [Google Scholar]
- [31].Xie X and Sun S, “Multi-view clustering ensembles,” in International Conference on Machine Learning and Cybernetics, ICMLC 2013, Tianjin, China, July 14–17, 2013, 2013, pp. 51–56. [Google Scholar]
- [32].Jegelka S, Gretton A, Schölkopf B, Sriperumbudur BK, and von Luxburg U, “Generalized clustering via kernel embeddings,” in KI 2009: Advances in Artificial Intelligence, 32nd Annual German Conference on AI, 2009, pp. 144–152. [Google Scholar]
- [33].Tremblay N, Puy G, Gribonval R, and Vandergheynst P, “Compressive spectral clustering,” in Proceedings of The 33rd International Conference on Machine Learning, 2016, pp. 1002–1011. [Google Scholar]
- [34].Kato T and Rivero R, “Mutual kernel matrix completion,” in arXiv:1702.04077v2, 2017. [Google Scholar]
- [35].Gretton A, Borgwardt KM, Rasch MJ, Schölkopf B, and Smola AJ, “A kernel method for the two-sample-problem,” in NIPS, 2006, pp. 513–520. [Google Scholar]
- [36].von Luxburg U, “A tutorial on spectral clustering,” Statistics and Computing, vol. 17, no. 4, pp. 395–416, 2007. [Google Scholar]
- [37].Liu H, Wu J, Liu T, Tao D, and Fu Y, “Spectral ensemble clustering via weighted k-means: Theoretical and practical evidence,” IEEE Trans. Knowl. Data Eng, vol. 29, no. 5, pp. 1129–1143, 2017. [Google Scholar]
- [38].Lovász L and Plummer MD, Matching Theory. Akadémiai Kiado, Nórth Holland, 1986. [Google Scholar]