Modeling Conformationally Flexible Proteins With X-ray Scattering and Molecular Simulations

Abstract

Proteins and protein complexes with high conformational flexibility participate in a wide range of biological processes. These processes include genome maintenance, gene expression, signal transduction, cell cycle regulation, and many others. Gaining a structural understanding of conformationally flexible proteins and protein complexes is arguably the greatest problem facing structural biologists today. Over the last decade, some progress has been made toward understanding the conformational flexibility of such systems using hybrid approaches. One particularly fruitful strategy has been the combination of small-angle X-ray scattering (SAXS) and molecular simulations. In this article, we provide a brief overview of SAXS and molecular simulations and then discuss two general approaches for combining SAXS data and molecular simulations: minimal ensemble approaches and full ensemble approaches. In minimal ensemble approaches, one selects a minimal ensemble of structures from the simulations that best fit the SAXS data. In full ensemble approaches, one validates a full ensemble of structures from the simulations using SAXS data. We argue that full ensemble models are more realistic than minimal ensemble searches models and that full ensemble approaches should be used wherever possible.

Graphical Abstract

Highlights

• •Conformationally flexible proteins are a major challenge for structural biologists.
• •Flexible proteins can be examined by combining molecular simulations and SAXS.
• •Minimal ensemble searches are a common way of combining simulations and SAXS.
• •Full ensemble methods use SAXS to validate simulations without curve fitting.
• •Full ensemble models are more realistic than minimal ensemble searches models.

1. Introduction

Proteins with high conformational flexibility and the complexes that they form are important participants in a wide range of biological processes [[1], [2], [3]]. Such processes include DNA replication and repair, transcription, protein synthesis, protein modification, protein degradation, signal transduction, and cell cycle regulation. This conformational flexibility can arise in a variety of different ways. For example, hinge regions between domains or subdomains allow open-to-closed transitions. These hinge-containing proteins usually explore a relatively narrow range of conformational space. Classic examples of such proteins include hexokinase [[4], [5], [6]] and DNA polymerases [7,8]. By contrast, long intrinsically disordered regions allow one or more domains to be tethered to each other or to binding partners. These partially or fully disordered proteins usually explore a wide range of conformation space. Classic examples of partially disordered proteins include histones [9,10] and the small, ubiquitin-like modifier (SUMO) [11,12].

Gaining a structural understanding of conformationally flexible proteins and the protein complexes that they constitute is arguably the greatest problem facing structural biologists today. This is a critical issue, because the conformational flexibility of such systems is often important for their biological function and their regulation. The goal of the structural biologist, when studying such a system, is to describe the full range of conformational states sampled by the protein or by the protein complex. Such a description would be an ensemble of individual structures with each structure detailing one conformational state that the protein can occupy. The difficulty here is that the basic experimental approaches used by structural biologists to obtain high-resolution structures are not well suited to this task. X-ray crystallography, for example, usually only provides a single structure of a protein or protein complex, and regions with high conformational flexibility are generally disordered and not visible in electron density maps. By contrast, NMR spectroscopy can yield an ensemble of individual structures of a protein and can be well suited to provide information about its conformational flexibility. NMR, however, is generally restricted to smaller protein (<50 kDa) [13]. Cryo-electron microscopy (cryo-EM) can reveal the structures of large proteins and protein complexes (>200 kDa) [13] and can yield an ensemble of individual structures. Cryo-EM, however, is not well suited to the task at hand because it is limited to individual structures that represent only highly populated conformational states (>5–10% of the total). Like X-ray crystallography, cryo-EM cannot generally resolve regions with high conformational flexibility.

Over the last decade, some progress has been made at gaining a structural understanding of conformationally flexible proteins using hybrid approaches. One particularly fruitful strategy has been a combination of small-angle X-ray scattering (SAXS) and molecular simulations [[14], [15], [16], [17], [18], [19], [20]]. In this review, we will briefly discuss SAXS and several types of molecular simulations, including all-atom molecular dynamics (MD) simulations to coarse-grained Langevin dynamics (LD) simulations. We will then consider two general approaches for combining SAXS data and molecular simulations. The first entails using the simulations to select a minimal ensemble of structures that best fit the experimental SAXS data. The second entails using the simulations to generate a full ensemble of structures that can be directly validated by the experimental SAXS data. As many recent reviews have focused on minimal ensemble approaches [[14], [15], [16], [17], [18], [19], [20]], this review will dwell more on full ensemble approaches.

2. Small-angle X-ray Scattering

2.1. The Basics of SAXS

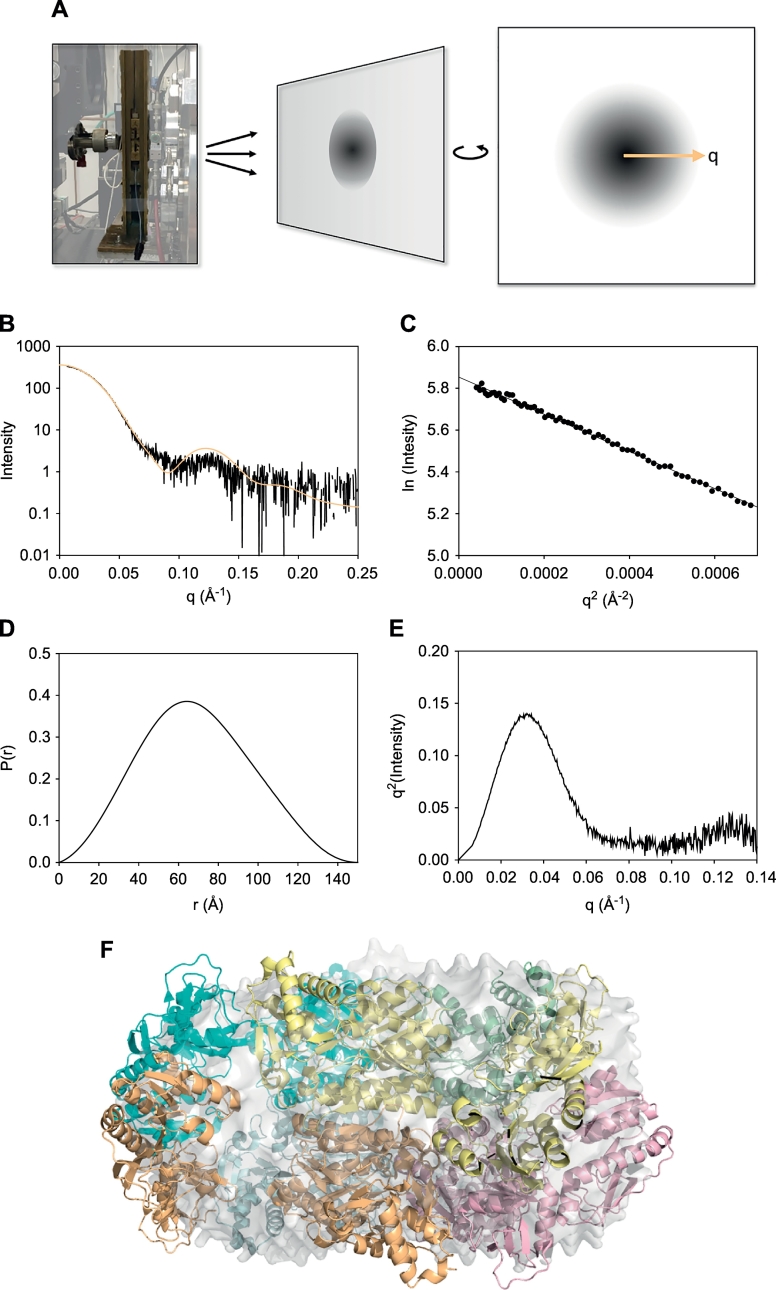
To collect SAXS data, one places a solution containing the protein of interest in an X-ray beam and records the intensity of the scattered X-rays as a function of the scattering vector q, which represents the radial distance from the center of the detector (Fig. 1A) [15,21,22]. Unlike X-ray diffraction, the X-ray scattering in SAXS experiments is represented as a continuous function. One also must place an identical buffer solution not containing the protein of interest in the X-ray beam and record the scattering intensity as a function of q. By subtracting the scattering intensity of the buffer alone from that of the buffer containing the protein of interest at each q value, one obtains the scattering curve of the protein itself.

Fig. 1.

Small-angle X-ray scattering.

A. A photograph of a SAXS setup and an illustration of an X-ray scattering image. B. A plot showing the experimental SAXS curve for the E. coli ArnA protein collected at Argonne National Laboratory using the Advanced Photon Source beamline 18-ID (black) and the theoretical SAXS curve derived from the X-ray crystal structure of the E. coli ArnA protein (PDB ID: 1Z7E) (orange) [27]. C. The Guinier plot is shown for the E. coli ArnA protein. The R_g of the protein was 52 Å. D. The P(r) plot for the E. coli ArnA protein. The D_max of the protein was 150 Å. E. The Kratky plot is shown for the E. coli ArnA protein. F. The X-ray crystal structure of the E. coli ArnA protein (PDB ID: 1Z7E) [27] fit within the envelope obtained from ab initio shape predictions using DAMMIF [30]. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

In practice, SAXS data collection is often done in line with size exclusion chromatography (SEC) [23]. This experimental setup is referred to as SEC-SAXS. In SEC-SAXS, one collects scattering data before, during, and after the elution of the protein peak from the SEC column. Here, buffer subtraction is usually carried out with scattering curves collected prior to the elution peak. Programs such as PRIMUS from the ATSAS software suite and BioXTAS RAW have been developed to average multiple scattering frames from SEC-SAXS and to carry out buffer subtraction [[24], [25], [26]].

The scattering curve of the protein contains information regarding the size and shape of the protein in solution. If the protein possesses conformational flexibility, the scattering curve also contains information regarding the distribution of different conformations in solution. This curve is typically shown as a graph of the logarithm of the intensity of the scattered X-rays as a function of the scattering vector, q. As an example, we show the scattering curve obtained from SEC-SAXS of the ArnA protein (Fig. 1B), an E. coli enzyme involved in the biosynthesis of compounds required for resistance to certain antimicrobials [27]. This protein is also known for being a nuisance; it is a common contaminant that binds affinity columns containing divalent nickel or cobalt metals that are routinely used to purify His₆-tagged proteins.

The first step of analyzing scattering data is to generate a Guinier plot by graphing the logarithm of the scattering intensity in the low q region, i.e., nearest the center of the detector, as a function of q². The Guinier plot for ArnA is shown in Fig. 1C. If the protein is not aggregating, the Guinier plot will be linear. From the slope of this line, one can calculate the radius of gyration (R_g), which describes the protein's moment of inertia around its axis of rotation. Programs such as AUTORG have been developed to select the most suitable data range for Guinier analysis and to create Guinier plots [25].

An indirect Fourier transform of the scattering curve yields the pairwise distance plot, or P(r) plot. This plot is analogous to a histogram showing the magnitudes of all of the interatomic vectors of the protein. If one were to list all combinations of pairs of atoms and measure the distances between the atoms in each pair and generate a histogram showing the number of combinations of each distance, one would have an approximation of the P(r) curve. The P(r) plot for ArnA is shown in Fig. 1D. Programs such as GNOM have been developed to generate P(r) plots and to determine the maximal distance between two atoms in the structure (D_max) [25,28]. The D_max is the distance (r value) at which the P(r) curve returns to the x-axis.

2.2. Static Structures

If one assumes that the protein of interest is static – i.e., not conformationally flexible – SAXS can be a useful approach to examining its structure at low to moderate resolution. For example, ab initio approaches allow one to calculate an envelope of a protein that best fits the experimental scattering data. This provides the overall size and shape of the protein. Programs such as DAMMIF and GASBOR have been developed to calculate the envelop of proteins from SAXS data using different approaches [29,30]. DAMMIF, for example, uses a lattice of a thousand or more spheres packed tightly in an initial configuration. A predicted scattering curve is generated for this configuration of packed spheres and is compared to the experimental scattering curve. The configuration is altered in an iterative cycle that ideally will converge.

If one has a high-resolution structural model of the protein of interest – such as one derived from X-ray crystallography, NMR, or homology modeling – one can fit the high-resolution structure into the SAXS envelope. This can be particularly useful to determine whether the protein adopts a static conformation that is different from the one represented in the high-resolution structure. Programs such as CRYSOL and FoXS have been developed to calculate theoretical scattering curves from known high-resolution structures and to compare these curves with experimental scattering curves [31,32]. The best rigid-body fit of the X-ray crystal structure of ArnA [27] to the SAXS envelope obtained from ab initio shape predictions using DAMMIF is shown in Fig. 1F.

2.3. Dynamic Structures

SAXS is also useful for examining the overall degree of intrinsic disorder of a protein. One often does this by generating a Kratky plot, which is a graph of the scattering intensity multiplied by q² shown as a function of q. The shape of this curve provides a semi-quantitative characterization of the amount of intrinsic disorder of the protein [21]. A globular, folded protein will appear as a Gaussian (bell-shaped) peak that returns to the baseline. A fully disordered protein will reach a plateau in the high q region – i.e., farthest from the center of the detector – and will not return to the baseline. A partially disordered protein will appear as a Gaussian peak that either reaches a plateau and does not return to the baseline or gradually returns to the baseline. The Kratky plot for ArnA shows that the protein is globular and folded (Fig. 1E).

3. Molecular Simulations

While SAXS data are generally low resolution, one can either fit them to high-resolution models or validate them with high-resolution models by combining them with molecular simulations. There are two broad classes of molecular simulations that one can use in conjunction with SAXS: molecular dynamics (MD) simulations and Langevin dynamics (LD) simulations. Here, Brownian dynamics (BD) simulations are considered as a subset of LD simulations in which there is no inertia. In this section, we will briefly discuss these classes of molecular simulations.

3.1. Molecular Dynamics

In MD simulations, one starts with a high-resolution structural model of the protein of interest. Usually, this initial model is obtained directly from an X-ray crystal structure or an NMR structure of the protein. However, in the absence of a high-resolution structure, homology models often suffice. Online tools such as SWISS-MODEL and Phyre2.0 are useful when constructing homology models [33,34]. Typically, one has to add loops and extended, flexible tails that were not present in a crystal structure either due to such regions being disordered in the electron density maps or being removed from the protein to facilitate crystallization. These loops and tails can be added using programs such as LOOPY [35]. Hydrogen atoms, which are not present in crystal structures, also need to be added. An example of constructing an initial model for molecular simulations of a protein containing two long, flexible tails is described below (see Section 5.1).

Once the initial high-resolution, all-atom model is constructed and placed in an explicit (i.e., all-atom) solvent, one then carries out the MD simulations using programs such as GROMACS [36] with force fields such as AMBER, CHARMM, or GROMOS [[37], [38], [39]]. Force fields are sets of potential energy functions and the values of the parameters used in these functions. The basic idea of MD simulations is that one has a list of the positions and momentums of all of the atoms (protein and solvent). The software calculates the forces acting on each of the atoms and then applies Newton's laws of motion to determine how these atoms change position and momentum over a very short time step of approximately 1 fs. The forces in question come from both bonded and non-bonded atomic interactions. The bonded interactions include bond length potentials, bond angle potentials, and torsional angle potentials. The non-bonded interactions include van der Waals interactions (described by Lennard-Jones potentials) and electrostatic interactions (described by Coulomb's law). Because these calculations typically are performed in 1 fs time steps, achieving 100 ns of simulation time, which is the approximate time frame of side chain movements and loop movements, requires 10⁸ consecutive time steps.

One major limitation of MD simulations is the length of simulated time that can be achieved in a reasonable amount of actual time. The amount of actual time required for each time step calculation depends on the number of atoms being simulated. A very common way of increasing the achievable length of simulated time is to remove the solvent atoms from the simulation and replace them with an implicit, continuous solvent. The implicit solvent allows one to set the ionic strength of the solution as well as the dielectric constant for the solvent and for the interior of the protein. However, these implicit solvent MD simulations do not consider collisions between solvent atoms and the atoms of the protein. To do this, LD simulations are necessary.

3.2. Langevin Dynamics

Whereas MD simulations are deterministic, LD simulations introduce stochastic elements into the simulations. The basic idea of LD simulations is very similar to that of MD simulations. One has a list of the positions and momentums of all of the atoms in the simulation, and the software calculates the forces acting on each of the atoms to determine how they change position and momentum over a very short time step. The key difference between LD and MD simulations, however, is that in LD simulations, the atoms of the protein are randomly nudged during the time step calculations to mimic collisions with solvent atoms [40,41]. As stated above, BD simulations are a simplified, subset of LD simulations in which there is no inertia. This essentially means that the momentum of each atom is ignored in the time step calculations and only the positions of each atom and the forces acting upon them are considered.

LD simulations are well suited to coarse-graining. In a coarse-grained (CG) model, entire amino acid residues can be replaced by one or more CG bead (or pseudoatoms). These CG beads can retain the relevant charges and, in some cases, the relevant sizes and shapes of the amino acid residues they replaced [42]. Moreover, Go potentials are often included in LD simulations to enforce the conformational stability of folded regions of proteins [[43], [44], [45]]. The critical point here is that coarse-graining greatly reduces the number of atoms (or CG beads) used in the calculations and, therefore, reduces considerably the amount of actual time needed to carry out the simulation. An example of constructing a CG model of a large protein and carrying out LD simulations of it are described below (see Section 5.1).

An important feature for simulating conformationally flexible regions of proteins is the inclusion of hydrodynamic effects resulting from the motion of solvent. MD simulations with an implicit solvent and many LD simulations do not model hydrodynamics. LD simulations, however, can be used to successfully model hydrodynamic effects by correlating the stochastic forces that act on neighboring or nearby atoms in loops and other conformationally flexible regions [42]. As described below (Section 5), LD simulations of such systems that include hydrodynamics have been shown to be highly consistent with experimental SAXS data.

4. Minimal Ensemble Approaches

Conformationally flexible proteins cannot be modeled as individual structures. Instead, they must be modeled as an ensemble of individual structures with each structure representing a distinct conformational state of the protein. Each of the individual structures, moreover, must be given a weighting factor to represent the fraction of time that the flexible protein is found in that conformational state. The most common way to generate the potential individual structures for inclusion in the ensemble is by MD simulations or LD simulations. Programs such as BilboMD have been developed to sample the potential conformational states of flexible proteins using MD simulations [46].

The major problem with the analysis of SAXS data is the limited amount of information one obtains from the experiment. A typical SAXS scattering curve is believed to contain only 10 to 30 independent data points [21]. This leads to a high risk of over fitting the data. This is particularly problematic when using molecular simulations to fit the data. Consider how one might fit SAXS data using molecular simulations. One could extract a large number of individual structures from the ensemble derived from the simulations. Each one of these structures would then be assigned a weighting factor representing the frequency with which that individual structure appears. The number of degrees of freedom of the model would greatly exceed what is statistically justifiable given the limited information content of the experimental data.

There are a variety of approaches, such as ensemble optimization and minimal ensemble searches, that have been developed to fit SAXS data using the results of molecular simulations in ways that minimize the risks of over fitting the experimental data. Several outstanding and recent review articles describe these methods in detail [[14], [15], [16], [17], [18], [19], [20]]. For this reason, we will briefly discuss minimal ensemble approaches and limit our remarks to minimal ensemble searches.

The most widely used approach to combine SAXS data and molecular simulations is to perform a minimal ensemble search. In a minimal ensemble search, one starts with a large ensemble derived from a molecular simulation. The software then searches through each of the individual structures in the starting ensemble to find the one that best fits the scattering data. Next, the software searches through all linear combinations of two structures, each with its own weighting factor, to find the ones that when combined best fit the data. This process is repeated for three structures, four structures, and so on. The goal is to find the minimal ensemble (the fewest number of individual structures) that best fit the scattering data. This process ends when the inclusion of additional structures in the model no longer improves the quality of fit substantially. The end result is typically three or four individual structures, each with a weighting factor, that when combined best match the experimental scattering data. Programs such as FoXS have been developed to compute theoretical scattering curves from individual high-resolution structures (such as the structures derived from the simulations) and to perform minimal ensemble searches [32].

The main drawback of minimal ensemble approaches is that the minimal ensembles are highly unrealistic. The conformational space explored by these flexible proteins is represented by only a few individual structures. While these results are not taken to literally mean that there are only a few highly populated conformations in solution, this is effectively how such approaches model these proteins. A great deal of information about the existence and frequency of many conformational states, which may by critical for the function or regulation of the protein in question, is not obtainable from minimal ensemble models. This places serious limits on the questions we can address concerning conformationally flexible proteins. This drawback has been the motivation for recently attempting full ensemble approaches.

5. Full Ensemble Approaches

A less common, but arguably better way of avoiding the over fitting problem is to not fit the data at all. Instead of using molecular simulations to generate structural models for fitting experimental SAXS data, one can use experimental SAXS data to validate structural models generated using molecular simulations. To do this, one does not merely generate a minimal ensemble comprised of a few structures. Instead, one generates a full ensemble comprised of thousands of individual structures. A distinct advantage of full ensemble approaches is that they produce more realistic structural models of conformationally flexible proteins than do minimal ensemble approaches.

To our knowledge, the earliest application of a full ensemble approach of the type highlighted here was with the restriction endonuclease EcoO109I [47]. This study compared the results of a 150 ns all-atom MD simulation with an explicit solvent to experimental SAXS data. This was followed by a similar study with the DNA-binding core of replication protein A (RPA), the eukaryotic single-stranded DNA binding protein [48]. This study compared the results of a 200 ns all-atom MD simulation without an explicit solvent to experimental SAXS data. Since then, larger proteins have been simulated for longer times (up to 10 μs) using coarse-grained models. In this section, we will briefly describe how the results of coarse-grained LD simulations are generated and analyzed in order to validate them with experimental SAXS data, and then we will discuss a few recent examples.

5.1. The Basics of Full Ensemble Approaches

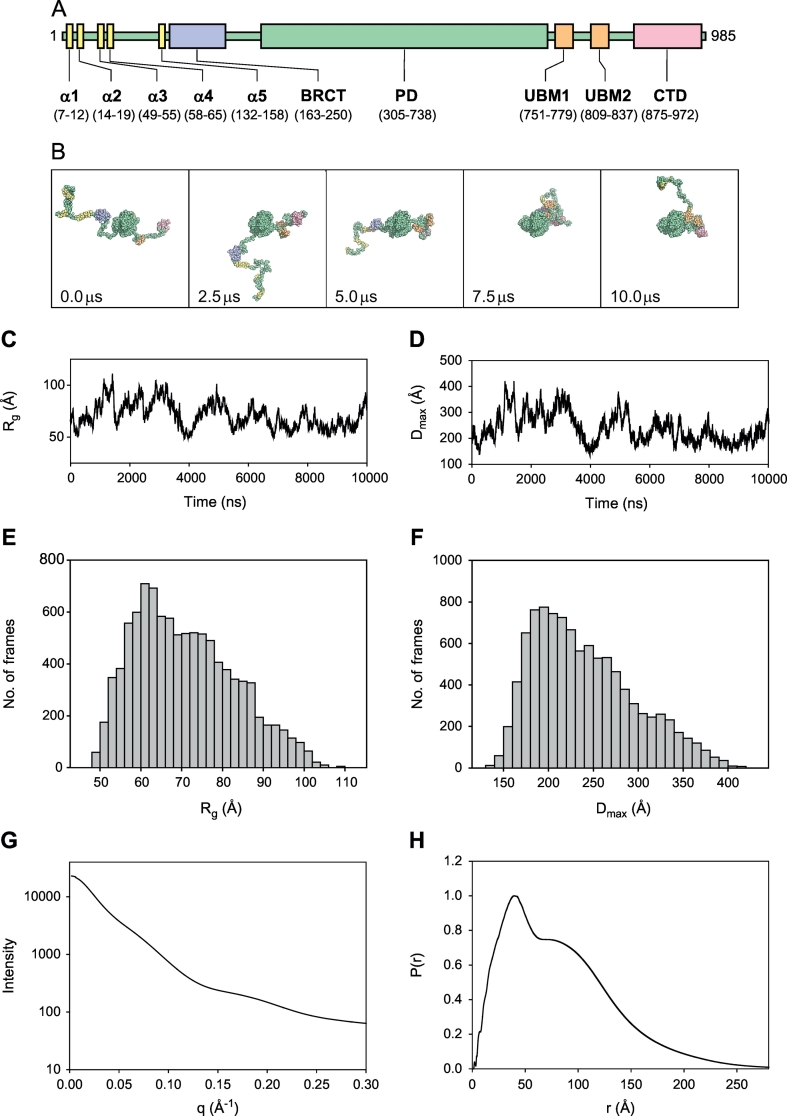
Here we use the yeast Rev1 protein, a translesion synthesis DNA polymerase required for DNA damage-induced mutagenesis [49,50], as an example to illustrate briefly how the molecular simulations are carried out and analyzed. Because of the inability to obtain sufficient quantities of purified Rev1, experimental SAXS data is not available to compare with the computational results. Nevertheless, this protein provides an excellent example to illustrate how predicted SAXS data are obtained from full ensembles. More detailed procedures for initial model building, molecular simulations, and data analysis are described elsewhere [51]. Rev1 has a complicated overall structure (Fig. 2A). Its primary structure can be divided roughly into thirds. The first third is the unstructured N-terminal region containing a small, folded BRCT domain. The second third is the structured polymerase domain. The final third is the unstructured C-terminal region containing two small, folded ubiquitin-binding motifs (UBMs) and a small, folded C-terminal domain.

Fig. 2.

Analysis of Langevin dynamics simulations.

A. The structural elements of yeast Rev1 showing the positions of five putative α-helices (yellow), the BRCT domain (blue), the polymerase domain (PD) (green), two ubiquitin-binding motifs (UBMs) (orange), and the C-terminal domain (CTD) (red). B. Snapshots of the LD simulations of the yeast Rev1 protein after 0.0, 2.5, 5.0, 7.5, and 10.0 μs of simulation time. The structural elements are colored as described above. C. A plot showing the R_g of each snapshot of the LD simulations of the yeast Rev1 protein as a function of time. D. A plot showing the D_max of each snapshot of the LD simulations of the yeast Rev1 protein as a function of time. E. A histogram showing the distribution of R_g values of the snapshots in the full ensemble of the yeast Rev1 protein. F. A histogram showing the distribution of D_max values of the snapshots in the full ensemble of the yeast Rev1 protein. G. A plot showing the theoretical SAXS curve derived from the full ensemble of the yeast Rev1 protein. H. The theoretical P(r) plot derived from the full ensemble of the yeast Rev1 protein. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

The initial model of Rev1 was derived from the X-ray crystal structures of the yeast Rev1 BRCT domain (PDB ID: 4ID3) [52] and the yeast Rev1 polymerase domain (PDB ID: 3BJY) [53] as well as homology models of the two UBMs and the C-terminal domain built with SWISS-MODEL [33] using the X-ray crystal structures of the human DNA polymerase iota UBM (PDB ID: 2L0G) [54] and the human Rev1 C-terminal domain (PDB ID: 2LSY) [55] as templates. The unstructured N-terminal region also contained five putative α-helices identified by Phyre2.0 [34]. All of these structural elements were connected in a stepwise manner using LOOPY [35].

Because of the large size of Rev1, all-atom MD simulations for several μs are not currently feasible. For this reason, the initial model was converted to a coarse-grained model as described previously [42,51]. Depending on the size, shape, and charge of the side chain, each amino acid residue was represented by one to four coarse-grain (CG) beads. LD simulations were then carried out using the program uiowa_BD [42,45,56] with 125 fs time steps with snapshots (PDB files) recorded every ns for 10 μs of simulation time, which is the approximate time frame of many domain motions. The LD simulation resulted in a sequence of 10,000 structural snapshots, which constituted the full ensemble. Several snaps shots of Rev1 are shown in Fig. 2B.

To examine the conformational flexibility of the N-terminal and C-terminal regions of Rev1, we used CRYSOL [31] to generate predicted scattering curves and MOLEMAN [57] to generate predicted P(r) plots for each individual structure (snapshot) in the ensemble. The R_g and D_max values for each snapshot were obtained from these graphs using AUTORG and GNOM [25,28], respectively. We graphed the R_g and D_max values as functions of simulation time (Fig. 2C and D). These graphs show that the conformation of Rev1 changes significantly during the simulation. The lack of an upward or downward trend, however, suggests that the system is at equilibrium and that the unstructured regions are not in the process of extending outward or collapsing inward. We further generated histograms showing the distribution of R_g and D_max values during the course of the simulation (Fig. 2E and F).

Visual examination of the snapshots reveals that the vast majority (~94%) of the structures constituting the ensemble have R_g and D_max values near their average value. In these structures, one or both of the unstructured regions are in partially extended states. Only a small number of structures (~3%) have R_g and D_max values near their minimum values. In these structures, both of the unstructured regions are in compact states. Similarly, only a small number of structures (~3%) have R_g and D_max values near their maximum values. In these structures, one or both of the unstructured regions are in highly extended states.

To obtain the predicted scattering curve of the full ensemble, the individual scattering curves for all 10,000 individual structures were averaged (Fig. 2G). The P(r) plot for the full ensemble was obtained by adding all the inter-atomic distances in all 10,000 structures using MATLAB (Fig. 2H). The R_g and D_max values for the full ensemble were obtained from these graphs using AUTORG and GNOM, respectively [25,28].

5.2. Ubiquitin-modified PCNA

Proliferating cell nuclear antigen (PCNA) is a homotrimer that forms a sliding clamp around double-stranded DNA and is an essential protein in DNA replication [[58], [59], [60]]. When the replication fork encounters DNA damage, ubiquitin is attached to Lys-164 of PCNA, and this post-translational modification promotes translesion synthesis [61,62]. Both PCNA and ubiquitin are almost completely structured. Despite this, ubiquitin-modified PCNA is conformationally flexible because there is a short, unstructured linker between the ubiquitin and PCNA moieties.

To model the conformational flexibility of ubiquitin-modified PCNA, coarse-grained LD simulations were run for 10 μs of simulation time [63]. The results from the simulations were analyzed as described above for Rev1. The predicted R_g for the full ensemble was equal to 42.5 Å, and the predicted D_max for the full ensemble was equal to 139 Å [63]. Overall, the ubiquitin moieties sampled many different positions and orientations around the side and back face of the PCNA ring. However, no evidence of preferential ubiquitin-binding sites along the sides and back of the PCNA ring was found. Experimental SAXS data was used to validate the simulations, and excellent agreement was achieved between the LD simulations and the experimental SAXS data. For example, the experimental R_g was equal to 42.4 Å, and the experimental D_max was equal to 140 Å [63].

The predicted scattering curve and P(r) plot from the full ensemble overlaid nicely with the experimental scattering curve and P(r) plot. In fact, the predicted scattering curve derived from the full ensemble approach fit the data better than the predicted curve derived from a minimal ensemble approach [63]. The χ² for the full ensemble approach was 2.65. This is a substantial improvement over the χ² for the minimal ensemble approach, which was 9.03 and resulted in an ensemble of three structures.

5.3. DNA Polymerase Eta

DNA polymerase eta (pol η) is a translesion synthesis polymerases that catalyzes the replication of thymine dimers [64]. It has a structured polymerase domain comprising ~80% of the protein and an unstructured C-terminal region comprising ~20% of the protein. The C-terminal region is not required for enzymatic activity in vitro, but is required for protein function in vivo [65]. This is because the protein-protein interaction motifs necessary for pol η's function are located within the C-terminal region. These include a small, structured ubiquitin-binding zinc finger (UBZ) which binds the ubiquitin moiety of ubiquitin-modified PCNA [66] and a short unstructured PCNA-interacting protein (PIP) motif which binds the PCNA moiety of ubiquitin-modified PCNA [65]. This has led to the notion that the C-terminal region of pol η acts as a long, flexible tether attaching the polymerase domain to the DNA replication machinery.

To model the conformational flexibility of the unstructured C-terminal region of pol η, coarse-grained LD simulations of full-length pol η were run for 10 μs of simulation time [51]. The predicted R_g for the full ensemble was equal to 38.2 Å, and the predicted D_max for the full ensemble was equal to 164 Å [51]. Overall, the C-terminal unstructured region sampled many conformational states, the vast majority of these were somewhere between largely extended states and largely compact ones. Experimental SAXS data was used to validate the simulations, and excellent agreement was achieved between the LD simulations and the experimental SAXS data. For example, the experimental R_g was equal to 37.6 Å, and the experimental D_max was equal to 165 Å [51].

The predicted scattering curve and P(r) plot overlaid nicely with the experimental scattering curve and P(r) plot, and the predicted scattering curve derived from the full ensemble approach fit the data better than the predicted curve derived from a minimal ensemble approach [51]. The χ² for the full ensemble was 3.65. This is a substantial improvement over the χ² for the minimal ensemble, which was 6.16 and contained three structures.

6. Summary and Outlook

Based on its clear advantages, we believe that the full ensemble approaches should be used wherever possible. First, full ensemble approaches avoid the over fitting problem by not fitting the data at all. Second, they represent the conformational flexibility of proteins in a more realistic way. Instead of representing this flexibility by an ensemble containing only three to five structures, they represent it by an ensemble containing tens of thousands of structures, each related to one another by a series of time steps in a molecular simulation. Third, the conformational space sampled by the protein depends on the forces acting on the atoms and the structure of the protein itself without a need for weighting factors.

So far full ensemble approaches have been used successfully with a variety of systems. They have worked with EcoO109I, a protein with a simple, hinge-like motion [47]. They have worked with ubiquitin-modified PCNA and SUMO-modified PCNA, proteins that have the ubiquitin and SUMO moieties attached by short, flexible likers [63]. They have worked with RPA, a protein containing multiple folded domains joined by short flexible linkers [48]. They have worked with pol η, a protein containing an extended region of intrinsic disorder [51]. Taken together, these studies suggest that full ensemble approaches may be more widely applicable than it might at first seem.

One particularly exciting future possibility is to combine full ensemble approaches with small-angle neutron scattering (SANS) [[67], [68], [69]]. SANS is a powerful, emerging technology that allows one to study multi-protein complexes using static, minimal ensemble, and full ensemble approaches. Unlike X-rays, which are scattered by electrons, neutrons are scattered by atomic nuclei, and the ability of a nucleus to scatter neutrons depends on the identity of the nucleus. This allows contrast matching. For example, if one purifies a protein containing roughly 75% of its hydrogen nuclei being H² (deuterons) and 25% being H¹ (protons), this protein will scatter the same as 100% deuterated water. This is important, because one can form a multi-protein complex with some component proteins being 75% deuterated and other proteins being nearly 100% protonated. The SANS data that one would obtain after buffer subtraction would only include scattering from the mostly protonated proteins.

Given this, one can modify the way in which the full ensemble derived from MD or LD simulations is analyzed. The simulations of the full protein complex can be run. However, when one calculates the scattering curve or the P(r) plot, one can ignore any proteins that were 75% deuterated in the SANS experiment and therefore obtain the plots for only the nearly 100% protonated proteins. This would allow one to directly validate the conformational flexibility of each individual protein component of a multi-protein complex within the context of the complex itself as opposed to isolated in solution.

Comparing the scattering curves for proteins components of a multi-protein complex isolated and within the complex itself will be extremely informative. It will show whether the conformational flexibility observed in solution is similar to or different from that observed in the complex. Moreover, it will allow us to have a complete description of the conformational space explored by the individual components and the entire complex as a whole. Such an achievement would move us closer to overcoming what arguably is the greatest problem facing structural biologists today – understanding the structure of conformationally flexible protein complexes to gain novel biological insights into their functions.

Conflict of Interest

The authors declare that they have no conflict of interest.