Abstract
The firing rate of speed cells, a dedicated subpopulation of neurons in the medial entorhinal cortex (MEC), is correlated with running speed. This correlation has been interpreted as a speed code used in various computational models for path integration. These models consider firing rate to be linearly tuned by running speed in real-time. However, estimation of firing rates requires integration of spiking events over time, setting constraints on the temporal accuracy of the proposed speed code. We therefore tested whether the proposed speed code by firing rate is accurate at short time scales using data obtained from open-field recordings in male rats and mice. We applied a novel filtering approach differentiating between speed codes at multiple time scales ranging from deciseconds to minutes. In addition, we determined the optimal integration time window for firing-rate estimation using a general likelihood framework and calculated the integration time window that maximizes the correlation between firing rate and running speed. Data show that these time windows are on the order of seconds, setting constraints on real-time speed coding by firing rate. We further show that optogenetic inhibition of either cholinergic, GABAergic, or glutamatergic neurons in the medial septum/diagonal band of Broca does not affect modulation of firing rates by running speed at each time scale tested. These results are relevant for models of path integration and for our understanding of how behavioral activity states may modulate firing rates and likely information processing in the MEC.
SIGNIFICANCE STATEMENT Path integration is the most basic form of navigation relying on self-motion cues. Models of path integration use medial septum/diagonal band of Broca (MSDB)-dependent MEC grid-cell firing patterns as the neurophysiological substrate of path integration. These models use a linear speed code by firing rate, but do not consider temporal constraints of integration over time for firing-rate estimation. We show that firing-rate estimation for speed cells requires integration over seconds. Using optogenetics, we show that modulation of firing rates by running speed is independent of MSDB inputs. These results enhance our understanding of path integration mechanisms and the role of the MSDB for information processing in the MEC.
Keywords: entorhinal cortex, medial septum, path integration, speed cells, speed signal
Introduction
Path integration (or dead reckoning) is a very basic form of navigation that is highly conserved across species and relies on self-motion cues (Mittelstaedt and Mittelstaedt, 1980; Etienne et al., 1998; Etienne and Jeffery, 2004). Path integration relies on continuously updating memory of the animal's location by integrating speed and running direction. The neuronal correlate of such a path integrator has been hypothesized to be the regular hexagonal spatial firing pattern of grid cells in the medial entorhinal cortex (MEC; Fyhn et al., 2004, 2008; Hafting et al., 2005). Modulation of conjunctive grid cells by head direction and running speed (Sargolini et al., 2006) supports the hypothesis of grid cells functioning as path integrators (McNaughton et al., 2006). The emergence of the periodic grid-cell firing pattern has been modeled using continuous attractor models (McNaughton et al., 1991; Fuhs and Touretzky, 2006; Burak and Fiete, 2009) or oscillatory interference models (Burgess et al., 2007; Burgess, 2008).
Oscillatory interference and attractor dynamics models both require a linear running speed signal to update position continuously in time. The running speed of an animal has been shown to positively modulate the spiking rates of a number of different functional classes of neurons in the hippocampus (McNaughton et al., 1983; O'Keefe et al., 1998) and MEC (Sargolini et al., 2006; Wills et al., 2012; Kropff et al., 2015; Hinman et al., 2016). A functionally dedicated population of neurons in the MEC has been proposed to code running speed by firing rate in a linear and context-invariant manner and have been termed “speed cells” (Kropff et al., 2015), which are generally assumed to provide the linear speed signal required for path integration by grid cells. However, many speed-modulated cells in the MEC have been shown to be better fit by a saturating exponential than a linear speed tuning curve (Hinman et al., 2016). Moreover, speed tuning curves are generated by integration over long time periods, thus leaving the question unanswered whether the animal's position in space is continuously and accurately updated at every moment in time. Data presented here demonstrate (1) the firing-rate modulation by running speed is linear at each time scale, even if the overall speed tuning curve appears to be exponentially saturating; (2) speed modulation of firing rates differs across time scales, with steeper speed tuning curves at longer time scales compared with shorter time scales; (3) firing-rate estimation for most speed cells requires integration over seconds; and (4) the speed scores of most speed cells peak when firing rates are computed over second-long time windows. Because of these temporal constraints required for accurate firing-rate estimation, we conclude that the firing modulation by running speed observed in speed cells reflects different activity states on a seconds-long time scale rather than providing an accurate moment-to-moment speed code on the subsecond time scale.
The speed signal has been hypothesized to be conveyed by speed-modulated activity of neurons in the medial septum/diagonal band of Broca (MSDB), which has major projections to the entorhinal cortex (Alonso and Köhler, 1984). The theta burst frequency of the majority of MSDB neurons correlate with running speed (King et al., 1998). Lesions and pharmacological inactivation of the MSDB disrupt theta (6–10 Hz) rhythm in the hippocampal formation (Rawlins et al., 1979; Mitchell et al., 1982; Mizumori et al., 1990), and inputs from the MSDB pace theta oscillations (Buzsáki, 2002; Hangya et al., 2009). Theta oscillation frequency and amplitude correlate with running speed in rodents (Jeewajee et al., 2008; Hinman et al., 2011). Oscillatory interference models of path integration hypothesize that the slope of the theta frequency versus running speed correlation reflects the presence of velocity-controlled oscillators whose frequencies increase with running speed (Burgess, 2008). Computational models suggest a possible role of cholinergic modulation in coding of novelty, spatial location, and running speed in the entorhinal cortex (Hasselmo et al., 2017). The y-intercept of the theta frequency versus running speed relationship is affected by anxiolytic drugs (Wells et al., 2013; Monaghan et al., 2017), whereas environmental novelty (Wells et al., 2013) and muscarinic cholinergic signaling (Newman et al., 2013) have been shown to specifically affect the slope of the theta frequency to running speed relationship. Cholinergic modulation has been shown to increase visual cue detection (Gritton et al., 2016) and to enhance sensory processing by nicotinic enhancement of afferent input (Gil et al., 1997; Hsieh et al., 2000; Disney et al., 2007; Niell and Stryker, 2010; Fu et al., 2014). Furthermore, acetylcholine contributes to the integration of idiothetic cues in head direction cells (Yoder et al., 2017). However, pharmacogenetic activation of medial septum cholinergic neurons (Carpenter et al., 2017) did not affect firing-rate modulation by running speed, whereas pharmacological inactivation of the whole MSDB decreased speed modulation of intrinsic theta frequency while firing rates of MEC neurons became more strongly modulated by running speed (Hinman et al., 2016). To test the role of cholinergic modulation on speed tuning, we used an optogenetic silencing approach to inactivate the cholinergic MSDB subpopulations or the whole MSDB in mice with high temporal precision during voluntary exploration of an open-field environment. Our data show that firing-rate modulation by running speed in MEC does not depend on MSDB inputs.
Materials and Methods
Subjects.
Before surgery, mice and rats were habituated to the experimenter and testing room. All experimental procedures were approved by the Institutional Animal Care and Use Committee for the Charles River Campus at Boston University.
The data from rats used for analysis in this study were previously acquired (Monaghan et al., 2017). Adult male Long–Evans rats (350–450 g at day of surgery; Charles River Laboratories) were housed individually in Plexiglas cages and maintained on a 12 h light/dark cycle at 85% of their ad libitum weight during the data collection period.
The data from mice were collected for the purpose of this study. Mice were purchased from The Jackson Laboratory (wild-type, C57BL/6J; ChAT-IRES-Cre, B6;129S6-Chattm2(cre)Lowl/J; PV-IRES-Cre, B6;129P2-Pvalbtm1(cre)Arbr/J; vGluT2-IRES-Cre, Slc17a6tm2(cre)Lowl/J). Transgenic mice were maintained as homozygous, and both homozygous and heterozygous mice were used for experiments. For data collection, adult male mice were housed in Plexiglas cages together with their siblings before surgery, but separated for individual housing after surgery, and maintained on a reversed 12 h light/dark cycle.
Viral transduction.
For cell-type-specific targeting of either cholinergic, GABAergic, or glutamatergic MSDB neurons for optogenetic silencing, we used stereotactically targeted virus injections of rAAV S9 FLEX-CAG-ArchT-GFP (Lot AV6222b, UNC Vector Core) into the MSDB of either ChAT-Cre, PV-Cre, or vesicular glutamate transporter 2 (vGluT2)-Cre mice. For targeting the whole MSDB, an unconditional version of the same construct was used (rAAV S9 CAG-ArchT-GFP, Lot AV6221D, UNC Vector Core). For control experiments with mock-silencing, Cre-transgenic mice were injected with a conditional rAAV coding for GFP (rAAV S9 FLEX-CAG-GFP, Lot AV5220b, UNC Vector Core), and wild-type mice were injected with the unconditional version of the same construct (rAAV S9 CAG-GFP, Lot AV5221, UNC Vector Core). Virus injection was performed under isoflurane anesthesia two weeks before the microdrive implantation to allow for sufficient opsin expression. Virus solution (2 × 250 nl) was injected at two ventral sites within the MSDB. To that end, a craniotomy was performed 1 mm anterior and 0.7 mm lateral to bregma, and the injection needle was lowered 4.8 and 4.4 mm at a 10° polar and −90° azimuth angle, following stereotactic coordinates from Paxinos and Franklin (2008). The injection needle (34 g, beveled; WPI) was left in place for 3 and 5 min after the first and second injections (100 nl/min; UMP3 electrical pump, WPI) to prevent backflow of the injected virus solution.
Surgery for microdrive implantation in rats.
Rats were implanted with recording drives housing up to 20 individually moveable tetrodes, of which four were used as reference tetrodes, targeted to the deep and superficial layers of MEC. The details of surgical procedures for neural recordings in rats are given by Monaghan et al. (2017). Briefly, rats were anesthetized with isoflurane and an initial injection of ketamine/xylazine/acepromazine mixture (ketamine: 12.92 mg/kg, acepromazine: 0.1 mg/kg, xylazine: 1.31 mg/kg) and buprenorphine (50 μg/kg). Two craniotomies were performed: one for implantation of a drug delivery cannula aimed toward the MSDB for use in another set of experiments (0.5 mm anterior, 3.0 mm lateral to bregma, lowered 6.0 mm from brain surface at a 25° polar and −90° azimuth angle), and one for implantation of the microdrive just anterior of the transverse sinus (most lateral and posterior corner, where the left bone ridge and lambda suture meet, angled 25° in the posterior direction (25° polar, 180° azimuth angle). One to two ground screws were implanted above the cerebellum, and 10 anchoring screws were positioned across the skull. Once the implant was firmly secured with dental cement, tetrodes were lowered 2–3 mm from the dorsal brain surface at surgery. Animals were allowed 1 week to recover fully after surgery before beginning of recordings.
Surgery for light fiber and microdrive implantation in mice.
Mice were injected with buprenorphine (0.1 mg/kg, s.c.) and atropine (0.1 mg/kg, i.p.), and chronically implanted under isoflurane anesthesia with 8-channel Axona microdrives carrying two movable tetrodes.
One ground screw was implanted above the cerebellum, five anchoring screws were positioned across the skull, and two craniotomies were performed for implantation of the light fiber (200 μm core, NA: 0.22; MFC_200/240-0.22_8mm_SMR_FLT, Doric Lenses), 1.0 mm anterior and 0.7 mm lateral to bregma, and for implantation of the microdrive, 0.3 mm anterior to the edge of the transverse sinus, 3.3 mm lateral to the midline. The light fiber was lowered 4.0 mm from the brain surface at an 8° polar and −90° azimuth angle and cemented on the animal's skull. Tetrodes were then implanted with a 4° polar and 0° azimuth angle, lowered 0.6 mm into the brain, and cemented onto the skull. Animals were given buprenorphine (0.1 mg/kg, i.p.), enrofloxacin (7.5 mg/kg, i.p.), and ketoprofen (3 mg/kg, i.p.) during a 5 d postsurgical care period and allowed 1 week in total to fully recover after surgery before beginning of recordings.
In vivo electrophysiological recordings.
Before implantation, impedance of tetrodes [12.7 μm nichrome wire (California Fine Wires) for rats, 17 μm platinum wires (California Fine Wires) for mice] was adjusted by electroplating to < 150 kΩ. Recordings were performed on the left hemisphere. Tetrodes were lowered daily by 35 μm in rats or 50 μm in mice, until theta rhythmic cells could be recorded indicating that tetrode tips were located in the deep or superficial cell layers of MEC, and recording sessions began. After each recording day, tetrodes were lowered further to advance through the cell layer until no further spiking activity could be recorded. Neural signals were pre-amplified by unity-gain operational amplifiers located on each animal's head.
For rats, signals were AC-coupled to digital amplifiers of the 64-channel Cheetah Digital Lynx acquisition system (NeuraLynx). When a signal crossed threshold, all four channels of the tetrode were digitized at 32 kHz and recorded. Information about position and head direction of the rat was obtained at 30 Hz via an overhead video camera that monitored a red (anterior) and green (posterior) LED attached to the headstage.
For mice, signals were AC-coupled to an Axona recording system. When a signal crossed threshold all four channels of the tetrode were digitized at 48 kHz and recorded. Information about position and head direction of the mouse was obtained at 50 Hz via an overhead video camera that monitored a small (right) and big (left) infrared LED attached to the headstage. EEG signal was recorded single-ended with the ground screw as reference at a 4800 Hz sampling rate.
Spikes were clustered using spike clustering software (for mice: DacqUSB/Tint, Axona; for rats: Offline sorter, Plexon). All further off-line analyses were performed using MATLAB (MathWorks) and custom-written MATLAB scripts.
Behavioral testing.
All recordings were performed while animals foraged for small pieces of Froot Loops (Kellogg) in the open-field environment. A typical recording session lasted 20 min for rats and 46 min for mice.
Rats were familiarized with foraging for pieces of Froot Loops in an open-field environment (1 × 1.5 m) with three black and one white painted wall. Distal cues surrounding the environment were visible to the rat.
Mice were trained to forage for pieces of Froot Loops in an open-field environment (1 × 1 m) with 60 cm high black walls and a white letter-size cue card at one wall. The recording environment was surrounded by black curtains.
Laser stimulation for optogenetic silencing of MSDB neurons.
For laser stimulation in mice, we used a fiber-coupled 532 nm laser (OBIS FP, Coherent), which was digitally modulated via the recording software. Laser light was delivered into the brain via a system of fiber patch cords (Thorlabs) and a rotary joint (FRJ_1×1_FC-FC, Doric Lenses). The last connection was a magnetic connection to the implanted light fiber. The laser light power entering the implanted light fiber was measured before and after every recording session and adjusted before the recording session to yield an estimate of 15–25 mW laser power delivered into the MSDB. Laser stimulation was applied in alternating 120 s Laser OFF and 145 s Laser ON periods until the end of the recording session (a typical recording session lasted 2770 s with 11 Laser OFF and 10 Laser ON periods).
Histology.
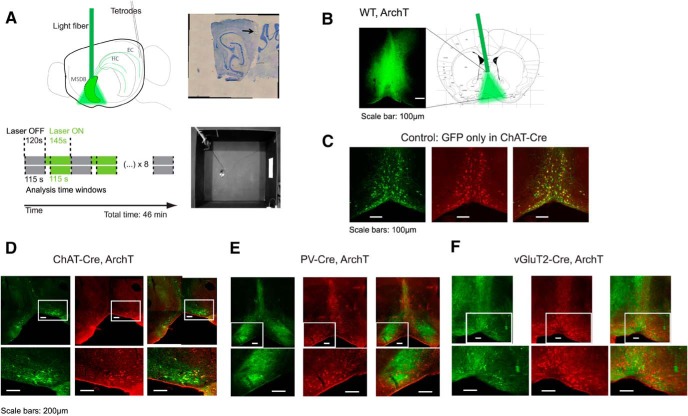
After the end of electrophysiological data collection, animals were deeply anesthetized by isoflurane or intraperitoneal injection of Euthasol (390 mg/kg), followed by electro-lesions (20 μA, 16 s) through one channel of each tetrode and subsequent transcardial perfusion with saline followed by 10% buffered formalin (SF100-4, ThermoFisher Scientific). Brains were extracted and stored in fixative for 1 d. Cresyl violet staining was performed on 50 μm sagittal slices of MEC to visualize tetrode tracks.
For immunolabeling of ArchT-GFP and ChAT in the MSDB, 50 μm coronal sections of the MSDB were incubated with first antibodies (goat anti-ChAT affinity purified polyclonal antibody, catalog #AB 144P, Merck Millipore, diluted 1:500; rabbit anti-GFP affinity purified polyclonal antibody, catalog #ab6556 OR ab290, Abcam, diluted 1:1000), followed by secondary antibodies (Cy3-conjugated donkey anti-goat-IgG polyclonal antibody, catalog #AP180C, Merck Millipore, diluted 1:1000; FITC-conjugated donkey anti-rabbit-IgG polyclonal antibody, catalog #711-096-152, Dianova, diluted 1:1000).
Calculation of running speed, instantaneous firing rate, and speed scores.
The animal's running speed was estimated by applying a Kalman filter to the positional data obtained from the video tracking (Fyhn et al., 2004; Kropff et al., 2015). To obtain an instantaneous firing rate signal, we calculated the instantaneous firing rate as the number of spikes per video frame period (33 ms for rats, 20 ms for mice), and smoothed this signal with a 125 ms Gaussian filter. Speed tuning curves (STCs) were created by binning the firing rate into 1 cm/s speed bins ranging from zero to the 99th percentile of running speeds.
The speed score was calculated as the Pearson's product moment correlation between firing rate and running speed (Kropff et al., 2015).
Filtering of running speed and firing rate to obtain speed tuning at different time scales.
To analyze speed tuning at different time scales in the range from 0.125–0.25 s up to 256–512 s in rats or 512–1024 s in mice, we applied time-domain filters to the running speed and instantaneous firing-rate signals. For filtering at a time scale [t1, t2], the signal smoothed with a t1-sized window was subtracted from the signal smoothed with a t2-sized window. This results in a demeaned time-domain filtered signal. Time scale-dependent STCs were then calculated for the filtered running speed and filtered firing-rate signal.
Classification of speed-modulated neurons.
In a first step, time scale-dependent speed scores were calculated for each cell at time scales ranging from 1 to 2 s up to 256–512 s in rats or 512–1024 s in mice. In a second step, hierarchical clustering of cells based on the Euclidean distance between time scale-dependent speed scores was computed using the clustergram function of the bioinformatics toolbox in MATLAB. The minimal linkage distance for separation of clusters was arbitrarily set to 0.9 (mouse dataset) or 0.95 (rat dataset) to create a reasonable number of clusters. The results of this hierarchical clustering approach for identification of speed-modulated neurons were compared with the classification results of a more classical shuffling procedure: chance-level statistics for determination of significant speed modulation were constructed by a shuffling procedure where the 20 ms (mouse data) or 33 ms (rat data) binned spike train of a given cell was randomly shifted in time in a circular manner, so that spikes exceeding the recording length after shifting were added at the beginning of the shifted spike train (Ye et al., 2018). The shuffling procedure was repeated 1000 times for each cell to create a null distribution of overall speed scores. A cell was classified as significantly speed modulated (negatively or positively) if its speed score was below the first or above the 99th percentile of that null distribution, respectively.
Maximum likelihood estimates of linear and exponentially saturating speed tuning curves.
Maximum likelihood estimates (MLEs) of linear and exponentially saturating fits were obtained as previously described in detail (Hinman et al., 2016) for all speed-modulated neurons using the mle function in MATLAB. If a speed-modulated cell's firing rate was significantly better predicted by the exponentially saturating fit compared with the linear fit at an α level of 0.05, the cell was classified as saturating exponentially tuned. Otherwise, it was classified as linearly tuned.
Calculation of Poisson-distributed spike trains.
For each cell and for each time point (20 ms time bins) a random number of spikes was drawn from a Poisson distribution with the parameter λ set to the expected firing rate given the animal's running speed at that time point based on the linear fit STC for that cell.
Decoding of running speed from firing rates of speed-modulated neurons.
We implemented a linear decoder as described in detail by Kropff et al. (2015) for decoding running speed from the firing rates of simultaneously recorded speed-modulated neurons. The linear decoder was trained on the first half of the dataset and tested on the second half of the dataset. To decode the raw running speed signal, we used the instantaneous firing-rate signal and the raw running speed signal as inputs. To decode time-scale-dependent running-speed signals, we used the time-scale filtered firing-rate signals and time-scale filtered running-speed signals as inputs. Accuracy of decoding was measured as the Pearson product-moment correlation coefficient between the decoded and observed speed signals.
General likelihood framework for estimation of firing rates.
To compute a firing rate, a spike train has to be smoothed using a kernel with a given bandwidth. The choice of the bandwidth parameter artificially imposes assumptions regarding the time scale of meaningful changes in firing rate (Prerau and Eden, 2011). To find the bandwidth that most accurately integrates spike times in a given spike train to create a firing-rate estimate, we used the general likelihood framework for characterizing the time course of neural activity developed by Prerau and Eden (2011). This method requires selection of a kernel and a bandwidth parameter which determines the temporal range over which the kernel smoothing procedure integrates information about the spike train to convert a discontinuous spike train into a continuous firing-rate estimate. For each spike in the spike train, a firing-rate estimate is computed by kernel smoothing over the surrounding spikes leaving the data point in the center out. The firing-rate estimate obtained from this procedure is then used to calculate the log-likelihood of a spiking event at the omitted time point. The log-likelihoods for all time points in the spike train are summed and the whole process is repeated for another bandwidth parameter. The bandwidth parameter which maximizes the summed log-likelihood is considered the optimal bandwidth for firing-rate estimation. We used a Hann kernel w, as follows:
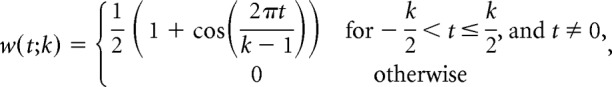 |
where k is the bandwidth parameter (length of the kernel) in units of time t.
Oscillatory interference model of grid cell firing.
To model the impact of integrating running speed over time on grid cell spatial periodicity, we used the oscillatory interference model of grid cell firing developed by Burgess et al. (2007) and studied further by Hasselmo et al. (2007) and Giocomo et al. (2007). This model depends on appropriate speed- and direction-dependent inputs to generate a grid-like firing pattern in two-dimensional space.
LFP analysis.
LFP data were downsampled to 600 Hz and power spectral density analyses were performed using custom written MATLAB scripts and the FieldTrip toolbox (Oostenveld et al., 2011).
Time-frequency analysis.
Time-frequency analysis of LFP power was performed using the FieldTrip multitaper method based on Slepian sequences with adjustable time windows containing 10 numbers of cycles per frequency in 0.2 Hz steps, and time increments of 0.1 s.
To analyze effects of rhythmic optogenetic silencing on LFPs, time-frequency analysis was performed (see above), and z-scores were assigned to each time and frequency bin of the resulting spectrograms using the full-epoch-length single-trial baseline correction method developed by Grandchamp and Delorme (2011). For each stimulation frequency, we computed the differences of the z-scores at those stimulation frequencies and the mean z-scores of the adjacent frequencies (±10% of the stimulation frequencies) and averaged the resulting values across sessions. To assess significance, we tested whether LFP effects were significantly locked to the time of rhythmic stimulation. To that end, we computed a surrogate distribution of all possible 120 s epochs, and computed p values based on the rank of the observed data within that surrogate distribution.
Quantification of theta peak power.
The theta peak power in the smoothed power spectrum was measured relative to a baseline defined by the linear interpolation between the values at frequencies surrounding the theta peak.
Instantaneous theta frequency versus running speed.
A theta frequency range was determined for each animal based on the range of the theta peak in the power spectral density plot (lower bound: 6.22 ± 0.82 Hz, higher bound: 10.21 ± 0.67 Hz). The LFP signal was then bandpass filtered at this theta frequency range with a third-order Butterworth filter, and the instantaneous theta amplitude and phase were determined via a Hilbert transform. Based on the instantaneous theta phase information, an instantaneous theta frequency was calculated for each point in time and matched with running speed information. To analyze changes in the theta frequency versus running speed relationship, we binned theta frequency by running speed at a bin width of 1 cm/s, and calculated the y-intercept and slope of the linear regression.
Experimental design and statistical analysis.
Details on statistical analyses on each experiment are reported in Results or Materials and Methods. Details on the MLE linear and saturating exponential fits were provided by Hinman et al. (2016). Details on data collection from rats were provided by Monaghan et al. (2017). In experiments using optogenetic silencing, if not mentioned otherwise, we excluded the first 5 s after laser offset and the first 30 s after laser onset from analyses to account for activation and deactivation kinetics of effects mediated by G-protein-coupled receptors.
Code accessibility.
Custom MATLAB code used for data analysis can be found at https://github.com/hasselmonians or can be made available upon request.
Results
Firing-rate modulation by running speed in entorhinal cortex speed cells differs across time scales
To study firing-rate modulation by running speed of entorhinal cortex speed cells at different time scales, we recorded activity from single units (n = 665) in the medial entorhinal cortex of rats (n = 11) during exploration of an open-field environment (1 × 1.5 m; see Materials and Methods) and applied a novel filtering approach (see Materials and Methods) to differentiate between time scale-dependent changes in running speed and firing rate at time scales ranging from 0.125–0.25 s up to 256–512 s (Fig. 1). Using the convention introduced by Kropff et al. (2015) we defined a speed score as the Pearson correlation coefficient between the animal's running speed and a cell's firing rate. However, this speed score does not reflect possible differences of speed modulation across time scales. Therefore, in addition to an overall speed score, we calculated time scale-specific speed scores for each time scale. This allowed us to use an unbiased hierarchical clustering approach (see Materials and Methods) to identify clusters of cells with similar time scale-dependent speed scores. Using this hierarchical clustering approach, we identified a set of neurons showing clear positive speed modulation of firing rate (n = 182 of 665 cells, 27.4%, Clusters A and B; Fig. 2A,B) with a smaller fraction (n = 6 of 665 cells, 1%, Cluster A) of very strongly speed-modulated neurons and a larger fraction (n = 176 of 665 cells, 26.5%, Cluster B) of moderately to strongly speed-modulated neurons. Together, these cells formed a smaller, but more precisely defined speed-cell cluster compared with the result of a classification method that uses an arbitrarily set threshold of the 99th percentile of a null distribution of speed scores from spike trains randomly shifted in time (n = 282 cells of 665, 42.4%; see Materials and Methods). Yet, n = 181 cells of 182 (99.5%) identified as speed-modulated using the clustering approach were also classified as speed-modulated by the speed score threshold approach. Consistent with earlier reports (Kropff et al., 2015; Hinman et al., 2016) we also identified a smaller fraction of neurons showing negative speed modulation of firing rate (n = 45 of 665 cells, 6.8%; Fig. 2A,B, Cluster F).
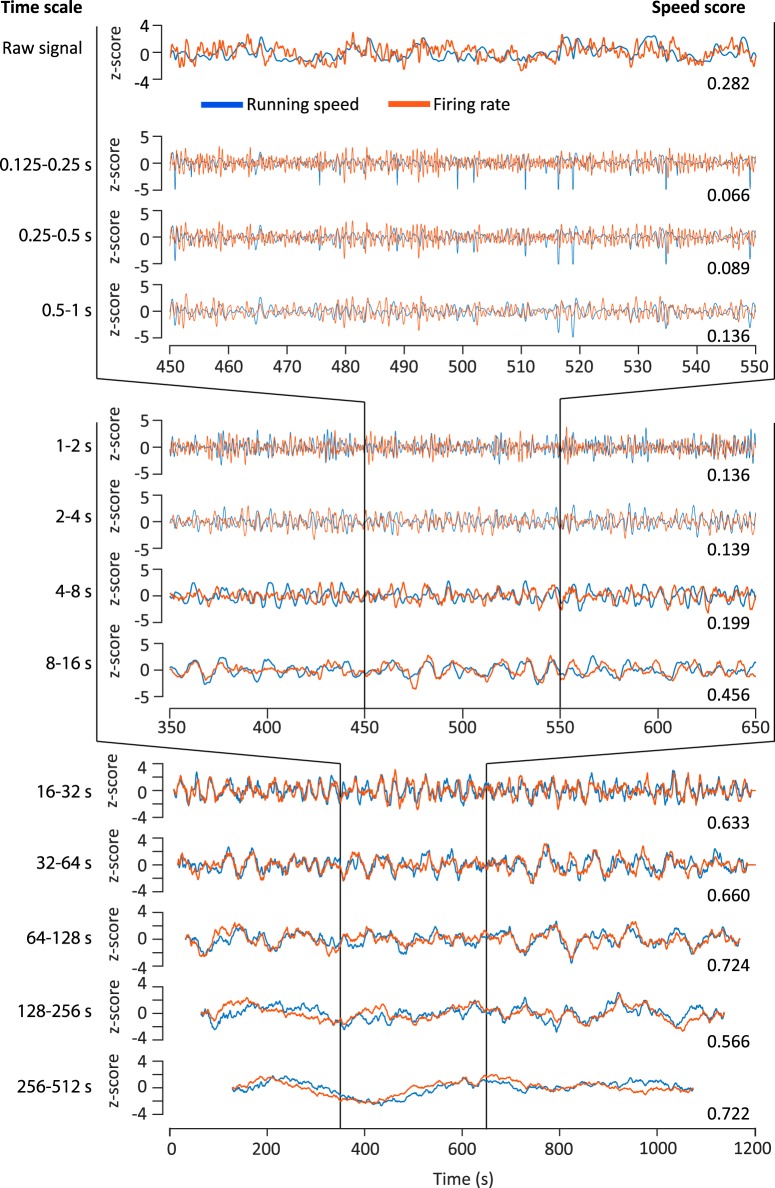
Figure 1.
Filtering of speed and firing-rate signals distinguishes between speed modulation at different time scales. Speed modulation of firing rate at different time scales shown for an example neuron of the rat dataset (same example neuron in Fig. 2). The top row shows unfiltered data (instantaneous running speed and firing-rate signal). The following rows show time scale-filtered data with the time scales indicated on the left. Speed scores calculated at each time scale are given at the bottom right of each row. For better comparison of running speed and firing rate, data are presented as z-scores. Blue traces represent z-scores of time-scale filtered running speed; red traces represent z-scores of time-scale filtered firing rate. The top four rows show 100 s of data, the middle four rows show 200 s of data, and the bottom five rows show data on the entire 20 min recording session.
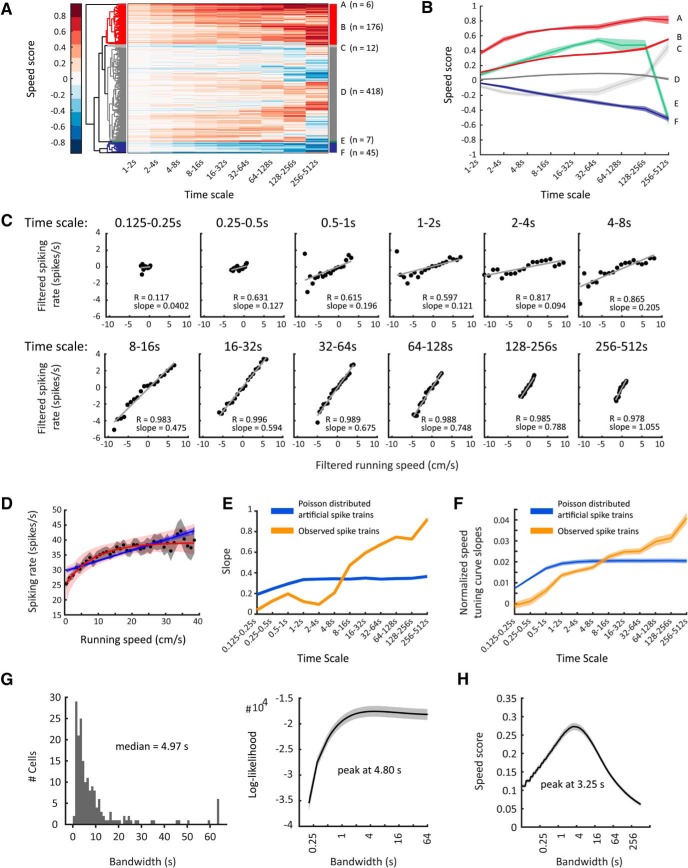
Figure 2.
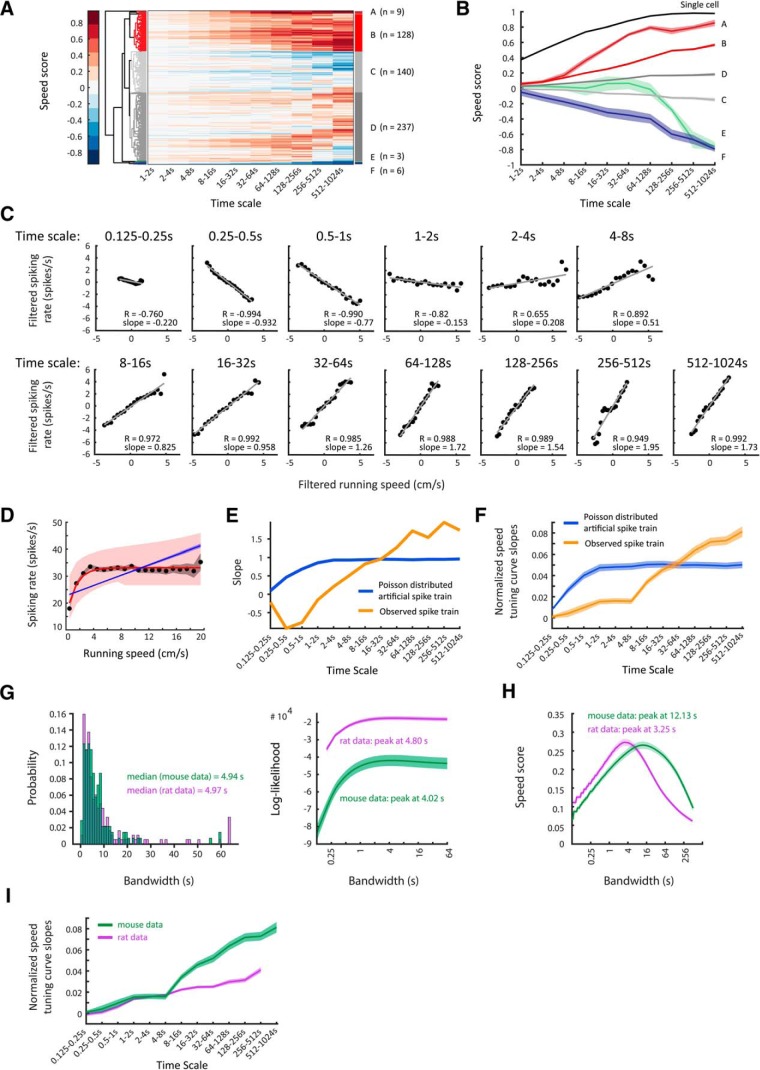
Firing-rate tuning by running speed in the entorhinal cortex of rats differs across time scales. Time scale-dependent speed scores allow clustering of neurons recorded in the rat entorhinal cortex into different speed-cell categories. A, Clustergram showing hierarchical clustering of 665 single units recorded in MEC of 11 rats. Each row depicts color-coded speed scores calculated for each time scale ranging, exponentially increasing, from 1 to 2 s up to 256–512 s (see Materials and Methods). Distinct clusters of clearly speed-modulated neurons can be identified. B, Mean ± SEM of time scale-dependent speed scores of clusters identified in A. C–E, Data on one speed-modulated example cell in Cluster B. C, Time scale-dependent speed tuning. Black dots show binned data (time-scale filtered firing rate vs time-scale filtered running speed); red lines show the least-square linear fits to binned data, r = Pearson correlation coefficient. D, The overall speed tuning curve of the example cell. Black dots and gray shading show mean values and 95% confidence intervals of speed-binned firing-rate data; blue and red lines show the best MLE linear (blue) and saturating exponential (red) fit functions obtained by temporal binning of firing rate, shadings indicate 95% confidence intervals. E, Slopes of observed time scale-dependent speed tuning curves for the example cell (orange curve) compared with mean ± SEM of slopes derived from 100 artificially created linearly tuned Poisson-distributed spike trains (blue line, SEM within line). F, Mean ± SEM of mean-normalized speed tuning curve slopes across all cells (orange, positively speed-modulated cells of Clusters A and B; blue, artificially created Poisson-distributed spike trains, one Poisson train per cell, n = 182). Observed spike trains differ significantly from artificial ones, F(11,4344) = 26.00, p = 0.0000, two-way ANOVA interaction effect. G, Left, Distribution of optimal bandwidths for firing-rate estimation. Right, Population average (mean ± SEM) of bandwidth-dependent log-likelihoods of firing-rate estimates. H, Population average (mean ± SEM) of bandwidth-dependent speed-score distributions.
Our data demonstrate that the absolute speed scores increase with time scales for all identified clusters (Fig. 2B) indicating that speed modulation by firing rate becomes more accurate when integrating a speed-modulated cell's firing rate over longer periods of time. Speed modulation by firing rate is generally assumed to be reflected in the cell's STC (Fig. 2D). However, STCs are generated by integrating over the whole recording time, which typically ranges from several minutes up to 1 h (Wills et al., 2012; Kropff et al., 2015; Hinman et al., 2016). Therefore, STCs do not differentiate between fast changes of firing rates on short time scales, which can be assumed to be important for path integration mechanisms versus slow changes of firing rates on longer time scales, which may reflect changes of metabotropic neuromodulatory input associated with different behavioral activity states.
The observed increase in time-scale-dependent speed scores with longer time scales raises the question whether a proposed speed code by firing rate, as reflected by a cell's STC, is accurate at shorter time scales. To address this, we calculated an STC for each time scale by binning time scale-dependent firing rate by time scale-dependent running speed to investigate whether STCs change across time scales. Interestingly, the slopes of time scale-dependent STCs become steeper at longer time scales (Fig. 2E,F for mean-normalized slopes) indicating less accurate coding of running speed at short time scales.
Speed coding by firing rate becomes inaccurate at short time scales
One possible explanation for less-accurate speed coding at shorter time scales may be Poisson noise of spike timing. To determine whether our findings of flatter STC slopes and lower speed scores at shorter time scales are simply due to Poisson noise or instead reflect a genuine lack of speed tuning accuracy at shorter time scales, we simulated Poisson-distributed artificial spike trains based on the MLE linear fits of the speed-modulated cells. These artificial Poisson distributed spike trains were thus designed to be perfectly speed modulated with their STCs matching the MLE linear fits given by the observed data. Notably, STC slopes approached zero at subsecond time scales in both the observed and simulated data, indicating the dominance of noise at subsecond time scales. In contrast to the observed data, the simulated Poisson-distributed spike trains did not show differential speed coding for second-long time scales as revealed by similar normalized STC slopes across second-long time scales (Fig. 2E,F). The difference between the observed data and the simulated control data was highly significant (two-way ANOVA interaction effect, F(11,4344) = 26.00, p = 0.0000) indicating that the observed increases in time scale-dependent STCs are real and not an artifact of our filtering approach.
In summary, these data show that (1) speed tuning is linear at each individual time scale, (2) STC slopes of most speed-modulated cells become steeper at longer time scales indicating that a proposed speed code by firing rate is less accurate at short time scales, and (3) this lack of accuracy at short time scales cannot be explained by the Poisson nature of neuronal firing.
The smoothing parameter maximizing the prediction of spiking events given the firing rate is on the order of seconds
Firing rate is a convenient mathematical construct rather than a biologically observable signal and thus it is impossible to empirically evaluate the accuracy of a firing-rate estimate (Prerau and Eden, 2011). To overcome this problem, we used the general likelihood framework for estimation of firing rates from neural spike train data developed by Prerau and Eden (2011). This general likelihood framework identifies the smoothing parameter (bandwidth of a Hann kernel; see Materials and Methods) for a firing-rate estimate, which allows the best statistical prediction of spiking events. This parameter is thus solely based on the spike train itself. The optimal bandwidth is found by maximizing the log-likelihood of the firing-rate estimate. The optimal bandwidths for firing-rate estimation in the rat dataset followed a log-normal distribution with a median of 4.97 s (Fig. 2G, left). Likewise, the bandwidth-dependent log-likelihoods of firing-rate estimates peaked on average at 4.80 s (Fig. 2G, right). These data indicate that second to subsecond short time scales are too short for providing a meaningful readout of firing rates.
The smoothing parameter maximizing the correlation of firing rate and running speed is on the order of seconds
The general likelihood framework described above is independent of any external physical world variable. Because we were specifically interested in the relationship between firing rate and running speed, we additionally asked which smoothing parameter (bandwidth) maximizes the correlation between firing rate and running speed. To that end, we calculated a speed score for a range of bandwidths. The speed scores of speed-modulated neurons in rat MEC peaked on average at 3.25 s (Fig. 2H).
The entorhinal speed code by firing rate differs across time scales
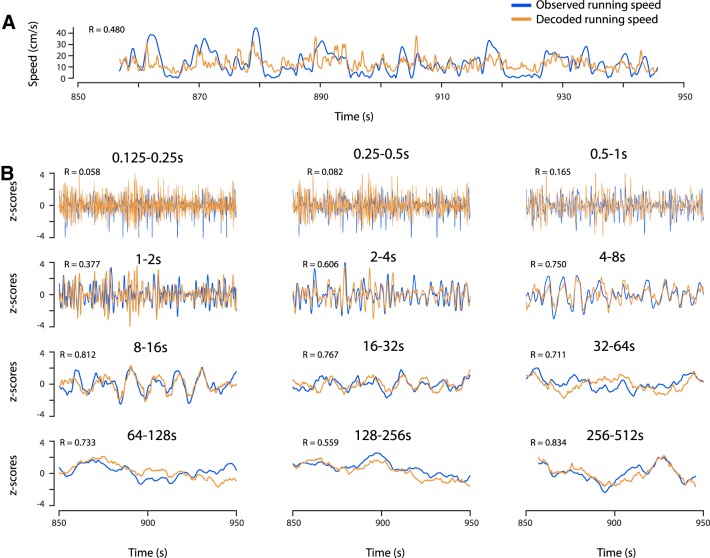
The previous data indicate that the running speed code by firing rates of speed-modulated neurons in the MEC differs across time scales and reflects changes of running speed at second-long, but not subsecond-long time scales. To test this hypothesis further, we tested whether running speed can be decoded separately at each time scale. To that end, we used a linear decoder (see Materials and Methods) to decode running speed from the firing rates of 12 simultaneously recorded speed-modulated MEC neurons (Fig. 3A). We applied the same linear decoder to the time scale-filtered firing rates. Decoding of running speed was poor at short time scales (Fig. 3B). Notably, decoding of running speed works best at second-long time scales.
Figure 3.
Running speed can be decoded separately at each time scale. Running speed is decoded from the firing-rate information of n = 12 simultaneously recorded speed-modulated neurons in MEC. Blue traces show the observed running speed; brown traces show decoded running speeds. Speed scores are given in top left corners. A, Running speed decoded from the instantaneous firing rate. B, Time scale-dependent running speeds decoded at time scales ranging from 0.125 to 0.25 s up to 256–512 s.
Together, these data show that the speed code by firing rate differs across time scales and can only provide accurate information for decoding of running speed at seconds-long, but not subsecond-long time scales.
The speed code by firing rate is too slow to maintain grid cell spatial periodicity in an oscillatory interference model of grid-cell firing
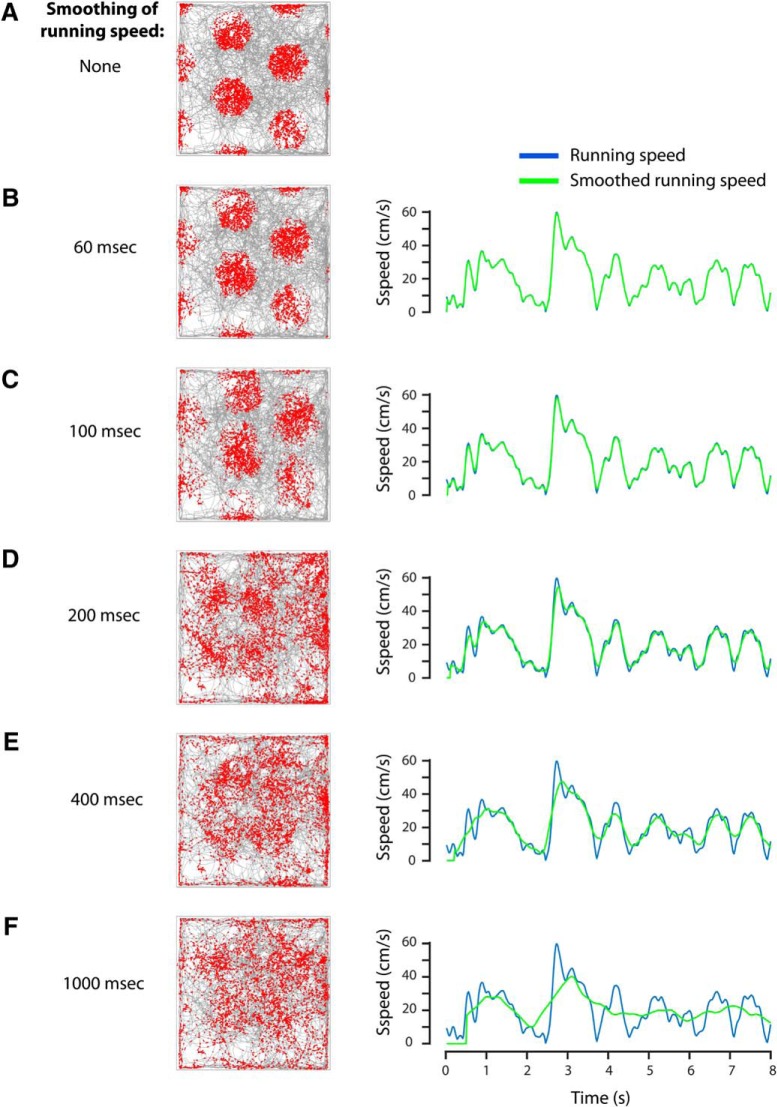
Speed cells in the MEC have been proposed to be the source of the linear running-speed signal required for path integration by grid cells. However, models of path integration and grid-cell firing do not consider the temporal constraints of integrating firing rates over time for accurate decoding of running speed. We therefore asked how smoothing the running speed signal affects the spatial periodicity of grid-cell firing in the oscillatory interference model (Burgess et al., 2007). We demonstrate that smoothing of the running speed signal with boxcar filters >∼200 ms severely disrupts the hexagonal firing pattern of grid cells (Fig. 4). These results indicate that the speed code by firing rate is too slow to provide an accurate running-speed signal needed for grid-cell firing in a model based on integration of velocity.
Figure 4.
Grid-cell spatial periodicity cannot be maintained in an oscillatory interference model of grid cell firing, when running speed is integrated over >∼200 ms. Grid-cell firing was modeled using the oscillatory interference model (see Materials and Methods). Left, Random trajectory (gray lines) of an animal exploring a rectangular arena (1 × 1 m in size); red dots indicate spiking events of the modeled grid cell. Right, The unsmoothed running speed signal (blue) compared with smoothed running speed signals (green). A, No smoothing; B, 60 ms smoothing; C, 100 ms smoothing; D, 200 ms smoothing; E, 400 ms smoothing; F, 1000 ms smoothing of running speed.
Using optogenetics to investigate the contribution of the medial septum to speed coding by firing rate in the entorhinal cortex
Our finding of steeper time scale-dependent STC slopes at longer compared with shorter time scales supports the hypothesis that the slower time scale of metabotropic receptor-mediated neuromodulatory effects, in particular cholinergic signaling, might play a central role in affecting firing rates of speed-modulated neurons in the entorhinal cortex. Because lesion studies and pharmacological inactivation of MSDB activity used in previous studies lack temporal precision and cell-type specificity, we decided to use an optogenetic silencing approach using rAAV transduction of medial septum cholinergic neurons with Cre-dependent Archaerhodopsin T (ArchT) 3.0 in mice expressing Cre recombinase under the control of the choline acetyltransferase (ChAT) promoter (Fig. 5). After viral transduction, mice were implanted with a 200 μm core light fiber to deliver light of 532 nm (15–25 mW) into the MSDB to silence ArchT-expressing neurons in the MSDB (see Materials and Methods). Because we could not exclude that visual effects of scattered laser light may affect the mouse behavior or electrophysiological data, we performed control recordings, in which laser light was prevented from entering the brain to mimic effects of scattered laser light on vision without directly affecting MSDB neurons. In the following, we refer to this group as the laser control group. In addition to visual effects, delivery of laser light into brain tissue results in local heating of brain tissue (Arias-Gil et al., 2016; Shin et al., 2016), which can affect brain activity, most likely resulting in a local increase of neuronal firing rates. To control for heating and other possible unwanted effects of laser light delivery into the brain, we performed control experiments in ChAT-Cre mice conditionally expressing green fluorescent protein (GFP) in cholinergic MSDB neurons, mimicking the sparse expression of virally transduced protein observed in the experimental groups for optogenetic silencing of MSDB subpopulations. In the following, we refer to this group as the GFP control group. To exclude that laser stimulation or optogenetic manipulation of cholinergic MSDB neurons affect exploratory behavior, in particular running speed, we computed the mean running speed across sessions for each mouse and compared a 60 s baseline period with the 145 s laser stimulation and a 60 s poststimulation baseline period. When data contained at least five mice per group, we also computed the average across mice. Running speed was not affected in any group tested (Table 1) and no other behavioral effects of laser stimulation were observed.
Figure 5.
Optogenetic silencing of MSDB neurons in combination with single-unit recordings in the MEC. A, Schematic of laser stimulation in MSDB and single-unit recordings in MEC of the left hemisphere (top left). Positional data and single-unit recordings are acquired while the mouse is freely moving in a 1 m2 open-field environment (bottom right). Baseline (Laser OFF; gray) periods (120 s) are alternating with laser stimulation (Laser ON; green) periods (145 s); see Materials and Methods for details of laser stimulation. A typical recording session lasts 46 min. Only the last 115 s of each baseline or laser stimulation period are analyzed in account of slow time scales of muscarinic receptor-mediated effects. Tetrode positions are confirmed by post hoc electro-lesions and cresyl-violet staining (top right). B, Unconditional ArchT-GFP expression (ArchT) in the MSDB of one example mouse, and schema of light fiber placement to deliver light into the MSDB. Scale bar, 100 μm. Schematic adapted from Paxinos and Franklin (2008). C–E, Immunofluorescence data showing expression of GFP or ArchT-GFP (FITC; green signal, left), and ChAT (Cy3; red signal, middle), and merged signals (right). C, Example data showing cell-type-specific expression of GFP in cholinergic neurons of the MSDB of a ChAT-Cre mouse. Scale bars, 100 μm. D, Example data showing cell-type-specific expression of ArchT-GFP in cholinergic MSDB neurons of a ChAT-Cre mouse. Scale bars, 200 μm. E, Example data showing no overlap of GFP and Cy3 signals in PV-Cre mice, indicating ArchT is conditionally expressed in GABAergic MSDB neurons after viral transduction of PV-Cre mice. Scale bars, 200 μm. F, Example data showing no overlap of GFP and Cy3 signals in vGluT2-Cre mice, indicating ArchT is conditionally expressed in glutamatergic MSDB neurons after viral transduction of vGluT2-Cre mice. Scale bars, 200 μm.
Table 1.
Running speed is not affected by optogenetic silencing of MSDB neurons
| Group | Mean ± SD |
n | Df; factor, error | F statistic | p | |||
|---|---|---|---|---|---|---|---|---|
| Running speed before laser stimulation, cm/s | Running speed during laser stimulation, cm/s | Running speed after laser stimulation, cm/s | ||||||
| Average across mice | Laser control | 8.24 ± 3.23 | 8.09 ± 3.36 | 8.74 ± 3.82 | 7 | 2, 18 | 0.07 | 0.93 |
| GFP control | 6.35 ± 1.11 | 6.44 ± 1.41 | 6.32 ± 1.06 | 5 | 2, 12 | 0.01 | 0.99 | |
| ChAT-Cre | 8.41 ± 3.62 | 8.76 ± 3.27 | 8.72 ± 3.73 | 10 | 2, 27 | 0.03 | 0.97 | |
| Average across sessions | Wild-type, ArchT | 7.29 ± 3.65 | 7.25 ± 3.84 | 7.51 ± 3.63 | 15 | 2, 42 | 0.02 | 0.98 |
| 3.43 ± 1.34 | 3.23 ± 1.08 | 4.57 ± 1.97 | 11 | 2, 30 | 2.53 | 0.10 | ||
| 10.53 ± 1.84 | 12.26 ± 2.49 | 12.13 ± 2.88 | 9 | 2, 24 | 1.41 | 0.26 | ||
| 9.51 ± 3.43 | 8.06 ± 2.31 | 11.99 ± 6.97 | 9 | 2, 24 | 1.63 | 0.22 | ||
| PV-Cre | 9.67 ± 4.95 | 10.00 ± 5.45 | 9.73 ± 4.74 | 4 | 2, 9 | 0 | 1.00 | |
| 10.27 ± 3.17 | 10.94 ± 2.92 | 10.46 ± 2.94 | 9 | 2, 24 | 0.12 | 0.89 | ||
| 13.43 ± 4.98 | 11.03 ± 3.33 | 11.70 ± 3.82 | 5 | 2, 12 | 0.46 | 0.65 | ||
| vGluT2-Cre | 6.73 ± 1.91 | 6.19 ± 1.69 | 5.61 ± 1.49 | 5 | 2, 12 | 0.53 | 0.60 | |
| 7.77 ± 2.17 | 7.13 ± 1.20 | 6.89 ± 1.88 | 24 | 2, 69 | 1.55 | 0.22 | ||
| 6.04 ± 1.90 | 5.07 ± 2.01 | 5.78 ± 1.32 | 10 | 2, 27 | 0.80 | 0.46 | ||
Df, Degrees of freedom; n, sample size. Statistics were performed across mice if the number of mice ≥5, otherwise across sessions per mouse.
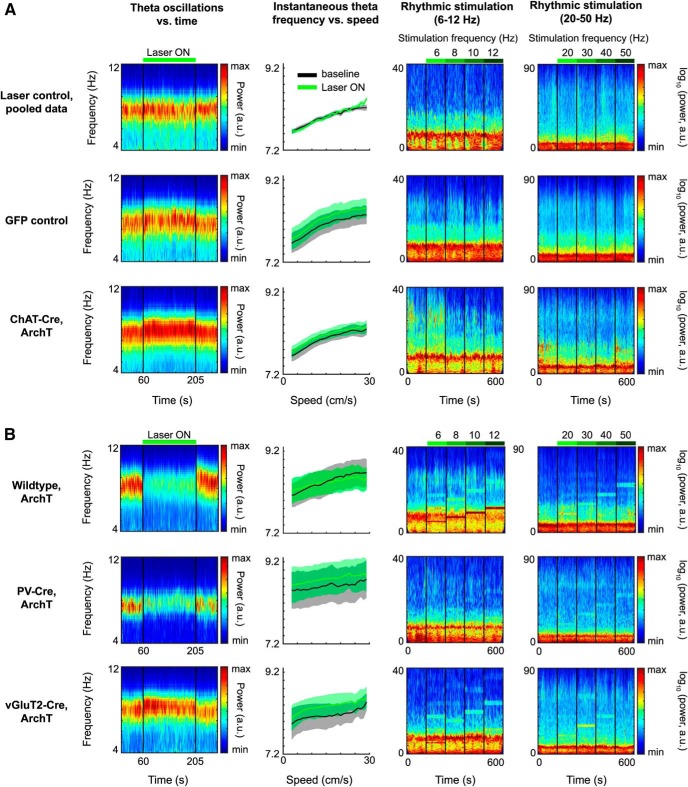
Having confirmed that laser stimulation or optogenetic silencing of cholinergic MSDB neurons does not affect behavioral running speed, we investigated the effects of laser stimulation and optogenetic silencing on LFP dynamics in the MEC. One well known major electrophysiological effect of MSDB manipulations are changes in theta rhythmic activity. In particular, theta rhythmic activity is strongly reduced in animals with MSDB lesions as well as during pharmacological inactivation of the MSDB. We therefore investigated how continuous optogenetic silencing of cholinergic MSDB neurons affected theta rhythmic activity. To that end, we computed spectrograms to visualize changes of theta frequency and power over time during continuous laser stimulation (Fig. 6, first column) and computed the relative theta peak power during baseline and optogenetic silencing epochs for quantification purposes (see Materials and Methods). Theta power was not affected by laser stimulation in animals of the laser control and GFP control groups (Fig. 6A; Table 2). However, theta frequency was slightly increased during laser stimulation in the GFP control as well as the cholinergic inhibition group (Table 3), presumably caused by heating of tissue. This change in theta frequency was independent of running speed, as evident by the significant change in y-intercept, but not the slope of the running speed versus theta frequency relationship (Table 3). In contrast, y-intercept and slope of the running speed versus theta frequency relationship was not significantly changed during laser stimulation in the laser control group (Table 3). Cholinergic silencing showed no detectable effects on LFP theta dynamics, which prompted us to perform positive control experiments to verify the effectiveness of optogenetic silencing. Experimental data show a strong role of GABAergic, but not cholinergic or glutamatergic, MSDB neurons in pacing theta rhythmic activity (Dannenberg et al., 2015; Robinson et al., 2016; Zutshi et al., 2018). We therefore investigated whether optogenetic silencing of either the whole MSDB, or GABAergic or glutamatergic MSDB neurons reduce LFP theta power in the MEC. We observed strong reductions of theta power with either silencing the whole MSDB or the GABAergic MSDB subpopulations over the entire 145 s time period of laser stimulation (Fig. 6B, first column; Table 2). No such reduction was found in either ChAT-Cre or vGluT2-Cre mice (Fig. 6; Table 2). As for the GFP control group and the group with silencing of cholinergic MSDB neurons, we observed an increase in y-intercepts during inactivation of the whole MSDB as well as glutamatergic or GABAergic MSDB neurons. Whereas the slope of the running speed versus theta frequency relationship remained unaltered during inactivation of glutamatergic or GABAergic MSDB neurons, it was reduced with inactivation of the whole MSDB (Table 3). These differential effects caused by silencing different MSDB subpopulations indicate that our optogenetic silencing approach is (1) effective and (2) cell-type specific.
Figure 6.
Effects of optogenetic silencing of MSDB neurons on LFP dynamics in entorhinal cortex. First column, Spectrograms of theta oscillatory power in MEC during baseline and continuous light stimulation of MSDB. Thirty second baseline activity followed by 145 s continuous laser stimulation, followed by 30 s poststimulation baseline activity. Color scale reflects power in arbitrary units. Panels show averages across mice; see Table 2 for statistics. Second column, Instantaneous theta frequency versus running speed plots, baseline (black) compared with continuous laser stimulation (Laser ON; green), data depicted as mean ± SEM across mice; see Table 3 for statistics. Third column, Spectrograms of LFPs in MEC during baseline (first 60 s) and rhythmic laser stimulation in the range of 6–12 Hz (four 60 s periods of stimulation at 6, 8, 10, and 12 Hz). Color scale reflects logarithmic power in arbitrary units; see Table 4 for statistics. Fourth column, Spectrograms of LFPs in MEC during baseline (first 60 s) and rhythmic laser stimulation in the range of 20–50 Hz (four 60 s periods of stimulation at 20, 30, 40, and 50 Hz). Color scale reflects logarithmic power in arbitrary units; see Table 4 for statistics. A, Data on control groups and cholinergic silencing. First row, Data for recording sessions, where the laser light was prevented from entering the brain to control for laser stimulation effects on vision (laser control group), mice pooled across different transgenic backgrounds. Visual effects of scattered laser light does not affect theta power (first panel), nor theta frequency (second panel), and has no or little effects on LFP dynamics in MEC (third and fourth panels; Table 2). Second row, Control data from mice in which only GFP was conditionally expressed in ChAT-Cre neurons (GFP control group). Laser light delivery into the MSDB slightly increases theta frequency (first panel) independent of running speed (second panel). Rhythmic laser stimulation has no or little effects on LFP dynamics in MEC (Table 2). Third row, Data for ChAT-Cre mice conditionally expressing ArchT in cholinergic MSDB neurons. B, Positive control for optogenetic silencing by manipulations of other than cholinergic MSDB subpopulations. First row, Data for wild-type mice unconditionally expressing ArchT in the MSDB. Optogenetic silencing of the whole MSDB decreases theta power during continuous laser stimulation (first panel). Rhythmic laser stimulation induces LFP oscillations in MEC exactly at the stimulation frequency for all frequencies tested (third and fourth panels). Second row, Data on PV-Cre mice conditionally expressing ArchT in GABAergic MSDB neurons. Silencing of GABAergic MSDB neurons decreases theta power during continuous laser stimulation (first panel). Rhythmic laser stimulation induces LFP oscillations in MEC, particularly at higher frequencies (third and fourth panels). Third row, Data for vGluT2-Cre mice conditionally expressing ArchT in glutamatergic MSDB neurons. As the case for GFP control mice, laser light delivery into the MSDB slightly increases theta frequency during continuous light stimulation (first panel) independent of running speed (second panel). Rhythmic laser stimulation induces LFP oscillations in MEC, particularly at lower frequencies.
Table 2.
Changes in theta peak power during optogenetic silencing
| Group | Change in theta peak amplitude, % |
n | Df | t Statistic | p | Effect size, Cohen's d | |
|---|---|---|---|---|---|---|---|
| Mean ± SD | |||||||
| Average across mice | Laser control | 3.69 ± 18.57 | 6 | 5 | 0.487 | 0.647 | 0.20 |
| GFP control | 12.38 ± 28.3 | 5 | 4 | 0.978 | 0.383 | 0.44 | |
| ChAT-Cre | 25.36 ± 45.94 | 10 | 9 | 1.746 | 0.115 | 0.55 | |
| Average across sessions | Wild-type, ArchT | −19.57 ± 29.11 | 15 | 14 | −2.603 | 0.021 | 0.67 |
| −52.95 ± 27.38 | 8 | 7 | −5.470 | 0.001 | 1.93 | ||
| −54.50 ± 26.98 | 9 | 8 | −6.060 | 0.000 | 2.02 | ||
| −61.60 ± 16.22 | 9 | 8 | −11.295 | 0.000 | 3.80 | ||
| PV-Cre | −40.49 ± 13.13 | 3 | 2 | −5.341 | 0.033 | 3.08 | |
| −68.59 ± 21.85 | 6 | 5 | −7.690 | 0.001 | 3.14 | ||
| −27.52 ± 11.77 | 5 | 4 | −5.227 | 0.006 | 2.34 | ||
| vGluT2-Cre | −6.97 ± 27.19 | 5 | 4 | −0.573 | 0.597 | 0.26 | |
| 8.49 ± 15.39 | 24 | 23 | 2.703 | 0.013 | 0.55 | ||
| 18.33 ± 19.18 | 10 | 9 | 3.021 | 0.014 | 0.96 |
Df, Degrees of freedom; n, sample size. Statistics were performed across mice if the number of mice ≥5, otherwise across sessions per mouse.
Table 3.
Changes in y-intercept and slope of running speed versus theta frequency relationship during optogenetic silencing
| Group | Mean ± SD |
n | Df | t Statistic | p | Effect size, Cohen's d | |||
|---|---|---|---|---|---|---|---|---|---|
| Baseline | Laser stimulation | Difference | |||||||
| Y-intercept, Hz | |||||||||
| Average across mice | Laser control | 7.63 ± 0.25 | 7.58 ± 0.27 | −0.06 ± 0.09 | 6 | 5 | −1.597 | 0.171 | −0.652 |
| GFP control | 7.68 ± 0.58 | 7.79 ± 0.62 | 0.11 ± 0.09 | 5 | 4 | 2.873 | 0.045 | 1.285 | |
| ChAT-Cre | 7.67 ± 0.45 | 7.78 ± 0.44 | 0.11 ± 0.09 | 10 | 9 | 3.913 | 0.004 | 1.237 | |
| Average across sessions | Wild-type, ArchT (n = 4 mice) | 8.03 ± 0.67 | 8.17 ± 0.67 | 0.14 ± 0.19 | 38 | 37 | 4.409 | 0.000 | 0.715 |
| PV-Cre (n = 3 mice) | 8.36 ± 0.94 | 8.50 ± 0.89 | 0.14 ± 0.10 | 12 | 11 | 4.946 | 0.000 | 1.428 | |
| vGluT2-Cre (n = 3 mice) | 8.39 ± 0.99 | 8.53 ± 0.91 | 0.14 ± 0.18 | 39 | 38 | 4.647 | 0.000 | 0.744 | |
| Slope, Hz/(cm/s) | |||||||||
| Average across mice | Laser control | 0.0232 ± 0.0067 | 0.0270 ± 0.0059 | 0.0038 ± 0.0060 | 6 | 5 | −1.542 | 0.184 | −0.629 |
| GFP control | 0.0268 ± 0.0079 | 0.0290 ± 0.0079 | 0.0022 ± 0.0020 | 5 | 4 | 2.378 | 0.076 | 1.064 | |
| ChAT-Cre | 0.0239 ± 0.0109 | 0.0220 ± 0.0111 | −0.0019 ± 0.0042 | 10 | 9 | 1.435 | 0.185 | 0.454 | |
| Average across sessions | Wild-type, ArchT (n = 4 mice) | 0.0213 ± 0.0132 | 0.0118 ± 0.0119 | −0.0094 ± 0.0135 | 38 | 37 | −4.291 | 0.000 | −6.96 |
| PV-Cre (n = 3 mice) | 0.0088 ± 0.0053 | 0.0115 ± 0.0074 | 0.0027 ± 0.0053 | 12 | 11 | 1.771 | 0.104 | 0.511 | |
| vGluT2-Cre (n = 3 mice) | 0.0103 ± 0.0116 | 0.0137 ± 0.0114 | 0.0034 ± 0.0125 | 39 | 38 | 1.678 | 0.102 | 0.269 | |
Df, Degrees of freedom; n, sample size. Statistics were performed across mice if the number of mice ≥5, otherwise across sessions.
Previous studies have shown that rhythmic activation of GABAergic (Dannenberg et al., 2015; Zutshi et al., 2018) or glutamatergic MSDB neurons (via a GABAergic relay in the MSDB; Robinson et al., 2016) can drive rhythmic LFP activity in the hippocampal formation. To further validate the use of optogenetics for inhibition of MSDB neurons, we analyzed effects of rhythmic laser stimulation on LFPs. When applying rhythmic laser stimulation in form of 2 min long 20 ms laser pulse trains at either 6, 8, 10, and 12 Hz, or 10 ms pulses at either 20, 30, 40, and 50 Hz, we observed strong rhythmic LFP activity at exactly the stimulation frequency and its harmonics when rhythmically silencing either the whole MSDB, the GABAergic neurons, or the glutamatergic neurons (Fig. 6B; Table 4). In contrast, rhythmic optogenetic silencing showed no or very weak effects on MEC LFP dynamics in the laser control and GFP control groups (Fig. 6A; Table 4). Interestingly, a small, but statistically significant, effect was observed at 10 Hz stimulation frequency in both control groups indicating that visual input alone can affect theta rhythm dynamics in MEC. Rhythmic silencing of cholinergic MSDB neurons showed weak effects across the entire range of stimulation frequencies with effect sizes being larger at lower stimulation frequencies (Fig. 6A; Table 4). Although these effects were statistically significant, effect sizes were too small to be clearly visible in non-normalized spectrograms. In general, stimulation at 12 Hz proved most effective in all groups, and effects were strongest when targeting the whole MSDB. Beyond that, rhythmic silencing of glutamatergic MSDB neurons proved more effective at lower compared with higher stimulation frequencies. In contrast, rhythmic silencing of GABAergic MSDB neurons proved more effective at higher compared with lower stimulation frequencies.
Table 4.
Effects of rhythmic optogenetic silencing on LFPs
| Group | n | 6 Hz | 8 Hz | 10 Hz | 12 Hz | 20 Hz | 30 Hz | 40 Hz | 50 Hz |
|---|---|---|---|---|---|---|---|---|---|
| Laser control | 5 sessions, 4 mice | ||||||||
| Mean | 0.11 | 0.04 | 0.22 | 0.52 | 0.06 | 0.14 | −0.01 | −0.10 | |
| SD | 0.26 | 0.34 | 0.68 | 0.60 | 0.20 | 0.21 | 0.13 | 0.16 | |
| p value | 0.9020 | 0.3745 | 0.0399 | 0.2840 | 0.9735 | 0.0159 | 0.7464 | 0.9604 | |
| Cohen's d | 0.44 | 0.12 | 0.33 | 0.87 | 0.30 | 0.68 | −0.07 | −0.62 | |
| GFP control | 18 sessions, 5 mice | ||||||||
| Mean | 0.16 | 0.07 | 0.17 | 0.21 | 0.13 | 0.08 | 0.03 | −0.02 | |
| SD | 0.36 | 0.40 | 0.55 | 0.62 | 0.37 | 0.33 | 0.17 | 0.23 | |
| p value | 0.0539 | 0.1564 | 0.0412 | 0.2673 | 0.0760 | 0.6703 | 0.9194 | 0.9745 | |
| Cohen's d | 0.44 | 0.17 | 0.30 | 0.34 | 0.35 | 0.25 | 0.18 | −0.11 | |
| ChAT-Cre | 11–16 sessions, 6–7 mice | ||||||||
| Mean | 0.65 | 0.34 | 0.53 | 0.51 | 0.19 | 0.10 | 0.16 | 0.18 | |
| SD | 0.67 | 0.76 | 0.68 | 0.79 | 0.58 | 0.53 | 0.48 | 0.43 | |
| p value | 0.0065 | 0.0095 | 0.0055 | 0.0209 | 0.0032 | 0.0142 | 0.3497 | 0.0098 | |
| Cohen's d | 0.97 | 0.45 | 0.77 | 0.64 | 0.34 | 0.19 | 0.32 | 0.41 | |
| Wild-type, ArchT | 7–8 sessions, 4 mice | ||||||||
| Mean | 0.74 | 1.18 | 1.80 | 2.18 | 1.26 | 0.84 | 1.08 | 0.81 | |
| SD | 0.67 | 0.60 | 0.39 | 0.12 | 0.53 | 0.63 | 0.52 | 0.48 | |
| p value | 0.008 | 0.007 | 0.003 | 0.010 | 0.000 | 0.002 | 0.000 | 0.000 | |
| Cohen's d | 1.10 | 1.97 | 4.58 | 17.72 | 2.38 | 1.35 | 2.08 | 1.70 | |
| PV-Cre | 5 sessions, 5 mice | ||||||||
| Mean | 0.14 | 0.12 | 0.54 | 0.87 | 0.57 | 0.51 | 0.60 | 0.40 | |
| SD | 0.20 | 0.43 | 0.50 | 0.43 | 0.60 | 0.25 | 0.42 | 0.16 | |
| p value | 0.0446 | 0.0576 | 0.0018 | 0.0095 | 0.0139 | 0.0035 | 0.0012 | 0.0082 | |
| Cohen's d | 0.69 | 0.27 | 1.09 | 2.01 | 0.95 | 2.04 | 1.42 | 2.58 | |
| vGluT2-Cre | 9–13 sessions, 3 mice | ||||||||
| Mean | 0.99 | 0.96 | 0.87 | 0.82 | 1.19 | 1.38 | 0.45 | 0.12 | |
| SD | 0.77 | 0.74 | 0.65 | 0.61 | 0.44 | 0.65 | 0.74 | 0.36 | |
| p value | 0.0062 | 0.0000 | 0.0062 | 0.0082 | 0.0000 | 0.0000 | 0.0038 | 0.0072 | |
| Cohen's d | 1.29 | 1.29 | 1.34 | 1.34 | 2.67 | 2.13 | 0.61 | 0.34 |
Statistics on z-scores of spectral power estimates (see Materials and Methods).
Together, the differential effects observed during continuous or rhythmic optogenetic silencing of MSDB subpopulations together with our immunohistochemistry results provide evidence for cell-type-specific expression of ArchT in genetically defined cholinergic, GABAergic, or glutamatergic MSDB neurons and effective optogenetic silencing of MSDB neurons.
Speed coding by firing rate in the entorhinal cortex does not depend on cholinergic medial septum inputs
Having demonstrated that our optogenetic silencing approach is both specific and effective, we used it to investigate a contribution of MSDB cholinergic neurons to speed coding by firing rate in the MEC. For this purpose, we compared speed scores of identified speed-modulated neurons during baseline and laser stimulation periods. Because many effects of acetylcholine in the MEC are likely to be mediated by activation of G-protein-coupled receptors with estimated onset time constants of 1–2 s and decay constants between 10 and 20 s (Hasselmo and Fehlau, 2001), we excluded the first 5 s after laser offset and the first 30 s after laser onset from the analysis.
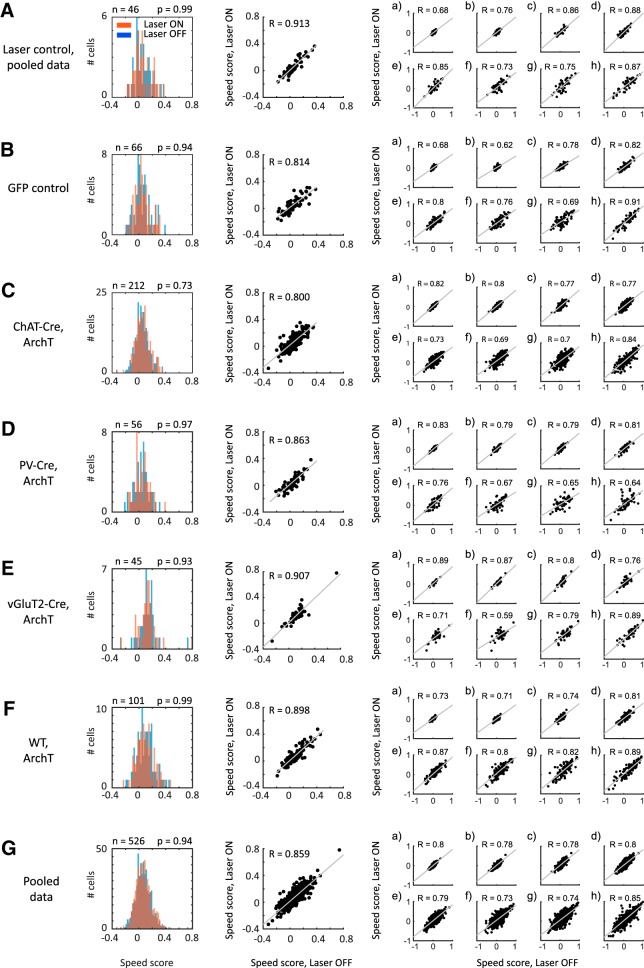
Surprisingly, silencing of cholinergic MSDB neurons (n = 212 cells from 9 mice; Fig. 7C) did not affect the speed scores of entorhinal cortical neurons. This was seen on the population level [Fig. 7C, histogram; Kolmogorov–Smirnov (KS) test; p = 0.73] as well as on the level of individual cells (Fig. 7C, scatter plot). Similar results were obtained for laser control sessions, in which the laser light was prevented from entering the brain tissue (n = 46 cells from 7 mice; Fig. 7A; KS test, p = 0.99), and in recordings of GFP control mice (n = 66 cells from 3 mice; Fig. 7B; KS test, p = 0.94).
Figure 7.
Firing-rate speed tuning does not depend on medial septum inputs. Speed scores of speed-modulated neurons in the MEC do not differ significantly during baseline and optogenetic silencing of MSDB neurons at each time scale tested. First column, Histogram plots showing the distribution of overall speed scores during baseline (Laser OFF; blue) and laser stimulation (Laser ON; red) periods. No significant differences exist on the population level, p values of KS test shown in the figure. Second column, Scatter plots showing the speed scores during baseline (Laser OFF) and laser stimulation (Laser ON) periods for all cells, significant correlations (p < 0.0001) observed for all groups, Pearson correlation coefficient (R) shown in the figure. Third column, Scatter plots of speed scores during baseline (Laser OFF) and laser stimulation (Laser ON) periods for different time scales, (a) 1–2 s, (b) 2–4 s, (c) 4–8 s, (d) 8–16 s, (e) 16–32 s, (f) 32–64 s, (g) 64–128 s, (h) 128–256 s, and (i) 256–512 s. Pearson correlation coefficients (R) for each time scale shown in figure. A, Laser control data from sessions where the laser light was prevented from entering the brain tissue. Data from n = 46 cells from seven mice. B, Control data from mice in which only GFP was expressed in ChAT-Cre neurons, n = 66 cells from three mice. C, Data from ChAT-Cre mice expressing ArchT in cholinergic MSDB neurons, n = 212 cells from nine mice. D, Data from PV-Cre mice expressing ArchT in GABAergic MSDB neurons, n = 56 cells from four mice. E, Data from vGluT2-Cre mice expressing ArchT in glutamatergic MSDB neurons, n = 45 cells from two mice. F, Data from wild-type mice unconditionally expressing ArchT in MSDB neurons, n = 101 cells from two mice. G, All cells from all groups pooled together, n = 526 cells from 21 mice. This is the dataset used for the further investigation of time scale-dependent speed coding.
Speed coding by firing rate in the entorhinal cortex does not depend on GABAergic or glutamatergic medial septum inputs
The absence of effects of cholinergic silencing on speed scores of speed-modulated neurons in the MEC prompted us to reject the cholinergic hypothesis on speed modulation in the MEC. However, other subpopulations of the MSDB or the MSDB as a whole might contribute to speed modulation in the MEC. To address this question, we first performed rAAV injections in parvalbumin (PV)-Cre and vGluT2-Cre mice for conditional expression of ArchT in GABAergic and glutamatergic MSDB neurons, respectively, as well as rAAV injections of an unconditional ArchT variant in wild-type mice for silencing of the whole MSDB (Fig. 2). We then tested whether silencing of GABAergic or glutamatergic MSDB neurons (n = 56 cells from 4 PV-Cre mice, n = 45 cells from 2 vGluT2-Cre mice, respectively), or the whole MSDB (n = 101 cells from 2 WT mice) affects speed scores of speed-modulated neurons in the MEC. No effects were observed in any condition tested. (Fig. 7D–F). This was seen on the population level (Fig. 7D–F, histograms; KS test; p = 0.97, p = 0.93, p = 0.99 for silencing PV+, vGluT2+, or whole medial septum cell populations, respectively) as well as on the level of individual cells (Fig. 7D–F, scatter plots).
Because our earlier results showed that speed tuning can differ across time scales, MSDB inputs might differentially affect speed tuning at different time scales. We therefore analyzed whether optogenetic silencing of MSDB subpopulations affected speed scores at individual time scales. Neither silencing of cholinergic, GABAergic, or glutamatergic MSDB neurons, nor silencing the whole MSDB showed differential effects on time scale-dependent speed tuning (Fig. 7, far right column, and plots a–h). Together, our findings using optogenetic silencing of medial septum subpopulations demonstrate that speed tuning of speed-modulated neurons in the MEC does not depend on inputs from MSDB neurons.
Validation of differential time-scale-dependent speed tuning in mice
Because optogenetic silencing of medial septum subpopulations did not affect modulation of firing rate by running speed in speed-modulated MEC neurons in any terms measured in this study, we pooled all available data on speed-modulated neurons (Fig. 7G) and used this dataset to validate our earlier results derived from the rat dataset on differential time-scale-dependent speed tuning. Our mouse dataset included data from n = 526 cells recorded from n = 21 mice during exploration of an open-field environment (1 × 1 m; see Materials and Methods). Because our recording sessions in mice had a duration of 46 min, we could extend our analysis of time scales to include an additional 512–1024 s time scale. Using the same hierarchical clustering approach as used for the analysis of the rat dataset, we identified clusters of speed-modulated neurons in mice with very similar characteristics both in terms of speed-score distribution across time scales as well as proportions of cells assigned to these clusters (Fig. 8A,B). A small cluster of cells showed strong speed modulation (1 single cell and Cluster A, n = 9 cells of 526), and a larger cluster showed moderate to strong speed modulation (Cluster B, n = 128 cells of 526). Notably, Clusters A and B of the mouse dataset strongly resemble Clusters A and B of the rat dataset. In total, 138 of 526 cells (26%) were identified as speed modulated using the hierarchical clustering approach. In comparison, 184 of 526 cells (35%) were identified as speed modulated by defining a speed score threshold at the 99th percentile of a null distribution of speed scores from spike trains randomly shifted in time; n = 113 cells were classified as speed modulated by both the hierarchical clustering and the speed score threshold approach. As for the rat dataset, the cells identified as speed modulated by the hierarchical clustering approach define a smaller, but more precisely defined fraction. Yet, n = 113 of 138 (82%) cells identified as speed modulated using the clustering approach were also classified as speed modulated by the speed score threshold approach. Figure 8C–E shows data on time-scale-dependent speed tuning for an example cell of Cluster A of the mouse dataset. As in the rat dataset, the slopes of time-scale-dependent STCs increase at longer time scales (Fig. 8F), indicating less accurate coding of running speed by firing rate at short versus long time scales.
Figure 8.
Validation of data on time scale-dependent speed tuning curves in mice. A, Clustergram showing hierarchical clustering of 526 neurons recorded in layer II/III of entorhinal cortex of 21 mice. Each row depicts color-coded speed scores calculated for each time scale ranging from 1 to 2 s up to 512–1024 s (see Materials and Methods). As in the rat dataset, distinct clusters of speed-modulated neurons can be identified. B, Mean ± SEM of time scale-dependent speed scores averaged across units of single clusters. A single most positively speed-modulated cell together with cells of Clusters A and B were defined as positively speed-modulated neurons (138 of 526 cells, 26.2%). Cluster F contains clear negatively speed-modulated neurons (6 of 526 cells, 1.1%). C–F, Data on one speed-modulated example cell in Cluster A. C, Time scale-dependent speed tuning curves of the example cell. Black dots show binned data (time-scale filtered firing rate vs time-scale filtered running speed), red lines show the least-square linear fits to binned data; r = Pearson correlation coefficient. D, The overall speed tuning curve of the example cell. Black dots and gray shading show mean values and 95% confidence intervals of speed-binned firing-rate data; blue and red lines show the best MLE linear (blue) and saturating exponential (red) fit functions obtained by temporal binning of firing rate, shadings indicate 95% confidence intervals. E, Slopes of observed time scale-dependent speed tuning curves (orange curve) compared with mean ± SEM of slopes derived from 100 artificially created linearly tuned Poisson-distributed spike trains (blue line; SEM within line). F, Mean ± SEM of mean-normalized speed tuning curve slopes (orange: positively speed-modulated cells of the single most positively speed-modulated cell, Clusters A, and Cluster B; blue: artificially created Poisson-distributed spike trains, one Poisson train per cell, n = 138). Observed spike trains differ significantly from artificial ones: F(12,3562) = 26.25, p = 1.6 × 10−57, two-way ANOVA interaction effect. G–I, Mouse data (green) are shown compared with rat data (purple). G, Left, Distribution of optimal bandwidths for firing-rate estimation. Right, Population average (mean ± SEM) of bandwidth-dependent log-likelihoods of firing-rate estimates. H, Population average (mean ± SEM) of bandwidth-dependent speed-score distributions. I, Mean ± SEM of mean-normalized speed tuning curve slopes.
Moreover, the median of optimal bandwidths for firing-rate estimation determined by the general likelihood framework is 4.94 s (Fig. 8G, left) in the mouse dataset. Likewise, the population average of the log-likelihoods of bandwidths peaks at 4.02 s (Fig. 8G, right), and the population average of the distribution of bandwidth-dependent speed scores peaks at 12.13 s (Fig. 8H). Together, these data on mice validate our finding in rats that subsecond time scales are too short for providing a meaningful readout of firing rates.
Linear and exponentially saturating speed cells operate at similar time scales.
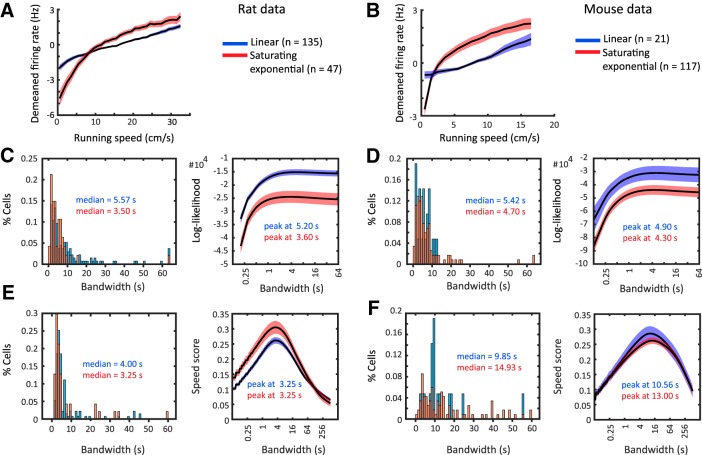
It has recently been shown that STCs are often fit better by a saturating exponential model than a linear model (Hinman et al., 2016). In the rat dataset, n = 47 of 182 speed-modulated neurons (26%) showed exponentially saturating speed tuning at an α level of 0.05, and consequently n = 135 of 182 cells (74%) showed linear speed tuning (Fig. 9A). In the mouse dataset, n = 117 of 138 speed-modulated neurons (85%) showed tuning curves that were best fit by an exponentially saturating fit (significance level α = 0.05), whereas 21 of 138 cells (15%) showed linear tuning (Fig. 9B).
Figure 9.
Exponentially saturating and linearly tuned speed-modulated cells operate at similar time scales. A, C, E, Data on rats. B, D, F, Data on mice. Each plot shows data on linearly tuned cells (blue), and exponentially saturating tuned cells (red). A, B, Average of mean-normalized speed tuning curves; line and shading show mean ± SEM. A, Data on mice, n = 21 linearly tuned and n = 117 exponentially saturating tuned cells. B, Data on rats, n = 135 linearly tuned and n = 47 exponentially saturating tuned cells. C, D, Left, Distributions and median values of optimal bandwidths for firing-rate estimation determined by a general likelihood framework (Prerau and Eden, 2011). Right, Population average (mean ± SEM) and peak values of bandwidth-dependent log-likelihoods of firing-rate estimates determined by the general likelihood framework. E, F, Left, Distributions and median values of bandwidths maximizing the speed score. Right, Population average (mean ± SEM) and peak values of bandwidth-dependent speed-score distributions. See text for statistics.
We therefore compared the optimal bandwidths for firing-rate estimation as well as the optimal bandwidths for maximizing speed scores between linearly and exponentially saturating tuned cells. In the rat dataset, we found that the distribution of optimal bandwidths of exponentially saturating tuned cells was slightly shifted to shorter bandwidths compared with the distribution of optimal bandwidths of linearly tuned cells (Fig. 9C, left; median values 3.50 and 5.57 s, respectively, p = 0.0055, KS test). However, the distribution of bandwidths maximizing the speed score for exponentially saturating tuned cells did not significantly differ from the distribution of bandwidths from linearly tuned cells (Fig. 9E, left; median values 3.25 and 4.00 s, respectively, p = 0.1885, KS test). Likewise, no significant differences between exponentially saturating and linearly tuned cells were found in the mouse dataset for distributions of optimal bandwidths for firing-rate estimation (Fig. 9D, left; median values 4.70 and 5.42 s, respectively, p = 0.9478, KS test), and for the distributions of bandwidths maximizing the speed score (Fig. 9F, left; median values 9.85 and 14.93 s, p = 0.4293, KS test). Similar values were obtained for the peaks of the population averages of log-likelihoods for firing-rate estimation as well as bandwidth-dependent speed-score distributions for both mice and rats (Fig. 9C–E, right). These data show that both linear and exponentially saturating speed tuning operates at similar slow time scales in the seconds range.
In summary, these results show that the speed code by firing rate in the entorhinal cortex differs across time scales and is most accurate at seconds-long time scales. Alternatively, the firing rates of most speed cells may be modulated by behavioral activity states rather than providing an accurate real-time speed code.
Discussion
Data on speed modulation at different time scales presented in this study show that speed modulation of firing rate happens on a time scale of seconds. This is consistent with a previous study showing that MEC neurons dynamically vary their coding properties to become more informative about position, head direction, or both position and head direction in response to faster running speeds (Hardcastle et al., 2017). Moreover, the brain's response to sensory input as well as plasticity can be improved by activity and behavioral states of arousal and attentiveness, generally associated with activation of the basal forebrain neuromodulatory system (for review, see Lee and Dan, 2012), as shown in the primary visual cortex of mice (Goard and Dan, 2009; Niell and Stryker, 2010; Fu et al., 2014; Kaneko and Stryker, 2014).
The MSDB is a necessary component for critical aspects of temporal and spatial processing in the hippocampal formation, most prominently theta oscillations (Buzsáki, 2002). Theta oscillations are the electrophysiological hallmark of running behavior and are modulated in frequency and amplitude by running speed (Vanderwolf, 1969; McFarland et al., 1975; Sławińska and Kasicki, 1998; Maurer et al., 2005; Jeewajee et al., 2008; Newman et al., 2014). Theta rhythmic activity has been proposed to be associated with properties of spatial navigation including generation of grid-cell firing patterns and path integration (Burgess et al., 2007; Burgess, 2008). Lesions or pharmacological inactivation of the MSDB reduces theta activity and disrupts grid-cell firing patterns (Brandon et al., 2011; Koenig et al., 2011). Furthermore, passive transport abolishes both velocity modulation of theta oscillations and grid-cell firing patterns (Winter et al., 2015). It is tempting to speculate that medial septum neurons are a necessary component for the transfer of a speed signal to the hippocampal formation. Cholinergic, GABAergic, and glutamatergic septohippocampal projection neurons form a complex network within the MSDB with potential contributions of each subpopulation to different aspects of spatial navigation including speed coding (for review, see Hinman et al., 2018). Optogenetic activation of glutamatergic (Robinson et al., 2016) or cholinergic (Dannenberg et al., 2015) MSDB neurons in mice can modulate rhythmicity of hippocampal theta oscillations via activation of GABAergic MSDB neurons. Furthermore, optogenetic activation of glutamatergic MSDB neurons can initiate locomotion (Fuhrmann et al., 2015), and activity of glutamatergic MSDB neurons has been hypothesized to provide a speed signal to neurons in the entorhinal cortex (Justus et al., 2017). In fact, firing rates of MSDB neurons are correlated with running speed and 65% of rhythmically bursting MSDB neurons have been reported to show a significant correlation between the interburst frequency and the animal's running speed (King et al., 1998). Moreover, medial septum lesions disrupt behavior in a path integration experiment, increasing the variability of temporal pacing of linear speeds on homeward trajectories (Martin et al., 2007), providing evidence for the involvement of the MSDB in path integration. Pharmacological inactivation of the MSDB abolishes hypothalamic stimulation-induced locomotion onset (Oddie et al., 1996), impairs the ability of rats to estimate linear distances based on self-motion information resembling effects observed after MEC lesions (Jacob et al., 2017), and disrupts an oscillatory speed signal based on spiking rhythmicity of MEC neurons (Hinman et al., 2016). In contrast, pharmacological inactivation of the MSDB reduced the variability in the firing-rate speed signal of entorhinal speed cells (Hinman et al., 2016).
We tested the hypothesis that the modulation of firing rates observed in a subset of cells in the MEC (previously described as speed cells;Kropff et al., 2015) might be because of changes in sensory or motor input or because of changes in cholinergic neuromodulatory signaling associated with running speed or activity states. To elucidate the latter hypothesis of a specific contribution of cholinergic signaling arising from the activity of cholinergic MSDB neurons on speed modulation of firing rates in the MEC, we used an optogenetic silencing approach. We show that STCs of speed-modulated neurons in the entorhinal cortex is not affected by transient silencing of either the cholinergic subpopulation of the MSDB, nor by transient silencing of the whole MSDB. We validated the efficiency of the optogenetic silencing approach by investigating effects of optogenetic manipulations on the LFP level after targeting GABAergic and glutamatergic MSDB subpopulations as well as the whole MSDB as expected from previous studies (Dannenberg et al., 2015; Robinson et al., 2016; Zutshi et al., 2018). Our data using transient and temporally precise optogenetic silencing of medial septum subpopulations demonstrate that speed tuning of firing rates in the entorhinal cortex does not depend on medial septum inputs. One caveat of optogenetic studies is that the delivery of laser light into brain tissue results in local heating (Arias-Gil et al., 2016; Shin et al., 2016), which most likely results in a local increase of neuronal firing rates. Nevertheless, our data using optogenetic silencing of cholinergic neurons are consistent with previous experimental data from experiments using less temporally precise pharmacogenetic modulation of medial septum cholinergic neurons (Carpenter et al., 2017). Consistent with our data on the inactivation of the whole MSDB, a previous study using pharmacological inactivation of the MSDB (Hinman et al., 2016) also showed no significant effect of pharmacological MSDB inactivation on the slope of speed tuning curves of MEC speed cells, although MSDB inactivation by muscimol infusions did disrupt the speed modulation of theta spiking rhythmicity. Whereas the same study also reported a slight increase of the firing rate versus running speed correlation during pharmacological MSDB inactivation, we did not observe this effect using optogenetic silencing of MSDB neurons. Studies using optogenetic activation of glutamatergic MSDB neurons suggested that glutamatergic MSDB neurons convey a firing-rate speed signal to neurons in the entorhinal cortex (Fuhrmann et al., 2015; Justus et al., 2017). However, optogenetic silencing of neither glutamatergic nor the whole MSDB disrupts speed coding by firing rate in the MEC suggesting that activity of glutamatergic MSDB neurons is not necessary for conveying a speed signal to the entorhinal cortex.
Most animals are able to return to the starting point of a journey simply relying on signals that derive from their own locomotion (Etienne and Jeffery, 2004). This ability to keep track of linear and angular self-motion and continuously update the internal representation of space based on the combined information about running direction and running speed has been termed path integration. Grid cells in the medial entorhinal cortex have been hypothesized to act as path integrators (McNaughton et al., 2006), and disruption of grid cells indeed impairs path integration (Gil et al., 2018). The majority of computational models of grid cells employ a path integration mechanism to generate the regularly repeating hexagonal firing patterns of grid cells. Firing-rate speed signals are found in continuous attractor dynamics models (McNaughton et al., 2006; Burak and Fiete, 2009; Giocomo et al., 2011; Widloski and Fiete, 2014). Alternatively, oscillatory interference models of grid-cell generation make use of the frequency of theta-range membrane potential oscillations varying as a function of running speed (Burgess et al., 2007; Blair et al., 2008; Burgess, 2008; Hasselmo, 2008). Importantly, both the continuous attractor and oscillatory interference models require the speed signal to be linear. This assumption has been recently challenged by the observation that the firing rates of many speed-modulated cells are better described by an exponentially saturating instead of a linear STC (Hinman et al., 2016). Furthermore, a speed signal by firing rate requires integration of spiking events over time, yet the time scale of this integration has not been directly studied so far.
To investigate STC characteristics over short to long time scales, we applied a novel approach of filtering a cell's firing rate and the animal's running speed signals at different time scales. We find that many cells show linear speed tuning at multiple time scales, but the relationship of firing rates and running speed appears to be most accurate when integrated over seconds. Importantly, for the majority of speed-modulated cells, the slopes of STCs increase with longer time scales indicating that the decreased speed tuning accuracy at short time scales cannot be attributed to Poisson noise alone. If coding accuracy would be limited on a short time scale by Poisson noise alone, this limitation could be overcome by fast spiking interneurons or by averaging over a larger population of speed cells. In fact, the majority of speed cells in the entorhinal cortex are fast-spiking interneurons (Kropff et al., 2015; Hinman et al., 2016; Ye et al., 2018). However, our findings suggest that the accuracy of firing-rate modulation by running speed genuinely increases at longer time scales. Consistently, a study of speed-modulated neurons in rat hippocampal CA1 found that firing rates of pyramidal cells are too low to provide a reliable speed code by firing rate, even if firing rates are correlated with running speed (Góis and Tort, 2018). Our data regarding entorhinal speed cells in mice and rats indicate that the vast majority of speed cells, including fast spiking interneurons, are modulated by running speed on a seconds-long time scale, but do not code for running speed in real-time. Using the oscillatory interference model of grid cell firing, we further demonstrate that such long integration time windows would disrupt the spatial periodicity of grid-cell firing.
These results have important consequences for computational models of path integration, which face two major challenges: First, they require a linear speed signal. However, it has been shown that STCs are often fit better by an exponentially saturating model than a linear model (Hinman et al., 2016). Moreover, the linear speed tuning at individual time scales shown in this study comes at the cost of integrating over second-long time windows resulting in firing-rate estimates, which cannot be used for real-time speed coding. Second, current path integration models require the coding of movement direction, which is often assumed to be given by the activity of head direction cells. However, head direction does not always align with movement direction, and in these cases, head direction cells primarily code for head direction, but not movement direction (Raudies et al., 2016). These results may explain the lower contribution of speed in predicting the spikes of mixed selectivity cells in the entorhinal cortex (Hardcastle et al., 2017), because only a small subpopulation of speed-modulated cells might be able to code for speed accurately on a short time scale. Finally, we hypothesize that modulation of firing rate by speed on long time scales may reflect changes of activity states such as attention and arousal rather than precise real-time coding of speed.
Footnotes
This work supported by the National Institutes of Mental Health, Grants R01 MH60013 and R01 MH61492, by the Office of Naval Research MURI N00014-16-1-2832 and DURIP N00014-17-1-2304, and by the Deutsche Forschungsgemeinschaft 322014644.
The authors declare no competing financial interests.
References
- Alonso A, Köhler C (1984) A study of the reciprocal connections between the septum and the entorhinal area using anterograde and retrograde axonal transport methods in the rat brain. J Comp Neurol 225:327–343. 10.1002/cne.902250303 [DOI] [PubMed] [Google Scholar]
- Arias-Gil G, Ohl FW, Takagaki K, Lippert MT (2016) Measurement, modeling, and prediction of temperature rise due to optogenetic brain stimulation. Neurophotonics 3:045007. 10.1117/1.NPh.3.4.045007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blair HT, Gupta K, Zhang K (2008) Conversion of a phase- to a rate-coded position signal by a three-stage model of theta cells, grid cells, and place cells. Hippocampus 18:1239–1255. 10.1002/hipo.20509 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brandon MP, Bogaard AR, Libby CP, Connerney MA, Gupta K, Hasselmo ME (2011) Reduction of theta rhythm dissociates grid cell spatial periodicity from directional tuning. Science 332:595–599. 10.1126/science.1201652 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burak Y, Fiete IR (2009) Accurate path integration in continuous attractor network models of grid cells. PLoS Comput Biol 5:e1000291. 10.1371/journal.pcbi.1000291 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgess N. (2008) Grid cells and theta as oscillatory interference: theory and predictions. Hippocampus 18:1157–1174. 10.1002/hipo.20518 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgess N, Barry C, O'Keefe J (2007) An oscillatory interference model of grid cell firing. Hippocampus 17:801–812. 10.1002/hipo.20327 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsáki G. (2002) Theta oscillations in the hippocampus. Neuron 33:325–340. 10.1016/S0896-6273(02)00586-X [DOI] [PubMed] [Google Scholar]
- Carpenter F, Burgess N, Barry C (2017) Modulating medial septal cholinergic activity reduces medial entorhinal theta frequency without affecting speed or grid coding. Sci Rep 7:14573. 10.1038/s41598-017-15100-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dannenberg H, Pabst M, Braganza O, Schoch S, Niediek J, Bayraktar M, Mormann F, Beck H (2015) Synergy of direct and indirect cholinergic septo-hippocampal pathways coordinates firing in hippocampal networks. J Neurosci 35:8394–8410. 10.1523/JNEUROSCI.4460-14.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Disney AA, Aoki C, Hawken MJ (2007) Gain modulation by nicotine in macaque v1. Neuron 56:701–713. 10.1016/j.neuron.2007.09.034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Etienne AS, Jeffery KJ (2004) Path integration in mammals. Hippocampus 14:180–192. 10.1002/hipo.10173 [DOI] [PubMed] [Google Scholar]
- Etienne AS, Maurer R, Berlie J, Reverdin B, Rowe T, Georgakopoulos J, Séguinot V (1998) Navigation through vector addition. Nature 396:161–164. 10.1038/24151 [DOI] [PubMed] [Google Scholar]
- Fu Y, Tucciarone JM, Espinosa JS, Sheng N, Darcy DP, Nicoll RA, Huang ZJ, Stryker MP (2014) A cortical circuit for gain control by behavioral state. Cell 156:1139–1152. 10.1016/j.cell.2014.01.050 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuhrmann F, Justus D, Sosulina L, Kaneko H, Beutel T, Friedrichs D, Schoch S, Schwarz MK, Fuhrmann M, Remy S (2015) Locomotion, theta oscillations, and the speed-correlated firing of hippocampal neurons are controlled by a medial septal glutamatergic circuit. Neuron 86:1253–1264. 10.1016/j.neuron.2015.05.001 [DOI] [PubMed] [Google Scholar]
- Fuhs MC, Touretzky DS (2006) A spin glass model of path integration in rat medial entorhinal cortex. J Neurosci 26:4266–4276. 10.1523/JNEUROSCI.4353-05.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fyhn M, Molden S, Witter MP, Moser EI, Moser MB (2004) Spatial representation in the entorhinal cortex. Science 305:1258–1264. 10.1126/science.1099901 [DOI] [PubMed] [Google Scholar]
- Fyhn M, Hafting T, Witter MP, Moser EI, Moser MB (2008) Grid cells in mice. Hippocampus 18:1230–1238. 10.1002/hipo.20472 [DOI] [PubMed] [Google Scholar]
- Gil M, Ancau M, Schlesiger MI, Neitz A, Allen K, De Marco RJ, Monyer H (2018) Impaired path integration in mice with disrupted grid cell firing. Nat Neurosci 21:81–91. 10.1038/s41593-017-0039-3 [DOI] [PubMed] [Google Scholar]
- Gil Z, Connors BW, Amitai Y (1997) Differential regulation of neocortical synapses by neuromodulators and activity. Neuron 19:679–686. 10.1016/S0896-6273(00)80380-3 [DOI] [PubMed] [Google Scholar]
- Giocomo LM, Zilli EA, Fransén E, Hasselmo ME (2007) Temporal frequency of subthreshold oscillations scales with entorhinal grid cell field spacing. Science 315:1719–1722. 10.1126/science.1139207 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giocomo LM, Moser MB, Moser EI (2011) Computational models of grid cells. Neuron 71:589–603. 10.1016/j.neuron.2011.07.023 [DOI] [PubMed] [Google Scholar]
- Goard M, Dan Y (2009) Basal forebrain activation enhances cortical coding of natural scenes. Nat Neurosci 12:1444–1449. 10.1038/nn.2402 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Góis ZH, Tort ABL (2018) Characterizing speed cells in the rat hippocampus. Cell Rep 25:1872–1884.e4. 10.1016/j.celrep.2018.10.054 [DOI] [PubMed] [Google Scholar]
- Grandchamp R, Delorme A (2011) Single-trial normalization for event-related spectral decomposition reduces sensitivity to noisy trials. Front Psychol 2:236. 10.3389/fpsyg.2011.00236 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gritton HJ, Howe WM, Mallory CS, Hetrick VL, Berke JD, Sarter M (2016) Cortical cholinergic signaling controls the detection of cues. Proc Natl Acad Sci U S A 113:E1089–E1097. 10.1073/pnas.1516134113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hafting T, Fyhn M, Molden S, Moser MB, Moser EI (2005) Microstructure of a spatial map in the entorhinal cortex. Nature 436:801–806. 10.1038/nature03721 [DOI] [PubMed] [Google Scholar]
- Hangya B, Borhegyi Z, Szilágyi N, Freund TF, Varga V (2009) GABAergic neurons of the medial septum lead the hippocampal network during theta activity. J Neurosci 29:8094–8102. 10.1523/JNEUROSCI.5665-08.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hardcastle K, Maheswaranathan N, Ganguli S, Giocomo LM (2017) A multiplexed, heterogeneous, and adaptive code for navigation in medial entorhinal cortex. Neuron 94:375–387.e7. 10.1016/j.neuron.2017.03.025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasselmo ME. (2008) Grid cell mechanisms and function: contributions of entorhinal persistent spiking and phase resetting. Hippocampus 18:1213–1229. 10.1002/hipo.20512 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasselmo ME, Fehlau BP (2001) Differences in time course of ACh and GABA modulation of excitatory synaptic potentials in slices of rat hippocampus. J Neurophysiol 86:1792–1802. 10.1152/jn.2001.86.4.1792 [DOI] [PubMed] [Google Scholar]
- Hasselmo ME, Giocomo LM, Zilli EA (2007) Grid cell firing may arise from interference of theta frequency membrane potential oscillations in single neurons. Hippocampus 17:1252–1271. 10.1002/hipo.20374 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasselmo ME, Hinman JR, Dannenberg H, Stern CE (2017) Models of spatial and temporal dimensions of memory. Curr Opin Behav Sci 17:27–33. 10.1016/j.cobeha.2017.05.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinman JR, Penley SC, Long LL, Escabí MA, Chrobak JJ (2011) Septotemporal variation in dynamics of theta: speed and habituation. J Neurophysiol 105:2675–2686. 10.1152/jn.00837.2010 [DOI] [PubMed] [Google Scholar]
- Hinman JR, Brandon MP, Climer JR, Chapman GW, Hasselmo ME (2016) Multiple running speed signals in medial entorhinal cortex. Neuron 91:666–679. 10.1016/j.neuron.2016.06.027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinman JR, Dannenberg H, Alexander AS, Hasselmo ME (2018) Neural mechanisms of navigation involving interactions of cortical and subcortical structures. J Neurophysiol 119:2007–2029. 10.1152/jn.00498.2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsieh CY, Cruikshank SJ, Metherate R (2000) Differential modulation of auditory thalamocortical and intracortical synaptic transmission by cholinergic agonist. Brain Res 880:51–64. 10.1016/S0006-8993(00)02766-9 [DOI] [PubMed] [Google Scholar]
- Jacob PY, Gordillo-Salas M, Facchini J, Poucet B, Save E, Sargolini F (2017) Medial entorhinal cortex and medial septum contribute to self-motion-based linear distance estimation. Brain Struct Funct 222:2727–2742. 10.1007/s00429-017-1368-4 [DOI] [PubMed] [Google Scholar]
- Jeewajee A, Barry C, O'Keefe J, Burgess N (2008) Grid cells and theta as oscillatory interference: electrophysiological data from freely moving rats. Hippocampus 18:1175–1185. 10.1002/hipo.20510 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Justus D, Dalügge D, Bothe S, Fuhrmann F, Hannes C, Kaneko H, Friedrichs D, Sosulina L, Schwarz I, Elliott DA, Schoch S, Bradke F, Schwarz MK, Remy S (2017) Glutamatergic synaptic integration of locomotion speed via septoentorhinal projections. Nat Neurosci 20:16–19. 10.1038/nn.4447 [DOI] [PubMed] [Google Scholar]
- Kaneko M, Stryker MP (2014) Sensory experience during locomotion promotes recovery of function in adult visual cortex. eLife 3:e02798. 10.7554/eLife.02798 [DOI] [PMC free article] [PubMed] [Google Scholar]
- King C, Recce M, O'Keefe J (1998) The rhythmicity of cells of the medial septum/diagonal band of Broca in the awake freely moving rat: relationships with behaviour and hippocampal theta. Eur J Neurosci 10:464–477. 10.1046/j.1460-9568.1998.00026.x [DOI] [PubMed] [Google Scholar]
- Koenig J, Linder AN, Leutgeb JK, Leutgeb S (2011) The spatial periodicity of grid cells is not sustained during reduced theta oscillations. Science 332:592–595. 10.1126/science.1201685 [DOI] [PubMed] [Google Scholar]
- Kropff E, Carmichael JE, Moser MB, Moser EI (2015) Speed cells in the medial entorhinal cortex. Nature 523:419–424. 10.1038/nature14622 [DOI] [PubMed] [Google Scholar]
- Lee SH, Dan Y (2012) Neuromodulation of brain states. Neuron 76:209–222. 10.1016/j.neuron.2012.09.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin MM, Horn KL, Kusman KJ, Wallace DG (2007) Medial septum lesions disrupt exploratory trip organization: evidence for septohippocampal involvement in dead reckoning. Physiol Behav 90:412–424. 10.1016/j.physbeh.2006.10.007 [DOI] [PubMed] [Google Scholar]
- Maurer AP, Vanrhoads SR, Sutherland GR, Lipa P, McNaughton BL (2005) Self-motion and the origin of differential spatial scaling along the septo-temporal axis of the hippocampus. Hippocampus 15:841–852. 10.1002/hipo.20114 [DOI] [PubMed] [Google Scholar]
- McFarland WL, Teitelbaum H, Hedges EK (1975) Relationship between hippocampal theta activity and running speed in the rat. J Comp Physiol Psychol 88:324–328. 10.1037/h0076177 [DOI] [PubMed] [Google Scholar]
- McNaughton BL, Barnes CA, O'Keefe J (1983) The contributions of position, direction, and velocity to single unit activity in the hippocampus of freely-moving rats. Exp Brain Res 52:41–49. [DOI] [PubMed] [Google Scholar]
- McNaughton BL, Chen LL, Markus EJ (1991) “Dead reckoning,” landmark learning, and the sense of direction: a neurophysiological and computational hypothesis. J Cogn Neurosci 3:190–202. 10.1162/jocn.1991.3.2.190 [DOI] [PubMed] [Google Scholar]
- McNaughton BL, Battaglia FP, Jensen O, Moser EI, Moser MB (2006) Path integration and the neural basis of the “cognitive map”. Nat Rev Neurosci 7:663–678. 10.1038/nrn1932 [DOI] [PubMed] [Google Scholar]
- Mitchell SJ, Rawlins JN, Steward O, Olton DS (1982) Medial septal area lesions disrupt theta rhythm and cholinergic staining in medial entorhinal cortex and produce impaired radial arm maze behavior in rats. J Neurosci 2:292–302. 10.1523/JNEUROSCI.02-03-00292.1982 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mittelstaedt ML, Mittelstaedt H (1980) Homing by path integration in a mammal. Naturwissenschaften 67:566–567. 10.1007/BF00450672 [DOI] [Google Scholar]
- Mizumori SJ, Perez GM, Alvarado MC, Barnes CA, McNaughton BL (1990) Reversible inactivation of the medial septum differentially affects two forms of learning in rats. Brain Res 528:12–20. 10.1016/0006-8993(90)90188-H [DOI] [PubMed] [Google Scholar]
- Monaghan CK, Chapman GW 4th, Hasselmo ME (2017) Systemic administration of two different anxiolytic drugs decreases local field potential theta frequency in the medial entorhinal cortex without affecting grid cell firing fields. Neuroscience 364:60–70. 10.1016/j.neuroscience.2017.08.056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newman EL, Gillet SN, Climer JR, Hasselmo ME (2013) Cholinergic blockade reduces theta-gamma phase amplitude coupling and speed modulation of theta frequency consistent with behavioral effects on encoding. J Neurosci 33:19635–19646. 10.1523/JNEUROSCI.2586-13.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newman EL, Climer JR, Hasselmo ME (2014) Grid cell spatial tuning reduced following systemic muscarinic receptor blockade. Hippocampus 24:643–655. 10.1002/hipo.22253 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niell CM, Stryker MP (2010) Modulation of visual responses by behavioral state in mouse visual cortex. Neuron 65:472–479. 10.1016/j.neuron.2010.01.033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oddie SD, Stefanek W, Kirk IJ, Bland BH (1996) Intraseptal procaine abolishes hypothalamic stimulation-induced wheel-running and hippocampal theta field activity in rats. J Neurosci 16:1948–1956. 10.1523/JNEUROSCI.16-05-01948.1996 [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Keefe J, Burgess N, Donnett JG, Jeffery KJ, Maguire EA (1998) Place cells, navigational accuracy, and the human hippocampus. Philos Trans R Soc Lond B Biol Sci 353:1333–1340. 10.1098/rstb.1998.0287 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oostenveld R, Fries P, Maris E, Schoffelen JM (2011) FieldTrip: open source software for advanced analysis of MEG, EEG, and invasive electrophysiological data. Comput Intell Neurosci 2011:156869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paxinos G, Franklin KBJ (2008) The mouse brain in stereotaxic coordinates, compact: the coronal plates and diagrams, Ed 3 Amsterdam: Academic. [Google Scholar]
- Prerau MJ, Eden UT (2011) A general likelihood framework for characterizing the time course of neural activity. Neural Comput 23:2537–2566. 10.1162/NECO_a_00185 [DOI] [PubMed] [Google Scholar]
- Raudies F, Hinman JR, Hasselmo ME (2016) Modelling effects on grid cells of sensory input during self-motion. J Physiol 594:6513–6526. 10.1113/JP270649 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rawlins JN, Feldon J, Gray JA (1979) Septo-hippocampal connections and the hippocampal theta rhythm. Exp Brain Res 37:49–63. 10.1007/BF01474253 [DOI] [PubMed] [Google Scholar]
- Robinson J, Manseau F, Ducharme G, Amilhon B, Vigneault E, El Mestikawy S, Williams S (2016) Optogenetic activation of septal glutamatergic neurons drive hippocampal theta rhythms. J Neurosci 36:3016–3023. 10.1523/JNEUROSCI.2141-15.2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sargolini F, Fyhn M, Hafting T, McNaughton BL, Witter MP, Moser MB, Moser EI (2006) Conjunctive representation of position, direction, and velocity in entorhinal cortex. Science 312:758–762. 10.1126/science.1125572 [DOI] [PubMed] [Google Scholar]
- Shin Y, Yoo M, Kim HS, Nam SK, Kim HI, Lee SK, Kim S, Kwon HS (2016) Characterization of fiber-optic light delivery and light-induced temperature changes in a rodent brain for precise optogenetic neuromodulation. Biomed Opt Express 7:4450–4471. 10.1364/BOE.7.004450 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sławińska U, Kasicki S (1998) The frequency of rat's hippocampal theta rhythm is related to the speed of locomotion. Brain Res 796:327–331. 10.1016/S0006-8993(98)00390-4 [DOI] [PubMed] [Google Scholar]
- Vanderwolf CH. (1969) Hippocampal electrical activity and voluntary movement in the rat. Electroencephalogr Clin Neurophysiol 26:407–418. 10.1016/0013-4694(69)90092-3 [DOI] [PubMed] [Google Scholar]
- Wells CE, Amos DP, Jeewajee A, Douchamps V, Rodgers J, O'Keefe J, Burgess N, Lever C (2013) Novelty and anxiolytic drugs dissociate two components of hippocampal theta in behaving rats. J Neurosci 33:8650–8667. 10.1523/JNEUROSCI.5040-12.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Widloski J, Fiete IR (2014) A model of grid cell development through spatial exploration and spike time-dependent plasticity. Neuron 83:481–495. 10.1016/j.neuron.2014.06.018 [DOI] [PubMed] [Google Scholar]
- Wills TJ, Barry C, Cacucci F (2012) The abrupt development of adult-like grid cell firing in the medial entorhinal cortex. Front Neural Circuits 6:21. 10.3389/fncir.2012.00021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winter SS, Mehlman ML, Clark BJ, Taube JS (2015) Passive transport disrupts grid signals in the parahippocampal cortex. Curr Biol CB 25:2493–2502. 10.1016/j.cub.2015.08.034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ye J, Witter MP, Moser MB, Moser EI (2018) Entorhinal fast-spiking speed cells project to the hippocampus. Proc Natl Acad Sci U S A 115:E1627–E1636. 10.1073/pnas.1720855115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoder RM, Chan JHM, Taube JS (2017) Acetylcholine contributes to the integration of self-movement cues in head direction cells. Behav Neurosci 131:312–324. 10.1037/bne0000205 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zutshi I, Brandon MP, Fu ML, Donegan ML, Leutgeb JK, Leutgeb S (2018) Hippocampal neural circuits respond to optogenetic pacing of theta frequencies by generating accelerated oscillation frequencies. Curr Biol 28:1179–1188.e3. 10.1016/j.cub.2018.02.061 [DOI] [PMC free article] [PubMed] [Google Scholar]