Neutropenia dynamics in a case of T‐LGL lymphoproliferation illustrate rapid turnover of granulocyte progenitors

Abstract

Objectives:  To elucidate the natural history of T‐cell large granular lymphocyte (T‐LGL) lymphoproliferation, we followed changes in associated fluctuating neutropenia for 3 years in an untreated patient presenting with the disease.

Materials and methods:  We report a nonlinear mathematical analysis of irregular neutrophil fluctuation, using iterative data maps, to detect long‐term regulation of the neutrophil population.

Results:  This geometric analysis indicated that variations of this sequence of neutrophil counts followed bounded deterministic dynamics around a fixed low level equilibrium, a situation similar to that previously observed for cultured mouse early bone marrow progenitor cells.

Conclusion:  These findings illustrate how the deleterious effect of T‐LGL on neutrophils is balanced, over periods of years, by pulses of compensatory neutrophil production, potentially accounting for the commonly observed prolonged indolent course of the disease.

Introduction

T‐cell large granular lymphocyte (T‐LGL) proliferation constitutes a rare group of diseases involving clonal expansion of cytotoxic T cells. It is associated with symptoms of T‐cell‐mediated autoimmunity, ranging from isolated neutropenia, through cytopenia with various autoimmune disorders (including arthritis), to outright T‐LGL leukaemia when one immunodominant clone escapes, generally after several years of indolent disease (1, 2). Neutropenia is a prevalent feature in all cases. We investigated the natural history of T‐LGL lymphoproliferation, by following changes in fluctuating neutropenia for 3 years in an untreated patient presenting with the disease.

Production of all normal blood cell lineages in vivo fluctuates spontaneously with a low amplitude about every 2 months (3, 4, 5). These oscillatory patterns are the result of the system of feedback and feedforward regulatory loops, with delays, controlling blood cell homeostasis. Characteristics of the oscillations provide information concerning the system as a whole. For instance, these fluctuations are amplified in tumoral blood cells (6) and become cyclic in periodic haematological diseases (7). A patient with LGL proliferation‐associated oscillating thrombopenia was recently described (8). We have observed similar fluctuations in rate of cell proliferation associated with bone marrow cell production in vitro (9). In this study, we report an analysis of neutropenia dynamics in a patient presenting typical T‐LGL proliferation. The study was retrospective, and blood samples were taken at irregular time intervals, as is often the case in clinical settings. The resulting sampling frequency precluded accurate interpolation of data and period detection by spectral analysis. Based on the particular temporal characteristics of these data, peaks and troughs of cell counts should be considered as local extrema specific to the sample. In other words, these peaks and troughs are the maxima and minima for this particular sequence of data but not for the actual continuously changing neutrophil population of the patient. Our aim was therefore to analyse this sequence of cell counts without any a priori hypotheses concerning the periodic, stochastic or chaotic behaviour of the system. Instead, we aimed to determine whether there was a deterministic structure underlying the sequence of counts. In such cases, geometric nonlinear analysis has three advantages: it provides a qualitative description of the oscillatory system without requiring prior knowledge of the distribution of data and noise, it is independent of sampling interval (order of the data being important instead), and is based on raw data with no requirement for a curve‐fitting hypothesis. We found that peaks and troughs of neutrophil counts were related to stationary points, consistent with a pattern of regulation similar to that previously observed in primary cultures of mouse early bone marrow progenitors (9). Our findings suggest that there is robust and flexible long‐term control of accelerated turnover of granulocytes in this condition.

Methods

Analytical procedure

Detailed explanations of the procedure and previous results are provided in the Appendix and Appendix S1–S3. We used a classical recurrent representation of cell counts on a one‐dimensional map, with cell count x _i plotted on the x‐axis, and the next cell count x _i+1 plotted on the y‐axis. Resulting consecutive points are then joined, generating a succession of vectors. In this representation, if the cell count x _i is a local minimum (x _i < x _i−1 and x _i < x _i+1), then the vector on the map runs in a south‐east to north‐west direction. Similarly, if the cell count x _i is a local maximum (x _i > x _i−1 and x _i > x _i+1), then the vector runs in a north‐west to south‐east direction. To compare orientation and amplitude of all vectors, the line bisecting each vector (the line perpendicular to the vector, intersecting at its midpoint) was drawn. Lines bisecting peak vectors point south‐west on the map and lines bisecting trough vectors point north‐east. The relatively small set of observations was insufficient for accurate Monte‐Carlo simulation and permitted only descriptive analysis. However, observed regulation of dynamics was similar to those previously reported for bone marrow cells and for progenitor cell production in vitro; these similarities provide support for the validity of our analysis (9, 10, unpublished data).

Data trends

Determination of trends was not straightforward as irregular fluctuations could not be smoothed even by high‐order polynomials, and the very uneven time intervals prevented use of regular moving averages. In an attempt to discern possible reciprocal changes in granulocyte and lymphocyte production described in other studies (12), we used two steps to search for trends. First, we arbitrarily excluded the few cell counts obtained less than 8 days after the preceding count, retaining only the first data point for a group of repeated determinations; this resulted in more homogeneous time intervals of about 45 days (mean 45 ± 30 days). Second, with this more regular data set, and with time intervals plotted along the x‐axis, we calculated moving averages (MA, nine data windows, resulting finally in 19 points). The resulting trends could be approximated by fourth‐order polynomials.

The patient

A 55‐year‐old woman presented with sigmoiditis and mild neutropenia (936/mm³). After 1 year of progression, marked by recurring dental infections, fatigue and untreated hip pain, she was given peritendinous injections of corticosteroids [3.75 mg cortivazol (CAS: 1110‐40‐3)/week, for 3 weeks] to treat periarthritis of the hip. Over the next 2 years, mild neutropenia, thrombopenia, and lymphocytosis, hand and ankle pain, and episodic purpura persisted. These symptoms led to diagnosis of T‐LGL lymphoproliferation. Cell phenotype analyses indicated proliferation of CD2+ CD3+ CD5+ CD7+ CD38+ CD45+ CD56− CD57+ CD57/CD8+ TCRab+(76%) and TCRgd+(18%) (Vdelta1) mature T cells, and clonal TCR rearrangement was detected. The only treatments administered were NSAID and antibiotics as clinically appropriate. The patient gave informed consent for the publication of this blood cell‐count analysis.

Results

Cell counts

Irregular fluctuations of cell counts were observed over the 3 years. Neutropenia and lymphocytosis (Fig. 1) remained moderate: mean counts ± SD for 31 time points, excluding time points 1 (pre‐disease) and 13 (transient steroid treatment), were 1185 (±304)/mm³ for neutrophils and 4056 (±1175)/mm³ for lymphocytes. Fluctuations in production of cells of the two lineages were shifted relative to each other. WBC count normalized completely after the incidental 3‐week course of local steroid injections, at the end of the first year (point 13, arrow), however, neutropenia and lymphocytosis rapidly recurred. Approximation of the respective changes in the two cell populations is illustrated by the trends obtained after filtering the data to smooth irregularity of time intervals. Trends highlighted a decrease in two phases of neutrophil population, negatively related to coinciding two‐phase increase in lymphoid population (Fig. 2). We detected no periodicity, not even of a complex nature, in cell count fluctuations, although frequency of one peak/every 50–80 days or so was observed over time. We also found no clear distribution or correlation function to suggest that the data were stochastic. These observations led us to apply nonlinear analysis to the data.

Figure 1.

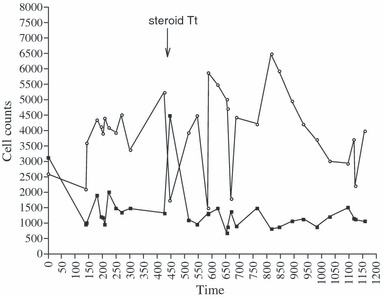
  White blood cell counts/mm ³ . Lymphocytes, open circles; neutrophils, dark squares. X‐axis in time (days), Y‐axis cell counts/mm³ (Local steroid treatment: arrow).

Figure 2.

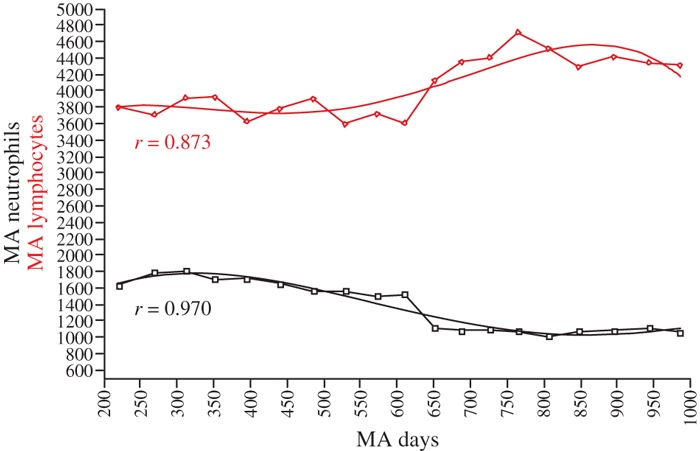
  Trend analysis. Lymphocytes, red diamonds; neutrophils, black squares. X‐axis: moving average (MA) for time (days); Y‐axis: MA for cell counts/mm³.

Nonlinear analysis based on return maps

The space phase of the iterative maps portrays long‐term evolution of cell populations and allows detection of determinism, if present, in the dynamics. In this representation of the data, the trajectory is independent of time interval and depends solely on absolute value of cell counts and their order. The maps obtained provided evidence of bounded deterministic dynamics of neutrophil counts. Lines bisecting peak vectors (n = 9) of neutrophil counts intersected on the diagonal of the map at two levels (Fig. 3a). We calculated intersections of bisecting lines on the diagonal, using the relationship:

Figure 3.

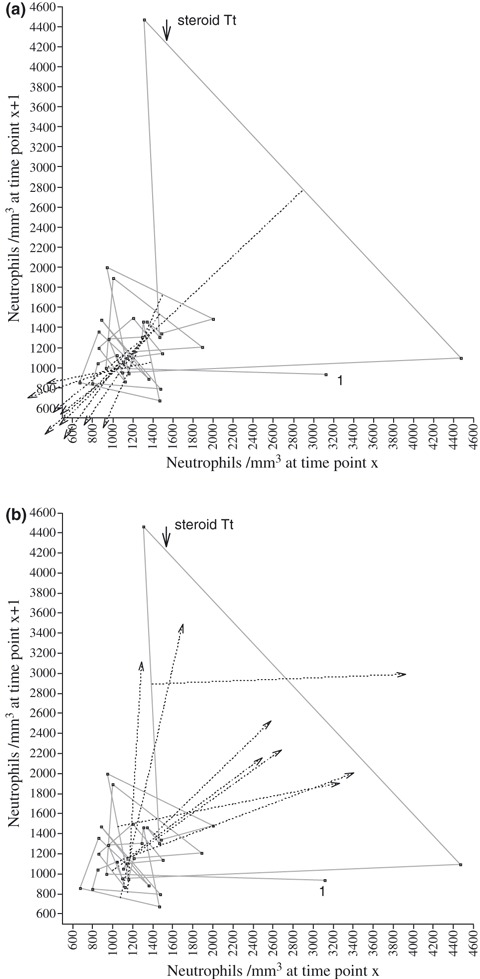
  Topological representation of neutrophil counts. X‐axis, cell count/mm³ (x _i); Y‐axis, the cell count/mm³ (x _i+1). (a) Bisecting lines (dotted) of vectors representing peaks of neutrophil counts, oriented downwards, meeting at coordinates 1203/1203 (n=5) and 913/913 (n=4). (b) Five lines (dotted), bisecting troughs oriented upwards, meeting at coordinates ∼1150/1150. Vector following steroid treatment is between points 12 and 13 (arrow).

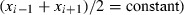(see Appendix, relationship (A1))

We found that five peaks converged on a first point at 1203 (±79.99) and four peaks converged on a second point at 913.1 (±68.07). Lines bisecting five of the eight trough vectors intersected on the diagonal of the map at coordinates 1150/1150 (Fig. 3b). Points on the map diagonal are fixed points (x _i = x _i+1), that is, steady levels. Therefore, fluctuations of neutrophil counts all share a relationship with these fixed levels. This set of observations was relatively small and insufficient for accurate Monte‐Carlo simulation; only descriptive analysis was possible. However, this geometric pattern is similar to that previously shown for blood progenitors, providing support for the validity of our analysis (9, unpublished data). We observed no such regulation in fluctuations of the lymphocyte population.

Discussion

Curves constructed from consecutive neutrophil and lymphocyte counts

The curves revealed irregular fluctuations, with moderate persistent neutropenia and lymphocytosis. The interval of around 60 days between peaks is consistent with frequency of previously described oscillations of blood cell counts (7, 11). However, given the temporal characteristics of the data (unevenly spaced sampling at long intervals ∼45 days), it is clear that peaks and troughs observed are local extrema specific to this particular sequence of cell counts, rather than actual extrema relating to continuous changes in neutrophil population of the patient. With this in mind, we chose not to carry out period detection by spectral analysis, deciding instead to focus on qualitative geometric analysis. Cell‐count fluctuations were irregular, but estimated trends showed that the two cell populations changed in opposite ways. Reciprocal changes in production of lymphoid and myeloid cells of the marrow, resulting in a shift in peripheral counts of lymphocytes and neutrophils, have been demonstrated previously (12). The negative effect of T‐LGL proliferation on neutrophils has been clearly demonstrated and involves both repression of neutrophil production and increase in neutrophil destruction via the Fas‐ligand (13, 14, 15, 16). Our patient is heterozygous for the canonical factor V Leiden mutation on 1q23.2, which maps to the same gene cluster as the Fas‐ligand. However, this association has not been described elsewhere and may be fortuitous. Lymphocytosis remained moderate over time (range 1460–6464/mm³), possibly reflecting stabilization that regulates polyclonal proliferation. Recent studies have shown that mixing clonal populations strongly inhibits early‐stage neoplastic progression observed for isolated clones (17). This may also reflect a putative intrinsic protective mechanism activating spontaneous apoptosis when the tumour clone expands, as shown in recurrent cycling of a case of lymphoma (18). Accordingly, neutropenia remained moderate over the 3 years, remaining at a clinically safe level most of the time (range 670–1999/mm³).

Nonlinear analysis based on return maps

Neutrophil dynamics displayed a particular pattern, with two fixed points coordinating maxima of cell counts, and one partly coordinating the minima. A fixed point on the diagonal of the map constitutes equilibrium level (where x _i = x _i+1) to which data are related, and we have shown for other cell types that this pattern of converging bisecting lines of peaks/troughs on fixed points is indicative of a deterministic system (9, 10). Here, it should be noted that the resulting orbits of neutrophil counts are established around a low, but clinically safe, level of about 1100 cells/mm³. This level may not be fortuitous. Various studies have shown that vigorous synthesis of G‐CSF occurs when neutropenia drops below a threshold of about 1000–1100 cells/mm³ (19, 20). Our interpretation of the results is that a feedback loop promotes episodic synthesis of G‐CSF when cytotoxic T‐LGLs decrease neutrophil count below this threshold of about 1100 cells/mm³, resulting in major mobilization of granulocyte progenitors. Three observations provide strong support for this interpretation: (i) chronic neutropenia results in surges of G‐CSF, increasing input from the progenitor compartment into the granulocytic pathway, with reduced marrow transit time for early precursors, and mobilization of granular progenitors into the blood (19, 20, 21, 22); (ii) the patient’s neutrophil dynamics, displaying fluctuations coordinated by fixed points, are similar to those of mouse early bone marrow progenitors in vitro (9); (iii) three cell counts obtained after this series, provided evidence for presence of circulating myelocytes and promyelocytic neutrophils, consistent with enhanced neutrophil turnover. Interestingly, brief normalization of cell counts after administration of steroid treatment to the patient is consistent with known effects of steroids on WBC (23) and implies that cell population dynamics readily reverted to normal patterns of behaviour at that point.

The Mackey model for regulation of neutrophil numbers fits well these long‐term changes in neutropenia, as it predicts various dynamics, from stable through periodically oscillating to a chaotic regime, depending on duration of delay for the feedback signal (7). Observations by Mackey’s group (7, 24) on cyclic neutropenia have illustrated the periodic regime of neutrophil oscillations. Occurrence of small stochastic fluctuations – that is, stability with noise – was described long ago for normal neutrophils (3, 4, 5). We believe that repair delays of repeated episodes of LGL‐induced neutropenia resulted in deterministic, possibly chaotic, fluctuations of neutrophil counts, potentially providing information about these delays. However, we cannot definitively exclude a random pattern. With such a small natural data set, it would be difficult to draw firm conclusions about stochastic or deterministic nature of the dynamics. Furthermore, various descriptions of natural systems have demonstrated alternate behaviour. Finally, such clinical data are inevitably mixed with some noise, stochasticity being involved at various levels: neutrophil production, death rate and margination, as well as irregular time intervals and noise in data determination.

Our reasoning, that coordination of this sequence of neutrophil counts is deterministic, is based on three points. First, the organized geometric pattern on the map suggests a determined structure. The time dimension is embedded in the map, with only numbers and their succession determining the geometric pattern. A sinusoidal pattern would display bisecting lines superimposed on the diagonal, bi‐rhythmic oscillations resulting in two bisecting lines converging on the diagonal, and random, noisy, dynamics are not coordinated at all (examples of these situations are illustrated in complementary figures at the end of the Appendix). Second, we have previously observed similar patterns of convergence in repeated series of liver cancer cells and bone marrow cells. We also showed that surrogate series of data, including at least eight peaks or troughs, could result in similar convergence of bisecting lines of vectors, representing peaks or troughs of cell population in less than 1.5% of the random series (9, 10). Third, we detected no periodicity, not even of a complex nature, in this sequence of unevenly spaced data, and we observed no clear distribution suggesting that the data were stochastic. Our various analyses and findings suggest that the observed dynamics reflect strong feedback regulation based on peripheral availability of neutrophils, itself the end result of mixed regulated and stochastic influences.

Conclusion

Nonlinear geometric analysis has revealed that dynamics of LGL‐associated neutropenia remain both flexible and tightly controlled in the first few years of LGL lymphoproliferation. This particular equilibrium restrains effects of the aggressive T‐clone, and presumably explains both the prolonged indolent phase of the disease, commonly lasting several years, and the rapid return to normal cell counts when proliferation of the T‐clone is contained by immunomodulatory therapy. However, such dynamics are prone to sudden destabilization (24), which may occur when the rogue T‐clone reaches a critical size, initiating leukaemic phase of the disease. No other long‐term observation of LGL‐associated neutropenia dynamics has been reported. Our conclusion that, in this case, neutrophil fluctuations were deterministic opens up new possibilities for studying mechanisms of T‐LGL effects on the marrow. However, the data set was too small for development of a mathematical model or assessment of the probable fit of the Mackey model. We need to collect larger series of data to understand the complex cell population dynamics associated with these rare diseases.

Supporting information

Appendix S1. Construction of a one‐dimensional map using clonogenic potential data as space‐phase coordinates. This map shows changes in clonal capacity of a liver cancer cell line in culture. Each week (day 0), 200 cells were seeded, and number of colonies was counted 15 days later. Top: changes in clonal capacity with time. Bottom: transformation to a one‐dimensional map, by plotting data x_i versus data x_{i +1}. As a result, each segment of the curve, from one passage to the next, is transformed as a point on the map, with coordinate x_i (number of clones at time x_i, that is, first point of the segment of curve) on the x‐axis, and coordinate x_{i +1} (number of clones at passage x_{i +1}, that is, endpoint of this segment of curve) on the y‐axis. Different situations on the curve (local maxima, local minima) can be further defined on the map as vectors: local maxima represented by vectors pointing south‐east, as illustrated here by segments 11 and 12 of the curve. Position and size of each vector is further analysed by drawing its bisecting line (perpendicular line, intersecting at midpoint of the vector).

Appendix S2. Examples of one‐dimensional map for sinusoidal dynamics (top) and bi‐rhythmic dynamics (bottom). In the case of sinusoidal oscillations (top), vectors for local minima and local maxima are superimposed and perpendicular to the diagonal, and their bisecting lines, which are oriented upwards for local minima, and downwards for local maxima, are superimposed on the diagonal. In bi‐rhythmic oscillations (bottom), there are two vectors representing the two local extrema, and two vectors representing the two local minima, and their superimposed bisecting lines intersect on the diagonal at two fixed points, at a high fixed point for troughs and a low fixed point for peaks.

Appendix S3. Maps of lymphocytes counts of the same patient. Bisecting lines for vectors of peaks (top) and for vectors of troughs (bottom) are randomly disordered.

Please note: Wiley‐Blackwell are not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.

Supporting info item

Supporting info item

Supporting info item

Supporting info item

APPENDIX: Detailed method of analysis (Appendix S1)

Recurrent representation of proliferation data

(i) We represented long‐term change in cell populations by plotting x _i (cell count at i‐th passage) on the x‐axis versus x _i+1, on the y‐axis. Let M _i be a point of coordinates (x _i, x _i+1). Consecutive points are joined. In this representation, if x _i is a local minimum (trough of proliferation), that is, if x _i < x _i−1 and x _i < x _i+1, then the segment M _i M _i+1 runs from south‐east towards north‐west. Similarily, if x _i is a local maximum (peak of proliferation), that is, if x _i > x _i−1 and x _i > x _i+1, then the segment M _i M _i+1 runs from north‐west to south‐east. (ii) We then drew the bisecting line (that is, line perpendicular to the vector, intersecting at its midpoint) for each vector on the map, to determine orientation of the vectors illustrating local minima (troughs) and local maxima (peaks).

Analytical expression of the control mechanisms

In a previous study (ref 10), analysing proliferation of hepatoma cells, we discovered the following control mechanisms: all bisecting lines of segments M _i M _i+1, corresponding to different minima x _i, converged on a fixed point situated on the diagonal of the coordinate axes. However, bisecting lines corresponding to the local maxima did not converge. The opposite pattern was observed in a second study analysing dynamics of proliferation of cultures of mouse bone marrow early progenitors (ref 9); we observed similar control mechanisms, with a low fixed point coordinating peaks of marrow cell counts, and a high fixed point partly coordinating troughs of cell counts.

Analysis.  On rectangular coordinates, consider points M _i−1(x _i−1, x _i) and M _i(x _i, x _i+1), where x _i is a local minimum (x _i < x _i−1 and x _i < x _i+1). Let H be the midpoint of M _i−1 M _i, such that H has coordinates x _H = (x _i−1 + x _i)/2, y _H = (x _i + x _i+1)/2. We assume that the line orthogonal to M _i−1 M _i cuts the diagonal line at fixed point F (f, f). The slope of line M _i−1 M _i is s ₁ = (x _i+1 − x _i)/(x _i − x _i−1) and slope of line HF is s ₂ = (f − y _H)/(f − x _H). As HA and M _i−1 M _i are orthogonal lines, s ₁ = −1/s ₂. This relationship, with the above values of s ₁ and s ₂, gives, after developing the terms and simplifications,

Thus, if all bisecting lines of segments M M′ corresponding to local maxima converge on a fixed point, then the mathematical law for the dynamic would be

(A1)

Relationship (A1) is simpler than the complete geometric construction, and allows an approximate statistical assessment of dispersion of the intersections of bisecting lines with the diagonal, and between them. However, the geometric construction provides a better illustration of central control, and it is that construction that led us to discover the control mechanism. It also permits a more critical, visual analysis of the position of each vector and of out‐of‐range data points.

We used two statistical tests of control mechanisms for fixed points of the dynamics of hepatoma cells and bone marrow progenitors (9, 10):

(i) We designed a computer program to determine intersections of the bisecting lines of trough vectors, by successively pairing all of them in each series. Mean and variance of x and y coordinates of all scattered points of intersection were calculated. The same was performed with vectors for local maxima. This calculation confirmed the strong convergence of the vectors of local minima of hepatoma cells on a point located on the diagonal of the map, that is, a fixed point. The same confirmation was obtained for the two fixed points of marrow progenitor dynamics.

(ii) We used a Monte Carlo procedure to show that the relationship (A1) results from deterministic control. Letting y _i = (x _i−1 + x _i+1)/2, we calculated quantities y ₁, y ₂,..., y _p corresponding to the different minima of the series and tested the hypothesis that set y _i is constant, that is of variance (or standard deviation, SD) zero. Let s ₀ be SD of set (y _i). We performed a random perturbation of order of the series x _i, then identified local minima and calculated quantities y _k of the perturbed (uncontrolled) series. Letting s ₁ be SD of these new y _k, by repeating the same procedure, we calculated new SDs s _2, s ₃,..., of several new series, obtained each time from the initial series by randomly shuffling the order. Our hypothesis is highly probable if only a very small number of s _i with i = 1, 2, …, are smaller than the observed valued s ₀. The same calculus was performed for local maxima. The same method was applied for all series of data. However, we gave explicit calculations only (i) for the 29‐week series of bone marrow cultures: probability of s _i ≤ s ₀ was 0.008; and (ii) for the 6‐ to 9‐month culture series of hepatoma cells: only 1.5% of s _i were ≤s ₀. Therefore, probability that a random sequence provides s _i more extreme than the observed s ₀ is very small, and we may have confidence that law (A1) expresses a deterministic structure. The other time series were shorter, or lacked one or two time points, and we chose to use the longest series in these two studies.

Characteristics of the map method

Due to recurrent representation of cell counts x _i versus the next cell count x _i+1 on the map, only numbers (x _i, x _i+1, x _i+2...x _n) and their order of succession determine the geometric pattern, time dimension being embedded in the map. The geometric pattern is thus independent of regularity and size of the time intervals. Sinusoidal oscillations of cell counts – that is, recurrent identical values – would display peak and trough vectors as a single line perpendicular to the diagonal, with bisecting lines superimposed on the diagonal. The bi‐rhythmic oscillations result in two bisecting lines converging on the diagonal, and random, noisy, dynamics were not coordinated at all. Examples of these situations are illustrated in Appendix S2 and S3 of this Appendix.