Impact of oxygen environment on mesenchymal stem cell expansion and chondrogenic differentiation

Abstract

Introduction:  In vitro expansion and differentiation of mesenchymal stem cells (MSC) rely on specific environmental conditions, and investigations have demonstrated that one crucial factor is oxygen environment.

Objectives:  In order to understand the impact of oxygen tension on MSC culture and chondrogenic differentiation in vitro, we developed a mathematical model of these processes and applied it in predicting optimal assays.

Methods and results:  We compared ovine MSCs under physiologically low and atmospheric oxygen tension. Low oxygen tension improved their in vitro population growth as demonstrated by monoclonal expansion and colony forming assays. Moreover, it accelerated induction of the chondrogenic phenotype in subsequent three‐dimensional differentiation cultures. We introduced a hybrid stochastic multiscale model of MSC organization in vitro. The model assumes that cell adaptation to non‐physiological high oxygen tension reversibly changes the structure of MSC populations with respect to differentiation. In simulation series, we demonstrated that these changes profoundly affect chondrogenic potential of the populations. Our mathematical model provides a consistent explanation of our experimental findings.

Conclusions:  Our approach provides new insights into organization of MSC populations in vitro. The results suggest that MSC differentiation is largely reversible and that lineage plasticity is restricted to stem cells and early progenitors. The model predicts a significant impact of short‐term low oxygen treatment on MSC differentiation and optimal chondrogenic differentiation at 10–11% pO₂.

Introduction

Mesenchymal stem cells (MSC) are multipotent progenitor cells capable of differentiating into bone marrow stromal cells, osteoblasts, chondrocytes, myocytes, and adipocytes. In some tissue types, such as bone marrow stroma, fat, skeletal muscle, and synovium, MSCs persist in adult life without losing their capacity to proliferate and differentiate (1). Under appropriate conditions, they can multiply and transform into specialized cell types. These processes have been found to be at least partially reversible, demonstrating a limited but significant plasticity of MSCs (2).

During the recent years, application of MSCs in tissue engineering has become a major subject of regenerative medicine, in particular, concerning cartilage and bone regeneration (3). Maintenance of MSCs as well as their differentiation, relies on specific environmental cues, such as growth factor supply and matrix elasticity (4, 5). Interestingly, there is growing evidence that stem cells are adapted to limiting metabolic conditions (6).

In agreement with this observation, low oxygen supply has been suggested to preserve early progenitor states in vitro (7). Accordingly, MSC‐derived cell populations show higher proliferative activity when cultured under low oxygen tension (2–5% pO₂) compared to high oxygen tension (20–21% pO₂) [human MSCs (7), mouse MSCs (8), rat MSCs (9)]. Cell populations expanded at low oxygen tension show a faster and more directed differentiation into osteoblasts, adipocytes (human MSCs (10), rat MSCs (9)), and chondrocytes (human MSCs (11, 12)). However, studies on the direct impact of the oxygen tension on differentiation in two‐ and three‐dimensional cultures has resulted in controversial findings. Malladi et al. (13) found for adipose‐derived mouse MSCs that osteogenesis in monolayers and chondrogenesis in pellet culture are significantly impaired at 2% pO₂ compared to 21% pO₂. According to results by D’Ippolito et al. (7), this applies also to osteogenesis of human bone marrow‐derived MSCs at 3% pO₂. In contrast, Lennon et al. (9) found no significant differences in osteogenesis between rat bone marrow‐derived MSCs cultivated at 5% and 20% pO₂, respectively. Moreover, human adipose‐derived MSCs in alginate bead culture have shown increased production of chondrogenic matrix molecules at 5% pO₂ compared to 20% pO₂ (14).

A large number of theoretical approaches to tissue engineering aim at quantitatively describing culture conditions concerning oxygen distribution, and the impact on processes such as matrix formation (15 and references therein). While many innovative tissue engineering strategies rely on stem cell expansion and differentiation, theoretical models of these systems are rather rare (16, 17). In order to provide reliable predictions on the dynamics of such systems, theoretical approaches are required that account for both: (i) composition and structure of the individual cell environment and (ii) particular stem cell properties such as lineage plasticity. To our knowledge, such models are currently not available.

Here we explain oxygen‐related phenomena of MSC expansion and differentiation, by a hybrid multiscale computer model. Following the stem cell concepts of Loeffler and Roeder (18, 19), we use a pedigree‐free approach. Within our model two properties – the cell proliferation rate and the amplitudes of cellular state fluctuations – determine organization of a stationary population structure with respect to cell differentiation. While both properties are assumed to be differentiation state‐specific, only cell state fluctuations are assumed to be sensitive to the oxygen environment. The model assumes that cell adaptation to non‐physiological high oxygen tension results in decreased cell state fluctuations and accumulation of cells in differentiated states. In contrast, low oxygen tension conserves stem cell and progenitor states. We simulate the experimentally observed impact of low oxygen expansion on subsequent differentiation in pellet culture, as a result of limited lineage plasticity of MSC‐derived cell populations. Thereby, our computer simulations closely follow standard in vitro expansion protocols and may be viewed as experiments ‘in silico’ (on the computer), so that results can directly be compared to those found from experiments.

Model

Modelling MSC differentiation and lineage specification

Differentiation.  In our model, cell differentiation is defined as loss of stem cell properties. It can be accompanied by, but is not identical to lineage commitment (see paragraph on Lineage commitment). Cell differentiation is quantified by a continuous state variable α that can adopt values between 0 (full stem cell competency) and 1 (completely differentiated cell). Each value of α may represent a set of regulatory network activation patterns. From the molecular point of view, α may depend on abundance and subcellular localization of proteins and RNAs, as well as other types of signalling and metabolic molecules (20). In general, cell differentiation is assumed to be reversible (19) and to occur independently of cell proliferation as found in progenitor systems (21).

In our model, each cell's α‐value fluctuates randomly with a state‐dependent noise amplitude σ(α) (Fig. 1a). From its current α‐value a cell adopts a new value α′ with a randomization rate R. α′ is drawn from a Gaussian distribution p(α′ | α), centred around α with standard deviation σ(α). Consequently, cells tend to accumulate in low noise states. The state dependence of σ(α) is assumed to be determined by the environment. Hence, a differentiation‐inducing environment reduces noise in high‐α states causing accumulation of differentiated cells.

Figure 1.

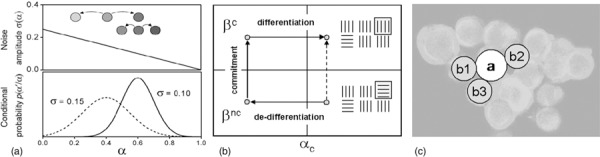
Hybrid multiscale model. (a) Modelling fluctuations of the differentiation state. Upper panel: A decrease of noise amplitude of the Gaussian conditional probability function p(α′|α) with α results in an accumulation of cells at higher values of α. Lower panel: Gaussian distribution p(α′|α) for α = 0.4 and α = 0.6. (b) Modelling lineage specification. Different states of lineage activity β^c and β^nc may be characterized by different activation patterns of the regulatory network (small boxes). A transition between the states is assumed to be impossible for α > α_c (dotted line) but may occur subsequent to de‐differentiation. (c) Cell–cell interaction. The induction of a chondrogenic phenotype of cell (a) requires a sufficient differentiation of the cell itself and that a defined number of neighbour cells are within the same lineage, here (b1), (b2), and (b3).

Lineage commitment.  MSCs are capable of differentiating into different lineages. At each differentiation state diverse lineages can be distinguished by their characteristic regulatory network activation patterns. Thus, characterization of cellular state requires introducing a second state variable β, which specifies the lineage. That is, whether a cell expresses markers of a specific lineage, e.g. the Sox‐9 transcription factor for chondrogenic lineage (22), depends on the value of β. According to the experimental observation that an entire spectrum of regulatory states may contribute to a defined lineage (23), a continuous state variable was chosen. We assume that the β‐value fluctuates as long as a cell is not fully committed. Lineage commitment is modelled as a cellular response to changing environmental conditions leading to a restriction of the accessible values of β. This can be understood as a consequence of large‐scale transcriptional silencing of the genome of these cells (24). We assume that a chondrogenic differentiation assay, as applied in our study, restricts β in a way that only a spectrum of states {S _chondro} remains accessible, which is specific to chondrogenic lineage. Dynamics of the chondrogenic lineage commitment are characterized by the transition rates W(β^nc→β^c, α) from non‐chondrogenic states β^nc into chondrogenic states β^c ∈{S _chondro}. These transitions are assumed to be irreversible under conditions of the assay. Sufficiently differentiated cells cannot switch lineage. Thus, transition rates W(β^nc→β^c, α) are larger than zero for undifferentiated cells only. For simplicity, they were set to be equal W₀ for α < α_c and zero otherwise (Fig. 1b).

Induction of a functional phenotype.  In our model, differentiation and lineage commitment are necessary but not sufficient to induce a lineage‐specific functional phenotype of a cell. Experimental observations suggest that cell–cell interactions via N‐cadherins are essential for induction of a functional chondrogenic phenotype in MSC‐spheroids (25). Hence, within our model induction of the chondrogenic phenotype is assumed to require (i) chondrogenic specification of the cell (β ∈ {S _chondro}); (ii) sufficient differentiation (α > α_d); and (iii) a minimum number N_c of neighbouring cells in the same lineage (Fig. 1c). This phenotype induction is reversible due to the general reversibility of differentiation in the model.

Individual cell‐based model

We aim at analysing induction of the chondrogenic phenotype in pellet cultures. In such spheroid cultures, the number of cell–cell contacts varies depending on cell position within the aggregate. Cells close to the surface have less cell–cell contacts than those in the interior. Moreover, oxygen and nutrient supply of a cell depends on its position within the multicellular aggregate. It decreases with its distance to the spheroid surface. Induction of a functional chondrogenic phenotype of individual cells depends on all these environmental properties, which, consequently, have to be considered in a reliable model. Motivated by previous work on growing multicellular spheroids (26), we use an individual cell‐based model, which appears to be perfectly suited to represent all these requirements.

Cell biophysics.  Cells in suspension and three‐dimensional aggregates often adopt a spherical shape (27). In our approach, individual cells are modelled as elastic spheres (28). We assume that cell volume in suspension cannot be smaller than a minimum value V ₀. In our model a cell can move actively by migration and passively by being pushed, can deform, adhere to other cells or a substrate, and can grow and divide. A proliferating cell divides if its volume has grown to twice the volume V ₀.

Elastic deformation of a cell subject to compression by other cells or substrate is modelled by the Hertz Model (29). This approximates an isolated cell by a homogeneous elastic sphere. It is parameterized by the Young modulus and the Poisson ratio and relates a cell's deformation and its contact area to neighbouring cells (or the substrate) to radial interaction forces exerted by neighbouring cells (or the substrate). We further assume that cells adhere to each other according to an adhesion energy that is proportional to the Hertz contact area (see Appendix).

Cell proliferation.  Cell proliferation is modelled assuming a two‐phase cell cycle: During interphase, a cell doubles is volume by stochastic increments. This growth process results in an approximately Γ‐distributed growth time τ of cells (26). During the mitotic phase, a cell divides into two daughter cells of equal volume. The population average of the growth time τ can easily be measured in vitro.

In particular, cell proliferation is assumed to depend on the differentiation state α of a cell. In our model it is restricted to intermediate differentiation states α with: 0 < α_s < α < α_d < 1. For these states, we assume identical growth time τ. Stem cells (α < α_s) and differentiated cells (α > α_d) do not proliferate. During the growth process cells may frequently switch between proliferative and non‐proliferative states. This results in an effective cell growth time larger than τ. Additionally, a cell undergoes growth arrest if the sum of the forces on it exceeds a critical threshold value F_c (see Appendix).

Systems dynamics.  We simulate cell motion by a stochastic equation of motion (‘Langevin equation’) for each cell. Active motion of a cell is represented as a random force modelled by white noise. Small Reynolds numbers in the regime of single cells allow us to neglect their inertia (30), leading to a system of linear stochastic differential equations for cell velocities. Thereby, velocity v_i of cell i is given by

(1)

where the sums run over all neighbouring cells j in direct contact to cell i. γ_is denotes the effective friction coefficient with suspension and substrate, and γ_ij the cell–cell friction coefficients. They are assumed to be proportional to respective contact areas given by the Hertz Model. The effective friction summarizes passive friction and active migration. 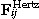and 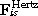denote the forces between cell i and cell j and cell i and the substrate respectively, and 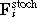the stochastic Langevin force on cell i.

It was demonstrated that growth behaviour of a simulated cell population on long timescales is neither affected by details of the assumptions on the precise shape of the interaction forces between cells nor by details of the cell cycle model (31). Therefore, we expect that the results obtained in this paper will be robust against changes of these model details.

Oxygen distribution.  We use a reaction‐diffusion equation for oxygen concentration c(r, t) similar to Drasdo and Höhme (26):

(2)

where D _O2 is the diffusion constant of oxygen within the cell aggregate, C _O2 denotes oxygen consumption rate of a single cell and n(r, t) represents cell density. We use the Forward Euler Method on a cubic lattice for numerically solving the reaction‐diffusion equation and assume the oxygen concentrations to be constant and equal in all lattice sites exterior to the spheroid. The parameters are chosen according to Malda et al. (32) and Zhao et al. (33) (Table 1).

Table 1.

  Model parameters used in simulations

Model	Parameter	Value	Simulation	Source
Stem cell dynamics	Randomization rate, R	2.5e–4/s	2D/3D	Fitted
	Stem cell state fluctuation strength, σ0	0.15	2D	Fitted
	Differentiation threshold, αd (αs= 1 – αd)	0.85	2D/3D	Set
	Minimal number of neighbours, Nc	6	3D	Set
	Transition rate, W 0	0.01/s	3D	Fitted
	Transition threshold, αc	0.15, 0.5, 0.85	3D	Set
Individual cell‐based model	Minimal cell radius, R 0	8 µm	2D/3D	Measured
	Minimal cell volume, V 0	V(R 0)	2D/3D
	Proliferation rate, r	1.5–2.1/day*	2D	Fitted
	Young modulus, E	450 Pa	2D/3D	34
	Contact inhibition threshold, Fc	1 × 10−9 N	2D/3D	Fitted
	Poisson ratio, ν	0.4	2D/3D	35
	Friction constant, ηij	3 × 107 Ns/m3	2D/3D	Set
	Cellular diffusion coefficient, DC	4 × 10−12 cm2/s	2D/3D	36
	Cell–cell anchorage, ɛ	6 × 10−5 N/m	2D/3D	37
	Cell–substrate anchorage, ɛ	6 × 10−5 N/m	2D	37
Diffusion	Oxygen diffusion coefficient, D O2	0.175 × 10−9 m2/s	3D	38
	Oxygen consumption rate, C O2	30–65 fmol/cell/h	3D	32, 33, 38

2D, two‐dimensional; 3D, three‐dimensional. *The fit of the CFU‐F data was achieved assuming a proliferation rate for all cells of 1.5/day for 20% pO₂ and a 1:1 mixture of cells with proliferation rates of 1.5/day and 2.1/day for 5% pO₂.

Materials and methods

Experiments

Isolation and culture of MSCs from ovine bone marrow aspirates.  Bone marrow aspirates were obtained with 15‐gauge Jamshidi needles from the iliac crest of 18‐ to 24‐month‐old Merino sheep. Heparinized aspirates (500 I.U./ml; Ratiopharm Ulm, Germany) were diluted 1 : 3 with phosphate‐buffered saline (PBS; Gibco, Karlsruhe, Germany) and agglutinates were removed by filtration with a 70‐µm pore filter. Samples were carefully poured into a Leucosep® tube with a porous barrier (Greiner Bio‐one, Frickenhausen, Germany), onto a Ficoll separating solution (density 1.077 g/ml; Biochrom, Berlin, Germany) and centrifuged 10 min at 1000 g at 20 °C. Enriched mononuclear cells including MSCs above the porous barrier were harvested and washed twice in PBS by centrifugation for 5 min at 500 g. Cells were resuspended and seeded at 2 × 10⁴ cells/cm² in tissue culture flasks with high‐glucose Dulbecco's modified Eagle's medium (DMEM; Gibco) supplemented with 10% foetal calf serum, 100 U/ml penicillin, and 100 µg/ml streptomycin (both Biochrom). Cultures were maintained at 37 °C in a humidified atmosphere containing 95% air and 20% O₂–5% CO₂ or 5% O₂–5% CO₂ balanced with N₂ in a tri‐gas incubator (Thermo Fisher Scientific, Dreieich, Germany). Medium was changed twice weekly. After 14 days at near confluence of cultures, cells were detached using trypsin/EDTA (0.25%/0.05 mm; Biochrom) and used for single cell cloning (see next paragraph) or for subculture. For that, cells were passaged at 5000 cells/cm² and cultured to reach 80–90% confluence of passage 2 before final trypsinization and use for chondrogenic differentiation in pellet culture.

Clonal expansion assay.  Single cell clones were generated by using a limited dilution method. Therefore, cells were seeded at one cell per well in a 96‐well plate at 5% and 20% pO₂. Each well was checked and all wells that contained just one single cell were marked. After 5 days, cell numbers of 30 single cell‐derived clones of 5% and 20% pO₂ cultures were counted using microscopy.

CFU‐F assay.  After isolation of the mononuclear fraction from bone marrow by Ficoll density gradient centrifugation, 2 × 10⁴ mononuclear cells/cm² were seeded in 10 cm Petri dishes. After 14 days, colonies were washed twice in PBS and were fixed in methanol for 5 min. After removal and air drying (5 min), cultures were incubated for 5 min in Giemsa stain solution (1 : 2 in aqua dest; Sigma‐Aldrich, Deisenhofen, Germany). Cultures were washed twice in water and colonies with more than 50 cells were counted.

Pellet preparation and culture.  Pellets were prepared according to protocols by Mackay et al. (47) and Yoo et al. (48). Briefly, a total of 0.5 × 10⁵ MSCs was placed in a 15‐ml conical polypropylene tube, centrifuged at 500 g for 5 min at 20 °C and resuspended in DMEM without serum for washing. After a further centrifugation step, cells were resuspended in serum‐free, chondrogenic medium (Chondrogenic Differentiation BulletKit®, Lonza, Wuppertal, Germany) supplemented with 10 ng/ml transforming growth factor beta3 (Lonza, Wuppertal, Germany) and cultured for 2, 7 and 14 days. Chondrogenic medium was changed twice a week.

Immunohistochemistry.  Immunohistochemistry on cryosections (8 µm) was performed using the two‐step indirect method. Samples were fixed in 4% formaldehyde for 20 min and in 100% ice‐cold methanol for 10 min. They were then washed three times in PBS and then blocked for 30 min in sheep serum (1 : 10 diluted in PBS). Preparations were incubated with primary antibody overnight at 4 °C [collagen type II: mouse monoclonal antibody (Clone: II‐4C11; MP Biomedicals, Solon, OH, USA), diluted 1 : 2000 in PBS/0.3% Triton X; Sox 9: mouse monoclonal antibody (Millipore, Schwalbach, Germany), diluted 1 : 200 in PBS/0.3% Triton X]. After washing in PBS, secondary antibodies Alexa Fluor® 488 goat anti‐mouse immunoglobulin G (IgG) for collagen type II and Alexa Fluor® 555 goat anti‐rabbit IgG for Sox 9 (diluted 1 : 1000 in 0.1 µg/ml DAPI/PBS/0.3% Triton X‐Solution) were added for 1 h at 37 °C (both antibodies were from Invitrogen, Karlsruhe, Germany). Finally, after washing in PBS, sections were coated with 90% glycerol in aqua dest. for fluorescence stabilization. Fluorescence was examined using microscopy (Axiovert 200, Carl Zeiss Jena GmbH, Jena, Germany).

For staining with peroxidase‐conjugated secondary antibody (Fig. 3b) after incubation with primary collagen type II antibody (see paragraph above) and washing in PBS, secondary antibody of peroxidase‐conjugated goat anti‐mouse IgG (diluted 1 : 50 in PBS; Jackson ImmunoResearch, Cambridge, UK) was added for 1 h at 37 °C. Immunostaining was developed by 3‐amino‐9‐ethyl‐carbazol substrate. Cell nuclei were counterstained after staining with Mayer's haematoxylin (Lillie's Modification; DakoCytomation, Hamburg, Germany).

Figure 3.

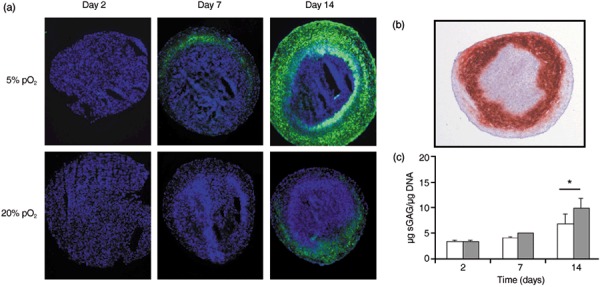
Experimental results on chondrogenic differentiation of mesenchymal stem cells at 20% pO₂. (a) Collagen II expression in pellet of cells expanded at 5% (upper row) and 20% (lower row) pO₂. Collagen II (green), DAPI (blue). Interestingly, differentiation starts in a defined layer beneath the surface. (b) This behaviour is confirmed by a second collagen II staining. (c) Glycosaminoglycan concentration of chondrogenic differentiated pellets. Sulphated glycosaminoglycan levels were normalized to DNA content. After 14 days sulphated glycosaminoglycan levels of cultures expanded at α 5% pO₂ cells were significantly higher compared to cultures expanded at 20% pO₂. *P < 0.05; (Student's paired t‐test); n = 4.

DNA quantification of pellet cultures (PicoGreen assay).  To assess proliferation of MSCs within pellet cultures, DNA concentration was measured by Quant‐iT™ PicoGreen® dsDNA Assay Kit (Molecular Probes, Eugene, OR, USA) according to the manufacturer's instructions. For preparation, each pellet sample was resuspended in 200 µl papain digestion buffer and digested for 16 h at 60 °C. After digestion, samples were diluted in Tris/Borate/EDTA buffer for DNA measurement. For quantification, a well‐defined DNA stock solution was used (Lambda‐DNA, Molecular Probes). Fluorescence of negative, cell‐free controls was subtracted from fluorescence values of samples.

Sulphated glycosaminoglycan quantification.  Pellets were digested in 0.2 ml papain digestion buffer (5 mm l‐cysteine, 5 mm EDTA, 100 mm Na₂HPO₄, pH 6.5) and incubated for 16 h at 60 °C in a thermomixer (Eppendorf, Hamburg, Germany) with 5 µl papain solution (10 mg/ml; Sigma‐Aldrich). Samples of 40 µl were assayed for proteoglycan contents by quantifying sulphated glycosaminoglycan content using 500 µl of 1,9‐dimethyl‐methylene blue dye (0.016 g/l DMMB, 5 ml/l C₂H₅OH, 2 g/l NaCOOH, 2 ml HCOOH, pH 3.0) binding assay (Roche, Basel, Switzerland). Absorbance was determined at 595 nm in a photometer and concentration of glycosaminoglycan was extrapolated from a standard curve based on shark chondroitin sulphate, within a range of 10–100 µg/ml. Sulphated glycosaminoglycan quantities of pellet cultures were normalized to DNA content, measured by PicoGreen assay.

Statistical analysis.  Experiments were performed using MSCs from at least four donors. Results were expressed as mean ± standard deviation. Significance of results was analysed using Student's t‐test, with P < 0.05 considered as significant.

Results

Low oxygen tension increases proliferation and colony forming potential of MSCs

Experiments.  We analysed growth dynamics of ovine MSCs applying different expansion assays. Figure 2a shows a typical result of CFU‐F assay performed with mononuclear cells from bone marrow isolates. After 14 days, cells expanded at low oxygen tension showed twofold higher CFU‐F potential compared to those expanded at high oxygen tension. Moreover, they formed larger and more extended colonies indicating a shorter doubling time of these cells, on average. We confirmed this observation selecting individual cells from analogue cultures and analysing size distribution of small colonies growing from them. We found that cells at low oxygen tension formed significantly larger colonies compared to those under atmospheric conditions. Colony size distributions after 5 days are summarized in Fig. 2(b,c) for 5% pO₂ and 20% pO₂, respectively.

Figure 2.

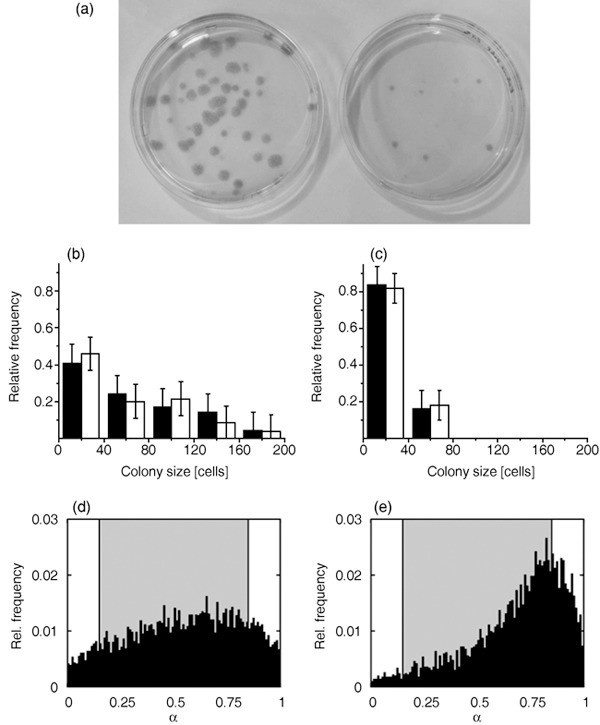
Growth dynamics of mesenchymal stem cell populations at different oxygen tensions. (a) CFU‐F assay for mononuclear cells from bone marrow isolates at 5% pO₂ (left) and 20% pO₂ (right). Growth time: 14 days. (b,c) Monoclonal expansion assay: size distribution of colonies grown from single cells at 5% and 20% pO₂, respectively. Experimental results (black columns) are compared with simulated results (white columns). Growth time: 5 days. For model parameters, see Table 1. (d,e) Simulated equilibrium distribution of the differentiation states at 5% and 20% pO₂, respectively. Shaded regions indicate proliferative states (0.15 < α < 0.85).

Simulations.  Motivated by the observed CFU‐F dependency on oxygen tension we assume an oxygen level‐specific control of the differentiation state fluctuations. Hence, we assumed the noise‐amplitude σ(α, pO₂) to depend on the oxygen tension pO₂:

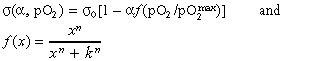(3)

with σ₀ denoting the stem cell state fluctuation strength and f being a Hill function approaching 0 and 1 at low and high pO₂, respectively. 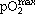refers to atmospheric oxygen tension. Simulated MSC colony growth thus depends on the randomization rate R, the stem cell state fluctuation strength σ₀, and the parameters of the Hill function (n and k) and those specifying proliferation rate (r and α_d with α_s = 1 – α_d). We performed extensive simulations to explore sensitivity of the simulation results with respect to the model parameters. We found that the average size of MSC clones depends sensitively on the proliferation rate r.

In general, where growth rate varies throughout the population, accumulation of rapidly proliferating cells occurs in the population. This effect is more pronounced in a low oxygen environment where cells enter proliferative states more frequently. This applies already for initial expansion of the mononuclear cells isolated from bone marrow (see Materials and methods section). Thus, in order to obtain quantitative agreement with experimental data, it was necessary to assume that cells prepared at 5% pO₂ have a slightly higher proliferation rate on average compared to those prepared at 20% pO₂. An appropriate fit of the experimental data was achieved applying the parameter set given in Table 1 (Fig. 2b,c). Our simulation results refer to highly motile cells. Less motile cells would form more dense colonies and contact inhibition of growth would strongly reduce their proliferation activity. Due to our observation that the colonies were rather sparse after 5 days growth, the simulation parameters were chosen to avoid contact inhibition of growth at both 5% and 20% pO₂.

Simulated MSC population structures at equilibrium are given in Fig. 2(d,e). Note the different shape of the relative frequency distribution at 5% and 20% pO₂, respectively. While at 5% pO₂ a significant fraction of about 9% of non‐proliferative stem cells (defined by α < 0.15) is conserved, at 20% pO₂ this fraction amounts to 3% only. On the other hand, the model predicts a fraction of about 14% non‐specific differentiated, non‐proliferative cells (defined by α > 0.85) at 5% pO₂ compared to 26% at 20% pO₂. Identifying these cells as potentially premature senescent cells, the obtained fractions are larger than those identified experimentally by senescence‐associated β‐galactosidase staining in monolayer cultures (39). However, the ratio found between low and high oxygen tension culture is comparable. In contrast to the simulated colony sizes, results for the population structures showed themselves to be robust against moderate changes in the proliferation rate (Appendix, Fig. S1).

Expansion at low oxygen tension increases chondrogenic differentiation potential of MSCs

Experiments.  We demonstrated chondrogenic differentiation of these ovine MSCs by gene expression analysis (aggrecan, collagen type II, X) and immunohistochemistry (Sox‐9, aggrecan, collagen type II). As an example, Fig. 3(a,b) show results of collagen type II expression during chondrogenic differentiation at 20% pO₂. Expression of this essential marker of chondrogenic differentiation is strongly increased in pellets of cells expanded at 5% pO₂ compared to pellets of cells which were expanded at 20% pO₂. Sulphated glycosaminoglycans represent a further prominent marker of chondrogenesis. In order to quantify accumulation of chondrogenic extracellular matrix in pellet cultures, we determined sulphated glycosaminoglycan concentrations by DMMB assay and normalized them to DNA content. We found that after 14 days pellets of cells expanded at 5% pO₂ had a 1.4‐fold higher sulphated glycosaminoglycan concentration (9.8 ± 2.0 µg/µg; P < 0.05) when compared to pellets of cells expanded at 20% pO₂ (6.9 ± 1.9 µg/µg DNA; Fig. 3c).

Simulations.  We hypothesized that observed differences in synthesis of chondrogenic proteins are due to different structure of MSC populations after expansion at 5% and 20% pO₂. In order to support this hypothesis, we simulated the differentiation process within MSC spheroids using simulated population structures of expansion assays as initial conditions. However, simulations of a spheroid system require some additional assumptions concerning the system under consideration, in particular, with regard to regulation of cell proliferation and oxygen supply.

Experimentally, we found that cell proliferation stops throughout the pellets within a few days. After 7 days, proliferation activity was localized at the periphery only (Fig. 4a). Analysing DNA content of the pellets, effective cell loss was observed (Fig. 4b). However, from day 7 onwards the number of cells stayed nearly constant. Accordingly, we decided to perform all simulations of the differentiation assay without considering cell proliferation.

Figure 4.

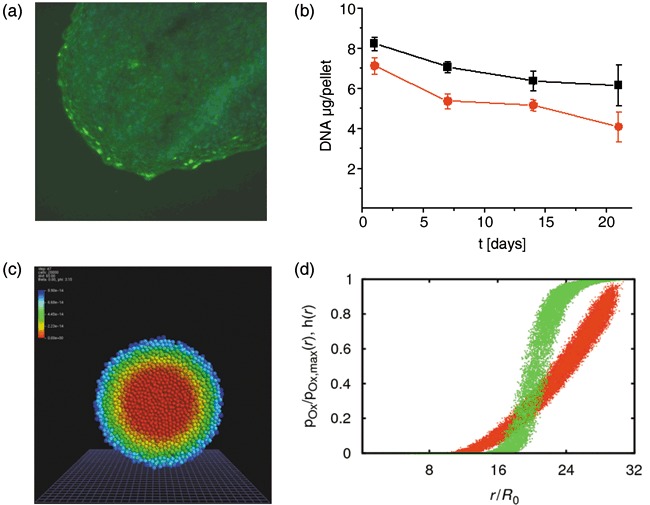
Properties of the chondrogenic pellet culture. (a) KI67 staining in a spheroid after 7 days. Proliferation occurs in some cells of the periphery only. (b) DNA content of pellets of cells expanded at 5% (black) and 20% (red) pO₂. During the first 7 days, the number of cells decreases. At later times it remains approximately constant. (c) Simulated equilibrium oxygen distribution within a mesenchymal stem cell spheroid using a oxygen consumption rate of 65 fmol/h per cell. High oxygen tension: blue, low oxygen tension red. (d) Oxygen concentration within the spheroid shown in (c) versus radial distance from the spheroid centre r for all cells (red). Additionally, the Hill function f(pO₂(r)) is shown (green, hill coefficient n = 5, dissociation constant k = 0.3, eqn 3). Note that both curves are smeared out due to the finite lattice constant.

In monolayer culture oxygen can be considered to be abundant. In spheroids oxygen diffuses into the spheroid from its border; hence, an oxygen gradient is established with decreasing oxygen concentration towards the interior of the spheroid. Consequently, cells in the interior of the spheroid may suffer from lack of oxygen (26). For oxygen consumption rates (C _O2, eqn 2) of MSCs and chondrocytes, a broad range between 1 and 100 fmol/h per cell was reported (32, 33, 38). In our simulations we assumed oxygen consumption to be equal in MSCs and chondrocytes. Consequently, the oxygen gradients within the spheroids do not change during the simulated differentiation process. Thus, the oxygen consumption rate defines only how steep this stable gradient is. In a first‐order approximation, the simulated differentiation processes of cells depend only on local available oxygen concentration. Thus, the oxygen consumption rate (C _O2) can be used to scale the width of the observed differentiation pattern in order to match with experimental values. Simulated equilibrium oxygen distributions are shown in Fig. 4(c,d).

In simulation series, we analysed the dynamics of chondrogenic differentiation of MSCs. Thereby, we assumed vanishing chondrogenic lineage activity β_c in initial populations. We started with setting the threshold value α_c of the lineage commitment model to 0.5. Yet, only stem cell and early progenitor cells with α < 0.5 are capable of changing to chondrogenic lineage.

Assuming sufficiently large lineage transition rates W compared to the basal randomization rate R (Table 1), we found differentiation dynamics in qualitative agreement with our experimental results. This is demonstrated in Fig. 5 showing the spatio‐temporal occurrence of functional differentiated chondrocytes.

Figure 5.

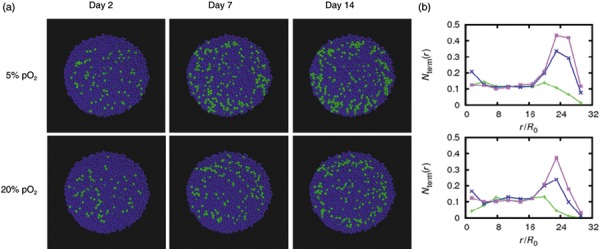
Simulated chondrogenic differentiation of mesenchymal stem cells in pellet culture at 20% pO₂. (a) Spheroids of cells expanded at 5% pO₂ (upper row) and at 20% pO₂ (lower row). Functional differentiated chondrocytes are shown in green, other cells in blue. (b) Fraction of chondrocytes versus radial distance from the spheroid centre at days 2 (green), 7 (blue) and 14 (magenta). At day 14, the total number of chondrocytes in pellets of cells expanded at 5% pO₂ is about 1.5 times larger then in pellets of cells expanded at 20% pO₂.

Stable chondrocyte clusters appear first in a layer beneath the spheroid surface. Accordingly, related chondrogenic matrix synthesis (e.g. of collagen type II) can be assumed to start at the same position in good agreement with our experimental results. This can be understood as follows. In the central region of the spheroids, differentiation state of cells fluctuates due to high noise‐amplitudes associated with low oxygen supply (eqn 3). Accordingly, cells in this region, although primed for chondrogenic lineage (Fig. 6a,c), do not reach a stable functional differentiated state. Stable differentiated cells can be frequently found at the periphery of the spheroids where the oxygen concentration is high (Fig. 6a,b). However, cells at the periphery, which were initially in an non‐specific differentiated state, stay in this state due to the small probability of starting de‐differentiation and switching into chondrogenic lineage at high oxygen tension. As a result, these cells rarely reach a chondrogenic differentiated state. Moreover, they prevent chondrogenic differentiation of neighbouring cells by limiting the number of their chondrogenic specified neighbours. Optimal conditions for chondrogenesis are therefore realized within an intermediate layer, where on one hand probability for lineage commitment is large and on the other differentiation is sufficiently high. We obtained an oxygen tension of about 10–11% pO₂ within this layer. This optimal oxygen concentration is quite robust against variation in lineage transition rate W ₀ and the oxygen consumption rate C _O2 (Appendix, Fig. S3).

Figure 6.

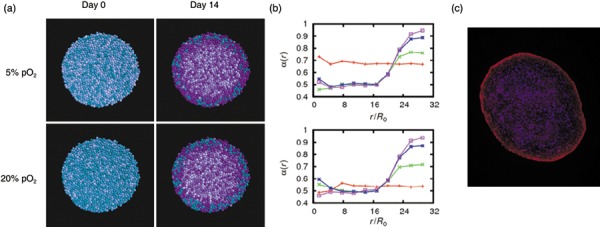
Lineage specification of mesenchymal stem cells in pellet culture at 20% pO₂. (a) Simulated – distribution after 0 and 14 days for cells expanded at 5% and 20% pO₂. Cells committed to the chondrogenic lineage are shown in magenta. The colour saturation is a marker of the differentiation level. Chondrogenic commitment is seen throughout the spheroid except of some cells at the periphery. (b) Averaged differentiation versus radial distance from the spheroid centre at day 0 (red), 2 (green), 7 (blue) and 14 (magenta). (c) Expression of the chondrogenic transcription factor SOX‐9 (red) after 14 days demonstrates the predicted chondrogenic commitment throughout the spheroid. A typical pellet of cells expanded at 20% pO₂ is shown (blue: DAPI staining).

According to the described scenario, observed differences in differentiation dynamics between populations expanded at 5% and 20% pO₂ can be mainly attributed to the different number of pre‐differentiated cells in these populations. The higher number of these cells within populations expanded under atmospheric conditions and their maintenance in non‐specific differentiation states (Fig. 6a) is, thus, suggested to account for impaired chondrogenesis of these populations. The proposed scenario is not observed assuming a considerable higher threshold value of lineage specification of, for example, α_c = 0.85 (Appendix, Fig. S2). In this case, only premature senescent cells cannot switch to the chondrogenic lineage. This limitation is too weak to account for the observed significant differences in differentiation dynamics. Thus, our model suggests that plasticity of MSCs and their progeny with respect to lineage commitment is restricted to stem cells and early progenitors.

Short‐term exposure of MSCs to low oxygen tension mimics continuous expansion at these conditions

In further simulations, we analysed consequences of short‐term exposure of MSCs to low oxygen. For that purpose, we studied dynamics of the de‐differentiation process that occurs in a high oxygen expansion culture (20% pO₂) decreasing the oxygen tension to 5% pO₂. Our simulations predict that cell adaptation to the changed environment is already finished by about 24 h (Fig. 7). After this time an equilibrium population structure is reached. Thus, our model predicts that even short‐term exposure of MSCs to low oxygen tension should result in improved chondrogenic potential of these populations. This is in agreement with recent findings by Martin‐Rendon et al. (11).

Figure 7.

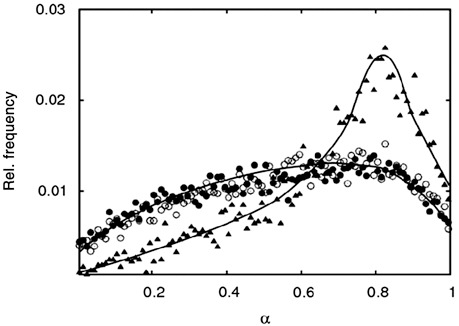
Simulation of low oxygen induced de‐differentiation of mesenchymal stem cells. The equilibrium distribution of differentiation states α in a monolayer population at 20% pO₂ (triangles) approaches the equilibrium distribution at 5% pO₂ (circles) after about 24 h cultivation under 5% pO₂ (open circles).

Low oxygen tension impairs MSC differentiation

According to our model, low oxygen tension during the differentiation process conserves progenitor states throughout spheroids and thus, impairs induction of a stable chondrogenic phenotype. Simulation results on MSC differentiation in pellet culture at 2% pO₂ are shown in the Appendix (Fig. S4 online). They are in agreement with experimental findings by Malladi et al. (13).

Discussion

We introduced a hybrid multiscale computer model of MSC expansion, differentiation and lineage commitment which consistently allows explation of a panel of experimental results. In particular the model explains: (i) why low oxygen level improves expansion of MSCs and (ii) why MSC populations expanded under low oxygen show improved potential in subsequent chondrogenic assays. The key assumptions of our model are that oxygen environment changes the population structure of expanding MSCs with respect to differentiation and that sufficiently differentiated cells can not switch lineage.

Our approach is based on a pedigree‐free concept of stem cell differentiation (19). Stem cell and progenitor cell differentiation are driven by stochastic fluctuations. Thus, these processes are reversible in general. Recently, we applied the concept of noise‐driven dynamics to differentiation of promyolytic progenitors and demonstrated that it represents an alternative to common molecular network approaches describing cell adaptation processes (40). According to our first key assumption, high oxygen tension reduces stochastic state fluctuations (noise) of differentiated states, thereby partly inducing differentiation of cells. Such differentiation would also result assuming that high oxygen tension increased fluctuation of stem cells states. In this case cells stressed by non‐physiological high oxygen tension would increase their potential for phenotypic transition. We here assume that they become more fixed in their states.

A different way of explaining impact of the oxygen environment on MSC expansion could be to assume that low oxygen tension strongly increases proliferation rate of the cells. Accordingly, low oxygen tension would increase the portion of progenitors within populations as in the simulations presented here. However, proliferation is stopped in MSC pellet culture. As a consequence, differentiation would occur independently of oxygen tension. This is in contrast to (i) our experimental observation that cells in low oxygen regions of the pellet centre do not differentiate and (ii) more general results on impaired chondrogenesis at low oxygen tension by Malladi et al. (13). While the first effect could be explained also by low growth factor or glucose concentrations and related signalling in these regions, the second strongly suggests that a proliferation effect alone cannot explain the impact of oxygen tension on MSC expansion.

However, there exists an effect of low oxygen culture on proliferation rates, in that at low oxygen accelerated selection of fast proliferating cells occurs. Accordingly, we performed further computer simulations to study the effect of a moderately increased average proliferation rate at low oxygen compared to high oxygen tension simulating colony growth. We found that these model details only marginally affect the population structure in these assays. Thus, the observed effects of oxygen tension during expansion on subsequent chondrogenic differentiation are not caused by this selection process. However, long‐term cell culture may potentiate the effect. Consequently, ongoing selection of highly proliferative cells may become substantial also for differentiation properties of the populations.

According to our second key assumption, sufficiently differentiated cells stay in their lineage state and are not sensitive to external stimuli of a differentiation assay. Consequently, a high number of non‐specific predifferentiated cells impairs differentiation potential of an MSC population. Our mathematical model predicts that accumulation of predifferentiated cells during MSC expansion can be avoided either by providing stem cell niche‐like conditions or by strongly activating proliferation. A complementary strategy would be to induce chondrogenic priming already in the expansion culture (e.g. by overexpression of SOX‐9) (41). Recent results by Martin‐Rendon et al. (11) on SOX‐9 gene expression indicate chondrogenic priming as a result of low oxygen supply. Clearly, assuming such priming would profoundly increase effects of low oxygen expansion of MSCs on their subsequent differentiation in our simulations. We here demonstrated that low oxygen culture improves their chondrogenic potential independent of such preceding priming.

Our results predict optimal oxygen tension for chondrogenic differentiation of about 10–11% pO₂, which is in the upper range measured at the surface of articular cartilage (42) and below optimal pressure of about 15% pO₂ found for cartilage formation of rabbit periosteal cells (43). Advanced chondrogenic assays should ensure high oxygen perfusion to guaranty this oxygen concentration throughout the probe. We expect that these results can be generalized for osteochondral differentiation of MSCs of different origin and from different species. Oxygen tensions of 2–3% pO₂ used by Malladi et al. (13) and D’Ippolito et al. (7) are too low and lead to impaired MSC differentiation. A value of about 5% pO₂ may either be comparable (9) or, as found for alginate bead culture (14), even better than 20% pO₂. Expansion at oxygen tensions below 1% pO₂ has been shown to induce adipocyte‐like phenotypes in human MSCs (44) and to impair their subsequent osteogenesis (45). Such behaviour cannot be described by our current mathematical model.

In the present study, we identified the site of matrix deposition with position where functionally differentiated cells appear, and compared the amount of synthesized matrix proteins with the number of these cells. Other models describe processes like that of matrix deposition in more detail (46). In particular simulations of long‐term matrix deposition (> 14 days) have to account for local accumulation and degradation effects. Such modelling requires detailed knowledge of matrix protein diffusion and degradation as well as cellular production rates.

In the present study, we aimed at better understanding of the basic principles of in vitro MSC expansion, differentiation and lineage specification as a prerequisite of reliable quantitative models of these processes.

Appendix

Simulations

Cellular dynamics.  Cellular motion is governed by a system of equations for all cells derived from eqn 1. Because non‐diagonal entries represent direct cell–cell contacts, the system is very sparse allowing use of memory and time saving optimized libraries for sparse matrices (49, 50). Note that dynamic control of the time step in simulations was required to guarantee numerical stability.

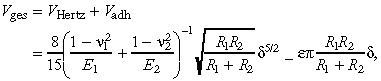
Cell–cell and cell–surface interactions are modelled by a modified Hertz‐Potential V, that consists of the classic Hertz‐Potential V _Hertz and an adhesive term V _adh:

(4)

where in the first term on the right‐hand side ν_i denotes cell i's Poisson's ratio, E_i its Young's modulus, R_i its radius and δ the surface deformation, while the second term models adhesion proportional to the Hertz contact area (29), where ɛ is the adhesion energy per unit area. The interaction force appearing in eqn 1 can be derived by partial differentiation of total potential V with respect to space coordinates x, y, and z.

The friction coefficients γ_is and γ_ij in eqn 1 are given by

(5)

where x denotes the type of contact (cell–cell, cell–substrate or cell–suspension), A_ix the corresponding contact area and η_ix the contact‐type dependent friction constant.

Contact inhibition is modelled similar to Drasdo et al. (31). Cell i stops growth and division if sum of the magnitudes of contact forces on the cell is larger than a threshold value F_c:

(6)

where the sum runs over all neighbouring cells j. F _ij and F _is denote contact forces exerted on cell i by a cell j and the substrate, respectively.

Oxygen distribution.  Oxygen distribution is calculated by solving the diffusion equation on a cubic lattice. For computational simplicity we use the explicit forward Euler scheme. The lattice constant was set to maximal cell diameter. As computation of diffusion appears to be the limiting time step for computation, it was implemented parallelized. In order to keep the simulations feasible, we decided to simulate spheroids of 20 000 cells.

Model parameters and robustness

For a first step, model parameters of the monolayer expansion system were adjusted in order to fit experimental results of the clonal expansion assays at 5% and 20% pO₂. For expansion at 20% pO₂, the best fit was achieved assuming cell population with proliferation rate of r = 1.55/day for each cell. Simulating expansion at 5% pO₂ we found a good fit assuming proliferation rate of r = 1.55/day for one‐half and of r = 2.1/day for the other half of the cells. This assumption can be motivated as discussed in the text. As shown in Fig. S1, variation of proliferations rates within the considered range only marginally affects distributions of differentiation states α.

As a second step, we used the parameter set of monolayer expansion simulations and adjusted additional parameters of the spheroid system, enabling the model to reproduce our experimental data. We obtained a fit assuming lineage specification threshold α_c = 0.5. A threshold α_c = 0.85 does not result in a significant difference in numbers of cells differentiated to the functional phenotype between populations expanded at 5% and 20% pO₂. On the other hand α_c = 0.15 gives a differentiation process that is much too slow (Fig. S2).

Interestingly, the prediction of optimal oxygen tension for chondrogenic differentiation neither depends on explicit choice of the lineage transition rate W ₀ nor on oxygen consumption rate C _O2 of cells. In all simulations, we found the fraction of cells entering the functional phenotype to peak at about 10–11% pO₂ (Fig. S3).

Simulations of chondrogenic differentiation at 2% pO₂ demonstrate inefficient differentiation of cells at low oxygen tension. After a fast saturation period, only about 10% of all cells enter the functional phenotype. This result is in agreement with the findings of Malladi et al. (13).

Supporting information

Figure S1. Dependence of the distribution of differentiation states α on the proliferation rate. Simulation results for expansion at 5% pO₂ (left) and 20% pO₂ (right) are shown. The results for the maximum proliferation rate of 2.1/day (solid lines) used in the simulations are compared with those for the minimum rate of 1.55/day (dashed lines).

Figure S2. Dependence of the terminal differentiation on the lineage‐specification threshold. For Fc = 0.85 (left) no significant difference between the fractions of terminal differentiated cells emerges. Assuming Fc = 0.15 (right) does not results in a significant amount of terminal differentiated cells within 14 days. Simulations for cells expanded at 20% pO₂ (open circles) and 5% pO₂ (filled triangles) are compared.

Figure S3. Dependence of the terminal differentiation on the lineage‐transition rate and oxygen consumption rate. The fraction of terminal differentiated cells is shown as function of the oxygen tension for varying lineage transition and oxygen consumption rates. Height and position of the peaks indicating the optimal oxygen tension for chondrogenic differentiation change only slightly. Left: expansion at 5% pO₂, right: 20% pO₂. Upper line: The lineage transition rate is varied by an order of magnitude (0.05/s: circles/dashed, 0.01/s: squares/solid, 0.005/s: triangles/dotted). Lower line: Oxygen consumption rates of 65 (open squares), 50 (filled triangles) and 30 fmol/h per cell (open circles) are compared). For 30 fmol/h per cell a minimum oxygen tension of 6% pO₂ was observed in the centre of the spheroid.

Figure S4. Chondrogenic differentiation at 2% pO₂. The number of cells in a functional phenotype saturates after a few hours. Strong fluctuations throughout the culture suppress further differentiation.

Please note: Wiley‐Blackwell are not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.

Supporting info item

Supporting info item

Supporting info item

Supporting info item