Abstract
Abstract. Objectives: Tumour progression has been described as a sequence of traits or phenotypes that cells have to acquire if the neoplasm is to become an invasive and malignant cancer. Although genetic mutations that lead to these phenotypes are random, the process by which some of these mutations become successful and cells spread is influenced by tumour microenvironment and the presence of other cell phenotypes. It is thus likely that some phenotypes that are essential in tumour progression will emerge in the tumour population only with prior presence of other different phenotypes. Materials and methods: In this study, we use evolutionary game theory to analyse the interactions between three different tumour cell phenotypes defined by autonomous growth, anaerobic glycolysis, and cancer cell invasion. The model allows us to understand certain specific aspects of glioma progression such as the emergence of diffuse tumour cell invasion in low‐grade tumours. Results: We have found that the invasive phenotype is more likely to evolve after appearance of the glycolytic phenotype which would explain the ubiquitous presence of invasive growth in malignant tumours. Conclusions: The result suggests that therapies, which increase the fitness cost of switching to anaerobic glycolysis, might decrease probability of the emergence of more invasive phenotypes.
INTRODUCTION
Cancer cells display characteristic traits acquired in a stepwise manner during carcinogenesis. Some of these are autonomous cell population growth, induction of neo‐angiogenesis, and invasion and metastasis (Hanahan & Weinberg 2000). Further characteristics of cancer cells include altered glucose metabolism, tumour cells commonly switch to glycolysis for energy production (Warburg 1930). FDG‐PET (fiuoro‐D‐deoxyglucose positron emission tomography) and MRS (magnetic resonance spectroscopy) imaging allow for in vivo analysis of glucose metabolism and lactate concentrations. Clinical use of PET imaging and MRS has largely confirmed the ubiquitous switch to glycolysis in many cancers including malignant gliomas (Herholz et al. 1992; Padma et al. 2003; McKnight 2004). Glycolysis is less efficient than the citrate cycle in terms of energy, but allows cell survival in hypoxic environments, that is, when oxygen demands by the growing number of tumour cells are no longer met by the tumour's vascular supply. In addition, cells with glycolytic metabolism can change pH of the local microenvironment to their advantage. Cells with non‐glycolytic metabolism will often undergo apoptosis or necrosis after prolonged exposition to acidic conditions. It has been suggested that tumour cells with glycolytic metabolism evolve because of this fitness advantage over other cells (Gatenby et al. 2006).
The prevalence of glycolysis in invasive tumours suggests that its presence could help the emergence of invasive phenotypes. Mathematical tools such as game theory (GT) can be used to study how interplay between different phenotypes affects the outcome of tumour progression. GT models, first formalized by von Neumann & Morgernstern (1953), have a comparatively long tradition in the social and economic sciences. It has also been successfully applied to the study of evolutionary dynamics in nature (Nowak 2006) and, more recently, GT has emerged as a tool in theoretical medicine. GT studies interactions between entities called ‘players’ where the fitness of each player depends on what the player decides to do (its strategy) as well as what the other players do; players obtain a fitness payoff as a result of these interactions. Maynard Smith (1982) helped to establish evolutionary GT (EGT) as a tool for the study of equilibria in ecosystems. In EGT, strategies of the players (i.e. their phenotypes), are not the result of rational analysis but rather due to behaviour shaped through natural selection.
Here, we introduce an EGT model in which we explore the hypothesis put forward by Gatenby et al. (2006) that glycolysis precedes tumour invasion and we place results in the context of gliomas, tumours of the central nervous system derived from glial cells. We have previously used a cellular automaton model to describe growth of gliomas (Hatzikirou et al. 2005; Hatzikirou & Deutsch 2007). The model did not include any provision for the various glioma malignancy grades and malignant progression; in contrast, the present study specifically focuses on these latter aspects of cancer biology. We start at a stage in tumorigenesis with cells that no longer require external growth factors and ignore external growth inhibitory signals (autonomous growth). We postulate that additional genetic mutations will either result in an invasive phenotype or a switch to glycolytic metabolism. The results show that a motile/invasive phenotype is more likely to evolve with the presence of glycolytic cells.
MATERIALS AND METHODS
We have assumed that all tumour cells are initially characterized by autonomous growth (AG phenotype). Cells could switch to anaerobic glycolysis for energy production (GLY phenotype), or become increasingly motile and invasive (INV phenotype). We make no assumptions concerning what genetic changes would be necessary for mutations to occur. The fitness of a cell with a given phenotype depends on its interaction with other cells that may have a different phenotype. Interactions between phenotypes are described in Table 1. Base payoff, 1, represents maximum fitness for a tumour cell under ideal circumstances in which it has to share nutrients and space with no other cell. The table is parametrized using variables: k, n and c. Variable k represents fitness cost incurred by the switch to less efficient glycolytic metabolism (GLY), n represents both, loss of fitness for a non‐glycolytic cell to live in an acid environment as well as fitness gain for a glycolytic cell that increases acidity of the microenvironment. Finally, c is the cost in motility incurred by cells with the INV phenotype resulting from the reduced proliferation rate of motile/invasive cells (Giese et al. 1996).
Table 1.
Payoff table that represents the change in fitness of a tumour cell with a given phenotype interacting with another cell
| AG | INV | GLY | |||
|---|---|---|---|---|---|
| AG |
|
1– c |
|
||
| INV | 1 |
|
1 – k | ||
| GLY |
|
1 – c |
|
The three phenotypes in the game are autonomous growth (AG), invasive (INV) and glycolytic (GLY). The base payoff in a given interaction is equal to 1 and the cost of moving to another location with respect to the base payoff is c. The fitness cost of acidity is n and k is the fitness cost of having a less efficient glycolytic metabolism. The table should be read following the columns, and thus the fitness change for an invasive cell interacting with an autonomous growth would be 1 – c.
Table 1 needs to be read following the columns. For instance, fitness payoff for an AG cell interacting with another AG, E(AG, AG), is 1/2 because AG cells have to share available resources. When an AG cell meets an INV cell then the INV cell will leave for another location, obtaining the base payoff minus the cost of motility 1 – c, whereas the AG cell gets access to all the available resources and thus the base payoff in full. When an AG cell meets a GLY cell, they both have to share the available resources. Furthermore, the AG cell loses fitness due to acidification of the environment. GLY cells never get the full base payoff because their metabolism is less efficient.
RESULTS
We have adopted a standard EGT analysis to study equilibria between the different phenotypes in two scenarios: (1) mutation(s) leading to invasive cells capable of motility in a tumour composed of autonomous growth cells (AG, INV) and (2) a tumour containing autonomous growth, motile and glycolytic cells (AG, INV, GLY).
Scenario 1: AG and INV
This scenario studies the situation in which a mutation can confer motility/invasiveness on tumour cells that already are capable of autonomous growth, that is, the tumour is populated by AG cells, which can acquire the INV phenotype.
A population of AG cells is immune to invasion from a mutant INV phenotype if the fitness of two AG cells interacting together is greater than that of the mutant INV cell's interaction with an AG cell. Alternatively, if the fitness of an AG cell playing with a second one is the same as that of an INV cell playing an AG cell, then the AG cell might still be immune to invasion if the payoff of an AG cell playing an INV cell is greater than that of an INV cell playing another INV cell. The payoff table shows that as long as motility represents a non‐negligible cost, then the only thing required of a population of AG cells to be immune to invasion by an INV phenotype is that the fitness payoff of two AG cells is greater than or equal to the fitness payoff for an INV cell interacting with an AG cell. That is, the AG phenotype is immune to invasion only if c ≥ 1/2. In many cases, a polymorphism of INV and AG phenotypes will result. In these cases, the fitness of the INV phenotype should be the same as that of the AG phenotype. If p is the proportion of invasive (INV) cells in the tumour, AG refers to the autonomous growth phenotype and W(P) to the fitness of phenotype P:
Scenario 2: AG, GLY and INV
Here, we study a tumour in which all three phenotypes coexist. Assuming that p refers to the proportion of INV cells and p′ to the proportion of AG cells, the fitness of each of the phenotypes can be calculated as:
In equilibrium, fitness of the three phenotypes is the same. The values of p and p′ can be deduced from these equations. From these equivalencies:
Figure 1 shows that the proportion of INV cells in the tumour, p, changes when we alter values of the cost of having the GLY phenotype (k) and the cost of a normal cell, living next to a GLY cell (n). For low values of k and high values of n the INV cells displace other phenotypes from the tumour. This means that conditions favouring anaerobic glycolysis also favour tumour invasion. One possible explanation for this phenomenon is that presence of glycolytic cells that increase the acidity of the environment will indirectly and comparatively reduce the costs of motility.
Figure 1.
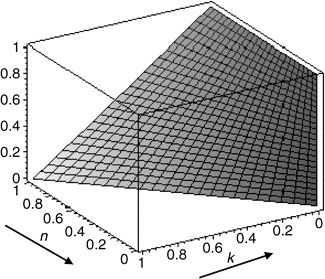
Proportion of invasive cells in a tumour with three phenotypes (autonomous growth, invasive and glycolytic). k is the cost in terms of fitness for adopting glycolytic metabolism, whereas n is the fitness cost of a normal cell when staying with a glycolytic cell.
Figure 2 shows how proportion of AG cells in the tumour population changes for variables k and n under four different scenarios for the cost of motility c. Proportion of AG cells increases as the cost of having a glycolytic metabolism increases, or as costs of living in an acid environment decreases, thus reducing the proportion of both INV and GLY cells in the tumour. Interestingly, as the cost of motility increases the proportion of AG cells shrinks: higher costs of motility lead to more glycolytic cells that reduce the fitness of autonomous growth cells.
Figure 2.
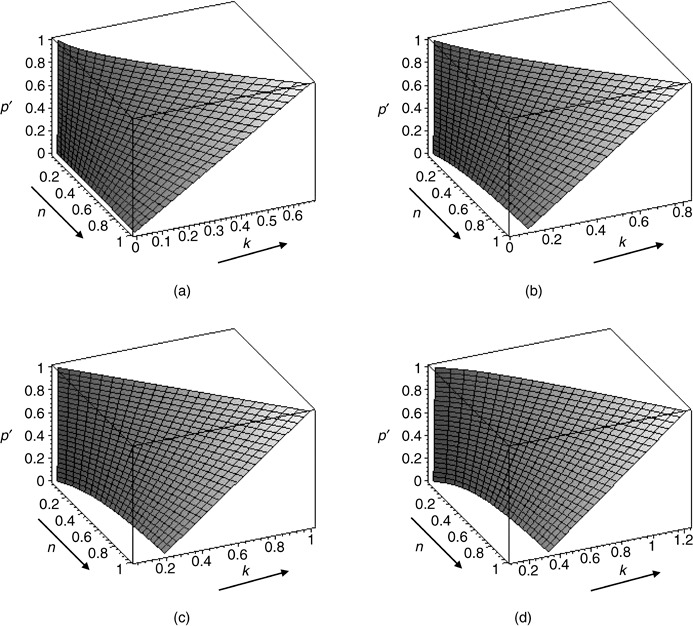
Figures imply that a higher cost of motility leads towards tumours with a small proportion of AG cells. The figures (a), (b), (c) and (d) show the proportion of autonomous growth cells in a tumour in which the three phenotypes (autonomous growth, invasive and glycolitic) are possible. Each scenario is characterized by a different value of c, the cost of motility: (a) c = 0; (b) c = 1/4; (c) c = 1/2; (d) c = 3/4.
DISCUSSION
Mathematical and computational models have been used to study tumour morphology and growth (Moreira & Deutsch 2002; Anderson et al. 2006; Sanga et al. 2007) and therapy (Abbott & Michor 2006). EGT has long been used to study the evolution of species but has only recently been applied to the analysis of evolutionary aspects of cancer. Tomlinson and Bodmer (Tomlinson 1997; , Tomlinson & Bodmer 1997) were the first to apply GT in cancer research. Their models study several cancer‐related problems, such as angiogenesis and evasion of apoptosis. Subsequent research by Bach and colleagues extended this idea to interactions between three players (Bach et al. 2001) as well as the effect of spatial dynamics (Bach et al. 2003) on their angiogenesis game. Gatenby & Vincent (2003) adopted a game theory approach, influenced by population dynamics, to study tumour–host interactions in colorectal carcinogenesis. More recently, Mansury et al. (2006) have employed a non‐evolutionary GT approach to study how interactions between proliferative and migratory phenotypes in a tumour affect a number of features of tumour growth dynamics.
To the best of our knowledge, ours is the first attempt to use evolutionary game theory to analyse the interplay of different tumour cell phenotypes, with respect to tumour invasion; our model makes certain predictions that can be compared to clinical observations. Virtually, all gliomas, including low‐grade tumours, display some degree of invasion. Tumour cell in filtration of several cerebral lobes is occasionally seen and our model provides a simple explanation for this observation, and an apparent difference from many other cancers. The model predicts that motile/invasive (INV) and autonomously growing cells (AG) will co‐exist as long as the fitness costs of motility are not too high when compared to the fitness increase obtained by moving to a new location. Glioma invasion in the brain is facilitated by the presence of white matter tracts that lower the costs of motility (Giese & Westphal 1996). Relatively, higher costs of motility are incurred by epithelial cancer cells, which have to transfer across a formal barrier (the basal membrane separating the epithelial layer from surrounding tissues), when compared to glioma cells. Furthermore, an invasive glioma cell will arrive in a surrounding very similar to the location from which it originated, that is, in brain tissue. In contrast, an epithelial cancer cell leaves the context of other epithelial cells in order to grow among soft tissue cells and intracellular matrix molecules which may mean further fitness costs.
Malignant progression is common and more than 50% of low‐grade tumours eventually become malignant (Schmidt et al. 2003). In the model, emergence of the glycolytic phenotype is the correlate of malignant progression. FDG‐PET and SRS imaging has shown a close correlation between histological malignancy grades and anaerobic glycolysis in gliomas (Herholz et al. 1992; Padma et al. 2003; McKnight 2004).
The results indicate that in a tumour populated by glycolytic cells (which in this model correlate with malignancy), invasive cells have a better chance of success (Fig. 1). Circumstances that favour the glycolytic phenotype also promote the emergence of the invasive phenotype. The proportion of invasive cells does not depend on the costs of motility, if all three phenotypes (AG, GLY, INV) are analysed in combination. This may reflect one of the fundamental tenets of malignant tumour progression. Malignant (glycolytic) tumour cells will also invariably, regardless of the specifics of the costs incurred, display a highly invasive phenotype. Invasion is a pre‐requisite for metastasis and, in the vast majority of cases, characterizes malignant tumours. Gatenby and co‐workers have suggested a direct link between the glycolytic phenotype and tumour invasion and have provided experimental evidence to support this hypothesis (Gatenby et al. 2006).
Invasive growth is not as closely related to malignancy in gliomas. As pointed out above, in the absence of glycolytic cells, the costs of motility do influence the emergence of the invasive phenotype, possibly reflecting the very specific environment of the brain. Hence, the model provides an explanation for the frequently invasive growth of slowly growing (benign AG) low‐grade gliomas. Invasive growth is usually not seen in most other cancers with the AG phenotype. Malignant glial tumours (glial tumours with a GLY phenotype) infiltrate the surrounding brain parenchyma, as predicted by the model. Importantly, glycolysis has been shown to support astrocytoma invasion in a tissue culture model (Beckner et al. 2005).
A mathematical model is necessarily a simplification of the complex situation found in a real tumour. Nevertheless, mathematical models provide theoretical frameworks in which to study tumour progression qualitatively and quantitatively (Gatenby & Maini 2003; Anderson et al. 2006). Probably, the most significant omission in our model is the lack of spatial consideration. Our previous research (Basanta et al. 2008) shows that game‐theoretical models of tumour invasion can have a similar predictive power as spatial ones based on cellular automata. Another possible future enhancement of the model would include changes in the way in which the fitness payoffs are considered. At the moment, the costs of motility, acidity and glycolysis are considered to be constant. A more realistic approach would be to express these costs in terms of functions that could cover facts such as the increase in the costs of motility as the tumour grows leaving less space in which to move. Such enhancement would undoubtedly enrich the model but also make the analysis more difficult. Further research may also include the use of a larger number of phenotypes in the model, which are defined by molecular genetic aberrations (or sets thereof), in order to allow for predictions of other important milestones in carcinogenesis.
Our model explains in mathematical terms‐specific aspects of glioma growth, which is invasion already present in slowly growing tumours, and puts them in a more general context. In addition, mathematical modelling of tumour progression may enhance our understanding of cancer and provide new insights for us. Our findings suggest that strategies, such as improving tissue oxygenation, which increase the relative fitness costs of switching to anaerobic glycolysis, may prevent invasion and metastasis.
ACKNOWLEDGEMENTS
We would like to acknowledge the help from Michael Kücken from Technische Universität Dresden. The research was supported in part by funds from the EU Marie Curie Network ‘Modelling, Mathematical Methods and Computer Simulation of Tumour Growth and Therapy’ (EU‐RTD IST‐2001–38923). We also acknowledge the support provided by the systems biology network HepatoSys of the German Ministry for Education and Research through grant 0313082C.
The authors declare no conflicts of interest.
REFERENCES
- Abbott LH, Michor F (2006) Mathematical models of targeted cancer therapy. Br. J. Cancer 95, 1136–1141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson A, Weaver A, Cummings P, Quaranta V (2006) Tumor morphology and phenotypic evolution driven by selective pressure from the microenvironment. Cell 1, 905–915. [DOI] [PubMed] [Google Scholar]
- Bach LA, Bentzen SM, Alsner J, Christiansen FB (2001) An evolutionary game model of tumour cell interactions: possible relevance to gene therapy. Eur. J. Cancer 37, 2116–2120. [DOI] [PubMed] [Google Scholar]
- Bach LA, Sumpter DJT, Alsner J, Loeschke V (2003) Spatial evolutionary games of interaction among generic cancer cells. J. Theor. Med. 5, 47–58. [Google Scholar]
- Basanta D, Hatzikirou H, Deutsch A (2008) Studying the emergence of invasiveness in tumours using game theory. Eur. Phys. J. B. 3, 393–397. [Google Scholar]
- Beckner M, Gobbel G, Abounader R, Burovic F, Agostino N, Laterra J, Pollack I (2005) Glycolytic glioma cells with active glycogen synthase are sensitive to PTEN and inhibitors of PI3K and gluconeogenesis. Lab. Invest. 85, 1457–1470. [DOI] [PubMed] [Google Scholar]
- Gatenby R, Gawlinski E, Gmitro A, Kaylor B, Gillies R (2006) Acid‐mediated tumor invasion: a multidisciplinary study. Cancer Res. 66, 5216–5223. [DOI] [PubMed] [Google Scholar]
- Gatenby R, Maini P (2003) Cancer summed up. Nature 421, 321. [DOI] [PubMed] [Google Scholar]
- Gatenby R, Vincent T (2003) An evolutionary model of carcinogenesis. Cancer Res. 63, 6212–6220. [PubMed] [Google Scholar]
- Giese A, Loo M, Tran N, Haskett SW, Berens ME (1996) Dichotomy of astrocytoma migration and proliferation. Int. J. Cancer 67, 275–282. [DOI] [PubMed] [Google Scholar]
- Giese A, Westphal M (1996) Glioma invasion in the central nervous system. Neurosurgery 39, 235–250. [DOI] [PubMed] [Google Scholar]
- Hanahan D, Weinberg R (2000) The hallmarks of cancer. Cell 100, 57–70. [DOI] [PubMed] [Google Scholar]
- Hatzikirou H, Deutsch A (2007) Cellular automata as microscopic models of cell migration in heterogeneous environments. Curr. Top. Dev. Biol. 81, 401–434. [DOI] [PubMed] [Google Scholar]
- Hatzikirou H, Deutsch A, Schaller C, Simon M, Swanson K (2005) Mathematical modelling of glioblastoma development. Math. Mod. Meth. Appl. Sci. 15, 1779–1794. [Google Scholar]
- Herholz K, Heindel W, Luvten P, Den Hollander J, Pietrzyk U, Voges J, Kugel H, Friedmann G, Heiss W (1992) In vivo imaging of glucose consumption and lactate concentration in human gliomas. Ann. Neurol. 31, 319–237. [DOI] [PubMed] [Google Scholar]
- Mansury Y, Diggory M, Deisboeck TS (2006) Evolutionary game theory in an agent based brain tumor model: exploring the genoype phenotype link. J. Theor. Biol. 238, 146–156. [DOI] [PubMed] [Google Scholar]
- Maynard Smith J (1982) Evolution and the Theory of Games. Cambridge, UK: Cambridge University Press. [Google Scholar]
- McKnight T (2004) Proton magnetic resonance spectroscopic evaluation of brain tumor metabolism. Semin. Oncol. 31, 605–617. [DOI] [PubMed] [Google Scholar]
- Moreira J, Deutsch A (2002) Cellular automaton models of tumor development: a critical review. Adv. Compl. Syst. 2–3, 247–267. [Google Scholar]
- Von Neumann J, Morgernstern O (1953) Theory of Games and Economic Behaviour. Princeton, NJ: Princeton University Press. [Google Scholar]
- Nowak M (2006). Evolutionary Dynamics: Exploring the Equations of Life. Boston, MA: Belknap. [Google Scholar]
- Padma M, Said S, Jacobs M, Hwang D, Dunigan K, Satter M, Christian B, Ruppert J, Bernstein T, Kraus G, Mantil J (2003) Prediction of pathology and survival by FDG PET in gliomas. J. Neurooncol. 64, 227–237. [DOI] [PubMed] [Google Scholar]
- Sanga S, Frieboes HB, Zheng X, Gatenby R, Bearer EL, Cristini V (2007) Predictive oncology: a review of multidisciplinary, multi‐scale in silico modeling linking phenotype, morphology and growth. Neuroimage 37 (Suppl. 1), S120–S134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmidt M, Berger M, Lamborn K, Aldape K, McDermott M, Prados M, Chang S (2003) Repeated operations for infiltrative low‐grade gliomas without intervening therapy. J. Neurosurg. 98, 1165–1169. [DOI] [PubMed] [Google Scholar]
- Tomlinson IPM (1997) Game theory models of interactions between tumour cells. Eur. J. Cancer 33, 1495–1500. [DOI] [PubMed] [Google Scholar]
- Tomlinson IPM, Bodmer WF (1997) Modelling the consequences of interactions between tumour cells. Br. J. Cancer 75, 157–160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warburg O (1930) The Metabolism of Tumors (English translation by F. Dickens). London: Constable. [Google Scholar]


