Experimental analysis and modelling of in vitro proliferation of mesenchymal stem cells

Abstract

Objectives:  Stem cell therapies based on differentiation of adult or embryonic stem cells into specialized ones appear to be effective for treating several human diseases. This work addresses the mathematical simulation of proliferation kinetics of stem cells.

Materials and methods:  Sheep bone marrow mesenchymal stem cells (phenotype characterized by flow cytometry analysis) seeded at different initial concentrations in Petri dishes were expanded to confluence. Sigmoid temporal profiles of total counts obtained through classic haemocytometry were quantitatively interpreted by both a phenomenological logistic equation and a novel model based on a one‐dimensional, single‐staged population balance approach capable of taking into account contact inhibition at confluence. The models’ parameters were determined by comparison with experimental data on population expansion starting from single seeding concentration. Reliability of the models was tested by predicting cell proliferation carried out starting from different seeding concentrations.

Results and discussion:  It was found that the proposed population balance modelling approach was successful in predicting the experimental data over the whole range of initial cell numbers investigated, while prediction capability of phenomenological logistic equation was more limited.

Introduction

Transplantation procedures represent a suitable biological/surgical technique when restoration of damaged native tissues and organs is impossible (1). In this framework, current research is focused on the use of stem cells, which once having proliferated in vitro, may be implanted to regenerate injured areas in vivo, as fast as possible.

Specifically, autologous stem cells may be obtained from tissues (skin, muscle, retina, neural, liver, intestine, mammary glands and others) of individual patients so that re‐implantation of in vitro cultured cells/tissues would avoid rejection problems. In particular, mesenchymal stem cells are multipotent stem cells, residing mainly in bone marrow, which can be harvested from organs and cord blood, grown in culture as a homogeneous adherent population of fibroblast‐like cells, and induced to differentiate into multiple cell types (cf. 2, 3, 4, 5, 6, 7, 8, 9, 10).

While it has been reported that systemic administration of autologous or allogeneic mesenchymal stem cells in healthy animals leads to their migration and engraftment in a plethora of non‐haematopoietic tissues (11), injury models have shown that mesenchymal stem cells migrate specifically to damaged sites and undergo tissue‐specific differentiation patterns (12, 13). Mesenchymal stem cells’ multilineage differentiation ability, together with their relatively easy isolation from bone marrow and extensive capacity for in vitro expansion, represents a powerful tool in the field of tissue engineering, as well as gene therapy, for a variety of congenital and acquired diseases (12). However, there is only limited information on the optimization of culture conditions required for their production. To properly stimulate these cells to expand to a sufficient amount for transplantation, kinetics of their proliferation during in vitro culture is needed. This information is particularly useful to design specific bioreactors where maximum yield of stem cell production during minimum culture time is achieved by optimizing culture conditions, such as medium perfusion velocity, nutrient and oxygen supply, and removal of wastes and catabolites, as well as by identifying optimal doses of differentiating factors for stimulating generation of specialized cell populations necessary for repairing damaged tissues.

Evaluation of intrinsic kinetics of cell proliferation may be performed using a static culture system (that is, in Petri dishes). Interpretation and analysis of corresponding experiments, which provide a clear contribution to understanding the complex biological mechanisms involved in stem cell expansion/differentiation, may be achieved by means of suitable mathematical models. Basically, two modelling approaches have been adopted so far in the technical literature. The first is based on formulation of phenomenological equations (like exponential growth, logistic and Gompertzian sigmoidal curves), which aim to quantitatively correlate lag, log and stationary phases naturally present in any growing population inside a batch, discontinuous environment like expansion of a stem cell culture system in Petri dishes. The second, more sophisticated modelling approach, known as population balance equations (PBE), is based on experimental evidence that the temporal behaviour of distribution of some intrinsic property (such as age, size, mass, DNA content, and more) of a cell population is able to describe kinetics of the system under investigation in a quantitative fashion.

The first approach basically consists of dividing a cell population into different and distinguishable compartments (such as proliferative, quiescent, mitotic, dead, and differentiating cells), which are proposed in order to give a sound, physical basis for adoption of the classic sigmoid phenomenological equations, which then result in being successful for a rough mathematical description of proliferation kinetics (cf. 14, 15, 16).

As for the PBE approach, age –versus size‐based equations are typically used (cf. 17, 18, 19, 20, 21, 22, 23). Moreover, unstructured versus structured PBE models have been also proposed (cf. 24). Finally, multistaged versions of PBEs may be found in the literature for tracking cells belonging to different phases of the cell cycle (cf. 23, 25, 26). As for the case of structured PBE, the multistaged approach naturally increases model complexity and introduces additional adjustable parameters, so that numerical solution as well as validation through comparison with suitable experimental data makes their adoption problematic. Despite this, complex combinations between these different PBE versions may also be found in, for example, Liu et al. (28), where a structured and multistaged PBE modelling analysis was performed.

A selection of references in recent literature on proliferating cultures, where comparisons between experimental data and model results have been given, is reported in Table 1. The PBE modelling approach has not been adopted for quantifying data from stem cell culture experiments. To the best of our knowledge, experimental data of proliferation kinetics of stem cells lineages are compared with model results where exponential growth is assumed.

Table 1.

 Literature references on proliferating cultures where comparison between experimental data and model results is presented

Mathematical modelling approach	Model system	Comparison with experimental data	Reference
PBE (age, multistaged)	CHO and mouse–mouse hybridoma cell lines	Total cell count temporal profile	Abu‐Absi and Srienc (20)
Exponential growth with cell loss	Muscle‐derived stem cells	Total cell count temporal profile (fitting)	Deasy et al. (14)
PBE (DNA content, multistaged)	Human cancer cell line	Distributions of DNA content (fitting)	Basse et al. (26)
PBE (mass, structured, multistaged)	Hybridoma and animal cell lines	Total cell count, substrates, and products temporal profiles (fitting)	Sidoli et al. (24)
PBE (mass)	Human cancer cell lines	Total cell count, tumour radius and mass temporal profiles (fitting)	Busini et al. (27)
PBE (volume, structured, multistaged)	Myeloma cell line	Total cell count, substrates, products, and cell phase fractions temporal profiles (fitting) Distributions of DNA content (qualitative comparison)	Liu et al. (28)
PBE (age, multistaged)	Human leukaemia cells	Cell phase fractions temporal profiles (fitting)	Sherer et al. (23)
PBE (protein content, multistaged)	Yeast	Distributions of protein content (qualitative comparison)	Hatzis and Porro (29) Cipollina et al. (21)

PBE, Population Balance Equation.

In this work, our attention was focused on the kinetic study of ovine mesenchymal stem cell proliferation in static systems. Phenotypic characterization by flow cytometry analysis was performed to ensure that differentiation during long‐term culture did not take place. In particular, the ovine model has been chosen as the cell system to investigate, since it is more appropriately similar to the human model in terms of size and DNA than the classical murine model. Expansion kinetics were experimentally followed through classical haemocytometry for temporal evolution of total counts at different levels of seeding concentration. Proliferation kinetics were interpreted by means of a simple, generalized logistic equation as well as through a novel mass‐based PBE model capable to simulate of stem cell proliferation up to confluence in Petri dishes.

The PBE model adopted is derived from that developed by Mantzaris et al. (19), which has been modified in order to take into account cell growth limited by contact inhibition as the population increases, under the assumption of an excess of nutrients and oxygen supply. Model solutions were fitted to the temporal evolution of experimental total cell counts to determine values of model parameters and this was followed by prediction runs in order to test model reliability.

Materials and methods

Isolation of ovine bone marrow‐derived stem cells

Fifteen millilitres of bone marrow aspirate, taken from the iliac crest of sheep, were diluted with equal volume of phosphate‐buffered saline (PBS, Sigma, St. Louis, MO, USA). This solution was layered on top of Hystopaque 1077 (Sigma), and centrifuged at 1500 g for 30 min to obtain the mononuclear cell fraction. The interface between the hystopaque and plasma below was carefully recovered using a pipette and placed in a separate centrifuge tube, then diluted 1 : 1 with PBS and centrifuged at 400 g for 10 min. Supernatant was discarded, and possible residual red blood cells were lysed using a commercial lysing solution (BD Pharm lyse, Milano, Italy). After centrifugation at 200 g for 10 min, the pellet was resuspended in complete culture medium constituted by alpha minimal essential medium (Sigma), 20% foetal bovine serum (Sigma), 1% penicillin‐streptomycin solution (Sigma), and 2 mm l‐glutamine. Nucleate cells were counted using a haemocytometer and plated at a density of 0.6–1 × 10⁶ cells/cm² in uncoated Petri dishes.

After overnight incubation at 37 °C in a humidified atmosphere containing 5% carbon dioxide, non‐adherent cells were removed and fresh medium was added. By removing the remaining non‐adherent cells through complete exchange of the culture medium every 3 days, cultures were maintained for 2 weeks (that is, up to 80–90% confluence). Then, cells were harvested by the use of 0.1% trypsin and 0.04% EDTA for 8 min at 37 °C and replated at a density of 1.5 × 10⁴ cells/cm². Medium was changed every 2 days, and cells from passage 6 were used for the proliferation studies.

Count protocol for proliferation studies

Ovine bone marrow‐derived stem cells were plated in 8‐cm² Petri dishes (Corning, Corning, NY, USA) at a density of 1.25 × 10³, 2.875 × 10³ and 4.6 × 10³ cells/cm², corresponding to 1.0 × 10⁴, 2.3 × 10⁴, and 3.68 × 10⁴ total cells, respectively. Cells from three plates for each culture density were harvested day‐by‐day with the use of 218 µl of 0.1% trypsin and 0.04% EDTA for 8 min at 37 °C. Action of trypsin was stopped with 436 µl of complete medium, and Petri dishes were washed with 436 µl of PBS. Cells were counted using a haemocytometer in total volume of 1.09 ml. Experiments were repeated at least three times.

Phenotypic characterization of stem cell culture

Cells harvested by treatment with 0.1% trypsin and 0.04% EDTA were fixed in 4% paraformaldehyde for 20 min, washed with PBS, then resuspended in PBS containing 0.1% bovine serum albumin. Cell aliquots (10⁵/100 µl) were incubated for 20 min on ice with monoclonal antibody followed by two washes in PBS containing 0.1% bovine serum albumin and when necessary, a further incubation with conjugated secondary antibody for 20 min at room temperature was performed. Fluorescein isothiocyanate‐conjugated monoclonal antibodies against hCD34, hCD44 (Immunotech, Marseille, France), unconjugated monoclonal antibodies specific for mammalian vimentin (BD Pharmigen), hCD105 (DakoCytomation, Glostrup, Denmark) and hCD117 (Biosource, Nivelles, Belgium), and secondary fluorescein isothiocyanate‐conjugated sheep F(ab′)2 fragment anti‐mouse immunoglobulin G antibody (Chemicon International, Milano, Italy) were used. Flow cytometry was performed on a fluorescence‐activated cell sorter (BD FACSCalibur, BD Biosciences, Franklin Lakes, NJ, USA). CellQuest Pro was the software used for flow cytometry data analysis (BD Bioscience, CA, USA).

Mathematical modelling

Mathematical modelling represents a useful tool for interpreting and analysing experimental data obtained from proliferation kinetics of a stem cell system; thus, this helps us to find optimal operative conditions and, simultaneously, contributes to the understanding of biological mechanisms and stem cell behaviour. Ultimately, the goal is the reliable and safe design/scale‐up of bioreactors in static as well dynamic regimes, which permits controllable and reproducible expansion of stem cell cultures under optimized operating conditions. To this aim, simple models are particularly attractive. In the following, two models are applied and compared for quantitative description of proliferation kinetics of ovine mesenchymal stem cells, up to confluence.

Generalized logistic

The generalized logistic equation is a phenomenological model proposed by Tsoularis and Wallace (30) and is defined by the following:

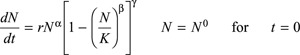(1)

where α, β, γ, K and r are positive real numbers that represent adjustable parameters to be determined by comparison with the temporal evolution of total number of cells N. Tsoularis and Wallace (30) demonstrated that several other forms of phenomenological growth equations may be derived from the generalized logistic (for example, exponential growth, an autocatalytic reaction, is obtained with α = 1 and β = γ = 0). While exponential growth is able to simulate the initial growth, not being adequate for describing confluence condition, the generalized logistic represents a growth curve based on the classic Verhulst equation, which, dating back to 1838, was the first one where the parameter K, the ‘carrying capacity’ for limiting exponential growth to a saturation upper boundary, is taken into account, thus enabling simulation of typical sigmoidal behaviour (cf. 16).

PBE approach

The mathematical model proposed in the present work describes cell growth and proliferation (expansion by mitosis) during culture in batch systems by means of the following PBE:

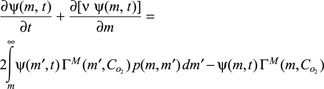(2)

along with the initial and boundary conditions

(3)

(4)

Here ψ(m, t) represents the number concentration density distribution of cell mass m at time t, which is assumed to be spatially uniform. Other symbols’ significance are reported in the ‘Abbreviations’ section, below. In eqn (2), the two terms of the left‐hand‐side represent accumulation and the cell growth term, respectively. On the other hand, first term of the right‐hand‐side of eqn (2) represents birth one (two daughter cells obtained by division of a larger mother cell), while the second term represents corresponding removal of the mother cell due to mitosis. Cell death by apoptosis is neglected in this equation, since it may be relevant only in the case of apoptotic/necrotic cells. While in eqn (3)ψ⁰ (m) represents initial distribution of cells, the physical meaning of the boundary condition for the PBE model, given by eqn (4) is that there exist no cells of zero mass at any time (cf. 19).

The adopted model is a single‐variable, unstructured, single‐staged PBE. The distributed property is the cell mass, although several examples of age‐structured PBE models can be found in the literature. Since model validation through comparison with experimental data is difficult when age is selected as a characteristic variable, because of the well‐known inability to easily measure age distribution within a population of cells (cf. 18, 19, 23), the choice of adopting cell mass as internal coordinate seems to be fully justified.

Unstructured and single‐staged characteristics of the adopted PBE approach are aimed to minimize model complexity, which reflects lowering the number of adjustable parameters. Indeed, without distinguishing among cells belonging to different cell cycle phases and by neglecting complex intra‐ and extracellular biochemistry, the proposed model permits one to track the essential features of the proliferation (cell number increases) taking place, and to simulate confluence limitation due to contact inhibition when a saturation level is reached within the Petri dish.

As is well known, differently from age‐based PBE, the adopted mass‐based PBE (2) needs to specify the three generally unknown functionalities; namely, cell mass growth (ν), cell division rate (Γ^M), and partitioning distribution of mother cell into daughters (p). The last expresses conditional cell mass density function for a daughter cell given the size of a mother cell at mitosis. In particular, following the approach described in detail in our previous works (cf. 31, 32, 33), unequal partitioning continuous distribution functionality, first proposed by Hatzis et al. (25), is taken into account:

(5)

where β(q, q) is the symmetrical beta function:

(6)

and Γ(q), is the gamma function:

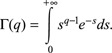(7)

Depending on specific value of parameter q, this partitioning function depicts, as most probable, the division of mother cell mass (m′) into two, equal daughter cells with mass m (equal partitioning, m = m′/2). In particular, equal partitioning is obtained when a very high value is assigned to parameter q, while, at relatively smaller values, a uniform probability is assigned to any sized couple of daughters. In the case of equal partitioning, the function p(m, m′) becomes the Dirac delta function δ[m – (m′/2)] centred at m = m′/2 (cf. 25).

According to Hatzis et al. (25), if distribution of mitotic cells is known, cell division rate Γ^M may be determined (and vice versa) by means of the following relationship derived from Koch and Schaecter (34):

(8)

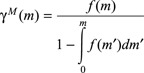(9)

where cell mass is used to predict cell division. In particular, if it is assumed that cell division occurs only when the cell reaches a critical mass, the probability density function of a cell with mass m to divide, f(m), may be expressed as a Dirac delta function (deterministic division). On the other hand, by relaxing this model constraint in order to account for heterogeneity in cell cycle distribution (statistical division), the function f(m) may be represented by normal distribution of dividing mass around a mean µ with variance σ² (cf. 17, 19):

(10)

According to eqn (8), mitotic rate depends on growth rate, so that if ν increases, cell division rate is also augmented. This is perfectly consistent with adoption of mass‐based distribution of cells at mitosis (f(m)), since by increasing the growth of cell mass, the deterministic or statistical condition at the critical mass for the occurrence of cell division is reached faster (mitotic rate increases).

Finally, the time rate of change of cell mass, ν, is expressed as reported below:

(11)

where, according to the postulate of von Bertalanffy, the anabolic (positive) term for a single cell is proportional to its surface area (m ^2/3), while the catabolic term (negative) is proportional to cell mass (m) (cf. 31, 35). The limiting supply of oxygen (nutrient) is taken into account by classic Monod kinetics (cf. 17, 28). However, the experimental procedure adopted in this work guarantees constant concentration of nutrients supplied to the expanding culture, so that relevant oxygen material balance is not taken into account. Moreover, in order to simulate contact inhibition that progressively slows down culture expansion when reaching confluence in the Petri dish as proliferation progresses, a limiting factor (Φ(t) ≤ 1) appearing in the anabolic term is proposed. As a consequence, according to eqn (8), this limiting factor reduces not only cell mass growth rate but also division rate Γ^M (rate of cell proliferation). Following modelling of adhesion kinetics for anchorage‐dependent cells (cf. 36, 37), the limiting factor is naturally related to available superficial area between cells on the Petri dish surface, assuming that ovine stem cells used in this work tend to distribute themselves as a monolayer. In order to account for this behaviour, a geometric limiting factor may be defined through the following power‐law:

(12)

where ϕ(t) represents the area occupied by cells and interstices (increasing with time as proliferation progresses), ϕ_a available area (corresponding to the Petri dish area), and α_P adjustable parameter. Accordingly, area occupied by cells and their interstices is roughly calculated as the bidimensional projection of a monolayer culture of spherical cells as follows:

(13)

where factor 4/π is the ratio between the surfaces of a square (cell and interstices) and the inscribed circle (the cell) within it, while V is culture volume, and d_c is cell mass density. Equation (13) could be easily modified to account for cell adhesion, stretching and deformation (cf. 36). However, this is beyond the scope of the present work.

It is worth highlighting the similarity between power‐laws used for geometric limiting factor Φ(t) defined in eqn (12) and saturation term of the generalized logistic (see eqn 1), which contains the ‘carrying capacity’K. However, while in generalized logistic the carrying capacity is merely an adjustable parameter representing the upper boundary of a growing total number (zero‐th moment of a distribution) of proliferating cells, eqn (13) assigns a precise physical meaning to sigmoid growth in a batch system. In particular, it is specified that surface extension of the Petri dish used for culture gives the maximum available surface for monolayer growing cells (and interstices between them), that is a limit for the moment of order 2/3‐th of the mass‐based distribution.

Numerical solution and fitting procedure

Equation (1) is an ordinary differential equation (ODE), which is integrated as an initial value problem by means of standard numerical libraries (Gear method, International Mathematical and Statistical Library).

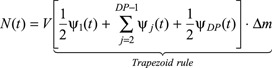
Equation (2) is a partial integro‐differential equation in the variables t and m along with the initial and boundary conditions (3), (4), respectively. In particular, the m domain of integration ranges from zero to +∞, since in general cells of any positive size (mass) may theoretically exist. Of course, this upper limit is not tractable by numerical analysis. Actually, a relatively high but finite value may be safely chosen if cell distribution ψ(m, t) is entirely contained in the resulting m domain. During its dynamic behaviour, in this paper, the upper limit (named m _max) was set equal to 16 ng. The method of lines (cf. 38) is a powerful tool for solving partial differential equations. Once its upper, finite limit is chosen, m domain is divided using a constant step size mesh, and only the partial derivative with respect to m is discretized by backward finite difference. Thus, the partial integro‐differential eqn (2) is transformed into a system of ordinary integro‐differential equations in time. The i‐th ODE for any fixed grid point of the mesh along the m domain is reported in the Appendix for the sake of clarity. In particular, all integrals appearing in model equations are numerically evaluated by means of trapezoid rule. Finally, the system of ODEs reported in the Appendix is integrated in time by means of standard numerical libraries (Gear method, IMSL) as an initial value problem. One hundred grid points (named DP) in the mass domain are typically used for numerically solving the PBE model, since finer grids have been shown not to provide significant improvements in accuracy.

The fitting procedure adopted for determining the unknown, adjustable parameters of the two models (the generalized logistic equation and PBE approach) consisted of minimizing the following cost function F:

(14)

defined as the sum of squared percentage errors between total number of cells experimentally measured N^Exp(t_k) at culture time t_k and the corresponding theoretical value N^Th(t_k), calculated by numerically solving the model equations. Here, NS represents the number of experimental data measurements. Minimization of cost function F is carried out by means of standard numerical libraries (Optimization, IMSL). For the case of PBE model, the total number of cells is calculated as follows:

(15)

while cell distribution, normalized with respect to total number of cells, is determined as (Vψ(m, t))/N(t).

Results and discussion

Phenotypic characterization of sheep bone marrow stem cells is considered first. In particular, flow cytometric analyses performed for seeded cells (at initial time), and for cells harvested after long‐term culture (14 days) are reported in Figs 1a and 1b, respectively. Phenotype of sheep stem cells can be analysed only using a few markers since a restricted number of antibodies is available for this cell lineage. In this paper, the markers tested by Mrugala et al. were used (39). These antibodies are specific for ovine or cross‐reacting human epitopes. Cells at passage 6 were shown to be negative for CD34 both at initial culture time and after 14 days, indicating that cells were not of haematopoietic origin at seeding and maintained this phenotypic characteristic even after long‐term culture. Cells were found to be highly positive for vimentin, and positive for CD105 and CD44, respectively, which are characteristic markers of mesenchymal stem cell lineages, as well as for CD117, a marker for progenitor cells. On the basis of these results, it can be concluded that sheep bone marrow stem cells considered in this work did not differentiate during long‐term culture in Petri dishes, and thus, proliferation with monolayer tendency was the only biological phenomenon taking place during the experimental runs performed.

Figure 1.

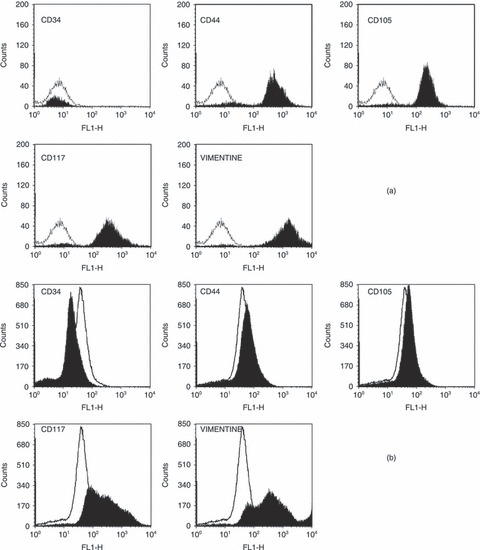
  Phenotypic characteristics of sheep bone marrow stem cells at time equal to day 0  (a) and after 14 days of culture in Petri dishes (b). The white area indicates isotypic control (unstained cells) and black area indicates positive staining.

The selected initial cell distribution is a log‐normal distribution, ψ⁰(m) = (N ⁰/V)/(mσ⁰√2π) exp{–1/2[(ln(m) – ln(µ⁰))/σ⁰]²}, characterized by mean value (µ⁰) and standard deviation (σ⁰). The first is assumed to be equal to 2 ng, which corresponds to spherical cells having density and diameter of 1.14 × 10⁶ ng mm⁻³ (cf. 40) and around 15 µm, respectively. The latter is approximately the average size of cells used in this work, as experimentally evaluated by microscopic analysis. Standard deviation, on the other hand, was chosen equal to 0.4 so that small daughter cells and large mother cells would both be present in the seeded population. However, as will be seen below, chosen values of parameters of the initial distribution affects cell number only at early stages of culture. Normalized initial cell distribution, i.e. (V ψ⁰(m))/N ⁰(t), is plotted in Fig. 2. Such distribution was used in all simulations of the PBE approach. PBE and generalized logistic models have been compared with experimental data obtained by culturing a cell colony for 14 days constituted of 3.68 × 10⁴ cells, as evaluated by counting using microscopy. Model parameters used for simulations of the PBE modelling approach are reported in Table 2. Some are taken from literature. In particular, the adopted value for parameter q of partitioning function corresponds to a relatively more probable division of a mother cell into two equal smaller cells than any other combination of daughters’ sizes. Moreover, mean of normal distribution of mitotic fraction (µ in eqn 10) is assumed equal to around twice the value of the mode (µ⁰) of initial distribution shown in Fig. 2. This seems a reasonable choice (cf. 19). Indeed, since no synchronization by either physical or biochemical means has been performed on the cell population, mode of the initial distribution should correspond to mean size of the daughters (which are typically many more than any other cell belonging to S or G₂/M cell cycle phases). Value assigned to variance of normal distribution in the mitotic fraction (i.e. σ in eqn 10) is chosen so that its ratio with the mean (µ) belongs to the typical range [0.2 ÷ –0.3] found in the literature (cf. 18, 19, 24).

Figure 2.

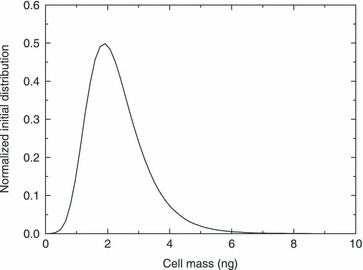
  Normalized initial cell mass distribution used in all simulations of the population balance equation modelling approach.

Table 2.

 Model parameters for population balance equation (PBE) modelling approach used in the simulation. Parameters µ′ and α_P were obtained by fitting model results and experimental data for experiments carried out when initial cell number was equal to 3.68 × 10⁴ (Run 1). These parameters have been also used to test the model predictive capability for experiments performed starting with 2.3 × 10⁴ and 1.0 × 10⁴ (i.e. Runs 2–3) as initial cell number

Parameter	Value	Unit	Reference
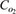
	0.203 × 10−6	mmol/mm3	Schumpe et al. (41)
Cm	0.006 × 10−6	mmol/mm3	Obradovic et al. (42)
dc	1.14 × 106	ng/mm3	Jakob et al. (40)
N 0	Run 1: 3.68 × 104	Cells	This work
	Run 2: 2.3 × 104
	Run 3: 1.0 × 104
q	40	–	Mantzaris et al. (19)
V	800	mm3	This work
αP	10.8	–	This work (tuned parameter)
ϕa	800	mm2	This work
µ	3.8	ng	This work
µ0	2	ng	This work
µc	1.0 × 10−3	1/h	Munteanu et al. (43)
µ′	97.4	ng/(mm2 h)	This work (tuned parameter)
σ	1.125	ng	This work
σ0	0.4	ng	This work

When using the PBE model, two parameters have been determined using a nonlinear fitting procedure: the proportionality constant, µ′, of cell mass rate (cf. eqn 11), and order α_P of the power law given in eqn (12). The comparison between model and experimental data is illustrated in Fig. 3, where the total number of cells, N(t), is reported as a function of time. The temporal profile of geometric limiting factor Φ(t) defined in eqn (12) is also plotted. The relative error (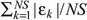 where ɛ_k=[N^Th(t_k) –N^Exp(t_k)]/N^Exp(t_k) is the k‐th relative error) obtained by fitting procedure for PBE model approach is equal to around 8.8%, while values of fitted model parameters are reported in Table 2. Additionally, the result of non‐linear regression analysis performed using the generalized logistic equation (cf. eqn 1) is given in Fig. 3. In this case, relative error is approximately 6.2%, while obtained values of model parameters are also given in Table 3.

Figure 3.

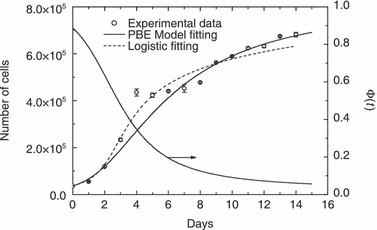
  Comparison between model results and experimental data for cell culture in Petri dishes starting with 3.68 × 10⁴ cells. Data are expressed as mean ± standard deviation. Temporal evolution of geometric limiting factor Φ(t) defined by eqn (12) also plotted.

Table 3.

 Model parameters for generalized logistic equation used in the simulation. Parameters obtained by model results and experimental data for experiments carried out when initial cell number was equal to 3.68 × 10⁴ (i.e. Run 1). These parameters have also been used to test the model predictive capability for experiments performed starting with 2.3 × 10⁴ and 1.0 × 10⁴ (Runs 2–3) as initial cell number

Parameter	Value	Unit	Reference
K	2.7 × 109	Cells	This work (tuned parameter)
N 0	Run 1: 3.68 × 104	Cells	This work
	Run 2: 2.3 × 104
	Run 3: 1.0 × 104
r	5.15 × 10−8	d−1 cells1–α	This work (tuned parameter)
α	2.53	–	This work (tuned parameter)
β	1.05	–	This work (tuned parameter)
γ	4.8 × 104	–	This work (tuned parameter)

To test predictive model capability, experimental data obtained when culture was carried out by starting with 2.3 × 10⁴ and 1.0 × 10⁴, respectively, as initial number of cells were simulated. Model parameters used in these simulation runs were the same as reported in 2, 3. It is important to remark that for these other initial cell numbers no parameters have been adjusted. In particular, with respect to the PBE modelling approach, values of µ′ and α_P were not changed since they should not depend on different initial conditions. On the other hand, since experimental runs were different from each other only for the initial cell number, the same normalized distribution given in Fig. 2 was adopted for the remaining seeding concentration levels investigated. 4, 5 illustrate comparisons of model results with these experimental runs. As can be seen, PBE modelling approach acceptably predicts temporal profile of number of proliferating cells at varying seeding concentrations. Relative error is 16.4% and 15.8%, for the data reported in 4, 5, respectively. On the other hand, generalized logistic equation does not provide good agreement when predicting experimental data reported in Fig. 5 (74.2% relative error), while relative error for predicting data reported in Fig. 4 is 8.85%. Actually, tuned values of some of its parameters reported in Table 3 seem unreasonable. In particular, value of parameters α and K are too high, since the former would indicate a percentage mitotic fraction higher than unity (which is not possible), while the latter corresponds to the ‘carrying capacity’ of an 8‐cm² Petri dish which is too large for the typical size of ovine stem cells used in this work. It should be recognized, however, that number of model parameters in the PBE approach is definitively higher than in generalized logistic equation. Nevertheless, by determining only two adjustable parameters instead of five, by means of population balance modelling it is possible to achieve a prediction capability definitively superior to that obtained using a phenomenological equation.

Figure 4.

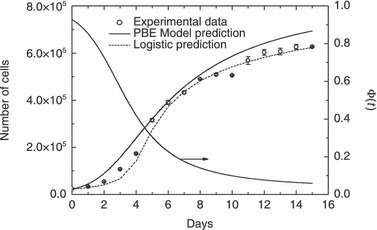
  Comparison between model predictions and experimental data for cell culture in Petri dishes starting with 2.3 × 10⁴ cells. Data are expressed as mean ± standard deviation. Temporal evolution of geometric limiting factor Φ(t) defined by eqn (12) also plotted.

Figure 5.

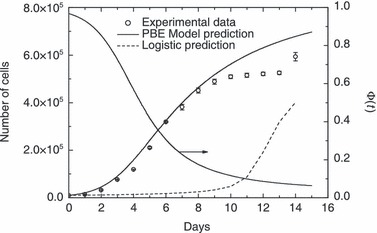
  Comparison between model predictions and experimental data for cell culture in Petri dishes starting with 1.0 × 10⁴ cells. Data are expressed as mean ± standard deviation. Temporal evolution of geometric limiting factor Φ(t) defined by eqn (12) also plotted.

In Fig. 6 normalized cell distribution at different culture times is reported for the case of an initial total cell number equal to 3.68 × 10⁴ cells (cf. Fig. 3) along with the term γ^M(m), which contains the effect on mitotic rate Γ^M (cf. (8), (9)) by adopted functionality for distribution of cells at mitosis (f(m)). As can be seen, the so‐called state of ‘balanced growth’, i.e. time‐invariant property distribution of cell population, is practically reached in 1 day of culture and maintained throughout the proliferation runs reported in 3, 4, 5. This result is consistent with conclusions reached by Mantzaris et al. (19), who found a periodic solution (cells continuously bouncing from the mitotic to the G₁ phase) only for the case of equal partitioning and a linear growth rate. Analyses of Fig. 6 show that, at ‘balanced growth’ stationary cell distribution is almost equal to the initial one. This is due to significant overlapping between initial cell and γ^M(m) distributions which reflects presence of a mitotic fraction in the initial cell population seeded into the Petri dish. Indeed, when overlapping was not initially present, death and birth terms of right hand side of PBE (2) disappear, since Γ^M results to be equal to zero, according to eqn (8). As a consequence, in the absence of an initial mitotic fraction, the PBE (2) would simulate only cell mass growth (cells increasing their sizes, without proliferation) until overlapping between cell distribution and Γ^M is reached, so that total cell number may then increase due to mitosis. This behaviour is shown in Fig. 7 where simulation results from the PBE modelling approach are reported for the case of narrow initial cell (i.e. σ⁰ = 0.053 ng) and γ^M(m) (i.e. f(m) with σ = 0.1 ng) distributions (all other model parameters are kept constant as reported in Table 2). This initial condition, corresponds to synchronization of cell population in G₁ phase. As can be seen in Fig. 7a, proliferation starts only after about 1 day of culture (induction time), which corresponds to temporal interval necessary for the population of cells gaining weight to reach a mitotic size, as shown in Fig. 7b. Due to the extremely narrow character of two relevant distributions, cell distribution actually displays transient behaviour, thus moving back and forth as mitosis and growth take place. As shown in Fig. 7a, this is reflected in an oscillating temporal profile of the total number of cells (even though always monotonically increasing), characterized by stationary periods followed by incremental steps, until oscillations were damped when balanced growth was reached (after about 10 days of culture). During this transient period, cells have a bimodal distribution, as can be seen in Fig. 7b from distribution of cells at 2 and 5 days of culture.

Figure 6.

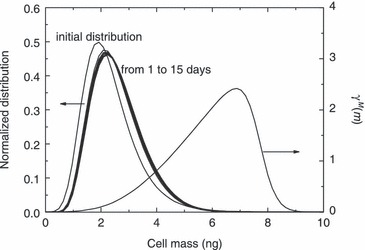
  Normalized cell mass distribution as a function of time for the experimental run carried out starting with 3.68 × 10⁴ cells. The γ^M(m) distribution defined in eqn (9) also plotted.

Figure 7.

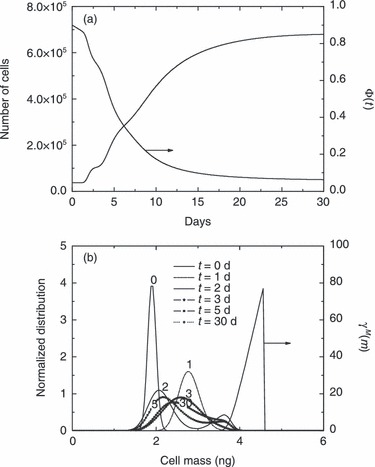
  Temporal profiles of total cell number and geometric limiting factor Φ(t) (a) and normalized cell mass distributions at different culture times (i.e. 0, 1, 2, 3, 5 and 30 days) (b), for the case of 3.68 × 10⁴ initial total cell number. The γ^M(m) distribution defined in eqn (9) also plotted in (b). Initial normalized cell mass and γ^M(m) distributions narrower than those depicted in Fig. 6 are considered.

Since the PBE approach is characterized by a significant number of model parameters, it is worth performing a sensitivity analysis, where the effect of every single parameter is evaluated. The analysis is performed in terms of percentage variation of model output, i.e. cell number after 15 days of culture, with respect to corresponding values obtained for the base case, when considered parameters are modified by ± 50%. The chosen base case is represented by cell number after 15 days of culture, i.e. model output, obtained using parameters reported in Table 2 for the case of N ⁰ = 3.6 × 10⁴. As can be seen from Fig. 8, significant sensitivity of the model output is ascribed to the order (α_P) of power law for geometric intrinsic factor. Indeed, by decreasing order of the power law in eqn (12), the geometric limiting factor decreases more slowly during cell proliferation (confluence is achieved later) and, therefore, cell number increases. The model is less sensitive to other parameters such as µ′ and µ, whose variations produce opposite effects on cell number, as expected. In fact, by decreasing µ′, growth rate proportionally decreases, and, according to eqn (9), division rate slows down, so that only a lower number of cells may be found in the Petri dish after the same culture time. On the other hand, by decreasing µ, cells need to grow less to reach maturity and divide by mitosis. Thus, reduction of parameter µ corresponds to augmentation of mitotic rate, and, finally, to higher cell number. Parameters as µ_c, d_c, c_m, , q, and those related to shape of initial cell distribution (N ⁰/V, µ⁰, and σ⁰) have almost negligible effect on model output. It is not actually surprising that cell number after 15 days of culture is not affected at all by the parameters related to the shape of initial cell distribution. In fact, a stationary condition (‘balanced growth’) is always reached in the Petri dish after few days under different sets of parameters investigated. On the other hand, the effect of initial cell distribution parameters is relevant when addressing cell number after only 1 day of culture. If such model output is considered to perform the sensitivity analysis, the results shown in Fig. 9 are obtained. As expected, by increasing initial seeding concentration (i.e. N ⁰/V), cell number after 1 day of culture is augmented. A similar effect is obtained through mean cell size (µ⁰) at seeding. Indeed, a larger value of µ⁰ means that, in average, cells are initially closer to the mitotic mass µ, so that mitotic rate increases. On the other hand, a larger σ⁰ produces a lower cell number. This is presumably due to the widening of initial cell distribution towards smaller cells, which have to grow more to reach maturity at mass µ when mitosis may finally take place.

Figure 8.

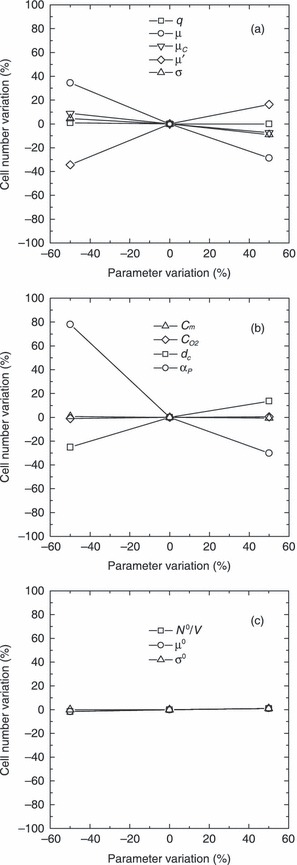
  Sensitivity analysis on cell number after 15 days of culture by varying parameters q, µ, µ_C, µ′, and σ (a), C_m, , d_c, and α_P (b), and N ⁰/V, µ⁰, and σ⁰ (c). Base case is related to model parameters reported in Table 2 when N ⁰ = 3.6 × 10⁴.

Figure 9.

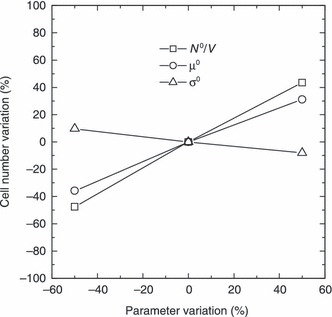
  Sensitivity analysis on cell number after 1 day of culture by varying parameters N⁰/V, µ⁰, and σ⁰. Base case is related to model parameters reported in Table 2 when N ⁰ = 3.6 × 10⁴.

Following the considerations above related to the performed sensitivity analysis, choice of µ′ and α_P as adjustable parameters seems appropriate. On the other hand, even if the value of the mean of the normal distribution of mitotic fraction (µ of f(m), represents a parameter to which the model is sensitive, its value was a priori chosen on the basis of sound consideration reported above.

Concluding remarks

Mathematical modelling and simulation of proliferation kinetics of stem cells expanded to confluence in Petri dishes is addressed in this work. The sigmoid temporal profiles of total counts are quantitatively interpreted by the phenomelogical logistic equation and a new model based on a one‐dimensional population balance approach able to take into account contact inhibition at confluence. The proposed population balance modelling approach is successful in predicting proliferation kinetics at the different initial seeding concentrations investigated experimentally. On the other hand, the logistic equation failed in predicting cell culture expansion for the case of relatively low initial seeding concentrations. Thus, the proposed model based on PBE approach represents a first step towards quantitative interpretation of stem cell proliferation, which may be applied when simulating perfusion in a bioreactor for tissue engineering applications, where the occlusion of pores in a three‐dimensional scaffold, due to cell proliferation, may progressively affect perfusion fluid‐dynamics. Thus, this mutual influence between intrinsic kinetics and perfusion fluid‐dynamics when approaching high proliferation yield may necessitate a temporal recalibration of operative conditions for optimally running the bioreactor.

Work is in progress for extending experimental validation of the proposed model, which can be, in our view, easily extended to the case of human cells, where specific values of model parameters will change accordingly to such cell lineages. In particular, temporal evolution of cell mass distributions experimentally determined using an automated electronic counting device (Coulter counter, Milano, Italy) will allow validation of model predictions for the balanced growth condition reached after 1 day in the static regime. Subsequently, the proposed model may be improved by splitting the whole culture into several populations of cells belonging to different cell cycle phases in order to enhance matching with experimental data. Since additional parameters related to transition rates between cell subpopulations will be introduced, flow cytometry analysis on DNA content distributions will be adopted for providing experimental data necessary for their safe and reliable determination.

Abbreviations

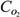
	concentration of O2 at saturation condition, mmol/mm3
Cm	oxygen concentration at half‐maximal consumption, mmol/mm3
dc	mass density, ng/mm3
DP	number of grid points for m domain discretization of PBE model
f(m)	division probability density function, 1/ng
Κ	saturation capacity of generalized logistic eqn (1), cells
m	single cell mass, ng
m′	mother cell mass, ng
m max	maximum cell mass value considered in numerical solution
N	cell number, cells
N 0	initial cell number, cells
NExp	cell number experimentally evaluated, cells
NTh	cell number evaluated from the adopted models, cells
p	partitioning function
q	coefficient appearing in symmetric beta function
r	rate constant of generalized logistic eqn (1), d−1 cells1–α
t	time, d
V	total cultivation volume, mm3
Greek letters
α	parameter of generalized logistic eqn (1)
αP	order of the power law given in eqn (12)
β(q, q)	symmetric beta function
β	parameter of generalized logistic eqn (1)
ϕ	occupied area by cells and interstices, mm2
ϕa	Petri dish area, mm2
Φ	geometric limiting factor
Γ(q)	gamma function
γ	parameter of generalized logistic eqn (1)
γΜ	distribution defined in eqn (9), 1/ng
ΓΜ	division rate function, 1/d
µ	average mass of dividing cells in eqn (10), ng
µ0	mean value of initial cell mass distribution in eqn (3), ng
µ′	maximum rate of cell growth, ng/(mm2 h)
µc	catabolic rate, 1/h
ν	time rate of change of cell mass m, ng/h
σ	standard deviation of the Gaussian distribution f(m) defined in eqn (10), ng
σ0	standard deviation of the initial cell mass distribution defined in eqn (3), ng
ψ	cell distribution function, cells/(ng mm3)

Appendix

According to the method of lines, the m domain has been divided using a constant step size [Δm = (m _max – 0)/(DP – 1) and m_i = Δm · (i – 1) with i ∈[1; DP]].

The system of ODEs resulting from the discretization of m domain in eqn (2) is:

(A1)

∀i∈[2; DP] and ψ₁(t) = ψ₁(0) = 0

with the initial condition

(A2)

where

(A3)

(A4)

(A5)

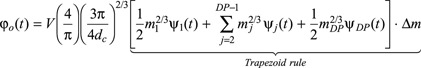(A6)

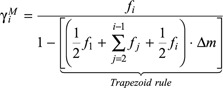(A7)

(A8)

(A9)

Equation (A1) is a system of ODEs in time that has been integrated as an initial value problem by means of standard numerical libraries (Gear method, IMSL).