Cell kinetic status of haematopoietic stem cells

Abstract.

The haematopoietic stem cell (HSC) population supports a tremendous cellular production over the course of an animal’s lifetime, e.g. adult humans produce their body weight in red cells, white cells and platelets every 7 years, while the mouse produces about 60% of its body weight in the course of a 2 year lifespan. Understanding how the HSC population carries this out is of interest and importance, and a first step in that understanding involves the characterization of HSC kinetics. Using previously published continuous labelling data (of Bradford et al. 1997 and Cheshier et al. 1999) from mouse HSC and a standard G₀ model for the cell cycle, the steady state parameters characterizing these HSC populations are derived. It is calculated that in the mouse the differentiation rate ranges between about 0.01 and 0.02, the rate of cell re‐entry from G₀ back into the proliferative phase is between 0.02 and 0.05, the rate of apoptosis from the proliferative phase is between 0.07 and 0.23 (all units are days⁻¹), and the duration of the proliferative phase is between 1.4 and 4.3 days. These values are compared with previously obtained values derived from the modelling by Abkowitz and colleagues of long‐term haematopoietic reconstitution in the cat (Abkowitz et al. 1996) and the mouse (Abkowitz et al. 2000). It is further calculated using the estimates derived in this paper and other data on mice that between the HSC and the circulating blood cells there are between 17 and 19.5 effective cell divisions giving a net amplification of between ~170 000 and ~720 000.

Introduction

The population of haematopoietic stem cells (HSC) gives rise to all of the differentiated elements of the blood: the white blood cells, red blood cells, and platelets. To understand the enormity of this production, consider that humans produce about 10 times their body weight in these haematopoietic cells over the course of a 70 years lifespan (cf. Appendix A). It is also important to realize how different this production is between humans and mice: one of the favourite tools of the experimental haematologist. In the mouse (Appendix A), the production amounts to about 60% of the mouse’s body weight in the course of a 2 year lifespan.

The fact that this production continues unabated for years, usually in a flawless fashion, makes the regulation of haematopoiesis (and the HSC in particular) an ideal system in which to study the control mechanisms that allow this seamless operation. In addition to using the HSC population for the study of cellular regulatory mechanisms, from a practical viewpoint it is also important to understand this population in as much detail as possible because of its importance in bone marrow transplantation, in the genesis of several periodic haematological diseases (cf. Haurie et al. 1998 for a review) such as periodic haematopoiesis (1999a, 2000, 1999b,Hearn et al. 1998), periodic leukaemia (Fortin & Mackey 1999), and cyclical platelet production (Santillan et al. 2000,Swinburne & Mackey 2000), and its potential role in gene therapy.

Unfortunately, identification of the haematopoietic stem cell is an uncertain business and must rely on indirect measures since morphological characteristics of the HSC are unknown. Consequently, over the past few years progressively more primitive candidates for the HSC have been identified.

In this paper, we take recently published flash and continuous labelling data for putative HSC’s from Bradford et al. (1997) and Cheshier et al. (1999) and analyse these data within the context of a G₀ model of the cell cycle. This model is used to derive quantitative estimates of the steady state rate of cellular re‐entry (β) from G₀ back into the proliferative phase, the rate of apoptosis (γ) from the proliferative phase, the rate of differentiation (δ) from G₀, and the duration (τ) of the proliferative phase.

Data

Bradford et al. (1997) studied a subclass of lineage negative (Lin⁻) bone marrow cells from CB57BL mice that showed low Hoechst 33342 fluorescence. These cells were further subdivided into categories RI, RII, and RIII based on their Rhodamine 123 fluorescence, and they argued that these cells are haematopoietic pluripotential stem cells with the RI cells being the most primitive. It is this class of RI cells for which we list the cell kinetic data in Table 1.

Table 1.

Data and results. Above the break are the primary mouse data used in this study, as extracted from Bradford et al. (1997) and Cheshier et al. (1999). The value of the labelling index f_L is from pulse labelling data, and the value of the fraction of G₀ phase cells, f_N, corresponds to the fraction of cells with 2N DNA as determined by cell sorting. The proliferating fraction f_P ≡ 1 − f_N. The fourth line of the table gives the decay coefficient b for the fraction of unlabeled cells f_U(t) = 1 − f_L(t) fit to the relation f_U(t) = ae^−bt, as determined from the published data. To obtain these values, the data of Bradford et al. (1997, Fig. 5) and Cheshier et al. (1999, Fig. 2) were scanned and digitized, and the values of f_L(t) determined using ghostview. Then the curve fitting routine of gnuplot was used to obtain values of a and b. The results of analysing these data are given in the second and third columns. The quoted value of the DNA synthesis time t_S is t_S,av ± Δt_S where t_S,av = t_S,min + Δt_S and Δt_S = (t_S,max − t_S,min)/2. The values of all of the other parameters correspond to the values calculated using t_S,av, and the range of values in parentheses corresponds to the values obtained using the range of t_S values. From Figure 1, γ is the apoptotic rate, β is the rate of cell entry from the G₀ phase into the proliferative phase, and δ is the rate of differentiation from the HSC into all cell lines. τ is the length of time that cells spend in the proliferative cycle.

Parameter	Mouse Bradford et al. (1997)	Mouse Cheshier et al. (1999)
fL	0.01	0.05
fN	0.93	0.94
fP	0.07	0.06
b (day−1)	0.0305	0.0768
tS (day)	0.54 ± 0.7	1.14 ± 0.24
γ (day−1)	0.069 (0.200)	0.228 (0, 0.599)
β (day−1)	0.020 (0.015, 0.031)	0.053 (0.038, 0.077)
δ (day−1)	0.010 (0, 0.015)	0.024 (0, 0.038)
τ (day)	4.25 (3.40, 9.86)	1.41 (1.15, 1.67)

Later, Cheshier et al. (1999) separated a subclass of Lin⁻ bone marrow cells from CB57BL mice for cell kinetic study that they also categorized as haematopoietic stem cells. The data on this subfraction of the bone marrow are also listed in Table 1. There is no indication of the extent to which these two populations of cells studied in Bradford et al. (1997) and Cheshier et al. (1999) may overlap in their functional nature.

The data collected by Bradford et al. (1997) and Cheshier et al. (1999) are of particular utility in estimating parameters of the haematopoietic stem cell compartment (HSC) in mice, since they continuously labelled DNA with bromodeoxyuridine (BrdU) for a long period of time (12 weeks in Bradford et al. (1997) and 6 months in Cheshier et al. (1999)) to determine the fraction of labelled cells f_L(t) as a function of time t, and also determined the pulse labelling index (f_L), and the fraction of cells in the non‐proliferative phase of the cell cycle, f_N.

ANALYSIS, METHODS AND RESULTS

The data of Bradford et al. (1997) and Cheshier et al. (1999) listed in Table 1 are analysed within the context of a standard (Burns & Tannock 1970) G₀ model of the cell cycle as depicted in Figure 1. Specifically, the goal of this study is to determine the steady state values of the rate of apoptosis (γ), the rate (δ) of differentiation from G₀, the rate (β) of re‐entry of G₀ phase cells into the proliferating phase, and the duration (τ) of the proliferating phase of the cell cycle consistent with the data of Table 1.

Figure 1.

A schematic representation of the G₀ stem cell model. Proliferating phase cells (P) include those cells in S (DNA synthesis), G₂, and M (mitosis) while the resting phase (N) cells are in the G₀ phase. δ is the rate of differentiation into all of the committed stem cell populations, while γ represents a loss of proliferating phase cells due to apoptosis. β is the rate of cell re‐entry from G₀ into the proliferative phase, and τ is the duration of the proliferative phase. See Mackey (1978),Mackey (1979),Mackey (1996) for further details.

The equations governing this model are presented in Appendix B, along with an analysis of the steady state situation, and the response of such a model tissue to pulse and continuous labelling protocols are given in Appendix C.

As shown in Appendix C, for long times the fraction of unlabelled cells in a continuous labelling experiment should decay exponentially according to f_U(t) ∼ e^−(β+δ)t. Since the continuous labelling data of both Bradford et al. (1997) and Cheshier et al. (1999) are accurately fit by an equation of the form f_U(t) ∼ e^−bt, we have f_U(t) ∼ e^−bt ∼ e^−(β+δ)t and we therefore identify b of Table 1 with β + δ.

The data of Bradford et al. (1997) and Cheshier et al. (1999) lack any determination of the DNA synthesis time t_S. As can be seen from (6), (10), (16), t_S is required in conjunction with f_L, f_N, f_P and γ in order to calculate β, δ, and τ. However, we can use the estimations of Equation 29 in Appendix D in conjunction with the Bradford et al. (1997) data from Table 1 to give t_S = 0.54 ± 0.17 days, while the Cheshier et al. (1999) data give t_S = 1.14 ± 0.24 days.

Having determined permissable ranges for the DNA synthesis time t_S, we determine the value of the apoptosis rate γ from Equation 12 and then we may then easily determine β, δ and τ from (11) (6) and (10), respectively. Approximations that are appropriate for the situation in which the labelling index f_L and the apoptosis rate γ are both small are given in Appendix E. (The procedures for these determinations are all carried out in the freeware gnuplot, and copies of the full gnuplot routines are available from the author).

The second and third columns of Table 1 give the results of this computation for the data of Bradford et al. (1997) and Cheshier et al. (1999), respectively. The calculated values of γ, β and δ from the data Cheshier et al. (1999) are two to three times larger than the corresponding values from the data of Bradford et al. (1997) while the computed value of τ from the data of Bradford et al. (1997) is about three times larger than that of Cheshier et al. (1999). The range of values estimated for γ, β, and δ all overlap, whereas the ranges for τ do not.

Discussion

Abkowitz et al. (1995) experimentally studied the reconstitution of the haematopoietic system in cats for six years following lethal irradiation and an autologous transplant. Zhong et al. (1996) have carried out the same experiment in mice over a 30‐week period. The only quantitative estimates of HSC parameters that have appeared (to my knowledge) before the ones obtained here are those of 1996, 2000 analysing these data in a stochastic modelling context. However, these stochastic modelling estimates did not give any indication about the length of time (τ) cells might spend in the proliferative phase of the cell cycle. The current study complements the Abkowitz study by providing an estimate for τ (either 1.4 or 4.3 days), and also offers an independent estimation of the parameters (γ,β,δ) for comparison with the estimations obtained from a repopulating situation. In Table 2 we list the values of the parameters γ, β and δ determined in 1996, 2000 for mice and cats, respectively. A comparison of the results in Tables 1 and 2 show that all three murine studies result in ranges of HSC parameters that overlap with each other (and with the feline estimates), while the ‘best’ values of β and δ are relatively close to one another, and these values are also similar to those estimated for cats. The biggest discrepancies for the different parameter estimates are in the ‘best values’ for the apoptotic rates, reflecting the wide ranges on γ. This clearly points out the desirability of having other, independent, estimates of γ derived from more direct kinetic observation of apoptotic cells.

Table 2.

Values of γ, β and δ for mouse and cat. This table gives, for comparison, the values arrived at by Abkowitz et al. (2000) in the mouse and the cat Abkowitz et al. (1996), respectively. In these two columns, the single quoted figure is the value arrived at that gave the ‘best fit’ to the data based on several criteria, while the figures within parentheses give the range of values that provided an ‘acceptable fit’ to the data.

Parameter	Mouse Abkowitz et al. (2000)	Cat Abkowitz et al. (1996)
γ (day−1)	0.007 (0, 0.071)	(0, 0.034)
β (day−1)	0.057 (0.022, 0.08)	0.018 (0.005, 0.047)
δ (day−1)	0.042 (0.011, 0.075)	0.011 (0.002, 0.043)

Nečas et al. (1998) have examined the efficiency of murine cell production (defined as the ratio of the actual production to that which would have been expected on the basis of measured cell kinetic parameters) in several different cell types by examining the rate of cell replacement after population ablation with hydroxyurea. Using the model development of Appendix B and the parameter values in Table 1, we can determine the efficiency of these stem cell populations studied in Bradford et al. (1997); Cheshier et al. (1999) using Equation 14. With this, the efficiency of the population of stem cells studied by Bradford et al. (1997) is 92% while for the Cheshier et al. (1999) data it is 45%. Other data and calculations have given an efficiency of about 45% in the post mitotic neutrophil compartment of humans (Aprikyan, Dale & Mackey, unpublished).

We can offer more insight into the nature of the replicative process between the HSC and the circulating cells in the blood. Novak & Nečas (1994) have made an extensive compilation of the available data on haematopoiesis in the mouse, and from that constructed a likely scheme for blood cell production. They estimate that the bulk of the haematopoietic production in terms of absolute numbers of cells is, as in humans, confined to granulocyte and erythrocyte production. From their figures, the granulocyte production rate is GPR ≅ 2.4 × 10⁹ cells/kg‐day, while the erythrocyte production rate is EPR ≅ 5.1 × 10⁹ cells/kg‐day to give a overall haematopoietic production rate of HPR ≅ 7.5 × 10⁹ cells/kg/day. If the average effective amplification (A) in cell numbers between the HSC and the circulation is given by A = 2^q, then in a steady state we must have HPR ≅ δN* × 2^q, where N* is the steady state number of G₀ phase cells.

We have estimates of δ in Table 1, and to obtain a value of N* we use the following. Let the frequency of HSC in the bone marrow be given by F _hsc = h × 10^−m HSC/nucleated BM cells, and the density of nucleated bone marrow cells be given by T_bm = b × 10ⁿ nucleated BM cells/kg. Then the total population of HSC in the G₀ phase of the cell cycle will be given by

Both Abkowitz et al. (2000) and Bradford et al. (1997) give a value for the HSC frequency of F _hsc ≅ 8 HSC/10⁵ nucleated BM cells, and Novak & Nečas (1994) give a value for the nucleated BM cells in the mouse of T_bm ≅ 1.4 × 10¹⁰ nucleated BM cells/kg, virtually identical with the value of T_bm ≅ 1.1 × 10¹⁰ given by Boggs (1984). Thus, putting all of this together we calculate that the effective amplification between the HSC and the circulation in the mouse is given by A = 2^q ≅ 7.2 × 10⁵, which corresponds to an effective number of divisions q ≅ 19.5 between the HSC studied by Bradford et al. (1997) and the circulation. Using the parameters derived from the Cheshier et al. (1999) data, an amplification of A = 3 × 10⁵ is calculated corresponding to q = 18.2 effective divisions between the stem cells they studied and the circulation. Finally with the Abkowitz et al. (2000) figures we have A = 1.71 × 10⁵ with an effective number of q = 17.4 divisions.

Acknowledgements

I would like to thank Prof. Emanuel Nečas, Institute of Pathophysiology, Charles University, Prague for his helpful comments, Prof. J. Abkowitz, Department of Medicine, University of Washington, Seattle, U.S.A. for her comments and a preprint of Abkowitz et al. (2000) and Prof. Helmut Schwegler, Institute of Physics, Universität Bremen, Germany for his hospitality and support during the time this work was completed. This work was supported by the Mathematics of Information Technology and Complex Systems (MITACS, Canada), the Natural Sciences and Engineering Research Council (NSERC Grant No. OGP‐0036920, Canada), the Alexander von Humboldt Stiftung, and Le Fonds pour la Formation de Chercheurs et l’Aide à la Recherche (FCAR Grant no. 98ER1057, Québec).

APPENDIX A. LIFETIME HEMATOPOEITIC PRODUCTION IN HUMANS AND MICE

To appreciate the enormity of haematopoietic production, as well as the differences between species, consider the following.

In the adult human the total leukocyte production is 1.5 × 10⁹ cells/kg‐day Dancey et al. (1976). Thus for a nominal adult weighing 70 kg and living 70 years, the total granulocyte production rate (GPR) is

Similarly, with a red blood cell density of 5 × 10⁶ cells/mm³ blood, an erythrocyte lifespan of 120 days Beutler et al. (1995), and a blood volume of 71 ml/kg Dancey et al. (1976) for a 70 kg adult we have an erythrocyte production rate (EPR) of

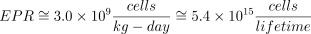
Finally, with a platelet density of 300 000 cells/mm³ of blood and a circulating platelet lifespan of 10 days Beutler et al. 1995 we have a platelet production rate (PPR) of

Thus we have a combined haematopoietic production rate (HPR = GPR + EPR + PPR) on the order of

It is difficult to conceptualize 10¹⁶ cells, but translating that number to a weight helps. The volume of an erythrocyte is 92 fl or 92 × 10⁻¹² cm³. If we assume that the density of an erythrocyte is that of water (a pretty good assumption), then one red blood cell weighs 92 × 10⁻¹² g and the total lifetime erythrocyte production in terms of weight is given by

Platelets have a volume of about 8 fl, and the analogous calculation gives a platelet production in weight of

Finally for neutrophils the volume is about 60 fl so we have

In other words a 70 kg adult produces on the order of 689 kilograms of haematopoietic cells in the course of a 70 years lifespan, or approximately their body weight in haematopoietic cells (white cells, red cells, and platelets) every seven years of life.

The situation is dramatically different in the mouse. Using the data from Novak & Nečas (1994), and assuming a 2 year life span for mice, we have

and

Thus in the mouse there is a total haematopoietic production rate of

Assuming a body weight of 25 g, this means that a mouse produces about 60% of their body weight in haematopoietic cells in the course of their lifetime.

APPENDIX B. STEM CELL MODEL

The dynamics of the HSC model of Figure 1 are governed Mackey 1978, 1979,1996 by the coupled differential delay equations

(1)

(2)

where τ is the time required for a cell to traverse the proliferative phase, N_τ ≡ N(t − τ), and the resting to proliferative phase feedback rate β is taken to be a function of P, N, or P + N. The notation β_τ is used to indicate that the argument of β is delayed by a time τ.

For any cell renewal system, the labelling index is defined as

(3)

where the subscript ‘L’ denotes labelled, the proliferating fraction is given by

(4)

and the fraction of cells in G₀ is given by

(5)

The steady state of the system (1) − (2) is defined by (dN/dt) ≡ (dP/dt) ≡ 0. We will always use the subscript * to denote a steady state. From Equation 2, in a steady state we have

(6)

while Equation 1 gives

(7)

Note also that in a steady state the proliferating fraction is given by

(8)

APPENDIX C. LABELLING RELATIONS

C.1 Pulse Labelling

For the situation in which we pulse label the cells, the system is in a quasi steady state. Since the only labelled cells are in the S phase,

(9)

We can solve (8), (9) for τ and β as functions of γ and t_S to give

(10)

and

(11)

respectively.

We determine the value of the apoptosis rate γ from the implicit relation obtained by writing out β + δ explicitly from (6), (10), (11) and then setting β + δ = β, or:

(12)

With γ from Equation 12, we may then easily determine β, δ and τ from (11), (6) and (10) respectively.

Note that the production (in cells/kg‐day) from the model of Figure 1 is simply δN_* or

(13)

However, the efflux in the absence of any apoptosis (γ ≡ 0) is just P_S/t_S, so the efficiency (defined as the ratio of the efflux with apoptosis present to that without apoptosis) is immediately given by

(14)

There is only a certain allowed range of values for γ. Clearly the lower bound is γ= 0, and at this minimal value for γ we have

(15)

The upper bound on γ is obtained by first noticing that since δ and β must both be strictly non‐negative, from Equation 6 we must have 2e^γτ − 1 > 0 or

(16)

However, combining this with Equation 10 gives

(17)

or finally

(18)

At this upper limit on γ we have

(19)

(20)

C.2 Continuous Labelling

In deriving an expression for the labelling index as a function of time in the case when cells are continuously labelled, we must consider two different time intervals. Since the cells are being continuously labelled, the cells that are initially labelled occupy an interval of the cell cycle of length t_S. As time progresses, all cells in S phase are continuously acquiring label so the interval of the cell cycle occupied by labelled cells steadily increases until a time (τ − t_S) has passed, at which point the labelled cells start to enter the G₀ phase.

During this initial phase (for 0 ≤ t ≤ τ − t_S) the density of labelled cells in the population (remember that they are all in the proliferating phase) obeys the differential equation

(21)

and must satisfy the initial condition

(22)

Solving Equation 21 with the initial condition (22) gives

(23)

so the labelling index is given by

(24)

For times t > τ + t_S, all of the cells in the proliferative phase are labelled, and the number of labelled cells N_L(t) in the G₀ phase must satisfy

(25)

where the first term on the right hand side is the loss of labelled cells and the second term is the gain in newly labelled cells coming from the proliferative phase. Realizing that the initial condition for Equation 25 is N_L(τ − t_S) = 0, we can easily solve the equation to give

(26)

This solution, in turn, allows us to write the second portion of the labelling index as

(27)

Combining (24), (27), we have the following expression for the continuous labelling index as a function of time:

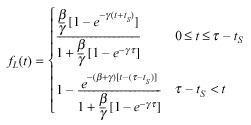(28)

APPENDIX D. BOUNDS ON THE DNA SYNTHESIS TIME T_S

Since we know that the parameter b describing the exponential decrease in the unlabelled population of cells in the continuous labelling experiment should be identified with β + δ[b = β + δ] then we also must have bt_S = (β + δ)t_S. Since δ must be positive we know that 0 ≤ γ ≤ γc and applying the limits in (15), (20) to β + δ we can place lower and upper bounds on t_S consistent with the data, yielding

(29)

APPENDIX E. APPROXIMATE RELATIONS

In the situation where the labelling index f_L is small (f_L ≪ 1) we can approximate the relations derived in the preceeding appendices to give easily calculable equations. Thus the approximation to the DNA synthesis time is given by

(30)

while

(31)

With these relations and the additional assumption that the apoptosis rate γ is ‘small’ we easily derive

(32)

(33)

(34)

Comparison of the values calculated with (30), (31), (32), (33), (34) shows excellent agreement with the values in Table 1.