In silico study of the impact of cancer stem cell dynamics and radiobiological hypoxia on tumour response to hyperfractionated radiotherapy

Abstract

Objectives

Advanced head and neck carcinomas (HNCs) are aggressive tumours, mainly due to hypoxia and a cancer stem cell (CSC) subpopulation. The aim of this study was to simulate tumour growth and behaviour during radiotherapy of three HNC groups (governed by different growth kinetics, hypoxia levels and CSC division pattern) to determine correlation between resistance factors and responses to hyperfractionated radiotherapy.

Methods

An in silico HNC model was developed based on biologically realistic input parameters. During radiotherapy simulation, three parameters were studied: growth kinetics, hypoxia and probability of CSC symmetrical division. Both independent and combined effects on tumour response to hyperfractionated radiotherapy were assessed.

Results

Oxic and very mildly hypoxic HNCs were revealed to be controlled by hyperfractionated radiotherapy, irrespective of growth kinetics and CSC division pattern. Moderately hypoxic tumours had different responses to radiotherapy: while slowly proliferating HNCs were still controllable, tumours with higher cell turnover were more resistant. In rapidly proliferating tumours, the number of fractions needed for tumour control increased exponentially with the probability of CSC symmetrical division, whereas in moderately growing HNC, this behaviour was linear. Severely hypoxic tumours could not be controlled by radiotherapy alone. Tumours with CSCs in a severely hypoxic niche required adjuvant therapies to be eradicated.

Conclusions

Growth kinetics strongly influence tumour responses to treatment. Slowly growing tumours showed linear dependence between dose and hypoxia/CSC, whereas rapidly growing tumours followed exponential behaviour.

Introduction

The challenge of cancer stem cells (CSC) in head and neck cancer

Head and neck cancers (HNC) are radiobiologically challenging due to well‐established factors, such as hypoxia and accelerated repopulation. Despite the general knowledge on the impact of the above‐named factors on tumour response to treatment, their quantitative assessment is still limited.

There is a growing body of evidence towards the existence of cancer stem cells (CSCs), which represent a subpopulation of tumour cells that hold the ability to proliferate indefinitely 1, are more quiescent than non‐cancer stem cells 1, can create all lineages of the original tumour 2 and can regenerate via both symmetric (giving birth to two stem‐like cells) and asymmetric division (one stem‐like cell and another non‐stem cancer cell) 3. Due to their ability to respond to triggers, these cells are considered to be accountable for treatment resistance, failure and even tumour recurrence. However, there is insufficient quantitative information in the literature regarding the kinetics and dynamics of CSCs in order to adapt treatment protocols to overcome their impact on tumour control.

Experimental studies undertaken on tumour cell lines have shown that the percentage of CSC varies drastically among tumours of different histopathological type 4. The first identification of CSC in HNC is linked to the study by Prince et al. 5, who have isolated a cellular subgroup exhibiting stem‐like properties. To date, there are very few quantitative reports in the literature on the percentage of CSC in head and neck cancer. In the experiments conducted by Tang et al. 6, the CSC proportion in various head and neck cell lines ranged between 1.7% and 13.5%. Another experiment undertaken on HNC cell lines by Harper et al. 7 has indicated that the proportion of CSC in CaLH3 cell line is 12.3%. These findings illustrate that there are significant differences among the studied head and neck cell lines.

Current clinical studies on CSC focus on the characterization of CSC cells through stem cell markers in order to establish the clinical significance of their expression. Since the number of such studies is sparse and the results inconclusive 8, there is a need for additional information to help elucidate the impact of treatment‐resistant CSC populations within head and neck tumours on treatment outcome.

Clinical background of radiotherapy for head and neck cancer

Given that cancer stem cells have the ability to regrow the tumour, to achieve complete tumour control, all CSCs must be eradicated. Conventionally fractionated radiotherapy was shown to be unsuccessful in providing high locoregional tumour control in head and neck cancer 9. Instead, altered fractionation schemes have demonstrated better tumour control without increasing normal tissue toxicity 9, 10.

Being rapidly proliferating tumours, HNC needs a more aggressive treatment to overcome repopulation between subsequent fractions. To a certain extent, tumour hypoxia can also be overcome with smaller and more frequent doses. These rationales have justified the implementation of hyperfractionated radiotherapy schedules in HNC management. Furthermore, head and neck tumour cells have a high cell turnover, therefore a relatively short cell‐cycle time. Cellular redistribution along the cell cycle for rapidly proliferating tumours consents to a more uniform cell kill than in slowly growing tumours, also justifying the choice for hyperfractionation 11.

Hyperfractionated radiotherapy for advanced head and neck cancer within the RTOG 9003 trial has led to a higher rate of locoregional control and no significant increase in late toxicity when compared with standard treatment regimens 10, 12. The results of a meta‐analysis conducted by Bourhis et al. 9 have also demonstrated the advantage of hyperfractionation over standard and accelerated radiotherapy.

However, to date, there is no optimal fractionation schedule that would eradicate advanced head and neck cancers, mainly due to hypoxia‐induced radioresistance and CSC resistance. This study aims to illustrate the influence of three critical factors on tumour response to therapy:

1. tumour growth kinetics,

2. hypoxia and

3. CSC dynamics.

Models of cancer stem cells in the literature

Models of tumour growth and response to treatment can be classified into two main categories: analytical and stochastic. There are several mathematical models that have employed a discrete approach via differential equation to simulate growth dynamics of a hierarchical tumour model 13, 14, 15, 16 or hybrid cellular automaton models 17. Other mathematical models have gone into more depth and studied the multi‐step process of tumorigenesis 18, 19 by considering mutation sequences leading to cancer 20. The main focus of these mathematical models was on the role of genetic instability in initiating cancer and the number/sequence of mutations in hierarchical tissues leading to stem‐like properties.

The effect of dedifferentiation on carcinogenesis in stem cell‐driven cancers has been recently modelled by Jilkine and Gutenkunst using a hybrid stochastic‐deterministic model of mutation accumulation in stem cells as well in progenitor cells 21. They suggest that dedifferentiation could play an important role depending on the way stem cell homeostasis is maintained, showing that dedifferentiation beyond a critical threshold leads to exponential growth of the stem cell population due to symmetrical division. Morton et al. have indicated that while CSCs play an important role in tumour progression, the kinetics of tumour growth as a whole is tempered by the dynamics of differentiated cells (i.e. non‐stem cancer cells) 22. As illustrated by their model, even small variations in the proliferative ability of these non‐stem cancer cells can lead to notable changes in tumour growth kinetics.

Cellular automaton models are popular due to their flexibility that allows incorporation of various spatial growth features and of agent‐based therapy simulations guided by pre‐established rules. By using experimental data on tumour kinetics, cellular automaton models can predict the growth curve of tumours, which facilitates further analysis of tumour behaviour during treatment. Thus, one of the main goals of cellular automaton models is to enable the understanding of the mechanisms guiding tumour growth and development, as well as invasion and metastases. These models allow for easy implementation of diverse experimental measurements.

A three‐dimensional multi‐scale mathematical model of cancer stem cell within tumour development has been designed by Li et al. with the aim to investigate the behaviour of CSCs during tumour progression and response to treatment 23. They have showed that drug therapy increases the fraction of CSCs to about 3‐fold, concluding that specific CSC targeting would be needed for tumour control in cancers with subpopulations of high self‐renewal ability. Another cellular automaton model has been reported by Monteagudo and Santos, describing a grid‐like tumour growth model guided by the main hallmarks of cancer growth 24. Their simulation has showed that proliferation of differentiated cells within the tumour is triggered by treatment, which in turn, stimulates CSCs to differentiate. This observation could be interpreted as ‘the survival of the fit’, whereby cancer cells use any of their available tools to outlive and repopulate the tumour.

With a few exceptions, majority of these models have focused on cancer stem cells in solid tumours, in general, rather than particular anatomical locations. Since growth kinetic parameters are a major starting point in tumour development, to fulfil the aim of individualized treatment, this study has considered a group of tumours having a common histopathology (i.e. head and neck squamous cell carcinomas).

Nowadays, in silico models focus on complex biological parameters, often neglecting fundamental elements that dictate the basic tumour behaviour. This study will show that tumour growth kinetics is an important factor influencing treatment outcome. Furthermore, the model also comes to emphasize the need of predictive assays for proliferative potential among head and neck carcinomas.

The aim of this study

Given the radiobiological challenges presented by head and neck carcinomas, such as accelerated repopulation and tumour hypoxia, this study aims to elucidate some aspects regarding the impact of cancer stem cells on treatment response.

To fulfil this aim, the project has followed these subsequent goals:

1. To grow in silico head and neck cancers with various growth kinetics

2. To evaluate inter‐patient variation of tumour response to hyperfractionated radiotherapy as a function of growth kinetics

3. To assess the interplay between CSCs and the hypoxic microenvironment during radiotherapy

Methods

Simulation of tumour growth

In this study, head and neck tumours were grown starting from one seed stem cell up to a clinically detectable size. The development algorithm follows a Monte Carlo method making probabilistic decisions based on parameter values taken from the literature. An earlier implementation of the tumour growth algorithm 25 has been revisited, and a more efficient model has been developed considering new radiobiological findings such as the impact of cancer stem cells on tumour response to treatment (Fig. 1).

Figure 1.

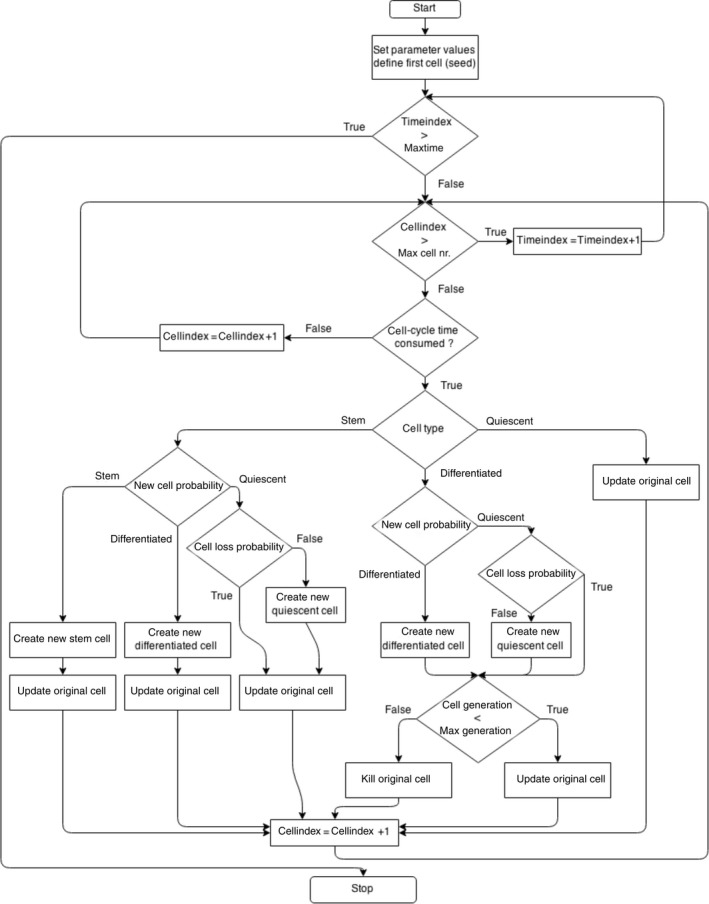
Flow chart of tumour growth model starting from one stem cell.

The model is based on an hourly evaluation of every cell within the tumour. If a cell is found to have consumed its cell‐cycle time, the model invokes the generation module. In this module, actions are taken based on the type of cell that has invoked the subroutine. The module generates a probabilistic value for the type of new cancer cell to be created. The hierarchical cell lineage comprises (i) cancer stem cells that divide both symmetrically and asymmetrically, (ii) differentiated cells, which are short‐lived non‐stem cancer cells, and (iii) quiescent or resting cells. As a result of multiple iterations, the value of 1.9% has been determined as the probability of the original stem cells to divide symmetrically, such that the biologically valid tumour kinetics is maintained throughout the simulation. Natural cell loss is 85%, also in accordance with the literature.

Stem cells have an ability to procreate indefinitely, while differentiated cells are only able to contribute to tumour growth for three generations after which they die (i.e. short‐lived). Quiescent cells are stagnant in the G₀ phase outside the cell cycle and represent about 85% of the total cell population, value that has been obtained through multiple iterations.

At every new cell generation, both the original and the new cells are assigned a new cell‐cycle time. The values of cell‐cycle time are created according to an asymmetrical Gaussian distribution truncated at 1 standard deviation towards lower values and 2 standard deviations towards higher values. This approach is in accordance with the literature data whereby the average head and neck cell‐cycle time (cct) is 33 h, ranging from 20 to 60 h 26. In order to study the role of cell kinetics on tumour growth and behaviour during radiotherapy, three groups of head and neck tumours have been simulated, each having different mean cell‐cycle time: HNC with fast proliferation (20 h), moderate proliferation (33 h) and slow proliferation (60 h). Figure 2 illustrates the Gaussian distributions of the cell‐cycle time for the average (33‐h mean cct) growing tumour.

Figure 2.

Gaussian distribution of cell‐cycle times (cct) around the mean value when the mean cct is 33 h. Cell‐cycle times are represented on the abscissa and the number of tumour cells on the ordinate.

All random generators employed by the model are making use of the Mersenne Twister algorithm, a pseudorandom number generator. The Mersenne Twister algorithm in its mt19937 implementation in the C++ library can generate random numbers uniformly spread within a given range, with a period of 2¹⁹⁹³⁷ – 1 27. This process is completed without adding significant time to the compilation.

To exclude the effect induced by different strings of random numbers and to allow the observation of input variable changes on final results, all simulations have employed the same initial seed for the random number generator engine. The tumour has been grown until a clinically detectable size of 10⁷ cells.

In an agent‐based computational model like the one used in this study, each cell is an individual entity and stochastic decisions are made at this level. The overall behaviour of the tumour results from the added effect of the decisions made at cellular level, which is closer aligned to biological reality. A limitation of this study is the absence of cellular bystander effects and cell‐to‐cell interaction.

Radiotherapy simulation, CSC kinetics and hypoxia

To simulate the effect of radiation on tumour cells, different surviving fractions (SF) have been defined for each cell type and each cell‐cycle stage using the linear quadratic model, according to their radiosensitivity. A mean surviving fraction after 2 Gy of 0.54 26 has been implemented for non‐stem cancer cells. According to the study by Phillips et al. 28 on breast cancer where they have investigated the clonogenic survival of CSC versus non‐stem cancer cells, CSC surviving fractions were found to be 0.19–0.26 larger than SF for non‐stem cancer cells. An analogy has been applied for HNC due to the lack of literature data regarding CSC resistance in squamous cell carcinomas. Thus, in the current model, the CSCs have a mean surviving fraction after 2 Gy of 0.77 (with 0.23 larger than SF for non‐stem cells).

Since hyperfractionated radiotherapy was shown to be the most efficient radiotherapy schedule for advanced head and neck cancers 9, this fractionation schedule has been modelled in this study. Hyperfractionated radiotherapy involves two fractions daily of 1.2 Gy per fraction given 5 days a week, over 7 weeks, thus totalling a dose of 84 Gy. SFs after 1.2 Gy have been determined based on the linear quadratic model. An SF mean value of 0.73 has been obtained for non‐stem cells and 0.85 for CSC. When the radiation module is applied, the cell array is parsed and cells are killed according to the above‐mentioned surviving fraction parameters.

The model considers various hypoxia levels as a function of the mean partial oxygen tension, from 3 mmHg (severely hypoxic) to 10 mmHg (well oxygenated). Surviving fractions of hypoxic cells are determined by the formula:

$${\text{SF}}_{\mathrm{hypoxic}}=1-(1-{\text{SF}}_{\mathrm{normoxic}})/\text{OER},$$

where OER is the oxygen enhancement ratio and has a value of 3, as known from early radiobiological findings 29.

Based on the above‐described virtual tumour growth, the following can be summarized.

The in silico HNC is composed of the following:

• Cancer stem cells (or tumour‐initiating stem cells)

• Differentiated cells

• Resting or quiescent cells

and displays the following properties:

• Head and neck carcinoma‐like kinetics

• Distinct radioresistance for non‐stem cells and the subpopulation of CSC

• Hypoxic, with various levels of hypoxia

The main parameters studied in this study are tumour growth kinetics, hypoxia and CSC division pattern, particularly the probability of symmetrical division. Therefore, tumour response to hyperfractionated radiotherapy has been analysed for these factors that can vary within the ranges specified in Table 1.

Table 1.

Tumour‐related parameters influencing cancer response to treatment and their corresponding values as modelled in this study

Tumour‐related parameters	Values/ranges
Cell‐cycle time	20, 33, 60 h
Hypoxia	3–10 mmHg
Probability of symmetrical division	1.9–10%

Results

Head and neck tumour growth

The growth curves corresponding to the three groups of head and neck tumours simulated as described above are represented in Fig. 3, illustrating the differences in growth speed as dictated by each tumour's independent cell kinetics.

Figure 3.

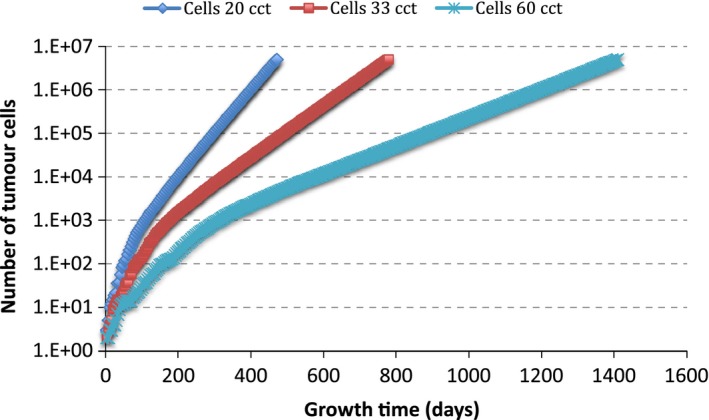
Exponential tumour growth curves for three groups of head and neck cancer with different growth kinetic parameters.

Tumour growth parameters are listed in Table 2 compared with the literature data. Certain parameters, such as cell division rate, are model‐driven, and therefore, no literature values are indicated for comparison. However, all listed parameters are interrelated in the model, so the in silico endpoint (i.e. the final tumour population) is in accordance with the in vivo characteristics of a head and neck neoplasm.

Table 2.

Tumour growth parameters according to the model

Parameters	Tumour group 1	Tumour group 2	Tumour group 3	Literature data (range) (reference)
Length of S phase	6.67 h	11 h	20 h	11 h 26
				13.7 h (7.3–37.5) 30
Mean cell‐cycle time (range)	20 h (12–36)	33 h (20–60)	60 h (36–108)	33 h (20–60) 26, 31
Volume doubling time	31 days	52 days	96 days	45 days (33–150) 32
Labelling index	4.71%	4.69%	4.67%	8% (1.2–30) 30
Cell division rate (24 h)	2.3%	1.3%	0.74%	— (derived from the model)
Pre‐treatment percentage of cancer stem cells	5.37%	5.42%	5.36%	Tang et al. 6
				Harper et al. 7
Cell loss factor	85%			85% 33

The influence of CSC dynamics and radiobiological hypoxia on tumour response to hyperfractionated radiotherapy

Hyperfractionated treatment has been simulated on the virtual tumour (1.2 Gy twice a day, 5 days a week, over 7 weeks, totalling 84 Gy) grown in various hypoxic conditions and having different cancer stem cell fractions. The following scenarios (with the parameters presented in Table 1) have been modelled and interpreted:

1. Tumour response in oxic environment with variable CSC division pattern

2. Tumour response in variable hypoxic environment with constant CSC division pattern

3. Tumour response in variable hypoxic environment with variable CSC division pattern

Tumour response to hyperfractionated radiotherapy in oxic environment with variable CSC division pattern

CSC division pattern refers to the probability of symmetrical division in mitosis. While this ability is an important property of CSCs, there are no quantitative data in the literature that would indicate the proportion of CSC undergoing symmetrical division in HNC. In the model, the probability of CSC symmetrical division has been varied from the initial 1.9% up to 10%. Very small increments showed no significant difference in treatment response (not shown here); therefore, larger values have been modelled (5% and 10%).

For a better illustration of the impact of tumour parameters on treatment response, the results are expressed as a function of the number of 1.2 Gy fractions needed to eradicate the tumour. Since hyperfractionated radiotherapy delivers an overall dose of 84 Gy in 35 treatment days, the number of 1.2 Gy fractions during a complete treatment is 70. Therefore, any values exceeding 70 fractions are interpreted as non‐efficient.

Figure 4 illustrates tumour response as a function of growth kinetics and CSC division pattern for oxic tumours. Minimal differences among tumours with different probabilities of symmetrical division are observed. Tumours are controlled, as all cancer cells are destroyed during treatment. The number of 1.2 Gy fractions necessary for tumour kill varies between 46 (55.2 Gy) and 57 (68.4 Gy), which are below the prescribed dose in a hyperfractionated setup. However, this clinical situation is rare, as HNCs are known to be usually hypoxic 34, which increases tumour resistance to radiation.

Figure 4.

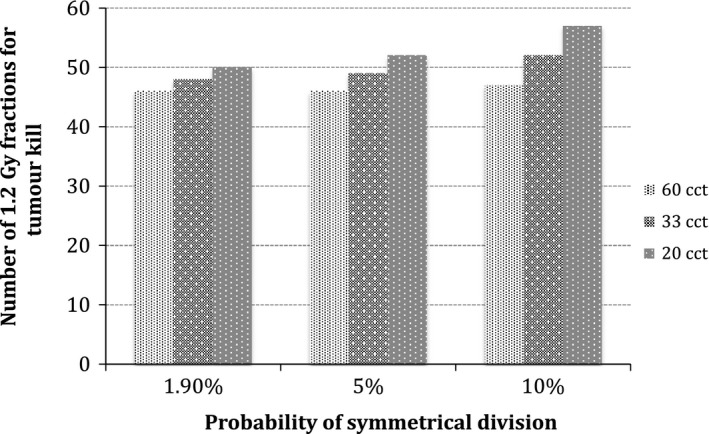
Tumour response as a function of growth kinetics and CSC division pattern for oxic tumours.

Tumour response to hyperfractionated radiotherapy in variable hypoxic environment with constant CSC division pattern

In order to study the influence of hypoxia on tumour control, an unperturbed CSC division pattern has been considered (pre‐treatment symmetrical division probability of 1.9% is also kept during treatment). Tumour hypoxia has, therefore, been modelled for three scenarios: severely hypoxic (3 mmHg), moderately hypoxic (6 mmHg) and mildly hypoxic tumours (9 mmHg) for the three tumour groups with different growth kinetics (20‐, 33‐ and 60‐h cell‐cycle time).

Although Fig. 5 shows a very strong influence of hypoxia on treatment response (as compared to the influence of symmetrical division probability for oxic conditions in Fig. 4), no significant variations among tumours with different growth kinetics have been found (7% in both mild and moderately hypoxic conditions), excepting the case of severe hypoxia, where the variation in the number of fractions among tumours was 12%. Tumours with severe hypoxia differ significantly based on their growth kinetics. None can be controlled with hyperfractionated radiotherapy‐only, all of them requiring adjuvant therapies.

Figure 5.

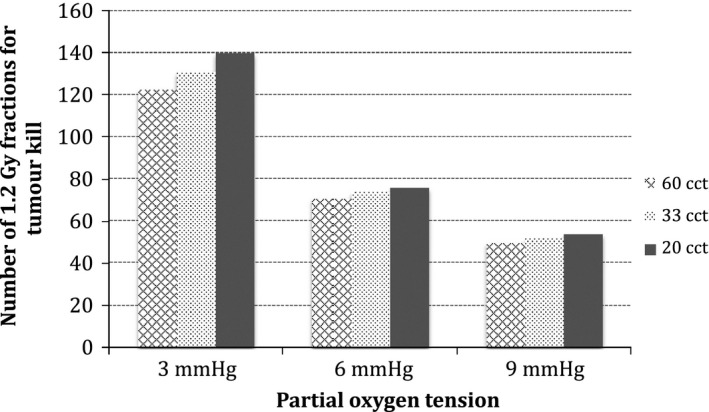
Tumour response as a function of growth kinetics and hypoxia.

This study was taken further to evaluate the above processes for a higher probability of symmetrical stem cell division (i.e. 5%). Comparison of tumour response among cancers with different kinetics as a function of CSC division pattern (1.9% versus 5% probability of symmetrical division) is shown in Fig. 6.

Figure 6.

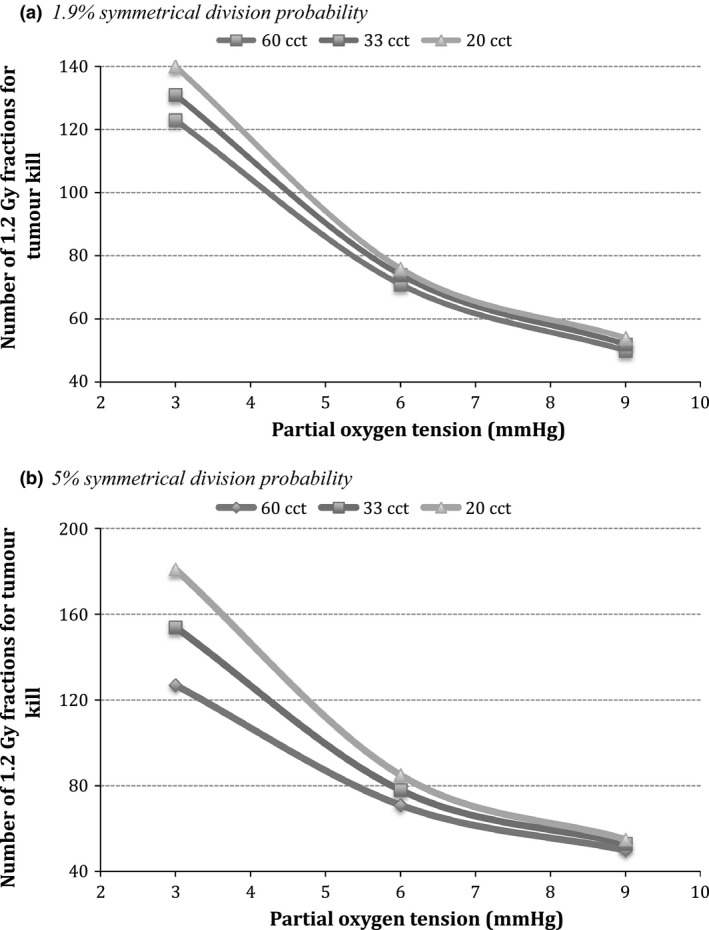
Comparison of tumour response among cancers with different kinetics as a function of CSC division pattern. (a) 1.9% symmetrical division; (b) 5% symmetrical division.

The trend for tumour response to hyperfractionated radiotherapy when CSCs divide symmetrically with a 5% probability is similar to the initial case of 1.9%. The level of hypoxia is shown to be, once again, a strong predictor of treatment response. The more severe the hypoxia, the greater the role played by growth kinetics. The difference in response between slower growing HNC (60 cct) and faster proliferating HNC (20 cct) is 54 fractions of 1.2 Gy, which represents about 30% of the number of fractions required to eradicate the tumour.

This is nevertheless a hypothetical schedule, as no patient could be subjected to such high doses of radiotherapy. The aim of the simulation was to illustrate the interplay between growth kinetics and tumour hypoxia when altered fractionation schedules are administered and to emphasize the need for predictive assays for optimal patient stratification in order to increase tumour control and find the most suitable adjuvant therapies.

Tumour response to hyperfractionated radiotherapy in variable hypoxic environment with variable CSC division pattern

This section has evaluated the interplay between the three factors that dictate tumour growth and behaviour during treatment: growth kinetics, hypoxia and CSC division pattern.

Figure 7 is a comparative representation of tumour response to hyperfractionated radiotherapy for the three studied tumour groups and hypoxia levels as a function of CSC symmetrical division probability.

Figure 7.

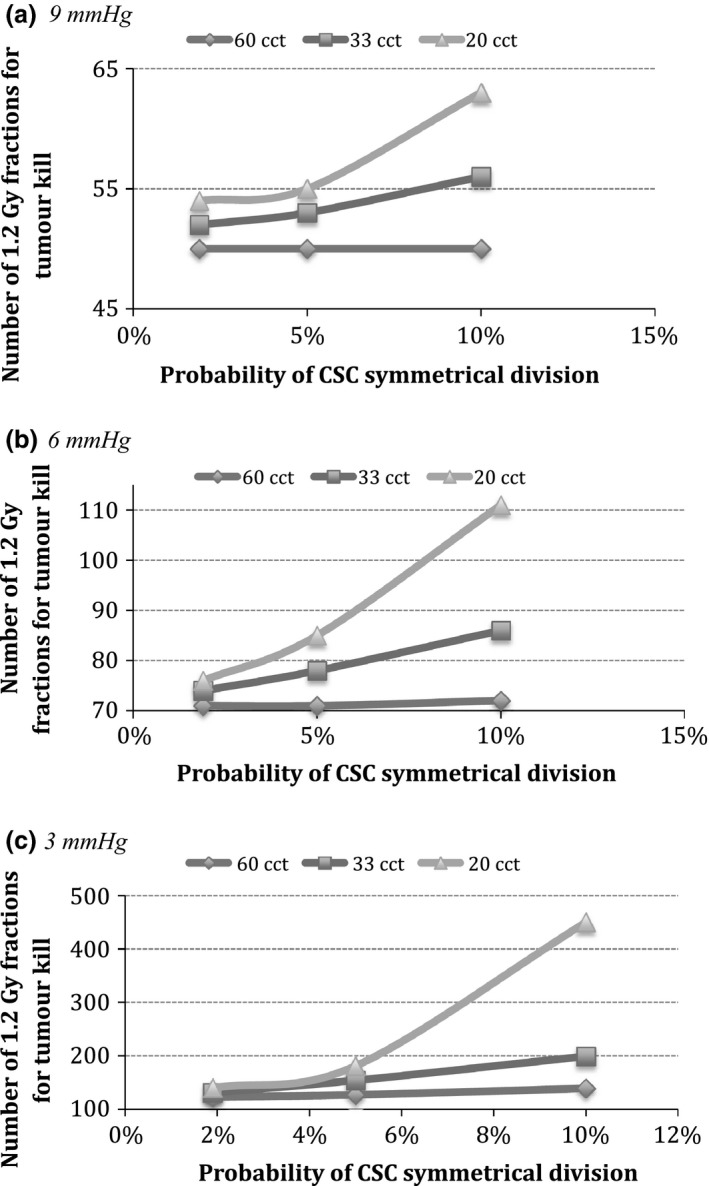
Comparison of tumour response among cancers with different kinetics as a function of CSC division pattern and tumour hypoxia. Note that the ordinate has been adjusted for each graph to further show the difference between the linear and exponential curves. (a) 9 mmHg, (b) 6 mmHg and (c) 3 mmHg.

Hyperfractionated radiotherapy appears to be an effective treatment method as a sole agent for tumours with mild hypoxia, irrespective of growth kinetics or CSC division pattern (up to the modelled value) (Fig. 7a). This is not the case for higher levels of hypoxia: Moderately hypoxic and slowly proliferating tumours can be controlled with hyperfractionated radiotherapy alone; however, faster proliferating HNC cannot be fully eradicated (Fig. 7b). Furthermore, Fig. 7c shows that irrespective of growth kinetics, none of the severely hypoxic tumours can be fully controlled with the hyperfractionated schedule.

Discussion

Advanced head and neck carcinomas are aggressive tumours due to various factors. Beside tumour hypoxia which is known to be a negative prognostic factor for treatment outcome, the subpopulation of CSCs contributes to the poor response due to their specific properties that confer radioresistance and self‐renewal ability. It has been showed that out of all known mechanisms behind accelerated tumour growth, namely cell recruitment, accelerated cell division, abortive division and loss of asymmetrical division (thus enabling symmetrical division), the latter one has the greatest impact on tumour response to treatment 35, 36. The aim of this study was to simulate the growth and behaviour during hyperfractionated radiotherapy of three groups of head and neck cancers governed by different growth kinetics, hypoxic fractions and CSC subpopulations. Various levels of hypoxia and cancer stem cell division pattern have been modelled, showing that there is a strong synergistic effect between these two factors, particularly in tumours with high cell turnover.

The results of this study have indicated that tumour growth kinetics influences tumour response to treatment. As hypoxia and CSC division pattern are better expressed, they gradually achieve a synergistic effect on tumour response among cancers with different growth kinetics. Slowly growing tumours show a linear dependence of treatment dose with hypoxia/cancer stem population, whereas rapidly growing tumours follow an exponential curve.

As shown in Fig. 7, tumours with CSCs in a severely hypoxic niche will not be eradicated by radiotherapy‐only, irrespective of the initial growth kinetic parameters. Fast proliferating tumours have a remarkable resistance to treatment due to the interplay of these critical factors: hypoxia, CSC subpopulation resistance, accelerated repopulation (via symmetrical division, shortening of stem cell‐cycle time and cell recruitment) and repopulation via asymmetrical division of non‐stem cancer cells.

Based on the above model, the following can be summed up:

• Oxic and very mildly hypoxic HNC can be controlled by hyperfractionated radiotherapy, irrespective of growth kinetics and CSC division pattern (note that this study has modelled up to 10% probability of CSC symmetrical division).

• Tumours with moderate hypoxia show different responses to radiotherapy: while slowly proliferating HNC (60 cct) are still controllable, tumours with higher cell turnover show more resistance. This radioresistance is dictated by the joint effect of hypoxia and CSC subpopulation. In rapidly proliferating tumours (20 cct), the number of fractions to achieve tumour control increases exponentially with the probability of CSC symmetrical division, whereas in moderately growing HNC (33 h), this behaviour is linear.

• Severely hypoxic tumours cannot be controlled by radiotherapy‐only. Tumours with CSCs in a severely hypoxic niche require more targeted, adjuvant therapies to be eradicated.

The overall dose of 84 Gy given in 1.2 Gy fractions during hyperfractionated radiotherapy is already a large dose for the normal tissue, which would not tolerate further dose escalations. Therefore, these tumours need additional radiosensitising agents to increase the therapeutic response.

The most significant finding of this study is the linear dependence between hypoxia/cancer stem population and dose needed for total tumour control in slowly growing tumours, while the same dependence in rapidly growing cancers is exponential. Thus, fast proliferating HNCs do not simply change the slope of the dependence curve, but they behave according to a new, exponential type of distribution.

Considering that one of the accelerated repopulation mechanisms is the shortening of the stem cell‐cycle time 37 leading to faster cell turnover (not modelled), tumours with average cell‐cycle time (33 cct) can easily become fast proliferating, thus changing the shape of their treatment response curve from linear to exponential. HNCs that present fast proliferation (20 cct) before beginning of treatment will only exacerbate the exponential trend requiring an enormous dose of radiation, obviously clinically impossible. These findings highlight the paramount importance of differentiating between slow and fast proliferating tumours among the same histopathological type.

The above modelling results, in accordance with international trials on HNC, come to emphasize the need for predictive assays on proliferative ability and growth kinetics among the same histopathological tumour group.

In conclusion, differences in treatment response of various HNC models due to CSCs, hypoxia and their interplay with growth kinetics show the importance to identify resistant subpopulations within the tumour. Consequently, head and neck tumours should be treated differentially as a function of the aforementioned characteristics, given that the magnitude of radiation dose adjustment and the addition of adjuvant therapies depend on such parameters.