The geometry of proliferating dicot cells

Abstract.

The distributions of cell size and cell cycle duration were studied in two‐dimensional expanding plant tissues. Plastic imprints of the leaf epidermis of three dicot plants, jade (Crassula argentae), impatiens (Impatiens wallerana), and the common begonia (Begonia semperflorens) were made and cell outlines analysed. The average, standard deviation and coefficient of variance (CV = 100 × standard deviation/average) of cell size were determined with the CV of mother cells less than the CV for daughter cells and both are less than that for all cells. An equation was devised as a simple description of the probability distribution of sizes for all cells of a tissue. Cell cycle durations as measured in arbitrary time units were determined by reconstructing the initial and final sizes of cells and they collectively give the expected asymmetric bell‐shaped probability distribution. Given the features of unequal cell division (an average of 11.6% difference in size of daughter cells) and the size variation of dividing cells, it appears that the range of cell size is more critically regulated than the size of a cell at any particular time.

Introduction

Developmental biologists have described several differences between plants and animals and perhaps the most significant one is that plant cell walls are cemented together while animal cells can change position (Steeves & Sussex 1989; reviewed in Korn 1993a). The developmental consequence of intercellular fixity in plant tissues is four‐fold. First, cells in the same vicinity grow at the same rate, although this rate can vary across a tissue. Second, tissue growth must be exponential because all cells are growing and dividing. For growth to be arithmetic or linear, growing cells will multiply resulting in some growing and colleagues not in order for the tissue to remain at a constant rate; this would lead to cases of growing cells contiguous to nongrowing cells and subsequent tissue tearing. Also, wall growth has been measured and found to be exponential (Korn 1998). Third, neighbouring cells cease growing at the same time upon maturation. A corollary to this feature is that individual cells cannot leave the mitotic cycle as do animal cells. Fourth, some special types of differential growth are permitted such as new cell plates do not grow for one generation and differentiated cells such as hairs and stomates cease growing as do walls facing an injury, however, walls adjacent to these loci undergo faster than average compensatory growth (Korn 1993a). During growth and division of plant cells, values of several parameters are conserved: epidermal cells growing in two dimensions average 6.0 (anticlinal) facets and have three‐rayed vertices, three‐dimensionally growing cells average 14.0 facets while manifesting intersecting vertices of four facets. (Cooke & Lu 1991), and cells express a limited range of sizes (Korn 1993b).

Since cells of a proliferating plant tissue are in different stages of the cell cycle (Korn 1993b) and cease growing at the same time (point 3 above), a mature population is composed of cells at different ages or stages in the cell cycle. Also, since cells become larger with age, cells of different ages will be of different sizes. A number of features of proliferating cells can be reconstructed from a tissue of mature, nondividing cells. The probability distribution frequencies (pdf) of cell sizes can be determined by direct cell measurement. (Korn 1993b). Also, pairs of daughter cells can be identified (Fig. 1A) and by measuring their size, the extent of inequality of cell division can be calculated (Korn 1993b). Trios of cells of one sister and its sister’s daughter cells can be identified and by their sizes the relationship of cell size to the time of division can be determined (Fig. 1A). Here daughter cells are noticeably different in size from unequal cell division, a condition which is compensated for by the smaller daughter having a longer cell cycle than the larger daughter. By this means cell size is restricted otherwise very small, dysfunctional and large, collapsible cells would be produced (Korn 1980, 1993a).

Figure 1.

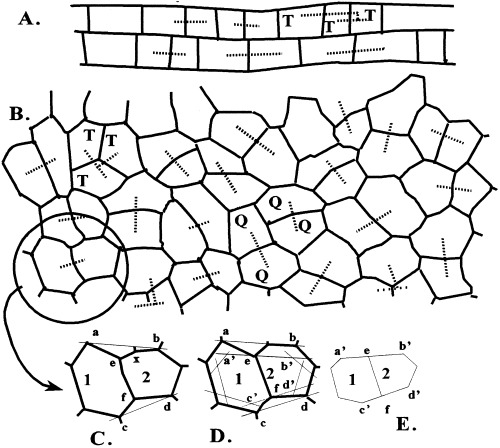
(A) Upper leaf epidermal cells of the monocot Zebrina. Dashed lines drawn between sister cells. ×50. (B) Upper leaf epidermal cells of the dicot jade. Dashed lines between sister cells, one group of which is a trio (T) with the two smaller daughter cells on the left and the largest, aunt cell on the right. A quartet of granddaughter cells (Q). Reconstruction of original cell area and shape. (C) Lines drawn (and) between vertices adjacent to cell plate vertices (e,f). (D) Lines drawn through plate vertices and parallel to first constructions. (E) Final reconstructed state of walls of new sister cells.

These types of studies have been conducted on epidermal cells of elongating monocot leaves where cell size is taken simply as cell length (Fig. 1A). By contrast dicot epidermal cells are isodiametric (Fig. 1B) which complicates analysis significantly but, as will be shown, also offers additional reconstruction possibilities to find the absolute sizes of mother and daughter cells as well as generation times, approaches not possible in elongating cells. Hence it is important to extend this type of cell cycle analysis to dicot tissues. It would also be desirable to develop a useful mathematical expression of the pdf by an equation that includes only a few essential values.

MATERIALS AND METHODS

Specimens of the common jade plant, Crassula argentae L., the New Guinea impatiens, Impatiens wallerana (Dazzler®), and the typical bedding begonia, Begonia semperflorens (Link and Otto), were purchased from a local nursery. Imprints of the upper (adaxial) epidermis were made with clear fingernail polish (Sampson 1961) and 500 cells of each were drawn with the aid of a camera lucida. In addition, 250 pairs of daughter cells were drawn. Cut‐outs of camera lucida drawings of cells were weighted and their absolute areas calculated by comparison to the weight of a piece of paper of known magnified area in µm². Computer programs were written in Visual Basic 4.0.

RESULTS

Cell size data

Epidermal cells of jade are highly geometric with distinctive, straight walls and three‐rayed vertices making tracing the cell outline easy and accurate (Fig. 1B). The average cell size is 1850 µm² and cell size ranges more than fivefold from 680 to 3790 µm² (Fig. 2a, Table 1). A useful value for making comparison is the coefficient of variation which is the standard deviation over the mean times a hundred (CV = 100 ± SD/mean). Here the CV is 100 × 700/1850, or 37. Comparable data for impatiens are a mean and standard deviation of 4075 µm² and 1245 µm² for a CV of 31, and for begonia the values are 2030 µm², 539 µm² and 31 (Table 1). The pdf for cell size of jade is an asymmetric distribution with a distinct tail to the right (Fig. 2A).

Figure 2.

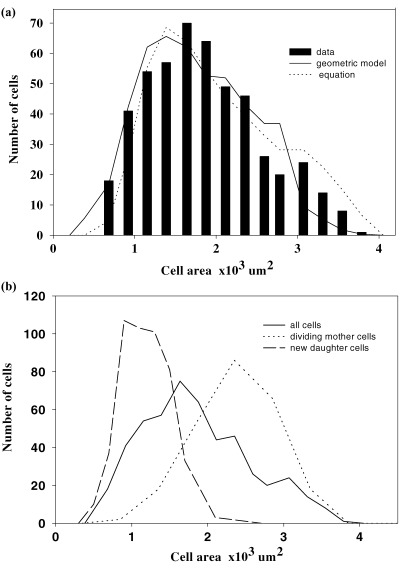
Cell sizes of jade. (A) Obtained data and expected frequencies from computer graphics model and equation. (B) Obtained data on all cells, reconstructed dividing mother and new daughter cells. Different sample sizes for the three groups of cells.

Table 1.

Cell sizes in µm² of the upper epidermis of the leaves of jade, impatiens and begonia

Feature	Plant
	Jade	Impatiens	Begonia
All cells
Range	680–7390	11,200–4700	520–3,400
Average	1850	4075	2,033
Standard deviation	700	1245	539
Coefficient of variation	37	31	31
Mother cells
Range	850–4350	2,400–5750	1,400–3,400
Average	2440	4020	2,323
Standard deviation	600	840	401
Coefficient of variation	25	21	17
Daughter cells
Range	1,000–5000	950–3650	650–1,850
Average	1200	2082	1,165
Standard deviation	340	576	315
Coefficient of variation	28	27	27
% difference in pairs	11.8	10.4	9.9

The arrangement of cells reveals sister cell pairs. Generally the cell plate is the longest facet of a cell and two contiguous cells with the same longest wall is good evidence of paired sister cells. When sister cell pairs are identified in a field of cells all cells can be accounted for with the exception where a trio of cells is found because one sister has divided before the other (Fig. 1A, B, letter T). Having identified daughter cells, the size of their mother at the time of division can be reconstructed. Cell plates do not grow for one generation thereby creating three angles approaching 120° at vertices rather than remaining at the original 90°–90°–180° values. Hence, the plate has not enlarged since the mother cell was partitioned. To determine the size of the dividing mother cell first lines 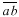and 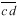are drawn through adjacent vertices of 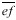the plate that existed at the time of cell division (Fig. 1C). Next a line 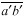is drawn through a vertex e of the cell plate and parallel to line 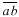and a second line 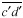is also drawn parallel to line 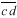and through the other vertex f of the plate (Fig. 1D). Finally, lines are drawn parallel to the other walls of the two daughter cells at a distance that separate 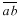from 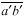(Fig. 1E). The resultant two figures have the original size and shape of the two daughter cells and therefore that of their mother cell. These are not the true values of the meristematic cells as they have enlarged about sevenfold after proliferation during leaf maturation, however, the relative size of cells to each other in the tissue remains unchanged.

A total of 250 cell pairs were reconstructed for jade and their areas determined. Daughter cells of jade have an average of 1200 ± 340 µm² for a CV of 28 while mother cells averaged 2440 ± 600 µm² for a CV of 25 (Table 1). The average difference in daughter cell size is 11.6%, that is, about 6% off the expected 50 : 50 ratio. Comparable data for impatiens and begonia are given in Table 1 and, in general, the CV for daughter cells is less than the CV for mother cell, and that for mother cells is less than that for all cells.

The range of sizes for mother and daughter cells are given in (Fig. 2B) and clearly there is an overlap of these two groups. Also, the profile on the left side of the daughter cell group matches that for all cells, and the right side of the mother cell group matches that for all cells. Since the sizes of all cells was measured directly and those for mother and daughter cells are from reconstruction, these parallel profiles give validity to the reconstruction method.

Of 30 cell trios examined where one sister divided and the other had not, the larger of the two sister cells divided first in all cases.

Quartets of granddaughter cells can also be identified and their outlines used to determine cell generation times of individual cells (1, 3). An initial daughter cell (A_d) becomes a mother cell (A_m) that divides into two daughter cells (B_d and C_d). Then B_d and C_d grow into sister mother cells (B_m and C_m), respectively. One sister mother cell (B_m) divides into two sister granddaughter cells (D_d and E_d) as the other sister cell (C_m) divides into another pair of daughter cells (F _d and G_d). It is the durations in relative iterations of growth of the two sisters when they become mother cells (B_d→ B_m and C_d→ C_dm) that are calculated. First, the original mother cell (A_m) is identified, then its two sister daughters (B_d and C_d) are reconstructed, and next these two sisters as mothers (B_m and C_m) are drawn (Fig. 3A). The increase in size of cells over their life is measured and the extent of increases (I_B = B_m/B_d, I_C = C_m/C_d) is calculated. The logarithm of the increase is divided by the logarithm of the growth rate (log I/log k) to give the duration of a cell life as measured in iterations of growth. For example, daughter cells B and C are 18 and 22 units in size and divided as mother cells when they were 41 and 38 units. The growth rate of 0.035/per iteration was selected to double size over 20 iterations (1.035²⁰ = 2.0), 20 iterations was selected for convenience as they give a reasonable range of cell sizes (12–32) for identifying type, or shape, of the pdf because its extremes have frequencies close to zero and less than 1/10 that of the peak. The cell cycle duration of cell B is then calculated as cc_B = log (41/18)/log (1.035) = log 2.27/log 1.035 = 23.7 intervals and the duration of cell C is cc_C = log(38/22)/log (1.035) = 15.7. A total of 100 cells were measure for cycle duration and their pdf is given in Fig. 3B. The pdf is nearly a symmetrical distribution with an average of 19.1 with a standard deviation of 3.6 for a CV of 18.8. The average number of intervals is less than 20, because dividing cells do not exist, except as smaller daughter cells.

Figure 3.

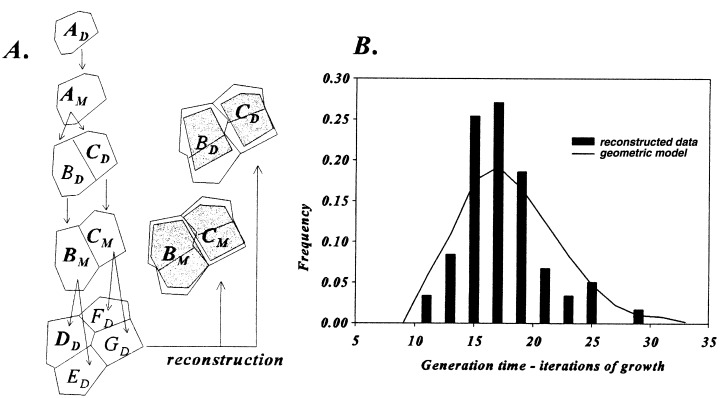
Generation time from Q cells in Figure 1B. (A) Reconstruction (shaded areas) of cells (B) and (C) at their inception and later at time of division. See text for method of calculations. B. Probability distribution of cell cycle duration.

Geometric model of cell size

A computer graphic model for two‐dimensional proliferation of cells was previously developed for determining the rules of cell growth and division (Korn 1993a). Proliferation was based on logarithmic growth of walls except for new cell plates that do not expand for one generation. And cell division is expedited by the cell plate passing through the cell centre and connecting orthogonally to the longest wall (Fig. 4). Values of cell sizes for this model were calculated and converted to those for jade by first factoring the difference in average cell size (Fig. 2A). Comparison of cell sizes in this model to those of jade by the χ² (= 13.8) method gave an acceptable fit of P > 20%. Cell generation times as the number of iterations from cell birth to time of division of individual cells were also tabulated and a symmetrical distribution was obtained, similar to that of the actual data (Fig. 3B).

Figure 4.

Cell arrays from computer graphics model. (A) Initial cell. (B) First daughter cells after 10 iterations. (C) Final array after 85 iterations.

Probability distribution of cell size

Mitchison (1971) described the pdf for cell age as a negative exponential distribution truncated on the right, f(a) = 2^1.0–a, where age, a, is measured in cell cycles from 0 to 1.0 (Fig. 5A). This relation was extended to cell size (s) by the doubly truncated expression f(s) = 2S/s with mother and daughter cells sizes 2S and S, respectively (Korn 1993b). The expression of this truncated distribution can be restated in the discrete form of a geometric distribution for size of growing cells (s_g).

Figure 5.

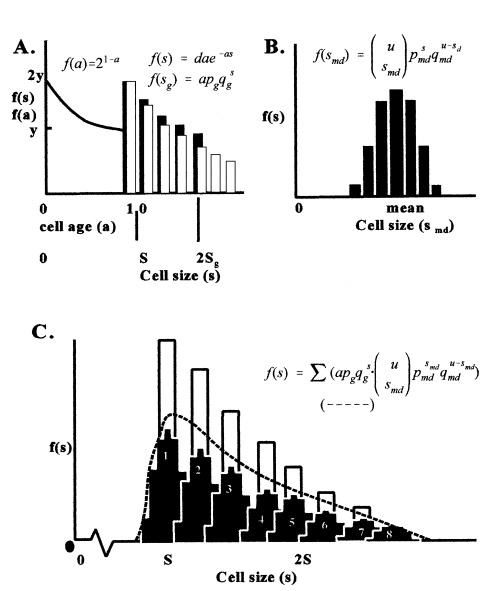
Graphs of steps in developing the equation for cell size. Equations are explained in text. (A) Mitchison’s model for cell age (line), Korn’s model for cell size (dark bars), and new discrete geometric model of growth/age (white bars). Equations are for both a continuous (f(s_g) = dae^−as) and discrete (f(s_g) = ap q_g ^{s − (1)}). (B) Model for new cells as a compound binomial distribution (black bars). (C) Joint distribution of growth (white bars), daughter cell cohort at different times (sets of black bars) and the cumulation of cells from different age cohorts of the same size (dashed line) corresponding to what is observed in actual tissue.

(1)

where p is adjusted so f(S)/2 = (f)2S, a normalizes the total to unity, S is the left point of truncation and 2S is the right limit of mother cells (Fig. 5A). Actually the limit of mother cell size is not 2S as can be seen in Fig. 2(B) but is a bell‐shaped distribution of sizes. The frequency value at 2S is then replaced by a binomial distribution for frequencies of mother cell sizes (s_m), or

(2)

As this equation replaces the value of 2S so all s‐values in (1) will be replaced by this equation because all cells eventually come from mother cells.

Also, cell division is not equal as the average difference between daughter cell sizes is about 12% (Table 1), ranging from 0% to 35%. The value of S for daughter cells in equation 1 is then replaced by another binomial distribution for size of daughter cells (s_d) so

(3)

Equations 2 and 3 can be treated jointly with u = M + N and the modified daughter cell (s_md) distribution becomes

(4)

These daughter cells form a cohort of cells of the same age (a = 0) although expressing a normal distribution of sizes. The cohort formed during the previous iteration will have a greater average size as it has grown over the period before the new cohort was formed (Fig. 5C). This previous cohort of larger cells will also be a smaller percent of all cells because the population has increased in size by half the number of new daughter cells since each mother is replaced by two daughters. Consecutively older cohorts have a progressively larger average size and represent a smaller frequency of the population. In developing the final model cohorts then replace cells of the same size and age in the truncated geometric equation 1. Equations 1 and 4 can be joined to give the pdf for cell size of the whole population

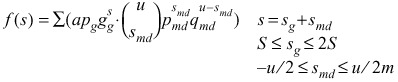(5)

To compare the values of jade to the expected ones from equation 5, u is taken as 18, the average of 1.414S becomes 1850 µm², and then the values of s were calculated (Fig. 2A). These values compared well with the jade data statistically (χ² = 22.7, P > 20%).

DISCUSSION

The geometric features of proliferating cells in two‐dimensions as in the case of dicot epidermal cells examined here are similar to those examined previously in one dimension as previously described for monocot epidermal cells (Korn 1993b). First, both types of cells undergo somewhat unequal division with paired monocot daughter cells differing in size by about 7.5% in Zebrina (wandering jew) and here the values are 11.8%, 10.4% and 9.9% for jade, impatiens and begonia, respectively. Second, the pdf for cell size in both monocots and dicots express an asymmetric profile skewed to the right. Thirdly, the range from smallest to largest cells is at least about a factor of four (Zebrina) to as much as six (begonia). Fourth, there is some overlap of cell sizes for daughter cells with those of mother cells, and the overlap involves about 8% of the cells in Zebrina and 19% in jade. Similar features have been found for various animal tissues. Unequal division appears to be universal in animals, and the distribution of sizes for all cells is single‐peaked with a noticeable tail to the right (Nachtwey & Cameron 1968). Also, the CV for daughter cell size is greater than that for mother cells (Koch & Schaechter 1962; Nanninga et al. 1982).

The opportunity to reconstruct the geometry of dividing mother cells and new daughter cells from an array of mature cells is based in the fact that cell plates do not grow for one cell generation and provides valuable data on the dynamics of cell size change and cell cycle duration. This assumption about the cell plate not growing (Korn 1973) was criticized by Cooke & Lu (1991) as physically untenable but later it was shown to occur by actually following living cells over two generations (Korn 1993a). The binomial distribution of daughter and mother cell sizes indicates the idea of deterministic S‐sized daughter cells and 2S‐sized mother cells is unrealistic. That the ranges of mother and daughter cells overlaps also indicates size alone does not explain regulation of the cell cycle. However, size does play some role in regulating cycling as shown by finding that the larger daughter cell divides before the smaller one.

Age also does not play the critical role in cycle regulation. New daughter cells in the three species examined express a CV greater than those for dividing mother cells. This increase in order indicates the cohort of new daughter cells does not become the cohort of dividing cells later, dividing cells must come from different daughter cohorts that have some feature in common. Further evidence for age playing some but not the sole cause for cell division is seen by the pdf for cycle duration (Fig. 3B). Hence, dividing cells have neither cell age nor cell size in common, however, both parameters are related to the timing of cell division.

It was suggested earlier that animal cells pass through two phases of growth, phase A expresses a transitional probability for shifting into a deterministic phase B. (Burns & Tannock 1970; Smith & Martin 1973). Phase A appears to be during the G₁ phase as its distribution profile matches that of the population age of cells (Shields & Smith 1977). Sennerstam & Strömberg (1996) proposed a different pair of phases, one for growth that is probabilistic in duration and one for DNA synthesis that is deterministic. Here the two are assumed to be weakly coupled at several points to restrict the duration of the cell cycle. A ‘sloppy size control’ model was proposed by Tyson (1986) for yeasts where the first phase is deterministic and the second is indeterministic with the probability of division onset increasing with time.

Any probabilistic model has to explain the bell‐shaped distribution of sizes and ages of dividing mother cells. A population of n cells that will divide with probability p have np cells siphoned off from the population by division after the first interval of time. At the next interval p(np) cells will divide and consecutively fewer to express a geometric distribution, p ^tq, where t is the number of intervals of time. This is not the observed bell‐shaped distributions. If the probability of division increases with time, f(p) = k_t, then a bell‐shaped distribution is realized; initially a few cells divide because p is small, then many cells divide because p and n are intermediate in values and later few cells divide once again because n has become small. Tyson’s sloppy size model satisfies the observed pattern but Burns & Tannock (1970) and Smith & Martin (1973) suggest a process they characterize ‘like radioactive decay’ that underlies the transition probability which will give a negative exponential distribution, an unacceptable profile. The model of Sennerstam & Strömberg (1996) is also unacceptable for this reason. There appears to be differences as to the profile of cell cycle times with a normal distribution for bacteria (Kelly & Rahn 1932), yeast (Miyata et al. 1978) and human amnion cells (Sisker & Moraca 1965) and with a negative exponential decay profile found in the distributions for rat sarcoma (Smith & Martin 1973), mouse fibroblasts (Shields 1977), and bacterial cells (Shields 1978). In the plant tissues examined here no dramatic, additional exponential decay is found as an extended right‐handed tail for dividing cell size and age.

An indeterministic expression comes from either a biological mechanism behaving as a random number generator as seen in mendelian segregation or time of seed germination or from noise acting on a system such as variation in stem diameter or thickness of cell wall along their lengths. The former cases reflect a strategy and express a relatively large CV (10–50) whereas those of noise are unregulated and the CV is much less (<10). Mother cell size and cell age fall into the first category of indeterminism, but it is not clear why there is so much variation in cycle times and cell sizes. The strategy for indeterminism in mendelian segregation of alleles and timing of seed germination over several years is clear but what advantage there is for a range of cell cycle duration and cell size is not clear. Perhaps there is no simple method by which a cell can monitor its size and what method has evolved relates more to restricting the range because very small and very large cells are dysfunctional. Range may be more significant than any other parameter in cell cycling.

A model can be proposed that explains both the basis of probabilistic behaviour and generates the appropriate pdf of size of mother cells. Since neither cell size nor cell age alone dictates time of division, nor does their joint effect (that would give an even greater dispersion), a third feature needs to be introduced and that is some cytoplasmic, particulate factor that increases in number exponentially and at some critical multiplicity they induce the onset of cell division. The growth rate of these factors increases with cell size because there is more cytoplasmic precursors and decreases with number of factors per cell that have to share the precursors. When a cell divides daughter cells are unequal and probabilistic for size as well as for the number of these factors according to mother cell size and chance segregation. Cell size and factor number is coupled by the growth rate of the factors as the rate is a function of cell size and number of factors present. Cell size and factor number are uncoupled at division by unequal cell division and chance segregation of factors into daughter cells. The dynamics of these factors would be like those of chloroplasts both as to their increase in number and segregation at division. A simple computer model was constructed to test this hypothesis with the following parameters.

f = number of factors in a cell

s = size of cell

k_s= growth rate of cell (0.07 per interation)

k_p= growth rate of factors (0.005f–0.0005 s) [couples cell size and number of factors]

x= number of factors that induce onset of division (20)

s_d1/(s_m− s_d2) < = >1 gives unequal cell division [uncouples cell size and number of factors]

f_d1/(f_m− f_d2) < = >1 gives random segregation of factors among daughter cells

When this algebraic model was run to produce some 16 000 cells over 1600 generations, the pdf of cell sizes was an asymmetric distribution with overlap of mother and daughter cell sizes and the CV for daughter cells is larger than that for mother cells. The advantage of this model over others is in the mother size distribution from known size and age of daughter cells. Nurse (1980) proposed a somewhat similar cytoplasmic hypothesis but he had only one large division‐inducing entity that enlarges and when completed binds to some critical site. The probability feature lies in the time required for the entity to become successfully bound. This system, however, would give a negative exponential distribution, one not recognized here for dividing cell size and age.

A significant difference between animal and plant cell sizes lies in the role of size in cell differentiation. Animal cells can leave the cycle without geometric (physical) consequences because they have slippage whereas plant cells are fixed together and growth of one cell must match that of contiguous cells. Actually some plant cells leave the cycling process to either (a) continue growing without further cell division or (b) continue growing but at a different rate. One example of the first case is the epidermal stone cell that ceases dividing about three cell cycles before the tissue itself ceases proliferation leading to the formation of a large cell that forms a single crystal (Mauseth 1988). Apparently cells of any size can leave cycling to become these specialized stone cells. A second example is that of the procambial initial cell which ceases division about four cycles before the rest of the tissue ceases growth and division resulting in a cylindrical cell that later divides longitudinally into elongated xylem and phloem cells of veins, structures having the proper shape for transport of solutes (Korn 1998). An example of the later case are stomates that form one to three cycles before the epidermis ceases growth and division and during this time the contiguous epidermal cells radially elongated by compensatory growth (Korn 1993a). In one sense, the development of the entire plant is making and deploying contiguous cells of various sizes into one geometrically compatible whole. It is then of interest to identify the initial array of cell sizes in proliferating tissues and then to follow individual cells of this array as they specialized to create tissue patterns, such as the branching pattern of veins within an organ and the checkerboard array of stomates on a leaf surface.

Acknowledgements

Collection of data on mother and daughter cell sizes by Lee Crush from jade, April Fowler from impatiens and Mi Suke Kim from begonia is gratefully acknowledged.