Abstract
The folding free energy landscape of the C-terminal β hairpin of protein G has been explored in this study with explicit solvent under periodic boundary condition and oplsaa force field. A highly parallel replica exchange method that combines molecular dynamics trajectories with a temperature exchange Monte Carlo process is used for sampling with the help of a new efficient algorithm P3ME/RESPA. The simulation results show that the hydrophobic core and the β strand hydrogen bond form at roughly the same time. The free energy landscape with respect to various reaction coordinates is found to be rugged at low temperatures and becomes a smooth funnel-like landscape at about 360 K. In contrast to some very recent studies, no significant helical content has been found in our simulation at all temperatures studied. The β hairpin population and hydrogen-bond probability are in reasonable agreement with the experiment at biological temperature, but both decay more slowly than the experiment with temperature.
Understanding protein folding is one of the most challenging problems remaining in molecular biology (1–5). Recent advances in experimental techniques that probe proteins at different stages during the folding process have shed light on the nature of the physical mechanisms and relevant interactions that determine the kinetics of folding, binding, function, and thermodynamic stability (2–5). However, many of the details of protein folding pathways remain unknown. Computer simulations performed at various levels of complexity ranging from simple lattice models, models with continuum solvent, to all atom models with explicit solvent can be used to supplement experiment and fill in some of the gaps in our knowledge about folding pathways. Much of today's theoretical understanding has been tested in minimalist lattice or off-lattice models. All-atom simulations of protein unfolding at high temperatures have also revealed many important features about the protein folding process, even though they are limited by the fact that the free energy landscape explored at high temperature might be very different from the landscape at biological temperatures. All-atom protein folding in explicit solvent still remains a challenge in computational biology.
The free energy landscape of native proteins in explicit solvent is believed to be partially rugged and funnel-like (6) because of the energy barriers caused by van der Waals repulsions and torsional energy barriers. At room temperature (RT), protein systems get trapped in many local minima. This trapping limits the capacity to effectively sample configurational space. Many methods have been proposed to enhance the conformation space sampling (7). In this work, we use the replica exchange or parallel tempering method (8) to increase barrier crossing events.
As one of the smallest naturally occurring systems, which exhibits many features of a full size protein and also is a faster folder (it folds in 6 μs), the C-terminal β hairpin of protein G has received much attention recently on both the experimental and theoretical fronts (2–5, 9–15). It is believed that understanding the folding of the key protein secondary structures, β sheet and α helix, will be a foundation for investigating more complex proteins. The breakthrough experiments by the Serrano (2, 3) and Eaton groups (4, 5) have recently established the β hairpin from the C terminus of protein G as the system of choice to study β sheets in isolation. These pioneering experiments have inspired much theoretical work on this system by using various models (9–12, 16). For example, Pande and coworkers have studied high-temperature and mechanically induced unfolding by using explicit solvent (9) and recently have studied folding by using an implicit solvent model (10); Karplus and coworkers (11) have explored the free energy landscape by using the charmm force field (CHARMM19) with a continuum solvent model; Garcia and Sanbonmatsu (12) have also studied the free energy landscape of this system in explicit solvent by using the amber force field (AMBER94) with a short cutoff (9 Å) in Coulomb interactions; and Klimov and Thirumalai (16) have studied this system with their off-lattice model and Langevin dynamics. However, there are questions yet to be resolved. The different simulations disagree on the relative importance of the interstrand hydrogen bonds in comparison with the hydrophobic core formation, the existence of such intermediates as the helical structures during the folding process, at what temperatures the free energy barriers disappear and the landscape becomes funnel-like, etc.
In this paper, we use a highly parallel replica exchange method combined with an efficient molecular dynamics (MD) algorithm, particle–particle particle–mesh Ewald (P3ME)/reference system propagator algorithm (RESPA) (17), to explore the free energy landscape of β hairpin in explicit water with all-atom oplsaa force field and periodic boundary condition. A total of 64 replicas of the solvated system consisting of 4,342 atoms are simulated with temperatures spanning 270 to 695 K. Because the force field is normally parameterized with RT properties, we do not expect it to yield accurate results for higher temperatures; nevertheless, these replicas permit the system to rapidly cross the energy barriers and thus lead to efficient sampling at lower temperatures. To our knowledge, this is the first all-atom simulation with the oplsaa force field and periodic boundary conditions for this β hairpin. It is found that the hydrophobic core and the β strand hydrogen bonds form at roughly the same time. The free energy landscape is rugged at low temperatures and becomes a smooth funnel-like landscape at about 360 K. No significant helical content has been found in our simulation at any of the temperatures studied. The β hairpin population and hydrogen-bond probability are in reasonable agreement with experiment at the biological temperature, but both decay much more slowly than the experimental data with temperature, as found in other studies by using charmm and amber force fields.
Methodology
The replica exchange method (REM) has been implemented in the context of the molecular modeling package impact (17, 18) following Okamoto's approach (8) by combining MD with a temperature exchange Monte Carlo process. Replicas are run in parallel at a sequence of temperatures. Periodically, the configurations of neighboring replicas are exchanged, and acceptance is determined by a Metropolis criterion that guarantees detailed balance. The acceptance criterion used in REM is identical to those in Jump Walking (J-Walking) methods (18). Because the high-temperature replica can traverse high energy barriers, there is a mechanism for low-temperature replicas to overcome the quasi-ergodicity they would encounter in a one-temperature walk. The replicas themselves can be generated by Monte Carlo, by MD-based Hybrid Monte Carlo (HMC) as was used in our recent implementation of J-Walking and Smart Walking (S-Walking) (18), or by velocity rescaling as used by Okamoto et al. (8). Although we could have used the HMC method, for simplicity we use velocity rescaling MD for the folding simulation, which also utilizes some of the recent advances in efficient coupling of multiple time step algorithms with particle mesh Ewald (RESPA/P3ME) (17).
The replica exchange method can be summarized as the following two-step algorithm.
(i) Each replica i (i = 1, 2, … M) at fixed temperature Tm (m = 1, 2, … M) is simulated simultaneously and independently for a certain number of Monte Carlo or MD steps.
(ii) Pick a pair of replicas and exchange them with the acceptance probability,
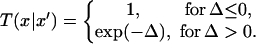 |
1 |
where Δ = (β − β′)(V(x′) − V(x)), β and β′ are the two reciprocal temperatures, x is the configuration at β, x′ is the configuration at β′, and V(x) and V(x′) are potential energies at these two configurations, respectively. After the exchange, go back to step i.
In the present work, MD is used in step i, and all of the replicas are run in parallel on M processors (M = 64); in step ii, only exchanges between neighboring temperatures are attempted because the acceptance ratio decreases exponentially with the difference of the two βs.
Results and Discussion
The β hairpin under study is taken from the C terminus (residue 41–56) of protein G (Protein Data Bank ID code 2gb1). The 16-residue β hairpin is capped with the normal Ace and Nme groups, resulting in a blocked peptide sequence of Ace-GEWTYDDATKTFTVTE-Nme, with total of 256 atoms. The solvated system has 1,361 water molecules [simple point charge (SPC) water, with density 1.0 g/cm3] and also three counter ions (three Na+ ions) for neutralizing the molecular system, which results in a total of 4,342 atoms per replica. All of the MD (canonical ensemble, constant NVT) simulations are carried out with impact (17, 18) using OPLSAA force field (19). The long-range electrostatic interactions with periodic boundary condition are calculated by the P3ME method, with a mesh size of 36 × 36 × 36 (grid spacing about 1.0 Å). A time step of 4.0 fs (outer time step) is used through an efficient combination of multiple time step algorithm RESPA with P3ME (RESPA/P3ME) (17). A total of 64 replicas, with temperatures ranging from 270 to 695 K, are simulated. A conjugate gradient minimization is performed first for each replica. Then a two-stage equilibration, each stage consisting of 100-ps MD, is followed with temperature ramping from 0 K to the specified temperature for each replica by Berendsen velocity rescaling and Andersen thermostat. In the first stage, the β hairpin is frozen in space, so only the solvent molecules are equilibrated, and in the second stage, all atoms are equilibrated. The final configurations of the above equilibration are then used as the starting points in the 64 replicas. Each replica is run for 2.0 ns for data collection, with replica exchanges attempted every 0.4 ps. Protein configurations were saved every 0.08 ps, giving a total of 1.6 million configurations. The total MD integration time of all replicas is 0.128 μs.
The optimal temperature distributions in the replica exchange method should be exponential and can be obtained easily by running a few short trial simulations. In this study, we set the acceptance ratio at about 30–40%, which resulted in a temperature series of 270, 274, 278, … , 685, 695 K, with gaps from 4 to 10 K. We observe that the “temperature trajectory” for one replica (e.g., replica nine starting at 310 K) visits all of the temperatures many times during the 2-ns MD run and, at a given temperature (e.g., 310 K), all of the replicas are also visited many times during the same MD run, indicating that our temperature series are reasonably optimized.
The free energy landscape is determined by calculating the normalized probability, P(X) = Z−1exp(−βW(X)) from a histogram analysis (12), where X is any set of reaction coordinates. W(X2) − W(X1) = −RTlog(P(X2)/P(X1)) is the relative free energy or so-called potential of mean force (12). We will describe the free energy surface as a function of various reaction coordinates, including the number of β strand hydrogen bonds, the hydrophobic core radius of gyration, the fraction of native contacts, the radius gyration of the entire peptide, the rms deviation (rmsd) from the native structure, and the principal components (PC) from PC analysis (12, 20).
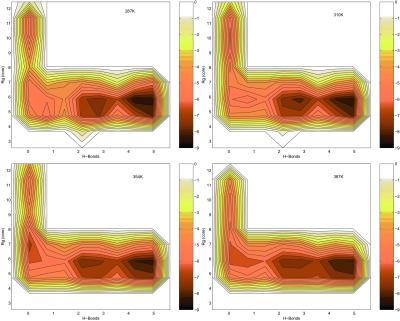
Fig. 1 shows the free energy contour map
with two reaction coordinates, the number of β strand hydrogen bonds
(N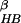 ), and the radius of
gyration of the hydrophobic core
(Rgcore).
N
), and the radius of
gyration of the hydrophobic core
(Rgcore).
N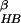 is defined as the number
of backbone–backbone hydrogen bonds, excluding the two at the turn of
the hairpin (five of a total of seven hydrogen bonds; see below).
Rgcore is the radius of gyration of
the side chain atoms on the four hydrophobic residues, W43, Y45, F52,
and V54. The free energy surfaces reveal several interesting features
of this β hairpin folding: (i) there are four states, or
local energy minima, in this two-reaction coordinate representation at
310 K: the native folded state (F), the unfolded state (U), and two
intermediates, a “molten globule” state, which is similar to
Pande and Rokhsar's state H (9), and a partially folded state (P);
(ii) the intermediate state P shows a compact hydrophobic
core, which has a radius of gyration of about 5.5 Å, similar to the
native state F, and also has two to three β strand hydrogen bonds of
the total of five; (iii) as the temperature increases, the
energy barrier separating these states decreases, and at about 360 K,
the barrier height is within the range of 0.5 RT, which means at this
temperature, the folding process can be described as “sliding down a
funnel-like free energy surface.” It should be pointed out that even
at 310 K, the local minima in the free energy landscape are visited
frequently within 2-ns MD; in other words, the barriers are crossed a
large number of times, thus we believe that our conformational space
sampling is adequately converged.
is defined as the number
of backbone–backbone hydrogen bonds, excluding the two at the turn of
the hairpin (five of a total of seven hydrogen bonds; see below).
Rgcore is the radius of gyration of
the side chain atoms on the four hydrophobic residues, W43, Y45, F52,
and V54. The free energy surfaces reveal several interesting features
of this β hairpin folding: (i) there are four states, or
local energy minima, in this two-reaction coordinate representation at
310 K: the native folded state (F), the unfolded state (U), and two
intermediates, a “molten globule” state, which is similar to
Pande and Rokhsar's state H (9), and a partially folded state (P);
(ii) the intermediate state P shows a compact hydrophobic
core, which has a radius of gyration of about 5.5 Å, similar to the
native state F, and also has two to three β strand hydrogen bonds of
the total of five; (iii) as the temperature increases, the
energy barrier separating these states decreases, and at about 360 K,
the barrier height is within the range of 0.5 RT, which means at this
temperature, the folding process can be described as “sliding down a
funnel-like free energy surface.” It should be pointed out that even
at 310 K, the local minima in the free energy landscape are visited
frequently within 2-ns MD; in other words, the barriers are crossed a
large number of times, thus we believe that our conformational space
sampling is adequately converged.
Figure 1.
Free energy contour map versus the number of β sheet H bonds
N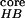 and the
hydrophobic core radius gyration Rgcore. A
hydrogen bond is counted if the distance between two heavy atoms (N and
O in this case) is less than 3.5 Å and the angle
N—H⋅⋅⋅O is larger than 150.0°. The contours are
spaced at intervals of 0.5 RT. We used RT instead of kcal/mol for
energy intervals across various temperatures, because it might be
easier to quantify the barriers at different temperatures.
and the
hydrophobic core radius gyration Rgcore. A
hydrogen bond is counted if the distance between two heavy atoms (N and
O in this case) is less than 3.5 Å and the angle
N—H⋅⋅⋅O is larger than 150.0°. The contours are
spaced at intervals of 0.5 RT. We used RT instead of kcal/mol for
energy intervals across various temperatures, because it might be
easier to quantify the barriers at different temperatures.
These results are generally consistent with what has been found by others (2, 4, 9, 11, 12, 16), but there are also some significant differences. One important difference is in the folding mechanism. Eaton and coworkers (4, 5) developed a helix-coil-type model to provide a structural interpretation for their equilibrium and kinetic data. The model suggests a mechanism in which folding is initiated at the turn and propagates toward the tails by forming hydrogen bonds, so that the hydrophobic clusters, from which most of the stabilization derives, form relatively late in the process (11). Our simulation shows no evidence of this hydrogen-bond-centric model. Also, Pande and Rokhsar (9), by using the charmm force field with a short cutoff (9.0 Å) in the electrostatics, found that the β hairpin system first folds into a compact H state, which has a formed hydrophobic core but only zero to one hydrogen bond. Garcia and Sanbonmatsu (12) found similar results, i.e., there is a well defined state H where the hydrophobic core is formed but with only zero to one hydrogen bond. The folding mechanism in these simulations is interpreted as a hydrophobic-core-centric one: the hydrophobic core is being formed first, and then the hydrogen bonds appear. In our simulation, we found that both the H and P states have a well formed hydrophobic core, but state P (two to three H bonds) has a significantly higher population than the intermediate state H (zero to one H bond). The heavy population in the partially folded state P implies that the final hydrophobic core and β strand hydrogen bonds are being formed nearly simultaneously. This can also be seen from the free energy barrier from state H to state P. The barrier is less than 0.5 RT (at 310 K, this is about 0.3 kcal/mol), which implies the transition from state H to state P is smooth at 310 K. From a Langevin dynamics simulation with an off-lattice model, Klimov and Thirumalai (16) also found that the lag time between collapse and hydrogen bond formation is very short, and the two processes occur nearly simultaneously, which agrees with our findings. The previously proposed H state, which has a well formed core but no β sheet hydrogen bonds (9, 12), is not well populated in our model. Thus, our results suggest the following folding mechanism: after an initial collapse of the peptide, it quickly adopts a partially folded state with two to three hydrogen bonds before it finally folds into the native state. Our model is in essence a blend of the hydrogen-bond-centric and the hydrophobic-core-centric models for this hairpin. Interestingly, this mechanism is supported by Pande and coworkers' latest MD folding simulation by using an implicit solvent model (10).
Another important difference lies in the transition temperature. Karplus and coworkers (11) found that there is no significant free energy barrier even at the biological temperature. Garcia and Sanbonmatsu (12) found that the free energy barrier disappears around 330 K. In contrast, we find this transition temperature to be around 360 K. We think the difference is mainly because of the different force fields used. Karplus and coworkers used the CHARMM19 force field, Garcia and Sanbonmatsu used the AMBER94 force field, and we used the OPLSAA (2000) force field. Also, protein folding is believed to be sensitive to solvation and to the treatment of long-range electrostatic interactions, and these are treated differently in the different simulations. Karplus and coworkers (11) used a continuum solvent model, Garcia and Sanbonmatsu (12) used explicit solvent but with a short cutoff (9.0 Å) in the long-range Coulomb interaction, and we used explicit solvent and the P3ME method for electrostatic interactions with periodic boundary condition. Which of the transition temperatures to smooth barrier crossing, 300, 330, or 360 K, is closer to reality is thus still an open question.
One interesting question regarding the folding intermediates is: To what extent do α helical structures form during the folding process? Early experiments and theoretical simulations have not found significant helical content (2–4, 9, 11). Very recently, Garcia and Sanbonmatsu (12), by using the AMBER94 force field, found that significant helical content exists (15–20%) at low temperatures and that these conformations are only slightly unfavorable energetically with respect to hairpin formation at biological temperatures. Pande and coworkers (10) also found significant helical intermediates at 300 K from their folding simulation with continuum solvent model and an old version of the OPLS united atom force field (no percentage is reported, but from their figures it appears to be significant). It is interesting to see whether this remains the case for the all-atom oplsaa model with explicit solvent with no cutoff in the long-range electrostatic interactions. The number of residues in β sheet and α helices are calculated with the program stride (21), which uses both hydrogen bond energies and dihedral angles in assigning secondary structure to each residue (21). It is found that the number of helical residues (including both α helix and 310 helix) is typically less than or equal to three, and only 1–2% of the conformations show any helical content. All the temperatures we have examined from 270 to 695 K show similar results (the graphs are not shown but are published as supporting information on the PNAS web site, www.pnas.org). Furthermore, almost all of the helices we found are 310 helices near the original β turn (residues 47–49). Very few conformations are found to have helix residues in places other than the original β turn. This minimal helix content is in contrast to recent results of Garcia and Sanbonmatsu (12) and Pande and coworkers (10). We think this is mainly because of the force field parameters used. For example, AMBER94 tends to overestimate the stability of α helices, as also found by Beachy et al. (22). Our results seem to agree better with experiment, because no evidence has been found in experiment for the significant helical content (2–5).
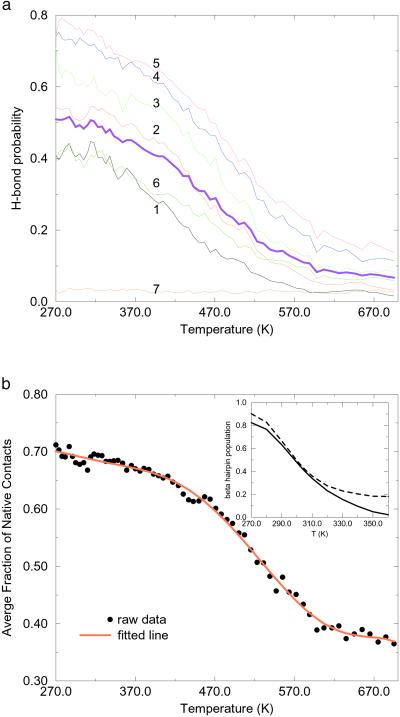
To determine which of the native hydrogen bonds play a significant role in the folding process, we calculated the probability of each individual hydrogen bond over a wide range of temperatures. All seven native backbone hydrogen bonds are included, and they are numbered from the tail to the turn [the same as in Karplus and coworkers (11) and Garcia and Sanbonmatsu (12)]; i.e., the one closest to the tail is numbered 1, and the one closest to the turn is numbered 7. Fig. 2a shows the probability of each hydrogen bond and their average as a function of temperature from 270 to 690 K. The average hydrogen bond probability decreases steadily with temperature, indicating a steady decrease of β sheet content (see below). The gradual decrease of hydrogen bond probability with temperature also indicates there is no cooperative transition in the hydrogen bonds with temperature and suggests that the hairpin formation is a broad two-state transition (4, 16). Hydrogen bonds 4 and 5 (which are closer to the turn) are the most stable, whereas 1 and 2 are much easier to break when water molecules “attack” the β sheet. Overall, the variations of hydrogen bond probabilities with temperature agree very well with Karplus and coworkers' results from the charmm force field (11) and also agree reasonably well with Garcia and Sanbonmatsu's (12) results from the amber force field except at the lower temperatures (below the biological temperature 310 K), where these authors found α helical structures and thus smaller β sheet hydrogen bond probabilities. The average probability of the β sheet hydrogen bonds in our model is 49% at 282 K, which is very close to the 54% found by Karplus and coworkers, and in reasonable agreement with the estimate of 42% from NMR experiment based on chemical shift data and 40% from Garcia and Sanbonmatsu's simulation by using the amber force field. Moreover, both our and Karplus and coworkers' results show that hydrogen bonds 7 and 6 have lower probabilities compared with other hydrogen bonds, because these hydrogen bonds are near the turn and find it harder to achieve an ideal N—H⋅⋅⋅O angle because of geometrical constraints. This differs from Klimov and Thirumalai's (16) results, where hydrogen bonds 7 and 6 have the highest probabilities of being formed, and from Garcia and Sanbonmatsu's (12) results, where the probabilities for hydrogen bonds 7 and 6 are not the highest but are much higher than hydrogen bonds 1 and 2. Except for hydrogen bonds 6 and 7, our hydrogen bond probabilities agree with Klimov and Thirumalai's (16) results reasonably well. Because hydrogen bond formation near the turns is more subtle, additional NMR experiments might be needed (16).
Figure 2.
(a) Temperature dependence of the probability of forming individual native hydrogen bonds. The thick solid line shows the average probability overall all native hydrogen bonds. (b) The average fraction of native contacts (population of β hairpin) as a function of temperature. The population of β sheet decreases monotonically but decays too slowly with temperature. The experimental results (solid line) (4) and simulation results from Klimov and Thirumalai (dashed line) (16) are shown (Inset).
The fluorescence quantum yield experiment determines the temperature dependence of the β sheet population for this hairpin (4). It is of interest to see whether all-atom force field simulations can reproduce this temperature dependence. Klimov and Thirumalai have used the average fraction of native contacts to estimate the β hairpin population (16), and here we follow their approach. Fig. 2b shows the average fraction of native contacts versus temperature. For comparison, we also plotted the experimental data and the simulation results from Klimov and Thirumalai (Fig. 2b Inset). Klimov and Thirumalai's simulation gives excellent agreement with experiment, even though a simple off-lattice model was used. The experimental data show that the β hairpin population decreases monotonically with temperature, with about 80% population at 270 K, 40% at 310 K, and about 0% above 360 K (4). Our simulation also shows a monoatomic decrease with temperature, but the population decays much more slowly than the experiment. The β hairpin population is about 71% at 270 K and 66% at 310 K, in reasonable agreement with experiment, but populations at higher temperatures are far higher than experiment. Interestingly, Karplus and coworkers (11) found a β hairpin population of about 75% at 300 K, 68% at 335 K, and 55% at 395 K by using charmm (ref. 23; A. R. Dinner, personal communication), which is similar to our oplsaa results. This agreement is consistent with the similar hydrogen bond probabilities from the two simulations, as pointed out earlier, because there is high correlation between the β hairpin population and the β strand hydrogen bonds, as seen from Fig. 2 a and b. Garcia and Sanbonmatsu (12) reported a 30% β hairpin population at 282 K and a 40% population at 300 K. This 30% β hairpin population at 282 K seems too low (because of significant α helix content at this temperature in their simulation); moreover, the temperature dependence at this temperature range, 270–310 K, is opposite to that of experiment. Garcia and Sanbonmatsu did not report the β hairpin populations for higher temperatures, but from similar hydrogen bond probabilities above 310 K, we speculate their β hairpin population also decays more slowly with temperature than does experiment. Thus, it seems that all three all-atom force fields, charmm, amber, and oplsaa, show slower decay in the β hairpin population at higher temperatures above 310 K, even though the population near the biological temperature might be reasonable. In addition, the amber force field predicts the low temperature dependence incorrectly. We think this reflects the way typical force fields are parameterized. The force field parameters are normally fit at RT, and it is not surprising that the resulting potential function cannot reproduce some properties at higher temperatures well. The SPC water model may also contribute to the errors in our simulation because, as pointed out recently by van Gusteren and coworkers, the properties of SPC water, such as the thermal expansion coefficient, heat capacity, and diffusion constants deviate significantly from experiments at higher temperatures (24). The same is probably true for the TIP3P water as used in Garcia and Sanbonmatsu's simulation. The constant volume simulation used both in our simulation and those of Garcia and Sanbonmatsu is also unrealistic at high temperatures. The high-temperature simulations at constant volume imply high pressures, which could stabilize the folded β hairpin if its volume change on unfolding is positive. The continuum solvent models also have problems at high temperatures, because at constant pressure, the water density decreases with temperature (except below 277 K), and most of the continuum solvent models do not have density-dependent parameters. More investigations with NPT simulations and also more force field reparametrizations might be very useful here.
To better compare our simulation results with those previously reported
for this β hairpin, we also calculated the free energy surfaces as a
function of the other reaction coordinates previously used. A total of
seven reaction coordinates were used in this study. In addition to the
two mentioned above (number of β strand hydrogen bonds
N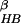 and core radius of
gyration Rgcore), five other reaction
coordinates were selected: the fraction of native contacts ρ, overall
radius of gyration Rg, first principal component PC1, second
principal component PC2 from principal component analysis (12, 20), and
overall rmsd.
and core radius of
gyration Rgcore), five other reaction
coordinates were selected: the fraction of native contacts ρ, overall
radius of gyration Rg, first principal component PC1, second
principal component PC2 from principal component analysis (12, 20), and
overall rmsd.
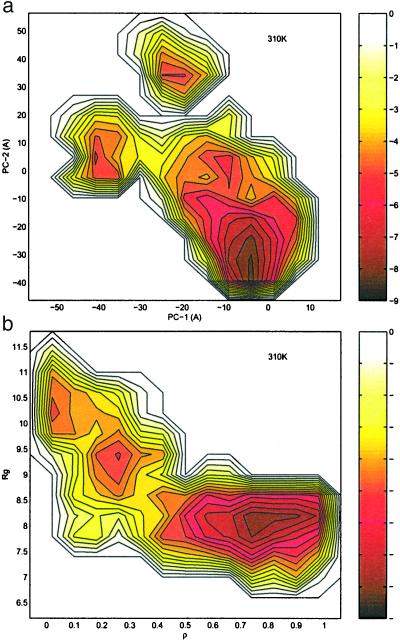
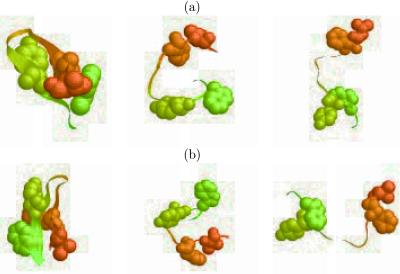
Fig. 3a shows the free energy contour map with respect to the first two principal components, PC1 and PC2, at 310 K (contour maps at other temperatures are published as supporting information on the PNAS web site). At low temperatures (T < 360 K), the free energy surfaces are rugged, with well defined local energy minima and high energy barriers separating these minima. At 310 K, there are three well defined local minima near (−8 Å, −35 Å) (near-native state), (−40 Å, 5 Å) (intermediate state), and (−21 Å, 32 Å) (fully extended state) in (PC1, PC2) coordinates. Fig. 4a shows three representative structures from these local minima. When the temperature is increased, the energy landscapes become less rugged, and there exist multiple paths connecting one local energy basin to another. At very high temperatures, T > 387 K, the landscape essentially becomes a one-basin surface. In contrast to Garcia and Sanbonmatsu's (12) results from AMBER94 (also by using PC1 and PC2 as reaction coordinates), our free energy landscapes are less rugged at low temperatures, and fewer local minima are found. Also, none of these local minima have helical content, as found in Garcia and Sanbonmatsu's structures. We find the transition temperature for smooth barrier crossing to be about 360 K in our simulation, which is slightly higher than Garcia and Sanbonmatsu's 330 K.
Figure 3.
Free energy contour map versus (a) the principal components PC1 and PC2 (Upper) and (b) the fraction of native contact ρ and the radius gyration of the entire peptide Rg (Lower) at 310 K. The contours are spaced at intervals of 0.5 RT. The contour maps at various other temperatures are published as supporting information on the PNAS web site.
Figure 4.
Representative structures from the local minima of the free energy contour map versus (a) the principal components PC1 and PC2 (Fig. 3 a and b) the fraction of native contacts and the radius of gyration of the entire peptide (Fig. 3b).
Fig. 3b shows the free energy contour map with respect to
the radius of gyration Rg and the fraction of native
contacts ρ at 310 K (contour maps at other temperatures are published
as supporting information on the PNAS web site, www.pnas.org). Similar
results are found from the energy surfaces in these two reaction
coordinates. At low temperatures (T < 360 K), the free
energy surfaces are rugged, with well defined local energy minima and
high energy barriers. At 310 K, there are also three well defined local
minima near (0.85, 8.0 Å) (near-native state), (0.26, 9.4Å)
(intermediate state), and (0.05, 10.4 Å) (fully extended state) in
(ρ, Rg) coordinates. Fig. 4b shows three
representative structures from these local minima. Both of the middle
structures in Fig. 4 a and b, i.e., the
intermediate states, show no well formed hydrophobic core or β strand
hydrogen bonds. In other words, there is no heavily populated state
with a hydrophobic core formed but no β strand hydrogen bonds formed
or vice versa. This also supports our blend view mentioned
above, i.e., the final hydrophobic core and β strand hydrogen bonds
are formed nearly simultaneously. When the temperature is increased to
about 387 K, the energy landscape essentially exhibits only one basin,
consistent with the above energy landscapes with respect to (PC1,PC2)
and also to (N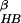 ,
Rgcore).
,
Rgcore).
Interestingly, Karplus and coworkers (11) found there is essentially no
energy barrier even at 310 K, as mentioned above. Their free energy
landscape shows an overall funnel-like surface with some local
roughness. They used the charmm force field and the
continuum solvent model and used the rmsd as the reaction coordinate.
Even though differing force fields and solvent models might contribute
significantly to the different shapes in free energy landscapes, as
discussed above, we believe the difference could also be exaggerated or
diminished by different choices of reaction coordinates. In other
words, some of the reaction coordinates might not be the best choices.
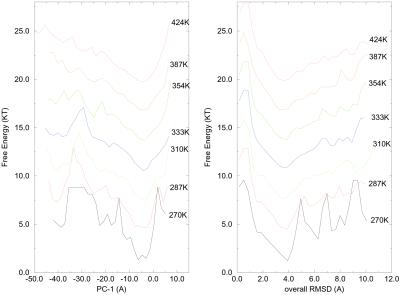
Fig. 5 shows plots of one-dimensional
(1-D) free energy curves versus two different reaction coordinates,
PC1, and overall rmsd. In the curve versus rmsd, the free energy
landscape at 270 K shows three sharp barriers separating local energy
minima, but these barriers quickly disappear, and the energy landscape
becomes funnel-like when the temperature is increased to 287 K. At 310
K, the energy landscape becomes smooth. On the other hand, the free
energy versus the principal component PC1 stays rugged until 354 K,
which is similar to Garcia's result. The observed smooth energy
landscape with respect to rmsd might be a coincidence for this system,
and the principal component PC1 might be a better choice for the
folding reaction coordinate, because it describes essential motions
during the folding process. The transition temperature determined from
PC1 is also consistent with the results from two-dimensional (2-D)
contour maps versus (N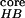 ,
Rgcore) (PC1, PC2), and (ρ,
Rg), as shown in Figs. 1 and 3 a and
b. It should be pointed out, however, that the 2-D contour
surfaces plotted versus rmsd and either Rg,
Rgcore, ρ, or PC1 are still rugged.
The free energy surface seems smooth only with 1-D plot versus rmsd.
,
Rgcore) (PC1, PC2), and (ρ,
Rg), as shown in Figs. 1 and 3 a and
b. It should be pointed out, however, that the 2-D contour
surfaces plotted versus rmsd and either Rg,
Rgcore, ρ, or PC1 are still rugged.
The free energy surface seems smooth only with 1-D plot versus rmsd.
Figure 5.
Free energy as a function of first principal coordinates PC1 (Left) and the overall rmsd from the native structure (Right) for various temperatures. Curves are shifted up from each other by 3 RT.
Conclusion
The energy landscape for a β hairpin folding in explicit solvent under periodic boundary conditions is studied in this paper. A highly parallel replica exchange method consisting of 64 replicas spanning from 270 to 695 K has been used with a very efficient P3ME/RESPA algorithm. The oplsaa force field with SPC water was adopted for this simulation, and the main conclusions are summarized in the following.
A blend view of hydrophobic-core-centric and hydrogen-bond-centric folding mechanism is proposed, which means that the final hydrophobic core and the β strand hydrogen bonds are being formed nearly simultaneously after initial collapse. In contrast to some very recent simulations (10, 12), no significant helical content has been found in our simulation at any temperatures, in agreement with experiment. The free energy landscape has been presented with respect to seven different reaction coordinates, and it is found that the free energy surface is rugged at low temperatures but becomes smooth and funnel-like at about 360 K. The population of β hairpin is found to be monotonically decreasing with temperature from about 71% at 270 K, in good agreement with fluorescence quantum yield experiments (80%). The average hydrogen bond probability is found to be 49% at 282 K, also in reasonable agreement with NMR experiments (42%). However, the decay of the β hairpin population and hydrogen bond probabilities with temperature are much slower than the experimental data at higher temperatures. It seems all three all-atom force fields, charmm, amber, and oplsaa, wrongly predict this temperature dependence.
This paper can be regarded as providing a test of some of the most frequently used force fields for solvated protein systems as well as emerging MD methodologies. This test is severe, because we, like several other groups, are using force fields and solvation models developed at RT to predict properties at higher temperatures. These force fields might be adequate for the predictions of properties at the temperatures for which they were developed, but it is clear that further work is needed in improving these models for a wider range of temperatures. Until such issues are addressed satisfactorily, it is important for those of us trying to extract temperature dependence from simulations to test our assumptions against experiment where possible, and one must be cautious in interpreting results obtained from models outside their realm of proven reliability.
Supplementary Material
Acknowledgments
We thank Angel Garcia and Yuko Okamoto for sending us preprints of their work. We also thank Jed Pitera, William Swope, Eric Sorin, and Vjay Pande for many useful comments. This work was supported in part by National Institutes of Health Grant GM43320 to B.J.B.
Abbreviations
- MD
molecular dynamics
- rmsd
rms deviation
- P3ME
particle–particle particle–mesh Ewald
- PC
principal component
- SPC
simple point charge
References
- 1.Fersht A. Structure and Mechanism in Protein Science. New York: Freeman; 1999. [Google Scholar]
- 2.Blanco F J, Rivas G, Serrano L. Nat Struct Biol. 1994;1:584–590. doi: 10.1038/nsb0994-584. [DOI] [PubMed] [Google Scholar]
- 3.Blanco F J, Serrano L. Eur J Biochem. 1995;230:634–649. doi: 10.1111/j.1432-1033.1995.tb20605.x. [DOI] [PubMed] [Google Scholar]
- 4.Munoz V, Thompson P A, Hofrichter J, Eaton W A. Nature (London) 1997;390:196–199. doi: 10.1038/36626. [DOI] [PubMed] [Google Scholar]
- 5.Munoz V, Henry E R, Hofrichter J, Eaton W A. Proc Natl Acad Sci USA. 1998;95:5872–5879. doi: 10.1073/pnas.95.11.5872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wolynes P G. Proc Natl Acad Sci USA. 1997;94:6170–6175. doi: 10.1073/pnas.94.12.6170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Berne B J, Straub J E. Curr Top Struct Biol. 1997;7:181–189. doi: 10.1016/s0959-440x(97)80023-1. [DOI] [PubMed] [Google Scholar]
- 8.Sugita Y, Okamoto Y. Chem Phys Lett. 1999;314:141–151. [Google Scholar]
- 9.Pande V S, Rokhsar D S. Proc Natl Acad Sci USA. 1999;96:9062–9067. doi: 10.1073/pnas.96.16.9062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zagrovic, B., Sorin, E. J. & Pande, V. S. (2001) J. Mol. Biol., in press. [DOI] [PubMed]
- 11.Dinner A R, Lazaridis T, Karplus M. Proc Natl Acad Sci USA. 1999;96:9068–9073. doi: 10.1073/pnas.96.16.9068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Garcia A E, Sanbonmatsu K Y. Proteins. 2001;42:345–354. doi: 10.1002/1097-0134(20010215)42:3<345::aid-prot50>3.0.co;2-h. [DOI] [PubMed] [Google Scholar]
- 13.Roccatano D, Amadei A, Nola A D, Berendsen H J. Protein Sci. 1999;10:2130–2143. doi: 10.1110/ps.8.10.2130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kolinski A, Ilkowski B, Skolnick J. Biophys J. 1999;77:2942–2952. doi: 10.1016/S0006-3495(99)77127-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Honda S, Kobayashi N, Munekata E. J Mol Biol. 2000;295:269–278. doi: 10.1006/jmbi.1999.3346. [DOI] [PubMed] [Google Scholar]
- 16.Klimov D K, Thirumalai D. Proc Natl Acad Sci USA. 2000;97:2544–2549. doi: 10.1073/pnas.97.6.2544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zhou R, Harder E, Xu H, Berne B J. J Chem Phys. 2001;115:2348–2358. [Google Scholar]
- 18.Zhou R, Berne B J. J Chem Phys. 1997;107:9185–9196. [Google Scholar]
- 19.Jorgensen W L, Maxwell D, Tirado-Rives J. J Am Chem Soc. 1996;118:11225–11236. [Google Scholar]
- 20.Garcia A E. Phys Rev Lett. 1992;68:2696–2699. doi: 10.1103/PhysRevLett.68.2696. [DOI] [PubMed] [Google Scholar]
- 21.Frishman D, Argos P. Proteins. 1995;23:566–579. doi: 10.1002/prot.340230412. [DOI] [PubMed] [Google Scholar]
- 22.Beachy M, Chasman D, Murphy R, Halgren T, Friesner R. J Am Chem Soc. 1997;119:5908–5920. [Google Scholar]
- 23.Dinner A R. Ph.D. thesis. Cambridge, MA: Harvard Univ.; 1999. [Google Scholar]
- 24.Walser P, Mark A E, van Gunsteren W F. Biophys J. 2000;78:2752–2760. doi: 10.1016/S0006-3495(00)76820-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.