Abstract
Objective
Traditional cancer initiation theory propounds evolution of a monoclonal population of fully transformed tumour cells to form a malignant tumour. Cooperation between surrounding stroma and the tumour also often leads to malignancy. This cooperation may exist as a result of sharing of growth signals or growth factors secreted by stromal cells, which can cause those with proliferative phenotypes to switch to motile phenotypes. Mathematical models of sharing of growth factors between cancer stem cells and stromal cells can allow for deeper understanding of tumourigenesis through cooperation. The study presented here describes a novel evolutionary game theoretical approach to investigate emergence of malignancy through interactions among cells of three different phenotypes, one of which produces growth factors.
Materials and methods
Three different scenarios have been considered, and types of behaviour of the three phenotypes during interactions, have been modelled in terms of cost and benefit variables. Phenotypic compositions of such a tumour at equilibrium have been analysed, and evolution of the population, with respect to time, has been investigated.
Results
Results suggest the role of cooperation in forming a malignant tumour and show, in all three cases, that emergence of triple polymorphism, two‐strategy polymorphism, and fixation of one phenotype, were possible at equilibrium. The models also suggest that under certain conditions, one phenotype may be completely eliminated from the population, thus leading to new possibilities for potential treatments.
Conclusions
This study explains some current experimental findings from a theoretical viewpoint, and may provide new approaches for future research in oncology.
Introduction
Carcinogenesis, transformation of healthy cells to malignant cells, is often recognized as an evolutionary process. Much traditional cancer theory states that tumours develop from a single progenitor cell, whose subsequent division and mutation result in creation of various subclones of partially transformed tumour cells 1. Genetic instability during the carcinogenic process allows for creation of subclones of such a phenotypically diverse population of cells. Development of malignancy subsequently requires the tumour to acquire a number of important mutational capabilities, through this evolutionary selection of aggressive subclones. These abilities include self‐sufficiency in generating growth signals, successful evasion of apoptosis and unlimited proliferative potential, amongst many others 2. Eventually, one subclone gains all the hallmarks necessary to form a fully malignant tumour mass 1.
Cancer stem cells (CSCs) are responsible for maintaining and initiating tumours and have also been found to play a role in tumour cell invasion and metastasis, through generation of tumour heterogeneity 3. The most recent model of cancer metastasis suggests that metastasis does not occur as a result of irreversible genetic changes, but of different gene expression programs that are imposed on the cancer cells by the tumour microenvironment 4. Current cancer research has shown that epithelial‐mesenchymal transition (EMT) leads to the rise of an invasive phenotype with properties akin to normal stem cells 5. Stromal signals, such as by transforming growth factor‐β (TGF‐β), can induce EMT in which proliferative tumour cells acquire an invasive phenotype 3. Two populations of EMT and non‐EMT CSCs can coexist and switch between the two phenotypes through EMT and, its reverse process, the mesenchymal‐to‐epithelial (MET) transition 3. Experimental studies have shown that phenotypic switching leads to onset of metastasis as a result of genetic reprogramming to invasive phenotypes 6. Phenotypic plasticity of CSCs suggests that they adopt an invasive phenotype to migrate to a secondary site 3. Once invasive cells have migrated to a new site, they may switch back to the proliferative phenotype and retain the proliferative phenotype or become dormant due to lack of signals to the contrary, from the microenvironment 4. Increasing evidence points to heterogeneity of the tumour as the reason why some tumours are resistant to drug treatment 4. Experimental evidence from examination of 86 melanoma cell lines in culture shows at least two major gene expression signatures – one presents itself in weakly invasive but rapidly proliferative phenotype that can be repressed by TGF‐β, and the other in a slowly proliferating but highly invasive phenotype that is resistant to TGF‐β growth‐inhibition signalling 7. Hoek et al. 8 discovered that cancer cell lines with fixed genetic profiles in culture, that were transplanted in vivo, generated heterogeneous tumours that contained both phenotypes. Carreira et al. 9 proposed that these different phenotypes of cancer cell exist in melanoma tumours due to different levels of microphthalmia‐associated transcription factor (Mitf) gene activity. Low expression of Mitf results in cells of invasive phenotype, while high Mitf expression yields cells with either proliferative phenotype or a pigment‐producing phenotype in melanoma 4. In breast cancer, increased regulation of TGF‐β signalling leads to decreased regulation of Mitf expression that subsequently triggers the switch from proliferative to an invasive phenotype 10.
In addition to the role of growth factors in phenotype switching 10, extensive cell cooperation that alters the surrounding non‐cancerous tissue has already been shown to exist between malignant cells and stromal cells of the tumour microenvironment 2. This cooperation arises through exchange of various types of growth signals or growth factors. An example of this type of cell communication can be found in carcinomas where cancer cells secrete platelet‐derived growth factor (PDGF), which recruits macrophages that in turn secrete TGF‐β. Overexpression of TGF‐β, then, activates carcinoma‐associated fibroblasts to stimulate cancer cell proliferation and invasion 11. Even in distant metastatic sites, endothelial cells and macrophages associated with lung cancer have been observed to express MMP9 (an agent that supports metastasis) when induced by cancer cell‐secreted VEGF of the primary tumour 12.
Axelrod et al. 13 have proposed that partially transformed tumour cells can cooperate through this sharing of growth factors, and therefore allow the tumour to reach malignancy before a fully transformed subclone emerges. Although increasing evidence has shown that tumours mostly originate from a single progenitor 1, there is also increasing evidence pointing to cooperation between stromal cells and CSCs as reason for initiation of metastasis 2. A recent study at the Weinberg lab 14 has found that an ‘instigator’ cell line is able to induce proliferation and metastasis of an ‘indolent’ cell line through secretion of osteopontin, a factor that caused initiation systemic effects that led to spreading. However, mutualism between different subclones has not yet been confirmed as paracrine signalling is often difficult to study in vivo. Because of complications in studying cancer mechanisms in human patients, mathematical models provide useful alternatives for preliminary investigations of tumour initiation, growth and metastatic spread.
Presently, game theory has risen to the forefront of cancer modelling due to understanding that cancer cells compete at some level over available space and nutrients. Pioneered by von Neumann and Morgenstern 15, game theory studies how players cooperate and compete by employing various strategies that affect their own fitness as well as the fitnesses of the other players. Evolutionary game theory (EGT), in particular, has been a tremendously useful tool in the biological sciences as it can be used to investigate evolution of a population where Darwinian fitness is determined by reproductive success of the population only, and assumes that players' strategies are not determined by rational payoff maximization, but by phenotypic traits. Traits themselves are acquired through adaptations resulting from natural selection, and the fitness of each individual is reproductive success 16. While EGT has been most frequently applied to evolution of competing animal species 17, its more recent applications include to bacteria 18 and virus 19 populations. During the past 10 years, the focus of EGT has been applied to modelling interactions among cancer cells. The use of EGT cancer models relies on the fact that a tumour is phenotypically diverse and is populated by cell ‘players’ that utilize different strategies to succeed in competition over available resources 20.
Previous studies using EGT models have focused on the competitive aspects of tumour cell interactions including effects of cytotoxins on neighbouring cells, and reproductive competition over available space 21, 22. More recent studies have acknowledged existence of phenotypic diversity in tumours 23. Both experimental and theoretical works cite existence of proliferative and migratory phenotypes in invasive tumours. According to current belief, benign tumours have proliferative cells, whereas invasive cells are only found in malignant tumours 24. Interestingly, cells that exhibit the proliferative phenotype cannot simultaneously become motile, and motile cells tend to be of a much lower proliferative level than cells at rest 25. Some prior studies have taken into account these two phenotypes in EGT models of glioma. Basanta et al. 26 looked at whether and how glycolytic cells may facilitate appearance of an invasive phenotype in a tumour populated by the proliferative phenotype, whereas Mansury et al. 27 investigated genotype–phenotype link in a population of migratory and proliferative cells. However, neither considered presence of growth factors and growth factor‐secreting phenotypes in their models. Although Tomlinson and Bodmer 28 used the concept of growth factors in game theory models of angiogenesis and programmed cell death, their models consisted only of cell genotypes that produce growth factors, and cells that cannot, without including other phenotypes that display either migratory or proliferative types of behaviour. Gatenby et al. 29 explored cooperation between tumour cells and normal stromal cells of the extracellular matrix, in creating a microenvironment for metastasis, although they did not look at cooperation between subclones of partially transformed tumour cells 29. During the past year, models have been created to study cancer stromal dependency 30 and cooperation among four phenotypes resulting from a combination of motile, glycolytic, and proliferative characteristics in glioblastoma multiforme 31. Currently, no study has yet specifically examined the various ways in which sharing of growth factors from stromal cells can impact the generation of a heterogeneous population of tumour cells, with the ability to metastasize.
The purpose of the study described here was to present a novel evolutionary game theory model to simulate cooperation among three distinctly unique phenotypes: proliferative, invasive and growth factor‐secreting (such as growth factor‐secreting stromal cells). The study sought to test which conditions can lead to rise of the invasive phenotype in a malignant tumour. In addition, the study looks at how cooperation affects proportions of the three phenotypes within the tumour. Growth factor signalling is present in all cancers, most prominently in highly invasive malignancies such as breast cancer, prostate cancer and glioblastoma during all stages of malignancy 32, 33, 34, 35, 36, 37. Thus, the article presents three cases in which the growth factor‐secreting and acceptance mechanisms are slightly different. This study seeks, on a broader scale, to contribute to a better understanding of tumourigenesis and ultimately lead to new treatments for the disease.
Materials and methods
Model design
The models presented in this study adopt evolutionary game theoretical analyses 17 to study equilibria among three different phenotypes of tumour cells in two different circumstances. Of the three phenotypes, it is assumed that two are the proliferative (present in benign tumours) and invasive or motile (present in malignant tumours) phenotypes because of their aforementioned importance in most tumours 24, 25, 38. These two phenotypes represent two subpopulations of cancer cells, one of which displays only the proliferative (PRO) phenotype and the other displays the invasive or motile (MOT) phenotype. The PRO phenotype proliferates at a rapid pace, but does not migrate, while the MOT phenotype does not proliferate as rapidly as the PRO phenotype, but actively migrates.
In addition, a third, growth factor‐secreting (GF or SGF) phenotype is present. Growth factors secreted by this phenotype act in both autocrine and paracrine fashions. Biologically, growth factors in the model could represent a number of factors that benefit the tumour cells that receive them. For example, hepatocyte growth factor/scatter factor (HGF/SF), when bound to the Met receptor tyrosine kinase, triggers increased proliferation or migration, depending on the cell type 38. However, for simplicity of the model, it is assumed only that growth factors secreted by the GF phenotype confer some variety of benefit to the receiving cells where they may act as proliferative or migratory signals.
In both models, the base payoff, the payoff received when cells are neither receiving any benefit nor sustaining any costs, is 1. Each cell is a player with a strategy determined by its phenotype. Cells engage in pairwise interactions. In addition, cell players may receive any of the following benefits or costs:
Cost of producing the growth factor, g where g > 0.
Benefit of receiving the growth factor, z where z > 0.
Cost of mobility, m where m > 0.
Cost of sharing space, d where d > 0.
Growth factor phenotype model
In the growth factor (GF) phenotype model, the growth factor phenotype secretes growth factors that are accepted by itself, the proliferative phenotype and the invasive phenotype via their surface receptors. A PRO cell incurs the cost of sharing space (d) when it interacts with another immotile cell because it does not migrate. An MOT cell incurs the cost of mobility (m) when interacting with any other cell because of its highly invasive and migratory tendency. A GF cell incurs the cost of producing the growth factor (g) and confers a benefit (z) to any cell it meets, and itself.
The following variables designate the proportion of each phenotype:
The proportion of cell type GF in the population is α.
The proportion of cell type PRO is β.
The proportion of cell type MOT is γ.
α + β + γ = 1
Table 1 illustrates possible interactions. Payoffs are given to cells in the leftmost column.
Table 1.
Payoff table represents the change in fitness of a tumour cell with a given phenotype after interacting with another cell. Three phenotypes (GF, PRO and MOT) are represented. Payoffs go to the cells in the leftmost column. For example, fitness change for a GF cell, interacting with an MOT cell is 1 – g + z
| Encounter with | |||
|---|---|---|---|
| GF | PRO | MOT | |
| Payoff to | |||
| GF | 1 − d − g + z | 1 − d− g + z | 1 – g + z |
| PRO | 1 – d + z | 1 − d | 1 |
| MOT | 1 – m + z | 1 − m | 1 − m |
Let W(GF), W(GF) and W(MOT) represent fitness of GF, PRO and MOT phenotypes, respectively, and E(GF, PRO) represent payoff to the GF cell after interacting with a PRO cell. Greater fitness represents greater reproductive potential of the phenotype. The same notations apply to all cases. Assuming that initial fitness, W 0, of each phenotype is equal, fitnesses of phenotypes, after participating in interactions depicted in the payoff table, can be computed:
| (1) |
| (2) |
| (3) |
At equilibrium, fitnesses are equal among all phenotypes. From this equilibrium, proportions of the three phenotypes can be deduced:
| (4) |
From α + β + γ = 1, it is possible to deduce:
| (5) |
| (6) |
In eqns ((4), (5), (6)), several conditions must hold for the three phenotypes to coexist:
Specific growth factor phenotype model
In real tumours, there exists the possibility that a particular phenotype did not acquire, through evolution, receptors for a type of growth factor that is beneficial to cells with the receptors. In fact, there is the possibility that the stromal cells only secrete proliferative growth factors that do not affect motile phenotypes. To test this scenario, a specific growth factor (SGF)‐secreting phenotype is introduced into the population to replace GF phenotype. Only itself and PRO phenotype may be able receive the specific growth factor. For this model, proportion of phenotype SGF in the population is designated δ. Costs and benefits are represented by the same variables as the previous model. This model studies whether malignancy can occur when only the benign phenotype (PRO) is able to receive a promoting factor. Note that in Table 2, the MOT cell is no longer able to obtain benefit of receiving growth factor (z) when it interacts with the SGF cell.
Table 2.
Payoff table represents change in fitness of tumour cells after interactions with other cells. Three phenotypes (SGF, PRO and MOT) are represented. Note specially that fitness change for an MOT cell interacting with an SGF cell is now 1 − m
| Encounter with | |||
|---|---|---|---|
| SGF | PRO | MOT | |
| Payoff to | |||
| SGF | 1 – d – g + z | 1 – d – g + z | 1 – g + z |
| PRO | 1 – d + z | 1 − d | 1 |
| MOT | 1 − m | 1 − m | 1 − m |
Once again, initial fitness of each phenotype is equal. Fitness of each phenotype at equilibrium is calculated to be:
| (7) |
| (8) |
| (9) |
At equilibrium:
| (10) |
| (11) |
| (12) |
In eqns (10–12), several conditions must hold:
Selective SGF phenotype model
If it is possible for stromal cells to only secrete growth factors that benefit the proliferative phenotype, it is also possible that the cells can only secrete migratory factors that benefit MOT cells. On the basis of experimental evidence that stromal cells will secrete factors that help cancer growth only after being activated by a certain factor secreted by the cancer cell 39, 40, the authors further assume that selective SGF (sSGF) stromal cells will only receive the benefit of the growth factor after being activated by the MOT cell. Table 3 illustrates dynamics of such a series of interactions.
Table 3.
Payoff table represents change in fitness of tumour cells after interactions with other cells. Three phenotypes (sSGF, PRO and MOT) are represented. Note specially that sSGF only secretes growth factors when it encounters an MOT cell
| Encounter with | |||
|---|---|---|---|
| sSGF | PRO | MOT | |
| Payoff to | |||
| sSGF | 1 – d − g | 1 – d − g | 1 – g + z |
| PRO | 1 − d | 1 − d | 1 |
| MOT | 1 – m + z | 1 − m | 1 − m |
Once again, initial fitness of each phenotype is equal. Proportion of MOT cells in the population is calculated to be:
| (13) |
In eqn (13), the following condition must hold:
Evolution of stable states in the population
To test stability of polymorphisms existing in the models over time, we present replicator equations 17 to analyse evolution of the population over time. This will allow us to see whether polymorphisms predicted by GF and SGF models prove to be stable evolutionary stable strategies (ESS) over many generations. Because of similarities between the SGF and sSGF models, we will only investigate evolution of the GF and SGF populations. Evolution of the population will be towards the stable states, given initial proportions of each phenotype and values of costs and benefits. Replicator equations for proportions of phenotypes in the GF model are as follows:
| (14) |
| (15) |
| (16) |
Where in eqns ((14), (15), (16)):
In the SGF model, equations for the three phenotypes are therefore:
| (17) |
| (18) |
| (19) |
Where in eqns ((17), (18), (19)):
Results
Due to complexity of the models, it is important to define several conditions. First, the game consists of only pure strategies, which means that no cell is able to switch between different phenotypes during the course of an interaction. Secondly, combinations of values of costs and benefits that result in negative phenotypic proportion values are rejected as they are biologically improbable. In addition, values of costs and benefits must follow: 1 + z ≥ g + m + d. Lastly, variables cannot be less than or equal to zero or greater than 1, as that may result in phenotypic proportions greater than 1.
Growth factor phenotype model
The select values of α, β and γ (representing the proportions of the GF, PRO and MOT phenotypes respectively) in Table 4 were obtained when the three phenotypes are at equilibrium. Initially, proportions are equal, and initial fitness, W 0, is assumed to be the same for all phenotypes. As shown in Table 4, equilibrium proportions are independent of initial proportions.
Table 4.
Dependence of equilibrium values of α (GF), β (PRO) and γ (MOT) on parameters d, g, m and z. Subscripts ‘i’ and ‘eq’ indicate initial and equilibrium values respectively. Triple polymorphism, two‐strategy polymorphism and fixations are depicted. Input values follow 1 + z = d + g + m
| Costs | Benefit | Initial values | Equilibrium values | ||||||
|---|---|---|---|---|---|---|---|---|---|
| d | g | m | z | αi | βi | γi | αeq | βeq | γeq |
| 0.50 | 0.35 | 0.50 | 0.35 | 0.33 | 0.33 | 0.33 | 0.00 | 1.00 | 0.00 |
| 0.50 | 0.50 | 0.50 | 0.50 | 0.33 | 0.33 | 0.33 | 0.00 | 1.00 | 0.00 |
| 0.52 | 0.86 | 0.48 | 0.86 | 0.33 | 0.33 | 0.33 | 0.00 | 0.92 | 0.08 |
| 0.54 | 0.32 | 0.47 | 0.33 | 0.33 | 0.33 | 0.33 | 0.03 | 0.84 | 0.13 |
| 0.55 | 0.31 | 0.48 | 0.34 | 0.33 | 0.33 | 0.33 | 0.09 | 0.78 | 0.13 |
| 0.55 | 0.10 | 0.55 | 0.20 | 0.33 | 0.33 | 0.33 | 0.50 | 0.50 | 0.00 |
| 0.55 | 0.15 | 0.55 | 0.25 | 0.33 | 0.33 | 0.33 | 0.40 | 0.60 | 0.00 |
| 0.58 | 0.60 | 0.58 | 0.75 | 0.33 | 0.33 | 0.33 | 0.21 | 0.79 | 0.00 |
| 0.59 | 0.27 | 0.52 | 0.38 | 0.33 | 0.33 | 0.33 | 0.29 | 0.59 | 0.12 |
| 0.61 | 0.44 | 0.39 | 0.44 | 0.33 | 0.33 | 0.33 | 0.00 | 0.64 | 0.36 |
| 0.62 | 0.24 | 0.55 | 0.41 | 0.33 | 0.33 | 0.33 | 0.41 | 0.47 | 0.11 |
| 0.65 | 0.05 | 0.65 | 0.35 | 0.33 | 0.33 | 0.33 | 0.86 | 0.14 | 0.00 |
| 0.67 | 0.33 | 0.33 | 0.33 | 0.33 | 0.33 | 0.33 | 0.00 | 0.50 | 0.50 |
| 0.68 | 0.78 | 0.32 | 0.78 | 0.33 | 0.33 | 0.33 | 0.00 | 0.47 | 0.53 |
| 0.70 | 0.33 | 0.47 | 0.50 | 0.33 | 0.33 | 0.33 | 0.33 | 0.33 | 0.33 |
| 0.70 | 0.16 | 0.63 | 0.49 | 0.33 | 0.33 | 0.33 | 0.67 | 0.23 | 0.10 |
| 0.70 | 0.20 | 0.30 | 0.20 | 0.33 | 0.33 | 0.33 | 0.00 | 0.43 | 0.57 |
| 0.70 | 0.05 | 0.35 | 0.10 | 0.33 | 0.33 | 0.33 | 0.50 | 0.00 | 0.50 |
| 0.74 | 0.12 | 0.67 | 0.53 | 0.33 | 0.33 | 0.33 | 0.77 | 0.13 | 0.09 |
| 0.75 | 0.29 | 0.25 | 0.29 | 0.33 | 0.33 | 0.33 | 0.00 | 0.33 | 0.67 |
| 0.76 | 0.10 | 0.69 | 0.55 | 0.33 | 0.33 | 0.33 | 0.82 | 0.09 | 0.09 |
| 0.76 | 0.75 | 0.25 | 0.76 | 0.33 | 0.33 | 0.33 | 0.01 | 0.32 | 0.67 |
| 0.81 | 0.05 | 0.74 | 0.60 | 0.33 | 0.33 | 0.33 | 0.92 | 0.00 | 0.09 |
| 0.81 | 0.55 | 0.25 | 0.61 | 0.33 | 0.33 | 0.33 | 0.10 | 0.21 | 0.69 |
| 0.85 | 0.04 | 0.85 | 0.74 | 0.33 | 0.33 | 0.33 | 0.95 | 0.05 | 0.00 |
| 0.90 | 0.22 | 0.81 | 0.93 | 0.33 | 0.33 | 0.33 | 0.76 | 0.13 | 0.11 |
| 0.90 | 0.55 | 0.42 | 0.87 | 0.33 | 0.33 | 0.33 | 0.37 | 0.09 | 0.54 |
| 0.94 | 0.52 | 0.08 | 0.54 | 0.33 | 0.33 | 0.33 | 0.03 | 0.05 | 0.92 |
| 0.97 | 0.69 | 0.16 | 0.82 | 0.33 | 0.33 | 0.33 | 0.16 | 0.00 | 0.84 |
| 0.98 | 0.71 | 0.28 | 0.97 | 0.33 | 0.33 | 0.33 | 0.27 | 0.01 | 0.71 |
There is strong evidence that initiation of metastasis is caused by primary migrating cancer cells that create pathways for other cells in the primary tumour 31. In this study, primary migrating cells are considered to exhibit the MOT phenotype. When γ > 0, metastasis is initiated as MOT cells appear in the population. While a stable triple polymorphism exists, the tumour becomes malignant when d > m. Two‐strategy polymorphism also occurs between any two of the three phenotypes. A two‐strategy polymorphism exists between GF and MOT when or m = αd. This is an interesting result because it suggests that the proportion of MOT cells depends directly on the proportion of GF cells in the tumour. Polymorphism also exists between GF and PRO when d = m. Finally, it results between PRO and MOT when g = z. Fixation of one phenotype arises when it becomes the only phenotype to remain in the population. Fixation of PRO phenotype exists when d = m and g = z. Fixations of GF and MOT phenotypes do not develop realistically because α eq = 1.00 when g = 0.00, m = d and γ eq = 1.00 when m = 0.00, g = z. This suggests that both GF and MOT need to cooperate with at least one other phenotype to survive as neither is an ESS in the population.
The following graphs take into account cases in which 1 + z ≥ d + g + m. Figure 1 shows that proportion of MOT cells in the tumour varies when values of cost of mobility (m) and cost of sharing space (d) are altered. High γ values emerge as a result of low values of m and high values of d. Proportion of GF cells in the population follows a similar pattern. Number of growth factor cells increases as benefit of receiving growth factor (z) becomes greater while cost of producing the growth factor (g) decreases.
Figure 1.
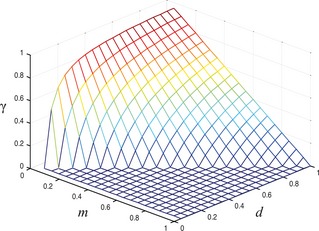
Proportion of phenotype MOT (γ) in cell population with regard to variations in m and d .
Figure 2 indicates how proportion of PRO cells in the tumour changes in four different cases. Values in which the proportion becomes greater than 1 are rejected. In case (a), proportion of PRO cells in the population increases as values of d and z decrease. Likewise, in case (c), as values of d and z decrease (to a certain point), value of the proportion increases. However, the opposite is true for cases (b) and (d): proportion of PRO cells increases as values of g and m increase.
Figure 2.
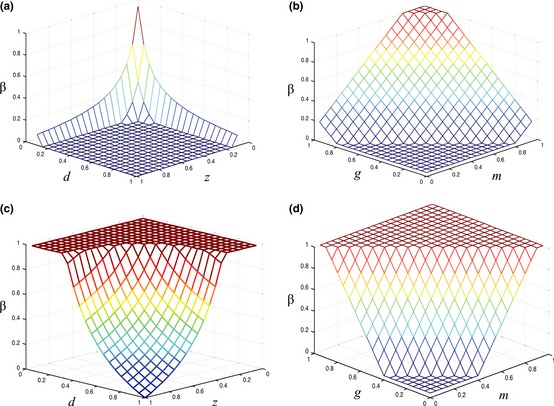
Proportion of phenotype PRO ( β ) in tumor population in four different cases. (a) g = m = 0.10, (b) d = z = 0.90, (c) g = m = 0.50, (d) d = z = 0.50.
Increase in proportion for the PRO phenotype means a subsequent decrease in proportion for either MOT or GF phenotype as PRO cells begin to dominate primary tumour resources. Thus, the tumour becomes less malignant as variables d and z decrease and variables g and m increase.
Specific growth factor phenotype model
Table 5 shows select equilibrium proportions of each cell type from simulation of the SGF model. Initial conditions and four parameters (d, g, m, and z) remain the same as in the previous model; however, proportion of the SGF phenotype has been designated δ.
Table 5.
Dependence of equilibrium values of δ, β and γ on parameters d, g, m and z. Subscripts “i” and “eq” indicate initial and equilibrium values respectively. Triple polymorphism, two‐strategy polymorphism and fixation can occur as values of variables vary. Input values follow 1 + z = d + g + m
| Costs | Benefit | Initial values | Equilibrium values | ||||||
|---|---|---|---|---|---|---|---|---|---|
| d | g | m | z | δi | βi | γi | δeq | βeq | γeq |
| 0.50 | 0.35 | 0.50 | 0.35 | 0.33 | 0.33 | 0.33 | 0.00 | 1.00 | 0.00 |
| 0.50 | 0.50 | 0.50 | 0.50 | 0.33 | 0.33 | 0.33 | 0.00 | 1.00 | 0.00 |
| 0.60 | 0.10 | 0.40 | 0.10 | 0.33 | 0.33 | 0.33 | 0.00 | 0.67 | 0.33 |
| 0.60 | 0.40 | 0.50 | 0.50 | 0.33 | 0.33 | 0.33 | 0.20 | 0.80 | 0.00 |
| 0.61 | 0.19 | 0.47 | 0.27 | 0.33 | 0.33 | 0.33 | 0.30 | 0.61 | 0.09 |
| 0.62 | 0.70 | 0.41 | 0.73 | 0.33 | 0.33 | 0.33 | 0.04 | 0.67 | 0.30 |
| 0.66 | 0.20 | 0.34 | 0.20 | 0.33 | 0.33 | 0.33 | 0.00 | 0.52 | 0.48 |
| 0.67 | 0.10 | 0.33 | 0.10 | 0.33 | 0.33 | 0.33 | 0.00 | 0.49 | 0.51 |
| 0.68 | 0.10 | 0.32 | 0.10 | 0.33 | 0.33 | 0.33 | 0.00 | 0.47 | 0.53 |
| 0.69 | 0.04 | 0.39 | 0.12 | 0.33 | 0.33 | 0.33 | 0.68 | 0.00 | 0.32 |
| 0.70 | 0.30 | 0.50 | 0.50 | 0.33 | 0.33 | 0.33 | 0.40 | 0.60 | 0.00 |
| 0.74 | 0.06 | 0.38 | 0.18 | 0.33 | 0.33 | 0.33 | 0.67 | 0.00 | 0.32 |
| 0.75 | 0.10 | 0.25 | 0.10 | 0.33 | 0.33 | 0.33 | 0.00 | 0.33 | 0.67 |
| 0.76 | 0.61 | 0.38 | 0.75 | 0.33 | 0.33 | 0.33 | 0.19 | 0.50 | 0.31 |
| 0.78 | 0.13 | 0.49 | 0.40 | 0.33 | 0.33 | 0.33 | 0.68 | 0.29 | 0.02 |
| 0.78 | 0.11 | 0.49 | 0.38 | 0.33 | 0.33 | 0.33 | 0.71 | 0.27 | 0.02 |
| 0.80 | 0.10 | 0.20 | 0.10 | 0.33 | 0.33 | 0.33 | 0.00 | 0.25 | 0.75 |
| 0.85 | 0.10 | 0.15 | 0.10 | 0.33 | 0.33 | 0.33 | 0.00 | 0.18 | 0.82 |
| 0.85 | 0.25 | 0.50 | 0.60 | 0.33 | 0.33 | 0.33 | 0.58 | 0.42 | 0.00 |
| 0.87 | 0.10 | 0.50 | 0.47 | 0.33 | 0.33 | 0.33 | 0.79 | 0.21 | 0.00 |
| 0.87 | 0.25 | 0.50 | 0.62 | 0.33 | 0.33 | 0.33 | 0.60 | 0.40 | 0.00 |
| 0.90 | 0.10 | 0.10 | 0.10 | 0.33 | 0.33 | 0.33 | 0.00 | 0.11 | 0.89 |
| 0.90 | 0.60 | 0.10 | 0.60 | 0.33 | 0.33 | 0.33 | 0.00 | 0.11 | 0.89 |
| 0.90 | 0.10 | 0.50 | 0.50 | 0.33 | 0.33 | 0.33 | 0.80 | 0.20 | 0.00 |
| 0.90 | 0.20 | 0.15 | 0.25 | 0.33 | 0.33 | 0.33 | 0.20 | 0.02 | 0.78 |
| 0.90 | 0.82 | 0.12 | 0.83 | 0.33 | 0.33 | 0.33 | 0.02 | 0.13 | 0.85 |
| 0.93 | 0.33 | 0.20 | 0.46 | 0.33 | 0.33 | 0.33 | 0.29 | 0.07 | 0.64 |
| 0.94 | 0.40 | 0.37 | 0.70 | 0.33 | 0.33 | 0.33 | 0.43 | 0.29 | 0.28 |
| 0.94 | 0.78 | 0.35 | 1.08 | 0.33 | 0.33 | 0.33 | 0.27 | 0.41 | 0.31 |
| 0.97 | 0.57 | 0.23 | 0.77 | 0.33 | 0.33 | 0.33 | 0.26 | 0.19 | 0.56 |
As in the GF phenotype model, triple polymorphism occurs under most circumstances at equilibrium. The tumour becomes malignant when d > m + z − g. Two‐strategy polymorphism results between PRO and MOT when g = z just as in the GF phenotype model. Two‐strategy polymorphism also occurs between SGF and MOT when . Fixation of a single phenotype in the population favours the PRO phenotype when d = z = m = g, although it is not restricted to this single case. Fixation of SGF and MOT phenotypes cannot realistically happen as γ = 1 when m = 0, g = z and δ = 1 when g = 0, d = m + z.
Because a major difference between the GF phenotype model and the SGF phenotype model is inability of MOT cells to directly accept the growth factor secreted by the SGF phenotype, it is most expedient to analyse the relationship of different values of z with phenotypic composition of the tumour (Fig. 3). This set of figures analyses cases when 1 + z ≥ d + g + m. Negative proportions are rejected as being biologically impossible.
Figure 3.

Proportion of the SGF , PRO , and MOT phenotypes in the tumor with regard to varying values of z . Four cases are take into account: (a) d = 0.65, g = 0.20, m = 0.20. (b) d = 0.65, g = 0.25, m = 0.25. (c) d = 0.65, g = 0.30, m = 0.30. (d) d = 0.65, g = 0.35, m = 0.35. Input values follow 1 + z ≥ d + g + m.
Both SGF and PRO in Fig. 3 increase in proportion with increasing values of z. However, γ decreases in value in all cases as value of z increases, suggesting inverse relationship between z and proportion of MOT cells in the population at equilibrium. The PRO phenotype increases across the four cases as both g and m increase. In contrast, proportion of SGF cells in the population decreases in a general trend. Whereas, in the first model, MOT phenotype was not directly affected by z, it is adversely affected by it now that the phenotype can no longer receive the growth factor. The PRO phenotype appears to be affected in relatively the same way as it was before, as its proportion increases in both models as g and m increase.
Selective SGF phenotype model
Results from the sSGF phenotype model differed slightly from the results of the SGF model. Because we are concerned with emergence of malignancy in the population, we shall only compare the pattern of resulting proportions of MOT cells in the population. Unlike the SGF model, proportion of MOT cells in the population increases when cost of producing the growth factor (g) increases and benefit of receiving the growth factor (z) decreases. The tumour becomes malignant whenever g>0. In reality, it is unlikely that cost of producing the growth factor will be zero as the stromal cell will need to use energy to produce the growth factors. Therefore, in this particular case, MOT cells will fill the population under most circumstances at equilibrium. This suggests that once stromal cells begin producing factors targeted for motile cells, the tumour will likely become malignant.
Evolution of stable states in population
An evolutionary game with three or more strategies may have no evolutionary stable strategy (ESS) that can resist invasion by outside mutants 17. Interestingly, only PRO can become a pure ESS when m > d in GF and SGF models. Although cells exhibiting MOT phenotype have often been considered an ESS due to their improved abilities to obtain nutrients and resources, the first two models presented here show the contrary, as the condition that W(MOT) > W(GForSGF) and W(MOT) > W(PRO) can never be satisfied. However interestingly, MOT may become an ESS in the sSGF model when g=z. Therefore, it is mathematically feasible for MOT to become fixated in the population in this particular case.
With regard to mixed strategy polymorphisms, the aforementioned results suggest that three kinds of polymorphisms exist in both the GF and SGF (and similarly in the sSGF) models. However, to see whether these polymorphisms are stable, we must see how the population of tumour cells evolves over time. Figures 4 and 5 show results after many successive generations. Time represents successive generations of the same population. We assume that the tumour starts out with equal proportions of GF (or SGF) and PRO cells (α = β = 0.5) and no MOT cells (γ = 0) as the tumour starts off non‐malignant. From the results, we can see that the three polymorphisms as predicted do exist in the populations under certain circumstances.
Figure 4.
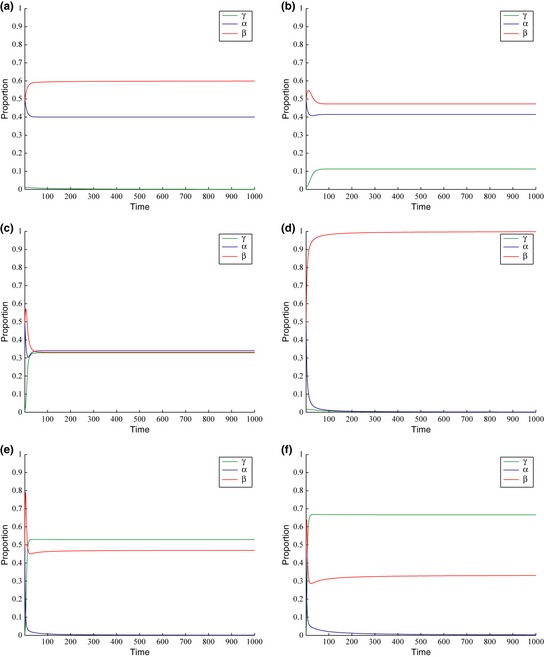
Evolution of stable states in the GF model with respect to time. Initial proportions of cells are as follows: α = 0.5, β = 0.5 and γ = 0. Time is dimensionless and represents one full cycle of replication. Values of parameters for each graph are: (a) d = 0.55, g = 0.15, m = 0.55, z = 0.25. (b) d = 0.62, g = 0.24, m = 0.55, z = 0. 41 (c) d = 0.70, g = 0.33, m = 0.47, z = 0.50. (d) d = 0.50, g = 0.50, m = 0.50, z = 0.50. (e) d = 0.68, g = 0.78, m = 0.32, z = 0.78. (f) d = 0.75, g = 0.29, m = 0.25, z = 0.29.
Figure 5.
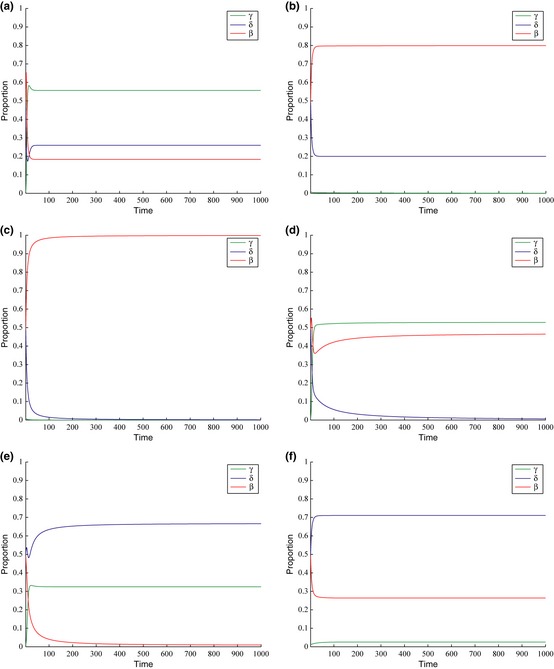
Evolution of stable states in the SGF model with respect to time. Initial proportions of cells are as follows: α = 0.5, β = 0.5 and γ = 0. Time is dimensionless and represents one full cycle of replication. Values of parameters for each graph are: (a) d = 0.97, g = 0.57, m = 0.23, z = 0.77. (b) d = 0.60, g = 0.40, m = 0.50, z = 0. 50 (c) d = 0.50, g = 0.35, m = 0.50, z = 0.35. (d) d = 0.68, g = 0.10, m = 0.32, z = 0.10. (e) d = 0.74, g = 0.06, m = 0.38, z = 0.18. (f) d = 0.78, g = 0.11, m = 0.49, z = 0.38.
Discussion
Results of the simulations have accomplished several objectives of the study. They have shown that cooperation among stromal cells that secrete growth factors and CSCs may exist and can lead to malignancy. Emergence of malignancy was established in all three models as the invasive or motile (MOT) phenotype [traditionally considered to be the phenotype associated with initiation of metastasis 41] became proportionately dominant under certain conditions. Fixation of the MOT phenotype can never happen in GF and SGF models, but it can occur in the sSGF model.
To cover a greater variety of growth factor mechanisms, the study presents three different models that have compared how release of a growth factor affects cells that directly receive it and cells that do not. In the GF model, all three phenotypes (GF, PRO, and MOT) were able to receive the growth factor; in the SGF model, only the SGF and PRO phenotypes were able to receive the factor; finally, in the sSGF model, only the MOT and sSGF phenotypes were able to receive the factors which the sSGF cells selectively secrete. Results and stability analysis show that the final proportional compositions of the tumour follow surprisingly similar patterns. Only PRO phenotype can become fixated in GF and SGF models, but MOT may become fixated in the sSGF model. But stable polymorphisms indicate that MOT phenotypes still depend on cooperation with other phenotypes to appear in the tumour population and remain in the population.
Although previous game theory models of tumour dynamics have dealt with competitive and cooperative nature of cancer cells, this study is the first to mathematically examine the validity of the role of growth factors secreted by tumour stromal cells, in initiating cooperation and ultimately malignancy in three different cases. In an attempt to further the use of EGT in theoretical oncology, this study presents a novel model for analyzing cooperation through sharing of growth factors in a population consisting of proliferative and invasive tumour phenotypes, and a growth factor‐secreting stromal phenotype. Emergence of cells that supply both autocrine and paracrine growth factors in the beginning, as well as in later stages of tumour malignancy emphasizes the need to understand growth factor dynamics. Because experimental studies of human patients may be unethical and often inconvenient, use of computational modelling provides a crucial alternative. Results suggest that under certain conditions, one phenotype may be completely eliminated from the population (as would occur in two‐strategy polymorphism), a conclusion that could lead to new therapeutic practices that would target one specific phenotype by altering tumour environmental conditions, rather than by attacking all phenotypes at once.
Although few experimental studies have been conducted on growth factors in terms of costs and benefits, the models still help explain some current experimental findings. The discovery that only certain cells can produce growth factors that the tumour as a whole needs, explains in homogeneous distribution of proteins in tumour tissue observed after immunohistochemical staining 42, 43. The demonstrated need for tumour cell cooperation across phenotypes verifies the importance of transferring some tumour‐derived cell lines at high concentrations 44. Because of the difficulty of studying paracrine signalling mechanisms 2, results of this study have no current experimental comparison. Therefore, the models provide suggestions for future in vivo and in vitro experiments based on altering environmental conditions to manipulate cancer cell polymorphism. For example, adding more nutrients to the microenvironment would decrease cost of sharing space, an increasingly acidic environment decreases cost of motility 45 and greater cell density increases cost of producing the growth factors.
In conclusion, over the course of this study, three scenarios were considered in which three different growth factor‐producing phenotypes were present. The purpose of the investigation was to examine whether theoretically, sharing of diffusible growth factors may contribute to tumour cell cooperation and emergence of malignancy, and whether presence of non‐receiving phenotypes affects tumour dynamics.
Even at this early stage, the study's findings may help predict some characteristics of tumourigenesis. Emergence of malignancy through cooperation is also implicated in all models. Furthermore, the models highlight key behavioural aspects of the different phenotypes. Among these aspects includes, among others, the implication that cells that can directly receive growth factors and those that cannot are both affected by the growth factor‐secreting phenotype. For instance, both GF and SGF models indicate existence of triple polymorphism, two‐strategy polymorphisms and fixation of the PRO phenotype, and the sSGF model suggests fixation by the MOT phenotype.
Although comprehensive in the number of scenarios taken into account, the models are still necessary simplifications of the complex processes in a real tumour. In future work, we plan to extend the model to include payoffs considered in terms of spatial constraints. Rather than varying payoffs randomly, future studies can take into account the possibility that payoffs vary in a pattern related to environmental conditions. For example, a space crowded with tumour cells of many different phenotypes might induce non‐motile cells to incur a greater cost of sharing space (because a greater concentration of cells means less nutrients per cell) than incurred if a cell is residing in a relatively sparse area.
The models presented in this study have the potential to enhance our understanding of tumourigenesis with emphasis on cooperation among different phenotypes of cancer cells. Although evolutionary game theory has had a relatively short history in the field of theoretical oncology, it may very well become an important and promising direction for future cancer research.
Acknowledgements
We thank Dr. Xiaowen Zhang for helpful review.
Primary research conducted at Edgemont High School.
References
- 1. Nowell PC (1976) The clonal evolution of tumor cell populations. Science 194, 23–28. [DOI] [PubMed] [Google Scholar]
- 2. Hanahan D, Weinberg RA (2011) Hallmarks of cancer: the next generation. Cell 144, 646–674. [DOI] [PubMed] [Google Scholar]
- 3. Biddle A, Liang X, Gammon L, Fazil B, Harper LJ, Emich H et al (2011) Cancer stem cells in squamous cell carcinoma switch between two distinct phenotypes that are preferentially migratory or proliferative. Cancer Res. 71, 5317–5326. [DOI] [PubMed] [Google Scholar]
- 4. Hoek KS, Goding CR (2010) Cancer stem cells versus phenotype‐switching in melanoma. Pigment Cell Melanoma Res. 23, 746–759. [DOI] [PubMed] [Google Scholar]
- 5. Scheel C, Weinberg RA (2011) Phenotypic plasticity and epithelial‐mesenchymal transitions in cancer and normal stem cells? Int. J. Cancer 129, 2310–2314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Almog N, Ma L, Raychowdhury R, Schwager C, Erber R, Short S et al (2009) Transcriptional switch of dormant tumors to fast‐growing angiogenic phenotype. Cancer Res. 69, 836–844. [DOI] [PubMed] [Google Scholar]
- 7. Hoek KS, Schlegel NC, Brafford P, Sucker A, Ugurel S, Kumar R et al (2006) Metastatic potential of melanomas defined by specific gene expression pro‐files with no BRAF signature. Pigment Cell Res. 19, 290–302. [DOI] [PubMed] [Google Scholar]
- 8. Hoek KS, Eichhoff OM, Schlegel NC, Dobbeling U, Kobert N, Schaerer L et al (2008) In vivo switching of human melanoma cells between proliferative and invasive states. Cancer Res. 68, 650–656. [DOI] [PubMed] [Google Scholar]
- 9. Carreira S, Goodall J, Aksan I, La Rocca SA, Galibert MD, Denat L et al (2005) Mitf cooperates with Rb1 and activates p21Cip1 expression to regulate cell cycle progression. Nature 433, 764–769. [DOI] [PubMed] [Google Scholar]
- 10. Giampieri S, Manning C, Hooper S, Jones L, Hill CS, Sahai E (2009) Localized and reversible TGF‐β signaling switches breast cancer cells from cohesive to single cell motility. Nat. Cell Biol. 11, 1287–1296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Egeblad M, Nakasone ES, Werb Z (2010) Tumors as organs: complex tissues that interface with the entire organism. Dev. Cell 18, 884–901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Hiratsuka S, Nakamura K, Iwai S, Murakami M, Itoh T, Kijima H et al (2002) MMP9 induction by vascular endothelial growth factor receptor‐1 is involved in lung‐specific metastasis. Cancer Cell 2, 289–300. [DOI] [PubMed] [Google Scholar]
- 13. Axelrod R, Axelrod DE, Pienta KJ (2006) Evolution of cooperation among tumor cells. Proc. Natl. Acad. Sci. USA 103, 13474–13479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. McAllister SS, Gifford AM, Greiner AL, Kelleher SP, Saelzler MP, Ince TA et al (2008) Systemic endocrine instigation of indolent tumor growth requires osteopontin. Cell 133, 994–1005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Von Neumann J, Morgenstern O (1944) Theory of Games and Economic Behavior. Princeton: Princeton University Press. [Google Scholar]
- 16. Sigmund K, Nowak MA (1999) Evolutionary game theory. Curr. Biol. 9, R503–R505. [DOI] [PubMed] [Google Scholar]
- 17. Maynard Smith J (1982) Evolution and the Theory of Games. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 18. Axelrod R, Hamilton WD (1981) The evolution of cooperation. Science 211, 1390–1396. [DOI] [PubMed] [Google Scholar]
- 19. Turner PE, Chao L (2003) Escape from Prisoner's dilemma in RNA phage phi 6. Am. Naturalist 161, 497–505. [DOI] [PubMed] [Google Scholar]
- 20. Merlo LMF, Pepper JW, Reid BJ, Maley CC (2006) Cancer as an evolutionary and ecological process. Nat. Rev. Cancer 6, 924–935. [DOI] [PubMed] [Google Scholar]
- 21. Tomlinson IPM (1997) Game‐theory models of interactions between tumour cells. Eur. J. Cancer 33, 1495–1500. [DOI] [PubMed] [Google Scholar]
- 22. Bach LA, Sumpter DJT, Alsner J, Loeschcke V (2003) Spatial evolutionary games of interaction among generic cancer cells. J. Theor. Med. 5, 47–58. [Google Scholar]
- 23. Dingli D, Chalub FACC, Santos FC, Van Segbroeck S, Pacheco JM (2009) Cancer phenotype as the outcome of an evolutionary game between normal and malignant cells. Br. J. Cancer 101, 1130–1136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Giese A, Loo MA, Tran N, Haskett D, Coons SW, Berens ME (1996) Dichotomy of astrocytoma migration and proliferation. Int. J. Cancer 67, 275–282. [DOI] [PubMed] [Google Scholar]
- 25. Godlewski J, Bronisz A, Nowicki MO, Chiocca EA, Lawler S (2010) microRNA‐451: a conditional switch controlling glioma cell proliferation and migration. Cell Cycle 14, 2742–2748. [PubMed] [Google Scholar]
- 26. Basanta D, Simon M, Hatzikirou H, Deutsch A (2008) Evolutionary game theory elucidates the role of glycolysis in glioma progression and invasion. Cell Prolif. 41, 980–987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Mansury Y, Diggory M, Deisboeck TS (2006) Evolutionary game theory in an agent‐based brain tumor model: exploring the ‘Genotype‐Phenotype’ link. J. Theor. Biol. 238, 146–156. [DOI] [PubMed] [Google Scholar]
- 28. Tomlinson IPM, Bodmer WF (1997) Modelling the consequences of interactions between tumour cells. Br. J. Cancer 75, 157–160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Gatenby RA, Vincent TL (2003) An evolutionary model of carcinogenesis. Cancer Res. 63, 6212–6220. [PubMed] [Google Scholar]
- 30. Basanta D, Scott JG, Fishman MN, Ayala G, Hayward SW, Anderson ARA (2012) Investigating prostate cancer tumour–stroma interactions: clinical and biological insights from an evolutionary game. Br. J. Cancer 106, 174–181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Basanta D, Scott JG, Rockne R, Swanson KR, Anderson ARA (2011) The role of IDH1 mutated tumour cells in secondary glioblastomas: an evolutionary game theoretical view. Phys. Biol. 8, 015016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Shapiro JR (1986) Biology of gliomas – heterogeneity, oncogenes, growth‐factors. Semin. Oncol. 13, 4–15. [PubMed] [Google Scholar]
- 33. Vona‐Davis L, Rose DP (2009) Angiogenesis, adipokines and breast cancer. Cytokine Growth Factor Rev. 20, 193–201. [DOI] [PubMed] [Google Scholar]
- 34. vanderValk P, Lindeman J, Kamphorst W (1997) Growth factor profiles of human gliomas – do non‐tumour cells contribute to tumour growth in glioma? Ann. Oncol. 8, 1023–1029. [DOI] [PubMed] [Google Scholar]
- 35. Chan JM, Stampfer MJ, Giovannucci E, Gann PH, Ma J, Wilkinson P et al (1998) Plasma insulin‐like growth factor I and prostate cancer risk: a prospective study. Science 279, 563–566. [DOI] [PubMed] [Google Scholar]
- 36. Xu XD, Wang B, Ye CS, Yao C, Lin Y, Huang XL et al (2008) Overexpression of macrophage migration inhibitory factor induces angiogenesis in human breast cancer. Cancer Lett. 261, 147–157. [DOI] [PubMed] [Google Scholar]
- 37. Plate KH, Breier G, Weich HA, Risau W (1992) Vascular endothelial growth‐factor is a potential tumor angiogenesis factor in human gliomas in vivo. Nature 359, 845–848. [DOI] [PubMed] [Google Scholar]
- 38. Gao CF, Xie Q, Su YL, Koeman J, Khoo SK, Gustafson M et al (2005) Proliferation and invasion: plasticity in tumor cells. Proc. Natl. Acad. Sci. USA 102, 10528–10533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Mueller MM, Fusenig NE (2004) Friends or foes—bipolar effects of the tumor stroma in cancer. Nat. Rev. Cancer 4, 839–849. [DOI] [PubMed] [Google Scholar]
- 40. Iwata M, Awaya N, Graf L, Kahl C, Torok‐Storb B (2004) Human marrow stromal cells activate monocytes to secrete osteopontin, which down‐regulates Notch1 gene expression in CD34 cells. Blood, 103, 4496–4502. [DOI] [PubMed] [Google Scholar]
- 41. Friedl P, Maaser K, Klein CE, Niggemann B, Krohne G, Zanker KS (1997) Migration of highly aggressive MV3 melanoma cells in 3‐dimensional collagen lattices results in local matrix reorganization and shedding of alpha2 and beta1 integrins and CD44. Cancer Res. 57, 2061–2070. [PubMed] [Google Scholar]
- 42. Bidard FC, Pierga JY, Vincent‐Salomon A, Poupon MF (2008) A “class action” against the microenvironment: do cancer cells cooperate in metastasis? Cancer Metastasis Rev. 27, 5–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Royuela M, Ricote M, Parsons MS, Garcia‐Tunon I, Paniagua R, De Miguel MP (2004) Immunohistochemical analysis of the IL‐6 family of cytokines and their receptors in benign, hyperplasic, and malignant human prostate. J. Pathol. 202, 41–49. [DOI] [PubMed] [Google Scholar]
- 44. Von Hoff DD, Clark GM, Forseth BJ, Cowan JD (1986) Simultaneous in vitro drug sensitivity testing on tumors from different sites in the same patient. Cancer 58, 1007–1013. [DOI] [PubMed] [Google Scholar]
- 45. Lagana A, Vadnais J, Le PU, Nguyen TN, Laprade R, Nabi IR et al (2000) Regulation of the formation of tumor cell pseudopodia by the Na+/H+ exchanger NHE1. J. Cell Sci. 113, 3649–3662. [DOI] [PubMed] [Google Scholar]


