Mathematical modelling of spatio‐temporal cell dynamics in colonic crypts following irradiation

Abstract

Objectives

Modelling the apoptotic process is essential for simulating and understanding tumour growth, as most tumour tissues carry mutations in apoptotic signalling pathways. Thus here, we have aimed to construct a mathematical model of colonic crypts that explicitly incorporates the apoptotic mechanism.

Methods

A murine colonic crypt was described as being a two‐dimensional rectangular surface model. In this system, three types of cells with different proliferating and differentiating potentials migrate. Apoptosis was described as a process activated by irradiation that progresses in a stepwise manner. Parameter values in the model were determined to be consistent with experimental data for changes in the apoptotic cell ratio within murine transverse colonic crypts following irradiation.

Results

First, we constructed a model reproducing cell proliferation dynamics in normal murine colonic crypts; next, we applied the apoptotic mechanism to this model. As a result, we succeeded in simultaneous reproduction of both spatial and temporal changes in distribution of apoptotic cells in murine colonic crypts by determining parameter values in numerical simulations. Through this adjustment process, we were able to predict that stem cells and transit amplifying (TA) cells in each generation must react distinctly from each other, to apoptosis‐inducing stimuli.

Conclusions

We constructed a mathematical model with which we could quantitatively describe cell proliferative and apoptotic dynamics in a murine colonic crypt. Using this model, we were able to make novel predictions that sensitivity to apoptosis‐inducing stimuli is dependent on cell type.

Introduction

In homoeostasis, number of cells in living tissues is controlled by balance between cell proliferation and cell loss by processes that include apoptotic and living cell extrusion 1. Studies of such homoeostasis are essential for understanding mechanisms of tumour growth and for developing novel anti‐cancer treatments. Thus, there have been many studies of homoeostasis of intestinal epithelial tissues, in which cells proliferate very frequently and migrate actively.

To quantitatively describe intestinal epithelial tissues as a dynamic system, dynamic parameters, such as cell‐cycle duration and speed of cell migration, need to be estimated. In conventional experimental methods, these dynamic parameters have been estimated indirectly by the statistical figures of fixed tissue samples based on several hypotheses generated using cell dynamics 2. To estimate the parameters directly, development of in vitro culture systems for intestinal tissues is required. Recently, some research groups have succeeded in culturing a single intestinal crypt in vitro 3, 4, where proliferating and migrating cells could be directly observed by microscopy.

As an alternative, mathematical modelling is a powerful method to understand dynamic systems behind experimental data. In earlier models, surface of the intestinal crypt has been characterized as a two‐dimensional rigid lattice with rectangular cell layouts 5, 6. Using this model, some cell dynamics have been described. However, this describes several unrealistic aspects inconsistent with real crypt dynamics; for example, migration of individual cells, as their movement would be restricted to discrete spatial steps. To resolve these difficulties, a two‐dimensional lattice‐free model has been proposed 7. Here, individual cell shape was depicted to result from location of the centre of the cell, and boundaries between all neighbouring cell centres were described using Voronoi diagrams. A further similar model for describing cell shape has been constructed 8. In this model, the Wnt signalling network was implemented; cell‐cycle and adhesion/repulsion forces between neighbouring cells are changed by distinct Wnt stimulation, which has been suggested in previous experimental results. Recently, a three‐dimensional model for murine small intestinal crypts has been developed 9. In this model, Wnt and Notch signals determined cell differentiation. Our group has also constructed a mathematical model to describe processes of cell proliferation and differentiation in a human colonic crypt, and has succeeded in simulating several experimental results 10.

In most of these previous crypt models, apoptosis occurred only at the top of the crypt to maintain crypt cell number. In contrast, considering that most tumour tissues carry mutations in apoptotic signalling pathways, modelling of the apoptotic process is needed for simulating and understanding tumour growth. Thus, in this study, to simulate tumour tissue development, we sought to construct a mathematical model of colonic crypts in which apoptotic mechanisms are incorporated. To achieve this, we attempted to integrate mechanism of apoptosis into our previously constructed model to describe tumour growth in which apoptosis is disordered. To validate the model quantitatively, experimental data relating to apoptosis are needed. However, apoptosis is rarely detected in healthy crypts 11. Therefore, we used data for apoptotic dynamics induced by irradiation. Irradiation experiments were intensively performed in the 1970s to investigate the process of tissue regeneration 12. In these experiments, apoptotic index (AI), percentage of cells showing apoptotic bodies in tissue, was obtained as quantitative data. In the present study, we found the apoptotic mechanism to be consistent with AI data obtained in the irradiation experiments.

Methods

Modelling cell proliferation and migration in murine colonic crypts

A colonic crypt was modelled as a hollow cylindrical shape, whose development is described as a two‐dimensional rectangular surface (Fig. 1a). On this surface, cells migrate and differentiate. The following three cell phenotypes were considered: stem, TA and differentiated cells.

Figure 1.

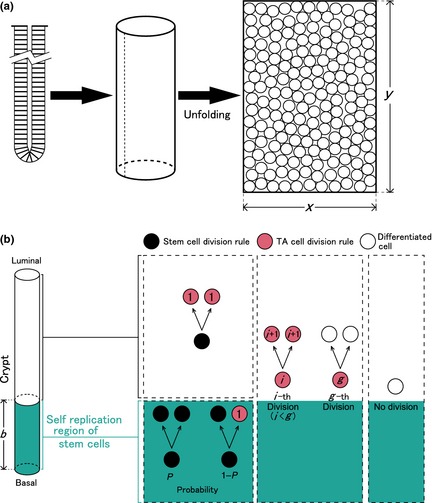
Model of murine colonic crypt. (a) Modelling of the crypt. A crypt is modelled as a cylindrical surface, which is unfolded to a two‐dimensional surface. Cells are spatially arranged on this rectangular surface whose width and height are given by x and y, respectively. (b) Scenario of cell proliferation and differentiation. Two regions are considered in a crypt. Lower portion of the crypt, whose height is b, is defined as the self‐replication region of stem cells. Within this region, a stem cell divides symmetrically and produces two stem cells with a probability P (0 ≤ P ≤ 1). When it divides asymmetrically, it produces a stem cell and a first‐generation transit amplifying (TA) cell with a probability 1 − P. Outside this region, a stem cell divides symmetrically and produces two‐first‐generation TA cells. Regardless of the region, a TA cell divides symmetrically and differentiates after g‐th divisions.

Among these, only stem cells can self‐replicate, and stem cell cycle time was defined as C _S. During the cell cycle, a cell doubles its size. That is, the cell radius r _t at time t is given by

$$r_t=\left(1+\left(\sqrt{2}-1\right)\frac{t}{C_{\mathrm{S}}}\right)\times r_0$$ (1)

where r ₀ is the initial cell radius value. The rule for division of stem cells depends on their position. The region from the crypt bottom to height of b is defined as ‘replication region of stem cells’. In this region, a stem cell divides symmetrically into two stem cells with a probability of P. Furthermore, a stem cell divides asymmetrically into one stem cell and one TA cell with a probability of 1 − P. At the upper end of this region, a stem cell always divides symmetrically into two TA cells.

A TA cell produced by a stem cell divides symmetrically a limited number of times. In the g‐th division, the TA cell differentiates into two differentiated cells; its cell cycle time is defined as C _TA. TA cell radius is also given by eqn (1). Differentiated cells never divide. Figure 1b summarizes cell proliferation and differentiation.

When a cell divides, its division axis, and centre positions of its daughter cells along division axis after division are determined 10. A dividing axis is determined as the axis passing through the centre of the dividing cell (mother cell) (x _M, y _M). Centres of daughter cells are determined as (x _D1, y _D1) and (x _D2, y _D2), respectively, where x _D1 = x _M + r ₀sinθ, y _D1 = y _M + r ₀cosθ, x _D2 = x _M − r ₀sinθ and y _D2 = y _M − r ₀cosθ. θ is an angle randomly sampled from the range of [−π, π] radian.

When daughter cells are generated by cell division, cells can overlap. To avoid overlaps, the ‘shoving’ algorithm, in which cells ‘shove’ each other to minimize overlapping area, is performed to arrange cell positions 10. In this algorithm, first, a cell (denoted by cell a) is chosen and its neighbouring cells (denoted by cells j; j = 1, 2, …, n _a) are determined as those attached to the first chosen cell. Next, the following sums are calculated:

$$\mathit{\delta }{x}^{(a)}=\sum _{j=1}^{n_a}\frac{x^{(j)}-x^{(a)}}{d^{(j)}}\left[\left(R^{\left(j\right)}+R^{\left(a\right)}\right)-d^{\left(j\right)}\right],$$ (2)

$$\mathit{\delta }{y}^{(a)}=\sum _{j=1}^{n_a}\frac{y^{(j)}-y^{(a)}}{d^{(j)}}\left[\left(R^{\left(j\right)}+R^{\left(a\right)}\right)-d^{\left(j\right)}\right],$$ (3)

where

$$d^{(j)}=\sqrt{{(x^{\left(j\right)}-x^{(a)})}^2+{(y^{\left(j\right)}-y^{(a)})}^2}$$

represents distance between centres of cells a and j, R ^(a) and R ^(j) represent radii of cells a and j, respectively, and (x ^(a), y ^(a)) and (x ^(j), y ^(j)) represent positions of cells a and j in two‐dimensional model space, respectively 10. Last, position of cell a is changed from (x ^(a), y ^(a)) to (x ^(a) + δx ^(a), y ^(a) + δy ^(a)). A set of these procedures is executed for all cells in the model, successively. In the present simulations, this procedure was repeated 1000 times for each shoving step.

As a result of the shoving algorithm, cells on average, move upwards. When cells arrive at the top of the crypt, they are removed from it. This removing process emulates the exfoliating process occurring at the top of real colonic crypts.

Calibrating parameters of cell proliferation and differentiation

To quantify cell proliferation in murine colonic crypts, many experiments using thymidine‐analogues have been conducted. In the 1970s, tritiated thymidine ([³H]dT) was injected into mice, and their large intestines (transverse colons) were dissected and fixed for autoradiographical analysis, where number of cells incorporating thymidine analogues was counted 13. In such experiments, labelling index (LI), defined as a ratio of labelled (thymidine analogues incorporated) cells, was given for each cell position in the crypt. We used such LI data, obtained experimentally in a previous study 13, for calibration of the model parameter values that determine cell dynamics in a crypt.

Calibration was executed by quantitatively comparing LI data obtained in the experiment with LI data calculated by model simulation, using a given parameter set. In the simulation, all S‐phase cells at the time of thymidine analogue injection were labelled. One hour after labelling, we calculated ratios of labelled cells in each cell position along a vertical (that is, crypt–villus) axis of the crypt. As shown in Fig. S1, vertical lines were drawn on the crypt surface at intervals of 5 μm. Next, on each line, labelling status (labelled or non‐labelled) of cells was recorded for each cell position, defined as number of cells counted from the bottom, along the line. Last, LI was calculated as n _i(%) (i = 1, 2, …) (Fig. S1).

As the existing ratio for each cell type can fluctuate around the mean value with time, LI depends on time when the thymidine analogue was injected. Therefore, in the present simulations, the thymidine analogue was injected at three different time points after the number of cells of each species reaches a steady state. Three LI curves calculated for a series of three thymidine analogue injections were averaged and used for calibration of the model parameter values.

Modelling apoptosis in colonic crypts

To describe by a constructed model, cell behaviour in colonic crypts after irradiation, implementation of the apoptosis process was essential. When a cell executes apoptosis in living tissues, several signalling pathways are activated and various reactions occur sequentially 14, 15. During apoptosis in colonic crypts, the reaction pathway shown in Fig. 2a is considered to progress in a stepwise manner. When cells are exposed to stresses such as hypoxia and irradiation, their DNA is damaged. When damage is too severe to be sustained, the cells initiate apoptosis. First, various apoptotic proteins such as BAX and BAK oligomerize on outer membranes of mitochondria, and these oligomers create pores. This is called mitochondrial outer membrane permeabilization and is irreversible. As a result, cytochrome c is released from inter‐membrane spaces of the mitochondria into the cytoplasm, and downstream reactions are activated sequentially. Finally, caspase‐3, the executor of apoptosis, is activated. Subsequently, this dismantles cells and causes cell death. Cell fragments – apoptotic bodies, are phagocytosed by macrophages and/or adjacent epithelial cells.

Figure 2.

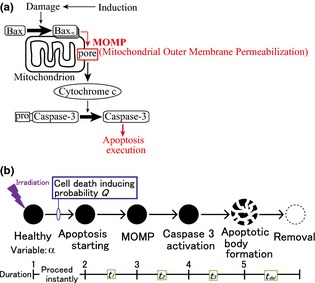
Modelling of the apoptotic process. (a) Schematic drawing of the apoptotic pathway, starting from DNA damage persisting after induction. This progresses in a stepwise manner. (b) Cells at each stage are assigned with a variable α. After irradiation, cells (α = 1) induce apoptosis with probability Q. Following this, the apoptotic process progresses sequentially with given time durations; between each stage these are assigned as t ₁, t ₂, t ₃, and t _del.

As apoptosis progresses in a stepwise manner, it has been subdivided into five stages in the present model (Fig. 2b). An integer variable α was assigned to each cell to describe the stage of apoptotic progression. Figure 2b shows the relationship between value of α and corresponding apoptotic stage. In cells with α = 1, no apoptotic process is activated. When cells are irradiated, a subset of cells undergoes apoptosis as a result of DNA double‐strand breaks, and the variable α is changed to 2. This change of α from 1 to 2 occurs stochastically with a probability of Q. Subsequent changes of α from 2 to 3, 3 to 4 and 4 to 5 occur as time elapses. Durations between states of α = 2, 3, 4 and 5 are defined as t ₁, t ₂ and t ₃, respectively. Cells with α = 5 are removed from the model crypt after duration t _del.

Calculation of apoptosis index

In previously reported experimental studies, AI has been measured along the cell position for a given time, to estimate apoptotic frequency within the crypt. AI at cell position i was defined as proportion of apoptotic cells found at i. AI curve provided in the literature 11 has been plotted in Fig. 5a (closed circles). In the same study 11, time courses of AI after irradiation, defined as ratio of apoptotic cells in a whole crypt, were also provided (closed circles in Fig. 5b). In the present model, cells with α = 4 or 5, corresponding to cells in which caspase‐3 was activated, were considered to be apoptotic cells. Using results the simulation, we calculated AIs along the cell positions at specified times corresponding to the experiments. We also calculated time course of AI in the crypt as a whole after apoptosis induced by irradiation. Finally, we compared these values with the corresponding experimental data 11.

Figure 5.

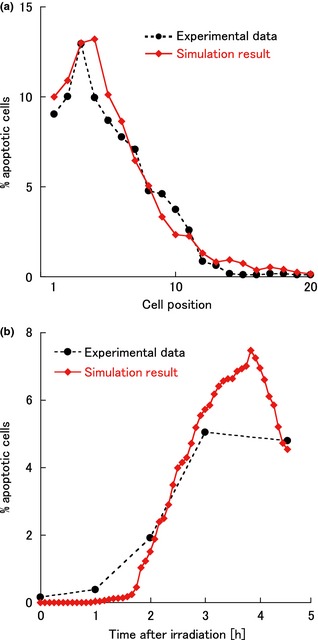
Spatial and temporal changes of apoptotic indices. (a) Apoptotic indices plotted against cell position (4.5 h after irradiation). (b) Apoptotic indices plotted against time after irradiation. These simulation results (red closed diamonds) were in good agreement with the experimental data 11 (black closed circles). Parameter values shown in Table 1 were used for the simulations.

In the simulation, a model crypt was stimulated by irradiation at a given time point after number of cells of each phenotype reached a steady state. For each given parameter set, three simulation results with different stimulation time points were averaged and the AI curve was obtained. We searched for parameter values in which the simulation results were consistent with the experimental data 11.

Assessment of fitness to experimental data

To quantify similarity of simulation results to experimental data (LI and AI), the value of D was used 10. D is defined as the absolute difference between simulation results and experimental data, averaged over cell positions i:

$$D=\sum _{i=1}^M|[\text{simulation results (LI or AI)}]-[\text{experimental data (LI or AI)}]|/M$$

where M is number of plots. To calibrate model parameters, we searched for the parameter set minimizing D by changing values of the parameters.

Results

Cell proliferation and migration

Initial cell radius, and width and height of the model crypt (r ₀, x and y, respectively) were determined to be consistent with previous reports measuring size of colonic crypts (Table 1) 13, 16. Following the method described above, model parameters relating to cell dynamics in the crypt were determined to be consistent with the experimental data. As shown in Fig. 3, the LI curve obtained with simulation results of the model was well adjusted to the experimental data 13 using the parameter values shown in Table 1.

Table 1.

Parameters of the murine colonic crypt model

Parameter	Symbol	Value
Crypt architecture
Crypt height	y	460 μm
Crypt circumference	x	230 μm
Number of cells in a crypt		684 cells
Initial cell radius	r 0	5 μm
Cell proliferation and differentiation
Self‐replication region of stem cell	b	20 μm
Stem‐cell cycle	C S	35 h (±5 h)
TA cell cycle	C TA	25 h (±5 h)
Maximum division count	g	3
Probability of symmetrical division of stem cells	P	0.9
Apoptotic process
Apoptosis‐inducing probability of stem cell	Q S	20%
Apoptosis‐inducing probability of TA cell (first generation)	Q TA1	70%
Apoptosis‐inducing probability of TA cell (second generation)	Q TA2	17.5%
Apoptosis‐inducing probability of TA cell (third generation)	Q TA3	0%
Minimum time duration between apoptosis starting and MOMP	t 1Min	80 min
Maximum time duration between apoptosis starting and MOMP	t 1Max	235 min
Time duration between apoptotic body formation and removal	t del	40 min

TA, transit amplifying; MOMP, mitochondrial outer membrane permeabilization.

Figure 3.

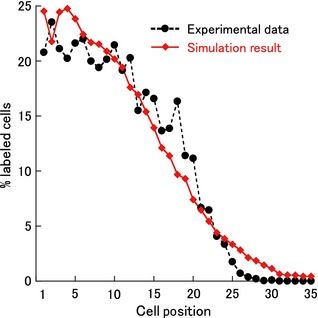
Labelling indices plotted against cell position. Simulation results (red closed diamonds and solid curve) were in good agreement with the experimental data (black closed circles and dashed curve) 13. To obtain these results, parameter values shown in Table 1 were used.

To investigate sensitivity of changing each model parameter on the resultant LI curve, we changed one of the five dynamic model parameters b, g, C _S, C _TA, or P while the others remained fixed. Results of sensitivity analysis are shown in Fig. S2a–e. When height of the self‐replication region of stem cells b was increased, LI values also increased globally (Fig. S2a). When maximum division count of TA cells g was increased, LI values in the upper part of the crypt increased dramatically (see Fig. S2b). When stem cell cycle C _S was reduced, as shown in Fig. S2c, LI values increased in lower and also in upper portions of the crypt. When TA cell cycle C _TA was changed, as shown in Fig. S2d, LI curve characteristically changed in response to C _TA. When C _TA decreased, LI values at the crypt base increased, while those in the upper portion reduced simultaneously. When probability of symmetrical division of stem cell P was changed, as shown in Fig. S2e, LI values slightly increased with increasing P.

Apoptosis in murine colonic crypts

Apoptosis is considered to be induced through a system that monitors damage in cells at each cell cycle checkpoint. Based on this consideration, in our model, we assumed that only dividing cells could execute apoptosis, and thus apoptosis not occurring in differentiated cells. In addition, we assumed that cell dynamics was not affected/hardly affected by damage caused by irradiation. Therefore, in the following simulations, we used the parameter values shown in Table 1.

First, we simulated cases in which apoptosis occurred in specific cell phenotypes. In cases where apoptosis occurred only in stem cells, it occurred only at bases of crypts (in cell positions 1–5); thus AIs could not be adjusted to the experimental data. If apoptosis occurred only in TA cells, it occurred at any region along the various cell positions, and AIs in middles of crypts were much larger than those in lower regions. Again, AIs could not be adjusted to the experimental data. These results indicate that apoptosis occurred in both stem cells and TA cells.

Therefore, we simulated a situation in which apoptosis occurred in both cell phenotypes. Although numbers of parameters to be calibrated was increased from one to two, that is, probability of inducing apoptosis following irradiation to stem cells and TA cells (Q _S and Q _TA, respectively), we could not adjust the resultant AI curve to the experimental data by any combination of Q _S and Q _TA values. As we noticed that apoptotic cells disappeared in cell positions higher than 15 in the experimental data, we investigated distribution of stem and TA cells in each generation along the cell positions (Fig. 4). Here, we classified TA cells into first, second and third generations with number of cell divisions following differentiation to a TA cell. In this figure, a dominant phenotype residing at a given cell position gradually changed from a stem cell to a differentiated cell as the cell position was increased.

Figure 4.

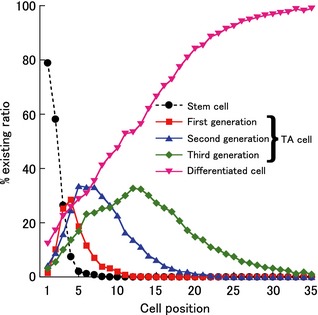
Existing ratio of each cell type. Existing ratios of stem (black circles), transit amplifying (TA) (first generation, red squares), TA (second generation, blue triangles), TA (third generation, green diamonds), and differentiated cells (pink inverted triangles) were plotted against cell position. To obtain these results, the parameter values shown in Table 1 were used.

By defining the parameter values of Q _TA independently for each generation of TA cells, we could adjust the resultant AI curve to the experimental data (Fig. 5a). In this case, apoptosis occurred only in stem cells and first and second generation of TA cells. Only this case, could simulation results be fitted to the experimental data. Values of apoptotic parameters, Q, t ₁, t ₂, t ₃, and t _del for each cell phenotype used in the simulation are summarized in Table 1.

To obtain these parameter values, two assumptions on values of t ₁, t ₂, t ₃ and t _del were made. In the first, values of t ₁, t ₂, t ₃ and t _del did not depend on cell phenotype, that is the same parameter values were used in stem cell and TA cells, in all generations. In the second assumption, values of t ₂ and t ₃ were determined by the value of t ₁. To calculate t ₂ and t ₃, relative ratio between t ₁, t ₂, and t ₃, which had been obtained experimentally in a study using HeLa cells 17, was used. To be specific, t ₂ and t ₃ were estimated by, t ₂ = (8.76/65.88) t ₁ and t ₃ = (25.36/65.88) t ₁, respectively.

At first, simulations were performed with a given set of values for durations t ₁, t ₂, t ₃. As there was clearly no apoptosis until time t ₁  + t ₂, under these conditions, it could not match the experimental data. Therefore, these time durations should be determined randomly from the assigned range. In the simulation, instead of calibrating values of t ₁, its maximum value, t _1Max, and its minimum value, t _1Min, were calibrated as fitting parameters. Using t _1Max and t _1Min, maximum and minimum values of t ₂ and t ₃ were calculated by t _2Max = (8.76/65.88) t _1Max, t _2Min = (8.76/65.88) t _1Min, t _3Max = (25.36/65.88) t _1Max and t _3Min = (25.36/65.88) t _1Min, respectively. Values of durations, t ₁, t ₂ and t ₃, were sampled randomly from the corresponding ranges [t _1Min, t _1Max], [t _2Min, t _2Max] and [t _3Min, t _3Max] by using uniform distribution. Furthermore, value of t _del was determined to be 40 min, as a result of simulations using various values of t _del (Fig. S3). Taken together, when parameter values were given by values shown in Table 1, simulation results [shown in Fig. 5 (closed diamonds)] could be fitted to the experimental data.

Discussion

Model parameter values related to cell proliferation and differentiation

As a result of the simulations, average stem cell cycle C _S and average TA cell cycle C _TA were estimated to be 35 and 25 h, respectively. According to previous reports, cell cycle duration of cells located from the base to middle to upper portions of the crypt was in the order of 36 h 18 and 20 h 13, 18, 19, respectively. Considering that intestinal stem cells reside in the bases of crypts 20, estimated values of C _S and C _TA are consistent with these previously reported data. In a more recent report, crypt base columnar cells, which are considered to coincide with stem cells in the small intestinal crypt, have mean cell cycle duration of 28.5 h 21. In a further recent report, cells at the base of the crypt expressing Lgr5, an intestinal stem‐cell marker, were shown to have a mean cell cycle of 21.5 h 22. Considering that the stem cell cycle in small intestinal crypts is shorter than that in colonic crypts 18, values of C _S and C _TA estimated in this study are very close to these published data.

Here, the probability of symmetrical division of stem cells, P, was estimated to be 0.9. This value was lower than 1, likely to be because stem cells sometimes divide asymmetrically in crypt bases. This prediction is consistent with a previous report that stem cells divide asymmetrically in mice and human colonic crypts 23.

The height of the self‐replication region of stem cells, b, was estimated to be 20 μm, implying that stem cells mainly reside in cell positions 1–2. This is consistent with the observation that stem cells reside at bases of colonic crypts 24, 25.

Model parameter values related to apoptosis

As shown in Table 1, apoptosis‐inducing probability Q in TA cells of the first generation (assigned as Q _TA1) was predicted to be larger than that of stem cells (Q _S) or second‐generation TA cells (Q _TA2).

Localization of suppressors of apoptosis is one of the possible reasons why Q _S was smaller than Q _TA1. Expression of Bcl‐2, a suppressor of apoptosis, has been reported to be confined to the base of the colonic crypt 26, where the stem cells expressing Lgr5 reside 25. Moreover, it was also reported that levels of both spontaneous and induced apoptosis in Bcl‐2‐null mice rose significantly and selectively at the bases of crypts, in comparison to crypts from wild‐type mice 26, 27.

Probability Q was reduced when generation of TA cells was increased (Table 1). We presumed this to be a mechanism to efficiently maintain healthy tissue by removing relatively long‐lived cells with persistent DNA damage, only. To the best of our knowledge, molecular evidence for this mechanism is lacking. We hope that this evidence will be revealed in future studies.

Relationship with other existing models

In this paper, we show that we have constructed a computational model for simulating apoptotic dynamics in murine colonic crypts. While other existing crypt models describe intestinal cell dynamics in normal crypts under a steady state 5, 6, 7, 8, 9, 10, 20, our present model focuses on transient processes after irradiation, and has succeeded in describing AI data obtained from previously performed quantitative experimental studies.

Several models published recently, introduced signalling pathways relating to growth, differentiation, proliferation and self‐replication such as Wnt, Notch and BMP 8, 9, 28. On the other hand, a model using a simple scenario for the mechanism of cell proliferation and differentiation has been able to describe satisfactorily cell dynamics in human colonic crypts 10. Because the present model focused on apoptotic dynamics, a simple scenario for proliferation and differentiation was used. If necessary, it is possible to incorporate more signalling pathways into our model.

Calibration methods

In our model, we calibrated parameter values to obtain reasonable simulation results by repeating simulations using various parameter values. However, there are more rigorous methods to calibrate model parameters. For example, a method using approximate Bayesian computation has been proposed. In previous studies, this method has been used for parameter estimation of a model describing DNA methylation pattern dynamics 29, 30. In principle, such a method can also be applied to the current crypt model. However, this application seems unrealistic at present as the computational load is too heavy. Thus, developing a novel strategy to apply such sophisticated methods to calibrate parameter values of complex computational models including ours developed in this paper, is expected.

In conclusion, in this study we developed a computational model of cell dynamics in a murine colonic crypt, with which we can quantitatively calculate spatial distributions of proliferative and apoptotic cells, within a crypt. We calibrated model parameter values to be consistent with previously reported experimental data, and found that parameter values related to the apoptotic process were dependent on the cell phenotype; this will shortly be validated experimentally.

Supporting information

Fig. S1 Illustration describing formation of a labelling index (LI) curve.

Fig. S2 Sensitivity analysis of model parameters.

Fig. S3 Sensitivity analysis of parameter t _del.