A novel view on stem cell development: analysing the shape of cellular genealogies

Abstract

Objectives:  The analysis of individual cell fates within a population of stem and progenitor cells is still a major experimental challenge in stem cell biology. However, new monitoring techniques, such as high‐resolution time‐lapse video microscopy, facilitate tracking and quantitative analysis of single cells and their progeny. Information on cellular development, divisional history and differentiation are naturally comprised into a pedigree‐like structure, denoted as cellular genealogy. To extract reliable information concerning effecting variables and control mechanisms underlying cell fate decisions, it is necessary to analyse a large number of cellular genealogies.

Materials and Methods:  Here, we propose a set of statistical measures that are specifically tailored for the analysis of cellular genealogies. These measures address the degree and symmetry of cellular expansion, as well as occurrence and correlation of characteristic events such as cell death. Furthermore, we discuss two different methods for reconstruction of lineage fate decisions and show their impact on the interpretation of asymmetric developments. In order to illustrate these techniques, and to circumvent the present shortage of available experimental data, we obtain cellular genealogies from a single‐cell‐based mathematical model of haematopoietic stem cell organization.

Results and Conclusions:  Based on statistical analysis of cellular genealogies, we conclude that effects of external variables, such as growth conditions, are imprinted in their topology. Moreover, we demonstrate that it is essential to analyse timing of cell fate‐specific changes and of occurrence of cell death events in the divisional context in order to understand the mechanisms of lineage commitment.

Introduction

Somatic stem cells play a central role in tissue maintenance and repair as well as in cancer initiation and progression. Therefore, these cells are potential targets of many clinically relevant treatment options. Although clinical applications like stem cell transplants are well established, a number of central questions about organizational principles are still unresolved. It is controversial how the balance of self‐renewal and differentiation within a stem cell population is generated at the single cell level. For example, it is an open question whether asymmetric cell division events play a functional role in this context or if the observed developmental patterns are induced by asymmetric cell fates that are not necessarily linked to the cell division event (1, 2). Moreover, there is only insufficient understanding of the nature of multipotency as well as of dynamic processes that initiate and regulate specification of the diversity of different functional cells (lineage specification) (3, 4). Experimental approaches based on cell population averages are mostly not able to answer these questions for two reasons: first, stem cell populations have a certain, hardly reducible, degree of inherent heterogeneity that makes it extremely difficult to initiate cultures of identical and synchronized cells; and, second, population approaches do not capture temporal evolution and chronology of cellular development as it occurs within a single cell. But it is precisely the development of each individual cell and its progeny that represents a possible realization of the developmental sequence and retains much of the necessary information: on the correlations between differentiation and cell‐cycle regulation, on timing of lineage specification processes and cell death events, as well as on the role of asymmetric developments (Fig. 1).

Figure 1.

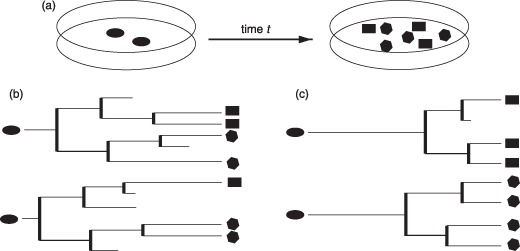
Cell cultures and genealogies. (a) Shows a typical cell culture experiment in which undifferentiated cells are exposed to certain conditions, and the final composition is evaluated after time t (possible changes of the cell fate are indicated by the shape of the sketched cells). Within this setup, it is not possible to analyse whether the initial cells contributed to more than one cell fate or whether there is an inherent predetermination of these cells. Furthermore, this approach does neither elucidate the role of cell death nor the timing of the expansion. The cellular genealogies shown in subfigure (b) and (c) represent two possible and rather distinct scenarios that match the above population results. Genealogies in (b) are characterized by early expansion, multipotency (initial cells contribute to more than one lineage fate) and significant cell death. In contrast, the genealogies in (c) show late expansion, unipotency (initial cells only contribute to one lineage fate) and reduced cell death.

It is here that the digital revolution in microscopy as well as increasing memory capacity of computer systems opens a new dimension for application of time‐lapse video microscopy for the analysis of cell cultures. Such high‐resolution technologies facilitate the tracing of a single cell, comprising all its progeny over extended time periods up to several days. This includes the temporal analysis of cell‐specific parameters like morphology, cell‐cycle time, motility or occurrence of cell death within the population context. Time‐lapse video monitoring with single cell tracking has been applied to cultures of haematopoietic (1, 5, 6) as well as neural (7, 8), muscle (9), and embryonic stem cells (10). In a recent study, it could be shown that identification of patterns in the in vitro cell‐cycle time distribution proved useful for enrichment of cells with higher repopulation potential in vivo (5). Continuing these ideas, fluorescence labelling of marker genes for differentiation and lineage specification will soon allow for better identification and temporal determination of central decision events in the developmental sequence (11, 12). All these different pieces of information on cellular development, divisional history, and differentiation can be comprised into a pedigree‐like structure in which the founder cell represents the root, and the progeny are arranged in the branches. Throughout this paper, these pedigrees are referred to as cellular genealogies. A comprehensive review about the importance and the perspectives of single cell tracking has been recently published by Rieger and Schroeder (13).

Automated analysis of time‐lapse videos from cell cultures allows tracking of a multitude of root cells. The resulting cellular genealogies represent unique examples of the developmental sequence as they occur under the particular assay conditions. Statistical analysis of these cellular genealogies can reveal typical patterns of cellular development as they are imprinted in the topology. However, to our knowledge there are no established measures for statistical analysis and comparison of this particular type of data. Therefore, the main objective of this work is the description of a set of measures that are specifically suited for analysis of cellular genealogies. In particular, the work focuses on topological characterization of the cellular genealogies with respect to the degree and symmetry of cellular expansion, and the occurrence as well as the relation of characteristic events such as cell death. Furthermore, we analyse how the reconstruction of lineage fate decisions can be biased by a retrospective assignment compared to a prospective approach.

For the application of the proposed measures to experimental data, a minimal set of requirements has to be met in order to substantiate the statistical arguments and to allow a comparison between different cell culture conditions. However, practical problems with the generation of sufficiently long and qualitatively analysable time‐lapse videos of suitable cell cultures, as well as difficulties in the automatic identification and tracing of single cells in current image‐processing techniques still limit the availability of experimentally derived cellular genealogies. Most of the above‐mentioned results that successfully applied time‐lapse video microscopy for different cell cultures are focused on a particular purpose and are, moreover, based on manual tracking of the individual cellular genealogies. This is a clear limitation to the quantity of available data but also a restriction to its comparability. To the best of our knowledge, there are currently no published sets of single cell tracking data that are sufficient in size for successful development and verification of novel statistical analysis methods. Due to these current limitations, we use simulated in silico cell cultures in order to illustrate our proposed measures. In particular, we obtain cellular genealogies from a single‐cell‐based computer model of haematopoietic stem cell organization, which is able to describe self‐renewal, differentiation and lineage specification within heterogeneous cell populations and which has been verified for different in vivo and in vitro situations (2, 14, 15, 16, 17). Based on this model, we show how changes in the particular (in silico) growth conditions influence topology of the cellular genealogies and how different methods for assignment of cellular fates alter the interpretation of critical events in lineage specification. Although this model has been developed for the haematopoietic system, the results can also apply to other differentiating and dividing cell types.

The analysis of tree‐like structures has a long tradition in phylogenetics and evolutionary biology (see the historical overview in Mooers & Heard (18)). Comparing different phylogenetic trees, the influence of external pressure on evolutionary development is characterized and linked to associated patterns in the tree shape. Although we develop the idea of shape measures in the Results section, the general approach in analysis of cellular genealogies starts from a different point: whereas in statistical phylogenetics a certain tree structure represents a unique set of events typical of a certain species, the analysis of cellular genealogies is based on comparison of many heterogeneous, albeit similar, pedigrees derived under identical culture conditions. Moreover, cellular genealogies incorporate information on temporal extension and spatial correlation that require additional coverage. In addition, interpretation of the typical events such as cell death/extinction and division/branching is different for cellular genealogies compared to phylogenetic trees, changing the focus to other relevant questions.

Methods

Cellular genealogies

Cellular genealogies are derived from tracking of a single, specified cell object (root cell) and its entire clonal offspring. Technically, a cellular genealogy is an unordered tree graph in which the edges c_i (i = 0 . . . N) represent cells and the branching points d_j (j = 1 . . . D) represent division events. Each genealogy is uniquely identified by its root cell c ₀, which is the cell that had been chosen as the initial cell for the tracking process. All its descendents are attributed as cells of the 1st to gth daughter generation, and are arranged in the branches. Furthermore, cells are characterized by their development (i.e. either a cell undergoes a division event giving rise to two daughter cells, or the cell's existence terminates without a further division). The latter option can be achieved either by a cell death event or by the termination of the tracking process. Such final cells are denoted as leaf cells. The relation r_pq between any two cells c_p and c_q is defined as a topological distance that measures the number of divisions between these cells. Daughter cells that share the same parental cell are termed siblings. A schematic representation of a cellular genealogy and an illustration of the distance measure are provided in Fig. 2.

Figure 2.

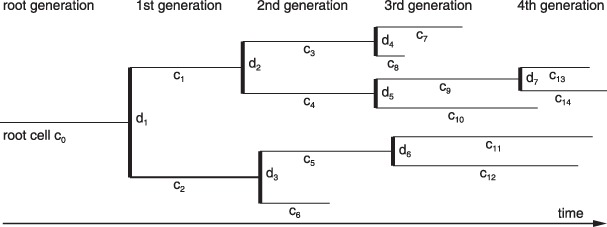
Schematic sketch of a cellular genealogy. Within the given five generation genealogies, the thin horizontal lines represent cells c_i whereas the divisions d_j are marked by the thick vertical bars. The horizontal dimension is time t with the founding root cell c ₀ indicated on the left hand side. Thus, the length of the horizontal lines represents duration of the cell's existence and is a measure of the cell‐cycle time (T _C). Final cells on the right hand side are called leaf cells. The degree of relation r_pq between any two cells c_p and c_q is given by the number of divisions between cells c_p and c_q. For example, cells c ₆ and c ₈ have a degree of relation r _6,8 = 4 (separated by the divisions d ₃, d ₁, d ₂, and d ₄). Using the same measure of relation the branch length from the root c ₀ to the leaf cells is determined. For the particular example, the longest branch is r _0,14 = 4 and the shortest branch is r _0,6 = 2.

Temporal dimension of the tracking process is usually encoded in length of the edges; however, this is an associate piece of information rather than a genuine topological parameter. Similarly, any additional information that has been recorded during the tracking process, such as spatial position, size of the cells, expression of certain lineage‐specific marker genes, or fluorescence activity of particular cell labels, can be attributed to the corresponding edges c_i. Specifically, in the case that data on the lineage commitment is available, a fate information Χ_i is assigned to the cell c_i. Different methods for this assignment and detailed examples are presented in the Results section.

Mathematical model of haematopoiesis

To illustrate the analytical potential of the measures that are introduced in the Results section, we use simulated cellular genealogies generated by a single‐cell‐based mathematical model of haematopoietic stem cell organization that has been developed in our group (14, 16, 17). Within the model, stem cells are able to switch reversibly between two characteristic states: proliferating (i.e. in phase G₁, S, G₂, or M of the cell cycle) and quiescent (i.e. in G₀). Generally, cells in the proliferating state have a cell‐cycle time T _C. However, due to (reversible) changes to the quiescent state, duration between two division events can be significantly prolonged (long periods of G₀) but also slightly shortened (rapid reactivation into cell cycle with a shortened G₁ phase, as preferentially realized in regenerating systems). Cells that have lost their propensity to change to the quiescent state continue regular cell divisions within a proliferation phase (differentiating cells) and are finally removed from the system after a subsequent maturation phase without further divisions. Lineage specification is described by intracellular propensities for development of particular lineage fates. Whereas the quiescent state equalizes the lineage‐specific propensities (uncommitted state), dominance of one or other lineage is established in a stochastic process during proliferation, indicating the process of lineage commitment. For further details, please refer to the Supporting Information.

To account for the occurrence of cell death events (e.g. apoptosis) and their impact on cellular genealogies, an additional mechanism has been included in our model. We assume that with a certain (low) probability p ^kill every proliferating cell in G₁ phase can be subject to cell death. Generally, such an effect might also occur in other stages of the cell cycle. However, here we focus on the (quantitative) characterization of the general impact of cell death events on cellular genealogies by appropriate topological measures rather than on details of the biological process. The simplifying assumption of restricting cell death events to G₁ phase does not qualitatively change our results (data not shown).

Generation of cellular genealogies

To develop and test different methods for their statistical analysis, we apply three different in silico conditions, inspired by typical cell growth scenarios. In order to minimize impact of the particular haematopoiesis model and to test robustness of the proposed statistical methods, the three scenarios are chosen to represent rather different dynamic regimes. First, the model system is initialized with one ‘model stem cell’ that undergoes massive expansion. This is referred to as the growth scenario. Thereafter, the model system establishes a stable pool of self‐renewing cells that simultaneously contribute to a pool of differentiating cells. This is referred to as the homeostatic scenario. Changing system parameters so that self‐renewal ability of the cells is lost, the whole population of cells undergoes final differentiation and subsequent cell death. This is referred to as the differentiation scenario, which is inspired by in vitro cultures of stem and progenitor cells lacking self‐renewal promoting conditions. Lineage specification is realized such that each of the three possible lineage fates occurs with the same probability.

For derivation of the cellular genealogy in the growth scenario, 400 independent model realizations are tracked for 300 h, each initialized with one single stem cell. In contrast, for the homeostatic scenario and for the differentiation scenario, all cells in the homeostatic stem cell compartment of one particular model realization are uniquely marked and subsequently tracked for the next 300 h. Typically around 400 cells are tracked in this process, similar to the 400 independent realizations in the growth scenario. A schematic representation of the cell population dynamics for the different scenarios and a typical characteristic cellular genealogy for each scenario is shown in Fig. 3.

Figure 3.

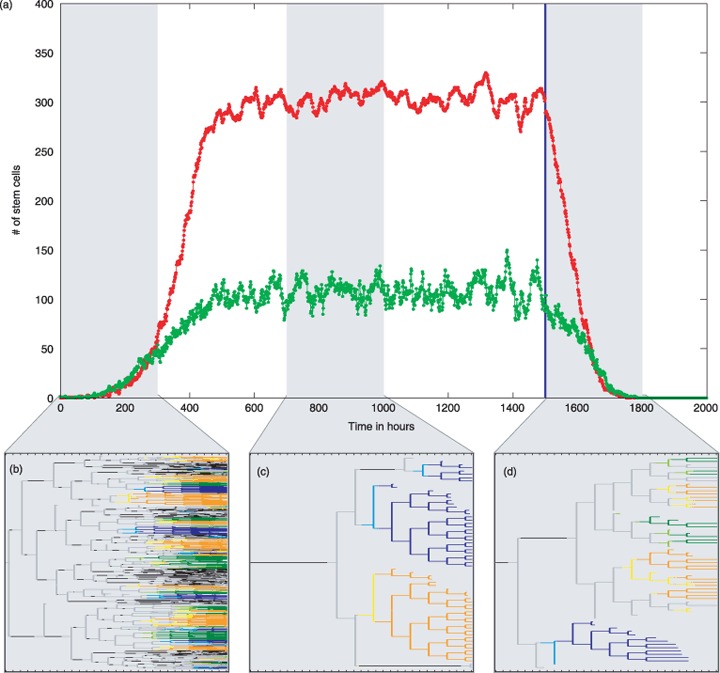
Populations dynamics for the three different scenarios and corresponding cellular genealogies. (a) Given are the simulated numbers of proliferating (green) and quiescent (red) stem cells. At time point t = 0, the cell culture is initialized by a single stem cells that subsequently undergoes massive expansion. The corresponding growth scenario is indicated by the first shaded area. Within this observation period of 300 h the cellular genealogies of 400 initial cells are tracked in independent realizations. Around t = 600 the system reaches a stable equilibrium with about 100 proliferating and about 300 quiescent stem cells. For the cellular genealogies of the homeostatic scenario, all stem cells present at time point t = 700 are uniquely marked and subsequently tracked for 300 h. This is indicated by the second shaded area. By changing differentiation and regeneration parameters at time t = 1500 (blue line), the self‐renewal ability of the stem cells is lost and they undergo terminal differentiation (differentiation scenario). As in the homeostatic scenario, cellular genealogies are derived by marking all stem cells present at time point t = 1500 prior to the change of parameters and their subsequent tracking for 300 h (third shaded area). (b)–(d) A characteristic genealogy for each scenario is given below the main graph (b, growth scenario; c, homeostatic scenario; d, differentiation scenario). Colours indicate cell‐cycle status of the undifferentiated cells and commitment to three possible lineages for differentiating cells: grey – undifferentiated proliferating cell; black – undifferentiated quiescent cell; yellow/orange – early/finally committed cell of the ‘orange lineage’; light/dark blue – early/finally committed cell of the ‘blue lineage’; light/dark green – early/finally committed cell of the ‘green lineage’.

Results

Topological measures for cellular genealogies

We propose a number of suitable topological measures for characterization and quantitative analysis of cellular genealogies. This way, it is possible to compare different sets of genealogies that have been derived under different experimental conditions or to quantify the heterogeneity that occurs within a set of genealogies that have been derived under the same conditions. Formal mathematical descriptions of the proposed measures are given in the Appendix.

Total number of leaves L and number of divisions D

The total number of leaves L is a suitable measure for the clonal expansion of a particular root cell. The index L counts all cells c_i of a certain genealogy that do not terminate with a further division. The number of divisions D that occur in the same genealogy is equally well suited for estimation of cellular expansion since D = L – 1. Population averages of these values are closely related to the overall expansion of the cell culture. However, beyond these average values, width of the distributions of the number of leaves L (or divisions D, respectively) originating from different cells under the same culture conditions is an indicator of population‐inherent heterogeneity in the clonal expansion potential that cannot be determined on the population level.

Box plots of distributions of total number of leaves L for the three scenarios –growth, homeostasis and differentiation– are given in Fig. 4a. Increased values of L in the growth scenario are plausible since initial expansion is characterized by high proliferative activity and shortening of the effective cell‐cycle time, which leads to increased number of cell divisions during the observation period for the cellular genealogies. In contrast, it is the homeostatic scenario that shows the widest variety of total number of leaves L. In this scenario, some cells show little expansion, due to prolonged phases of cellular quiescence, whereas other clones expand quickly under the same model conditions.

Figure 4.

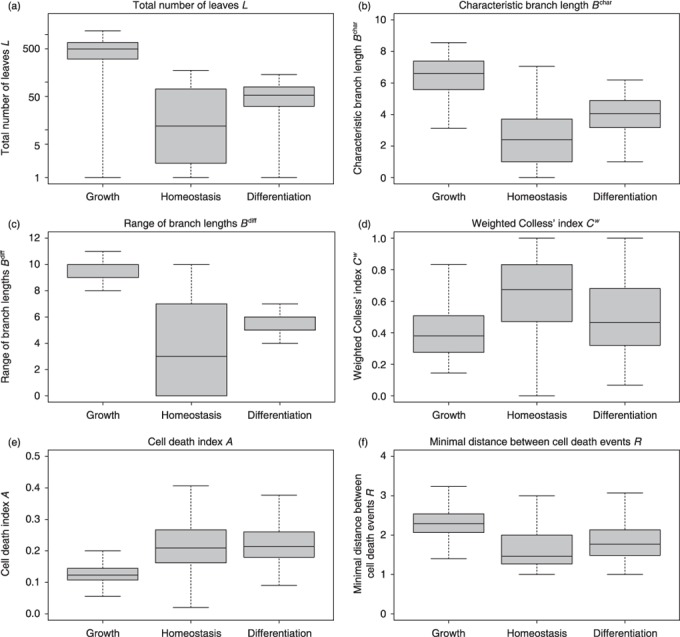
Characteristic measures of tree shape. Shown are box plots of distributions for the topological measures proposed in the Results section. (a) total number of leaves L (shown on a logarithmic scale) (b) characteristic branch lengths B ^char (c) range of branch lengths B ^range (d) weighted Colless’ index C^w (e) cell death index A (f) minimal distance between cell death events R. Median values are shown by the thick bars, boxes correspond to the first and third quartile. Whiskers extend to the most extreme data point which is no more than 1.5 times the interquartile range from the box. Detailed histograms of distributions are provided in the Supporting Information.

Branch lengths B

The branch length B_k measures the number of divisions between the root cell c ₀ and the leaf cell c_k. The complete set of branch lengths for all leaf cells of a given genealogy is a measure of the proliferative activity of the root cell, but, it also accounts for heterogeneity within a single expanding clone. We will briefly focus on both these aspects.

Due to the exponential nature of cellular expansion, the average branch length, mean(B_k), within a particular genealogy is dominated by the maximal branch lengths, max(B_k). To circumvent this inherent bias, we propose a characteristic branch length, B ^char, for which the different branch lengths, B_k, are normalized according to the generation in which the leaf cell occurs. Intuitively speaking, B ^char is the average branch length that one encounters by randomly following the genealogy from the root cell c ₀ to the leaves. Such a process ensures that longer and more ramified branches are weighted less, compared to shorter branches. Box plots of distributions for cellular genealogies derived under the three different culture scenarios are shown in Fig. 4b. Since the characteristic branch length, B ^char, is also a measure of the clonal expansion, ratios between the different scenarios closely resemble the results for the number of leaves, L, shown in Fig. 4a.

Distribution of branch lengths, B_k, within a particular genealogy characterizes the heterogeneity within the progeny of a single expanding (root) cell. However, these distributions are always dominated by the longer branches due to the exponentially increasing number of leaf cells. Therefore, we argue that relation between the extreme values – min(B_k) and max(B_k) – are more instructive. In particular, we have analysed the range of branch lengths between the minimal and the maximal branch lengths [B ^range = max(B_k) – min(B_k)] for the genealogies derived from different simulated culture scenarios. Box plots for the corresponding distributions are shown in Fig. 4c. In the growth and in the differentiation scenario, variance of this measure is rather small compared to that of the homeostatic scenario. Furthermore, the high absolute value indicates that uniform expansion in all branches is rarely observed and that genealogies in the growth and in the differentiation scenario are characterized by significant differences in branch lengths within individual genealogies. This effect is less pronounced in the homeostatic scenario. However, a number of smaller genealogies with low characteristic branch length B ^char (compare Fig. 4b) might skew this perspective.

Symmetry indices (weighted Colless’ index C^w)

Tree shape measures with a focus on symmetry have a long tradition in the analysis of phylogenetic trees (18, 19, 20). These measures are commonly used to detect imbalances that testify the regulation of diversity in ecological communities. Applied to the situation of cellular genealogies, these measures can provide understanding of the balance between self‐renewal and differentiation, as well as on action of cell death processes.

A particularly useful measure is the Colless’ index of imbalance, C (21). This index compares the number of leaves emerging from the two daughter cells, c _daughter 1 and c _daughter 2, resulting from a particular division d_j. Colless’ index C sums the difference in the number of leaves subtended by the two daughter cells for all divisions within the genealogy and normalizes by dividing with the largest possible score. Colless’ index increases from C = 0 for perfectly symmetric genealogies to C = 1 for completely asymmetric genealogies. However, the classical Colless’ index puts the same weight on asymmetries that occur late in development compared to earlier events. This is contrary to the common biological perspective of the balance between stem cell self‐renewal and differentiation, which assumes that asymmetries are most pronounced on the stem cell level. Especially in the case of large, exponentially expanding genealogies, such early events are underestimated by the classical Colless’ index compared to a vast amount of expansion events in latter stages of development. Therefore, we propose a weighted Colless’ index C^w that explicitly accounts for exponential expansion within cellular genealogies. In contrast to the classical Colless’ index C, the weighted Colless’ index C^w sums over the differences in number of leaves emerging from two daughter cells which are normalized according to the generation in which the asymmetry occurs.

As visualized in Fig. 4d, the weighted Colless’ index C^w shows highest absolute values in the homeostatic scenario. It is here that the balanced situation between quiescence and proliferation leads to a number of highly asymmetric genealogies (indicated by high values of C^w). However, width of the distribution indicates that at the same time, a number of almost symmetric genealogies appear. In these, the branches are committed equally to either continuous proliferation or quiescence (indicated by low values of C^w). Since cell proliferation is more likely in the growth and the differentiation scenario, average values of the weighted Colless’ index C^w are slightly reduced. It is mainly the occurrence of cell death events that accounts for observed asymmetries in these scenarios.

Cell death index A

Cell death events are regularly observed in cell cultures. Cell death index A measures the observed frequency of cell death events and, therefore, is an estimate of the probability of cell death occurrence. To account for systematic effects related to cellular development, it seems appropriate to consider cell death index A as a function of the current cell state and/or the generation g within the genealogy.

As a particular example, the cell death index A^g is calculated as the ratio of the number of cell death events observed for cells in generation g and number of all cells existing in the same generation. Unlike in the experimental situation in which the role of cell death and apoptosis potentially changes in the course of differentiation, the random occurrence of induced cell death process in our simulation model makes a distinction for different generations obsolete. For simplicity, we use a generalized cell death index A that averages over all generation‐depended values A^g for each genealogy (except the root cell generation). Box plots of the corresponding distributions are shown in Fig. 4d. Due to increased proliferation activation and the resulting shortening of G₁ phases in the growth scenario, cell death index A is reduced compared to the other scenarios.

In contrast to the cell death index A^g itself, a generalization to pairs of sibling cells allows identifying potential correlations of cell death events and, therefore, to reveal particular asymmetries in cell fates. The idea behind this is that in case of statistically independent events, probability of observing a particular combination of events in two siblings (i.e. cell death in none, one or both siblings) equals the product of the probabilities of the corresponding events for individual cells. Thus, if cell death events would occur independently of each other, the latter probabilities could be estimated by (1 – A^g)², 2A^g(1 – A^g), (A^g)², respectively. Using differences in the observed and the (under the independence assumption) expected frequencies of these pairwise events, it is possible to calculate the so‐called mutual information (MI) of all sibling pairs within a particular generation. The MI, which always has values between 0 and 1, is a measure of the information about one of the two events that is provided by the other one. In our particular case, MI = 0 would imply that one cannot obtain any information about cell death occurrence of one sibling cell from knowing the fate of the corresponding daughter cell, as expected under the applied model assumption of completely random cell death. For illustration of MI, two artificial genealogies are shown in Fig. 5. A formal definition of MI is given in the Appendix.

Figure 5.

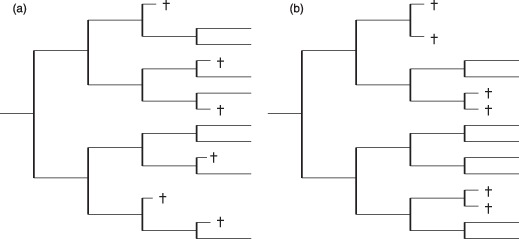
Mutual relation between cell death events. (a) and (b) show two examples of topologically similar cellular genealogies (L = 14, B ^char = 3.75, B ^range = 1, C = 0.05, A³ = 1/4, A⁴ = 1/3 for both genealogies, C^w = 0.068 (a) and C^w = 0.136 (b)). However, despite these similarities they differ considerably with respect to occurrence of cell death events. Whereas in (a) the cell death events are rather isolated, they always appear in sibling cells in (b). The mutual information measures MI^g and the minimal distance R are suitable measures to account for these correlations: (a) MI ³ = 0.036, MI ⁴ = 0.076, R = 3; (b) MI ³ = 0.244, MI ⁴ = 0.276, R = 1.

It should be noted that this approach can also be generalized to other events that characterize the fate of sibling cells. A related but less analytical approach to correlate fluorescence expression between closely related cells, indicating synchronized epigenetic remodelling in embryonic stem cells, has been published recently (10).

Minimal distance between characteristic events R

Cellular genealogies retain information about the relatedness of certain characteristic cellular events like the occurrence of cell death, changes in the cells morphology, or expression of cell fate characteristic markers. Beyond MI, we have identified the topological distance between such characteristic cellular events 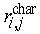as a suitable measure of their relation. In particular, minimal distance between a characteristic event of cell c_i and the closest similar event of cell c_j proved useful for identification of whether the events are rather isolated or appear to be closely related. Such a minimal distance R_i can be calculated for each characteristic event [R_i = min(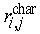)]. To provide a unique measure for each cellular genealogy, the average R over these minimal distances is calculated separately for each genealogy. Lower minimal distances R indicate a relation between the events, possibly due to similar developmental stages of the cells in question, whereas a tendency towards higher minimal distances is more likely to be caused by general effects that are independent of the cell state.

For illustration of this type of measure, we studied minimal distances between cell death events that occurred randomly in G₁ phase in the model scenarios. For each genealogy, the minimal distances R_i from each cell death event to the nearest other such event have been calculated. Subsequently, the average R has been calculated for each genealogy. Box plots in Fig. 4f show the distribution of these average minimal distances R in the three relevant model scenarios. By definition, genealogies with less than two cell death events are excluded from calculation of the minimal distance measure R. Generally, minimal distances between cell death events are rather similar for the three different model scenarios due to the underlying assumption of randomly occurring cell death events that act identically in all three scenarios. However, since cell death events are less likely in the growth scenario (compare cell death index A in Fig. 4e), average minimal distances R is slightly increased compared to the other two scenarios. Differences in minimal distances R are also outlined for the artificial genealogies shown in Fig. 5.

Some of the measures proposed above are not invariant under changes of the observation period. Especially in the case in which genealogies from experiments with different observation periods need to be compared, one needs to get an idea on how these measures scale with observation time. In the case of unconstrained development, measures like total number of leaves L scale exponentially with time while characteristic branch length B ^char scales linear with time. In contrast, weighted Colless’ index C^w and the cell death index A show almost constant values for genealogies obtained for different observation periods. However, even in the simulation model, the idealized situation of unconstrained development is not met (and not intended either). Already in the model situation, saturation effects (in the growth scenario) or exhaustion (in the differentiation scenario) play a dominant role and lead to a nonlinear divergence from the expected behaviour. It can be expected that influence of such effects is even more pronounced in the experimental situation. Therefore, we argue that appropriate rescaling of the measures, as we outline in the Appendix, should be advocated with great care and only in situations in which the effect of temporal changes within the cell culture is well understood and quantifiable. Since these conditions are violated, the measures in Fig. 4 compare genealogies with identical observation period. A discussion of the scaling properties is provided in the Appendix along with a detailed mathematical description of the different measures.

Assignment of lineage fates

Defining criteria of stem and progenitor cells are their ability to differentiate into different types of functional cells by a process of lineage specification. Within the simulation model, lineage specification is represented as a continuous process that progressively restricts the number of available developmental options. In order to allow simple phenotypic characterization, cells above a certain threshold for lineage propensities are attributed to a particular cell type although a small but continuously decreasing probability for conversion remains. This information about the ‘commitment state’ of a cell is available throughout the whole tracking process. Therefore, it can be represented in the cellular genealogies in a straightforward fashion, which is referred to as the prospective view: According to its internal state at a certain time point (t), a cell c_i is marked as undifferentiated Χ_i(t) = 0 or committed to a certain lineage fate Χ_i(t) = 1,2, . . . , M, with M denoting the number of possible lineages. Fig. 6a shows a typical cellular genealogy of the differentiation scenario with the prospective lineage assignment.

Figure 6.

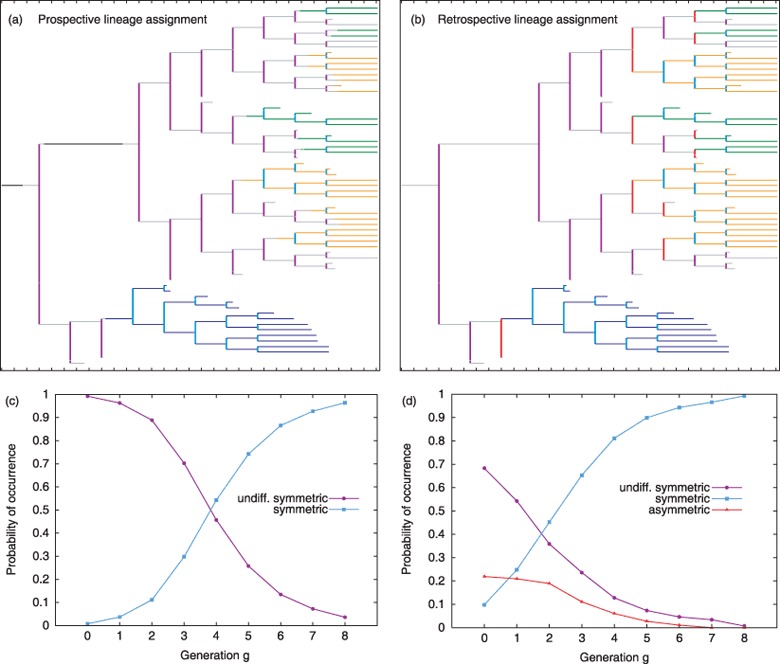
Prospective vs. retrospective view for the lineage assignment. (a) Lineage fate is assigned in situ for a chosen cellular genealogy of the differentiation scenario in the prospective view, e.g. ‘the colour coding’ of a cell might change during the cells existence if certain critical markers (lineage propensities in the simulation model) exceed a threshold level. In contrast, in subfigure (b) Lineage fate is assigned recursively based on the lineage fate of the daughter cells for the same genealogy as in subfigure (a). Colour‐coding of the cells is identical to Fig. 3 (neglecting the early committed stages), colours for the divisions are assigned as follows: undifferentiated symmetric divisions – magenta, symmetric divisions of committed cells – light blue, asymmetric divisions (only in the retrospective view) – red. In (c) and (d), the probability of occurrence of the particular division types for each generation g is given for the set of genealogies derived under the differentiation scenario. The colour‐coding is identical to (a) and (b).

All divisions d_j are characterized by comparing lineage specification state of the parent cell prior to division, to the daughter cells immediately after division. This results in two classes of division events: undifferentiated symmetric divisions if an undifferentiated parent gives rise to two undifferentiated daughters (Χ _parent = Χ _daughter 1 = Χ _daughter 2= 0) and symmetric divisions if a committed parent gives rise two daughters of the same fate (Χ _parent = Χ _daughter 1= Χ _daughter 2 > 0). Since cell divisions in the underlying model system are symmetric by definition, asymmetric divisions do not occur in the prospective view.

In contrast to the simulation model, lineage assignment is a difficult task in the experimental situation, especially if cellular genealogy needs to be maintained. Using classical time‐lapse microscopy of a differentiating cell culture, the only currently available, non‐invasive method for this assignment, is identification of cell type‐specific changes in the cell's morphology. However, changes in morphology are hard to identify and occur rather late compared to changes in transcriptional activity of cell fate‐specific genes. Novel techniques, which are already developed for haematopoietic stem and progenitor cells (11), allow targeted placement of genes coding for the expression of fluorescence proteins under the control of particular lineage‐specific promoters. By use of these reporter genes, it should be possible to obtain information about the lineage decisions during the tracking process. To our knowledge, this technique has not been used in the context of single cell tracking approaches; however, it is the most promising strategy for the prospective assignment of lineage fates in a cellular genealogy.

An already applied technique for identification of cellular fates in cellular genealogies relies on staining methods. This approach requires that the final, spatial configuration of the tracking procedure is preserved in order to allow unique mapping into the genealogy. This is only feasible for adherent cell cultures as they are used, for example, for tracking of neural stem and progenitor cells. However, this assignment of lineage fates refers only to the final configuration and earlier decision events have to be estimated in a retrospective fashion. Given that a lineage fate Χ_i is assigned to each leaf cell, the fate of all cells within the genealogy is determined recursively as follows: If both daughter cells of a parental cell belong to the same lineage, then the same lineage is attributed to the parent cell (Χ _parent = Χ _daughter 1 = Χ _daughter 2). The particular division is characterized as symmetric. In contrast, if the daughter cells are of different lineages or one is undifferentiated (Χ _daughter 1 ≠ Χ _daughter 2), then the parent cell is marked as undifferentiated (Χ _parent = 0) and the parental division is counted as asymmetric. Two undifferentiated daughter cells (Χ _daughter 1 = Χ _daughter 2 = 0) derive from an undifferentiated parent (Χ _parent = 0) due to an undifferentiated symmetric division. Given this notion of symmetric and asymmetric fates, the retrospective view is a generalization of classical ‘sibling analysis’ in which development of two daughters from a common parental cell is compared. Evaluating the same cellular genealogy as Fig. 6a in the retrospective view (i.e. only based on the lineage fate of the leaf cells), a modified version of the genealogy is obtained as shown in Fig. 6b in which progeny of a parental cell that only gives rise to one abstracted cell fate is always shown in the same colour.

Comparing the cellular genealogies, it appears that cells at certain positions are already marked as committed in the retrospective view, while the prospective view indicates that the lineage specification process has not reached a detectable threshold. For statistical evaluation, the occurrence of symmetric, asymmetric or undifferentiated symmetric division events, as outlined for the prospective and the retrospective view, is summarized in appropriate histograms in Fig. 6c and 6d. Starting from a population of rather undifferentiated cells, such histograms are plotted against the generation g in which the division event occurs. Although both fate assignments are based on the same set of underlying genealogies, in the prospective view (Fig. 6c) symmetric expansion of undifferentiated cells in early generations (shown in magenta) is more pronounced compared to the retrospective view (Fig. 6d). It is particular construction of the lineage assignment in the retrospective view (based on subsequent cellular development and decoupled from the actual intracellular differentiation state) that suggests a much earlier onset of lineage fixation compared to the prospective view. Although the propensity of a cell for development in one particular fate might already be skewed at such an early time point, the prospective view indicates that fixation is not yet accomplished. This bias is inherently present in any retrospective assignment of cellular characteristics and marks a central disadvantage to the prospective view in which critical steps of the lineage specification process are determined in their divisional context.

However, the retrospective view is a helpful tool to identify cells that give rise to more than one lineage fate (multipotent cells). Although multipotency is not based on the transcriptional state of the cell but on its future development, the retrospective lineage assignment is well suited to detect occurrence and timing of division events that give rise to different (asymmetric) cell fates. In this respect, the retrospective view illustrates difference between a functionally asymmetric division, which is by construction not occurring in the underlying model system, and an asymmetric cell fate, which is commonly detected in the resulting genealogies.

Discussion

Illustrated by the use of a mathematical model of stem cell organization, we show that the proposed topological measures particularly address the quantitative analysis of individual cell fate distributions, including the balance between stem cell proliferation, quiescence and cell death. The measures are suited to distinguish between cellular genealogies derived under different culture conditions, but they can also be applied for the estimation of inherent variation within a set of genealogies derived under identical conditions. In this respect, cellular genealogies and their topological characterizations are powerful tools to quantify clonal heterogeneity, and to distinguish whether stem cell populations are inherently heterogeneous or if they are composed of predefined homogeneous subsets.

The total number of leaves L as well as the characteristic branch length B ^char address expansion of a cell clone within a given time interval. Averaging over many genealogies, these measures can be used to characterize the degree of clonal expansion under different culture conditions. However, on top of this classical ‘population measure’, it is evident that heterogeneity within a cell population can only be estimated on the level of individual genealogies. For the example of the growth scenario, 400 independent model simulations have been traced, each initialized by individual, almost identical cells. It is variance of the total number of leaves (L; Fig. 4a) and of the characteristic branch length (B ^char; Fig. 4b) which indicates that the cells undergo initial expansion at a very different extent. This heterogeneity on the level of individual genealogies is equally pronounced in the homeostatic and differentiation scenario.

To address heterogeneity of expansion that occurs within a genealogy, extreme values of the branch lengths B_k are evaluated. In particular, we have studied the range of branch lengths B ^range between minimal and the maximal branch lengths. The observed high absolute values of this index together with the rather low variance indicate that heterogeneity in branch lengths is a general feature of cellular genealogies in almost all observed scenarios.

Colless’ index C and the weighted Colless’ index C^w address the question of how proliferation and quiescence are balanced on the level of individual cells. However, application of the classical Colless’ index C requires careful interpretation since all asymmetries are weighted equally, irrespective of whether they occur early or late in development. Therefore, we introduced a weighted Colless’ index C^w that accounts for the exponential expansion within the genealogy and puts higher weight on early asymmetries. Moreover, as we show in the Appendix, the weighted Colless’ index C^w does not depend on the observation period (compared to the classical Colless’ index, C) and, thus, resembles an invariant measure of imbalance in cellular genealogies. Width of distributions for the weighted Colless’ index C^w shown in Fig. 4d indicate that the population‐inherent heterogeneity ranges from almost symmetric genealogies to highly asymmetric counterparts.

Cell death events occur regularly in cell cultures and potentially play an important role in regulation of haematopoiesis in vivo. We introduced the cell death index A^g to estimate probability for the occurrence of cell death for a cell in a particular generation g within its genealogy. This measure can be used to account for changes of particular probability during the course of differentiation. Besides the simple observation of cell death events, it is not yet clear under which conditions these events have a functional role; for example, with respect to the final composition of cell populations in a culture (1, 3, 22). If it becomes possible to clearly identify cell death events (e.g. by monitoring activity of certain relevant genes in the apoptosis pathway, using fluorescence labelling methods), cellular genealogies are a unique tool to investigate this action in divisional and in the population context. We have proposed to study correlations of cell death events in siblings, using the MI measure, as well as the average minimal topological distance between such events R to directly address this issue. In the biological context, it is particularly interesting whether lineage specification is regulated by survival signals for particular early committed cell types (selective regulation) or if it is governed by cell‐intrinsic regulations accompanied by random cell death events (instructive regulation). In the first case, the internal ‘decision’ of a cell is unregulated and supports all possible lineage fates. Subsequently, certain lineages are promoted by virtue of survival signals, whereas cells committed to unfavourable lineages, undergo cell death. Since closer related cells within a cellular genealogy are more likely to share the same lineage fate, it could be speculated that selective cell death preferentially targets closely related cells. This should lead to increased values of MI and to smaller values of the minimal topological distance between cell death events R. In contrast, cell‐intrinsic regulation of lineage specification causes establishment of just a number of demanded cell lineages. In this case, cell death does not have a functional role for selection of lineages and the occurring cell death events are expected to be statistically independent (i.e. MI  0). This should also be reflected by higher values of the minimal topological distance measure R compared to the selective situation.

With regard to the balance between self‐maintenance of a stem cell population and differentiation into tissue cells, it is often hypothesized that asymmetric cell divisions play a functional role. This concept proposes that both aspects of stem cell organization are scheduled upon division, when one daughter cell remains a stem cell whereas the other is committed to differentiation. Such divisions are reported for a number of stem cell systems (23, 24). Also, for the haematopoietic system, it has been shown recently that certain cellular components can be segregated asymmetrically to the daughter cells (25). However, there is still no convincing evidence for functional asymmetry in distribution of molecular content in haematopoietic stem and progenitor cells. Especially with regard to these findings, it seems appropriate to replace the concept of asymmetric division by the more general concept of asymmetric cell fates. Within the latter concept, the (obviously existing) asymmetry of cellular development can, but does not have to be, related to cell division events. As in the applied model system, which has been used for derivation of the cellular genealogies, asymmetric fate is solely the result of the independent development of the two daughter cells after a functional symmetric division event.

Cellular genealogies are ideal representations in which to study asymmetries with respect to cell fate commitment. It seems tempting to define a global measure of this asymmetry as it has been done with the Colless’ index of imbalance C for the case of topological asymmetries. An adaptation of Colless’ index to cell fate decision (such as lineage commitment) fails since the maximum asymmetric situation, which is necessary for normalization, is critical to define. As we have shown in the Results section, it is more appropriate to study the occurrence of asymmetric fate decisions using a retrospective lineage assignment. Although the retrospective view is not necessarily coupled to the transcriptional state of differentiation (which is better represented in the prospective view), it allows detection of divisions that asymmetrically contribute to different cell fates and to evaluate them with regard to the generation in which they occur.

Apart from the elaborated analysis introduced above, availability of cellular genealogies would also allow for an exact characterization of individual cell‐cycle times T _C. Whereas classical estimates of cell‐cycle times are based on measurements of the fold increase in a population of differentiating cells, which neither account for the heterogeneity of individual cells nor for occurrence of cell death, the shape of distribution of cell‐cycle times can be reliably estimated from a sufficiently large set of cellular genealogies. Starting from a paternal division d_i, the time interval to the next division d_j is an exact measure of the cell‐cycle time T _C. Besides the global distribution of cell‐cycle times, representation of clonal development in a cellular genealogy allows evaluation of cell‐cycle times with respect to secondary parameters (e.g. according to the particular cell generation g or to cell fate‐specific information that accompany a particular genealogy). In the latter case, correlations between lineage fate and the change in cell turnover can be quantified circumventing the obstacles of a population average that potentially contains different cell types.

Using a tuneable mathematical model for the generation of cellular genealogies, we were able to test a large variety of possible measures on whether they are suited to identify differences in the generation scenarios. Based on such a strategy, we disqualified a number of such measures that performed poorly in comparison and characterization of cellular genealogies. However, using a mathematical model instead of biological data bears a number of risks and uncertainties. Some aspects, which are inherently present in experimentally derived data, cannot be studied on the basis of the particular simulation model. For example, the unique potential of cellular genealogies for the exact measurements of individual cell‐cycle times T _C and their potential correlation with developmental processes cannot be exemplified, since the model is based on the simplifying assumption of fixed cell‐cycle durations. However, the measures proposed in the Results section are based on topological structure (the parent–daughter relation) and, therefore, do also apply to the situation of varying cell‐cycle times. Furthermore, the simulated genealogies do not account for migration of cells since the employed stem cell model is not based on an underlying spatial structure. Therefore, neither spatial correlations between the existing cells nor their velocities, are accessible, and analysis of their influence on cell fate decisions cannot be studied using the current model implementation. Structural characterization of cellular genealogies, as it is presented above, can be easily extended to incorporate the spatial component. Preliminary approaches to address such influences are currently developed. Finally, the list of proposed measures is neither complete nor exclusive. Different biological questions might result in the development of novel measures that are particularly designed to reveal certain structures within the genealogies.

As mentioned in the introduction, cellular genealogies have been successfully used to determine fate‐related aspects of cellular development like asymmetric segregation of chromosomal content or identification of correlations between cellular quiescence and repopulation ability. We have carefully evaluated each of these studies whether they contain suitable data sets for an illustration of the proposed measures. However, since these studies address a diversity of biological phenomena under very different experimental conditions (including severe temporal and spatial restrictions), a comparison of different cell types based on such data sets would be misleading. In particular, the results would not illustrate differences between the different cell types used, but between the applied experimental protocols. To overcome such limitations, a minimal set of requirements for the experimental practice has to be in place, including generation of sufficiently large data sets (both in number and extend), a comparability of spatial and temporal restrictions, and identification of cell death events.

It can be expected that availability of time‐lapse video microscopy and establishment of efficient image‐processing methods will soon allow ‘high throughput’ tracing of single cells within cell cultures. Interpretation and management of the resulting cellular genealogies is a challenge to experimental and theoretical biologists alike. Therefore, we argue that development of efficient automated tracking routines on one side, but also establishment of a powerful analysis pipeline on the other, are both integral parts of a joint venture that need to be pursued in parallel. Although application of model data imposes certain risks for generalization of the results, it represents a unique tool to study the explanatory and the statistical power but also the limitations of certain analysis methods prior to generation of large amounts of data. Moreover, an in silico model can be tuned so as to pronounce certain developmental aspects like differentiation at the cost of self‐renewal or a bias towards particular lineage fates. Comparing the predicted model genealogies with their ‘real’ counterparts (as soon as they become available) is a powerful systems biological tool to uncover imprints of different developmental and/or regulatory processes that are hidden in the complex topological structure of this particular type of data.

Appendix

Topological definition of cellular genealogies

Cellular genealogies are unordered tree graphs G = (C, D) composed of a set of edges C = (c_i, i = 1 . . . n) representing cells and a set of branching points D = (d_i, i = 1 . . . m) representing division events. Unordered trees are characterized as trees in which the parent–daughter relationship is significant, but the order among the two daughter cells is not relevant. Within such a structure, cells are ordered into subset C^g according to their generation g, starting with the root cell c ₀ ∈ C ⁰ and followed by the daughter cells in the first to the gth generation (c_i ∈ C ¹, C ², . . .). To each cell c_i belongs either a subsequent division event d_j, giving rise to two daughter cells (c_i ∈ C ^div, with C ^div representing the subset of all cells that undergo division), or the cell's existence terminates without a further division either by cell death (c_i ∈ C ^death, with C ^death representing the subset of all cells that die within the observation period) or by termination of the tracking process (c_i ∈ C^term, with C^term representing the subset of all cells with censored observation, i.e. no information about future cell fate available).

Final cells are termed leaf cells (i.e. C^leaf = C^death ∪ C^term). The degree of relation r_pq between any two cells c_p and c_q is defined as a topological distance that measures the number of divisions between cells c_p and c_q. A fate information Χ_i, as well as any accompanying information (e.g. on cell shape, expression of fluorescence markers) can be assigned to the individual cells c_i.

Definitions of the topological measures for cellular genealogies

Total number of leaves L

The total number of leaves L counts all cells that terminate without further division within a particular genealogy:

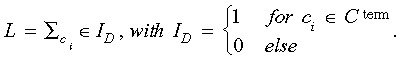In the case of unlimited growth, the total number of leaves L scales exponentially with the observation period. This scaling behaviour is verified for wide ranges of the observation period as shown by the log‐lin plot in Fig. 7a.

Figure 7.

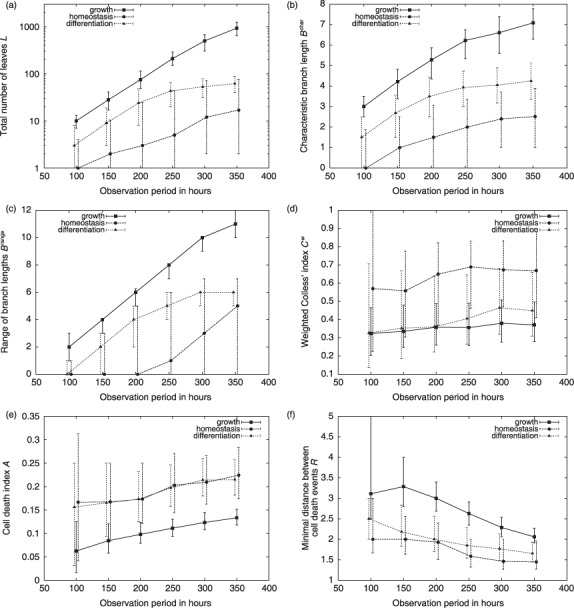
Scaling behaviour of the characteristic measures of tree shape. Median (dots) and first and third quartiles (error bars) are shown for the distributions of the topological measures proposed in the Results section as a function of the observation period (ranging from 100 h to 350 h, shown on the x‐axis) (a) total number of leaves L (shown on a logarithmic scale), (b) characteristic branch lengths B ^char, (c) range of branch lengths B ^range, (d) weighted Colless’ index C^w, (e) cell death index A and (f) minimal distance between cell death events R.

Branch lengths B_k

The branch length B_k is defined as the topological distance r _0,k between the root cell c ₀ and a leaf cell c_k ∈ C ^leaf. The characteristic branch length B ^char is calculated as 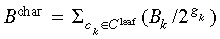in which g_k refers to the generation of leaf cell c_k. The range of branch lengths B ^range for a certain genealogy is given as B ^range = max_k(B_k) – min_k(B_k).

The characteristic branch length B ^char as well as the range of branch lengths B ^range scale linear with the observation period (compare Fig. 7b and 7c). For the latter measure, it is the maximal branch length, max(B_k), that accounts for the linear scaling since the minimal distance, min(B_k), reaches a constant value for sufficiently long observation period.

Symmetry indices (weighted Colless’ index, C^w)

The classical Colless’ index of imbalance C (21) is given 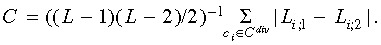as L_{i ,1} and L_{i ,2}
refer to the number of leaves subtended by the two daughter cells of cell c_i. In contrast, the weighted Colless’
index (C^w) is given as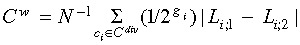 
with the normalization to the maximal possible value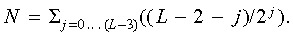

As Fig. 7d indicates, the weighted Colless’ index C^w is almost invariant against changes of the observation time. This is a central advantage compared to the classical Colless’ index C that converges to zero for larger genealogies.

Cell death index A

The cell death index A^g estimates the probability for a cell death event occurring in generation g of a certain genealogy. It is calculated as 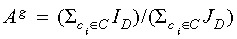in which the indicator function 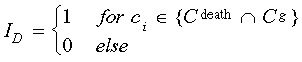is used to count the number of cell death events in generation g and the indicator function 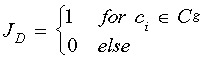to determine the total number of cells that exist in the same generation g. For the generalized cell index A used in Fig. 4e, A^g has been averaged over all generations except the root.

Cell death occurs with probability p ^kill = 0.02 at each time step (i.e. within 1 h) in the simulation model. For a typical G₁ phase of 12 h, the cumulative probability to encounter a cell death event within one cell cycle is calculated as PG1^−kill = (1–0.98¹²) = 0.215. This value is well approximated by the generalized cell death index A, which is measured from the available genealogies. As shown in Fig. 7e, the index values for the homeostatic and for the differentiation scenario converge towards this analytical estimate for sufficiently long observation periods. Lower index values for the growth scenario are plausible, since shortened cell‐cycle times reduce the probability of induced cell death.

The mutual information of two (discrete) random variables X and Y is defined as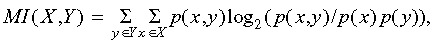
where p(x, y) is the joint probability distribution of X and Y, and p(x) and p(y) are the marginal distributions of X and Y, respectively. That is, the MI is the expected log‐likelihood differences between the bivariate model and the product of the marginal models. In the particular case of cell death events, we assume identical probability distributions for both sibling cells. Therefore, the expected probabilities for the three possible events (i.e. none (p ₀), one (p ₁) or two (p ₂) cell death events per sibling pair) under the hypothesis of statistical independence of the two siblings can be estimated by (1 – A^g)², 2A^g(1 – A^g), and (A^g)², respectively. Estimating the bivariate probabilities by the observed relative frequencies (f_i, i = 0, 1, 2) of the aforementioned events (p_i, i = 0, 1, 2) leads to the estimated mutual information per generation g:

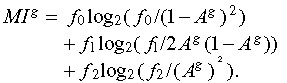Minimal distance between characteristic events R

The minimal distance between characteristic events R is an average over the topological distances from one characteristic event at cell c_i to the nearest similar event at cell c_j within the cellular genealogy G. These individual minimal distances are defined as 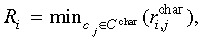in which C ^char refers to the set of cells for which a characteristic event has been observed and 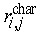is the topological distance between them. For genealogies with less than two such characteristic events index R is not defined.

As an example, we studied minimal distances between induced cell death events. In the case of randomly occurring cell death, as in the simulation model, the minimal distance R appears to stabilize around R = 2 for sufficiently long observation periods, as shown in Fig. 7f.

Supporting information

Appendix S1. 1 Mathematical model of haematopoiesis

Figure S1. Characteristic measures of tree shape. Shown are the histograms that correspond to the box plots in Fig. 4.

Table S1. Model parameters

Please note: Wiley‐Blackwell are not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.

Supporting info item