Oedema‐based model for diffuse low‐grade gliomas: application to clinical cases under radiotherapy

Abstract

Objectives

Diffuse low‐grade gliomas are characterized by slow growth. Despite appropriate treatment, they change inexorably into more aggressive forms, jeopardizing the patient's life. Optimizing treatments, for example with the use of mathematical modelling, could help to prevent tumour regrowth and anaplastic transformation. Here, we present a model of the effect of radiotherapy on such tumours. Our objective is to explain observed delay of tumour regrowth following radiotherapy and to predict its duration.

Materials and methods

We have used a migration–proliferation model complemented by an equation describing appearance and draining of oedema. The model has been applied to clinical data of tumour radius over time, for a population of 28 patients.

Results

We were able to show that draining of oedema accounts for regrowth delay after radiotherapy and have been able to fit the clinical data in a robust way. The model predicts strong correlation between high proliferation coefficient and low progression‐free gain of lifetime, due to radiotherapy among the patients, in agreement with clinical studies.

We argue that, with reasonable assumptions, it is possible to predict (precision ~20%) regrowth delay after radiotherapy and the gain of lifetime due to radiotherapy.

Conclusions

Our oedema‐based model provides an early estimation of individual duration of tumour response to radiotherapy and thus, opens the door to the possibility of personalized medicine.

Introduction

Diffuse low‐grade gliomas (DLGG), grade II gliomas according to the World Health Organization classification 1, are primary brain tumours that affect young adults. At the beginning of their evolution, they grow slowly and continuously, and absence of angiogenesis is assessed by lack of contrast enhancement detected on T1‐gadolinium MR images 2. At this stage, extent of these tumours can be estimated only on T2 weighted or Fluid Attenuated Inversion Recovery (FLAIR) images, that show maximal visible abnormalities 3. After several years growth, and despite treatment (surgery, chemotherapy and radiotherapy), angiogenesis is eventually triggered and DLGGs inexorably evolve into more aggressive forms, impeding social and professional life of the patients 4. A number of major clinical observations have been recently made concerning evolution of DLGGs:

1. They are invasive; isolated glioma cells can be found beyond MRI limits of signal abnormalities, including T2 weighted and FLAIR sequences 5, 6. This characteristic explains systematic recurrences observed after oncological treatment, including MRI‐based gross total removal 7.

2. Mean radius of the tumours measured on MRI images increases linearly with time 8, 9, and value of growth velocity is a prognostic factor for both malignant progression‐free survival and overall survival 9, 10, 11.

3. According to studies of correlation between histology and imaging, size of the T2 weighted abnormality (that we measure on MRI to assess size of the tumour), is not linked to glioma cell density but rather to density of associated oedematous fluid 12, 13, 14. This interstitial oedema appears on haematoxylin and eosin‐stained samples as ‘holes’ between loose fibres of the tissue 13, 15. It is probably created by glioma cells since it appears in tumour‐invaded tissues 15, 16.

4. In one recent study, dynamics of DLGG during and after radiotherapy (RT) have also been asssessed 17. In particular, it has been observed that, even after the end of RT, tumour radius continues to reduce, sometimes over a number of years. However, regrowth invariably occurred for all patients under investsigation. Strong negative correlation between proliferation coefficient and overall survival has also been revealed.

On the basis of these clinical observations, the work described here addresses the question of modelling evolution of DLGG treated by RT as first‐line oncological therapy, and in particular the question of delay in tumour regrowth after RT.

Stochastic models usually describe behaviour of a moderate number of glioma cells 18, 19, 20 whereas deterministic 21, 22, 23 and hybrid models 24, 25 are able to describe evolution of a real tumour, with a large number of cells. The archetypical model is one where migration of glioma cells is represented by a diffusion process. The simplest migration–proliferation model takes the form of a partial differential equation governing glioma cell density ρ (see eqn (1)) 21, 22, 26. This model is extremely simple but allows one to obtain estimates of medical interest. In particular, theoretical prediction from eqn (1) that radius r of the tumour increases linearly over time for extensive periods, has been verified by clinical data 8, 9. One can, therefore, easily estimate survival time of a given patient 27.

Modelling effects of RT has already been the object of previous research [for a review, see 28]. Sachs and collaborators 29 have presented a model for RT, based on what is known as the linear‐quadratic model for radiation efficiency 30. The model has no spatial structure and is thus only appropriate for description of homogeneous, well‐localized, tumours. Ribba and collaborators' approach is different, but it also relies on absence of spatial structure 31. Since an essential feature of DLGG is their capacity to invade surrounding normal tissue, it seems more accurate to use a model that involves a spatial structure, as in the work of Rockne and collaborators 32. Their starting point was the invasion‐proliferation model, with cell death term due to RT (present only while the therapy lasts). However, it appears that the basic migration–proliferation model, such as the one used by Rockne and collaborators for high‐grade gliomas 32, cannot account for the most striking feature of clinical follow up – radii following RT; reduction of tumour radius lasts much longer than the treatment itself. The same group has proposed a migration–proliferation model with oedema and angiogenesis for high‐grade gliomas that is closer to our approach 33.

Here, we present a model for the long‐term effect of RT on DLGG. We thus will not describe early and transient effects of RT, such as formation of cytotoxic oedema, probably related to blood–brain barrier disruption 34, 35. This oedema requires steroid administration during and after RT but can be tapered within the month after the end of RT 35.

We use a migration–proliferation model augmented by an equation describing appearance and draining of oedema in tumour‐invaded tissues 16. This model is based on clinical data obtained from analysis of tumour biopsies 14 and takes into account all clinical observations of DLGG listed above. Draining of oedema accounts for delay of the tumour's regrowth after the end of RT.

We show that our model is able to fit clinical data on the effect of RT, that all the parameters of the fit can in principle be estimated before RT, and that some predictions of time of regrowth after RT and gain of lifetime due to RT are possible.

Materials and methods

The patients

We had at our disposal a series of 28 patients with DLGG, diagnosed at the Sainte‐Anne Hospital (Paris, France) from 1989 to 2000. These patients were selected according to precise criteria detailed elsewhere 17. In short, only adults with typical DLGG (that is, no angiogenesis and thus no contrast enhancement on gadolinium‐T1 images), available clinical and imaging follow‐up before, during, and after RT and RT as their first oncological treatment except for stereotactic biopsies, were eligible.

Figure 1 top describes an example of tumour evolution. The patient had MRI follow‐up before, during and after RT (Fig. 1 bottom). Three tumour diameters in axial, coronal and sagittal planes on each MRI image with T2 weighted and FLAIR sequences, were measured manually. Mean radiological tumour radius is defined as half the geometric mean of these three diameters 8 and is plotted as a function of time (see Fig. 1 top). A good model should be able to capture regrowth delay after the end of RT, visible in Fig. 1 top.

Figure 1.

Top: Example of spontaneous velocity of radius expansion of a left temporo‐insular diffuse low‐grade glioma through the evolution of its mean tumour radius on MRI over time. Each point represents an MR examination. Before treatment by radiotherapy (a), the tumour grew spontaneously and continuously. Duration of radiotherapy is indicated by joined arrows. Following radiotherapy, tumour volume measured on follow‐up MRIs decreased for more than 5 years. Then, tumour progression was observed on MRI with a tumour regrowth. Bottom: MRI images corresponding to the times indicated by letters on the radius‐versus‐time curve.

The model and its parameters

Oedema‐based model for tumour growth

To build a model for RT, we needed a model that could account for glioma growth. As such, the migration–proliferation model, which describes evolution of glioma cell density ρ as a combination of diffusion and proliferation, has already proven its usefulness 21, 23, 26, 36, 37:

$$\frac{\mathrm{\partial }\mathrm{\rho }}{\mathrm{\partial }t}=D\mathrm{\Delta }\mathrm{\rho }+\mathrm{\kappa }\mathrm{\rho }(1-\mathrm{\rho })$$ (1)

where ρ (x, y, z, t) is glioma cell density, D diffusion coefficient of glioma cells, and κ their proliferation coefficient. Glioma cell density ρ is defined as ratio of glioma cell concentration C to maximum glioma cell concentration that can be handled by the tissue C _m (also called the tissue carrying capacity): ρ = C/C _m. In existing models of glioma growth, limit of MRI‐signal abnormality is usually assumed to be a curve of isodensity of glioma cells, and its position allows calculation of radius of the portion of tumour on visible on MRI (usually called the “tumour radius”). But experimental results suggest instead that abnormality seen on MRI images (with T2 weighted or FLAIR sequences) is not due to glioma cells but to oedema associated with glioma cells 12, 13, 14, 33. To illustrate importance of oedema in tumour tissues, two haematoxylin and eosin stained biopsy samples are presented in Fig. 2, one with fraction of oedema ~80%, close to the centre of the tumour, inside the limits of MRI‐defined abnormalities (represented here as a grey rectangle), and the other with no oedema, taken outside limits of the MRI‐defined abnormalities 27, 38. Thus, a model of tumour growth coupled to oedema appearance is in order, and to eqn (1) that describes evolution of glioma cell density, we have added a second equation that governs evolution of tumour‐associated oedema:

$$\frac{\mathrm{\partial }\mathrm{\xi }}{\mathrm{\partial }t}=\mathrm{\mu }\mathrm{\rho }\left({\mathrm{\xi }}_{\mathrm{m}}-\mathrm{\xi }\right)-\mathrm{\lambda }{\mathrm{\xi }}^{\mathrm{\gamma }}$$ (2)

where ξ(x, y, z, t) is the fraction of volume occupied by oedema, and μ, λ and γ are oedema parameters. The first term of the equation represents production of oedema. We have modelled the fact that presence of oedema is a consequence of presence of glioma cells, by having an oedema production coefficient that depends on glioma cell density. Oedema production depends also on oedema concentration and becomes zero when oedema reaches its maximal value. There is global conservation between glioma cells, oedema and healthy tissue: if V is total volume available occupied by the three components, we have V = V _g  + V _e  + V _t where indices g, e, t stand for glioma cells, oedema and healthy tissue. Dividing by V and introducing ξ_t for the fraction of total volume occupied by healthy tissue, we find ρC _m V ₀ + ξ_e + ξ_t = 1 where C _m is maximum glioma cell concentration introduced above, and V ₀ is volume of a single glioma cell. Putting α = C _m V ₀ we have finally conservation ξ_e + ξ_t = 1 – αρ. When oedema has replaced all healthy tissue, reaching its maximal value ξ_m, we have ξ_m = 1 – αρ. The second term in [2] models draining of oedema. Clearance of oedema is a complex phenomenon that involves a number of mechanisms such as drainage into the cerebrospinal fluid (corresponding to a constant drainage rate) or reabsorption into blood vessels in the oedematous tissue (corresponding to a drainage rate proportional to quantity of oedema) 16, 39, 40. For the sake of simplicity, we have opted for a phenomenological representation where the exponent γ = 0.1. This value has the advantage of being very close to constant‐rate draining, while ensuring that oedema concentration remains positive at all times (something impossible in the case of constant draining where a cut‐off must be applied ad hoc when value of concentration reaches 0).

Figure 2.

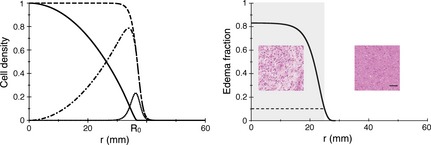
Left: Profiles of cell densities before and after RT. The dashed (respectively solid) black curve corresponds to the cell density profile just before (resp. after) RT. The cell density just after RT is obtained by multiplying the cell density just before RT by a parabola‐shaped function that crosses the horizontal axis at x = R ₀. The dotted‐dashed curve is the difference between the solid and the dashed black curves, and represents the cell density that has been killed by RT. The dotted black curve is the density of cells that has been created by proliferation during 6 weeks, between t = −0.12 year and t = 0. The parameters are common to all the curves: κ = 7.0 year⁻¹, D = 1.75 mm²/year, λ = 0.79 year⁻¹, x = 0.60. Right: Example of an oedema fraction curve, at the onset of RT. The parameters are the following: κ = 1.8 year⁻¹, D = 0.9 mm²/year, λ = 0.17 year⁻¹, x = 0.97 (patient 12). The value of oedema fraction 0.1 (dashed line) is the threshold between the visible part of the tumour on a T2‐weighted MR image (indicated by a grey rectangle) and the invisible part. For the same patient, samples from a biopsy (haematoxylin and eosin staining) inside the MRI‐defined abnormalities are associated with a high fraction of oedema in the tissue [80%, as measured in 14], whereas outside the MRI‐defined abnormalities, the fraction of oedema is lower and reaches zero for normal tissue. The black bar represents 50 μm.

For simplicity, we have assumed spherical symmetry of the tumour. Therefore, ρ and ξ depend on distance r to the centre of the tumour and at time t only.

$$\frac{\mathrm{\partial }\mathrm{\rho }}{\mathrm{\partial }t}=D\left(\frac{{\mathrm{\partial }}^2\mathrm{\rho }}{\mathrm{\partial }{r}^2}+\frac{2}{r}\frac{\mathrm{\partial }\mathrm{\rho }}{\mathrm{\partial }r}\right)+\mathrm{\kappa }\mathrm{\rho }\left(1-\mathrm{\rho }\right)$$ (3)

For numerical simulations it is more convenient to introduce an auxiliary variable. We put ρ = u/r and, multiplying both sides of (1.2) by r, we obtain the equation

$$\frac{\mathrm{\partial }u}{\mathrm{\partial }t}=D\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{r}^2}+\mathrm{\kappa }u\left(1-\frac{u}{r}\right)$$ (4)

where, because of the relationship between ρ and u, we must have u(r = 0, t) = 0 and (∂u/ðr)(r = 0, t) = ρ(r = 0, t). The problem is now reduced to a one‐dimensional one. We have solved eqn (4) by discretizing it over a radial mesh, size Δr = 0.01 mm (thus Δr is close to the radius of a single cell) with time step Δt = 0.01 year, using an implicit scheme for the diffusion component and a homographic‐type discretization for the logistic component. Standard Euler‐type integration was used for integration of oedema eqn (2). Once both equations were solved, profiles of tumour cells as well as of oedema density were obtained, at a given time step, and we defined tumour radius as distance r to the tumour centre where the fraction of oedema ξ crossed a fixed threshold c. Our oedema‐based model accounted for the limit of the MRI abnormality on T2 weighted images corresponding not to a threshold on density of glioma cells but rather to a threshold on fraction of tissue occupied by oedema 12, 13, 14.

Modelling the effect of RT

Next we turn to modelling of the radiotherapy process itself. Given the time scale of the whole process of tumour growth before and after therapy, we decided, for simplicity, to apply radiotherapy at a given point in time instead of spreading it over the duration (typically 6 weeks, or 0.11 year) of treatment in a real‐life situation (for comparison, mean re‐growth delay after radiotherapy for the patients we will present in what follows, is 1.25 year).

We assumed that cell density ρ(r, 0⁻) just before RT drops to ρ(r, 0⁺) = ρ(r, 0⁻) f(r) during RT (that occurs at t = 0).

It is useful to stress here that when we speak of “cell density ρ(r, t)”, we refer to cells that are able to proliferate, migrate and produce oedema, that is, cells that are alive. By killing cells, RT triggers a drop in density viable cells.

Function f(r) was chosen to obtain a profile of cells killed by treatment, ρ(r, t) (1 − f(r)), that is, close to zero at the centre of the tumour, and displays a maximum at the periphery of the tumour, where proliferating cells are located (see Fig. 2 left, dotted curve represents proliferating cells and dashed‐dotted curve represents cells killed by RT). A simple one‐parameter inverted parabola meets these requirements:

$$\left\{\begin{array}{c}f(r\le R_0)=1-{\left(r/R_0\right)}^2\\ f(r\ge R_0)=0\end{array}\right.$$

An example of the effect of RT can be visualized in Fig. 2 left: dashed curve represents the profile of cell density ρ(r, 0⁻) just before RT, whereas the solid curve represents the profile of cell density just after RT, ρ(r, 0⁺) = ρ(r, 0⁻) f(r).

The profile of cells killed by RT is: ${\mathrm{\rho }}_{\mathrm{K}}(r)=\mathrm{\rho }(r,0^{-})-\mathrm{\rho }(r,0^{+})=\mathrm{\rho }(r,0^{-}){\left(r/R_0\right)}^2$ for r ≤ R ₀ and ρ_K(r) = ρ(r, 0⁻) for r > R ₀ and is represented by the dotted‐dashed curve in Fig. 2, left. Parameter R ₀ is radius of action of RT: for r > R ₀, no cell is killed (see Fig. 2 left).

Number of glioma cells N ₋ in the tumour just before RT is calculated as $N_{-}=A{\int }_0^{\infty }\mathrm{\rho }(r,0^{-})r^2\mathrm{d}r$ where A is constant. Number of glioma cells N ₊ in the tumour just after RT is calculated as $N_{+}=A{\int }_0^{\infty }\mathrm{\rho }(r,0^{+})r^2\mathrm{d}r$. To characterize effects of treatment by a parameter more concrete than radius of the parabola R ₀, we defined 0 < x < 1 as fraction of glioma cells killed by RT: x = (N ₋ − N ₊)/N ₋. By using expressions N ₋ and N ₊, x can also be expressed as follows: $x=({\int }_0^{\infty }{\mathit{\rho }}_{\mathrm{K}}(r)r^2\mathrm{d}r)/({\int }_0^{\infty }\mathit{\rho }(r,0^{-})r^2\mathrm{d}r)$. If x is close to 0 (i.e. R ₀ = 0), no cell is killed and fraction of cells killed by RT increases with x: parameter x is, therefore, a measure of tumour sensitivity to RT.

The parameters

Once the model is fixed, we must address the question of its parameters, their number and their influence on the results. A first remark concerns variables of time and space. They were both calibrated so that time was counted in years and distances measured in mm.

The second remark concerns number of parameters in the model: from eqns (1) and (2) it is clear that the model introduced five parameters, κ and D control the natural tumour's growth, μ, λ and α define dynamics of oedema. Modelling RT brings one more parameter, x. Initial conditions can also introduce further parameters. While for oedema density the initial value is 0, for glioma cell density we started from an initial cell number. Finally, estimating radiological radius of the tumour necessitated introduction of one more parameter, namely threshold c. Thus naive counting lead to no fewer than eight parameters. However, we will show that we were able to fix some of them, reducing numbers of unknown parameters.

First, the term ξ_m = 1 – αρ. In 14, 41, value of C _m for low‐grade gliomas has been estimated to be around 10⁵ cells/mm³ and volume of a glial cell is 0.5 pL 42, which provides a value of 0.05 for α. Given that ρ < 1, the term αρ is negligible compared to 1 (except when ρ is close to 1). We thus simplified the model by approximating 1 – αρ – ξ by1 – ξ.

Second, number of cells in the initial mass. As we do not know what occurs at very early stages of tumour growth, we decided to start with one cell only, as in 27. Next we investigated the effect of threshold c. Analysis of stereotactic biopsies 14 suggested that this threshold should be set between 0.1 and 0.2. However, changing the value of c did not affect RT consequences in an appreciable way, so we chose to set c = 0.1, see Fig. 2 right.

Finally, five parameters remained: growth parameters D and κ, oedema parameters λ, μ, and RT parameter x. These three families of parameters (growth, oedema, RT) control different parts of the tumour radius‐versus‐time curve. In Fig. 3 left, we show simulated evolution radius of a DLGG before, during and after treatment. One can distinguish four parts in this evolution.

Figure 3.

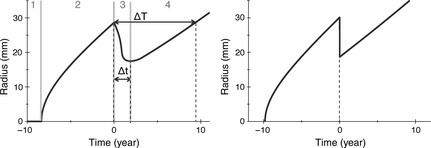
Left: Definition of the regrowth delay Δ t and of the gain of lifetime due to RT Δ T and of the four phases that compose the radius‐versus‐time curve. Right: A radius‐versus‐time curve, with the migration–proliferation model without oedema (the radius of the tumour visible on MRI is calculated from the cell density). The threshold of visibility on the cell density is set to 0.02 37. The parameters are the following: κ = 1.0 year⁻¹, D = 1 mm²/year, λ = 0.5 year⁻¹, x = 0.63.

The first, (number 1 in Fig. 3 left) is the invisible phase when oedema density is beneath detection threshold and the tumour cannot be discovered. We will not discuss this phase here as it has been studied in detail elsewhere 27.

The second part of the curve (number 2 on Fig. 3 left) is linear growth of tumour radius, before RT. It is well known that increase in radius of a tumour is governed by eqn (1) alone, and becomes asymptotically linear with time 22, velocity of the detectable tumour front being:

$$v=2\sqrt{D\mathrm{\kappa }}$$ (5)

This linear behaviour persists even in the case where growth is governed by the coupled system [1] and [2] as eqn (2) does not present any spatial dependence. For example, asymptotic velocities shown in Fig. 3 left (model with oedema), and right, (model without oedema) are the same. If, for a patient, the velocity of radial expansion v can be measured, we can fix the product of D and κ using eqn (5) and have only one effective parameter D/κ to be adjusted in our simulations.

The third part of the curve (number 3 in Fig. 3 left) corresponds to reduction in tumour radius after RT. Just after RT, number of glioma cells becomes dramatically lower. At the periphery of the tumour, cells that were producing oedema have been killed, thus draining of oedema is not compensated by its production, and radius of the tumour gets smaller. Meanwhile, remaining glioma cells proliferate, and when they reach sufficient density, the production term of oedema is again large enough to compete with draining, reducing velocity of reduction in tumour radius. After tumour radius has reached its minimum, its growth starts again when (and where) proliferation overcomes the draining. We defined the lower velocity v _d as the absolute value of the mean slope during the regrowth delay. This decreased velocity not only mainly depends on oedema production and draining coefficients but also on κ and D (see Fig. 4 top). Effects of lowering draining coefficient λ can be visualized in Fig. 4 top by comparing the solid thick black curve with the solid thin black one: decrease velocity v _d gets smaller. On the other hand, if production coefficient μ is lowered, decrease velocity v _d gets larger (compare the solid thick black curve with the thick dashed black one).

Figure 4.

Top: Influence of the parameters on the radius‐versus‐time curve. Thick solid black curve: κ = 1.0 year⁻¹, D = 1 mm²/year, μ = 1.0 year⁻¹, λ = 0.5 year⁻¹, x = 0.90; thick solid grey curve: same parameters as for the thick solid black curve, except κ = 2.0 year⁻¹; dashed grey curve: same parameters as for the thick solid black curve, except x = 0.74; thin solid black curve: same parameters as for the thick solid black curve, except λ = 0.1 year⁻¹; dashed black curve: same parameters as for the thick solid black curve, except μ = 0.65 year⁻¹. Bottom: Influence of the parameters of the model on ΔT (left) and on Δt (right). The variation of ΔT and Δt (year) obtained by simulation are plotted against the parameters of the model: white triangles for the oedema production coefficient μ (year⁻¹), grey squares for the diffusion coefficient D (mm²/year), crosses for the proliferation coefficient κ (year⁻¹), white circles for the fraction of glioma cells killed by RT x, black circles for the draining coefficient λ (year⁻¹). The solid lines are the best fits (with μ = 1 year⁻¹): ΔT = 7.7/D ^0.37; ΔT = 8.1/κ^0.72; ΔT = 2.6x/(1.05 − x)^0.68; ΔT = 7.8/(1.134 − λ)^−0.05.

The fourth part of the curve (number 4 in Fig. 3 left) corresponds to regrowth of the tumour. After the radius has reached its minimum, oedema production overcomes draining, and tumour radius returns to its pre‐RT linear evolution. In Fig. 4 top, influence of parameter x can be visualized by comparing the solid thick black curve (x = 0.90) with the thick dashed grey one (x = 0.74): if fewer cells are killed during RT, regrowth delay is reduced. Influence of parameter κ can be visualized by comparing the solid thick black curve (κ = 1 year⁻¹) with the solid thick grey one (κ = 2 year⁻¹): with a higher proliferation coefficient, glioma cells proliferate faster and regrowth occurs earlier. Natural growth velocity v is also larger in this case.

Oedema fraction

After a given time of evolution, cell density is saturated at the centre of the tumour and its value does not change further, see Fig. 2 right, solid black curve. Thus, even if, at the scale of the whole system, a steady state is not reached, locally at the centre of the tumour, where cell density is saturated, the oedema fraction reaches a steady value. Value of the oedema fraction at the centre of the tumour ξ_e can be deduced from eqn (2), with ∂ρ/∂t = 0 and ρ = 1. One finds that ξ_e is solution of the equation:

$$1-{\mathrm{\xi }}_{\mathrm{e}}=\frac{\mathrm{\lambda }}{\mathrm{\mu }}{\mathrm{\xi }}_{\mathrm{e}}^{0.1}$$ (6)

Fraction of oedema ξ_e depends only on the ratio λ/μ. In Fig. 2 right, for patient 12, μ = 1 and λ = 0.25, which yields ξ_e = 0.76. Conversely, if one can measure the fraction of oedema (for instance by an MRI‐based and spatially oriented stereotactic biopsy and using the method described in 14 to calculate the fraction of oedema), one can deduce the ratio λ/μ. For the same patient, we found that haematoxylin and eosin stained biopsy sample inside the limits of the MRI‐defined abnormalities materialized by the grey rectangle, is characterized by a fraction of oedema around 80%, whereas the sample taken outside the limits of the MRI‐defined abnormalities has no oedema (see Fig. 2 right) 27, 38.

Sensitivity to the parameters

To study the influence of the parameters on output of the model, we defined two variables, that can be measured both in simulations and on radius‐versus‐time curves from real patients: regrowth delay after RT, Δt, measures time from RT until onset of tumour regrowth and progression‐free gain of lifetime due to RT, ΔT, which is time interval between RT and when the tumour radius reaches the value it had just before RT, without any anaplastic transformation of the tumour (see Fig. 3 top left). Influence of the parameters can be visualized in Fig. 4 left (for ΔT) and right (for Δt). The parameter of oedema production μ has a very small influence on values of ΔT and Δt in the range 0.5–10 year⁻¹. Since all the patients lie in this range (see next section), we were able to simplify the model by fi Sin μ = 1 when fitting the clinical data. By contrast, the parameter that influences the most ΔT and Δt is fraction of cells killed by RT, x, indicated here with white circles.

Since for what follows, we needed fitting of the function ΔT (κ, D, μ, λ, x), we performed here the analysis of its limiting behaviours: for example, if x = 0 (no glioma cells killed), then ΔT (κ, D, λ, 0) = 0 (for finite values of the other parameters). If draining coefficient was λ > (1 − c)/c ^0.1 (i.e. λ > 1.133 with c = 0.1), value of the oedema fraction at equilibrium ξ_e calculated from eqn (6) becomes lower than the detection threshold c = 0.1 and detectable radius of the tumour is always zero. If λ is slightly smaller than (1 − c)/c ^0.1, after RT, regrowth occurs very late, as almost all produced oedema drained right away. So ΔT → ∞ when λ → (1 − c)/c ^0.1. If κ → 0, regrowth after RT occurred very slowly, and thus ΔT → ∞. On the other hand, if κ → ∞, regrowth after RT occurred almost instantaneously and thus Δt → 0. This analysis led us to assume that function ΔT can be approximated by a product of four one‐variable functions (with μ = 1) (see Fig. 4 left):

$$\mathrm{\Delta }T(x,\mathit{\lambda },\mathit{\kappa },D)=2.5x{(1.05-x)}^{-0.68}{(1.134-\mathit{\lambda })}^{-0.05}{\mathit{\kappa }}^{-0.72}{D}^{-0.3}$$ (7)

In eqn (7) ΔT is measured in year, λ and κ in year⁻¹ and D in mm²/year.

Fitting procedure

A total of 326 data points (326 couples time‐radius), that represented a mean of 11.6 data points per patient, was available. From the radius‐versus‐time curve of each patient, 3 variables are measured:

• ☐Slope of linear growth phase before RT, v.
• ☐Regrowth delay after RT, Δt.
• ☐Progression‐free gain of lifetime due to RT, ΔT.

As explained above, the model is comprised of five parameters: κ, D, μ, λ and x, but since value of v is used to fix the product κD, removing parameter D, only four parameters are varied to fit the clinical data. The four parameters were varied by steps of 10⁻¹ year⁻¹ for κ, μ and λ and of 10⁻² for x in the following ranges: 0.1 < λc ^0.1/(1 − c) < μ < 10 year⁻¹, 0.1 < κ < 15 year⁻¹ and 0 < x < 1 and mean of the square residual χ² is measured at each step.

The best quadruplet (κ, μ, λ, x) for each patient corresponded to a radius‐versus‐time curve that:

1. Fulfilled the following constraints, as in our previous work 27:

   • 1‐  Age constraint: age of the tumour can not exceed age of the patient.
   • 2‐  Linearity constraint: we require linearity of evolution of tumour radius from time the radius exceeds 15 mm onwards, that is, value of slope of the radius‐versus‐time curve at r = 15 mm should not exceed value of the asymptotic slope by more than 20%.

2. Minimizes χ².

3. Is characterized by progression‐free gain of lifetime due to RT, ΔT and regrowth delay, Δt, that are the closest possible to ones measured by clinical data.

Results

Comparison with a model without oedema

The first result of our model was to show that oedema is essential: we simulated evolution of a tumour with the migration–proliferation model without oedema (eqn (1) only), see Fig. 3 right. Since in this case, the tumour limit corresponded to an isodensity line of glioma cells, reduction of tumour radius was instantaneous when cells were killed by the treatment, and tumour regrowth occurred as soon as treatment is stopped. Therefore, the basic migration–proliferation model could not account for the regrowth delay after RT. In the following, we always used the oedema‐based model.

Application to clinical data

All our 28 patients were very well fitted to the model. Figure 5 displays superimposition of clinical data and best fit for six patients. Error bars for clinical data are set to ±1 mm. For some patients, with large uncertainty on the measure of Δt, several fitting solutions with comparable χ² were found (see Fig. 6 top right). In Fig. 6 top left, the 326 tumour radii obtained by simulations for the 28 patients are plotted against experimental radii measured from clinical images. Coefficient of determination of the linear regression is R ² = 0.96.

Figure 5.

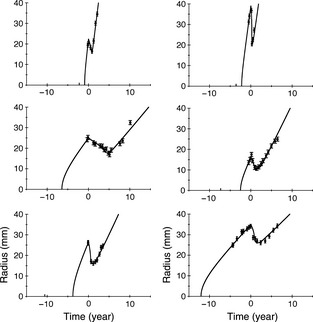
Superimposition of the tumour radius from patients (black dots) and the fit obtained with our model (solid line), versus time, for six patients. Top left: patient 1, κ = 15 year⁻¹, D = 4.8 mm²/year⁻¹, μ =2.8 year⁻¹, λ = 0.6 year⁻¹, x = 0.99; top right: patient 5, κ = 15 year⁻¹, D = 3.75 mm²/year⁻¹, μ = 3.2 year⁻¹, λ = 1.8 year⁻¹, x = 0.95; middle left: patient 12, κ = 1.8 year⁻¹, D =  0.89 mm²/year⁻¹, λ = 0.17 year⁻¹, x = 0.97; middle right: patient 19, κ = 4.2 year⁻¹, D = 1.06 mm²/year⁻¹, μ = 0.4 year⁻¹, λ = 0.2 year⁻¹; x = 0.97; bottom left: patient 16, κ = 3.2 year⁻¹, D = 1.6 mm²/year⁻¹, λ = 0.6 year⁻¹, x = 0.92; bottom right: patient 25, κ = 1.5 year⁻¹, D = 0.78 mm²/year⁻¹, λ = 0.5 year⁻¹, x = 0.82.

Figure 6.

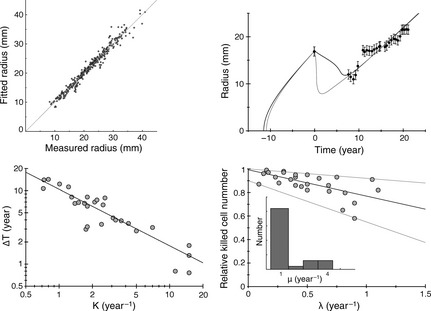
Top left: The tumour radii obtained by simulations for the 28 patients are plotted against the experimental radii measured on clinical pictures. The coefficient of determination of the linear regression is R ² = 0.96. Top right: Example of the series radius‐versus‐time for a patient, that can be fitted with different set of parameters, with a comparable mean square difference between the simulated and the experimental data, χ². In this case, the uncertainty on the measure of Δt is large (see Fig. 7 left, patient 4). Bottom left: The gain of lifetime due to RT ΔT is plotted against κ, in a log‐log scale. The equation of the linear regression is y = 10.4/x ^0.76. Bottom right, inset: histogram of distribution of the oedema production μ obtained when fitting all the patients. The relative cell number killed by RT is plotted against the draining coefficient λ, with the best linear regression (y = −0.22x + 0.99) and the two linear curves that comprise all the data points (y = −0.08x + 1 and y = −0.35x + 0.9).

Dependence of ΔT to κ

Variable ΔT (λ, x, κ, D) depended strongly on x and κ, but weakly on λ, the draining coefficient. Since standard deviation of x between the 28 patients was very small (σ_x = 9.910⁻², x = 0.88), the main contribution to the standard deviation of ΔT came from κ (σ_κ = 3.2 year⁻¹, κ = 3.5 year⁻¹). Therefore, even if all the parameters varied from one patient to another, variation of κ dominated, and the plot ΔT‐versus‐κ could be ficoul by the function, i.e. ΔT ∝ κ^−0.76 (see Fig. 6 bottom left), which is close to the function given by eqn (7): ΔT ∝ κ^−0.72.

Prediction of recurrence time

For 19 patients, duration of total survival after diagnosis was known 11. For these patients, we found that there was correlation between regrowth delay Δt and overall survival (R ² = 0.61) but also between gain of lifetime due to RT ΔT and overall survival (R ² = 0.66). Study of these two variables thus present clinical interest, and it is of the utmost importance to be able to predict them. In this section, we tried to discover whether it was possible to answer the following questions that are crucial for clinicians: would we be able to predict the time at which the tumour would start to regrow after RT, and progression‐free gain of lifetime due to RT?

To be able to perform predictions, parameters of the model need to be known well before regrowth, and ideally before the end of treatment.

Here, we show that it was possible to fix values of parameters μ and κ without greatly changing values of ΔT and Δt, that it was possible to measure the value of parameter λ at the time of RT, and that, from the value of the parameter λ, we were able to infer the value of the last parameter x.

Fixing μ

As shown in fig 4 bottom left, parameter μ had little influence on ΔT and Δt. It had stronger influence on decrease velocity after RT, v _d. However, if μ was fixed to 1 for example, we verified that decrease velocity could be reset to its initial value by changing the other oedema parameter λ. Moreover, the histogram of values of μ obtained after the fitting procedure in the general case shows that most patients were compatible with a value of μ close to 1 (see Fig. 6 bottom right). We thus decided to fix μ to 1 for all the patients.

The fitting procedure with μ = 1 provides new values of Δt and ΔT for each patient, that differed only by 7% on average for Δt and by 2% on average for ΔT from values obtained with the fitting procedure in the general case (range: 0–31% for Δt and 0–20% for ΔT).

Fixing κ

We could not fix κ to the same value for all the patients, since constraints of age and linearity were different for each patient. We thus fixed κ to the minimum value compatible with constraints of age and linearity for each patient. The fitting procedure with μ = 1 and κ set to its minimum possible value, gave new values of Δt and ΔT for each patient, that now differed by 13% on average for Δt and by 5% on average for ΔT from values obtained with the fitting procedure in the general case (range: 0–75% for Δt and 0–32% for ΔT). In Fig. 7 left (respectively right), values of Δt (resp. ΔT) corresponding to the general case appear as white circles, and values of Δt (resp. ΔT) corresponding to the case with μ = 1 and κ set to its minimum possible value, appear as crosses. Values of Δt and ΔT directly measured by the clinical data are represented with error bars as thick grey lines.

Figure 7.

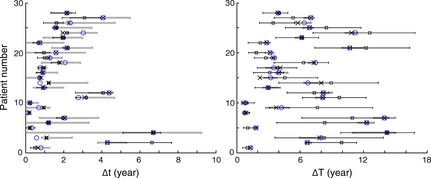
The different Δ t (left) and Δ T (right). The measured values with the associated error bars (thick grey lines), the simulated values in the general case with the four free parameters (white circles), the simulated values with μ fixed to 1 year⁻¹and κ fixed to its minimum value compatible with the constraints (crosses), the simulated values with μ fixed to 1 year⁻¹, κ fixed to its minimum value compatible with the constraints and x calculated from the linear relation with the draining coefficient (squares) (in this case, the error bars correspond to the different linear regressions, see Fig. 5 bottom right).

Measuring λ

We have seen that if cell density had been saturated for at least one year before RT (which is the case for all patients), value of the oedema fraction at the centre of the tumour ξ_e is the solution of the eqn (6) and depends only on the ratio λ/μ. Thus, if one can measure the fraction of oedema (for instance via a MRI‐based and spatially oriented stereotactic biopsy and using the method described in 14 to calculate the fraction of oedema) just before or at the time of RT, one can deduce the ratio λ/μ. As μ has been fixed to 1, this measure would directly give access to the value of the draining coefficient λ.

Estimating x

The last parameter to be estimated was the fraction of cells killed by RT. Values of x for all patients lay between 0.65 and 0.99, mean 0.88 standard deviation 10⁻¹. Since the standard deviation is small, we could have used the same value of x for all patients. However, to increase accuracy of our estimation, we preferred to use the linear correlation observed between fraction x of cells killed and draining coefficient, see Fig. 6 bottom right, to deduce the fraction of cells killed by RT, from the measured value of draining λ. All data points were included between two lines that underlay the uncertainty associated with the value of x, see Fig. 6 bottom right.

Parameters were now all fixed or measured: μ = 1 year⁻¹ for all the patients, κ fixed to its minimum value compatible with linearity and age constraints, λ given by the fraction of oedema at saturation that could be measured by biopsy performed just before RT, and value of x deduced from value of λ by a linear relation. Values of parameters could now be used in the simulation of tumour growth to “predict” regrowth delay Δt and gain of lifetime ΔT. “Predicted” values of Δt and ΔT corresponded to the case where all parameters were fixed or measured, and thus were the ones represented by squares in Fig. 7.

Mean relative error on Δt “predicted” compared to Δt in the general case is 21.7% (σ = 21.8%, range: 0–89%). However, the most representative error lies in comparison between Δt measured from clinical data and Δt “predicted” obtained with the simulation, see Fig. 7 left. When all parameters were fixed or measured, “predicted” Δt lay for all but one patients (patient 2) inside the experimental error bars. For all patients, there was an overlap between experimental values of Δt and simulated ones, with error bars.

Mean relative error on the “predicted” ΔT was 22.6% (σ = 18%, range: 0–79%). Since ΔT was more sensitive to x than Δt, error bars on the estimation of ΔT were larger. Even when “predicted” ΔT lay outside error bars of measured ΔT for several patients, there was overlap between experimental values of ΔT and simulated ones with error bars, for all patients, see Fig. 7 right. Moreover, the four patients with very short gain of lifetime (patients 1, 5, 8 and 10) were very well identified and their “prediction” of ΔT was good.

Discussion

In this article, we proposed an oedema‐based migration–proliferation model that described evolution of DLGG under RT. The model used for assessment of RT effects is admittedly a very simple one. Being simple offers the advantage of eschewing intricate mechanisms and restricting the number of parameters. As explained in the previous sections, the effective number of parameters, which may influence results in an appreciable way, is just four: two parameters for tumour growth, one for oedema production and draining and one for the RT process.

To test our model, we fitted clinical data. We showed that we were able to obtain very good fits of experimental data. The results are robust and are not due to high numbers of independent fitting parameters. This agreement does not fully validate our model, but we have shown that a model without oedema fails at fitting the data.

We showed that variation of κ dominateed variations of others parameters in the patient population and that there exists a strong correlation between high proliferation coefficient and low progression‐free gain of lifetime of the patients. This result is consistent with results of clinical studies on the same data where high proliferation rates were associated with poorer outcomes 17.

We found that, for our population of patients, RT killed around 88% glioma cell number, the remaining 12% being responsible for recurrence of the tumour. In our model, proliferating cells represent only a small part of cells killed by RT (8% on average), see Fig. 2 left, the dotted curve, and it is interesting to note that Ribba et al., with a different model, also predicted that RT may have killed not only proliferative cells but also quiescent ones 31. We found that there was weak linear correlation between draining coefficient and fraction of cells killed by RT: larger draining coefficient was associated with lower fraction of cells killed by RT. A hypothesis to explain this correlation would be that high draining coefficient washed out quickly factors released by irradiated cells, thus preventing them from killing other non‐irradiated cells by any bystander effect 43. However, a larger cohort of patients would be needed to confirm this hypothesis.

In addition, we showed that in theory, it should be possible to estimate all parameters of the model when RT starts. In this case, the model could predict future evolution of the tumour radius. The regrowth delay and the gain of lifetime due to RT could be predicted with an uncertainty of around 20%. However, any additional uncertainty on the estimate of the parameters can dramatically increased uncertainty of predictions. Due to these uncertainties inherent in any clinical data, the model could not be used to provide regrowth delay or gain of lifetime with high precision, but it certainly could provide an order of magnitude of its duration.

Estimating regrowth delay and gain of lifetime due to RT could be very useful for RT clinicians: first, it seems that these variables are correlated to overall survival of patients. Second, since RT has very strong side effects on patients, clinicians could use predicted regrowth delay to decide whether risks for patients' health outweigh benefits or not. If, for example, very short regrowth delay would be predicted, RT may be cancelled in favour of another more efficient oncological treatment. And third, during treatment, estimate of regrowth delay could help clinicians anticipate regrowth of the tumour. More frequent MRI scans could be planned at the approach of the estimated regrowth time. A new treatment could start just as growth resumes, when radius of the tumour would be close to its minimum, improving efficiency of this second treatment, and maybe delaying anaplastic transformation.

Our conclusions have been drawn for a particular set of patients and will have to be confirmed by studies performed on larger cohorts. Several improvements to our model also spring to mind. For instance, duration of RT could be modelled rather as a small but finite time interval. The pattern of cells removed during radiotherapy could be chosen differently from the one used here. Draining of oedema could be modelled in a way different from the one adopted here, perhaps based on more detailed experimental investigations. Although these suggested modifications may lead to an improvement of the model, their implementation would entail introduction of more parameters, something we have strived to avoid throughout this study.

Conflicts of interest

No potential conflicts of interest were disclosed.