Mathematical model for chemotherapeutic drug efficacy in arresting tumour growth based on the cancer stem cell hypothesis

Abstract

Abstract.  Objective: Cancer stem cells have been identified as the growth root for various malignant tumours and are thought to be responsible for cancer recurrence following treatment. Materials and methods: Here, a predictive mathematical model for the cancer stem cell hypothesis is used to understand tumour responses to chemotherapeutic drugs and judge the efficacy of treatments in arresting tumour growth. The impact of varying drug efficacies on different abnormal cell populations is investigated through the kinetics associated with their decline in response to therapy. Results and conclusions: The model predicts the clinically established ‘dandelion phenomenon’ and suggests that the best response to chemotherapy occurs when a drug targets abnormal stem cells. We compare continuous and periodic drug infusion. For the latter, we examine the relative importance of the drug cell‐kill rate and the mean time between successive therapies, to identify the key attributes for successful treatment.

INTRODUCTION

According to the cancer stem cell hypothesis, just as mature cells in some systems are maintained by self‐renewing stem cells, malignant tumours occur through mutations of healthy stem and early progenitor cells, in the corresponding abnormal cells (Al‐Hajj & Clarke 2004; Clarke 2004). Thus, understood, tumours consist of progeny of abnormal stem or progenitor cells (Reya et al. 2001; Pardal et al. 2003; Clarke 2004; Singh et al. 2004). A key contention of the hypothesis is that only a small subset of tumour cells has the ability to proliferate rapidly in many types of cancer. Consequently, because it is likely that cancerous stem cells are often responsible for recurrences that occur after conventional treatment, treatments must target cancer stem cells in order to eliminate the disease.

The transformation of stem cells into a malignant phenotype requires fewer mutations than are required to ectopically activate a more differentiated cell. Because stem cells are self‐renewing they often persist for longer periods and are thus more likely to accumulate mutations than a shorter‐lived progenitor or differentiated cell. Such progenitor cells inheriting mutations from a stem cell can also itself undergo further mutations to cause transformation. Malignant cells that arise after such mutations disrupt normal signalling pathways and usurp the self‐renewal machinery that is normally the property only of stem cells. Consequently, many pathways associated with normal stem cell renewal are also implicated in oncogenesis, for example, Bmi‐1 (Lessard & Sauvageau 2003; Molofsky et al. 2003), Sonic Hedgehog (Taipale & Beachy 2001) and Wnt (Polakis 2000; Taipale & Beachy 2001). The literature cites several techniques for mathematical modeling of haematopoietic, neural and embryonic stem cells (Viswanathan & Zandstra 2003), plus for cells of chronic myeloid leukaemia (CML) (Komarova & Wadarz 2005; Michor et al. 2005; Roeder et al. 2006). We (Ganguly & Puri 2006) have previously extended a compartmental method (Wichmann & Loeffler 1984) to formulate a predictive mechanistic mathematical model for a process based on a cancer stem cell hypothesis (Reya et al. 2001; Al‐Hajj & Clarke 2004; Clarke 2004; Singh et al. 2004).

Ineffective targeting of the abnormal stem cell population within tumours can lead to therapeutic failures and cancer recurrence (Al‐Hajj et al. 2004; Polyak & Hahn 2006). Most cytotoxic chemotherapeutic agents target the more rapidly proliferating progenitor cells during the cancer cell transit amplification stage (in which progenitor or amplifying cells expand the differentiating cell population through a series of symmetric divisions, Mackenzie 2005). Therefore, it is possible that the slower proliferating cancer stem cells can survive these treatments.

Our objective herein is to characterize tumour cell responses to chemotherapeutic drugs. We consider impact of different drug efficacies on various abnormal cell populations by observing the kinetics (e.g. imposed by the cell‐kill rate) associated with their reduction in response to therapy. Such observations can help provide insight into disease responsiveness and resistance (Huntly & Gilliland 2005; Michor et al. 2005). Overall efficacies of continuous and periodic drug therapy in arresting tumour growth are compared and different modes of drug infusion and their outcomes are also examined. Finally, the relative importance of the cell‐kill rate is demonstrated through a parametric study. These results could assist clinicians by providing comparative information on several possible chemotherapy modes and by identifying the key attributes of a successful therapy.

THE MODEL

Our model is schematically described in Fig. 1(a). It consists of two pathways, one normal and the other an abnormal path that occurs due to stem and early progenitor cell mutations. It is based on an evolutionary perspective, which assumes that cells regularly undergo mutations in their DNA. While the vast majority of these mutations are detrimental to cell survival, some cells, particularly those capable of self‐renewal, infrequently survive the mutations. They subsequently drive the formation and pathology of the neoplasia (Clarke 2004). The model incorporates the role of internal cell signalling during proliferation. Hence, it is self‐regulating; that is, normal cell signalling limits healthy cell proliferation to a steady value that is sufficient to replenish any steady death (apoptosis) of mature cells.

Figure 1.

(a) Cancer stem cell model showing the cell‐signalling pathway, and the action of a chemotherapeutic drug. (b) Instantaneous infusion rate ‘a’ for different modes of chemotherapeutic drug dosing, that is, continuous infusion, periodic infusion. Here, τ_drug denotes the time period between two consecutive drug doses, τ_cycle the duration of non‐zero infusion rate in a cycle, and a_max the instantaneous peak infusion rate.

Other than tissue evasion and metastasis (since it does not consider cell transport), the model accounts for the remaining five hallmarks of malignancy (Hanahan & Weinberg 2000), These include (i) self‐sufficiency in growth signals, (ii) insensitivity to antigrowth signals (which taken together represent the loss of regulation and signalling in abnormal cells), (iii) limitless replicative potential (i.e. the basis of the cancer stem cell hypothesis), (iv) acquisition of resistance to apoptosis and (v) sustained angiogenesis (here, we can incorporate different carrying capacities for the healthy and abnormal cell populations). We have previously used the model to confirm that mutations leading to malignant change are more significant when they occur in stem cells than in early progenitor cells. We have concluded in that investigation that cancer risk increases with increasing frequency of injury, for example, with a repeated insult that depletes the mature cell population (Ganguly & Puri 2006). While the model was deterministic (not stochastic), randomness could be readily included by changing various parameters [such as those reported in 1, 2 of Ganguly & Puri (2006)].

Table 1.

Parameters used in the model

Parameter	Ssymbls	Values
Cell cycle time for SC, EP, LP compartments	τSC, τEP, τLP	12 h
Cell maturation time for LP compartment	τm	40 h
Self‐renewal probability upper and lower limits for SC	Pmax,SC, Pmin,SC	0.6, 0.4
Self‐renewal probability upper and lower limits for EP	Pmax,EP, Pmin,EP	0.5, 0.5
Upper and lower limits of mitotic fractions for stem cells	αmax,SC, αmin,SC	1, 0.01
Upper and lower limits of mitotic fractions for EP cells	αmax,EP, αmin,EP	1, 0.3
Number of EP cell self‐renewals	k	5
Upper and lower limits of the number of mitotic cycles	nLP,max, nLP,min	3, 9
Death rate (apoptosis) of MC	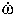0,MC (in AU)	0.01
Death Rate (apoptosis) of AP	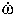0,AP (in AU)	0.01
Carrying capacity of healthy and abnormal cells	Θhealthy cells, Θa (in AU)	1000, 100
Rate at which drug becomes ineffective due to cell kill	γ (in AU)	0.01 for healthy cells 0.05 for abnormal cells
Drug decay rate	λ (in AU)	0.01
Duration of infusion in one therapy cycle	τcycλɛ	25 h
Peak infusion rate	amax (in AU)	0.5

Table 2.

SCA and AP size at t = 2000 h expressed as percentages of their corresponding populations in absence drug therapy (a_max = constant)

	SCA	AP
τdrug = ∞	100	100
τdrug = 500 h	85.7	85.1
τdrug = 100 h	43.1	46.8
τdrug = 25 h	11.6	14.9
τdrug = 0	5.6	8.5

Cell fate choices in the model are assumed to arise from soluble signals that establish a concentration gradient. This enables cells within the gradient to adopt alternate, ‘all‐or‐none’ fates at critical threshold signal levels (Jessel & Lumsden 1997; O’Neill & Schaffer 2004). We assume that the concentration gradient becomes negligible when the mature cell population reaches a desired sustainable level (there is an upper signalling threshold). The growth mechanisms and factors influencing stem cell self‐renewal are considered to be the same for both normal and abnormal stem cells (Oliver & Wechsler‐Reya 2004). Thus, self‐renewal probabilities for both normal and abnormal (or mutated) stem cells are identical, as are those for normal and abnormal early progenitor cells.

Stem cells (SC) are assumed to self‐renew an unlimited number of times (Al‐Hajj & Clarke 2004) with a self‐renewal probability P_SC. Those that do not self‐renew, differentiate to form early progenitor cells (EP). The self‐renewal probability varies between a maximum P_max,SC and a minimum P_min,SC depending on the stem cell, and early and late progenitor cell (LP) populations. Self‐renewal probability of early progenitor cells P_EP likewise lies between P_max,EP and P_min,EP depending on their respective cell populations. The model constrains early progenitor cells to self‐renew a limited number of times k (Al‐Hajj & Clarke 2004). Late progenitor cells undergo n_LP stages of cell division and produce mature cells (MC). Cell division regulatory feedback signalling controls the number of cell division stages between n_LP,min and n_LP,max. A regulatory signal is responsible for maintaining a steady population of mature cells. The mature cell population also provides feedback to the stem cells thereby influencing their mitotic fraction and self‐renewal rate. Regulatory feedback signals are represented by dotted lines that are numbered j through n in Fig. 1(a)[for which the mathematical representations are summarized in Table 2 of Ganguly & Puri (2006)].

The probabilities M_SC and M_EP represent occurrence of oncogenic mutation during DNA transcription for each cell division event involving stem cells or early progenitor cells. If mutation occurs, one daughter cell acquires the mutated gene following cell division while the other retains the original DNA. Thus mutation of SC leads to formation of abnormal stem cells (SCA). Abnormal early progenitor cells can be formed either due to mutation in EP cells, or through differentiation of SCA. Subsequent differentiation of EPA leads to formation of abnormal progeny (AP). In our model, this AP population is the precursor of malignancy. Any increase or reduction in its size is presumed to be an equivalent increase or decrease of the risk of malignancy. Cancer arises when a cell with a mutated gene acquires the ability to proliferate indefinitely through the accumulation of at least C mutations. Due to uncontrolled proliferation, thereafter the associated cell cluster produces a malignant tumour (Reya et al. 2001). We consider each cell type as a separate compartment that has an individual rate expression for its cell population growth. The model also considers rates of apoptosis 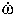_0,MC and 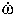_0,AP for MC and AP, respectively.

CHEMOTHERAPEUTIC TREATMENT

It is possible to design chemotherapeutic drugs with selective efficacies towards different cell populations. Hence, we assume that when a drug is supplied it influences a particular cell sub‐compartment with a specific efficacy. We therefore have assigned separate cell‐kill rates µ for different healthy and abnormal cell compartments to account for this selectivity. This assumption is consistent with previous observations, for example, imatinib inhibits more than 90% of CML progenitor cell growth in vitro in the 1–10 µM concentration range but shows little activity against normal haematopoietic progenitors (Huff et al. 2006).

MATHEMATICAL DETAILS

The basic model for healthy and cancer stem cell pathways is described by Ganguly & Puri (2006). In this paper, the effect of a chemotherapeutic drug on the cell population equation is included in terms of its cell‐kill rate µ. Each cell type has also been assumed to have its own carrying capacity Θ[an upper limit to which cell growth is limited, for example, by a bounded nutrient supply rate to the growing cell population, Byrne (2003)]. Thus, the cell proliferation relation accounting for drug therapy is

(1)

where N denotes the cell population, 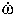 = (α/τ) ln(2) the cell division rate (where α is the proliferative fraction and τ the cell cycle time). The average drug concentration A is determined from the expression

(2)

Equation (2) indicates that the net rate of change of drug concentration in a cellular matrix is a function of the drug infusion rate a(t), the natural drug decay (due to chemical decomposition of the drug or its transport, both associated with the decay rate λ) and the rate γAN at which the drug becomes ineffective due to cell‐kill rate. The last terms in (1), (2) are related but γ and µ can have different numerical values. With the modification described in Equation (1), the rate of change in a cell population is also modified as follows.

Healthy cell compartments

For all healthy cell compartments (depicted on the upper pathway of the schematic diagram in Fig. 1a), an average cell‐kill rate µ_{healthy cells} and an average carrying capacity Θ_H are assumed.

Stem cell compartment (population N _SC):

(3)

Early progenitor compartment (consisting of k sub‐compartments, each with a population ):

(4a)

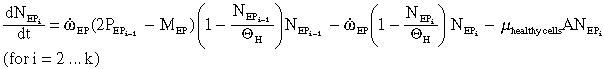(4b)

Total efflux of differentiated EP cells that enter the LP compartment:

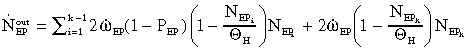(5a)

(5b)

Late progenitor cell compartment (population N _LP):

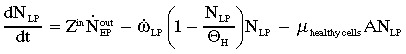(6a)

where and τ_g (=τ_LP/α_LPln2) and τ_m denote cell generation time and cell maturation time, respectively (Ganguly & Puri 2006).

(6b)

Mature cell compartment (population N _MC):

(7)

Abnormal stem cell compartment

Following Ganguly & Puri (2006), abnormal stem cells are assumed to have the same self‐renewal rates P_SC and proliferative fractions (therefore, the same values of 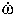_SC) as their healthy counterparts. Similarly, abnormal EP cells also have the same values of P_EP and 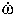_EP as healthy EP cells. For the abnormal cell population, the drug is assumed to have selective kill rates µ_SCA, µ_EPA, and µ_AP, respectively. A separate carrying capacity Θ_a is considered for the abnormal cells.

Abnormal stem cell compartment:

(8)

Abnormal early progenitor cell compartment:

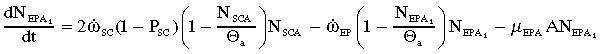(9a)

(9b)

The efflux of abnormal EP cells

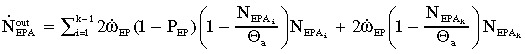(10)

Abnormal progeny compartment:

(11)

DISCUSSION

(2), (3), (4a), (4b), (5a), (5b), (6a), (6b), (7), (8), (9a), (9b), (10), (11) were numerically solved using a time marching scheme, and the parameters specified in Table 1 of Ganguly & Puri (2006). The model has previously been tested by Ganguly & Puri (2006) for its stability and steady state response. We have demonstrated that SC mutations have a much larger proliferation potential than mutations in EP cells. Thus, mutations leading to malignancy are more significant when they occur in stem cells than in early progenitor cells. The model predicts that repeated insult increases the proportion of the stem cell population that participates in cell division thereby enhancing the growth rate of abnormal progeny.

Here, we have modeled the effects of both the continuous and of the periodic infusion of a drug on (healthy and abnormal) cells. During continuous infusion, drug dose is constant over the entire duration of chemotherapy. During periodic dosing, drug infusion occurs every τ_drug hours and, consequently, the instantaneous drug concentration decays due to inactivation both through cell kill and to the natural decay of the drug. Perhaps, the simplest representation of temporal drug decay is through the saw‐tooth curve described schematically in Fig. 1(b), which we have incorporated into our model.

We have considered various periodic dosing times τ_drug. Drug infusion is initiated every τ_drug hours with a maximum infusion rate a_max that linearly decreases to 0 after τ_cycle hours. In order to analyze chemotherapeutic effects at different dosing frequencies, a_max can either be held constant irrespective of the value of τ_drug or it can be assumed to have an inverse relationship with it. In the latter case, the total amount of infused drug (a* = 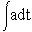) is conserved over a specified treatment time, that is, the same total dose is always infused irrespective of the dosing frequency. For the former type of periodic dosing (when a_max is maintained constant), a* is not conserved but is inversely proportional to τ_drug. In this case, the more frequent the dosing the larger the value of a*. Figure 1(b) illustrates three drug infusion models for which a* is conserved, one of which is continuous and the other two are periodic with values of τ_drug= 100 h and 250 h.

The overall drug efficacy is characterized through its effect on abnormal progeny size. Here, we have assumed that the size of a like cell mass is proportional to the cell population within a compartment. The dynamic response of our model is compared to experimental results of Michor et al. (2005) and Roeder et al. (2006). These teams have found that successful therapy exhibits a biphasic exponential decline in leukaemic cells in imatinib‐treated CML. Experimental data (◆, □ and ▴) in Fig. 2 demonstrate the heterogeneous response of the BCR‐ABL1 transcript levels. The primary effect (exhibited through a steep decline) was induced by initial reduction of proliferating BCR‐ABL1‐positive cells due to the assumed degradation effect. The later moderate decline was largely based on changes in regulatory response of the system due to reduced stem cell numbers. Roeder et al. (2006) successfully modeled this effect by assuming different values of imatinib‐induced degradation, r_deg. The closest analogue to the parameter r_deg in our model is the cell‐kill rate, µ_SCA. Results from our model presented in Fig. 2 predict a similar response for AP cells under continuous infusion for three different µ_SCA values (µ_SCA= 0.5, –·–; µ_SCA= 0.4, ··········; and µ_SCA= 0.5, —). Consistent with the experiments, the simulations show an initially rapid decline in AP cell population that is followed by a slower response. Results presented in Fig. 2 clearly suggest that our model predictions are consistent with clinically determined trends for chemotherapeutic response in imatinib‐treated CML cases.

Figure 2.

Response of the BCR‐ABL1 transcript levels in imatinib‐treated CML cases (the experimental data ◆ and ▴ are from Michor et al. 2005; □ is from Roeder et al. 2006). Our model (plotted against the secondary axis) also predicts a similar biphasic response using different cell‐kill rates (that are analogues of the parameter r_deg in Roeder et al. 2006), that is, µ_SCA= 0.3, –·– µ_SCA= 0.4, ········; and µ_SCA= 0.5, —.

Figure 3 depicts the response of the AP size to therapy. We have assumed that after a tumour is detected, therapy is initiated at 500 h and treatment continues until 2000 h. Both continuous and periodic infusion are examined with τ_drug= 100 h and τ_cycle= 25 h for the periodic case. Drug efficacies for the different abnormal cell populations are varied but the effect of the drug on healthy cells (µ_{healthy cells}= 0.01 in arbitrary units, AU) is always the same.

Figure 3.

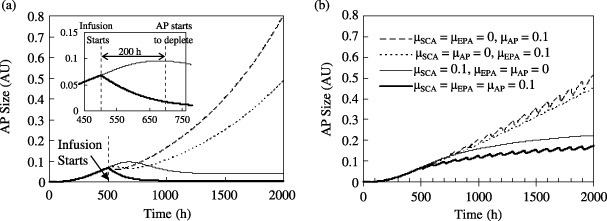
Effect of selective efficacy (represented in terms of the cell‐kill rate, µ) of the chemotherapeutic drug on the abnormal progeny size. The panels show the growth rate of AP over time with (a) a continuous injection rate of 0.5 units, and (b) periodic infusion of a_max= 0.5 units. Each session of drug infusion occurs over τ_cycle= 25 h, and the time period τ_drug between two consecutive infusions is 100 h. For both cases, µ_{healthy cells}= 0.01. Drug infusion begins at t = 500 h. The inset in Fig. 3(a) shows an enlarged view of the response lag of the AP population to a drug that is selective to AP alone in comparison with one that is selective to SCA only. The legends for the curves are identical for Fig. 3(a), its inset, and for Fig. 3(b).

The results show that the AP size diminishes by the largest extent when a drug has equally vigorous effects on the SCA, EPA and AP compartments (here µ_SCA=µ_EPA=µ_AP= 0.1). However, such equivalent effects of a drug on all three kinds of abnormal cell populations are not generally clinically feasible. Therefore, it is instructive to examine AP growth with different drug efficacies for the three abnormal populations. Figure 3 presents results when each of µ_SCA, µ_EPA and µ_AP are separately held at 0.1 with the other two values set to 0 (e.g. if µ_SCA= 0.1 then µ_EPA and µ_AP are both 0 and so on). Overall drug efficacy is based on the AP size at 2000 h (i.e. after 1500 h of therapy). When µ_SCA=µ_EPA= 0 and µ_AP= 0.1, the AP size is 0.80 AU with continuous injection and 0.51 AU for periodic injection. For the case µ_SCA=µ_AP= 0 and µ_EPA= 0.1, these values are 0.49 and 0.45 AU, respectively. A marked reduction in the AP size (0.04 AU for continuous infusion, 0.22 AU for periodic infusion) occurs when µ_SCA= 0.1 and µ_EPA=µ_AP= 0. There is very little improvement over these values (0.01 and 0.17 AU for continuous and periodic infusion, respectively) when µ_SCA=µ_AP=µ_EPA= 0.1. These results indicate that AP growth is most inhibited when a drug acts on the abnormal stem cells regardless of the mode of drug infusion.

Figure 3(a) shows that drug response immediately following infusion is progressively more sluggish when the drug acts on EPA or SCA alone instead of on AP. For example, when µ_AP= 0.1 (and µ_SCA=µ_EPA= 0) there is an immediate reduction in the AP size. In contrast, when the drug acts on the SCA compartment alone, the AP size continues to grow until 200 h following infusion. The inset of Fig. 3(a) shows that the AP population continues to grow from 0.068 AU at 500 h to 0.096 AU at t = 700 h before it starts to decline and eventually reduces to 0.012 AU at 2000 h. The delay in response of the AP population to the drug occurs because the amplification of the SCA population into AP transpires with its own time constant. Although targeting the SCA compartment produces a more sluggish initial response as compared to targeting AP cells, it ultimately has a much higher efficacy. This can be explained using the metaphor of the ‘dandelion phenomena’ (Jones et al. 2004; Huff et al. 2006). It logically states that in order to eliminate a dandelion both the stem (or visible portion) of the weed and its root must be removed. Therefore, therapies that offer the potential for the cure of cancers derived from stem cells must target the abnormal stem cells (i.e. the root) that are responsible for disease maintenance, because the elimination of mature cells (i.e. the stem) alone may not lead to a cure. This again explains the smaller overall efficacy of chemotherapy when AP cells instead of the SCA population are targeted by the drug.

As an example, breast tumours that exhibit a basal phenotype similar to healthy mammary progenitor cells are resistant to standard chemotherapy. This supports the hypothesis that therapeutic success in this case could depend on targeting cancer stem cells (Brenton et al. 2005). Imanitib was developed as part of a program to identify drugs that block unregulated activity of protein kinases in various types of cancers (Huff et al. 2006). It produces a rapid response in decreasing CML tumours due to its striking activity against CML progenitors (O’Brien et al. 2003). However, many of its early responses are not durable (Mauro et al. 2003; Cortes et al. 2004) because some CML patients relapse quickly when the drug is discontinued (Cortes et al. 2004) while others show evidence of progression despite continuing with the therapy (Mauro et al. 2003). This has been explained as CML stem cell resistance to Imanitib (Huff et al. 2006). On the other hand, primary activity of interferon may be confined to CML stem cells (Bonifazi et al. 2001), which produces a slow but often durable response in curbing CML (Pierce et al. 2001). because the rationale behind the cancer stem cell hypothesis is to identify the ‘roots’ of cancer and propose durable remedies, for the remainder of the discussion we will focus on drugs that have a specific selectivity towards the SCA population only.

We have noted that the AP population does not exhibit a ‘saw‐tooth’ waveform during periodic drug infusion when µ_AP= 0. When a drug does not act on the AP compartment, the AP population is solely controlled by the differentiation of EPA to AP and indirectly by the differentiation of SCA to EPA. Equation 11 (for the AP compartment) is a first order differential equation with a time‐constant t = 1/(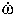 ₀+ m_APA). ^§ When µ_AP= 0 and the AP death rate ω₀= 0.01, this time‐constant is of the order of 100 h. Similar re‐arrangements of (9a), (9b) reveal that the time‐constant associated with each EPA sub‐compartment is t = 1/(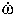 _EP + m_EPAA). Considering µ_EPA= 0 and 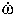= (a_EP/t_EP)ln2, the time‐constant for EPA ranges from 17 to 57 h when a_EP lies in the range 1–0.3 (Refer to Table 1). Thus, with µ_SCA= 0.1, and µ_EPA=µ_AP= 0, any variation in the SCA population with periodic dosing τ_drug is ‘smoothened’ as the fluctuation of the cell population propagates through k EPA sub‐compartments before being reflected in the transient response of the AP population. On the contrary, when µ_AP= 0.1 and the average drug concentration is 0.1 (as found from the simulations), the representative time‐constant for the AP compartment is τ= 1/(0.01 + 0.1 × 0.1) = 50 h. Thus, any ripple in the cell population with a larger time period (e.g. in the case reported in Fig. 3b with τ_drug= 100 h) is reflected in the form of a saw‐tooth profile for the time‐response curve of the AP population.

Effects of chemotherapy on abnormal as well as on healthy cell populations are portrayed in 4, 5 for different dosing frequencies. For all these cases, the drug is considered to have one order of magnitude lower cell‐kill rate for healthy cells (i.e. µ_SCA= 0.1 and µ_{healthy cells}= 0.01). Therapy is again assumed to extend from 500 h to 2000 h. Two dosing modes are considered. First, the maximum drug‐dosing rate a_max is specified – as in a case when a maximum tolerated dose that should not be exceeded is stipulated, in order to prevent systemic side effects (Mayer et al. 2006). For this type of dosing, the value of a* varies inversely with the dosing frequency.

Figure 4.

(a) Effect of drug infusion frequency on the AP size. The limiting cases are for no drug infusion (τ_drug=∞) and continuous drug infusion (τ_drug= 0). Each drug infusion session occurs for 25 h with a_max= 0.5 units. µ_SCA= 0.1, µ_EPA=µ_AP= 0, µ_{healthy cells}= 0.01. (b) Corresponding variations in the MC and SCA populations. Drug infusion begins at t = 500 h.

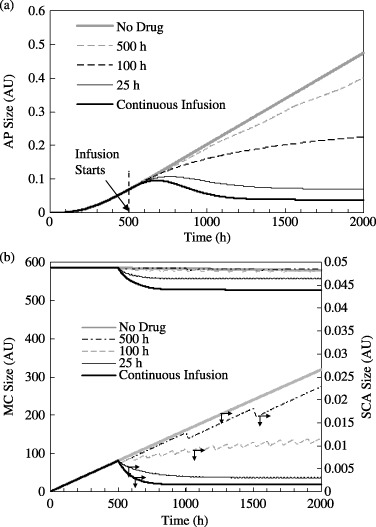
Figure 5.

Effect of drug infusion frequency on the (a) AP number and (b) SCA and MC populations. The limiting cases are for no drug infusion (τ_drug=∞) and continuous drug infusion (τ_drug= 0, a = 0.05 units). Each session of drug infusion occurs for 25 h. a_max is adjusted at different dosing frequencies such that a* = is constant for all dosing frequencies. For all cases, µ_SCA= 0.1, µ_EPA=µ_AP= 0, µ_{healthy cells}= 0.01. Drug infusion begins at t = 500 h.

Figure 4(a) presents the time‐response of AP to therapies with different periodicity, that is, τ_drug= 25 h, 100 h and 500 h. For all three cases a_max= 0.5 AU with each drug infusion session occurring over a period τ_cycle= 25 h. For comparison, AP response to continuous infusion over the same duration and with an identical dosing rate (0.5 AU), and for the case when there is no therapy, are also presented. These latter two cases establish the theoretical lower and upper limits for τ_drug and are, respectively, 0 and ∞. The corresponding MC and SCA population are plotted in Fig. 4(b). Next, the same cases are examined when the total drug administered a* is conserved between 500 and 2000 h for all the values of τ_drug (except, of course, when τ_drug=∞ for which a* = 0). The corresponding responses of the SCA, MC and SCA populations are plotted in Fig. 5.

As shown in Fig. 4(a), the AP population at the beginning of drug infusion is 0.068 AU. When no drug is administered, it grows to 0.47 AU at 2000 h. Recall from Fig. 3(a) that the AP population reaches 0.80 AU when µ_SCA=µ_EPA= 0 and µ_AP= 0.1 AU. This indicates that abnormal progeny size reduces significantly with chemotherapy that targets SCA cells instead of AP. Figure 4(a) indicates that the AP sizes (in AU) following 1500 h of chemotherapy are 0.47, 0.4, 0.22, 0.07 and 0.04 when τ_drug=∞ (i.e. when no drug is administered), 500 h, 100 h, 25 h and 0 h (or when there continuous infusion), respectively. This indicates that a_max being held constant, more frequent chemotherapy sessions have greater efficacy. Here, continuous infusion produces the best result, because consistent with intuition, the total amount of the dosed drug a* increases as τ_drug decreases.

The model considers the drug to have a low cell‐kill rate with respect to healthy cells (µ_{healthy cells}= 0.01), which leads to a steady depletion in the MC and other healthy cell populations. Any reduction in healthy cells from their equilibrium values stimulates regulatory feedback signals through (cf. Fig. 1a) and increases the SC (and therefore SCA) proliferation rates. This increase in the SCA population increases AP production, which could under certain conditions counterbalance abnormal progeny removal through chemotherapy. This indicates that a drug that targets AP cells alone can hypothetically exacerbate tumour treatment unless it has a large enough AP kill rate (i.e. a large value of µ_AP) or low enough side effects on healthy cells (with a low value for µ_{healthy cells}).

Mature cells and SCA populations for these cases are presented in Fig. 4(b). Continuous infusion leads to a small depletion in the MC population from an equilibrium value of 578.8 AU to 527.8 AU. This 8.8% MC decrease induces SC (and SCA) proliferation through feedback signalling. Regardless, the SCA population does not exceed, for any τ_drug value, the corresponding value for the case when there is no treatment (because the drug now directly targets the SCA population). The SCA population diminishes immediately after the drug is administered. The greatest response is again observed for continuous infusion with which the SCA population reduces to 22% of its initial size. As before, the SCA population does not decline as rapidly for larger τ_drug values. After initially declining, SCA size actually increases slightly with time, indicating that cell‐kill rate is lower than the SCA production rate when τ_drug > 100 h. In contrast, for τ_drug > 500 h SCA growth is only marginally arrested below the SCA build‐up without drug therapy. At 2000 h, SCA populations are respectively 0.0266, 0.0228, 0.0116, 0.0031and 0.0015 AU when τ_drug=∞, 500 h, 100 h, 25 h and 0 h. Table 2 presents final SCA and AP populations for different τ_drug values expressed as percentages of their respective sizes would have been in the absence of therapy. Correlation between the reduction in the AP and SCA populations under therapy is almost linear. AP behaviour, presented in Fig. 4(a), therefore follows a trend similar to the SCA activity in Fig. 4(b), but with a time‐lag.

When total infusion a* is constant irrespective of τ_drug, the response of the AP population to chemotherapy is much different. As shown in Fig. 5(a), the AP population at 2000 h is 0.11, 0.04 and 0.04 AU when τ_drug= 500, 100 and 25 h, respectively. Drug efficacy does not noticeably alter when τ_drug changes. However, periodic infusion produces large transient declines in the MC population (Fig. 5b). For instance, the MC population decreases from 585.4 to 335.8 AU immediately following infusion during each cycle when τ_drug= 500 h. This is due to the large a_max value (cf. Fig. 1b) imposed as τ_drug increases so as to maintain a constant a* value. Therefore, when τ_drug= 100 h the MC depletion is smaller (from 585.4 to 509.6 AU). Because depletion of mature cells is an undesirable side effect of therapy, particularly for sensitive populations, the results imply that administering large doses at infrequent periods could be detrimental to patient health. For example, survivors of medulloblastoma show signs of impaired neuropsychological activity in the first decade after chemotherapy and radiation treatment (Maddrey et al. 2005), both of which have the deleterious side effect of healthy brain tissue damage.

So far, we have considered an arbitrarily chosen constant value of µ_SCA (= 0.1) for our analysis. However, different drugs may have varying SCA kill rates. Thus, it is important to investigate how variations in µ_SCA can alter the results of chemotherapy for both continuous and periodic infusions with different values for τ_drug. Figure 6 presents the AP population at t = 2000 h as function of µ_SCA when a_max and a* are held constant, respectively. As before, the drug is administered from t = 500 h to t = 2000 h, and all the other parameters (e.g. τ_cycle, µ_{healthy cells}, etc.) are unchanged.

Figure 6.

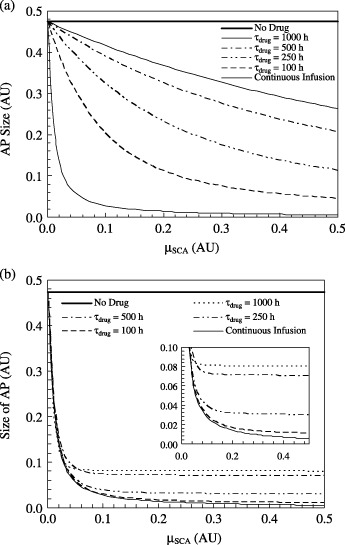
Efficacy of chemotherapy in diminishing the AP population as a function of the SCA kill rate µ_SCA for different drug infusion conditions: (a) a_max= constant for all frequencies and a* is not conserved, and (b) a_max is adjusted at different dosing frequencies so that a* is conserved. The plot indicates the AP size at t = 2000 h. Drug infusion occurs from t = 500 h to t = 2000h. The inset of Fig. 6(b) shows an enlarged view of the same plot.

Figure 6(a) indicates that for a continuous infusion process, significant improvement in drug efficacy is achieved when the value of µ_SCA is raised by even a very small value above 0. The post‐treatment AP size decreases by almost 95% from that in the absence of therapy when µ_SCA is raised from 0 to 0.12. However, further increase in µ_SCA does not alter efficacy as significantly and the final AP population is eventually almost insensitive to any further increases in µ_SCA. For τ_drug= 100 h, the effect of µ_SCA is less pronounced, because for µ_SCA= 0.5 the decline in AP size is 90.5% as compared to one in the absence of therapy. Unlike the case of continuous infusion, the AP versus µ_SCA curve continues to monotonically decrease within the range of the study. The slope of this curve decreases with increasing τ_drug. For example, with µ_SCA= 0.5, the AP sizes at t = 2000 h for τ_drug= 250 h, 500 h and 1000 h are 24%, 44% and 55% in comparison with the case when there is no therapy (Fig. 6a). Thus, when a_max= constant (i.e. a* is not conserved), a more vigorous drug is progressively less effective as the time between two consecutive infusion increases. On the contrary, when a* is conserved over the entire duration of therapy and µ_SCA is smaller than 0.04, the sensitivity of drug efficacy on µ_SCA at all τ_drug values is almost as satisfactory as that produced through continuous infusion.

Figure 6(b) indicates that increasing the value of µ_SCA from 0 to 0.04 can result in a more than 80% reduction in AP growth for all the τ_drug values considered here. Beyond a threshold of µ_SCA (0.3, 0.18, 0.12 and 0.06 for τ_drug= 100 h, 250 h, 500 h and 1000 h, respectively, as shown in the inset of Fig. 7b), AP size ceases to significantly deplete with any further increase in µ_SCA. This implies that for periodic therapy with conserved a*, an acceptable result is achieved when the drug has a threshold value of µ_SCA. A drug with a µ_SCA value lower than this threshold does not decrease the AP population to the maximum extent possible. In contrast, while a larger value of µ_SCA could produce more pronounced side effects, it would provide no tangible improvement in efficacy, for example, through drug resistance (Stordal et al. 2006).

Figure 7.

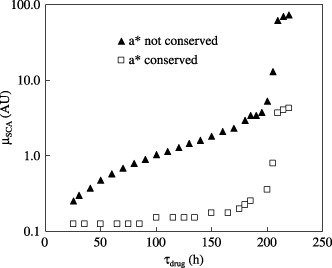
Drug efficacy in terms of the SCA cell kill rate, in AU, required to eradicate 95% of the SCA population plotted as a function of the time between two consecutive treatments during periodic drug infusion. For curve ▴, a_max is constant so that a* is not conserved. For curve □, a_max is adjusted such that a* is conserved. Chemotherapy begins at t = 500 h and continues until t = 2000 h. Each session of drug infusion occurs for 25 hours.

Continuous infusion yields better overall efficacy than periodic infusion. However, the latter is often the more feasible option from a mobility perspective. Nonetheless, there is a trade‐off. While a large value of τ_drug is desirable from a convenience perspective, it has lower efficacy. Choosing a large value for µ_SCA may not necessarily compensate for a large τ_drug interval, because values above a threshold value of µ_SCA do not provide significant therapeutic improvement. Therefore, the combination of τ_drug and µ_SCA that is selected is important.

Figure 7 presents the results of a parametric simulation to determine the minimum µ_SCA required to achieve 95% reduction in AP as a function of τ_drug. Within the range 25 h < τ_drug < 250 h, this µ_SCA value increases monotonically for both the two conditions: (i) when a_max= constant and a* is not conserved and (ii) when a* is conserved. Thus, to achieve the same treatment efficacy, a larger τ_drug period requires a larger value of µ_SCA. It is apparent from Fig. 7 that the average slope of the curve for the condition when a* is not conserved is much higher than that for when a* is conserved. For the first case the required value of µ_SCA increases from 0.25 for τ_drug= 25 h to 5.3 when τ_drug= 200 h. In contrast, this value increases from 0.125 when τ_drug= 25 h to 0.35 for τ_drug= 200 h when a* is conserved. Both plots exhibit sudden increase by almost one order of magnitude in the required µ_SCA values as τ_drug approaches 200 h, after which the curves plateau. This implies that it becomes chemotherapeutically challenging to control cancer if the time between two consecutive therapies exceeds 200 h for the specific conditions of our model. These results should be interpreted qualitatively because different therapeutic conditions applied in the model will yield other quantitative results.

CONCLUSIONS

Efficacy of chemotherapeutic drug therapy for cancer has been investigated using a predictive model based on the cell compartment method. Continuous and periodic drug infusions with different time periods between successive infusions were compared. The infused drug was considered to have either a constant maximum infusion rate a_max or a conserved total infusion quantity a*.

• 1For both continuous and periodic infusions drug efficacy for controlling AP cells is greater when the drug acts selectively on SCA alone, rather than on EPA or AP alone.
• 2When a drug acts on AP alone, the AP growth is immediately arrested. However, its longer‐term efficacy is relatively poorer than if the drug had acted on other compartments. On the other hand, if the drug has a selective efficacy towards SCA alone, although the reduction in the AP cell population is delayed, it is more pronounced. Hence, targeting a drug selectively to remove SCA cells is preferable to targeting EPA or AP cells alone.
• 3When a drug is administered periodically and the maximum dosing rate a_max is held constant (rather than the total infusion quantity a*) reduction in the AP population declines, as the time period τ_drug between consecutive therapies increases. At the upper limit, the higher efficacy is achieved for continuous infusion for which a* is also the largest.
• 4If periodic infusion is performed, such that a* is conserved, drug efficacy is not as strongly affected by τ_drug. However, in case of large τ_drug values, instantaneous drug infusion rate a_max must also be higher, leading to a large temporary decline in the healthy cell population due to side effects induced by the drug. Therefore, such a mode of therapy could be detrimental for populations more susceptible to side effects.
• 5During continuous infusion, drug efficacy is very sensitive to µ_SCA values when these are relatively small. Post‐treatment AP size decreases by almost 95% from that in the absence of therapy when µ_SCA is raised from 0 to 0.12. However, further increases in the values of µ_SCA do not alter the efficacy as significantly. After a critical value, the final AP population is eventually almost insensitive to any further increases in µ_SCA. With periodic infusion and with a* not conserved, even a more vigorous drug is not found to be effective at large value of τ_drug. On the contrary, when a* is conserved over the entire duration of therapy and µ_SCA is smaller than 0.04, the dependence of drug efficacy on µ_SCA is nearly identical for a wide range of τ_drug values (including for the case of continuous infusion).
• 6Achieving the same treatment efficacy with periodic therapy for larger τ_drug periods requires relatively larger values of µ_SCA. However, if τ_drug exceeds a value of 200 h, an order of magnitude larger value of µ_SCA is required. Such treatment could become chemotherapeutically challenging.