Exposing the Nucleation Site in α-Helix Folding: A Joint Experimental and Simulation Study

Abstract

One of the fundamental events in protein folding is α-helix formation, which involves sequential development of a series of helical hydrogen bonds between the backbone C=O group of residues i and the –NH group of residues i + 4. While we now know a great deal about α-helix folding dynamics, a key question that remains to be answered is where the productive helical nucleation event occurs. Statistically, a helical nucleus (or the first helical hydrogen-bond) can form anywhere within the peptide sequence in question; however, the one that leads to productive folding may only form at a preferred location. This consideration is based on the fact that the α-helical structure is inherently asymmetric, due to the specific alignment of the helical hydrogen bonds. While this hypothesis is plausible, validating it is challenging because there is not an experimental observable that can be used to directly pinpoint the location of the productive nucleation process. Therefore, in this study we combine several techniques, including peptide cross-linking, laser-induced temperature-jump infrared spectroscopy, and molecular dynamics simulations, to tackle this challenge. Taken together, our experimental and simulation results support an α-helix folding mechanism wherein the productive nucleus is formed at the N-terminus, which propagates toward the C-terminal end of the peptide to yield the folded structure. In addition, our results show that incorporation of a cross-linker can lead to formation of differently folded conformations, underscoring the need for all-atom simulations to quantitatively assess the proposed cross-linking design.

Graphical abstract

1. INTRODUCTION

Protein folding involves precise packing and organization of various secondary structural elements. This hierarchical structural assembly at the molecular level thus necessitates studying how and on what time scales protein secondary structures form in order to understand how proteins achieve their tertiary folds. In this regard, much effort has been devoted to elucidating the folding dynamics and mechanism of α-helix,^1–46 the most common structural motif found in proteins. The interest in studying the mechanism of α-helix formation is also motivated by the effort to design and develop individually folded, stable α-helices with novel biological functions and/or therapeutic utilities.^19,47–54

Within the framework of the one-dimensional Ising model,^{1,2,10,11,26–29} each residue in an α-helical peptide can be assumed to adopt either a helical (H) or a coil (C) state and, as a result, the microscopic conformational states of the peptide can be distinguished by the number and distribution of the H states within the peptide sequence of interest. By considering the statistical weights of these states, Zimm and Bragg,⁵⁵ as well as Lifson and Roig,¹ were able to calculate the partition function and hence the thermodynamic properties of the system. A key outcome of this theoretical treatment is that the formation of the first turn of the helix, stabilized by a hydrogen-bond (H-bond) formed between the amide units of residue i and i+4 is thermodynamically unfavorable.^11,55–59 However, the subsequent propagation steps that elongate this helical nucleus via sequential addition of helical H-bonds act to decrease the free energy of the system.^2,55,57,58 In other words, the α-helix folding kinetics can be described by a series of discrete steps where the nucleation event is the slowest and occurs first, followed by a faster elongation process. In this regard, many experimental studies^{4,5,7,8,12–14,16,19,20,23,25–28,31,34,35,38,41,42,59–61} have focused on the kinetics of α-helix formation, attempting to resolve those key conformational events. While taken together, these studies provided many microscopic details into the folding dynamics of α-helix, we still lack a complete understanding of the folding mechanism of this simple structural motif. One key remaining question is whether the productive nucleation event (i.e., the one leading to α-helix formation) occurs randomly or at a specific location within the peptide sequence.

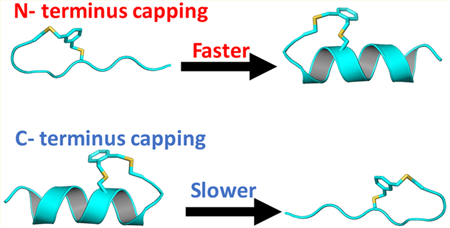
Even for a homopolypeptide, the corresponding α-helix structure is inherently asymmetric, due to the specific alignment of the helical H-bonds. Therefore, it has been hypothesized,⁶² and observed in simulations,^3,15,21,39 that the dominant α-helix folding flux arises from an N-to-C pathway, namely, the α-helical conformation is produced by elongating an α-helical nucleus formed at the N-terminus. Consequently, the reverse and unfolding process would run in a C-to-N manner. However, experimentally it has been difficult to directly validate this hypothesis due to the fact that there is not a distinct signal that only reports on the nucleation event.³⁷ Herein, we aim to provide new insights into the α-helix folding mechanism by studying the folding kinetics of three cross-linked, alanine-based peptides using laser-induced temper-ature-jump (T-jump) infrared (IR) spectroscopy⁶³ and molecular dynamics (MD) simulations.

Side-chain to side-chain cross-linking is a commonly used strategy to stabilize the α-helical conformation of short peptides by reducing the entropic cost associated with folding.^45,47,52 However, traditional cross-linking methods tend to leave flexible helical ends. We recently developed a strategy to constrain helix caps with bis-thioether macrocycles and have achieved high helical contents in short peptides (Figure 1).^54,64 Here, we take advantage of this approach and use it to “expose” the productive nucleation site in an alanine-based peptide.⁵² The name and sequence of the cross-linked peptides studied are given in Table 1. Our working hypothesis is that if the α-helix folding flux proceeds in a preferred direction, the folding rate of these cross-linked peptides would depend on the position of the cross-linker. Indeed, our spectroscopic measurements show that the cross-linker position has a profound effect on the conformational relaxation kinetics of the peptides. This effect is also observed in the MD simulations, which provide an atomistic view of the folding dynamics of those cross-linked peptides. Taken together, our experimental and simulation results support the N-to-C α-helix folding hypothesis. In addition, an unexpected finding arising from our study is that cross-linking may promote the peptide in question to populate differently folded helical conformations, highlighting the need for careful consideration of the peptide sequence and the cross-linker in designing capped or cross-linked α-helices.

Figure 1.

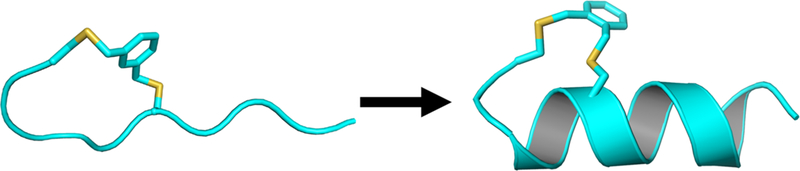
Illustration of the a-helix stabilization effect of a bis-thioether macrocycle at either the N- or C-terminus of a short peptide, where the sulfur atoms are colored yellow.

Table 1.

Name and Sequence of the Cross-Linked Peptides Studied, Where Underlines Represent the Cysteines with the Cross-Linker Attached and a Stands for D-Alanine

peptide	sequence
C-Cap	Ac-AAARAARACAAAaC-NH2
N-Cap1	Ac-CAAAACRAARAAAA-NH2
N-Cap2	Ac-CTPAQCRAARAAAA-NH2

2. EXPERIMENTAL SECTION

2.1. Peptide Synthesis.

The details of the peptide synthesis and purification are given in the Supporting Information. Briefly, the linear precursors of cross-linked peptides were synthesized using standard 9-fluorenylmethoxy-carbonyl (Fmoc) chemistry, and peptide cross-linking was achieved via cysteine alkylation reaction following previously published procedures.^47,52

2.2. Circular Dichroism (CD) and Fourier Transform Infrared (FTIR) Measurements.

CD spectra were measured on an Aviv 62A DS circular dichroism spectrometer (Aviv Associate, NJ) using a 1 mm quartz cuvette. FTIR spectra were collected on a Magna-IR 860 spectrometer (Nicolet, WI) using a homemade sample holder⁶⁵ composed of two CaF₂ windows and a 50 μm spacer. All peptide samples were prepared in deuterated 10 mM phosphate buffer solution (pH 7), and the final peptide concentrations were 4 mM for static and time-resolved IR experiments and 100 μM for CD measurements.

2.3. Infrared Kinetics Measurements.

The T-jump coupled transient IR setup has been described in detail elsewhere.⁶⁶ The only difference is that in the current setup the 1.9 μm T-jump pump pulse was generated from a Continuum Surelite OPO, which was pumped by the 1064 nm output of a Continuum Surelite-EX.

2.4. Molecule Dynamics Simulation.

Simulation Setup.

MD simulations of a total of ~668 μs were carried out using GROMACS 4.5.4⁶⁷ on the Folding@home distributed computing platform.⁶⁸ The AMBER ff99sb-ildn-NMR⁶⁹ force field was used in combination with the TIP3P explicit solvent model. NVT molecular dynamics was performed at 300 K, starting from 10 conformations taken from implicit-solvent replica-exchange molecular dynamics (REMD) simulations (Table S1 in the Supporting Information).

Markov State Model Construction.

Markov state model (MSM) approaches have been used with great success to model the conformational dynamics of protein folding as a kinetic network of metastable conformational states.^70–75 A key advantage of MSMs is the ability to infer complete information about folding thermodynamics and kinetics from ensembles of short, nonequilibirum trajectories. Briefly, constructing an MSM involves first identifying the metastable states, usually through geometry-based conformational clustering. Then, once the states have been defined, the probabilities T_ij^(τ) of transitioning between metastable states i and j over some lag time τ can be estimated from the number of observed transitions in the trajectory data. The matrix T(τ) (with elements T_ij) thus contains full information about the thermodynamics and kinetics. The equilibrium populations π are given by the stationary eigenvector Tπ = π, and the implied time scales τ_n of each relaxation eigenmode are obtained from the eigenvalues μ_n of T as τ_n = –τ/ln(μ_n). The rate matrix K of continuous-time rates between metastable states is related to the transition matrix by T = exp(Kτ), and the implied time scales τ_n are related to the eigenvalues of the rate matrix λ_n through τ_n = (–λ_n)^–1. The longest implied time scale corresponds to the folding relaxation rate of the system.

The MSMBuilder3 software package⁷⁶ was used to construct MSMs from the simulation data. The first 100 ns data were excluded to alleviate potential bias from nonequilibrated distribution of initial seeding for simulations (see Figure S1 in the Supporting Information for trajectory distribution). Time-structure-based independent component analysis^77,78 (tICA) was used to find an optimal low-dimensional subspace onto which the high-dimensional trajectory coordinate data could be projected for the purpose of conformational clustering. As inputs to tICA, we used 378 pairwise distances between Cα and Cβ atoms as input for tICA projection. The outputs of tICA are the set of time-lagged independent components (tICs) that best capture a low-rank approximation of the time-lagged correlation matrix. Thus, the tICs represent the degrees of freedom along which the longest-time scale conformational dynamics occurs. The MSM transition matrix can similarly be thought of as a time correlation matrix for orthogonal indicator basis functions;⁷⁹ and therefore, provided that the MSM decomposition is sufficiently fine-grained, the slowest MSM relaxation eigenmodes should correspond to the same slowest motions identified by tICA.

The optimal number of metastable states for MSM construction was determined using the generalized matrix Rayleigh quotient (GMRQ) variational cross-validation method⁷⁹ (Figure S2 in the Supporting Information). We used a tICA lag time of 5 ns and performed k-center clustering over four tICs to identify 500 metastable states for each crosslinked peptide. The maximum-likelihood estimator (MLE) in MSMBuilder (default setting) was used to estimate the MSM transition matrix from sliding-window counts. An MSM lag time of 20 ns was chosen for construction of the MSM model. Plots of implied time scales versus MSM lag time showed convergence near 20 ns, validating that dynamics was sufficiently Markovian.

3. RESULTS AND DISCUSSION

3.1. Stability Characterization.

The α-helix stabilizing role of the bis-benzylic cross-linker has been demonstrated previously by Wu et al.⁵⁴ Consistent with this notion, the CD spectra of both C-Cap and N-Cap1 peptides at 5 °C are characteristic of an α-helical conformation (Figure 2A). Interestingly, however, the CD spectrum of the N-Cap2 peptide shows a distinct difference, suggesting that this peptide can also sample other conformation(s) besides the expected α-helical and disordered structural ensembles (see below for further discussion). As expected (Figure 2B), the CD thermal-melting curves (T-melts) of these peptides, measured at 222 nm, indicate that the position of the cross-linker and peptide sequence has a profound effect on the thermodynamic stability of the α-helical structure. In particular, the results obtained for C-Cap and N-Cap1 peptides, which only differ in the cross-linker position, reveal that C-terminal cross-linking is more effective in stabilizing the α-helical structure than N-terminal cross-linking. To further assess this difference, we estimated the folding–unfolding thermodynamics of these two peptides by globally fitting their CD T-melts to a two-state model, which assumes that the folded CD baselines of these peptides, or the mean residue ellipticities of their folded states are identical. As shown (Figure S4 and Table S2 in the Supporting Information), this analysis yielded a thermal-melting temperature (T_m) of 8.3 °C for C-Cap, which agrees with that determined by Wu et al.,⁵⁴ and a T_m of –6.4 °C for N-Cap1. Because the thermal unfolding transition of N-Cap2 involves more than two conformational assembles, we did not attempt to fit its CD T-melt. In addition, it is worth noting that these alanine-based peptides contain a RAAR segment in the middle of the peptide sequence, which destabilizes the α-helical conformation due to charge repulsion. Therefore, unlike other α-helical peptides studied previously,⁴ which contain Lys residues that are four residues apart and hence lack such an effect, these short peptides do not show any appreciable folding without the cross-linker.⁵⁴

Figure 2.

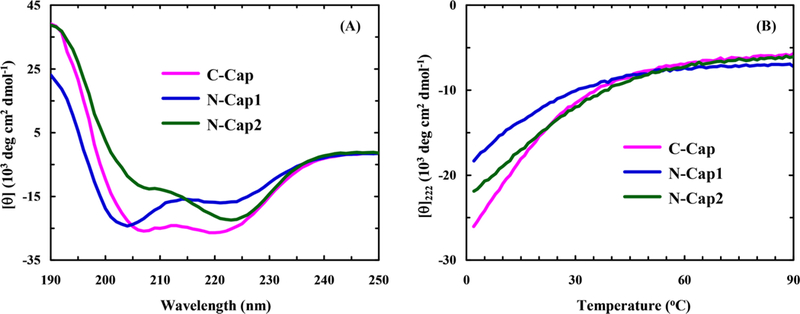
(A) CD spectra of the cross-linked peptides (100 μM) at 5 °C, as indicated, and (B) the corresponding CD thermal melting curves monitored at 222 nm.

3.2. Conformational Relaxation Kinetics.

As shown (Figure S5 in the Supporting Information), the amide Iʹ band of C-Cap loses (gains) intensity at ~1630 cm^–1 (~1665 cm^–1) with increasing temperature, which also manifests, as observed with other α-helical peptides,⁶ in the thermal unfolding of the underlying α-helical structure. Therefore, to assess the kinetics of this conformational transition, we measured the transient IR absorption kinetics of the peptide in question in response to a nanosecond T-jump pulse. As shown (Figure 3), the T-jump induced conformational relaxation kinetic traces of both C-Cap and N-Cap1 peptides, measured at 1640 cm^–1, can be satisfactorily described by a single-exponential decay function, whereas that of N-Cap2 requires a biexponential function to fit. Interestingly, as indicated (Figure 4), the relaxation rate constants of C-Cap and N-Cap1 peptides show quite different dependence on the final temperature. Moreover, around room temperature the T-jump induced conformational relaxation of N-Cap1 is significantly faster than that of C-Cap. For example, the relaxation rate constant of N-Cap1 is ~(162 ns)^–1 at 19.8 °C, compared to ~(472)^–1 for C-Cap at 20.3 °C.

Figure 3.

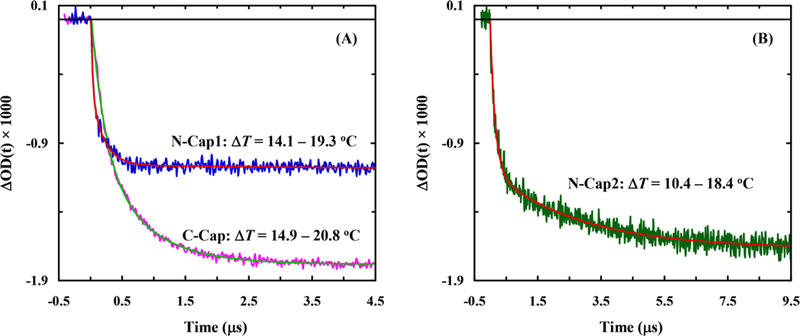
Representative conformational relaxation kinetics of C-Cap and N-Cap1 (A) and N-Cap2 (B) in response to a T-jump, as indicated. In each case, the smooth line corresponds to the best fit of the respective kinetic trace to a specific decay function: ΔmOD(t) = 1.78[exp(−t/472 ns) − 1] for C-Cap, ΔmOD(t) = 1.08[exp(−t/162 ns) − 1] for N-Cap1, and ΔmOD(t) = 1.66[0.66 exp(−t/180 ns) + 0.34 exp(−t/3020 ns) − 1] for N-Cap2.

Figure 4.

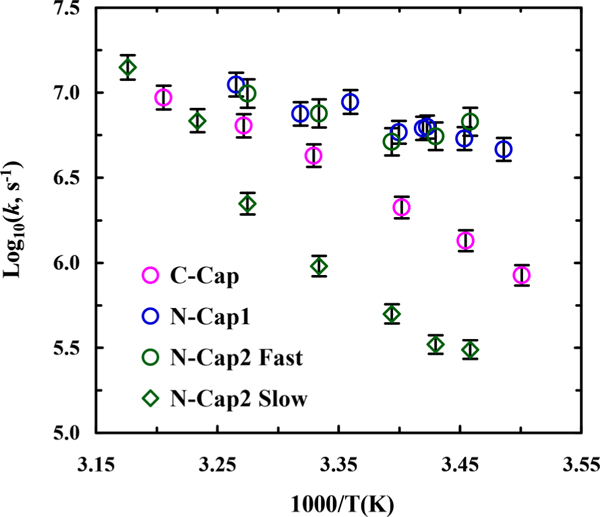
Temperature dependence of the T-jump induced relaxation rate constants of C-Cap, N-Cap1, and N-Cap2 peptides, as indicated.

The conformational relaxation rate constant (k_R) of a two-state system is the sum of the respective folding (k_f) and unfolding (k_u) rate constants. Therefore, to determine k_f and k_u from k_R measured at a specific temperature, one would also need to know the corresponding folding equilibrium constant (K_eq), which equals the ratio of k_f and k_u. For both C-Cap and N-Cap1 peptides, we were able to further decompose the experimentally determined k_R into k_f and k_u using the respective folding-unfolding thermodynamics estimated from their CD T-melts (Table S2 in the Supporting Information). As shown (Figure 5), the folding and unfolding rate constants of these two peptides not only differ in values but also exhibit different dependence on temperature. More specifically, those results indicate, in the temperature range of the experiment, that (1) the unfolding rate constant of C-Cap is not only slower but also more sensitively dependent on temperature than that of N-Cap1, suggesting that the unfolding process of the C-Cap α-helix involves a larger enthalpic barrier; (2) the folding rate constant of N-Cap1 is essentially temperature independent, suggesting that its folding process does not encounter a significant free energy barrier; and (3) around room temperature the α-helix folding rate of N-Cap1 is much faster than that of C-Cap. Taken together, these differences indicate that the role of an N-terminal cross-linker is to increase the α-helix folding rate, whereas that of a C-terminal cross-linker is to decrease its unfolding rate or to prevent it from unfolding. Moreover, it is worthy of mentioning that the role of the D-alanine residue in C-Cap is to provide further stabilization of the C-terminal end of the α-helix and that a previous study⁸⁰ has shown that an individual C-terminal d-alanine only marginally affects the folding rate of helical peptides. Considering the fact that the C-Cap α-helix is more stable than the N-Cap1 α-helix, these kinetic results also offer practical insight into the design of stable α-helices, namely, that decreasing the unfolding rate is a more effective strategy than increasing the folding rate to increase the α-helix stability.

Figure 5.

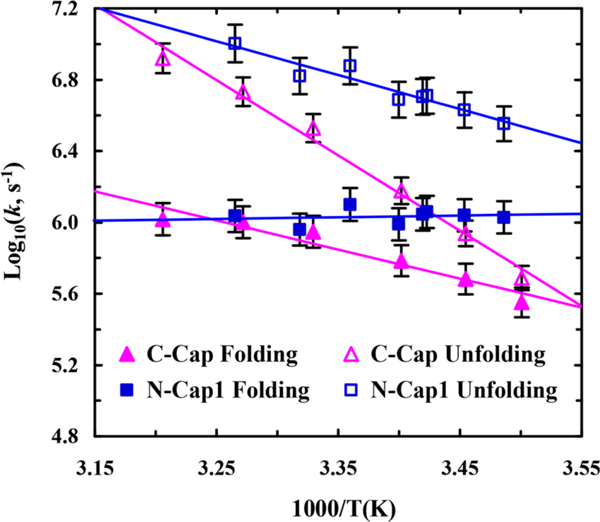
Temperature dependence of the folding and unfolding rate constants of C-Cap and N-Cap1 peptides, as indicated. Solid lines are a guide to the eye.

The kinetic results obtained with these two cross-linked peptides are also useful in understanding how linear α-helices fold. A previous study by Serrano et al. showed that the T-jump induced conformation relaxation rate of an alanine-based cyclic peptide (i.e., cyc-RKAAAD where the Lys and Asp side chains are connected via a cyclization reaction), which folds into a single-turn α-helix, is about (600 ns)^–1 at room temperature. Interestingly, this relaxation rate is similar to that of C-Cap but is significantly different from that of N-Cap1 (Figure 4). In fact, the conformational relaxation kinetics of C- Cap are quite similar to those of cyc-RKAAAD in the entire temperature range of the experiment (Figure S6 in the Supporting Information). Therefore, given the structural similarity between cyc-RKAAAD and the cross-linked region in C-Cap and N-Cap1 peptides, these results suggest that the T-jump induced conformational relaxation of C-Cap involves folding and unfolding of the capped region and hence is slower, whereas that of N-Cap1 does not and is therefore faster. In other words, the conformational transition of C-Cap involves a helical and a nonhelical state and, as shown above, its unfolding process encounters a larger enthalpic barrier. However, the conformational transition of N-Cap1 takes places between a helical and a partial helical state where the capped region is still folded and acts as a pre-existing helical nucleus. As such, the folding process of N-Cap1 is expected to be dominated by helical propagation events, leading to a faster and temperature-insensitive folding rate, as observed (Figure 5). Together, these findings support an α-helix unfolding mechanism wherein unfolding begins from the C-terminus, which in turn suggests that the most productive folding pathway begins with formation of an α-helical nucleus at the N-terminus. However, given the intrinsic complexity of the α-helix folding dynamics, there is always a possibility that the presence of a cross-linker will lead to a fundamental change in the underlying folding mechanism, hence making our interpretation incorrect.

In comparison to that of N-Cap1, the N-terminal TPAQ motif of N-Cap2 is designed to further promote helix initiation and also provide additional helix capping interactions.⁵⁴ Therefore, it is expected that the α-helical conformation of N-Cap2 is more stable than that of N-Cap1 (Figure 2B). However, given the similarity between these two peptides, it is unexpected that the T-jump induced conformation relaxation process of N-Cap2 occurs in a biexponential manner (Figure 3B). Theoretically, such kinetic behavior indicates that the folding process of N-Cap2 could proceed via one of the following mechanisms: (1) a single folding pathway involving an on-pathway intermediate; (2) a single folding pathway involving an off-pathway intermediate; (3) two connected folding pathways involving one folded state and two unfolded states; (4) two separate folding pathways involving two folded states and two unfolded states; (5) two connected folding pathways involving two folded states and one unfolded state. While distinguishing among these possibilities is difficult, the unique CD spectrum of N-Cap2 (Figure 2A) prompts us to suggest that the last mechanism is the most probable. In other words, N-Cap2 can fold into two different conformations, with one being an α-helix that is similar to that formed by N-Cap1. In support of this notion, as indicated (Figure 4), the rate constant of the fast component of the conformation relaxation kinetics of N-Cap2 is identical to that of N-Cap1 within experimental uncertainty. In addition, the fact that the slow relaxation component of N-Cap2 has a smaller rate constant than that of C-Cap (Figure 4) suggests that this kinetic phase is unlikely to arise from a conformation relaxation process involving unfolding of the capped region.

To better elucidate these mechanistic hypotheses, we next performed MD simulations to gain microscopic insight into the conformational relaxation kinetics of C-Cap, N-Cap1, and N- Cap2.

3.3. MD Simulations.

Comparison with experimental folding relaxation rates provides a stringent test of the ability of all-atom simulations to accurately predict folding kinetics. Using the Folding@home distributed computing platform, we obtained more than 200 μs of aggregate trajectory data for each of the three cross-linked peptides and analyzed the results by constructing MSMs of the folding kinetics, each comprising 500 metastable conformational states (see Experimental Section).

Predicted Relaxation Time Scales from MSMs Agree Well with Experiment.

An MSM is described by a matrix of transition rates T_ij(τ) corresponding to the probability of transitioning from state i to state j in some lag time τ. Since the accuracy of this coarse-grained description of kinetics depends on whether the lag time τ is long enough to approximate the dynamics as Markovian, it is typical to build a series of MSMs using a range of lag times to find the best choice. The implied time scales for each cross-linked peptide, plotted as a function of the MSM lag time, plateau after the lag time becomes sufficiently long, indicating an appropriate choice of lag time to be 20 ns for all three MSM models (Figure 6).

Figure 6.

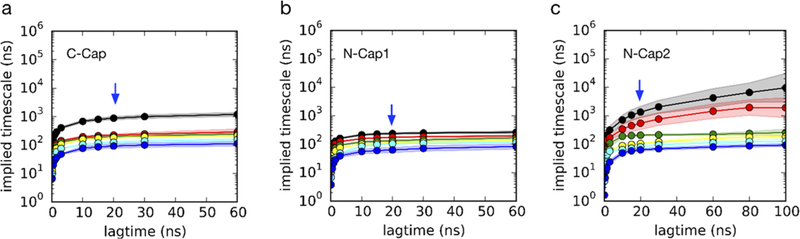
Implied time scale plots for (a) C-Cap, (b) N-Cap1, and (c) N-Cap2. Shown are implied relaxation times from MSMs built using different lag times. Six slow motions in total are shown in different colored lines. Uncertainty estimates (standard deviations shown as shaded regions) were calculated using a bootstrap procedure, whereby 20 different MSMs were constructed by sampling the input trajectories with replacement.

The slowest implied time scale of the MSM corresponds directly to the experimentally observed relaxation rate k_R = k_f + k_u. A comparison of experimentally measured relaxation times (i.e., τ_R = k_R^–1) and the slowest implied time scales predicted by the MSMs show remarkably good agreement (Figure 7). Absolute comparison of measured and predicted relaxation times at 300 K are, on average, within 0.6 orders of magnitude (i.e., rms deviations of log₁₀(τ_R). The absolute agreement improves to within 0.4 orders of magnitude if we compare the simulated relaxation times to experimental times measured at ~293 K. The larger uncertainty estimates for the slow kinetic phase of N-Cap2 are due to finite sampling error, as simulated transition times begin to approach the average trajectory length. Overall, the level of agreement between simulated and experimental folding times is comparable to the current state- of-the-art method³³ with the MSMs being able to correctly predict the rank order of folding times.

Figure 7.

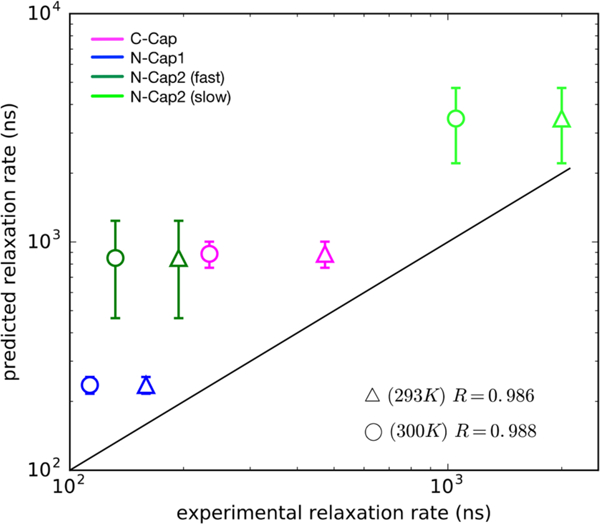
Comparison between the slowest relaxation time scales predicted from MSMs and experimentally measured relaxation time scales. Experimental measurements made at ~293 and 300 K are denoted by triangles and circles, respectively. Uncertainties in the predicted values (vertical bars) were calculated using a bootstrap procedure in which 20 different MSMs were constructed by sampling the input trajectory data with replacement. Coefficients of determination (R²) calculated for the two temperatures are shown on the lower right.

MSMs Reveal Non-native Interactions That Contribute to Misfolded States.

Remarkably, the MSMs were able to correctly predict the existence of slow and fast kinetic phases for N-Cap2 and single kinetic phases for C-Cap and N-Cap1. A hallmark of two-state folding is a gap between the slowest implied time scale and the next-slowest time scale, such that time-resolved experiments may only be able to detect single-exponential relaxation kinetics. Whereas C-Cap and N-Cap1 exhibit such a time scale gap, N-Cap2 does not (Figure 6), instead showing two slow relaxation time scales in the range detectable by the T-jump experiment.

To better understand the microscopic interactions that might contribute to the folding mechanism, we examined the structural features of long-lived kinetic intermediates contributing to population flux in the MSM. A powerful feature of the tICA approach is the ability to project high-dimensional simulation trajectory data to a low-dimensional subspace representing the slowest motions. Provided that the MSM is sufficiently fine-grained (in our case, 500 states), the most significant tICs should correspond to the slowest relaxation eigenmodes of the MSM, a fact that has been exploited in much previous work.^70–75 Projections onto the two largest tICA components show the broad contours of the folding landscape and reveal long-lived kinetic intermediates.

For the C-Cap peptide, partially folded metastable states are separated from the native state along largest tICA component (tIC₁), indicating that relaxation from these non-native states to the native folded structure correspond to the slowest folding relaxation (Figure 8). These non-native states are characterized by non-native backbone hydrogen-bonding interaction between Ala3/Ala4/Ala7 and Cys15/Ala14/Ala13 (upper left panel in Figure 8). The next-slowest motion, as seen from projections of the dynamics along tIC₂, is coupled to relaxations from another partially folded state stabilized by a π-cation interaction between the Arg8/Arg5 side chain and the aromatic ring on the capping group. Similar non-native interactions were observed in misfolded peptides simulated in previous work.⁶⁸ As evidenced by the smaller kinetic barriers along tIC₂, the MSM predicts a much faster relaxation time scale likely to be undiscernible by a T-jump experiment.

Figure 8.

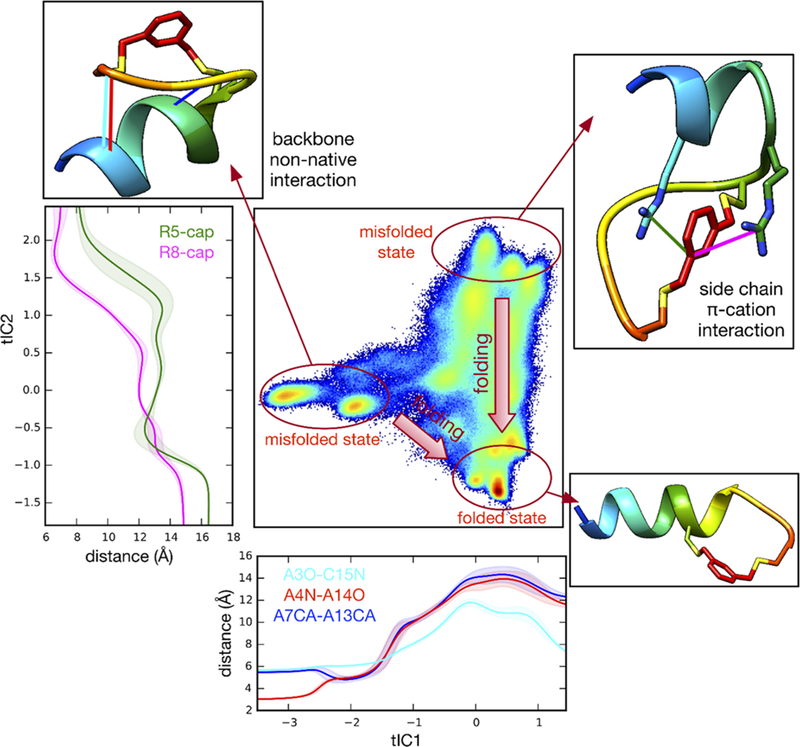
Trajectory data for C-Cap peptide projected to the 2D tICA landscape, along with average atomic distances Ala3(O)–Cys15(N) (cyan), Ala4(N)−Ala14(O) (red), and Ala7(Cα)−Ala13(Cα) (blue) as a function of tIC1 (bottom panel). Similarly plotted (left panel) are distances Arg8(Cζ)−capping group (magenta) and Arg5(Cζ)–capping group (green) as a function of tIC2. Selected snapshots (rainbow) are shown to represent featured conformation for typical microstates.

For the N-Cap1 peptide, the two slowest folding relaxations are similar in time scale and are both predicted to be faster than the slowest relaxation of the C-Cap peptide, consistent with the experimental results. Compared to the C-Cap peptide, the folding landscape is predicted to be more “downhill”, with the tICA projection showing multiple partially folded states contributing to the relaxation kinetics (Figure 9). The states most separated from the native helix structure on the tICA landscape include partially folded structures with either a folded N-terminus or a folded C-terminus. Each of these states has a low kinetic barrier for forming the native helical state, while remaining kinetically separated from each other. Both the fast relaxation kinetics and the shape of the tICA landscape are highly consistent with the hypothesis that the N-Cap1 cross-linker is able to lower the nucleation barrier to folding.

Figure 9.

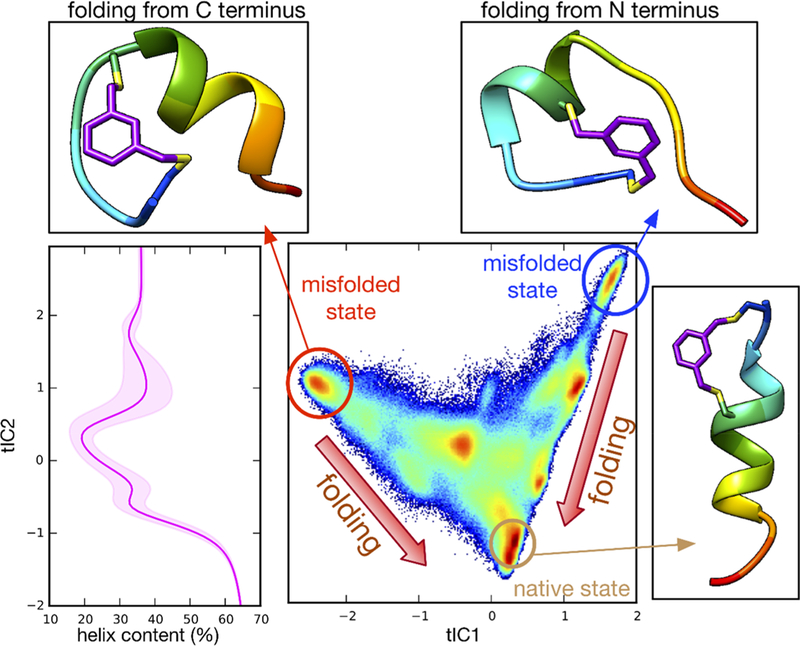
Trajectory data for N-Cap1 peptide projected to the 2D tICA landscape, along with average helix content computed using MDTraj algorithm along tIC1 and tIC2.

For the N-Cap2 peptide, the tICA landscape yields structural insight into the fast and slow kinetic relaxations observed in experiment. As hypothesized from the experimental kinetics and the unique CD spectrum, the slowest relaxation process (along tIC₁) appears to arise from the interconversion between two competing folded states: one state is the regularly folded α-helix, while the other is a misfolded state with a hairpin structure stabilized by the cross-linker (Figure 10). Unlike N-Cap1, which has polyalanine between the N-terminal cysteines, N-Cap2 contains the sequence TPAQ which is designed to serve as an effective N-terminal cap of the α-helix. The formation of this hairpin structure, which we do not observe for the other two peptides, may be encouraged by the presence of both threonine, an amino acid with β-sheet propensity, and proline, which can promote tight turns. The next-slowest relaxation (along tIC₂) is predicted to result from the transitions of unfolded structures to these two folded states. The time scale for this process is faster than, and more similar to, the folding relaxation seen for the C-Cap peptide, consistent with similar barrier-separated two-state folding to each competing folded state.

Figure 10.

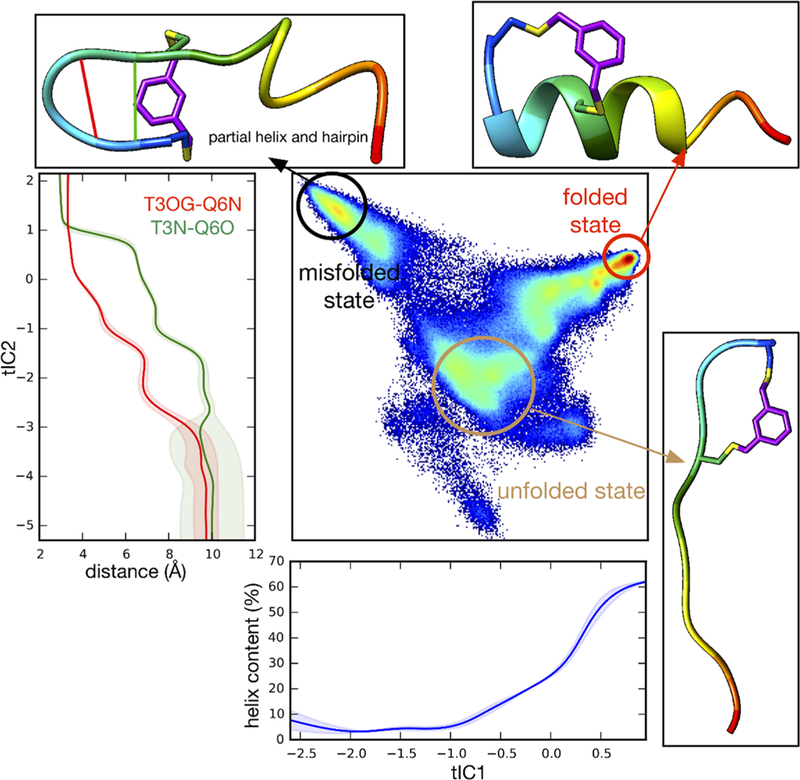
Trajectory data for N-Cap2 peptide projected to the 2D tICA landscape, along with average helix content (blue) as a function of tIC1 and average atomic distances Thr3(Oγ)−Gln6(N) (red) and Thr3(N)−Gln6(O) (green) as a function of tIC2.

4. CONCLUSION

While it has long been recognized that a-helices fold through a nucleation–propagation mechanism, it remains unclear whether the (productive) nucleation event occurs randomly or at a specific location within the peptide sequence. To provide insight into this question, herein we studied the folding kinetics and mechanism of three cross-linked, alanine-based peptides (i.e., C-Cap, N-Cap1, and N-Cap2) using T-jump IR spectroscopy and MD simulations. Our T-jump IR measurements revealed that N-Cap1 folds and unfolds faster than C- Cap. Since these two peptides differ only in their cross-linker position and both are more stable than their uncross-linked counterpart, these results demonstrate that a bis-benzylic cross-linker can promote α-helix formation by either increasing the folding flux from the N- to C-terminus or deceasing the unfolding flux from the C- to N-terminus. Our MD simulations not only validated this picture but also provided an atomistic description of the folding landscape of these peptides. Taken together, these findings support a folding–unfolding mechanism of linear peptides wherein the folding process begins by forming a productive helical nucleus at the N-terminus, whereas the reverse process or unwinding of the helical structure begins from the C-terminal end of the α-helix.

Interestingly, the T-jump induced relaxation kinetics of N- Cap2, whose sequence is only different from that of N-Cap1 in the N-terminal region, are more complex than those of N-Capl and C-Cap. Our MSM analysis indicated that this is because this peptide can populate two folded conformations, with one being a regular α-helix and the other being a hairpin structure. It is somewhat surprising that N-Cap2 may not fold uniquely to the intended α-helical state, as expected from the rational design of this peptide. Therefore, our results show the nontrivial challenge of designing cross-linked or stapled α-helices, and the need for all-atom simulations to quantitatively assess proposed designs. Another lesson underscored by this work is the synergistic nature of combing simulation methods with experiments to achieve an atomic-level understanding of folding. MSM-based approaches are a powerful tool for modeling long-time scale folding behavior and providing a mechanistically interpretable picture of these processes. The work presented here is further evidence of the level of quantitative predictive power such models can achieve: not only do the MSM models well predict absolute folding relaxation times, but they also correctly predict the rank order of folding times of the three different designed peptides, as well as the existence of slow and fast kinetic phases for N-Cap2. This quantitative accuracy, combined with the ability to rationalize the mechanisms, suggests a much larger role for all-atom simulation and MSM methods for peptide design, and the need for developing more robust and efficient MSM-based algorithms for this purpose.