Photovoltaic Pixels for Neural Stimulation: Circuit Models and Performance

Abstract

Photovoltaic conversion of pulsed light into pulsed electric current enables optically-activated neural stimulation with miniature wireless implants. In photovoltaic retinal prostheses, patterns of near-infrared light projected from video goggles onto subretinal arrays of photovoltaic pixels are converted into patterns of current to stimulate the inner retinal neurons. We describe a model of these devices and evaluate the performance of photovoltaic circuits, including the electrode-electrolyte interface. Characteristics of the electrodes measured in saline with various voltages, pulse durations, and polarities were modeled as voltage-dependent capacitances and Faradaic resistances. The resulting mathematical model of the circuit yielded dynamics of the electric current generated by the photovoltaic pixels illuminated by pulsed light. Voltages measured in saline with a pipette electrode above the pixel closely matched results of the model. Using the circuit model, our pixel design was optimized for maximum charge injection under various lighting conditions and for different stimulation thresholds. To speed discharge of the electrodes between the pulses of light, a shunt resistor was introduced and optimized for high frequency stimulation.

I. Introduction

ELECTRICAL stimulation can be applied to neurons in the central or peripheral nervous systems to treat neurological diseases or alleviate their symptoms, replace damaged sensory inputs, and control limbs and other organs. Applications of electrical neural stimulation are rapidly expanding, and they currently include the cochlear prosthesis [1], [2], deep brain stimulation [3], bladder control [4], disabling rheumatoid arthritis [5], stimulation of the lacrimal gland for treatment of dry eye syndrome [6] and treatment of obstructive sleep apnea [7], among many others.

Retinal degenerative diseases, such as age-related macular degeneration (AMD) and retinitis pigmentosa, lead to blindness due to the loss of photoreceptors [8]–[10]. However, a significant number of the inner retinal neurons survive in such diseases [11]–[13], raising the possibility of sight restoration with electrical stimulation of the remaining inner retinal neurons.

Two major types of retinal prostheses are used for this purpose—epiretinal and subretinal. Epiretinal implants [14]–[16] placed on the inner limiting membrane, aim at direct stimulation of the retinal ganglion cells (RGCs). Subretinal implants [17]–[19] are placed between the retina and pigmented epithelium to stimulate the first layer of neurons after the photoreceptors—the inner nuclear layer (primarily bipolar cells). A suprachoroidal approach, where the stimulating implant is placed further away from the retina—between the choroid and sclera is also being explored [20]. Both subretinal [21] and epiretinal [22] prosthetic systems restored some degree of sight in patients blinded by retinitis pigmentosa, with a visual acuity in the best cases of 20/550 and 20/1260, respectively. However, much better visual acuity (> 20/200) is required to make retinal prostheses useful for patients with AMD, since most of these patients have some degree of sight due to remaining peripheral vision.

Direct targeting of RGCs in epiretinal stimulation is best achieved with cathodic pulses of sub-ms duration [23]–[25]. Stimulation of the inner retinal neurons with a subretinal prosthesis, however, has the lowest thresholds and is most selective with much longer anodic pulses. For example, at 4 ms the stimulation threshold with subretinal electrodes is 1.3 μA, with selectivity exceeding a factor of 3 [23].

Wired transmission of power and data for electrical neural stimulation in general, and for retinal implants in particular, greatly complicates surgical procedures, and introduces multiple risk factors for post-surgical complications. Even when information and power are delivered to the ocular implant via radio telemetry, such as in ARGUS II, a very bulky receiving antenna and decoding electronics are still required; they are located under the conjunctiva and connected to the epiretinal arrays via trans-scleral cable [26]. Alternatively, subretinal implants by Retina Implant AG [18] are powered by an extra-ocular power supply via trans-scleral cables. Similar techniques are implemented in several other retinal prostheses [15], [16], [19], [29], [30]. Intraocular placement of the receiving RF antenna and signal decoder obviates the need for trans-scleral cables, but still involves rather bulky electronics and wiring [27], [28].

In our photovoltaic retinal prosthetic system the data and power are transferred to the implant by pulsed patterned near-infrared (NIR, 880 ≤ λ ≤ 915 nm) illumination, which is invisible to remaining photoreceptors in a diseased retina. Each pixel in the subretinal array photovoltaically converts pulsed light into pulsed electric current flowing through the retina to stimulate the nearby neurons. This design does not require any additional implantable electronics or wiring and is easily scalable to a large number of pixels. Retinal stimulation with photovoltaic arrays has been successfully demonstrated in vitro [31], where pulsed NIR illumination of subretinally located arrays elicited bursts of action potentials in rat retinas. Similarly, photovoltaic subretinal implants elicited response from the visual cortex in rats in vivo [33]. The photovoltaic approach can also be used for wireless neural stimulation in other translucent tissues, which comprise most of the human body, especially when powered by near-infrared light.

In this paper we describe the operation of such photovoltaic pixels in electrolyte. In particular, we developed a computational model of this system to guide its optimization for retinal stimulation and experimentally verified its performance. We demonstrate why high frequency stimulation leads to a reduction in injected charge and define the optimal shunt resistor values to maximize the injected charge for various pixel configurations.

II. Materials and Methods

A. Photovoltaic Pixel Arrays

Silicon photodiode arrays with pixel sizes of 70 or 140 μm (Fig. 1) were fabricated by a silicon-integrated-circuit/MEMS process [34]. Arrays were ~ 1 mm in diameter to allow for implantation in rat eyes and 30 μm thick – sufficient for significant absorption of NIR light (880–915nm) in silicon. Each pixel consisted of 1, 2 or 3 photodiodes, separated by 5 μm trenches filled with polysilicon. Photodiodes are connected in series between an active central electrode 18 or 36 μm in diameter and a circumferential return electrode 5 or 8 μm in width, respectively [Fig. 1(b) and (d)]. Central and return electrodes were coated with a 300 nm thick sputtered iridium oxide film (SIROF) to maximize the charge injection. Pixels were separated from the neighbors by 5 μm open trenches, which allowed nutrients to flow to the retina [31]. The return electrodes of the pixels were connected together by narrow platinum tracks on top of the oxide-coated silicon bridges (Fig. 2). More details about the device fabrication and design can be found in [34].

Fig. 1.

Photovoltaic pixel arrays with 140 μm pixels in (a) and (b) and 70 μm pixels in (c) and (d). 1 – central active electrode, 2 – return electrode, 3 – conductive bridges, 4 – filled trenches, 5 – open trenches. (e) Electric circuit of a 3-diode pixel.

Fig. 2.

Images of the 2- and 1-diode pixels. (a) 2-diode, 140 μm. (b) 1-diode, 140 μm. (c) 2-diode, 70 μm. (d) 1-diode, 70 μm.

In this paper we refer to the 70 μm pixels as small pixels (s) and to the 140 μm pixels as medium pixels (m). In the rest of the paper, we use abbreviations to denote different pixel types; e.g., s3 means a small pixel (70 μm) with 3 diodes.

B. Light-to-Current Conversion

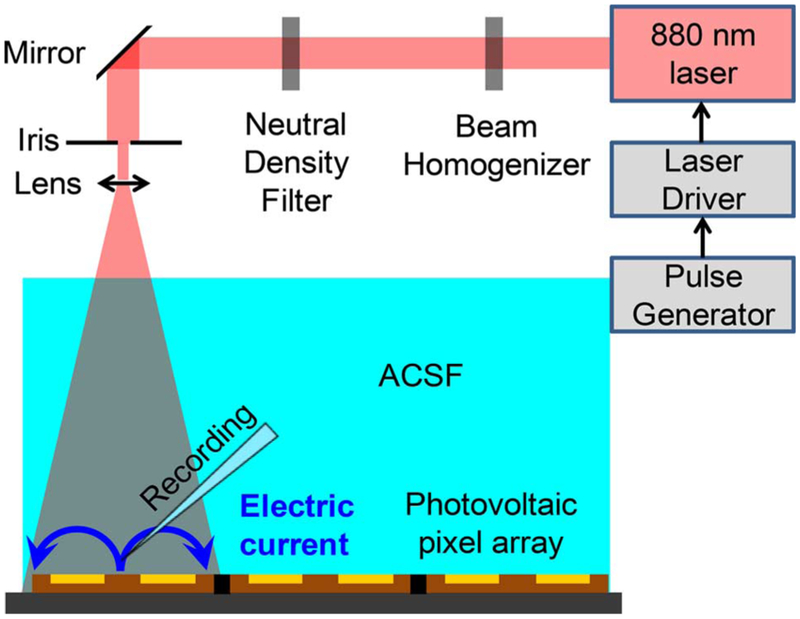
To characterize the electric currents generated by the photovoltaic pixels we used the setup shown in Fig. 3. A rectangular pulse generator modulates the output of a laser driver used to control a fiber-coupled 880 nm NIR diode laser bar (Jenoptik, Jena, Germany). The light beam passes through a microlens array (ED1-C20, Thorlabs Inc, Newton, NJ), which acts as a beam homogenizer, and a neutral density filter (ND-1 or ND-2, Thorlabs Inc, Newton, NJ). It is then coupled into the optical path of an upright microscope (Olympus BX51WI). An iris located in the conjugate image plane of the sample controls the beam diameter. A single pixel in the center of the array was illuminated in these measurements. Photovoltaic arrays were placed in a Petri dish filled with artificial cerebrospinal fluid (ACSF, containing in mM: NaCl 126, glucose 10, KCl 2.5, NaH₂PO₄ * H₂O 1.25, MgSO₄ * 7H₂O 1, CaCl₂ * 2H₂O 2, NaHCO₃ 26). The electric potential was measured with a glass pipette (~ 1 μm tip diameter) filled with ACSF solution and placed 5 μm or 25 μm above the active electrode of the illuminated pixel. An Ag/AgCl wire was placed inside the pipette, and a large Ag/AgCl return electrode was located in the Petri dish far from the photovoltaic array.

Fig. 3.

Diagram of the experimental setup for measurement of the electric current in electrolyte above the illuminated pixel.

Voltages measured with the pipette electrode above the photovoltaic pixels were converted into currents using a conversion factor defined in a similar set of measurements, but with wired electrodes. Array of bipolar and monopolar electrodes of 10, 20, 40 and 80 μm diameter were deposited on a glass substrate (see Fig. 4) and connected to the wiring pads at the edge of the array using lithographically defined platinum tracks. The exposed parts of the array (central discs and circumferential rings) were coated with SIROF. The platinum tracks were isolated by SiN_x. All circumferential electrodes were connected together and served as a return for the bipolar electrodes. Square pulses of current were applied to the 20 and 40 μm bipolar electrodes. A recording pipette with ~ 1 μm tip diameter was positioned 5 μm or 25 μm above the center of the active electrode. Voltage measurements were performed on 3 electrodes of each size, and the current-to-voltage conversion factor was found to be 0.09 ± 0.02 mA/V for 20 μm and 0.11 ± 0.02 mA/V for 40 μm electrodes at 5 μm height, 0.30 ± 0.05 mA/V for 20 μm and 0.33 ± 0.05 mA/V for 40 μm electrodes at 25 μm height.

Fig. 4.

Bipolar and monopolar wired electrodes on a glass substrate. The disc electrodes are 10, 20, 40 and 80 ìm in diameter.

III. Model of the Photovoltaic Pixels

A simplified diagram of a photovoltaic pixel with 3 diodes is shown in Fig. 5. The role and value of the shunt resistor are discussed in the “Shunt resistor” section below. Unless otherwise specified, its value is considered to be infinite. Since electric charge is carried in metals by electrons and in electrolytes by ions, the charge transfer between different types of charge carriers occurs at the electrode-electrolyte interface. The Debye double layer forming in the electrolyte near the electrode has a capacitance of about 1 μF/cm² for a polished metal surface [36]. Porous electrodes have a much larger surface area, and therefore can provide much larger capacitance. In addition, electrochemical reactions, which may or may not be reversible, can take place at the electrode-electrolyte interface [36]. A SIROF electrode exhibits both of these properties: it is very porous and allows for reversible oxidation of iridium, as well as other voltage-dependent Faradaic reactions in the physiological medium [36]. A microscopic model of such an interface would require consideration of the ion diffusion and the dynamics of each chemical reaction at the interface. We used a macroscopic model that describes the electrode-electrolyte interface as the combination of a capacitor (C) with a parallelFaradaic resistor (R_F) and a series access resistor (R_a), as illustrated in Fig. 5 [37]. Quantities with subscript 1 correspond to the active electrode; with subscript 2, to the return electrode. To account for the voltage-dependent characteristics of the Faradaic reactions, C and R_F are voltage dependent. Electrodes are connected by a voltage-independent resistor R_e representing conductance through the bulk of the medium.

Fig. 5.

Electrical circuit model of a photovoltaic pixel in electrolyte. R_a is the access resistance, R_F is the Faradaic resistance, C is the capacitance of the electrode-electrolyte interface, R_e is the bulk resistance of the electrolyte medium, R_s is the shunt resistance.

A. Electrode-Electrolyte Interface

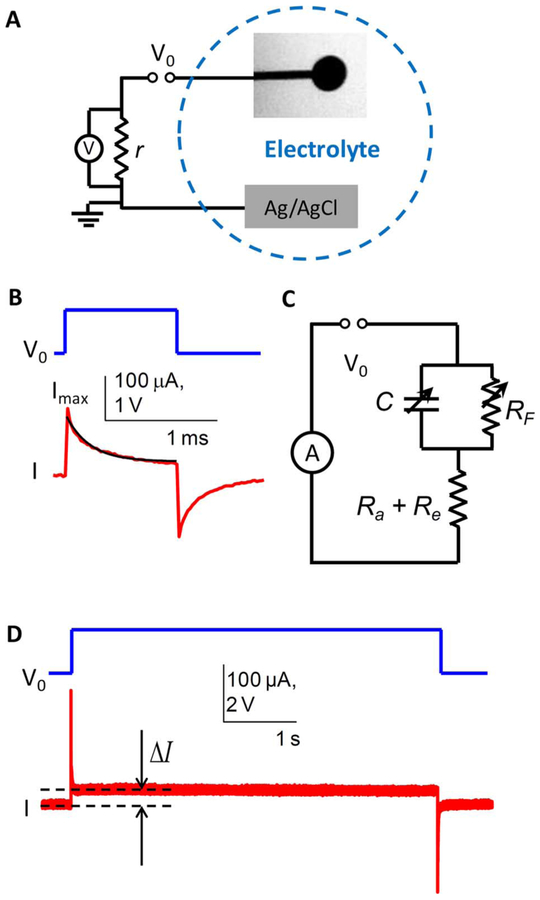
To find numerical values of the circuit elements at the electrode-electrolyte interface, we used SIROF-coated electrodes of the same sizes as in the photovoltaic pixels, and accessible by direct wiring (Fig. 4). A large (> 1 mm³) Ag/AgCl electrode placed in the medium was used as a return, and its resistance was assumed negligible due to its size. Rectangular voltage pulses from the pulse V₀ generator were first applied between the monopolar disc electrodes of 20, 40 and 80 μm diameter and a large Ag/AgCl return electrode in the ACSF solution [Fig. 6(a)]. Series resistors of 1 kΩ − 1 MΩ were used to record the current waveforms.

Fig. 6.

(a), (c) Circuit diagrams and (b), (d) current/voltage waveforms at the SIROF electrode-electrolyte interface with wired electrodes.

The equivalent circuit for these measurements is shown in Fig. 6(c). Here the electrolyte and access resistances are combined into a single variable resistance R_a + R_e, calculated by dividing the applied voltage by the peak current I_max [Fig. 6(b)]

$$R_a+R_e=\frac{V_0}{I_{\text{max}}}.$$

To assess capacitance of the electrode-electrolyte interface the current waveform was fitted with an exponential: I = I₀·e^−t/τ + I₁ [black curve in Fig. 6(b)], and the time constant τ was divided by the previously found resistance R_e + R_a to obtain C

$$C=\frac{\tau }{R_a+R_e}.$$

The voltage across this capacitor

$$V=V_0-I\left(R_a+R_e\right)$$

varies over time, and with pulse durations much longer than τ it reaches a steady state value. A series resistor r = 1 kΩ was used to measure the current waveforms in these experiments. To accurately measure the steady state current ΔI and determine R_F, pulses of 5–1000 seconds were applied.

$$R_F=\frac{V_0}{\Delta I}-\left(R_a+R_e\right)\approx \frac{V_0}{\Delta I}$$

Fig. 6(d) shows a current waveform for a 1.6 V pulse, which reaches steady state within a fraction of a second. However, at lower voltages reaching steady state required much longer times, in the hundreds of seconds.

Capacitance was assessed as a function of voltage for cathodic and anodic pulses of 1 ms and 10 ms duration using d = 20, 40 and 80 μm electrodes. The resulting capacitance per unit area is plotted in Fig. 7(a).

$$\frac{C}{S}=\frac{C}{\frac{\pi d^2}{4}}$$

where S is the electrode area.

Fig. 7.

(a) Voltage dependence of the capacitance, measured with 1 ms and 10 ms pulses on 3 different electrodes. Markers with dark fill correspond to 80 μm diameter electrodes, with light fill – to 40 μm, with white fill – to 20 μm electrodes. (b) Faradaic resistance of the 20 μm electrode as a function of voltage. (c) Electrolyte plus access resistance R_e + R_a for 80 μm electrode as a function of the inverse concentration of the electrolyte.

The voltage across the capacitor in these plots was estimated as the average value during the pulse. Capacitance increased with increasing voltage magnitude, although differently for positive and negative polarities. These findings reflect the increasing rate and number of chemical reactions at higher voltages and their asymmetry with respect to pulse polarity. Capacitance also increased with increasing pulse duration due to diffusion of the ions deeper into the SIROF pores, thereby accessing a larger surface area. More details about the processes taking place at the SIROF-electrolyte interface can be found in [36].

For anodic pulses, capacitance curves could be fitted well with exponential curves, however, for cathodic pulses the more complex shapes required fit with the cubic polynomials. The best fit functions defined by the least-squares method were calculated as following:

$$\begin{gathered} 10\text{ms}\text{anodic:}C/S=1.20\cdot e^{1.61\text{V}} \\ 1\text{ms}\text{anodic:}C/S=0.33\cdot e^{1.52\text{V}} \\ 10\text{ms}\text{cathodic:}C/S=-7.0V^3-18.5V^2-16.8V+1.20 \\ 1\text{ms}\text{cathodic:}C/S=-1.96V^3-4.03V^2-3.39V+0.33, \end{gathered}$$

where C/S is measured in mF/cm² and V in volts.

The Faradaic resistance [Fig. 7(b), shown for a 20 μm electrode] rapidly decreased with increasing voltage magnitude from a few GΩs to 1 MΩ for anodic pulses. For cathodic pulses this decrease was less rapid, but also significant. This decrease in Faradaic resistance, which was different for the two polarities, is due to an increasing rate of electrochemical reactions at higher voltages. Inside the water window of iridium oxide – between −0.6 V and 0.8 V relative to Ag/AgCl [36] – resistance values exceeded 4 GΩ, and the current through the Faradaic resistor becomes negligible. The data fitted with exponentials using the least-square method yielded the following functions:

$$\begin{gathered} \text{Cathodic:}{R}_{\text{F}}=3.0\cdot {10}^4\cdot e^{2.09V} \\ \text{Anodic:}{R}_{\text{F}}=1.1\cdot {10}^8\cdot e^{-14.1V}, \end{gathered}$$

where R_F is measured in MΩ and V in volts.

With long pulses at voltages outside the water window, the rate of chemical reactions was sometimes sufficiently high to produce visible bubbles or irreversibly change the color of the SIROF electrodes. In these cases the electrodes were replaced with new ones.

The series resistance R_a + R_e did not vary with voltage. Since R_e is proportional to the resistivity of the medium, its value could be measured by varying the solution concentration by adding distilled water, as illustrated in Fig. 7(c). Points in the figure represent the average of 12 measurements, while the error bars show standard deviation. Assuming that the resistivity is inversely proportional to concentration, we obtain R_e = K · 1/c + R_a, where c is the relative concentration of the medium (c = 1 for non-diluted ACSF). The intersection of the linear fit with the vertical axis corresponds to the access resistance (1.4 kΩ for 80 μm electrode diameter), which is one forth the total resistance at normal concentration of the medium (c = 1). Since the retinal resistivity is ~ 14 times that of ACSF, the relative contribution of R_a to the total resistance in the retina will be even smaller.

Properties of SIROF electrodes defined in these measurements correspond well to published data. Capacitance was found to increase with increasing pulse duration [38]. With 1 ms cathodic pulses of −2 V on 300 nm thick SIROF electrodes with 50 μm diameter biased at +0.6 V, capacitance was estimated to be 3.5 mF/cm² [38], which is slightly higher than the data shown in Fig. 7(a) for −1.5 V. Faradaic resistance measured in [38] on SIROF electrodes with 650 nm thickness and 400 μm diameter was 0.13 MΩ · cm² for 0.6 V and 0.07 MΩ · cm² for 0.7 V. Our data from Fig. 7(b) yields 0.08 MΩ · cm² and 0.02 MΩ · cm² for 0.6 V and 0.7 V, respectively.

B. Parameters of the Pixel Model Circuit

The voltage-dependent values of C and R_F, as well as voltage-independent R_e and R_a defined above, have been applied to compute the dynamics of the pixel circuit shown in Fig. 5. The resistance R_e1 of a disk electrode in a conductive medium scales with its radius a as following [39]:

$$R_{e1}=\frac{\rho }{4a}$$

where ρ is the resistivity of the solution. The hexagonal return electrodes connected to each other in the array have a surface area 120 times as large as that of a single active electrode for medium pixels, and 580 times as large for the small pixels. Therefore the contribution of their resistance R_e2 was assumed negligible compared to R_e1 in estimating the R_e for the complete circuit shown in Fig. 5. Similarly, the very large capacitance C₂ of the common return electrode, connected in series with the much smaller capacitance of the active electrode has a negligible effect on circuit dynamics. The very low voltage across this large capacitor results in a very high Faradaic resistance R_F2, which can therefore be disregarded.

Since Faradaic reactions take place in a thin interface layer in front of the electrode, its resistance was assumed to be inversely proportional to the surface area of the electrode, while capacitance was assumed to be proportional to the surface area. Since diffusion length scales as the square root of time, C was assumed to scale with the square root of pulse duration. Such dependence is supported by the published experimental observations: the data shown in Fig. 10 in [38] fits the power law C = τ^p, with p = 0.48.

Fig. 10.

Charge injected by 70 μm pixels in electrolyte of 1000 Ω · cm resistivity during 4 ms pulses as a function of light intensity. Lines depict the model calculations, and dots represent experimental data for s2 and s3 pixels. On the left is shown the optimum number of diodes per pixel corresponding to the minimum light intensity required to reach the target charge delivery.

$$R_F~\frac{1}{a^2},C~a^2\sqrt{\tau }$$

The current-voltage (I-V) curves of the photodiodes were measured as described in [30], and fitted with the curve

$$I_{PD}=-\alpha PS+I_{0}S\left(e^{V/n{V}_0}-1\right)$$ (1)

where P is the light intensity, S – photodiode surface area, α = 0.36 A/W – light-to-current conversion factor, I₀ = 6.1 · 10⁻⁵ μA/mm², n is the diode ideality factor, and V₀ = kT/e = 25.4mV at room temperature. The ideality factor n indicates the relative importance of generation-recombination in the depletion region (n = 2) to that in the quasi-neutral regions of the diode (n = 1). Generation-recombination at surfaces and interfaces, as well as contact and other series resistance can also affect the diode behavior. In the dark, n was measured to be 1.4 in s3 pixels and 1.1 in s1 pixels. However, photogenerated carriers can change the dominant recombination mechanism by saturating recombination centers, especially in the depletion region, and decreasing the relative importance of surface recombination. Therefore, n can decrease with increasing illumination and current flowing in the diode. For modeling of the photovoltaic pixels the ideality factor n was taken to be 1.2 for s3 pixels and 1 for s2 and s1 pixels.

Other model parameters are listed in Table I. It is important to emphasize that the dynamics of the electrode-electrolyte interface are very complex, and their microscopic description should take into consideration various voltage-dependent electrochemical reactions, as well as dynamics of diffusion into porous materials and the surrounding medium. Therefore the simplified circuit in our macroscopic approach with a few voltage-dependent elements is just a first-order approximation, which allows exploring the dynamics under various illumination conditions.

TABLE I.

Geometrical Parameters of the Photovoltaic Pixels

# of diodes in pixel	Total exposed photosensitive area per pixel (μm2)
	Small pixels	Medium pixels
1	2770	11900
2	1610	8510
3	1220	7650

IV. Dynamics of the Photovoltaic Circuits in Electrolyte

A. I-V Curves of the Circuit Elements

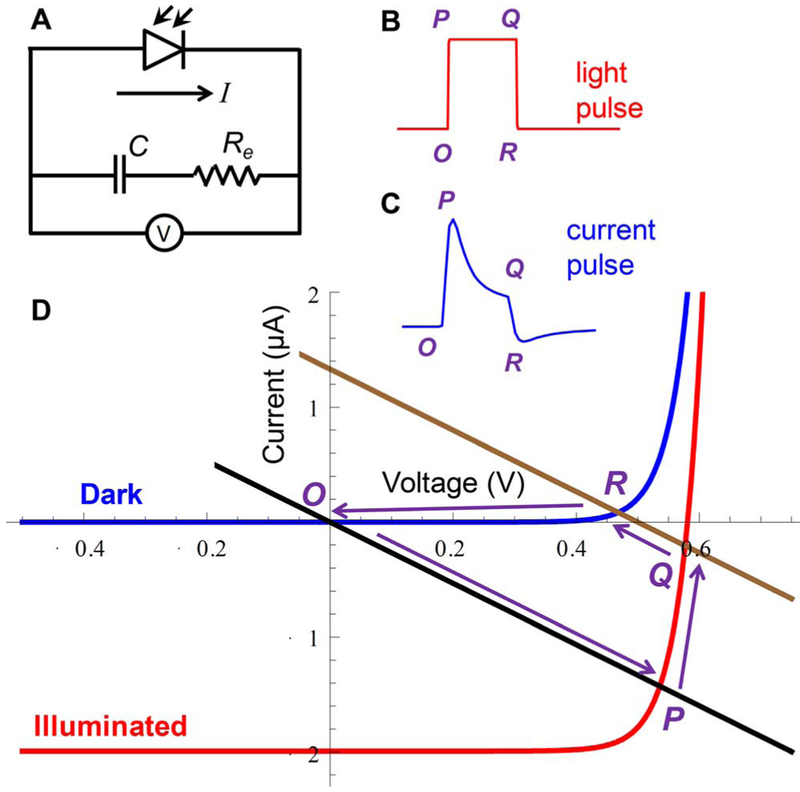
To better understand the role of each circuit element (Fig. 5) in shaping the current waveforms, we begin with the analysis of a simpler circuit, which consists of a single photodiode, resistor and capacitor [Fig. 8(a)]. Despite its simplicity, it captures many of the important properties of the more complete circuit [40]. Fig. 8(d) shows I-V curves of the dark and illuminated photodiodes (blue and red lines) and I-V curves for a resistor plus capacitor (black and brown straight lines). The path OPQRO (charging along the red curve and discharging along the blue one) yields the current in the circuit at any moment of time.

Fig. 8.

(a) A simplified circuit, consisting of a capacitor, a resistor and a photodiode, (b) illuminated by a rectangular pulse of light, produces (c) a current waveform. (d) I-V curves of the dark (blue) and illuminated (red) photodiode, and the resistor plus capacitor (discharged in black and charged in brown).

When the light is off, the circuit is defined by the intersection of the blue and black curves at point O, and after the light is turned on, the system very quickly switches to point P, corresponding to the current peak in Fig. 8(c). The current flowing in the circuit charges the capacitor, shifting the black line to the right. The brown line corresponds to the capacitor charged to 0.5 V (intersection point with the voltage axis). During the pulse of light the system moves from point P to point Q, and the current decreases, as shown in Fig. 8(c). When the light turns off, the system switches from point Q to R, with currents of smaller magnitude and opposite polarity flowing through the resistor, after which the capacitor slowly discharges back to point O. The large resistance of a photodiode at low voltage results in a long discharge time. Since no net charge can flow through the capacitor, the charge delivered during the positive phase (OPQ part of the loop) is equal and opposite in polarity to the charge flowing during the negative phase (RO part of the loop), so that the pulses are charge-balanced.

The regime in which the resistor + capacitor I-V curves (OP and QR) intersect the steep section of the illuminated photodiode I-V curve (as shown in Fig. 8(d) is called the voltage-limited regime. Here the photodiode acts similarly to a source of constant voltage of about 0.6 V. In this regime the pulse of current has a peak at the light onset and then decreases exponentially charging the capacitor [Fig. 8(c)]. Another example of the voltage-limited regime is shown in Fig. 9(c)–(d) for an s1 pixel. The voltage-limited regime is typically observed at high irradiances or with long pulse durations.

Fig. 9.

(a), (c) Calculated and (b), (d) measured current waveforms generated by small pixels in ACSF medium illuminated with 1 ms pulses of (a), (b) 0.1 mW/mm² and (c), (d) 2.7 mW/mm² irradiance. Scale bars are the same for the model and for experimental results.

The current-limited regime occurs when the resistor + capacitor I-V curves intersect only the horizontal section of the illuminated photodiode I-V curve. Here the photodiode acts as a source of constant current and the capacitor voltage increases linearly with time. The pulse of current in this regime has a rectangular shape [Fig. 9(a)–(b) and (c)–(d) for s2 and s3 pixels]. The current-limited regime is observed at low irradiances and with short pulse durations.

B. Waveforms Generated by Photodiode Pixels

With the voltage-dependent values of the resistors and capacitors described above, we can evaluate the dynamics of the more complex circuit shown in Fig. 5. Let V be the voltage across each photodiode, N the number of photodiodes in a pixel, I the current in the solution, V_c1 and V_c2 the voltages across capacitors C₁ and C₂, and q₁ and q₂ their respective charges. We can then write the following system of Kirchhoffs equations in addition to (1):

$$\begin{gathered} \{\begin{array}{l}{I}_{PD}=-\alpha PS+I_{0}S\left(e^{V/n{V}_0}-1\right)\hfill \\ I=-I_{PD}\hfill \\ NV=V_{C1}+V_{C2}+I\cdot \left(R_e+R_{a1}+R_{a2}\right)\hfill \end{array} \\ \{\begin{array}{l}{I}_{C1}=I-\frac{V_{C1}}{R_F\left(V_{C1}\right)}\hfill \\ V_{C1}=\frac{q_1}{C\left(V_{C1}\right)}\hfill \\ {\dot{q}}_1=I_{C1}\hfill \end{array} \\ \{\begin{array}{l}{I}_{C_2}=I-\frac{V_{C_2}}{R_F\left(V_{C_2}\right)}\hfill \\ V_{C_2}=\frac{q_2}{C\left(V_{C_2}\right)}\hfill \\ {\dot{q}}_2=I_{C2}\hfill \end{array}. \end{gathered}$$ (2)

This system of first-order differential equations was solved numerically using Wolfram Mathematica 7.0. We simulate the application of pulses of NIR (880 nm) light to a single pixel immersed in conductive medium with resistivity ρ = 70 Ω · cm(ACSF) or ρ = 1000 Ω · cm (representing the retina). Since water is practically transparent at this wavelength, light absorption by the few millimeters of the medium is considered negligible in the model.

Fig. 9 A depicts the calculated current for s1, s2 and s3 pixels irradiated by 1 ms-long pulses at 0.1 mW/mm² irradiance. The current follows the rectangular shape of the pulse of light, and its amplitude decreases with an increase in the number of diodes per pixel. This is due to the fact that diode area decreases with the introduction of additional diodes to the pixel, as can be seen in Figs. 1 and 2. Capacitors of all three pixel types are charged to a voltage lower than 0.1 V, and therefore they operate in the current-limited regime.

Results of the model correspond reasonably well to the waveforms recorded above the illuminated pixel, shown in Fig. 9(b). Since photovoltaic pixels have no direct connection to any external wires, the current was estimated from the measurements of the voltage in the medium above the pixel, using the calibration measurements performed with wired electrodes (shown in Fig. 4) in the same medium, as described above.

Fig. 9(c) shows calculated current waveforms of the photodiodes illuminated with 1 ms pulses at 2.7 mW/mm². Under such illumination the 3- and 2-diode pixels still produce rectangular pulses in the current-limited regime, while the 1-diode pixel reaches the voltage limit. The higher current of a 1-diode pixel charges the capacitor faster, and when it approaches the open-circuit voltage of a single photodiode, the current starts decreasing. This result corresponds reasonably well to the waveforms recorded above the pixel illuminated at such settings, as shown in Fig. 9(d).

The tilted slopes of the rising and falling edges of the experimental waveforms, unlike the vertical edges in the model, result from a low-pass filter in the measurement circuit. The recording pipette has a small diameter and therefore a high impedance, which, in combination with the parasitic capacitance of the system, yields a high RC time constant and low cut-off frequency f ~ 1/(RC) of the low-pass filter. With a larger pipette the pulse edges appear sharper, as expected (not shown).

C. Injected Charge

The strength-duration relationship of neural stimulation [23], [41] is often well fitted by the Weiss equation [42]

$$I_{stim}=I_{rh}\left(1+\frac{{\tau }_{ch}}{\tau }\right)$$

where I_stim is the stimulation threshold, τ is pulse duration, I_rh is the rheobase current, and τ_ch is the chronaxy. For pulses much shorter than the chronaxy (around 10 ms for the retinal network stimulation), injected charge is constant. The total charge injected by the photodiode pixels during the pulse is the integral of the current over the pulse duration

$$Q={\int }_0^{\tau }I\cdot dt.$$

The injected charge as a function of light intensity calculated for 70 μm pixels with 4 ms pulses and medium resistivity corresponding to retinal tissue (1000 Ω · cm, [43]) is depicted in Fig. 10, along with experimental measurements on s2 and s3 pixels. At low light intensities the s1, s2 and s3 devices operate in the current-limited regime, and the corresponding slopes of the curves are proportional to the area of a single diode in the pixel. At high intensities, the devices operate in the voltage-limited regime, and pixels with a larger number of diodes provide higher maximum charge due to their increased output voltage. Devices with fewer photodiodes saturate at lower light intensities since they generate higher currents at low intensities, and their electrode capacitors charge to the maximum voltage earlier. The maximum charge (saturation level in Fig. 10) is higher for pixels with a larger number of photodiodes because of (a) their higher output voltage and (b) their higher electrochemical capacitance at higher voltages, as shown in Fig. 7(a).

Experimental results with s3 pixels follow the theoretical curve very closely, but the s2 pixels, while properly matching the early linear regime and the very bright conditions, deviate from the model in the middle of the range.

If the retinal stimulation threshold was below 1 nC, s1 would require the least intense illumination. For stimulation in the range of 1 nC < Q < 4 nC, s2 pixels are optimal, and for a stimulation charge exceeding 4 nC the s3 pixels are required.

Stimulation threshold of the RCS retina with 70 μm 3-diode cathodic devices and was 5 mW/mm² for 4 ms pulses [31]. According to Fig. 10, this corresponds to injected charge of about 3 nC, for which the 3-diode devices are the optimal, providing a broad range of stimulation. With anodic s3 devices, the stimulation thresholds decreased to about 0.8 nC. The 2-diode devices in this case may provide robust stimulation significantly exceeding the threshold level (0.33 mW/mm² with 10 ms pulses [32]).

With very high Faradaic resistors at low voltages across the electrode-electrolyte interface, the resulting pulses of charge are perfectly balanced: positive charge accumulated in the electrode capacitors during the pulse of light is completely discharged during the dark phase, provided there is sufficient time between the pulses. However, at high voltages, when Faradaic resistance decreases to values comparable to the resistance of the electrolyte, the Faradaic current flowing in parallel with the capacitors is not compensated. Such a misbalance may result in irreversible electrochemical reactions damaging the electrode and/or the tissue. Accumulation of charge and associated high voltage across the electrodes can be avoided by adding a shunt resistor, as described in section E below.

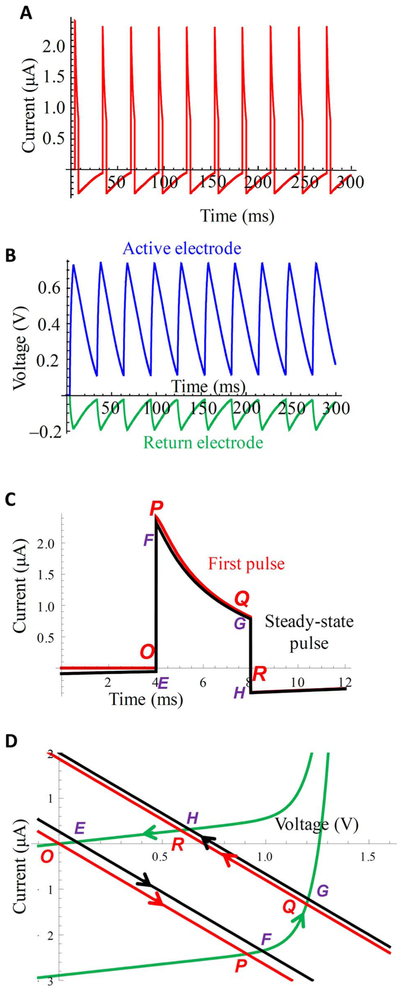
D. Repetitive Pulsing

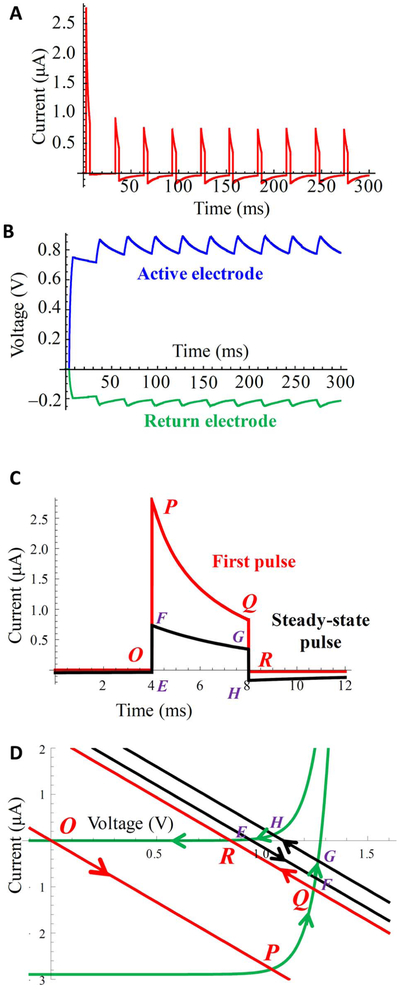
For efficient conversion of stroboscopic illumination into pulses of electric current at video rates (> 20 Hz) the electrode capacitors should discharge between the pulses and thereby avoid charge accumulation and the associated decrease of current with consecutive pulses, as illustrated in Figs. 11 and 12. Experimental waveforms shown in Fig. 11 illustrate that even under very bright illumination (18mW/mm²) delivered at 1 Hz repetition rate the electrodes fully discharge between both the 1 ms and 10 ms pulses, and therefore consecutive pulses have exactly the same shape. At 10 Hz the electrodes do not discharge completely, and the shape of the subsequent pulse starts deviating from that of the first pulse. This effect is exacerbated at 50 Hz, especially with 10 ms pulses.

Fig. 11.

Measured current generated by the 2-diode, 70 μm device (s2) under repetitive pulsed illumination of 18 mW/mm². The first pulse is shown in red, and the black waveforms represent 20 traces at 1 s intervals.

Fig. 12.

Model of an s2 pixel irradiated with 4 ms, 10 mW/mm² pulses at 33 Hz. (a) Current decreases over time. (b) Voltage across the active and return electrode capacitors. (c) The first (red) and steady-state (black) pulse shapes. (d) I-V curves illustrating the first pulse (OPQR loop) and the steady-state regime (EFGH loop).

Fig. 12 illustrates the effect of high frequency (33 Hz) pulsing on the system: the second pulse of current is already much smaller than the first one, and the current waveforms reach steady-state at a current about one fourth that of the first pulse [Fig. 12(a) and (c). Fig. 12(b) illustrates the reason for this effect: capacitors of the active and return electrodes charge during the pulse, but cannot discharge significantly between the pulses. The circuit operation is illustrated in Fig. 12(d): the first pulse starts from point O, proceeds to point P, and then to point Q where the capacitors are charged. When the light turns off, the system switches to point R, where the slow discharge towards point O begins. Since the resistance of the diodes at low voltage is very high, only a very small current flows through the circuit. If the next pulse arrives before the system reaches point O, the capacitors start charging again while they are still storing charge from the previous pulse. As a result, the system gradually shifts to the steady-state loop EFGH, which corresponds to lower current delivered to the tissue.

E. Shunt Resistor

To speed-up the electrode discharge between the pulses, a shunt resistor can be added to the circuit, as shown in Fig. 5. Equation I = −I_PD in (2) should then be replaced by

$$I=-I_{PD}-\frac{NV}{R_{sh}}.$$ (3)

All the other equations describing the model still hold true.

The waveforms illustrating the response of the s2 pixel shunted by 2 MΩ are shown in Fig. 13. The amplitude of the consecutive pulses decreases only slightly [Fig. 13(a) and (c)], and capacitors of the active and return electrodes are discharged almost completely [Fig. 13(b)]. When the light is turned off (point R in Fig. 13(d)), the electrode capacitors discharge much faster along the green curve, whose slope is now defined by the inverse value of the shunt resistor. This allows for almost complete discharge of the capacitors between pulses, and as a result, the steady-state cycle EFGH is very close to the first pulse cycle OPQR. Therefore, the amplitude and shape of the steady-state pulse are similar to those of the first pulse [Fig. 13(c)].

Fig. 13.

Modeling the s2 pixel performance under the same conditions as in Fig. 12, but with a 2 MΩ shunt resistor.

It is important to keep in mind that the shunt resistor also drains current during the light pulse, thereby reducing the current flowing through the medium. This can be seen in the diagram in Fig. 13(d): steeper green curves [compared to Fig. 12(d)] intersect with straight lines (points P and F) at lower current, corresponding to a lower peak current during the pulse of light. An optimal shunt resistance maximizes the total injected charge in the steady-state regime, and depends on pixel configuration, medium resistivity and lighting conditions. For example, Table II summarizes the optimal values of the shunt resistor for a 33 Hz repetition rate, 10mW/mm² light intensity, 4 ms pulse duration and resistivity of the retina of 1000 Ω · cm.

TABLE II.

Optimal Shunt Resistor Values (in MΩ) for 4 ms Pulses of 10 mW/mm² Applied to the Retina at 33 Hz

Pixel size	3-diode	2-diode	1-diode
70 μm Small	5	2	1
140 μm Medium	0.7	0.5	0.3

The shunt resistor can be optimized for the highest expected settings (light intensity, pulse duration and repetition rate), and it will discharge the capacitors efficiently at lower settings as well. The optimal shunt resistance varies relatively slowly with variation of the stimulation conditions. For example, with the shunt on the s2 pixel optimized for 4 ms, the injected charge during a 10 ms pulse will be only 13% lower than with the shunt optimized for 10 ms.

Besides increasing the charge delivery, shunt resistors also reduce the peak voltage across the capacitors, and thus significantly reduce the amount of unbalanced charge flowing through the Faradaic resistor, which, in turn, reduces the rate of irreversible electrochemical reactions.

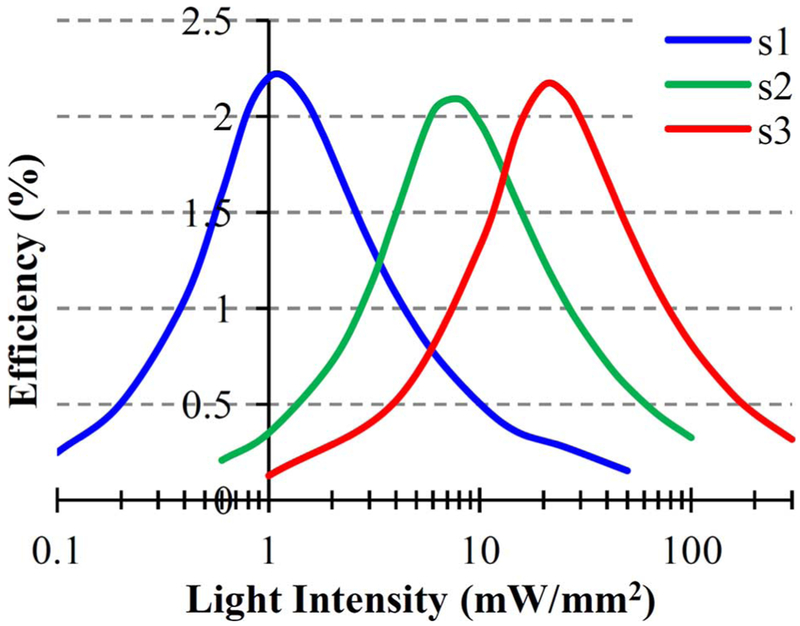
F. Energy Transfer Efficiency

Efficiency of the energy transfer from light to current in photovoltaic pixels is defined as the ratio of the energy of the pulse of current delivered into the electrolyte to the energy of the pulse of light incident on a pixel.

$$\eta =\frac{{\int }_0^{\tau }{I}^{2}R\cdot dt}{PS\cdot \tau }$$

where P and τ are intensity and duration of the light pulse, S is the pixel area, T is the inter-pulse period, and R the resistance of the electrolyte. Conversion efficiency depends on light intensity and its absorption in the pixel, the number of diodes and the losses of the photosensitive area due to electrodes, metal leads and trenches. Simulated efficiency of the energy transfer for 4 ms pulses and retinal resistivity is shown in Fig. 14 for s1, s2 and s3 pixels with the optimal shunt resistors listed in Table II. Peak efficiency of all three pixel types is around 2.2%, as shown in the plot.

Fig. 14.

Simulated efficiency of light-to-current conversion of small photodiode pixels.

Multiple factors affect the conversion efficiency. Metal leads, electrodes and trenches in the pixel reduce the silicon area collecting the incoming light by as much as 75% in s3 pixels, 67% in s2 and 44% in s1 devices. In addition, electron-hole recombination at the boundaries of thin and small photodiodes results in a 0.36 A/W light-to-current conversion factor—lower than that of a thick and large silicon wafer. The output power of the photodiode circuit is a product of the generated current and voltage. This product is low at the extremes of the photodiode I-V curve, where either the current or the voltage is very low. Peak efficiency occurs at the transition between the current-limited and voltage-limited regimes, which take place at lower intensities for pixels with smaller number of diodes, as shown in Fig. 14.

For larger pixels, a smaller fraction of light is lost on metal leads, electrodes and trenches, and the peak values of efficiency for 140 μm pixels illuminated from the front side reach 3.0 to 3.7%. If pixels were illuminated from the back (in applications other than subretinal prostheses), metal leads and electrodes on the front surface would not shadow the silicon, and efficiency would increase further.

Absorption of light in tissue and associated heating limit the applicable light intensities due to safety considerations. ANSI standards for ocular safety of NIR light limit the average retinal irradiance during prolonged exposure to ~ 5.2 mW/mm² for 905 nm wavelength [31]. For single pulses with durations in the range 0.05–70 ms, the peak irradiance limit is defined by the 285 · τ^−1/2, where τ is the pulse duration in milliseconds and the intensity in mW/mm² [31]. For example, the safety limit for 4 ms pulse duration is 202 mW/mm².

V. Conclusions

Photovoltaic pixels provide a very compact and convenient solution for wireless neural stimulation in translucent tissues. To avoid irreversible electrochemistry, the maximum voltage should not exceed the water window (about 1.4 V), and therefore the number of diodes per pixel is unlikely to exceed 3. The optimal number of diodes per pixel depends on the required charge, and thus may vary for different applications. Pixel performance at high repetition rates can be optimized using a proper shunt resistor, whose value depends on irradiance, repetition rate, pixel size and resistivity of the medium.

Biographies

David Boinagrov received the B.S. degree in applied physics and applied mathematics from the Moscow Institute of Physics and Technology, Dolgoprudny, Russia, and the M.S. degree in electrical engineering and Ph.D. degree in physics from Stanford University, Stanford, CA, USA, in 2007, 2012, and 2014, respectively.

Currently, he is a Postdoctoral Scholar in the Department of Physics and Hansen Experimental Physics Laboratory at Stanford University. His research interests include study of electro-neural interfaces and development of electronic retinal prostheses.

Xin Lei received the B.S. degree in microelectronics from Xi’an Jiaotong University, Xi’an, China, in 2011.

Currently, she is a graduate student in the Department of Electrical Engineering, Stanford University, Stanford, CA, USA.

Georges Goetz received the Diplome d’Ingenieur from Ecole Centrale Paris, Paris, France, and the M.S. degree in electrical engineering from Stanford University, Stanford, CA, USA, in 2011.

Currently, he is working toward the Ph.D. degree in the Department of Electrical Engineering and the Hansen Experimental Physics Laboratory at Stanford University. His research interests include information processing in the visual system and electro-neural interfaces for retinal prostheses.

Theodore I. Kamins (S’65–M’68–SM’79–F’91) received the B.S., M.S., and Ph.D. degrees in electrical engineering from the University of California, Berkeley, Berkeley, CA, USA.

Currently, he is a Principal Scientist in the Quantum Science Research Group at Hewlett-Packard Laboratories, Palo Alto, CA, USA, where he has conducted research on numerous semiconductor material and device topics. He is also a Consulting Professor in the Electrical Engineering Department, Solid State and Photonics Laboratory, Stanford University, Stanford, CA, USA. He has worked on epitaxial and polycrystalline silicon at the Research and Development Laboratory of Fairchild Semiconductor. His research interests include advanced nanostructured electronic materials and devices. He is the author of Polycrystalline Silicon for Integrated Circuits and Displays (Kluwer, 1998), and a coauthor of Device Electronics for Integrated Circuits (Wiley, 2003).

Dr. Kamins is a Fellow of the Electrochemical Society.

Keith Mathieson received the Ph.D. degree in physics from the University of Glasgow, Glasgow, Scotland, U.K., in 2001.

Since 2001, he has developed high-density micro-electrode arrays to study the response of retinal tissue to optical and electrical stimulation in collaboration with the University of California, Santa Cruz, Santa Cruz, CA, USA; the Salk Institute for Biological Studies, San Diego, CA, USA; and Stanford University, Stanford, CA, USA. Currently, he is a Reader in Neurophotonics and Head of Institute at the Institute of Photonics, University of Strathclyde, Scotland, U.K.

Dr. Mathieson was the recipient of a Scottish Government/Royal Society of Edinburgh personal research fellowship and an SU2P entrepreneurial fellowship funded through RCUK.

Ludwig Galambos received the B.S. and M.S. degrees in material science from the Polytechnic Institute of Engineering, Bucharest, Romania, in 1982 and 1984, respectively.

Currently, he is a Research Engineer in the Department of Electrical Engineering, Stanford University, Stanford, CA, USA.

James H. Harris, Jr. (S’65–M’69–SM’78–F’88)received the B.S., M.S., and Ph.D. degrees in electrical engineering from Stanford University, Stanford, CA, USA, in 1964, 1965, and 1969, respectively.

In 1969, he joined the Rockwell International Science Center, Thousand Oaks, CA, USA, where he was one of the key contributors in developing their preeminent position in GaAs device technology. In 1982, he joined the Solid State Electronics Laboratory, Stanford University, as a Professor of electrical engineering. From 1984 to 1998 and from 1985 to 1999, respectively, he served as a Director of the Solid State Electronics Laboratory and the Joint Services Electronics Program, Stanford University. Currently, he is the James and Ellenor Chesebrough Professor of Engineering at Stanford University. He has supervised more than 85 Ph.D. students. He has authored or coauthored work in over 750 publications. He is the holder of 18 U.S. patents. His research interests include the physics and application of ultrasmall structures and novel materials to new high-speed and spin-based electronic and optoelectronic devices and systems.

Dr. Harris is a Fellow of the American Physical Society and Optical Society of America. He was the recipient of the 2000 IEEE Morris N. Liebmann Memorial Award, 2000 International Compound Semiconductor Conference Walker Medal, IEEE Third Millennium Medal, and Alexander von Humboldt Senior Research Prize in 1998 for his contributions to GaAs devices and technology.

Daniel Palanker received the Ph.D. degree in applied physics from the Hebrew University of Jerusalem, Jerusalem, Israel, in 1994.

Currently, he is a Professor in the Department of Ophthalmology and in the Hansen Experimental Physics Laboratory at Stanford University, Stanford, CA, USA. He studies interactions of electric field with biological cells and tissues in a broad range of frequencies: from quasi-static to optical, and develops their diagnostic, therapeutic and prosthetic applications, primarily in ophthalmology. Several of his developments are in clinical practice worldwide: pulsed electron avalanche knife (PEAK PlasmaBlade), patterned scanning laser photocoagulator (PASCAL), and OCT-guided laser system for cataract surgery (Catalys). In addition to laser-tissue interactions, retinal phototherapy and associated neural plasticity, he is working on electro-neural interfaces, including retinal prosthesis, and electronic control of vasculature and of the secretory glands.