Vulnerability of Corneal Endothelial Cells to Mechanical Trauma from Indentation Forces Assessed Using Contact Mechanics and Fluorescence Microscopy

Abstract

Corneal endothelial cell (CEC) loss occurs with surgical anterior segment surgery and corneal transplantation tissue manipulation as well as from contact with synthetic materials like intraocular lenses and tube shunts. While several studies have quantified CEC loss for specific surgical steps, the vulnerability of CECs to isolated, controllable and measurable mechanical forces has not been assessed previously. The purpose of this study was to develop an experimental testing platform where the susceptibility of CECs to controlled mechanical trauma could be measured. The corneal endothelial surfaces of freshly dissected porcine corneas were subjected to a range of indentation forces via a spherical stainless steel bead. A cell viability assay in combination with high-resolution fluorescence microscopy was used to visualize and quantify injured/dead CEC densities before and after mechanical loading. In specimens subjected to an indentation force of 9 mN, the mean ± SD peak contact pressure P₀ was 18.64 ± 3.59 kPa (139.81 ± 26.93 mmHg) in the center of indentation and decreased radially outward. Injured/dead CEC densities were significantly greater (p ≤ 0.001) after mechanical indentation of 9 mN (167 ± 97 cells/mm²) compared to before indentation (39 ± 52 cells/mm²) and compared to the sham group (34 ± 31 cells/mm²). In specimens subjected to “contact only” – defined as an applied indentation force of 0.65 mN – the peak contact pressure P₀ was 7.31 ± 1.5 kPa (54.83 ± 11.25 mmHg)_. In regions where the contact pressures was below 78% of P₀ (< 5.7 kPa or 42.75 mmHg), injured/dead CEC densities were within the range of CEC loss observed in the sham group, suggesting negligible cell death. These findings suggest that CECs are highly susceptible to mechanical trauma via indentation, supporting the established “no-touch” policy for ophthalmological procedures. While CECs can potentially remain viable below contact pressures of 5.7 kPa (42.75 mmHg), this low threshold suggests that prevention of indentation-associated CEC loss may be challenging.

1. Introduction

The non-proliferative corneal endothelial cell (CEC) monolayer is located on the posterior surface of the cornea and maintains corneal transparency by controlling stromal hydration and thickness (i.e., by sustaining stromal deturgescence). CECs regulate corneal hydration levels through a combination of ion transport mechanisms, which counterbalance the passive flow of aqueous humor from the anterior chamber into the corneal stroma through leaky junctional barriers (Bonanno, 2003, 2012). While healthy corneas contain endothelial cell densities (ECD) ranging between 2,000 – 3,000 cells/mm², corneas with ECDs below ~750 – 500 cells/mm² are at risk of developing cloudiness or hazing due to decompensation – failure of CECs to maintain corneal thickness – which can lead to reduced vision and, in some cases, blindness. In the USA, the two most commonly reported indications for corneal transplantation are endothelial-related dystrophies (e.g. Fuch’s Dystrophy) and surgical complications (e.g. post-cataract surgical edema) (EBAA, 2016).

Unfortunately, clinical measurements of ECD after penetrating keratoplasty (PK), endothelial keratoplasty (EK), or cataract surgery show a steady uninterrupted decline over time that exceeds the physiological rate (0.6% per year). For example, studies assessing outcomes 2, 5 and 7 years after Descemet’s membrane endothelial keratoplasty (DMEK) reported EC losses of 45%, 44% and 65% (Ham et al., 2016; Peraza-Nieves et al., 2017; Schlogl et al., 2016). Similarly, ECD declined by 45% and 62% 5 and 10 years after Descemet stripping endothelial keratoplasty (DSEK) (Price et al., 2016; Wacker et al., 2015) and by 75% 10 years after PK (Lass et al., 2013). After cataract surgery, short-term (< 1 year) ECD losses of 2% – 20% (Abell et al., 2014; Amir-Asgari et al., 2016; Chen et al., 2017) and long-term (1 year) ECD losses of 4 – 6% (Storr-Paulsen et al., 2008) have been reported, and these losses depend on technique. In PK/EKs, endothelial decompensation increases risk for primary (Baydoun and Melles, 2016) or early-onset secondary graft failure (Mannis et al., 2013; Patel et al., 2010) while in cataract surgery, CEC loss increases risk of developing bullous keratopathy.

In vivo, the corneal endothelium is mostly isolated from mechanically stress. Exposing it to bending moments or external forces during ophthalmological procedures is thought to kill CECs. Thus, while much of the literature emphasizes ECD decline over time after eye surgery, a substantial proportion of EK, PK and cataract surgery-associated CEC loss occurs during the procedures themselves. For example, after PK, immediate CEC loss of 26% is observed, while DSEK kills 9% - 56% of CECs depending on insertion technique (Ide et al., 2007; Mehta et al., 2008; Price and Price, 2008; Terry et al., 2009a; Terry et al., 2013). Injection of DMEK grafts is associated with 27 – 32% CEC loss (Schallhorn et al., 2015). In cataract surgery, indentation of the endothelial surface due to collisions of rogue lens fragments (Amir-Asgari et al., 2016) is associated with CEC. Based on the reviewed literature, iatrogenic CEC loss seems to be largely dependent on the magnitude and type (e.g., indentation) of external mechanical forces experienced by the corneal endothelium.

Yet, the vulnerability of CECs to controlled, measurable mechanical forces imparted using materials testing equipment – in contrast with surgically-imparted forces that are difficult to control and quantify – has not been assessed. Thus, our long term goal is to characterize the types and magnitudes of mechanical forces necessary to kill CECs to inform novel adjustments in surgical techniques that reduce iatrogenic CEC loss. The first step towards accomplishing this goal was to develop a custom experimental testing platform wherein controlled mechanical forces could be applied onto the corneal endothelium. As a proof of concept, the vulnerability of CECs to indentation forces was explored. This type of mechanical force was chosen since it is relevant to multiple ophthalmological procedures. For example, PK and EK both require grabbing and holding a graft with forceps (e.g., to move the graft onto a glide or inserter from a trephination block), while in cataract surgery, floating lens fragments can make contact with the endothelium. In both cases, the corneal endothelium is exposed to indentation forces. Porcine corneas were subjected to millinewton forces and damage to the corneal endothelium was quantified. Our findings demonstrate that at applied contact pressures below 5.70 kPa (42.75 mmHg), CEC loss was negligible, indicating that CECs can survive contact with an indentor and that in the case of EK, it may be possible (though challenging) to grasp corneal grafts without CEC loss.

2. Materials & Methods

2.1. Study Design

Indentation forces were applied onto the corneal endothelium via a spherical indentor attached to a cantilever beam. Three experimental groups we assessed: a sham group (n = 10) where the specimen was loaded and unloaded from the mechanical tester without contact by the bead; 2) a contact-only group (n = 10) where the specimen touched the bead with a small but non-negligible “contact” indentation force of F_ind = 0.65 mN; and 3) an indentation group (n = 10) where following contact, the specimen was further displaced into the bead until an indentation force of 9 mN was applied to the corneal endothelium.

2.2. Specimen Preparation

Fresh porcine eyes were obtained from a local slaughterhouse, transported to the lab, and placed in a refrigerator at 4°C for storage prior to experimentation. Corneo-scleral rims were dissected from each eye less than 12 hours after slaughter. A detailed description of the dissection procedure is available in the supplementary materials (Figure S1). In summary, first the globe was cleared of all extraocular muscles and orbital fat with gross dissection scissors. The epithelium was gently scraped off the cornea using a #21 scalpel blade. The globe was cut open along the equator of the sclera to isolate the anterior segment. Using a pair of serrated forceps, the sclera was held in place and the ciliary body and iris were detached from the sclera using Castroviejo scissors. Once separated, the ciliary body, lens, and remaining vitreous humor were easily peeled off, exposing the corneal endothelium. Intact corneo-scleral rims were stained immediately after dissection.

2.3. Specimen Staining

CEC viability was assessed via fluorescence imaging of CECs stained with calcein-AM (Invitrogen, ex. 494 nm and em. 513 nm, P/N: C3100MP) and propidium iodide (PI, Invitrogen, ex. 493 nm and em. 636 nm, P/N: P3566). When calcein AM penetrates the cell membrane, it is cleaved by esterases and becomes both green fluorescent and membrane-impermeant. (In its cleaved form, this molecule is known simply as calcein.) Thus, calcein-stained cells appear green and indicate cells with intact membranes (i.e., live cells). In contrast, PI fluoresces in red and can only penetrate a ruptured membrane. Thus, PI-stained cells are either injured (i.e., cells with temporarily ruptured membranes) or dead. Corneo-scleral rims were placed endothelium side-up on top of a test tube cap to recreate the curved shape of the cornea, and 300 μL of balanced salt solution (BSS, Alcon, P/N: 0065079550) containing 10 μM calcein-AM was added to the endothelium drop-wise. The corneo-scleral rim was then covered from light and incubated for 35 minutes at 37°C. Both new and used BSS containers were obtained from the Flaum Eye Institute operating room at the University of Rochester Medical Center after cataract surgery. Used BSS contained 500 units of epinephrine. Containers were stored on the lab bench at room temperature exposed to light for 1 week – 3 months. Epinephrine has been shown to exhibit no toxic effects on CECs (Cakmak et al., 2010; Liou et al., 2002) and no significant differences were found when comparing experimental results between specimens in BSS and specimens in BSS containing epinephrine (Figure S2). BSS was chosen as a buffer since it is manufactured to mimic the chemical composition of aqueous humor and is used as an ophthalmic irrigation fluid during surgery. BSS did not appear to evaporate significantly during the staining procedure and covered the full endothelial surface. After staining, corneoscleral rims were gently rinsed twice in BSS and left submerged in a bath prior to mechanical indentation testing.

2.4. Mechanical Indentation Testing Protocol

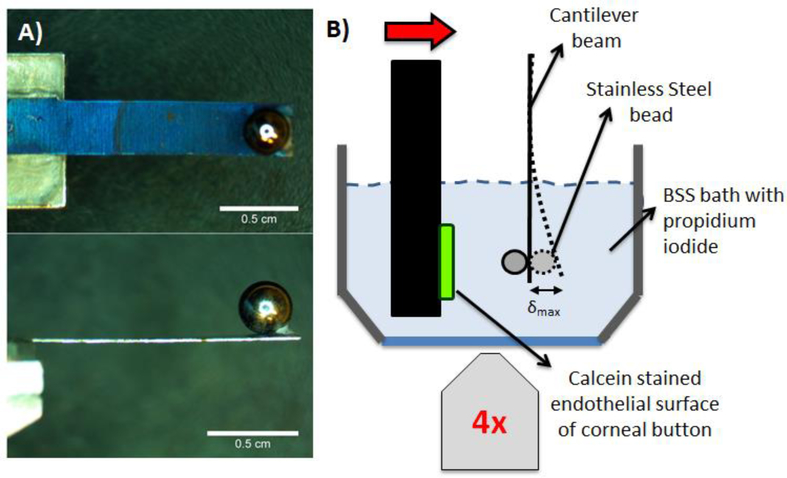
Central cylindrical corneal explants (buttons) 8 mm in diameter (~50 mm² surface area) were cut from the stained corneo-scleral rims using disposable biopsy punches (Integra Miltex, Plainsboro, NJ, USA, P/N: 33–37). After baseline images were taken to quantify the initial viability of the corneal endothelium (see subsection 2.5 titled “Fluorescence Imaging Protocols”), the button was placed onto a microscope-mounted mechanical testing device known as a Tissue Deformation Imaging Stage (TDIS, Harrick Scientific Products, Inc. Pleasantville, NY, USA) (Buckley et al., 2013; Ramirez-Garcia et al., 2017; Sloan et al., 2014). Specifically, the anterior side of the button was adhered to a rigid platen in the TDIS using small droplets of cyanoactylate (superglue). Note that the curvature of the button was removed by flattening it against the platen. In the TDIS, the rigid platen was positioned directly in front of a 3 mm diameter stainless steel spherical bead (McMaster-Carr, Ohio, USA, P/N: 1598K23) superglued as close as possible to the edge of a cantilever beam (Lyons Shim Stock, P/N: BTS-5) (Figure 1). Both the rigid platen and the cantilever beam were submerged in a BSS bath such that the button remained hydrated throughout the mechanical test. Cantilever beams were cut to a custom length and width. Thickness and Young’s modulus measurements were obtained from the manufacturer, and the area moment of inertia was calculated based on cantilever dimensions. The length, width, and distance between the edge of the cantilever beam to the center of the stainless steel bead were measured using stereo micrographs (Amscope) analyzed in ImageJ. Stainless steel beads were sonicated in distilled water to remove any dust or coatings before use. Beads were sterilized before and in between experiments by spraying with ethanol and wiping dry with a Kimwipe (VWR, P/N: 470224–038).

Figure 1:

Custom mechanical indentation device. A) A 3 mm diameter stainless steel bead was superglued to a pre-cut cantilever beam at its free end. B) The cantilever beam and bead were aligned to the center of an 8 mm diameter corneal button. The button was displaced against the cantilever beam and bead, as shown in A), until a cantilever beam deflection was measured corresponding to a desired deflection force, F_beam. The mechanical tester was mounted onto an inverted microscope to visualize the deflection of the cantilever beam.

The rigid platen was coupled to a piezoelectric actuator (Physik Instrumente (PI), Karlsruhe, Germany, P/N: P-62#.1) controlled by LabView (NI Instruments), enabling precisely defined motion towards and away from the bead (Figure 2B). The cantilever beam with the spherical bead was attached to an arm with three linear translation stages allowing for manual control of the bead position along three orthogonal directions. This allowed for precise positioning of the bead in relation to the center of the corneal button.

Figure 2:

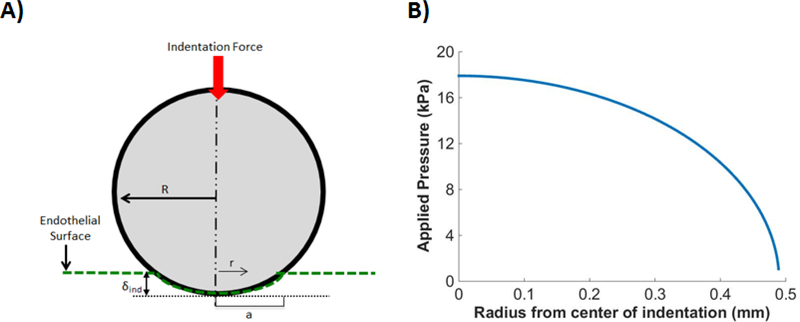
Schematic of Hertzian contact model. A) A stainless steel bead of radius, R, was indented against the corneal endothelial surface to an indentation depth δ_ind associated with a contact radius α. B) Spherical indention is associated with a radially dependent pressure distribution. The curve shown in the figure corresponds to the mean δ_ind of 160 μm from the 9 mN indentation group.

During testing, the TDIS was mounted onto the stage of an IX81 inverted microscope with fluorescence imaging capabilities (Olympus, Center Valley, PA, USA). Reflected white light imaging was performed using a 4× objective lens to monitor the position of the cantilever beam. After the specimen was attached to the device and the bead was positioned at or near the central axis of the button, the microscope objective was focused onto the bottom surface of the cantilever beam and the rigid platen was manually displaced against the bead until contact between the bead and the endothelium was made. “Contact” was defined as a 5 μm deflection of the cantilever beam, the smallest easily detectable beam displacement corresponding to an indentation force, F_ind, of 0.65 mN (see subsection 2.7 titled “Determining the Indentation Force” for a description of how indentation forces were calculated).

For higher indentation forces, immediately after contact was established, the rigid platen was further displaced at a rate of 9.98 μm/sec against the cantilever beam. The specimen was indented against the bead until the cantilever beam deflection, δ_beam, indicated that the desired indentation force, F_ind = 9 mN, was reached (see subsection 2.7 titled “Determining the Indentation Force”). Immediately afterwards, the rigid platen was manually retracted away from the bead and cantilever. Indentation experiments lasted approximately 15 seconds. The indentation depth, δ_ind, of the bead into the specimen was measured as the total distance the rigid plate travelled towards the bead minus the deflection of the cantilever beam.

At the conclusion of the experiment, the specimen was gently removed from the rigid platen and placed endothelial face-down in the retainer cup for additional fluorescence imaging to quantify CEC loss from indentation (see subsection 2.5 titled “Fluorescence Imaging Protocols”). From comparing the pre-indentation tile scan of the endothelium to the post-indentation tile scan, the site of indentation was identified as an area with radially-symmetric cell death near the center of the button.

2.5. Fluorescence Imaging Protocols

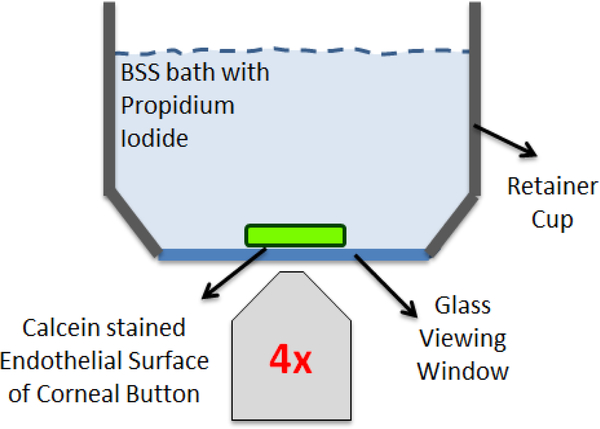
Immediately after staining and again after mechanical indentation, corneal buttons were placed endothelium side-down inside the retainer cup of the TDIS mounted on the fluorescence microscope. The cup was filled with a bath of BSS containing 15 μM PI (Figure 3A). The retainer cup consists of a stainless steel rim with a glass coverslip (Fisher Scientific, P/N: 12–546-2) at the base to serve as a viewing window. The first set of multichannel fluorescence tiled (stitched) images encompassing the complete button surface area (~ 35 – 30 tiles per image, 1990 × 1420 pixel resolution) was taken in order to quantify damage from dissection, staining and trephination. This set of images captured the baseline state of CEC viability prior to mechanical testing (Figure 4A). The second set of images was acquired after mechanical testing to assess damage from indentation (Figure 4B), and the third set of images was taken at the site of indentation (or geometric center of the button if no easily identifiable damage area was observed) in order to better visualize individual PI-labelled nuclei and calcein-stained cells for quantification (Figure 4C).

Figure 3:

Fluorescence imaging set-up. The retainer cup of the mechanical testing device, consisting of a stainless steel rim with a coverslip glass base, was placed on an inverted microscope to enable fluorescence imaging of the corneal endothelial surface. Cylindrical explants were laid endothelium-surface down inside the retainer cup. The endothelium was stained with calcein-AM to visualize live CECs in green, and submerged in a BSS bath containing PI in order to visualize injured/dead CECs in red. Three sets of multichannel fluorescence tiled images of the complete endothelial surface were obtained: 1) prior to mechanical indentation; 2) after mechanical indentation; and 3) after mechanical indentation but only at the site of indentation as an EFI projection to better visualize individual PI-labelled nuclei..

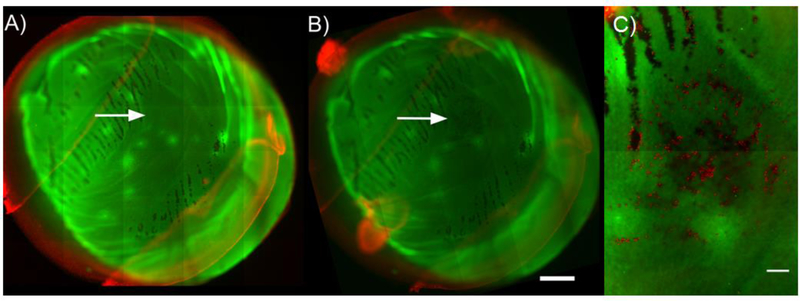
Figure 4:

Representative fluorescence image tiles of a specimen from the 9 mN indentation force group. Images A) and B) spanned the entire endothelial cell surface area (~50 mm², ~30 – 35 image tiles) and were taken A) after dissection, staining and trephination procedures, but prior to mechanical indentation (serving as a baseline image) and B) after mechanical indentation. The indentation images taken after indentation were translated and rotated to match the alignment of the baseline image to facilitate analysis. Arrows in A) and B) indicate site of indentation. C) A third multichannel tiled (~ 2 – 4 tiles) EFI projection of a z-stack was taken at site of indentation to facilitate quantification. Each red dot is an individual dead/injured CEC labelled with PI. The resolution of images used for quantification was 995 × 710 pixels (figure resolution was 498 × 355 pixels). The scale bar in A) and B) is 1 mm; scale bar in C) is 200 μm.

The third tile scan (Figure 4C) was taken as a set of extended focal image (EFI) projections from z-stacks with a step size of 40 μm. An EFI projection automatically detects regions in focus within each slice of the z-stack, blending them together to generate a single in focus image; thus all tiles comprising the tile scan were in focus. The third tile scan typically contained 2–4 tiled images stitched together with the site of indentation at its center, thus covering the full indentation site and its surroundings. This in-focus tile scan was required as folds in the Descemet’s membrane or variations in thickness in the underlying stroma would otherwise cause regions of the images to appear out of focus, making accurate quantification difficult.

Image acquisition took approximately 30 – 40 minutes per specimen. In order to minimize experimental downtime, specimens were dissected, stained, and tested in sets of three. Therefore, the last corneoscleral rim of a given set was submerged in BSS for a maximum of 2 hours prior to testing. CEC viability did not decrease after prolonged exposure in BSS (data not shown).

2.6. Quantification of Injured/Dead Cells

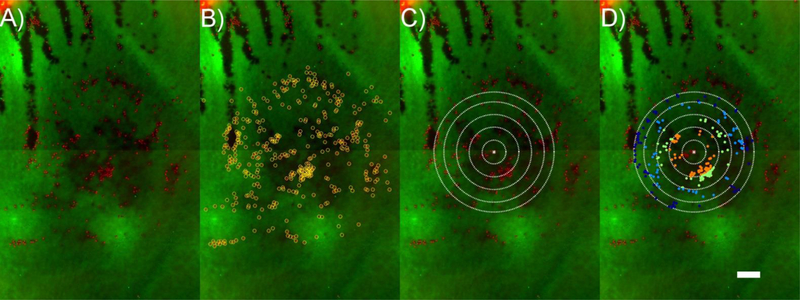
Quantification of CEC damage due to indentation was performed through a combination of image analysis techniques in ImageJ and MATLAB (Mathworks, version 2014b). First, all image sets were converted from 16-bit to 8-bit and reduced in size in ImageJ using the 2 × 2 average bin method to a resolution of 995 × 710 pixels in order to decrease computational processing time. Next, an intensity threshold was applied to the red fluorescent channel of the tiled EFI projections (Figure 5A) to convert them into binary images, such that as many PI positive cell nuclei (i.e. injured/dead cells) as possible were visible. The watershed algorithm was then applied to separate any adjoining cell nuclei. Using the particle analysis tool, the centroids (XY coordinates) of cell nuclei were recorded. However, if any cells were not captured through this method, then their centroids were manually determined in MATLAB using a counter (Romesh, 2015) (Figure 5B). After all injured cells’ coordinates were obtained, the centroid of the complete coordinate set was calculated.

Figure 5:

Quantification of CEC loss. A) EFI projections of a z-stack at the site of indentation were used for quantification. B) PI-labelled CEC nuclei were counted in ImageJ and MATLAB, outlined as yellow circles. C) Contact areas were overlaid at site of indentation. D) CECs within the contact area were quantified (shown as colored dots), while those extending beyond the contact area were not. CECs were then further separated into their corresponding annular regions (shown as distinct colored dots). Scale bar is 200 μm for all images.

Next, the baseline and after indentation image sets – which were each taken after the explant was placed at an arbitrary orientation in the glass bottom retainer cup – were aligned with one another to facilitate analysis. The MATLAB function fitgeotrans was first used to apply geometric transformations (translation and rotation) to align all image sets taken after indentation to the baseline image. The green fluorescence channel was used since it contained visible features (e.g., gaps in the endothelial surface) to aid as markers in the transformations (see Figure 4B compared to 4A). After these transformations, the transformPointsForward function was used to translate and rotate the coordinates of all identified PI positive cells such that their positions (and, consequently, the site of indentation) in the baseline image were known.

The next step consisted of calculating the applied contact pressures for each specimen. First, the contact area was determined (see subsection 2.8 titled “Determining the Applied Contact Pressure”). Then, using the contact area and experimentally measured beam force, the pressure distribution spanning the entire contact area was determined for each specimen (see subsection 2.8 titled “Determining the Applied Contact Pressure”). Next, contact areas were divided with concentric rings such that each annular region correspond to a prescribed interval of P/P₀, where P is the contact pressure at a given distance r from the center of contact and P₀ is the peak contact pressure (i.e., the contact pressure at the center of contact). The intervals of P/P₀ were determined by splitting the mean contact area of the 9 mN indentation force experimental group into annular regions increasing by Δr = 100 μm and calculating the corresponding values of P/P₀ at each radial increment. The same P/P₀ intervals were used for all experimental groups.

The final step was to quantify the cells that fell within the contact areas and annular intervals in order to assess injured cell densities. First, calculated contact areas were overlaid at the site of indentation (on EFI-projected images) with the assumption that the centroid of the coordinate set of PI positive cells matched the location of the center of the contact area (Figure 5C). PI positive cell nuclei located within the full contact area were used to determine the density of injured/dead cells (i.e., the number of injured/dead CECs divided by the full contact area in mm², Figure 6). Counted cells that extended beyond the contact area region were excluded from this measurement (Figure 5B versus Figure 5D). PI positive cell nuclei within the contact area were then further divided into their corresponding annular regions (Figure 5D), allowing for quantification of the density of injured/dead cells (the number of injured/dead CECs divided by the area of their corresponding annular region in mm²) as a function of P/P₀ (Figure 7). Finally, the contact area was overlaid at the site of indentation in the baseline image and, using a similar method as described above, all PI positive cell nucleus that fell within the contact area in the red channel were counted to obtain the baseline injured cell density (Figure 6).

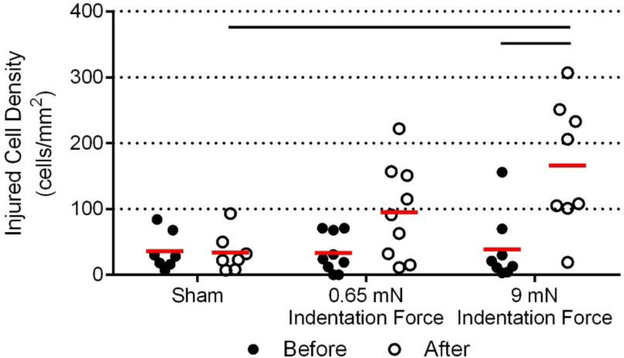
Figure 6:

Quantification of injured CEC densities within the full contact area for each experimental group before and after indentation. Mean values are denoted by the red line. CEC loss in the 9 mN indentation force group was significantly higher after indentation compared with before indentation (p ≤ 0.001) and compared to the sham negative control (p ≤ 0.001).

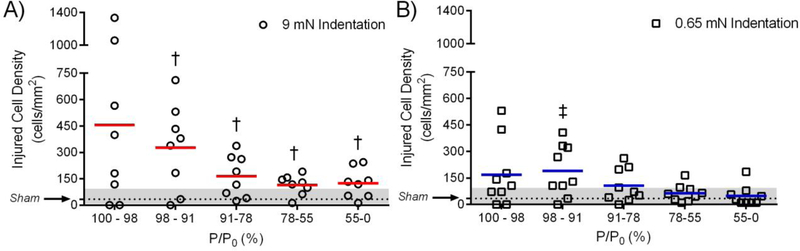
Figure 7:

Quantification of injured CEC densities as a function of percentage of applied pressure over peak applied pressure P/P₀. Separated CECs within each annular region (Figure 5D) were counted and divided over the annular area to obtain the pressure-dependent density of injured cells. The mean sham injured/dead CEC density after indentation (Figure 6) is represented by the dotted line and the gray area denotes the range of injured/dead densities in the sham. A) Injured CEC densities for the 9 mN indentation force group. Injured/dead CEC densities below 98% of P₀ were all significantly higher than the sham group (p < 0.05). B) Injured CEC densities for the 0.65 mN indentation force group (“contact only”). Injured/dead CEC densities below 78% of P₀ fell within the range of injured/dead CEC density in the sham group. Mean values denoted by the solid red and blue lines.

Specimens were not tested if the baseline image contained large calcein-negative (dark) regions, corresponding to stripped or non-viable CECs (>7% of the contact area). To determine the percentage of non-viable surface areas within the contact area, ImageJ and MATLAB thresholding tools based on the range of pixel intensity values in the contact area were used. No specimens were eliminated due to this criterion. Specimens analyzed contained on average < 3% of dark regions (i.e., >97% of the contact area contained viable CECs, Figure S3). Moreover, since alignment of the spherical bead to the middle of the specimen was performed manually, the site of indentation was occasionally off-centered. Thus, specimens were also not considered for analysis if indentation occurred near the edge of the button where swelling created uneven planar surfaces. Specifically, a circle drawing function (Chernov, 2009; Taubin, 1991) was applied to the post-indentation green fluorescence channel indentation image to find the center of the specimen, and the distance between the specimen center and the centroid of indentation was calculated. Only specimens with indentation sites less than 2 mm from the center of the specimen were considered for analysis (Figure S4). This region represents the inner 25% of the specimen. Finally, any outliers (mean ± 2 SD) in radial distance from the specimen center (9 mN indentation group: n = 1), injured cell density in the baseline image (“contact only” group: n = 1; sham group: n = 1; 9mN indentation group: n = 1), or injured cell density in the post-indentation image (sham group: n = 1) were also not considered for analysis.

For the sham negative control group, or those specimens where no easily identifiable indentation site was observed in the EFI projection, the centroid of the coordinate set of PI positive cells was taken to be the center of the EFI projection itself (i.e. the geometric center of the corneal button). Additionally, for the sham group, the contact areas assigned were the mean values from the 9 mN indentation force group.

2.7. Determining the Indentation Force

According to classical beam theory, the maximum deflection, δ_beam, produced by a concentrated load at a known distance from the free end of a cantilever beam is given by

$${\delta }_{beam}=\frac{F_{beam}}{6EI}\left(2l^3-3l^{2}x+x^3\right),$$ (1)

where F_beam is the concentrated load, l is the length of the beam, E is the Young’s modulus of the beam, I is the area moment of inertia of the beam, and x is the distance from the free edge of the beam to the location of the concentrated load. If δ_beam is known, then Equation (1) can be manipulated to determine the concentrated load:

$$F_{beam}=\frac{6EI{\delta }_{beam}}{\left(2l^3-3l^{2}x+x^3\right)}.$$ (2)

In our experiments, we used a cantilever beam with a spherical bead attached near its free end (Figure 1A). The external force deflecting the cantilever beam, F_beam, was applied by a corneal button with the endothelium facing the bead (Figure 1B). Under equilibrium, or static, conditions (maximum cantilever beam deflection), the sum of the forces on the bead is equal to zero and includes the force from the corneal button (equal and opposite to F_cornea, the force on the corneal button) and the force from the cantilever beam (equal and opposite to F_beam, the force on the cantilever beam). Thus,

$$-F_{cornea}-F_{beam}=\sum F_x=0.$$ (3)

Hence, the force the spherical indentor exerts onto the endothelium is equal to the force required to deflect the cantilever beam:

$$-F_{cornea}=F_{beam}=\frac{6EI{\delta }_{beam}}{\left(2l^3-3l^{2}x+x^3\right)},$$ (4)

where the negative sign indicates that F_cornea acts in the opposite direction to F_beam.

2.8. Determining the Applied Contact Pressure

Given that a spherical indentor was used to apply the indentation force, a simple analytical model based on Hertzian contact mechanics was used to determine the concentric distribution of contact pressures on the endothelial surface. The porcine button was assumed to be an infinite elastic half-space and the bead a rigid sphere with radius R indenting to a depth δ_ind. The contact radius, α, is equal to

$$a=\sqrt{R{\delta }_{ind}}.$$ (5)

The distribution of normal pressures in the contact area as a function of radial distance, r, from the centroid of indentation (Figure 2B) can be found from

$$P(r)=P_0{\left(1-\frac{r^2}{a^2}\right)}^{1/2},$$ (6)

where P₀ = P(r = 0) is the pressure at the centroid of indentation. P₀ is obtained from

$$P_0=\frac{3F_{ind}}{2\pi a^2},$$ (7)

where F_ind is the (normal) indentation force applied to the button. In our experiment, this force is equal in magnitude to the concentrated load (F_beam) applied to the cantilever (Eq. 4). In order to apply Hertzian contact mechanics, the following assumptions were made: (i) the button was taken to be an infinite elastic half-space; (ii) the corneal endothelium was taken to be planar since its radius of curvature is much greater than the indenting bead; (iii) frictionless sliding was assumed to occur between the indentor and the specimen; and (iv) strains imparted onto the tissue substrate were taken to be small. Assumptions (i) and (iv) are justified because the thickness of the buttons was >> δ_ind; assumption (ii) is justified because the button was attached in a manner that flattened the curvature of the cornea; and assumption (iii) is justified because the experiments were performed in fluid.

It should be noted that for the “contact only” group, δ_ind is unknown since the moment at which indentation first occurs (δ_ind = 0) cannot be accurately assessed. Importantly, δ_ind is necessary to determine the applied contact pressure distribution (Eqn. 6). However, the Hertz contact force-indentation relationship (Dias and Ziebarth, 2013; Last et al., 2012; Thomasy et al., 2014) can be used to calculate δ_ind for the “contact only” group:

$${\delta }_{ind}={\left(\frac{3F\left(1-v^2\right)}{4E\sqrt{R}}\right)}^{2/3},$$ (8)

where F is the loading force, E is the effective indentation modulus of the cornea, R is the radius of the spherical indentor, and v is the Poisson’s ratio of the cornea (assumed to be 0.49) (Dias and Ziebarth, 2013; Hatami-Marbini and Etebu, 2013b; Last et al., 2009; Last et al., 2012). First, the effective indentation modulus E of the cornea was estimated based on the experimental value of δ_ind from the 9 mN indentation group. We obtained an indentation modulus of 70 ± 20 kPa (mean ± SD), a nearly identical value (66 kPa) to that in published literature for the posterior stroma (Dias and Ziebarth, 2013). Then, using the calculated E and F_beam = 0.65 mN, δ_ind for the “contact only” group was determined (Eqn. 8).

2.9. Statistical Analysis

Two-way analyses of variance with Bonferroni post hoc adjustment was performed to compare the density of injured cells within the total contact area across time points (before indentation and after indentation) and across experimental groups (sham, contact only and indentation). Two-way ANOVA with Bonferroni post hoc adjustment was also performed to compare the density of dead/injured cells across annular regions and across experimental groups (sham and indentation). For all statistical tests, the threshold for significance was set to α = 0.05. Statistical tests performed in GraphPad Prism (GraphPad Software, La Jolla California USA, Windows version 6.07).

3. Results

The acquired baseline images confirmed that dissection and staining generally killed few CECs (Figure 4A). Indentation depths (δ_ind) due to 9 mN indentation forces were relatively consistent between specimens (160 ± 33 μm, mean ± SD), resulting in similar contact areas (0.753 ± 0.154 mm²) and peak compressive pressures (18.64 ± 3.59 kPa or 139.81 ± 26.93 mmHg). Indentation locations were also consistent, with the distance between the center of the cylindrical button and the centroid of indentation measured to be 756.3 ± 320 μm, or approximately the inner ~ 4% area of the corneal button. For the “contact only” group, δ_ind was estimated to be 27.7 ± 5.6 μm, with an estimated peak compressive pressure P₀ of 7.31 ± 1.5 kPa (54.83 ± 11.25 mmHg).

In both the sham and contact only groups, the density of injured/dead cells in the area of contact did not change after indentation (sham: 36 ± 29 cells/mm² before indentation versus 34 ± 31 cells/mm² after indentation; contact only: 33 ± 30 cells/mm² before indentation versus 96 ± 73 cells/mm² after indentation; Figure 6). However, in the 9 mN indentation group, the total number of injured/dead cells increased significantly (p ≤ 0.001) following indentation (39 ± 52 cells/mm² before indentation versus 167 ± 97 cells/mm² after indentation). Comparing across experimental groups, the density of injured/dead cells after indentation in the 9 mN force group was significantly greater (p ≤ 0.001) than in the sham negative control group (167 ± 97 cells/mm² versus 34 ± 31 cells/mm² respectively). Importantly, the density of injured/dead cells before indentation was similar between all of the experimental groups.

In the 9 mN indentation force group, cell injury/death was greatest closest to the center of contact where the contact pressures were highest (Figure 7A). Cell injury/death then progressively decreased with decreasing P/P₀, (i.e. decreasing percentage of the peak applied pressure). Still, at all locations, the density of injured/dead cells remained significantly higher (p ≤ 0.05) than the sham negative control (Figure 7A). Interestingly, injured/dead cell densities for the contact only group were close or within the range of the injured/dead cell densities of the sham group (Figure 7B). Injured/dead cell densities at P/P₀ < 91% were no longer statistically higher (p > 0.05) than sham, and injured/dead cell densities at P/P₀ < 78% (5.7 kPa or 42.75 mmHg) were within the range of the sham group (denoted as the gray area in Figure 7; the range was 7 cells/mm² - 99 cells/mm²).

4. Discussion

In this study, we successfully developed an experimental testing platform enabling a well-defined indentation force to be applied onto the corneal endothelium in a controllable and measurable manner. Indentation-type forces are applied to the corneal endothelium when a surgeon contacts a graft with forceps, e.g. when dragging a lenticule from a trephination block onto a Busin glide in DSEK (Busin et al., 2008) or when dislocated nuclear lens fragments touch the endothelium during cataract surgery (Amir-Asgari et al., 2016). To the best of our knowledge, this engineering-based approach – which delineates the effects of specific types and magnitudes of loading on the corneal endothelium – has not been previously pursued.

In the 9 mN indentation force group, significant cell loss was observed after mechanical loading (Figure 6). Because a spherical indentor was used, a pressure gradient was generated (Eqn. 6) within the circular contact area, where the peak pressure (P₀ = 18.64 kPa or 139.81 mmHg) was applied at the center of indentation (Eqn. 7) and decreased as a function of radius (Figure 4). This pressure gradient allowed us to assess CEC damage in a pressure-dependent manner within the contact area, and we found significant CEC loss (compared with the sham control) at all pressure ranges (Figure 7A). From these findings, we can conclude that CECs are vulnerable to contact pressures of 10.25 kPa or 76.88 mmHg (55% of P₀) and above.

To further refine these measurements and investigate lower contact pressures, the effects of minimal contact (F_beam = 0.65 mN) between the bead and the specimen were assessed. In this experimental group, significant cell loss was again observed after loading (Figure 6). However, analysis of pressure-dependent cell loss in the “contact only” group demonstrated that at contact pressures below 91% of P/P₀, or pressures less than 6.65 kPa or 49.88 mmHg, cell loss was no longer significantly higher than in the sham group (Figure 7B). Moreover, at P/P₀ below 78%, or pressures less than 5.7 kPa or 42.75 mmHg, the mean injured cell density fell within the range of CEC loss seen in sham groups. These findings suggest that CEC remain viable below a critical contact pressure threshold of approximately 5.7 kPa (~43 mmHg).

To quantify cell death, a fluorescent staining protocol was chosen based on its widespread use (Bernard et al., 2014; Hong et al., 2009; Pipparelli et al., 2011; Saad et al., 2008; Schallhorn et al., 2015; Terry et al., 2009b; Terry et al., 2013). However, differing from previous work, we calculated injured CEC densities by acquiring high-resolution fluorescence micrographs (1990×1440 pixels, 905.75 nm/pixel scale) of calcein/PI-stained buttons, counting the number of PI-labelled CEC nuclei and dividing by the contact area. This method contrasts the more common method of staining buttons with trypan blue/alizarin red S and determining the stained area fraction after thresholding (Pipparelli et al., 2011; Saad et al., 2008). This distinct approach was taken for two reasons: first, our main focus was on assessing damage at sites of indentation only; second, the high resolution of our images allowed for reliable visualization and quantification of individual CEC nuclei. The size of the contact areas was only ~1.5% of the total surface area the button. Thus, quantifying CEC loss for the full button was determined to be unnecessary and irrelevant given the study objective.

Unfortunately, similar challenges experienced in previously described methods persisted in our experiments. For example, accurate thresholding remained influenced by staining quality, while in out-of-focus regions, PI-labelled nuclei appeared blurry. To overcome these obstacles, extended focal imaging (EFI) based on a locally acquired z-stacks at the site of indentation (Figure 3C) was incorporated as part of the imaging procedure. This allowed for visualization of all nuclei accurately for counting. Additional challenges were faced during the execution of mechanical indentation experiments. The stationary grip with the cantilever beam had to be manually adjusted in three-dimensional space to align the bead with the center of the specimen. However, recorded distances between the center of the specimen (determined through a circle-drawing function in MATLAB) (Chernov, 2009) and the site of indentation were relatively small (719.3 ± 320 μm, Figure S4).

The staining incubation times, along with waiting periods throughout the experiment with corneas sitting in BSS, caused corneal specimens to swell. According to reflected light micrographs acquired of fixed and cut corneal buttons after swelling in PBS, the posterior stroma appeared to swell more than the anterior stroma. This differential swelling led to an outward bulging of the posterior stroma (Figure S6) (Muller et al., 2001). Interestingly, the peripheral edges of the button appeared to swell the most. Additionally, surface undulations leading to the presence of asperities in the posterior stroma (presumably due to swelling, Figure S7) were also observed. It is possible that these asperities caused uneven force distributions throughout the contact area during indentation experiments. Specifically, the presence of asperities could lead to increased contact pressure in convex (protruding) regions within the contact area and decreased contact pressure in concave (depressed) regions within the contact area. Since these effects should cancel out over large regions, they may not impact our measurements of total CEC loss over the entire contact area (Figure 6). However, local asperities are likely to affect local measurements of cell death (Figure 7). In fact, the presence of asperities could partially explain the large variability in the injured/dead CEC density measurements obtained for the 9 mN indentation force group (range: 19 – 307 injured/dead CEC/mm²).

Swelling may also have indirectly affected CEC loss measurements by reducing the Young’s modulus of the stroma(Hatami-Marbini and Etebu, 2013a) leading to an increased indentation depth δ_ind for a given F_ind according to ${\delta }_{ind}={\left(\frac{3F_{ind}}{4E{R}^{1/2}}\right)}^{2/3}$. An increase in δ_ind will cause the indentation contact area to increase (Equation 5) and the peak contact pressure to decrease (Equation 7). While the decrease in contact pressure should reduce CEC loss, the increase in contact area is expected to increase CEC loss. According to our data, the net effect is a positive correlation (r² = 0.23) between CEC loss and expected corneal thickness (see Supplementary Material). However, the effect of swelling appears to be small compared to specimen-to-specimen variability, and corneal thickness did not vary significantly between experimental groups.

Interestingly, one specimen from the sham negative control group and the 9 mN indentation group measured a decrease in injured cell density as compared to baseline (Figure S5). While this effect was rare, it may be explained by cells getting stripped off during the course of the experiment. Note that stripped cells are not counted in our analysis, which only quantifies dead (PI-positive) cells.

Certain specimens at the site of indentation also exhibited sites of decreased calcein intensity but no PI-labelled nuclei (Figure 5A). This would suggest that some amount of calcein was able to leak out of the cell, but PI was not able to enter. We considered these cells to be viable, but it is possible that they may be fundamentally altered in some way. A limitation of this study is that we only assessed immediate cell injury/death (i.e. no temporal component), and only assessed a specific form of mechanical insult. In surgery, there are multiple forms of mechanical trauma and often multiple sites of CEC loss throughout the entire corneal graft. Moreover, local damage could propagate due to the release of damage-associated molecular patterns (DAMPs) or other mechanisms. Whether damage from mechanical forces could spread over time to induce long-term cell loss via apoptosis or necrosis in neighboring CECs will be the subject of future work.

It is well established that during EK, incision size has a significant effect on CEC loss due to the high forces CECs experience while traversing the recipient wound (Price and Price, 2008; Terry et al., 2009a). Folding of donor tissue prior to insertion and the forces it experiences as it is being crushed are viewed as the primary culprits (Alqudah et al., 2013). These findings have led to the development of novel tools and techniques which minimize or avoid wound compression altogether (Busin et al., 2008; Khor and Kim, 2014; Kruse et al., 2011; Schallhorn et al., 2015; Terry et al., 2013; Terry et al., 2015). However, from an engineering standpoint, the mechanical environment that CECs are subjected to during wound insertion is highly complex and cannot be directly related to the findings of the current study. In particular, insertion involves not only indentation forces, but a combination of compressive forces, shearing forces and bending moments whose effects on CEC viability have not yet been investigated or decoupled.

Mechanical trauma to the corneal endothelium during cataract surgery is thought to increase risk of endothelial decompensation. For example, dislocated lens fragments can collide with the endothelium when cataracts are extracted. For this reason and others, ophthalmic viscoelastic devices (OVDs) are used to cover the endothelium acting as a ‘soft’ (Arshinoff, 1999) or ‘hard’ (Kim et al., 2017) physical barrier. While the current study investigated the vulnerability of CECs in the absence of OVDs, future studies will assess how OVDs impact the critical contact pressure required to kill CECs.

It is important to note that fluid pressures applied to the donor endothelium due to intraocular pressure (IOP) or air bubbles (used in EK to adhere grafts onto donor corneas) are distinct mechanical stimuli that are not necessarily identical to indentation-based contact pressure (as investigated in the current study). Specifically, air bubbles impact CEC viability in unique ways that do not apply to mechanical indentation. For example, most air bubble-induced CEC loss occurs at the periphery of a bubble due to surface tension differences between air and the endothelial layer (Kim et al., 1997). IOP exerts the same (normal) pressure on all parts of the corneal endothelium, while spherical indentation is associated with a spatially varying contact pressure (Equation 6). As a result, indentation forces induce complex distributions of shear and axial stresses in the endothelium that are distinct from the distributions of stress induced by fluid-mediated external pressures. The material interaction of stainless steel with the corneal endothelium may also impact the extent of cell loss (and the critical contact pressure for maintenance of CEC viability) such that different results may be expected in fluid-mediated loading of the endothelium. Nevertheless, our finding that the critical contact pressure for CEC death due to indentation was 5.7 kPa (~43 mmHg) is consistent with decreased ECD measurements after documented episodes of IOP levels greater than 40 mmHg (such as those recorded in patients with primary angle closure glaucoma) (Janson et al., 2017; Olsen, 1980; Sihota et al., 2003; Tham et al., 2006). Whether hydrostatic fluid pressure (i.e., IOP) above 43 mmHg can cause CEC loss will be the topic of future investigations.

The existence of a critical contact pressure threshold for CEC death suggests that the commonly held no-touch policy during corneal transplantation (Dapena et al., 2011) could be revisited. Though it is beyond the scope of the current study, ongoing work in our laboratory is aimed at determining the minimum indentation force a surgeon could impart with forceps onto a corneal graft to perform a specific maneuver (e.g., to move a graft onto a glide or inserter). Combined with the thresholds established in the current study, these measurements could inform the development of new tools designed to prevent application of CEC-damaging contact pressures (e.g., by spreading the indentation force over greater contact areas). Nevertheless, the value of the contact pressure threshold for maintenance of CEC viability (< 5.7 kPa or 42.75 mmHg) suggests that prevention of indentation-associated CEC loss may be challenging to achieve. In the most extreme case, consider a tool that spreads surgically-applied contact forces over the entire endothelial surface of an 8 mm diameter button (~50 mm²). Such a tool would need to apply a contact force below 0.287 N (slightly greater than the weight of a penny) to avoid CEC loss. Moreover, a more realistic tool with a smaller contact area would require even smaller forces to prevent CEC loss.

The experimental platform developed in this study to enable quantification of the vulnerability of CECs to indentation forces may have broad applications beyond the current investigation. For example, this system could be used to interrogate the vulnerability of CECs under different eye-banking conditions, including different death to preservation or storage times. This platform could also be used to screen exogenous treatments of corneal grafts by coating the endothelial surface with OVDs, pharmaceutical agents, or supplementing known irrigating/media solutions with additives and assessing their ability to protect CECs from mechanical injury.

5. Conclusion

Understanding the effects of isolated mechanical loading regimens on CEC viability is a crucial step in developing techniques to minimize surgical trauma. In this study, we developed an experimental testing platform where indentation forces could be applied onto the corneal endothelium in a controllable and measurable manner. We found that CEC are highly susceptible to mechanical trauma due to indentation, and only at very low applied contact pressures (< 5.7 kPa or 42.75 mmHg) can CEC remain viable. In practicality, these findings suggest the established “no-touch” policy may be the best solution for minimizing iatrogenic CEC loss during endothelial keratoplasty procedures.