Validation of tissue optical properties measurement using diffuse reflectance spectroscopy (DRS)

Abstract

The effectiveness of photodynamic treatment depends on several factors including an accurate knowledge of optical properties of the tissue to be treated. Transmittance and diffuse reflectance spectroscopic techniques are commonly used to determine tissue optical properties. Although transmittance spectroscopy technique is accurate in determining tissue optical properties, it is only valid in an infinite medium and can only be used for interstitial measurements. Diffuse reflectance spectroscopy, on the other hand, is easily adapted to most tissue geometries including skin measurements that involve semi-infinte medium. However, the accuracy of the measured optical properties can be affected by uncertainty in the measurements themselves and/or due to the uncertainty in the fitting algorithm. In this study, we evaluate the accuracy of optical properties determination using diffuse reflectance spectroscopy implemented using a contact probe setup. We characterized the error of the optical properties fitted using two fitting algorithms, a wavelength wise fitting algorithm and a full reflectance spectral fitting algorithm. By conducting systematic investigation of the measurements and fitting algorithm of DRS, we gained an understanding of the uncertainties in the measured optical properties and outlined improvement measures to minimize these errors.

INTRODUCTION

The effectiveness of photodynamic treatment depends on several factors including an accurate knowledge of optical properties of the tissue to be treated. To correctly determine the needed light dose, the values of tissue optical properties must be well known. Transmittance spectroscopy is commonly used to measure optical properties. Our group has developed a dual-motor continuous wave transmittance spectroscopy system for optical properties measurements [1] and it has been employed in several clinical settings to quickly determine in vivo tissue optical properties. Despite the high accuracy and simple instrumentation, this technique is only valid in an infinite medium. It can be used for interstitial measurements but is not practical in most clinical settings where invasive insertion of cathether is not an option. Continuous wave diffuse reflectance spectroscopy (DRS) is also commonly used to measure tissue optical properties. This technique can be easily adapted to most tissue geometries, including skin measurements, using either a contact probe or a noncontact probe setup. However, the accuracy of the measured optical properties can be affected by uncertainty in the measurements themselves and/or due to the uncertainty in the fitting algorithm.

In this study, we conduct a series of diffuse reflectance measurements from solid phantoms with a range of optical properties using a contact probe setup. Optical properties were extracted using two different fitting algorithms, a wavelength-wise fitting algorithm and a full reflectance spectral fitting algorithm. Optical properties determined using both methods are compared against the values determined using dual-motor transmittance spectroscopy to characterize the error for each method. By conducting systematic investigation of the measurements and fitting algorithms of DRS, we gained an understanding of the uncertainties in the measured optical properties and outlined improvement measures to minimize these errors.

METHODS

Phantom preparations

9 solid phantoms with different optical properties, μ_a = 0.1 – 1 cm⁻¹, μ_s’ = 5 – 20 cm⁻¹ were used in this study. The phantoms were made with room-temperature-volcanizing (RTV) silicone mixed with carbon powder and titanium dioxide. Specifically, RTV-12A was used as the base compound, RTV-12C was used as the curing agent, carbon powder was used as light absorbers, and titanium dioxide (TiO2) was used as light scatterers. The relationship between the amount of carbon powder and TiO2 to the final optical properties are as follow [2]:

Absorption formulation

$$Carbonrequired(mg)=\frac{{\mu }_a\left(c{m}^{-1}\right)+0.0068\left(c{m}^{-1}\right)}{0.0203\left(c{m}^{-1}\cdot m{g}^{-1}\right)}\times \frac{totalvolume(ml)}{1650(ml)}$$ (1)

Scattering formulation

$$TotalTiO2required(g)=3.6(g)\times \frac{{\mu }_S^{\prime }\left(c{m}^{-1}\right)}{7.5\left(c{m}^{-1}\right)}\times \frac{totalvolume(ml)}{1650(ml)}$$ (2)

A weight ratio of 20:1(RTV12A:RTV12C) for the matrix composition is recommended by the manufacturer. However, inthis study, an increased 10:1 volume ratio was used to accelerate the curing rate of the silicon matrix. To make the phantom, absorbers and scatterers solutions were prepared separately with RTV12C. 10mg of carbon black was dissolved in 10 ml of RTV12C to make carbon ink solution at the concentration of 1 mg/ml. 10g of TiO2 was dissolved in 100ml of RTV12C to make TiO2 solution at the concentration of 0.1g/ml. Both solutions were vortex for 30 seconds and sonicated in water bath for an hour. The weight of carbon black (X mg) and TiO2 (Y g) needed for the desired optical properties were calculated based on Eqs. (1) and (2). The volume of absorber and scatterer solution needed was X ml and 10Y ml. Assuming the total volume of the phantom solution (RTV12C and RTV12A mixture) is V ml, the matrix compounds needed were calculated as RTV12C = V/11-X-10Y (ml) and RTV12A=10×V/11 (ml). The matrix solution was then mixed with X ml of absorber solution and 10Y ml of scatterer solution. The final mixture was poured into molds, as shown in Figure 1. The molds were then placed inside a desiccator to cure for 72 hours. The dessicator was connected to a vacuum pump to remove any bubble trapped in the mixture.

Figure 1.

9 solid phantoms with different optical properties inside the curing molds.

Interstitial Transmittance Spectroscopy

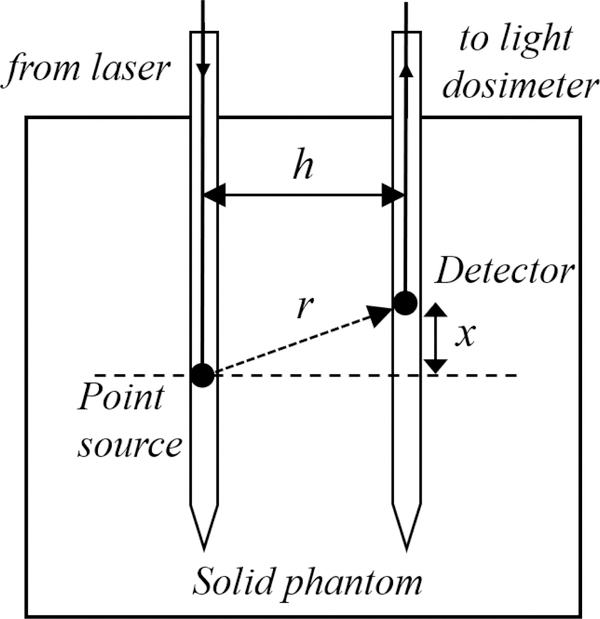
Experimental setup for the interstitial transmittance spectroscopic measurement system is shown in Figure 2. Generally, it consists of 2 transparent catheters (Flexi-needle, Best Industries, Inc., Springfield, VA) positioned at a fixed distance, h, parallel to each other. An isotropic point source was placed in one of the catheter and was connected to a 665nm laser (B&W Tek, Newark, DE). An isotropic detector was placed in the second catheter and was connected to a light dosimetry system, which consists of an array of photodiodes. Both the light source and detector fibers were controlled by a computer-controlled dual-motors platform (Velmex, Inc East Bloomfield, NY). This allows both the light source and detector to be moved to different locations in the phantom. During data acquisition, the position of light source was fix and the detector was scanned along its catheter at 0.05 mm interval. The profile of light fluence rate was recorded for 4 cm, 2 cm across both side of the light source. The dashed line in Figure 2 indicates x= 0 cm when detector was at the shortest distance perpendicular to the light source.

Figure 2.

Schematics of a light source and a detector placed inside 2 transparent catheters that are inserted into a solid phantom. The distance between two catheters is h. The position of light source is fixed during measurement, while the detector is scanned across the light source along the catheter. The distance between the detector to the light source is given by $r=\sqrt{x^2+h^2}$.

Using the diffusion approximation, the light fluence rate ϕ per source power S at a distance r from a point source can be expressed as [3]:

$$\frac{\varphi }{S}=\frac{{\mu }_{eff}^2}{4\pi r{\mu }_a}{e}^{-{\mu }_{eff}r}=\frac{3{\mu }_s^{\prime }}{4\pi r}{e}^{-{\mu }_{eff}r}$$ (3)

where S is the source power of the point source (in mW), ϕ(r) is the fluence rate in mWcm⁻² at r. r is the distance between the detector and light source and can be calculated as $r=\sqrt{x^2+h^2}$, where x and h are the parallel and perpendicular distances from the centre of the point source as shown in Figure 2. In theory, measurements of ϕ at two different distances r from the point source are sufficient to determine both μ_a and μ_s’. Since our measurments contain up to 800 distances, sample’s optical properties can be determined accurately. A differential evolution algorithm was used to fit Eq. (3) for optical properties with all free parameters, μ_a, μ_s’ and h, constrained to be positive values. More details about the system configuration and fitting algorithm can be found elsewhere [1].

Diffuse reflectance measurements with contact probe

Diffuse reflectance measurements were taken using an in-house built contact probe. The probe has two source fibers (one for narrowband fluorescence excitation and the other for broadband reflectance excitation) and 9 detector fibers at lateral distances between 0.7 – 8.1 mm away from the nearest source fiber. In this study, only one source fiber was used for broadband reflectance measurement. A tungsten lamp (Avalight, Avantes, Inc.) was used as excitation light source. A CCD-based spectrograph (Princeton Instruments, Princeton, NJ) was coupled to the detector fibers, recording a spectrum for each fiber. Measurements were taken by placing the probe on the surface of the phantom and triggering the data acquisition. This probe has been used to acquire optical properties in-clinic for human PDT cases [4, 5]. More details about the probe design and measurement configurations can be found elsewhere [6].

Wavelength-wise hybrid P3 Fitting Algorithms

Diffuse reflectance data is pre-processed by correcting for offset, background noise, and ambient light, before it can be used to fit for the optical properties. Two fitting algorithms were used to extract the optical properties, namely the wavelength-wise and the spectral fitting algorithms. For wavelength-wise fitting method, we use a model based on the hybrid P3 approximation developed by Hull and Foster [7]. By using this model, which models light propagation in turbid media, we are able to obtain values for μ_a and μ_s’. The fitting algorithm used to obtain values for optical properties from this model is a built-in MATLAB function called fminsearch. The results of this fitting process are the complete absorption and reduced scattering spectra of the sample for the desired wavelength range.

Spectral fitting algorithm

For spectral fitting method, we employed a multiwavelength fitting algorithm that simultaneously fits all reflectance spectra (wavelength range of 600 to 800nm used in this study) using multiple source-detector separation distances. Here, two assumptions were made about μ_a and μ_s’ to stabilize the analysis for optical properties determination: 1) μ_a(λ) = ∑_i c_iϵ_i(λ), and 2) ${\mu }_s^{\prime }=A{\lambda }^{-B}[8].{ϵ}_i(\lambda )$. ϵ_i(λ) is the molar spectral absorbance of the ith chromophores and c_i is the molar concentration of the ith chromophore. Only one chromophore, carbon black powder, was used in this study. The extinction coefficient of the carbon was determined by direct measurement of carbon dissolved in RTV12C using an absorption spectrometer. We directly reconstructed the concentration and the parameters A and B using a nonlinearly constrained optimization method, FMINCON, implemented in MATLAB. The optical properties at 665nm are determined by using the equations given above. This data analysis is based on the theory of diffuse approximation for a semi-infinite medium. The solution for diffuse reflectance from a semi-infinite medium as a function of optical properties (μ_a, μ_s’) and source-detector separation ρ can be found in [9].

RESULTS AND DISCUSSIONS

The optical properties at 665nm for 9 solid phantoms determined from transmittance and diffuse reflectance spectroscopic measurements and using different fitting algorithms are presented in Table 1. Diffuse reflectance at the same wavelength was calculated based on the measured μ_a and μ_s’ using the following analytical expression [10]:

$$R_d=0.4843a^{\prime }\cdot \left(1+e^{-4.428\sqrt{1-a^{\prime }}}\right)e^{-2.65\sqrt{1-a^{\prime }}}$$ (4)

where,

$$a^{\prime }=\frac{{\mu }_S^{\prime }}{{\mu }_a+{\mu }_S^{\prime }}$$ (5)

Table 1.

The expected optical properties of 9 solid phantoms.

Phantom	Expected optical properties (cm−1)
	Absorption coefficient, μa	Reduced scattering coefficient, μs’
1	0.09	4.2
2	0.09	8.5
3	0.09	16.9
4	0.25	4.2
5	0.25	8.5
6	0.25	16.9
7	0.45	4.2
8	0.45	8.5
9	0.45	16.9

Results from Table 2 show that there are discrepancies between the optical properties determined from transmittance spectroscopy and the expected values (Table 1) calculated using Eqs. 1 and 2. The differences between the measured and expected values could be due to uncertainties during sample preparation and batch variation in optical properties of the phantom materials (such as the carbon powder and the silicone curing and base compounds). Despite the differences, the optical properties determined from transmittance spectroscopy measurements are assumed to be the true optical properties of the phantoms for further analysis of this study. The phantoms’ absorption coefficients, determined using transmittance spectroscopy, range from 0.09 – 0.5 cm⁻¹ and the reduced scattering coefficients range from 3.9 – 16.4 cm⁻¹.

Table 2:

Optical properties at 665nm (μ_a, μ_s’) for 9 solid phantoms determined from transmittance spectroscopic measurements and diffuse reflectance spectroscopic measurements, fitted using wavelength-wise and spectral fitting algorithms. Calculated diffuse reflectance at 665nm were also included.

Phantom	Transmittance			Diffuse Reflectance - Contact Probe
	Interstitial			Wavelength-wise fit			Spectral fit
		μa	μs’	Rd	μa	μs’	Rd	μa	μs’	Rd
1	0.13	3.89	0.43	0.02	0.88	0.48	0.05	1.80	0.44
2	0.09	9.67	0.62	0.02	0.95	0.50	0.05	4.76	0.60
3	0.10	16.42	0.67	0.20	13.24	0.55	0.13	14.73	0.62
4	0.25	4.23	0.33	0.08	1.56	0.36	0.13	2.61	0.36
5	0.23	6.57	0.42	0.14	8.38	0.53	0.15	6.81	0.49
6	0.25	13.18	0.51	0.40	14.34	0.45	0.26	13.43	0.51
7	0.50	3.92	0.21	0.01	7.72	0.85	0.18	4.83	0.40
8	0.43	7.01	0.32	0.06	9.98	0.68	0.26	6.42	0.39
9	0.42	11.60	0.41	0.05	9.79	0.69	0.22	12.07	0.52

To assess the accuracy of optical properties determined from diffuse reflectance measurements, we compute the percentage difference (%) between the values obtained using wavelength-wise and spectral fitting algorithms to the values determined from transmittance spectroscopy. The percentage error of μ_a, μ_s’ and Rd at 665nm obtained using both fitting methods are presented in Table 3. For wavelength-wise fitting, the average percentage error was 77.1±18.7% for absorption coefficients, 49±31.8% for reduced scattering coefficients and 63.2±87.6% for calculated diffuse reflectance. For spectral fitting, the average percentage error was 40.6±16.9% for absorption coefficients, 21.6±19.7% for reduced scattering coefficients, and 19.4±25.8% for calculated diffuse reflectance. Results show that there are huge differences between the optical properties obtained from diffuse reflectance spectroscopy measurements and transmittance spectroscopy measurements. Nevertheless, the percentage errors for optical properties obtained using spectral fitting algorithm were smaller compared to using wavelength-wise fitting algorithm. Although results show that spectral fit is more accurate in determining sample’s optical properties, the percentage errors for both methods are somewhat high. The maximum errors for μ_a and μ_s’ are 98.8% and 97% for wavelength-wise fitting method and 64.3% and 53.7% for spectral fitting method. The maximum errors for Rd can be as high as 294.5% for wavelength-wise fitting method and 88.4% for spectral fitting method. These huge errors suggest there could be potential errors due to measurement uncertainties.

Table 3:

Percentage error (%) of optical properties (μ_a, μ_s’) and diffuse reflectance at 665nm, determined using wavelength-wise and spectral fitting algorithms, assuming that the results obtained from transmittance spectroscopy in Table 2 are correct.

Phantom	Wavelength-wise fit			Spectral fit
	μa	μs’	Rd	μa	μs’	Rd
1	84.2	77.4	13.4	57.3	53.7	3.0
2	76.5	90.2	20.4	43.5	50.8	3.0
3	96.1	19.4	18.0	27.5	10.3	6.7
4	68.4	63.1	7.5	48.0	38.3	8.3
5	36.1	27.5	26.1	33.3	3.7	16.9
6	59.5	8.8	11.8	3.6	1.9	0.5
7	98.8	97.0	294.5	64.3	23.2	88.4
8	86.8	42.4	109.2	40.1	8.4	21.1
9	87.8	15.6	68.1	48.1	4.1	27.1
Average (stdev)	77.1 (18.7)	49.0 (31.8)	63.2 (87.6)	40.6 (16.9)	21.6 (19.7)	19.4 (25.8)

To minimize errors due to measurement uncertainties, we carefully repeated the diffuse reflectance spectroscopy measurements. The room light is turned off and the phantom is completely shielded to prevent any signal contamination by ambient light. The contact probe is pressed firmly against the phantom surface to prevent potential light leakage during data acquisition. Special care is taken to ensure good contact of probe and phantom during measurement by avoiding regions of uneven phantom surfaces.

The optical properties and calculated diffuse reflectance at 665nm, determined from the repeated diffuse reflectance spectroscopic measurements for the same 9 solid phantoms are presented in Table 4. The percentage difference between the optical properties determined from the repeated diffuse reflectance spectroscopic measurements and transmittance spectroscopic measurements are presented in Table 5. For wavelength-wise fitting methods, the average percentage error was 20.9±10.3% for μ_a, 25.7±16.2% for μ_s’ and 14.0±18.4% for Rd. For spectral fitting method, the average percentage error was 10.1±9.7% for μ_a, 17.7±9.4% for μ_s’ and 7.8±3.6% for Rd. The percentage errors of the optical properties determined from the repeated diffuse reflectance spectroscopic measurements were significantly smaller compared to the first set of measurements. Despite the robustness of diffuse reflectance spectroscopic technique to be easily adapted to various tissue geometry using contact probe setup, this technique is prone to large measurement uncertainties if care is not taken during data acquisition.

Table 4.

Optical properties at 665nm (μ_a, μ_s’) for the same 9 solid phantoms determined from the repeat diffuse reflectance spectroscopic measurements, fitted using wavelength-wise and spectral fitting algorithms. Calculated diffuse reflectance at 665nm were also included.

Phantom	Diffuse Reflectance - Contact Probe
	Wavelength-wise fit			Spectral fit
	μa	μs’	Rd	μa	μs’	Rd
1	0.09	2.62	0.43	0.10	3.60	0.45
2	0.07	5.70	0.58	0.11	8.67	0.57
3	0.08	13.31	0.66	0.12	12.07	0.61
4	0.34	1.78	0.16	0.25	4.49	0.34
5	0.26	7.75	0.42	0.23	8.80	0.46
6	0.19	15.89	0.58	0.23	15.44	0.55
7	0.35	5.17	0.31	0.46	2.83	0.18
8	0.41	6.42	0.32	0.42	8.42	0.36
9	0.40	11.77	0.42	0.42	12.81	0.43

Table 5.

Percentage error (%) of optical properties (μ_a, μ_s’) and diffuse reflectance at 665nm, determined from the repeat diffuse reflectance spectroscopic measurements, assuming that the results obtained from transmittance spectroscopy in Table 1 are correct.

Phantom	Wavelength-wise fit			Spectral fit
	μa	μs’	Rd	μa	μs’	Rd
1	32.3	32.6	0.5	20.8	7.5	4.0
2	20.0	41.1	6.7	29.4	10.3	8.2
3	17.6	18.9	0.3	17.6	26.5	9.1
4	35.6	57.9	50.1	0.0	6.1	2.9
5	14.2	18.0	1.2	2.2	33.9	10.4
6	24.7	20.6	13.7	8.4	17.1	7.3
7	31.3	31.9	44.7	8.7	27.8	14.3
8	6.7	8.4	0.9	3.2	20.1	10.7
9	5.7	1.5	8.1	0.9	10.4	3.7
Average (stdev)	20.9 (10.3)	25.7 (16.2)	14.0 (18.4)	10.1 (9.7)	17.7 (9.4)	7.8 (3.6)

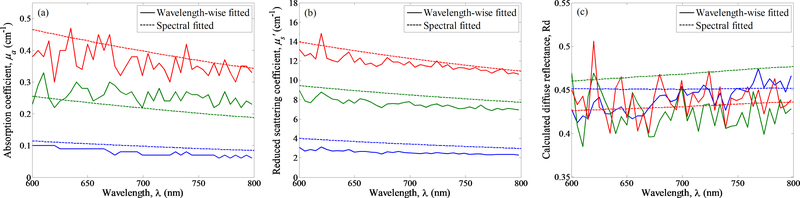
From Tables 3 and 5 we can see that for both sets of measurements, spectral fitting method was able to extract more accurate sample’s optical properties compared to wavelength-wise fitting algorithm. Beside producing more accurate optical proeprties at 665nm, spectral fitting algorithm can also reduce the crosstalk between the extracted μ_a and μ_s’ over the full range of wavelength used for fitting. Figure 3 (a) to (c) show the full spectra of reconstructed optical properties (μ_a, μ_s’) and diffuse reflectance over the range of wavelengths fitted using wavelength-wise and spectral fitting algorithms, for 3 phantoms. Blue lines are results for phantom #1, green lines are results for phantom #5 and red lines are results for phantom #9. Solid lines represent fitting results using wavelength-wise algorithm and dashed lines represent fitting results using spectral fitting algorithm. Generally, the spectra of optical properties obtained using spectral fitting are smoother (fewer crosstalks between μ_a and μ_s’) over the full fittng range compared to those obtained using wavelength-wise method. The fitting of diffuse reflectance data can be stabilized by utilizing the full spectral range and constraints based on the molar spectral absorbance of sample’s chromophore.

Figure 3.

Spectra of (a) absorption coefficient, μ_a, (b) reduced scattering coefficient, μ_s, and (c) calculated diffuse reflectance determined from diffuse reflectance spectroscopic measurements of 3 solid phantoms, over the range of wavelength used for fitting. Solid lines represent results obtained using wavelength-wise fitting algorithm and dashed lines represent results obtained using spectral fitting algorithm. Blue lines are phantom #1, green lines are phantom #5, and red lines are phantom #9.

Transmittance spectroscopy methods implemented using a dual-motor platform is an effective way to determine sample’s optical properties and decent accuracy in retrieveing μ_a and μ_s’ from turbid media has been demonstrated in our previous work [1]. This method requires insertion of catheter to guide the source and detector fibers and is suitable for interstitial measurements from tissue such as the prostate. Furthermore, the dual-motor design is also advantageous in allowing multiple measurements at different locations for the evaluation of optical properties heterogeneities within the probed volume. Despite the accuracy in optical properties determination and simple instrumentation, the invasiveness of catheter insertion makes this method not practical in most clinical settings including skin optical properties measurements. Diffuse reflectance spectroscopy implemented using a contact probe offers a noninvasive way of extracting tissue optical properties that can be easily adapted to various tissue geometries. However, this method is more prone to measurement uncertainties due to probe pressure, light leakage due to bad contact, and movement artefacts during data acquisition. Furthermore, the accuracy of measured optical properties can be affected by the fitting algorithm used, as shown in this study. We show that optical properties obtained using spectral fitting algorithm is more accurate than using wavelength-wise P3 approximation, compared to the values obtained from transmittance spectroscopy. However, spectral fitting method requires the priori information about the molar spectral absorbance of all sample’s chromophores. Since most chromophores in biological tissues are well identified and the molar spectral absorbance has been well characterized, we conclude that spectral fitting method is more suitable to be employed to extract optical properties from diffuse reflectance spectroscopic measurements. For samples with unknown constituents, wavelength-wise fitting algorithm can still be used to provide fairly accurate sample’s optical properties (with some crosstalks between μ_a and μ_s’) at each wavelength used in the fitting.

CONCLUSIONS

In this study, we evaluated the accuracy of optical properties determination using diffuse reflectance spectroscopy implemented using a contact probe setup. Our data show that the contact probe is susceptible to large measurement uncertainties, which can be minimized if special care is taken when data is being recorded. We characterized the error in the optical properties determined using wavelength-wise fitting algorithm and a full reflectance spectral fitting algorithm, and our results suggest that the latter can extract more accurate sample’s optical properties with less crosstalk between the μ_a and μ_s’. By conducting systematic investigation of the measurements and fitting algorithm of DRS, we gained an understanding of the uncertainties in the measured optical properties and outlined improvement measures to minimize these errors.