Abstract
We examine methods to reweight classical molecular mechanics solvation calculations to more expensive QM/MM energy functions. We first consider the solvation free energy difference between ethane and methanol in a QM/MM Hamiltonian from configurations generated in a cheaper MM potential. The solute molecules in the QM/MM Hamiltonian are treated with B3LYP/6–31G* and the solvent water molecules are treated classically. The free energy difference in the QM/MM Hamiltonian is estimated using Boltzmann reweighting with both the Non-Boltzmann Bennett method (NBB) and the Multistate Bennett Acceptance Ratio (MBAR) and the variance of each method is directly compared for an identical dataset. For this system, MBAR-derived methods are found to produce smaller overall uncertainties than NBB-based methods. Additionally, we show that to reduce the variance in the overall free energy difference estimate in this system for a fixed amount of QM/MM calculations, the energy re-evaluations in the Boltzmann reweighting step should be concentrated on the physical MM states with the highest overlap to the QM/MM states, rather than allocated equally over all sampled MM states. We also show that re-allocating the QM/MM re-evaluations can be used to diagnose poor overlap between the sampled and target state. The solvation free energies for molecules in the SAMPL4 solvation dataset are also calculated in the QM/MM Hamiltonian with NBB and MBAR, and the variances are marginally smaller for MBAR. Overall, NBB and MBAR produce similar variances for systems with poor sampling efficiency, and MBAR provides smaller variances than NBB in systems with high sampling efficiency. Both NBB and MBAR converge to identical solvation free energy estimates in the QM/MM Hamiltonian, and the RMSD to experimental values for molecules in the SAMPL4 solvation dataset decreases by approximately 28% when switching from the MM Hamiltonian to the QM/MM Hamiltonian.
GRAPHICAL ABSTRACT
1. Introduction
Molecular dynamics and Monte Carlo simulations have become ubiquitous tools in the field of computational chemistry and allow researchers to calculate numerous thermodynamic properties of interest such as solvation free energies,1–5 ligand binding,6–9 and protein folding.10–13 These computational techniques continue to experience increasing success in reproducing and even predicting experimentally measured properties, as demonstrated by recent blind prediction studies.4,5,14–29 The two primary challenges in matching computed estimates with experimental values are the efficiency of the simulation in sampling relevant system configurations and the accuracy of the Hamiltonian used to generate the samples.30
The ability to estimate free energy differences using expensive energy models, up to and including quantum mechanics, is often desirable because these ab initio potentials automatically incorporate degrees of electronic freedom, such as polarizability, which may be critical to describe the system of interest. Quantum mechanical methods also avoid the need to parameterize classical partial charges and intramolecular parameters on a per-atom basis. The importance of capturing the proper polarization, charges, and bonded parameters were re-emphasized in the recent SAMPL blind prediction studies.17,18,20,22–28 However, simulating directly in complex Hamiltonians with explicit polarization or quantum mechanical effects is often prohibitively expensive, which further aggravates the challenge to obtain a sufficient number of samples for converged thermodynamic quantities.
Warshel and others showed that one can avoid simulating directly in the expensive Hamiltonians by simulating in a cheaper energy function and calculating ensemble averages in the target Hamiltonian by reweighting each sampled configuration from the equilibrium distribution of the cheap potential to the Boltzmann distribution that would be characteristic of the expensive target potential.31–35 Most simply, one can sample from energy function 1 and calculate properties in another energy function 2 with importance sampling using the following equations:36
| (1) |
| (2) |
Where ΔU12(x) = U2(x) − U1(x) is the energy difference between energy function 1 and energy function 2, ΔA12 = A2 − A1 is the free energy difference between the two potentials, and O(x) is any observable of the system. These equations require only energy evaluations in the target Hamiltonian which avoids completely the computational expense of direct sampling in the expensive potential. When the target Hamiltonian is an expensive quantum-based potential, the rate limiting step in computing a free energy estimate using eq 2 is the energy evaluations of the cheap sampled MM configurations in the target potential. Although a large quantity of samples can easily be drawn from the cheap MM state, each configuration must be re-evaluated in the expensive potential before being used in equation 2. It is therefore critical to efficiently utilize the information from the MM sampling, as only a few configurations may have significant probability in the expensive potential. As can be seen in eq 2, if U12(x) varies significantly from one configuration to another, the average will be dominated by only a small set of configurations. All ensemble averages in the expensive potential, as well as the free energy estimate, will have large uncertainties if only a small number of configurations with high probability in the expensive potential are sampled.
A range of different alternate approaches to eq 2 have been used previously to improve the efficiency of reweighting from a cheap to expensive potential. As we review below, each of these approaches has a different bias and statistical efficiency. There is currently no clear consensus on which approaches are most efficient and have the lowest systematic error (bias), as evidenced by the numerous studies in the past decade which use a variety of different Boltzmann reweighting techniques, and we attempt to resolve this situation here.
The simplest method to obtain free energy differences via Hamiltonian reweighting involves reweighting from one sampled to one unsampled state, generally referred to as exponential reweighting or the Zwanzig equation,5,31,33–41 which is simply eq 1. This method produces asymptotically unbiased free energy differences in the limit of large sampling. However, this method suffers from the known issue of being numerically noisy and highly sensitive to the degree of phase space overlap and amount of sampling.42
In recent years, a series of reweighting techniques have been developed which use configurations from multiple sampled states simultaneously to more efficiency calculate the free energy difference between a cheap and expensive potential.43–45 Multistate reweighting techniques generally outperform Zwanzig approaches4,46 because information from two or more sampled states is used to probe the configuration space of the unsampled state. Two of the most widely used multistate reweighting methods are the Non-Boltzmann Bennett (NBB) method developed by König et al.4,24,44,47 and the Multistate Bennett Acceptance Ratio (MBAR) method developed by Shirts and Chodera.45,48 MBAR leads to free energy estimates identical to those from the weighted histogram analysis method in the limit of zero width bins,49 and also includes accurate asymptotic error estimates.46 With both MBAR and NBB, an estimate of the free energy difference between two states in the expensive potential is calculated by evaluating the energy in the expensive potential of all configurations from some set of cheap sampled states. Although NBB and MBAR use identical inputs, the differences in the formulation of each statistical estimator potentially lead to differences in the bias and uncertainty in the final free energy estimate. To obtain the optimal estimate of the free energy difference to an unsampled state given a set of configurations in a sampled state one should use the reweighting method which produces the lowest biases and uncertainties, and the decision between NBB and MBAR requires a direct comparison of the biases and uncertainties produced by both estimators.
In this study, we directly compare the NBB and MBAR methods, as well as several variants, on the same dataset to determine the most efficient ways to obtain an estimate of the free energy in an expensive Hamiltonian given sampling from a cheaper classical potential. A recent study suggests that the traditional exponential averaging method outperforms the multistate NBB method when reweighting between an MM and QM/MM potential.50 Here we extend this comparison by including the Multistate Bennett Acceptance Ratio method as well as logical variants of both MBAR and NBB. All methods are compared for an equal computational expense (an equal number of QM/MM energy evaluations, since all methods use the same MM simulations), and the statistical uncertainty is used as the benchmark for method efficiency. We first examine, in depth, a simple system of methanol and ethane in water and calculate the difference in solvation free energy between these two compounds using both NBB and MBAR. The same comparative analysis of the uncertainties between MBAR and NBB is then applied to the solvation free energy of the molecules in the SAMPL4 small molecule solvation dataset. In all cases, the molecules are simulated in a classical fixed-charge potential and the system is reweighted to a QM/MM Hamiltonian. A previous study using NBB showed that the QM/MM Hamiltonian provides a small but statistically significant improvement over standard MM force fields at matching experimental data.4,5,29 We evaluate whether the magnitude of this benefit changes when different methods are used to reweight the same MM configurations to the same QM/MM Hamiltonian.
With all multistate reweighting methods, the energy re-evaluations in the expensive potential are performed with configurations drawn from multiple different sampled states. A ‘state’ in the context of this paper consists of a temperature and volume as well as a specific Hamiltonian. This Hamiltonian at each state can correspond to a physical system, referred to as the end state, or can be one of many unphysical modified Hamiltonians, referred to as intermediate states. One possible allocation of these QM/MM calculations is to place an equal number of energy re-evaluations at each sampled end state and intermediate state. However, one could in theory place a larger fraction of the energy re-evaluations in a particular sampled state in order to lower the uncertainty in the final free energy estimate. Thus, we also test a variety of different allocations and assess whether we minimize the variance in the free energy difference estimate by evenly dividing the energy re-evaluations among all sampled states or placing more of the re-evaluations in a single state.
It is worth noting that a number of previous studies by Essex and coworkers have made modifications to the original Zwanzig relationship in order to overcome the large statistical uncertainty in eq 1 by using only the intermolecular interaction energies for ΔU12.5,38,39 The resulting free energy produced by eq 1 with this substitution reflects the difference in free energy between the pure MM state and an unsampled state with MM intramolecular interactions and QM/MM intermolecular interactions. The additional step to convert the intramolecular interactions from MM to QM/MM at each endstate is assumed to contribute negligibly to the overall free energy difference. The bias introduced by this approximation is in many cases small,5,38,39 but there is no rigorous bounds or systematic prediction of the size of the approximation. Understanding the limits of this uncontrolled approximation is beyond the goals of the present study and we instead focus on reweighting variants that use rigorously correct approaches with asymptotically unbiased free energy differences.
2. Theory
2.1. Non-Boltzmann Bennett
Bennett showed51 that the minimum variance estimate of the free energy between two states, given configurations sampled from both states, can be calculated with
| (3) |
where ΔA0,1 is the free energy difference between states 1 and 0, Ui is the energy of a configuration in state i, f denotes the Fermi function
| (4) |
and
| (5) |
where Ni denotes the number of configurations sampled from state i. The estimator shown in eq 3 is valid and asymptotically unbiased for any C, and thus will converge toward the correct free energy with any value, but the choice of C shown in eq 5 gives the lowest possible statistical uncertainty. If no samples are drawn from either of the states 0 or 1 then equation 3 cannot be used to estimate the free energy difference. We often encounter this situation when one or both of the states are in a quantum-based Hamiltonian where direct sampling is computationally infeasible.
In the Non-Boltzmann Bennett method, the energy difference between the two sampled states 0 and 1 in eq 3 is replaced with the energy difference between two unsampled states 0 and 1, and the configurations are drawn from two ‘biased’ states 0, b and 1, b. The bias in the potential energy for each sampled configuration in the biased state is
| (6) |
where Ubiased and U represent the potential energy in the sampled and unsampled Hamiltonian, respectively. The ensemble averages in the unsampled states 0 and 1 are recovered from the configurations sampled in the biased states using the relationship originally developed by Torrie and Valleau52,53 to calculate the unbiased ensemble average of a property X from samples collected in a biased state:
| (7) |
Calculating the ensemble averages in equation 3 with configurations in biased states reweighted with equation 7 leads to the NBB equation for calculating the free energy difference between two unsampled states:
| (8) |
Note that the minimum variance constant C is defined in terms of the number of samples from each of states 0 and 1. However, there are no samples from state 0 and 1. Since we cannot use Bennett’s original formula for the minimum variance choice of C, the choice used in previous NBB papers was to implicitly set N0 = N1. Since both N0 and N1 are in fact equal to each other (besides being equal to zero), this seems a natural choice, but the original derivation of the minimum variance C in eq 5 is no longer applicable. However, the formula will still converge to the correct answer in the limit of sufficient samples for all finite choices of C.
In many instances, the initial and final unsampled states of interest are connected through a series of intermediate states λ0, … , λK and the full free energy difference is computed through the sum of the free energy differences between each step along the entire thermodynamic path.
| (9) |
The computational overhead of computing free energies with eq 8 generally depends most sensitively on the number of energy evaluations in the expensive unsampled potential. Nominally, the QM energy of every configuration in each sampled intermediate state should be computed for NBB, and the total free energy difference is calculated as the sum across all unsampled intermediate states with eq 9. The NBB method that uses all intermediate unsampled states is referred to as ‘NBB-direct’ and a diagram for this method is presented in Figure 1. The term ‘direct’ in this context does not reflect that sampling is done directly in the expensive potential. Rather, this follows the naming convention used in a recent study by Min and coworkers in which ‘direct’ implies that the alchemical path connecting the end states includes intermediate states in the expensive potential.54 If a total of N samples are drawn from each of K intermediate states, the total number of QM energy evaluations with NBB-direct is KN.
Figure 1:
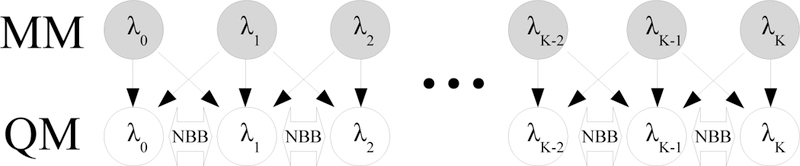
Illustration of the NBB-direct method in which each intermediate MM state is connected to an intermediate unsampled QM state. Grey nodes indicate sampled states and white nodes indicate unsampled states. Thin black arrows indicate where configurations from the sampled state are re-evaluated in the target state. Thick arrows indicate where free energy differences are evaluated. The NBB-direct method requires QM energies for all configurations from all sampled MM states.
In the systems studied in this work, the intermediate states along the thermodynamic path represent a mixed Hamiltonian of the two physical end states. All intermediate states are therefore unphysical and the QM/MM energies of configurations in these states are not well-defined. We instead assign energies to these intermediate states by first evaluating the QM/MM energy at both physical end states and then interpolate the energy in the intermediate state λk with:
| (10) |
where is the QM/MM energy of configuration x in the intermediate state λk , interpolating between the physical end states λ0 and λK , and y denotes the order of the mixing rule between the two states (generally assumed to be 1). Because a QM/MM energy evaluation is computed at both end states for each configuration, there are a total of 2KN QM/MM evaluations necessary for NBB-direct.
The number of QM evaluations can be reduced below 2KN by setting the bias, for all i ∈ {1..K − 1}. The intermediate unsampled QM states collapse to the sampled MM states and no QM energies need to be calculated at these states. The thermodynamic cycle in this reweighting scheme, referred to as ‘NBB-indirect’, is illustrated in Figure 2 and was adopted in all previously published studies employing NBB to save computational expense.4,24,44,47 NBB-indirect requires the QM energies of all N configurations sampled from states λ0, λ1, λn − 1, and λn for a total of 4N QM energy evaluations. No interpolation from equation 10 is needed for NBB-indirect because only the QM energies at one of the physical end states is needed for every reweighted configuration. Although NBB-indirect is the most commonly used variant of the Non-Boltzmann Bennett method, we have included the NBB-direct method for completeness because it utilizes additional QM/MM calculations which gives the potential for NBB-direct to outperform NBB-indirect.
Figure 2:
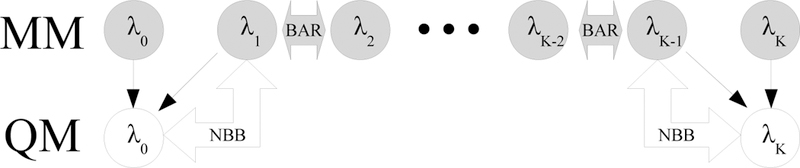
Illustration of the NBB-indirect method in which each intermediate MM state is connected through BAR except the fi two MM states which are reweighted to the unsampled QM state. Grey nodes indicate sampled states and white nodes indicate un-sampled states. Thin black arrows indicate that configurations from the sampled state are re-evaluated in the target state. Thick arrows indicate where free energy differences are evaluated. The NBB-indirect method requires QM energies for all configurations from λ0, λ1, λK−1, λK.
2.2. Multistate Bennett Acceptance Ratio
The Multistate Bennett Acceptance Ratio (MBAR) method was developed as an extension of the widely used Weighted Histogram Analysis Method (WHAM) in the limit of zero-width bins, and a generalization of the minimum variance Bennett Acceptance Ratio (BAR) method for more than 2 states. MBAR calculates the free energy differences between any number of sampled and unsampled states simultaneously and has been proven to have the lowest statistical error among all reweighting estimators.45,48 The MBAR estimate of the relative free energy of state i is
| (11) |
where xjn is the nth configuration sampled in state j, and Ui is the energy of the configuration in state i. A notable difference between the NBB estimator (eq 8) and the MBAR estimator (eq 11) is that MBAR sums over all sampled configurations in the ensemble averages at each state, while NBB uses only configurations sampled from state i when computing ensemble averages in state i (see Supporting Information section 2). The MBAR estimator therefore uses extra information about state i that is not utilized in the NBB estimator. To calculate the difference in free energy between two unsampled QM end states using samples from K intermediate states, MBAR requires the energy of every sampled configuration in each of the two unsampled states for a total of 2KN QM calculations, which is the same expense as NBB-direct. Unlike NBB-direct, there are no unphysical QM/MM intermediate states necessary for the full MBAR method. The sampled configurations need to be re-evaluated only in the two physical QM/MM end states. Potential energies of configurations at each MM state must also be calculated in all other MM states, but this expense is usually negligible compared to the expense of recomputing energies in the QM potential. The reweighting process for MBAR is illustrated in Figure 3.
Figure 3:
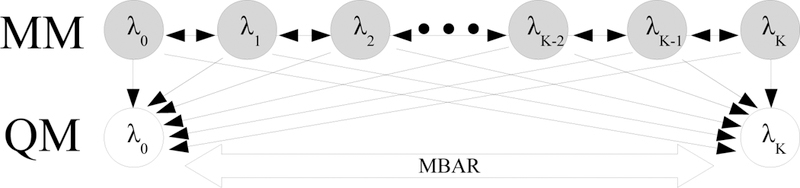
Illustration of the full MBAR method in which all sampled MM states are connected together and the free energies of all sampled and unsampled states are calculated simultaneously. Grey nodes indicate sampled states and white nodes indicate unsampled states. Thin black arrows indicate that configurations from the sampled state are re-evaluated in the target state. Thick arrows indicate where free energy differences are evaluated. The full MBAR method requires QM energies for all configurations from all sampled MM states.
The number of QM calculations necessary to estimate the free energy difference between the two unsampled states along a thermodynamic path with MBAR can be reduced by partitioning the thermodynamic path into three stages and computing the free energy difference across each section individually with MBAR. This reweighting scheme, which we call three-stage MBAR, is illustrated in Figure 4. The number of intermediate states used in the MBAR calculation on either end of the thermodynamic path in Figure 4 can vary anywhere between 1 and K/2 states. The total number of QM energy evaluations with three-stage MBAR can therefore be set anywhere between 2N and KN depending on the number of reweighted MM intermediate states. In the limit that 1 state is reweighted at each end, the three-stage MBAR method collapses to a Zwanzig reweighting between the physical QM and MM end states followed by MBAR across the entire range of MM states. For simplicity, we henceforth refer to the three-stage MBAR method with N reweighted states at each end of the thermodynamic cycle as three-stage MBAR(N). We note that for more complex calculations, what we describe as the three-stage MBAR method may contain more than three actual stages. For example, in the SAMPL4 dataset calculations described in Section 3.2 there are a total of four states, with the gas phase and solution phases each having one stage connecting the MM state to the QM/MM state and one stage connecting the MM state to an analytical reference.
Figure 4:
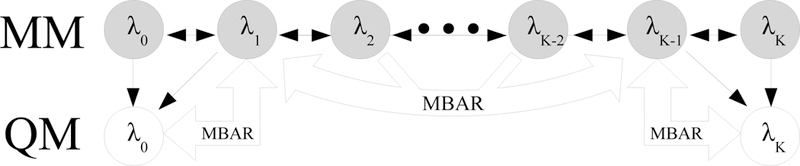
Illustration of the three-stage MBAR method in which the states are divided into three groups that are each solved simultaneously with MBAR. Grey nodes indicate sampled states and white nodes indicate unsampled states. Thin black arrows indicate that configurations from the sampled state are re-evaluated in the target state. Thick arrows indicate where free energy differences are evaluated. The three-stage MBAR method requires QM energies for all configurations from the MM states included in the groups with the unsampled QM states. The three-stage MBAR method with two reweighted states at each end is shown here, however the method can generally be applied to any number of reweighted states.
2.3. Effective Number of Samples
A final concept we will use in this paper is the number of effective samples. The number of effective samples provides a rough quantitative metric of the information gained in an unsampled state using samples from another state. If we have a weighted average , then Kish’s formula for calculating the number of effective samples is55
| (12) |
where the last step assumes normalized weights Σn Wn = 1. As can be seen from this formula, if one weight is significantly larger than all others, the number of effective samples approaches 1; if all weights are similar, the number of effective samples approaches N.
Ensemble averages calculated via MBAR can be expressed in terms of a weighted sum over the samples where the weights in state i are calculated as
| (13) |
where A is the Helmholtz free energy of each state (or Gibbs free energy for NPT simulations), U is the energy of each state, Nk is the number of samples from state k, and states k = 1 … K are sampled states. If state i has high overlap with the other K states, then the number of effective samples in state i will approach Σk Nk. If state i, has high overlap with only one state k, then the number of effective samples in state i will approach Nk. Finally, if state i has very little overlap with any state, then the number of effective samples in state i will approach 1.
3. Simulation Details
3.1. Ethane-Methanol
All simulations were conducted with CHARMM,56,57 using the CHARMM2258 force field. The QM and QM/MM calculations were performed with Q-Chem59 based on the CHARMM/Q-Chem interface.60
The implementation of the ethane-methanol free energy calculations follows the one presented in Reference 47. Solvation free energy differences between ethane and methanol were calculated using the standard thermodynamic cycle. Gas phase simulations were conducted with Langevin dynamics, using a friction coefficient of 5 ps−1 on all atoms and random forces according to a target temperature of 300 K. In solution, we used 862 water molecules and an octahedral box that was cut from a cube with a side length of 32.166 Å. The temperature was maintained at about 300 K by a Nosé-Hoover thermostat.61 Lennard-Jones interactions were switched off between 10 and 12 Å, while electrostatic interactions were computed with the Particle Mesh Ewald method.62 The time step was 1 fs and SHAKE was applied to all hydrogen atoms. In the gas phase, the cut-off radius was set to 998 Å.
Free energy differences were calculated based on simulations of 5 ns in gas phase and 1 ns in solution. Trajectories were written every 100 steps in gas phase and 20 steps in solution for a total of 10,000 samples from each phase. For the free energy calculations, eleven λ points were employed in both the gas phase and solution phase (0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0). Quantum potential energies were calculated for all trajectories. Each simulation was repeated four times, starting with different initial random velocities.
The dual topology hybrid of ethane and methanol was implemented using the MSCALE module of CHARMM.63 Energy evaluation was divided into three tasks:
Calculating the energy contributions of all bond, bond angle and Urey-Bradley terms of the full hybrid molecule, (this was done in the main MSCALE process to maintain the connectivity of the hybrid molecule).
dihedral angle and non-bonded contributions corresponding to state 0, (i.e., all atoms that are not part of ethane or the common environment were deleted)
dihedral angle and non-bonded contributions corresponding to state 1, (i.e., all atoms that are not part of methanol or the common environment were deleted). The λ states were generated by mixing those three energy contributions according to
The quantum-mechanical potential energies (UQM) were calculated with CHARMM and Q-Chem based on input files generated with the CHARMM-Q-Chem interface. B3LYP/6–31G* was used for the solute in both gas phase and the explicit solvent QM/MM calculations, and in solution, the solvent was treated classically. The standard QM/MM electrostatic embedding scheme was used such that the solute-solvent interactions were calculated with QM treating the water atoms as point charges.
To evaluate the potential energy of each frame of the gas phase trajectories, each calculation was divided into two tasks:
removing all atoms not corresponding to the initial state 0 (ethane) and calculating the potential energy, and
removing all atoms not corresponding to the final state 1 (methanol) and calculating the potential energy,. To calculate the potential energy of λ states, the two terms were mixed according to eq 10.
The corresponding explicit solvent QM/MM potential energy calculations (UQM/MM) were divided into two steps:
Calculating the QM/MM potential energy using a single box of water molecules that were centered around the solute for each frame of the trajectory . The quantum region consisted of the solute and the MM region consisted of the water molecules. Only the intramolecular solute-solute interactions and the solute-solvent interactions were considered. No cutoff was used. To generate the end states of the alchemical transformation, all atoms not corresponding to the end state were removed from the calculation, leading to for ethane and for methanol.
The solvent-solvent interactions were added by deleting the solute from the trajectory and calculating the potential energy using periodic boundary conditions . Thus, this approach neglects the long range solute-solvent and solute-solute interactions with the image atoms of the periodic system. However, the box size is larger than twice the standard CHARMM cutoff of 12 Åand therefore the non-bonded contribution from the periodic image with this setting is exactly zero.
To generate potential energies for each λ intermediate state, UQM/MM was evaluated once for the initial state and once for the final state , leading to for simulations in solution.
3.2. SAMPL4 subset
The data for the blind subset of the SAMPL4 hydration free energy challenge are based on the potential energy data used in reference 4. The blind subset originally consisted of 24 molecules, but 3 out of the 24 molecules (molecules 7, 8 and 18) had to be withdrawn from the challenge. As described in Ref. 4, the original simulations were conducted with CHARMM using the CHARMM General force field (CGenFF), version 0.9.6 beta. The thermodynamic cycle follows precisely the one described in Ref 4. Briefly, the gas and solvent phase molecules were driven to a non-interacting ideal gas state through a two step alchemical mutation. First, all charges of the solute were set to zero. Second, all Lennard-Jones interactions of the solute were set to zero. A total of 6 and 7 lambda points were used for each respective step of the transformation in the gas phase, and 12 and 13 lambda points were used for the transformation in the solution phase. The original QM and QM/MM calculations were performed with Q-Chem based on the CHARMM/Q-Chem interface. The QM and QM/MM data consists of calculations with B3LYP/6–31G* that were only performed for the first λ step of the MM alchemical uncharging transformation. This corresponds to simulations with normal CGenFF charges (λ=0.00) and with CGenFF charges that were scaled by a factor of 0.95 (λ=0.05) in both gas phase and solution. The gas phase data consisted of 45000 data points for each λ point, corresponding to a simulation time of 4.5 nanoseconds. The solvent phase data consisted of 10000 data points for each λ point, corresponding to a simulation times between 0.5 and 1 nanoseconds. To improve sampling, Hamiltonian replica exchange was used between the λ points. Other details of the alchemical simulations are described in Ref. 4.
3.3. Harmonic Oscillators
A toy system of 1-D harmonic oscillators is used in addition to the ethane-methanol system and the SAMPL4 molecule system to probe the uncertainties in free energy estimates using the various reweighting methods described in section 2. Harmonic oscillators provide a valuable testing ground for free energy estimators because the free energy difference between two oscillators can be calculated analytically, and samples from harmonic oscillators can be easily drawn. The potential energy and free energy of a 1-D harmonic oscillator are:
| (14) |
| (15) |
where U (x) is the potential energy of the harmonic oscillator at position x, k is the spring constant, is the equilibrium distance of the oscillator, and A is the absolute free energy. In this work, two harmonic oscillators are sampled (satisfying the NBB-indirect method requirements of two sampled states) and used to estimate the free energy difference between the second oscillator and a variety of different unsampled harmonic oscillators. In all simulations, the arbitrary parameter β is set to unity and 1000 configurations are drawn from each of the sampled harmonic oscillators.
The first oscillator test system studied here is a series of 11 oscillators which all have a mean position of and have evenly spaced harmonic spring constants ranging from k = 1.0 to k = 6.0. An illustration of the potential energy surface of the sampled and unsampled oscillators in this system are plotted in Figure 14. The increasing spring constants decrease the overlap with the sampled oscillators and mimic the physical effect a degree of freedom that is stiffer in the target state than the sampled state, such as a higher frequency bond vibration. The statistical estimators described in section 2 are applied to this oscillator system in two different cases. In the first case, the two oscillators with the smallest spring constants are sampled and reweighted to the stiffer unsampled oscillators. In the second case, the two harmonic oscillators with the largest spring constants are sampled and reweighted to the unsampled oscillators with weaker spring constants.
Figure 14:
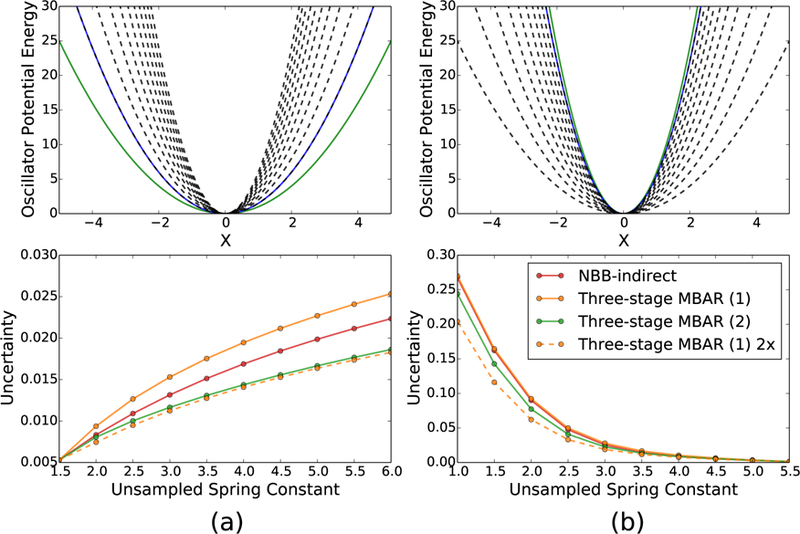
The uncertainties in the free energy difference between the sampled and unsampled oscillators increase for all methods as the spring constant of the sampled and unsampled oscillators become farther apart. The uncertainties are lower with three-stage MBAR (2) than with NBB-indirect for all values of the spring constant of the unsampled oscillator in each case. For an equal amount of energy re-evaluations, the method with the lowest variance involves placing all the re-evaluations in the sampled oscillator with the highest overlap and reweighting with the Zwanzig equation. The set of harmonic oscillators are shown above in which the offset is identical and the spring constant of the oscillators changes. The green and blue solid lines represent the first and second sampled oscillator, and the dashed lines indicate the set of unsampled oscillators. The sampled oscillators are reweighted to the un-sampled oscillators in two cases (a) the two oscillators with the smallest spring constant are sampled and (b) the two oscillators with the largest spring constant are sampled.
The second test system examined here is another series of 11 oscillators which all have a harmonic spring constant of k = 1.0 and evenly spaced mean offsets ranging from to . An illustration of the potential energy surfaces for these sampled and unsampled oscillators are shown in Figure 15. The varying offset for the unsampled oscillators mimics the physical effect of a degree of freedom with a different mean value in the target and sampled states, such as a longer average bond length.
Figure 15:
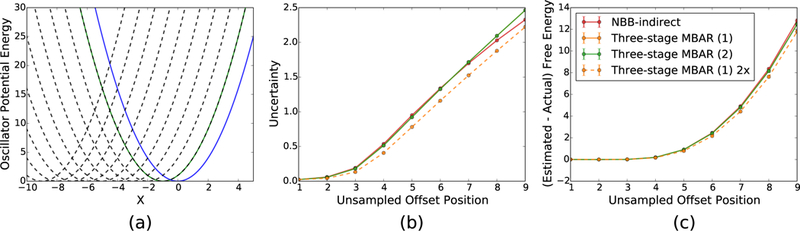
The uncertainties in the free energy estimates for offset oscillators are relatively large for all methods. The variance in the estimate for unsampled offsets above 6 are lower for NBB-indirect than three-stage MBAR (2). However, the bias in the estimate for offsets above 6 are much larger than the uncertainties and all estimates with all methods are essentially meaningless. The set of offset oscillators with identical spring constants are shown on the left. The green and blue lines represent the fi and second sampled oscillators and the dashed lines indicate the set of unsampled oscillators.
3.4. Uncertainty Analysis
All uncertainties in the free energy estimates produced by NBB and MBAR were calculated by computing the variance of 200 independent bootstrap iterations. The configurations were decorrelated before bootstrapping using the method of Chodera et al.64 Uncertainties in the uncertainties for the SAMPL4 dataset were estimated assuming a normal distribution using where σ2 is the variance in the free energy estimate and n represents the number of bootstrap iterations.46
4. Results and Discussion
4.1. Ethane-Methanol
The estimates of the difference in solvation free energy between ethane and methanol are shown in Figure 5, calculated with only the MM energies as well as with the QM/MM energies using both NBB and MBAR. The uncertainties with MBAR (0.022 kcal·mol−1) are 4 times smaller than the uncertainties with the NBB-direct method (0.088 kcal·mol−1) when applied to the same set of data. These uncertainties suggest that for this transformation, the full MBAR method is approximately 16x more efficient at producing the free energy estimate. This assumes we are in the limit that the squared uncertainties are inversely proportional to the number of reweighted configurations, which we generally do arrive at for most reweighting methods in the first few hundred samples.46 Under this relatively mild assumption, then, the NBB-direct method would require 16x more QM/MM energy evaluations in order to produce the same magnitude of uncertainties as the full implementation of MBAR.
Figure 5:

The solvation free energy difference estimate between ethane and methanol in the QM/MM Hamiltonian is statistically distinguishable from the estimate in the MM Hamiltonian for all methods except NBB-direct. The bootstrapped uncertainties for the MBAR-derived methods are smaller than the uncertainties using the NBB-derived methods. The parenthetical values for the three-stage MBAR method indicate the number of sampled states reweighted to each unsampled state.
In addition to larger uncertainties, the free energy estimate with the NBB-direct method is also dependent on the path connecting the unsampled states. The path dependence of the NBB-direct method occurs because the method requires an estimate of the free energies of all intermediate states in the QM/MM Hamiltonian. The free energy between the end state QM/MM states is calculated as a sum of the pairwise free energies between each adjacent intermediate QM/MM state shown numerically in equation 9 and graphically in Figure 1. The full MBAR method can in principle be used to estimate the free energies of these intermediate QM/MM states. However, the relative free energies of unsampled states are not dependent on the energies or free energies of any other unsampled state as can be seen from equation 11. Therefore, the estimate of the free energy difference between the physical ethane and methanol end states with full MBAR is not affected by the inclusion or exclusion of intermediate QM/MM states.
As one example of the path dependence in the NBB-direct method, a noticeable systematic error (bias) is introduced in the free energy difference estimate when the mixing rule used to calculate the intermediate QM/MM energies (eq 10) is increased above first order (shown in Figure 6). The free energy difference estimate with the quadratic and cubic mixing rule is statistically different from the estimate with the linear NBB-direct and the full MBAR method based on the bootstrapped uncertainty values. This suggest that using a non-linear mixing rule with NBB-direct method introduces a systematic error into the free energy estimation and not just an increase in the statistical uncertainty. With MBAR, the weights and free energy estimates depend only on the sampled states, and therefore the unsampled state free energies are independent of the number or location of the unsampled intermediate states. The larger uncertainties and the dependence on unsampled pathway for NBB-direct shown in Figure 5 and 6 demonstrate a clear advantage in using MBAR instead of the NBB-direct method to estimate the solvation free energy difference between methanol and ethane.
Figure 6:
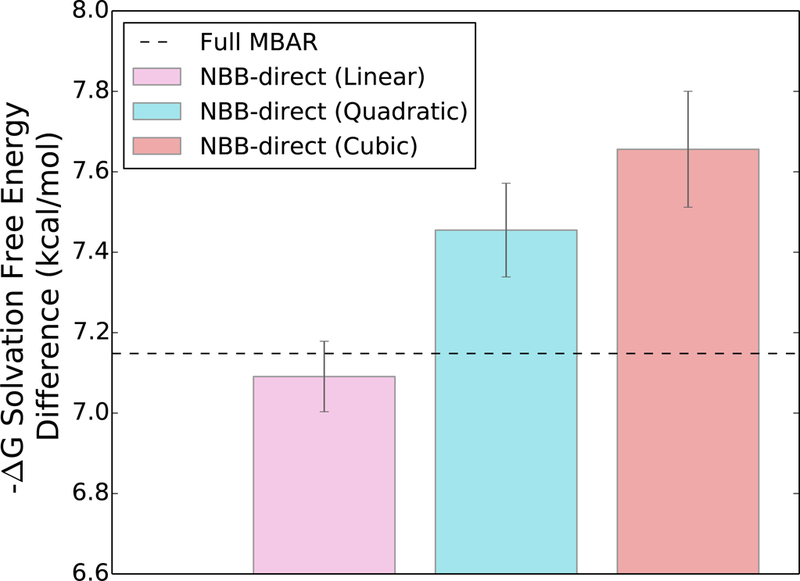
The free energy difference estimate with NBB-direct is dependent on the thermodynamic path connecting the unsampled states. Higher order mixing rules for the unsampled QM/MM intermediate states lead to statistically significant biases in the estimate. The dashed line indicates the free energy estimate using the full MBAR method.
The NBB-indirect and three-stage MBAR reweighting methods require significantly less computational expense than MBAR and NBB-direct because the QM/MM energy re-evaluations only need to be conducted at a subset of states near the physical end states of the thermodynamic cycle rather than at every ‘mixed’ intermediate state (see Figure 2 and 4). The three-stage MBAR method can be run with any number of reweighted states on either end of the thermodynamic path ranging from 1 to where K is the total number of sampled states. However the free energy difference estimate and uncertainty in this system are insensitive to the number of reweighted states (Figure 7), and the estimates with more than one reweighted state are statistically identical to the estimates with only the physical end states evaluated in the QM/MM potential.
Figure 7:
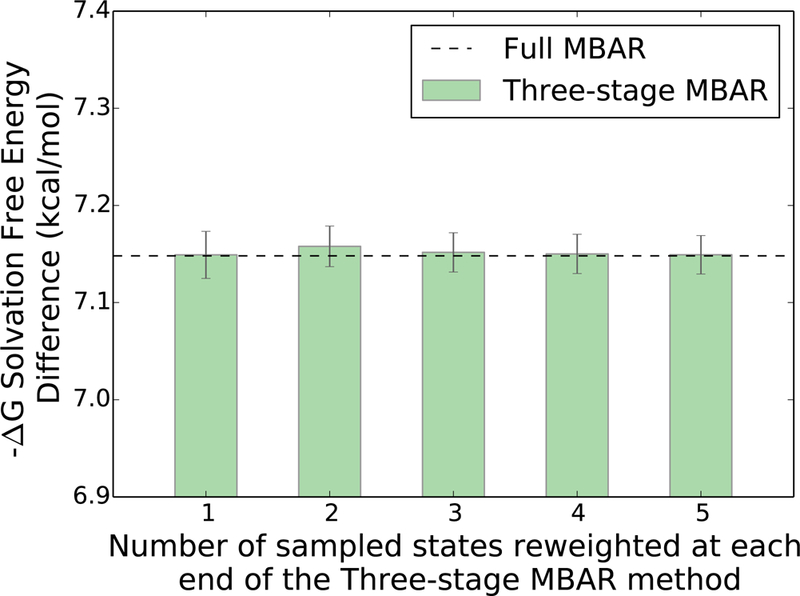
The free energy difference estimate with three-stage MBAR in the ethane-methanol system is insensitive to the number of states reweighted at each end of the thermodynamic path. The free energy estimate using any number of reweighted states is within the uncertainty of the value estimated by the full MBAR method which uses all of the available configurations.
The solvation free energy difference estimates with the NBB-indirect and three-stage MBAR methods are in good agreement with the estimate using the full QM/MM dataset generated with MBAR (Figure 5). The three-stage MBAR(2) method with 2 reweighted states at each end has the most natural comparison to NBB-indirect because both methods use exactly the same number of QM/MM energy evaluations. The uncertainty with three-stage MBAR(2) is 0.021 kcal·mol−1, while with NBB-indirect the uncertainty is 0.057 kcal·mol−1. This suggests that three-stage MBAR(2) is roughly 7x more efficient at producing the free energy estimate with the abridged dataset, again assuming that the the squared uncertainties are inversely proportional to the number of reweighted configurations. Overall, the data suggests that for transformations similar to the methanol-ethane system, the QM/MM evaluations should be conducted primarily at the end states of the alchemical path and that the reweighting analysis be conducted with three-stage MBAR (i.e. Zwanzig reweighting of end states to QM/MM plus MBAR for free energies of the intermediate states) rather than NBB-indirect to minimize the uncertainty in the free energy estimate while simultaneously maximizing efficiency.
For the methanol-ethane system, the solvation free energy difference estimate and uncertainty in the QM/MM potential with three-stage MBAR is statistically the same when re-evaluating configurations from all of the sampled states versus only re-evaluating configurations in the physical MM end states. The results from this system suggest that in free energy studies where two states in an expensive Hamiltonian are connected through a set of cheaper intermediate states, the energy re-evaluations in the expensive potential should likely be done primarily with configurations sampled at the end states of the thermodynamic path where the overlap to the expensive potential is the highest. In most cases, the end states are likely to have more overlap because they both represent physical states, but these results do not rule out exceptions, such as where a partially charged MM end state from an over-polarized force field resembles the QM potential more closely than the fully charged MM end state.
We compare in more detail this approach of only using end state samples for the reweighting step from the cheap to expensive potential with the alternative of using samples from multiple intermediate steps. We evaluated the free energy difference estimate and uncertainty for the ethane-methanol system in the QM/MM potential using three-stage MBAR for a fixed total of 15000 energy evaluations evenly drawn from N reweighted states at each end of the thermodynamic path. When N = 1, all 15000 samples are drawn from the physical end states and re-evaluated in the QM/MM potential along with equation 11 to estimate the solvation free energy difference between the physical QM/MM and MM state. When N = 5, 3000 samples are re-evaluated from each of the 5 MM intermediate states closest to the physical end state. Figure 8 shows that the uncertainty in the free energy estimate to move from the unsampled QM/MM state to the farthest reweighted MM state is lowest when all energy evaluations are done at the physical end states of the thermodynamic pathway.
Figure 8:
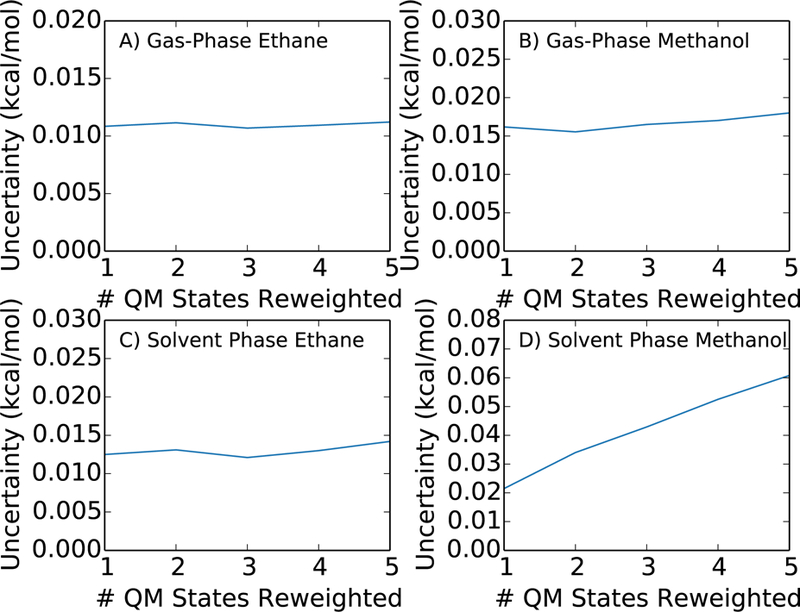
The bootstrapped uncertainty in the solvation free energy estimate with three-stage MBAR are lowest when all QM/MM re-evaluations are done only at the physical MM end states where the overlap to the QM states is highest. The uncertainties increase when re-evaluated samples are moved away from the physical MM end states. The increase is most pronounced for solvent phase methanol, because only the physical MM end state has high overlap to the QM/MM state. A total of 15,000 samples are taken evenly from each reweighted intermediate state and the uncertainties as a function of the number of reweighted states are shown for A) gas phase ethane, B) gas phase methanol, C) solvent phase ethane, and D) solvent phase methanol.
We note that the approach of reweighting only a single MM state to the QM/MM Hamiltonian is just the traditional Zwanzig reweighting scheme. Therefore, in this system of ethane and methanol, the solvation free energy difference is best estimated using the Zwanzig reweighting method rather than a multistate approach such as NBB or full MBAR for a fixed amount of energy re-evaluations. This is consistent with the recent study by Jia et al. in which the Zwanzig approach was seen to outperform the NBB approach.50 When samples are removed from the physical end states and spread out into the intermediate states, the uncertainty in the free energy estimate tends to increase because the physical end states have the highest overlap to the QM/MM potential. This effect is most pronounced in the solvent phase methanol state because only the physical MM end state has high overlap to the QM/MM state. A rigorous minimization of the uncertainty as a function of the distribution of re-evaluated configurations is outside the scope of the present study. However, this analysis demonstrates that to minimize the uncertainty and maximize computational efficiency, the energy re-evaluations should be conducted at the state with the highest overlap, which in this system is the end states of the thermodynamic pathway. It is difficult to determine the highest overlap state without running any simulations. However, a set of short simulations could in theory be used to identify the state with the highest overlap, and the subsequent full production simulations and QM energy re-evaluations can be run from this state alone.
We briefly note that if the mixed Hamiltonian MM states do not have good overlap with adjacent intermediate states, the overall uncertainty in the QM/MM free energy will be large regardless of the choice of state to reweight to the QM/MM Hamiltonian.
4.2. SAMPL4 subset
The analysis of the solvation free energy difference in the ethane-methanol system indicates that the uncertainties using MBAR are lower than the uncertainties using NBB for the same set of data. However, this relative uncertainty comparison could in theory reflect features specific to the ethane-methanol system rather than intrinsic properties of the analysis methods. To further generalize the results, we applied the same solvation free energy difference estimates to the SAMPL4 small molecule solvation dataset (shown in Figure 9) with both three-stage MBAR and NBB-indirect. To save computational expense, only the final two states of the path connecting the SAMPL4 molecules were re-evaluated in the QM/MM potential and therefore it is not possible to calculate the free energy difference using either NBB-direct or MBAR. However, the prior analysis with the ethane-methanol system suggests that reweighting with only 2 states is likely to be statistically equivalent to the full MBAR calculation (Figure 7).
Figure 9:
The molecules in the blind SAMPL4 solvation dataset examined in this work.
The solvation free energies and uncertainties for each SAMPL4 molecule with MM-only, NBB-indirect, three-stage MBAR(1), and three-stage MBAR(2) are shown in Figure 10 and Figure 11. The bootstrapped uncertainty values using three-stage MBAR(2) are lower than the corresponding uncertainties with NBB-indirect for 14 of the 21 molecules in the SAMPL4 molecule set. The uncertainty with NBB is on average 15% larger than the uncertainty with three-stage MBAR(2), suggesting that three-stage MBAR(2) is 28% more efficient at estimating the free energy difference using the same set of data. It is worth noting that the uncertainties with three-stage MBAR(1) are similar to those with three-stage MBAR(2) despite having half as many energy re-evaluations in the QM/MM Hamiltonian. The average uncertainty with three-stage MBAR(1) is 21% smaller than the average uncertainty with three-stage MBAR(2) for a fixed number of energy re-evaluations assuming that the uncertainties are proportional to the square root of the number of QM/MM calculations. This suggests that in the SAMPL4 dataset the Zwanzig approach is best for a fixed amount of QM/MM energy calculations, similar to the results shown earlier for the ethane-methanol system.
Figure 10:
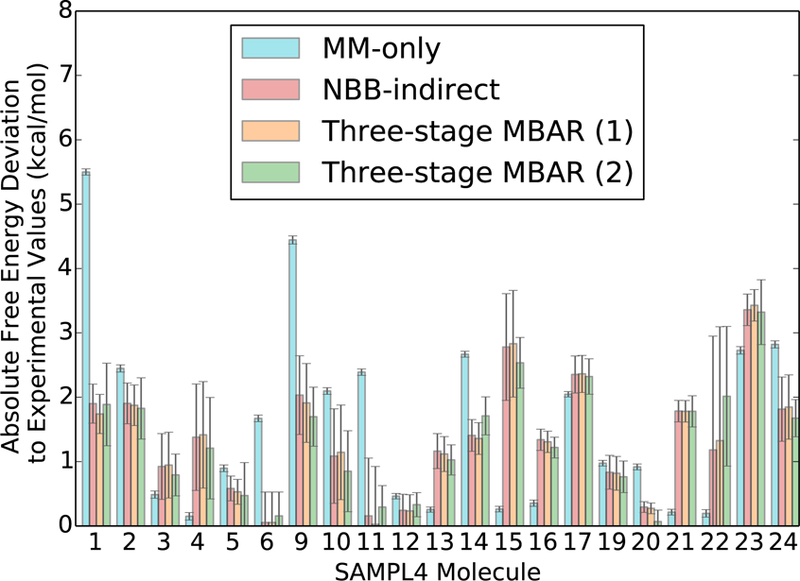
The absolute deviation between the experimental solvation free energy and the theoretical estimate are lower on average in the QM/MM potential than in the MM potential. The deviations in the estimates with MBAR are slightly lower on average than those with NBB. Uncertainties for each reweighting method are bootstrapped variances of the solvation free energy estimate. The parenthetical values for the three-stage MBAR method indicate the number of sampled states reweighted to each unsampled state.
Figure 11:

The uncertainties in the solvation free energy estimate of the molecules in the SAMPL4 dataset calculated with bootstrapping are larger on average with the NBB-indirect method (0.47 kcal·mol−1) than with three-stage MBAR (0.41 kcal·mol−1). Uncertainties in the uncertainties were estimated through standard error propagation assuming a normal distribution. The parenthetical values for the three-stage MBAR method indicate the number of sampled states reweighted to each unsampled state.
The larger uncertainties with NBB-indirect relative to three-stage MBAR(2) are qualitatively consistent with the trend observed in the ethane-methanol system. However the uncertainties with the two methods in the SAMPL4 dataset are noticeably closer in magnitude relative to the uncertainties in the ethane-methanol system. The MM and QM/MM Hamiltonians have significantly less overlap in the SAMPL4 molecules than in the ethane and methanol systems based on the larger uncertainties in the free energy estimate (Figure 11) as well as the smaller number of effective samples (Figure 12 and 13). The average number of effective samples in the solvent phase for the SAMPL4 molecules is 8.7, which is significantly lower than the solvent phase effective samples for ethane (5426) and methanol (779). Correspondingly, the average uncertainty in the solvation free energy for the SAMPL4 molecules with three-stage MBAR(2) is 0.41 kcal·mol−1, which is more than an order of magnitude larger than the uncertainty in the solvation free energy difference between ethane and methanol (0.021 kcal·mol−1). The bootstrapped uncertainty values for the SAMPL4 molecule solvation free energy estimates were on average 28% larger than the analytical uncertainty estimates calculated with MBAR. This discrepancy in error estimates suggests that the sampling in the SAMPL4 molecule dataset has not reached the point where asymptotic statistical variances apply. We therefore conclude that both NBB-indirect and three-stage MBAR(2) provide similar variances for systems with low overlap, but MBAR and three-stage MBAR(2) provide significantly lower variance estimates than NBB-indirect for systems with high overlap to the expensive potential.
Figure 12:
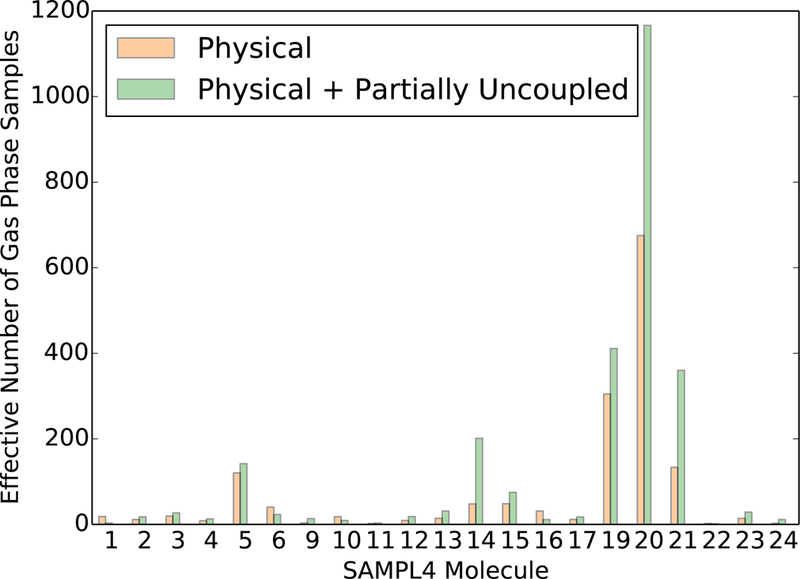
The number of effective samples in the QM/MM potential for the SAMPL4 molecules in the gas phase vary significantly and are all lower on average than the number of effective samples for ethane (6413) and methanol (7622). The numbers of effective samples were calculated using just the configurations from state 0 as well as using all configurations from state 0 and state 1.
Figure 13:
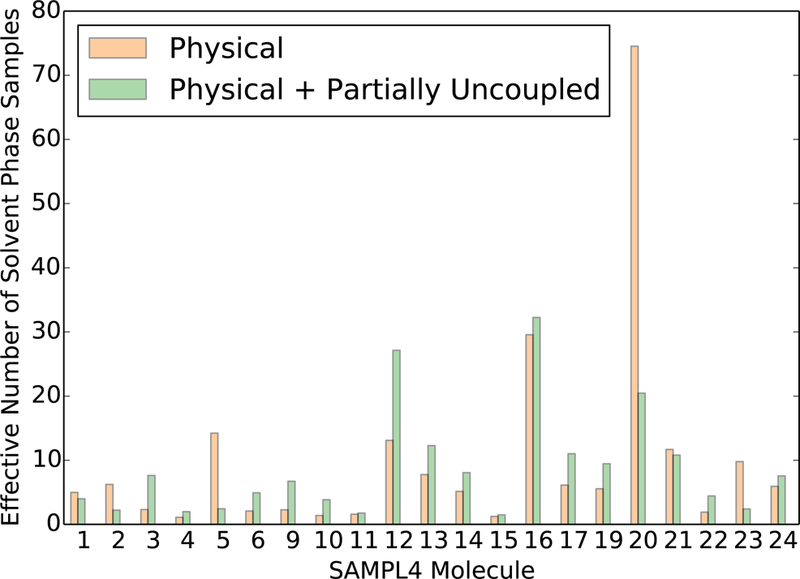
The number of effective samples in the QM/MM potential for the SAMPL4 molecules in the solvent phase are significantly lower on average than the number of effective samples for ethane (5426) and methanol (779). The numbers of effective samples were calculated using just the configurations from state 0 as well as using all configurations from state 0 and state 1. In 6 of the 21 molecules, the number of effective samples decreases when adding in the samples from state 1, suggesting that the QM/MM free energy estimates need significantly more samples before converging.
We also note that in all molecules where NBB has a noticeably lower variance than three-stage MBAR(2) in Figure 11, the number of effective samples for these molecules decreases when using samples from both the physical state 0 and the charge-scaled (by 0.95) state 1, rather than just state 0 (Figure 12 and 13). A decrease in the number of effective samples resulting from the addition of configurations can only be caused by a significant shift in the free energy estimate, as seen by inspection of the formulas for the weights (equation 13) and effective samples (equation 12). The free energy estimates in these molecules have therefore not yet well converged with the current sampling, and any estimate of the free energies or the uncertainties are likely to be spurious.
The large uncertainties and change in the number of effective samples can in theory be used as a quick test of whether the target state is being effectively sampled by the cheaper point-charge potentials. One can simply reweight using three-stage MBAR(1) as well as three-stage MBAR(2). If the number of effective samples decreases when adding in an additional state in the reweighting process or the free energy estimate changes beyond the uncertainty, this strongly suggests that the free energy estimate has not converged. If the number of effective samples increases and the free energy estimate remains unchanged, this suggests that the overlap between the point-charge and target potential is reasonable.
The overlap between the MM and QM/MM Hamiltonians in the SAMPL4 molecules could in theory be improved by designing new MM potentials for each molecule which more closely resemble the QM/MM potential energy surface. Poor overlap was observed even in the gas phase for some of the SAMPL4 molecules, as indicated by less than 10 gas phase effective samples for 4 of the molecules in the dataset. If gas phase simulations already have low overlap, it is unlikely that the overlap will be high when the solvent water molecules are added. This lack of configurational overlap even without the effects of the water molecules suggests that there are significant differences in even the intramolecular interactions between the MM and QM/MM Hamiltonians for these molecules. Indeed, the 5 SAMPL4 molecules with the highest number of gas phase effective samples have rigid aromatic and double-bonded structures which enforce similar intramolecular geometries at both the MM and QM/MM level of theory. Adjusting the intramolecular parameters in the MM potential to match the QM/MM Hamiltonian is likely to increase the configurational overlap in the remaining molecules, and the idea to adjust the MM potential has been pursued in multiple previous and ongoing research efforts,65–69 but it is outside the scope of the present work.
The solvation free energy differences in the QM/MM Hamiltonian for the SAMPL4 molecules agree favorably with the experimental values, as shown in Figure 10. When the QM/MM Hamiltonian with three-stage MBAR(2) is used instead of the pure MM potential, the RMSD between the theoretical and experimental solvation free energy differences decreases from 2.17 kcal·mol−1 to 1.57 kcal·mol−1 and the mean average deviation decreases from 1.62 kcal·mol−1 to 1.33 kcal·mol−1. This is consistent with the findings of König et al.4 and Essex et al.5 who saw that the deviation to experimental values decreased when reweighting to the QM/MM Hamiltonian. It is worth noting that although the deviation to experiments is smaller on average with the QM/MM potential, the estimates with only the MM energies were closer in 9 of the 21 SAMPL4 molecules as well as in the ethane-methanol system.
Both NBB-indirect and three-stage MBAR are asymptotically unbiased estimators, and for the SAMPL4 dataset both methods provide essentially equal improvement over the MM potential with respect to the experimental values. With three-stage MBAR(2), the average RMSD is 1.57 kcal·mol−1 and with NBB-indirect and three-stage MBAR(1) the average RMSD is 1.60 kcal·mol−1. The mean average deviation with three-stage MBAR(1) and three-stage MBAR(2) is 1.35 kcal·mol−1 and 1.33 kcal·mol−1, respectively, and the mean average deviation with NBB-indirect is 1.36 kcal·mol−1.
4.3. Harmonic Oscillators
As a final comparison of the NBB, three-stage MBAR(1), and three-stage MBAR(2) estimators (which in this test case is equivalent to MBAR), all three methods were used to calculate the free energy difference between a sampled and unsampled harmonic oscillator through an intermediate sampled harmonic oscillator. In the first test case, sampled harmonic oscillators with weak spring constants are reweighted to stiffer harmonic oscillators with larger spring constants. In the second test case, the two stiffest oscillators are sampled and reweighted to the oscillators with weaker spring constants. In the final test case, all oscillators have the same spring constant, but the two sampled oscillators and the unsampled oscillators have increasingly offset equilibrium positions.
In the first two cases, for all values of the spring constant the uncertainty with MBAR is lower than the uncertainty with NBB-indirect (Figure 14). The uncertainty is highest with the three-stage MBAR(1) approach. However this mostly reflects the fact that half as many sampled configurations are re-evaluated in the target state with the Zwanzig approach, corresponding with only one oscillator being used in the reweighting rather than both oscillators for NBB-indirect and three-stage MBAR(2). When the three-stage MBAR(1) approach is run with twice as many configurations sampled from the first oscillator, the free energy difference estimate has a lower uncertainty than both NBB-indirect and three-stage MBAR(2). This is consistent with the results from the ethane-methanol system and the SAMPL4 system, where the lowest variance free energy estimate (for a fixed amount of re-evaluations) came from placing all the re-evaluations into the one state with the highest overlap to the target unsampled state, which is equivalent to the Zwanzig approach(Figure 8). For all methods examined with these harmonic oscillators, the bias in the free energy estimate was negligible.
In the final case, when the offset of the unsampled oscillators is nonzero, a systematic error appears in the free energy estimate for all methods, and this bias becomes more significant as the offset increases (Figure 15). For a sufficiently large offset, the variance in the free energy difference estimate for NBB-indirect is smaller than the variance in the estimate with three-stage MBAR(2). However, this change occurs at an offset where the systematic error is so large that the free energy estimate is essentially meaningless. This is consistent with the findings from the SAMPL4 molecule dataset in which NBB-indirect produced lower variance free energy estimates only for molecules with poor or biased sampling.
Finally, we note that the lower uncertainties for NBB-indirect relative to three-stage MBAR(1) occurs in the limiting case that N1 = N2, where Ni is the number of samples drawn from sampled oscillator i and oscillator 1 represents the sampled state farther away from the unsampled states. When N1 > N2 the uncertainty for NBB-indirect is larger than both three-stage MBAR (1) and three-stage MBAR (2) (see Supporting Information section 1, and Fig. 3).
5. Conclusions
The solvation free energy difference between methanol and ethane was calculated in a QM/MM Hamiltonian by sampling in a cheap MM potential followed by Hamiltonian reweighting. The Hamiltonian reweighting was carried out using a variety of different algorithms derived from the Multistate Bennett Acceptance Ratio method and the Non-Boltzmann Bennett method, and the MBAR-based methods produce on average smaller uncertainties than the NBB-derived methods for identical sets of data. In addition to lower uncertainties, the MBAR method provides a more natural way to estimate the free energies between two or more unsampled states because the final estimate does not depend on the path connecting the unsampled states. Additionally, one needs to identify which MM state connects to the unsampled QM/MM state in NBB, but no such identification is required with MBAR.
The total solvation free energy difference estimate for the ethane-methanol system is the same, within uncertainty, when reweighting with only the physical end state configurations rather than reweighting all configurations from all intermediate states between ethane and methanol for both NBB and MBAR. The overall computational expense is significantly reduced when reweighting with only the configurations sampled at the end states because it avoids the costly step of re-evaluating the energy of all intermediate configurations in the expensive QM/MM Hamiltonian. Additionally, the lowest variance free energy estimate for a fixed amount of QM/MM energy evaluations occurs when all of the evaluations are conducted at the physical MM end states where the overlap to the corresponding QM/MM states is the highest. Both of these results motivate concentrating the energy re-evaluations on only the configurations sampled at the state with the highest overlap to the expensive potential in order to maximize computational efficiency. Although any intermediate state could, in theory, have the highest overlap with the QM states, it is natural to expect that a fully physical MM state (rather than an unphysical mixed state) would best represent the configurations in a fully physical QM state.
The solvation free energy differences were also estimated for molecules in the SAMPL4 small molecule solvation dataset, and the uncertainties with three-stage MBAR with 2 reweighted states are lower than with NBB-indirect in 14 of the 21 molecules tested. However, the difference in the uncertainties between three-stage MBAR and NBB-indirect were smaller for the SAMPL4 molecule dataset than for the methanol-ethane system. MBAR has been previously shown to have the lowest asymptotic variance possible among all reweighting estimators.45 We therefore hypothesize that the deviation from these asymptotic limits results from very poor sampling in the SAMPL4 dataset relative to the sampling in the methanol-ethane system. This hypothesis is supported by lower overall uncertainties and higher numbers of effective samples for methanol and ethane when compared with the molecules in the SAMPL4 dataset. It is also supported by the fact that molecules with a smaller statistical error with NBB than with MBAR have low, even single digit numbers of effective samples and free energy estimates that are not fully converged with the available samples as shown in Figures 12 and 13.
The observation of higher uncertainties for NBB-indirect relative to MBAR is also affirmed by a simple system of 1-D harmonic oscillators in which two sampled oscillators are reweighted to a series of unsampled oscillators. In all examined cases with low bias, the MBAR derived uncertainties are lower than the NBB-indirect uncertainties for a fixed amount of energy re-evaluations. The NBB-indirect method produces lower variance estimates only in cases where the bias is substantially higher than the uncertainty, similar to the results observed in some of the SAMPL4 molecules. In all three systems examined, the uncertainties are lowest for a fixed number of QM/MM calculations when all energy re-evaluations are placed at a single MM state with the highest overlap to the QM/MM Hamiltonian. This single-step reweighting approach is the three-stage MBAR(1) method, which is equivalent to the standard Zwanzig approach plus a multistate reweighting estimate of the cheap intermediate states.
Both NBB and MBAR provide an asymptotically unbiased estimate of the true free energy of the model, and both estimators produce solvation free energy differences in the QM/MM potential that more closely agree with experiments than the MM potential estimates on average. The mean average deviation in the SAMPL4 dataset decreases from 1.62 kcal·mol−1 to 1.36 kcal·mol−1 and 1.33 kcal·mol−1 when moving to the QM/MM potential with NBB-indirect and three-stage MBAR(2), respectively. Given the approximations used to construct the QM/MM Hamiltonian, however, the improvement to experiments relative to the MM potential may be fortuitous.
Based on the results presented in this study, we recommend that to reduce the variance in future free energy difference estimates in unsampled potentials using Hamiltonian reweighting, the sampling and energy re-evaluations should be focused primarily on the thermodynamic states with the highest overlap to the target potential, which are usually the cheaper potential’s physical end states. We also recommend that the subsequent reweighting analysis should be carried out with MBAR or the three-stage variant, which is equivalent to the Zwanzig approach at the end state in the limit of one reweighted state. We note, however, that without a sufficiently close match in configuration space overlap between the MM and QM/MM Hamiltonians, no reweighting method works particularly well.
Supplementary Material
6. Acknowledgments
The authors would like to thank Stefan Boresch and Lee Woodcock for insightful discussions on the current status of reweighting methods. We would also like to thank Ye Mei for carefully reading through this document and providing feedback, as well as generating the figure for the SAMPL4 molecule dataset. This work was partially supported by the intramural research program of the National Heart, Lung and Blood Institute of the National Institutes of Health and utilized the high-performance computational capabilities of the LoBoS and Biowulf Linux clusters at the National Institutes of Health. (http://www.lobos.nih.gov and http://biowulf.nih.gov). This work was also supported financially by NSF through the grant NSF-CBET 1351635.
Footnotes
7 Supporting Information
Supporting Information Available: An extended discussion of the harmonic oscillator system is provided. A discussion of the mathematical differences between NBB and MBAR is also included. This material is available free of charge via the Internet at http://pubs.acs.org
References
- (1).Kollman PA Chem. Rev 1993, 93, 2395–2417. [Google Scholar]
- (2).Mobley DL; Dumont E; Chodera JD; Dill KA J. Phys. Chem. B 2007, 111, 2242–54. [DOI] [PubMed] [Google Scholar]
- (3).Mobley DL; Bayly CI; Cooper MD; Shirts MR; Dill KA J. Chem. Theory Comput 2009, 5, 350–358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (4).König G; Pickard FC IV; Mei Y; Brooks BR J. Comput.-Aided. Mol. Des 2014, 28, 245–257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Genheden S; Cabedo Martinez AI; Criddle MP; Essex JW J. Comput.-Aided. Mol. Des 2014, 28, 187–200. [DOI] [PubMed] [Google Scholar]
- (6).Marelius J; Hansson T; Aqvist J Int. J. Quantum Chem 1998, 69, 77–88. [Google Scholar]
- (7).Jorgensen WL Science 2004, 303, 1813–1818. [DOI] [PubMed] [Google Scholar]
- (8).Gallicchio E; Levy RM Adv. Protein Chem. Struct. Biol 2011, 85, 27–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Wereszczynski J; McCammon JA Q. Rev. Biophys 2012, 45, 1–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).van Gunsteren WF; Bakowies D; Baron R; Chandrasekhar I; Christen M; Daura X; Gee P; Geerke DP; Glättli A; Hünenberger PH; Kastenholz MA; Oostenbrink C; Schenk M; Trzesniak D; van der Vegt NFA; Yu HB Angew. Chemie Int. Ed 2006, 45, 4064–4092. [DOI] [PubMed] [Google Scholar]
- (11).Onuchic JN; Wolynes PG Curr. Opin. Struct. Biol 2004, 14, 70–75. [DOI] [PubMed] [Google Scholar]
- (12).Karplus M; Mccammon JA Nat. Struct. Biol 2002, 9, 646–652. [DOI] [PubMed] [Google Scholar]
- (13).Karplus M; Kuriyan J Proc. Natl. Acad. Sci. U. S. A 2005, 102, 6679–6685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Lommerse JPM; Motherwell WDS; Ammon HL; Dunitz JD; Gavezzotti A; Hofmann DWM; Leusen FJJ; Mooij WTM; Price SL; Schweizer B; Schmidt MU; van Eijck BP; Verwer P; Williams DE Acta Crystallogr. Sect. B Struct. Sci 2000, 56, 697–714. [DOI] [PubMed] [Google Scholar]
- (15).Motherwell WDS; Ammon HL; Dunitz JD; Dzyabchenko A; Erk P; Gavezzotti A; Hofmann DWM; Leusen FJJ; Lommerse JPM; Mooij WTM; Price SL; Scheraga H; Schweizer B; Schmidt MU; van Eijck BP; Verwer P; Williams DE Acta Crystallogr. Sect. B Struct. Sci 2002, 58, 647–661. [DOI] [PubMed] [Google Scholar]
- (16).Day GM; Motherwell WDS; Ammon HL; Boerrigter SXM; Della Valle RG; Venuti E; Dzyabchenko A; Dunitz JD; Schweizer B; van Eijck BP; Erk P; Facelli JC; Bazterra VE; Ferraro MB; Hofmann DWM; Leusen FJJ; Liang C; Pantelides CC; Karamertzanis PG; Price SL; Lewis TC; Nowell H; Torrisi A; Scheraga HA; Arnautova YA; Schmidt MU; Verwer P Acta Crystallogr. B 2005, 61, 511–527. [DOI] [PubMed] [Google Scholar]
- (17).Nicholls A; Mobley DL; Guthrie JP; Chodera JD; Bayly CI; Cooper MD; Pande VS J. Med. Chem 2008, 51, 769–779. [DOI] [PubMed] [Google Scholar]
- (18).Guthrie JP J. Phys. Chem. B 2009, 113, 4501–4507. [DOI] [PubMed] [Google Scholar]
- (19).Day GM; Cooper TG; Cruz-Cabeza AJ; Hejczyk KE; Ammon HL; Boerrigter SXM; Tan JS; Della Valle RG; Venuti E; Jose J; Gadre SR; Desiraju GR; Thakur TS; van Eijck BP; Facelli JC; Bazterra VE; Ferraro MB; Hofmann DWM; Neumann MA; Leusen FJJ; Kendrick J; Price SL; Misquitta AJ; Karamertzanis PG; Welch GWA; Scheraga HA; Arnautova YA; Schmidt MU; van de Streek J; Wolf AK; Schweizer B Acta Crystallogr. B 2009, 65, 107–25. [DOI] [PubMed] [Google Scholar]
- (20).Geballe MT; Skillman AG; Nicholls A; Guthrie JP; Taylor PJ J. Comput.-Aided. Mol. Des 2010, 24, 259–279. [DOI] [PubMed] [Google Scholar]
- (21).Bardwell DA; Adjiman CS; Arnautova YA; Bartashevich E; Boerrigter SXM; Braun DE; Cruz-Cabeza AJ; Day GM; Della Valle RG; Desiraju GR; van Eijck BP; Facelli JC; Ferraro MB; Grillo D; Habgood M; Hofmann DWM; Hofmann F; Jose KVJ; Karamertzanis PG; Kazantsev AV; Kendrick J; Kuleshova LN; Leusen FJJ; Maleev AV; Misquitta AJ; Mohamed S; Needs RJ; Neumann MA; Nikylov D; Orendt AM; Pal R; Pantelides CC; Pickard CJ; Price LS; Price SL; Scheraga HA; van de Streek J; Thakur TS; Tiwari S; Venuti E; Zhitkov IK Acta Crystallogr. B 2011, 67, 535–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (22).Muddana HS; Varnado CD; Bielawski CW; Urbach AR; Isaacs L; Geballe MT; Gilson MK J. Comput.-Aided. Mol. Des 2012, 26, 475–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Klimovich PV; Mobley DL J. Comput.-Aided. Mol. Des 2010, 24, 307–316. [DOI] [PubMed] [Google Scholar]
- (24).König G; Brooks BR J. Comput.-Aided. Mol. Des 2012, 26, 543–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Lawrenz M; Wereszczynski J; Ortiz-Sa´nchez JM; Nichols SE; McCammon JA J. Comput.-Aided. Mol. Des 2012, 26, 569–76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (26).Mobley DL; Liu S; Cerutti DS; Swope WC; Rice JE J. Comput.-Aided. Mol. Des 2012, 26, 551–562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (27).Gallicchio E; Deng N; He P; Wickstrom L; Perryman AL; Santiago DN; Forli S; Olson AJ; Levy RM J. Comput.-Aided. Mol. Des 2014, 28, 475–490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (28).Mobley DL; Wymer KL; Lim NM; Guthrie JP J. Comput.-Aided. Mol. Des 2014, 28, 135–150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (29).Mikulskis P; Cioloboc D; Andrejić M; Khare S; Brorsson J; Genheden S; Mata RA; Söderhjelm P; Ryde U J. Comput.-Aided. Mol. Des 2014, 28, 375–400. [DOI] [PubMed] [Google Scholar]
- (30).Hansen N; Van Gunsteren WF J. Chem. Theory Comput 2014, 10, 2632–2647. [DOI] [PubMed] [Google Scholar]
- (31).Warshel A; Levitt M J. Mol. Biol 1976, 103, 227–249. [DOI] [PubMed] [Google Scholar]
- (32).Luzhkov V; Luzhkov V; Warshel A; Warshel A J. Comput. Chem 1992, 13, 199–213. [Google Scholar]
- (33).Vaidehi N; Wesolowski TA; Warshel A J. Chem. Phys 1992, 97, 4264–4271. [Google Scholar]
- (34).Rosta E; Klähn M; Warshel A J. Phys. Chem. B 2006, 110, 2934–2941. [DOI] [PubMed] [Google Scholar]
- (35).Olsson MHM; Hong G; Warshel A J. Am. Chem. Soc 2003, 125, 5025–5039. [DOI] [PubMed] [Google Scholar]
- (36).Zwanzig R J. Chem. Phys 1954, 22, 1420–1426. [Google Scholar]
- (37).Gao J; Xia X Science 1992, 258, 631–635. [DOI] [PubMed] [Google Scholar]
- (38).Beierlein FR; Michel J; Essex JW J. Phys. Chem. B 2011, 115, 4911–4926. [DOI] [PubMed] [Google Scholar]
- (39).Cave-Ayland C; Skylaris C-K; Essex JW J. Phys. Chem. B 2015, 119, 1017–1025. [DOI] [PubMed] [Google Scholar]
- (40).Fox SJ; Pittock C; Tautermann CS; Christ C; Malcom N; Essex JW; Skylaris C.-k. J. Phys. Chem. B 2013, 117, 9478–9485. [DOI] [PubMed] [Google Scholar]
- (41).Sampson C; Fox T; Tautermann CS; Woods CJ; Skylaris C-K J. Phys. Chem. B 2015, 119, 7030–7040. [DOI] [PubMed] [Google Scholar]
- (42).Lu N; Kofke DA J. Chem. Phys 2001, 115, 6866–6875. [Google Scholar]
- (43).Kumar S; Rosenberg JM; Bouzida D; Swendsen RH; Kollman PA J. Comput. Chem 1992, 13, 1011–1021. [Google Scholar]
- (44).König G; Boresch S J. Comput. Chem 2011, 32, 1082–1090. [DOI] [PubMed] [Google Scholar]
- (45).Shirts MR; Chodera JD J. Chem. Phys 2008, 129, 124105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (46).Paliwal H; Shirts MR J. Comput. Chem 2011, 7, 4115–4134. [DOI] [PubMed] [Google Scholar]
- (47).König G; Hudson PS; Boresch S; Woodcock HL J. Chem. Theory Comput 2014, 10, 1406–1419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (48).Tan Z J. Am. Stat. Assoc 2004, 99, 1027–1036. [Google Scholar]
- (49).Souaille M; Roux B Comput. Phys. Commun 2001, 135, 40–57. [Google Scholar]
- (50).Jia X; Wang M; Shao Y; Ko G; Brooks BR; Zhang JZH; Mei Y J. Chem. Theory Comput 2016, [DOI] [PubMed] [Google Scholar]
- (51).Bennett CH J. Comput. Phys 1976, 22, 245–268. [Google Scholar]
- (52).Torrie GM; Valleau JP Chem. Phys. Lett 1974, 28, 578–581. [Google Scholar]
- (53).Valleau JJ Comput. Phys 1977, 23, 187–199. [Google Scholar]
- (54).Min D; Zheng L; Harris W; Chen M; Lv C; Yang W J. Chem. Theory Comput 2010, 6, 2253–2266. [DOI] [PubMed] [Google Scholar]
- (55).Kish L Survey Sampling; Wiley: New York, 1965. [Google Scholar]
- (56).Brooks BR; Iii CLB; Mackerell AD; Nilsson L; Petrella RJ; Roux B; Won Y; Archontis G; Bartels C; Boresch S; Caflisch A; Caves L; Cui Q; Dinner AR; Feig M J. Comput. Chem 2009, 30, 1545–1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (57).Brooks BR; Bruccoleri RE; Olafson BD; States DJ; Swaminathan S; Karplus M J. Comput. Chem 1983, 4, 187–217. [Google Scholar]
- (58).MacKerell A; Bashford D J. Phys. Chem. B 1998, 102, 3586–3616. [DOI] [PubMed] [Google Scholar]
- (59).Shao Y; Molnar LF; Jung Y; Kussmann J; Ochsenfeld C; Brown ST; Gilbert ATB; Slipchenko LV; Levchenko SV; O’Neill DP; DiStasio RA; Lochan RC; Wang T; Beran GJO; Besley NA; Herbert JM; Lin CY; Van Voorhis T; Chien SH; Sodt A; Steele RP; Rassolov V. a.; Maslen PE; Korambath PP; Adamson RD; Austin B; Baker J; Byrd EFC; Dachsel H; Doerksen RJ; Dreuw A; Dunietz BD; Dutoi AD; Furlani TR; Gwaltney SR; Heyden A; Hirata S; Hsu C-P; Kedziora G; Khalliulin RZ; Klunzinger P; Lee AM; Lee MS; Liang W; Lotan I; Nair N; Peters B; Proynov EI; Pieniazek PA; Rhee YM; Ritchie J; Rosta E; Sherrill CD; Simmonett AC; Subotnik JE; Woodcock HL; Zhang W; Bell AT; Chakraborty AK; Chipman DM; Keil FJ; Warshel A; Hehre WJ; Schaefer HF; Kong J; Krylov AI; Gill PMW; Head-Gordon M Phys. Chem. Chem. Phys 2006, 8, 3172–3191. [DOI] [PubMed] [Google Scholar]
- (60).Woodcock L; Hodoscek M; Gilbert A; Gill P; Schaefer H; Brooks BR J. Comput. Chem 2007, 28, 1485–1502. [DOI] [PubMed] [Google Scholar]
- (61).Hoover WG Phys. Rev. A 1985, 31, 1695–1697. [DOI] [PubMed] [Google Scholar]
- (62).Essmann U; Perera L; Berkowitz ML; Darden T; Lee H; Pedersen LG J Chem Phys 1995, 103, 8577–8593. [Google Scholar]
- (63).Woodcock HL; Miller BT; Hodoscek M; Okur A; Larkin JD; Ponder JW; Brooks BR J. Chem. Theory Comput 2011, 7, 1208–1219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (64).Chodera JD; Swope WC; Pitera JW; Seok C; Dill KA J. Chem. Theory Comput 2007, 3, 26–41. [DOI] [PubMed] [Google Scholar]
- (65).Akin-Ojo O; Song Y; Wang F J. Chem. Phys 2008, 129, 064108. [DOI] [PubMed] [Google Scholar]
- (66).Pinnick ER; Calderon CE; Rusnak AJ; Wang F Theor. Chem. Acc 2012, 131, 1146. [Google Scholar]
- (67).Bentzien J; Muller RP; Florian J; Warshel A J. Phys. Chem. B 1998, 102, 2293–2301. [Google Scholar]
- (68).Plotnikov NV; Kamerlin SCL; Warshel A J. Phys. Chem. B 2011, 115, 7950–7962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (69).König G; Brooks BR Biochim. Biophys. Acta - Gen. Subj 2015, 1850, 932–943. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


