Sequence-based Prediction of Protein-Protein Interactions Using Gray Wolf Optimizer–Based Relevance Vector Machine

Abstract

Protein-protein interactions (PPIs) are essential to a number of biological processes. The PPIs generated by biological experiment are both time-consuming and expensive. Therefore, many computational methods have been proposed to identify PPIs. However, most of these methods are limited as they are difficult to compute and rely on a large number of homologous proteins. Accordingly, it is urgent to develop effective computational methods to detect PPIs using only protein sequence information. The kernel parameter of relevance vector machine (RVM) is set by experience, which may not obtain the optimal solution, affecting the prediction performance of RVM. In this work, we presented a novel computational approach called GWORVM-BIG, which used Bi-gram (BIG) to represent protein sequences on a position-specific scoring matrix (PSSM) and GWORVM classifier to perform classification for predicting PPIs. More specifically, the proposed GWORVM model can obtain the optimum solution of kernel parameters using gray wolf optimizer approach, which has the advantages of less control parameters, strong global optimization ability, and ease of implementation compared with other optimization algorithms. The experimental results on yeast and human data sets demonstrated the good accuracy and efficiency of the proposed GWORVM-BIG method. The results showed that the proposed GWORVM classifier can significantly improve the prediction performance compared with the RVM model using other optimizer algorithms including grid search (GS), genetic algorithm (GA), and particle swarm optimization (PSO). In addition, the proposed method is also compared with other existing algorithms, and the experimental results further indicated that the proposed GWORVM-BIG model yields excellent prediction performance. For facilitating extensive studies for future proteomics research, the GWORVMBIG server is freely available for academic use at http://219.219.62.123:8888/GWORVMBIG.

Introduction

Protein-protein interactions (PPIs) are playing key roles in the fields of biological processes. It is much important to have knowledge of PPIs that can provide a certain help in understanding molecular functions of biological processes and propose a new method for practical medical applications, and bring about a deep understanding of disease mechanisms. Despite many high-throughput methods like yeast 2-hybrid system,^1,2 protein chips³ and immunoprecipitation⁴ are commonly used to detect PPIs. However, these experimental approaches are both expensive and time-consuming. In addition, the approaches mentioned above result in high rates of false negatives and false positives.^5,6 Accordingly, a lot of computational approaches based on different types of data, such as protein domain, genomic information, and protein structure have been presented to detect PPIs. However, most of the aforementioned approaches are limited as they are difficult to calculate and depend on large amounts of homologous proteins. As a result, developing effective computational approaches based on protein sequence information to detect PPIs is much essential.

Till now, a lot of computational methods based on sequence have been proposed to identify PPIs. Yu and Guo⁷ reported a computational approach based on secondary structures to identify PPIs, which found that most of the interacting regions are taken up by helix and disordered structures. Pitre et al⁸ proposed a novel sequence-based computational approach called protein-protein interaction prediction engine (PIPE), which can detect PPIs for any target pair of the yeast Saccharomyces cerevisiae proteins. Xia et al⁹ presented a computational approach using protein sequence information, which combined rotation forest with autocorrelation descriptor to identify PPIs. Zhao et al¹⁰ proposed a model based on position-specific scoring matrix (PSSM) and auto covariance for predicting bioluminescent proteins and yielded a high test accuracy of 90.71%. Shi et al¹¹ proposed an effective method based on protein sequence, which employed a support vector machine (SVM) as classifier and used correlation coefficient (CC) transformation as a feature extraction method. Zahiri et al¹² proposed a novel evolutionary-based feature extraction algorithm for PPI prediction called PPIevo, which extracts the evolutionary feature from the PSSM of the protein sequence. In spite of this, there is still space to improve the accuracy and efficiency of the existing methods.

In this work, we proposed a computational method called GWORVM-BIG, which used Bi-gram (BIG) to represent protein sequences on a PSSM and GWORVM classifier to perform classification for predicting PPIs. More specifically, the proposed GWORVM model can obtain the optimum solution of kernel parameters using gray wolf optimizer (GWO) approach, which has the advantages of less control parameters, strong global optimization ability and ease of implementation compared with other optimization algorithms. The experimental results on yeast and human data sets demonstrated the good accuracy and efficiency of the proposed GWORVM-BIG method. The results showed that the proposed GWORVM classifier can significantly improve the prediction performance compared with the relevance vector machine (RVM) model using other optimizer algorithms including grid search (GS), genetic algorithm (GA), and particle swarm optimization (PSO). In addition, the proposed method is also compared with other existing algorithms, and the experimental results further indicated that the proposed GWORVM-BIG model yields excellent prediction performance. For facilitating extensive studies for future proteomics research, the GWORVM-BIG server is freely available for academic use at http://219.219.62.123:8888/GWORVMBIG.

Materials and Method

Data set

To verify effectiveness of the proposed GWORVM-BIG prediction model, yeast and human data sets were employed in the experiment, which can be obtained from the publicly available Database of Interacting Proteins (DIP).¹³ For better implementing the proposed approach, the protein pairs with less than 50 residues are removed, because they might just be fragments. The protein pairs with too much sequence identity are generally considered to be homologous; thus, the pairs which have ⩾40% sequence identity are also deleted for eliminating the bias to these homologous sequence pairs. As a result, 5594 positive protein pairs were selected to create the positive data set and 5594 negative protein pairs were selected to build the negative data set from the yeast data set. Similarly, we selected 3899 positive protein pairs to create the positive data set and 4262 negative protein pairs to build the negative data set from the human data set. Consequently, the yeast data set contains 11 188 protein pairs and the human data set contains 8161 protein pairs.

Position-specific scoring matrix

PSSM is a useful tool that was originally applied for detecting distantly related proteins. Each protein sequence can be transformed into a PSSM¹⁴ using the position-specific iterated BLAST (PSI-BLAST)¹⁵

$$PSSM=\left[\begin{array}{cc}\begin{array}{ccc}{P}_{1,1}& P_{1,2}& P_{1,3}\\ P_{2,1}& P_{2,2}& P_{2,3}\end{array}& \begin{array}{cc}\dots & P_{1,20}\\ \dots & P_{2,20}\end{array}\\ \begin{array}{ccc}M& P_{i,j}& M\\ P_{L,1}& P_{L,2}& P_{L,3}\end{array}& \begin{array}{cc}M& M\\ \dots & P_{L,20}\end{array}\end{array}\right]$$ (1)

where N represents the length of a protein sequence, 20 represents a total of 20 amino acids, and $P_{i,j}$ represents the probability of the $i\mathrm{th}$ amino acid mutates into the $j\mathrm{th}$ amino acid during the course of biological evolution. As a result, high probability indicates a well conserved position and low probability represents a weakly conserved position.

In this article, PSI-BLAST is employed to construct each protein sequence PSSM. To obtain highly and widely homologous sequences, the e-value parameter of PSI_BLAST was set 0.001, and 3 iterations were selected. Consequently, the PSSM of each protein sequence can be expressed as a 20-dimensional matrix that consists of L × 20 elements, where L represents the number of residues of a protein. The columns of the matrix represent the 20 amino acids.

BIG feature extraction method

The BIG has been applied for protein fold recognition.¹⁶ In the work, we employed BIG feature extraction method¹⁷ to represent a given protein sequence based on its PSSM. In detail, the BIG feature vector was computed through counting the BIG frequencies of occurrences in PSSM. A PSSM of a protein sequence contains L rows and 20 columns, where L is the length of protein sequence and 20 represents 20 amino acids. The function of BIG feature extraction method can be given as equation (2)

$$BI{G}_{mn}=\sum _{i=1}^{L-1}{P}_{i,m}{P}_{i+1,n}1\le m\le 20,1\le n\le 20$$ (2)

Equation (2) gives 400 frequencies of occurrences $(BI{G}_{mn})$ for 400 BIG transitions, the matrix BIG is called the BIG occurrence matrix, and the 400 elements represent the BIG feature vector¹⁷ as follows

$$BF=\left[\begin{array}{l}B{G}_{1,1},B{G}_{1,2},\dots B{G}_{1,20},B{G}_{2,1},\dots \\ B{G}_{2,20},\dots B{G}_{20,1},\dots B{G}_{20,20}\end{array}\right]$$ (3)

These BIG features can also be expressed as

$$BF=\left[{\mathrm{\phi }}_1,{\mathrm{\phi }}_2,{\mathrm{\phi }}_3,\dots ,{\mathrm{\phi }}_u,\dots ,{\mathrm{\phi }}_{\theta }\right]$$ (4)

where $\theta =mn=400$ is the dimensionality of the feature vector $BF$. Then, ${\mathrm{\phi }}_u$ can be represented as follows

$${\mathrm{\phi }}_u=\{\begin{array}{c}B{G}_{1,u}\left(1\le u\le 20\right)\\ B{G}_{2,u-20}\left(21\le u\le 40\right)\\ ⋮\\ B{G}_{20,u-380}\left(381\le u\le 400\right)\end{array}$$ (5)

Finally, each protein sequence was transformed into a 400-dimensional vector using BIG method.

Relevance vector machine

Relevance vector machine was always experimented on the binary classification.¹⁸ Given a train data with input ${\{x_n,t_n\}}_{n=1}^N$, $x_n\in R^d,$ where $t_n\in \{0,1\}$ represents the label of training data and $t_i$ is the label of testing data

$$t_i=y_i+{\epsilon }_i$$ (6)

$$y_i=w^T\mathrm{\phi }\left(x_i\right)=\sum _{j=1}^N{w}_{j}K\left(x_i,x_j\right)+w_0$$ (7)

where $y_i$ represents classification model and $i$ represents additional noise. Assuming that the training sets are independent and identically distributed, the vector $t$ obeys the following distribution

$$p\left(t|x,w,{\mathrm{\sigma }}^2\right)={\left(2\pi {\mathrm{\sigma }}^2\right)}^{-N/2}\exp \left[-\frac{1}{2{\mathrm{\sigma }}^2}{\left|\left|t-\mathrm{\phi }w\right|\right|}^2\right]$$ (8)

where $\mathrm{\phi }$ is expressed as follows

$$\mathrm{\phi }=\left(\begin{array}{cccc}1& k\left(x_1,x_1\right)& \cdots & k\left(x_1,x_N\right)\\ ⋮& ⋮& \dots & ⋮\\ 1& k\left(x_N,x_1\right)& \dots & k\left(x_N,x_N\right)\end{array}\right)$$ (9)

The label $t$ is employed to detect the testing set label $t_{*}$, given by

$$p\left(t_{*}|t\right)={\int }^{}p\left(t_{*}|w,{\mathrm{\sigma }}^2\right)p(w,{\mathrm{\sigma }}^2|t)dwd{\mathrm{\sigma }}^2$$ (10)

For the sake of making the value of most components of the weight vector $w$ zero and reducing the amount of calculation of the kernel, additional conditions are attached to the weight vector $w$. Assuming that $w_i$ obeys a distribution with a mean value of zero and a variance of ${\mathrm{\alpha }}_i^{-1}$, the mean $w_i~N(0,{\mathrm{\alpha }}_i^{-1})$ and $p(w|a)={\prod }_{i=0}^{\mathrm{N}}p(w_i|a_i)$, where $a$ represents a hyper-parameters vector of the prior distribution of the weight vector $w$

$$p\left(t_{*}|t\right)={\int }^{}p\left(t_{*}|w,a,{\mathrm{\sigma }}^2\right)p(w,a,{\mathrm{\sigma }}^2|t)dwdad{\mathrm{\sigma }}^2$$ (11)

$$p\left(t_{*}|w,a,{\mathrm{\sigma }}^2\right)=N(t_{*}|y\left(x_{*};w\right),{\mathrm{\sigma }}^2)$$ (12)

Because $p(w,a,{\mathrm{\sigma }}^2|t)$ cannot be obtained by integration, it must be resolved using the Bayesian formula, given by

$$p\left(w,a,{\mathrm{\sigma }}^2|t\right)=p\left(w|a,{\mathrm{\sigma }}^2,t\right)p(a,{\mathrm{\sigma }}^2|t)$$ (13)

$$p\left(w|a,{\mathrm{\sigma }}^2,t\right)=p\left(t|w,{\mathrm{\sigma }}^2\right)p\left(w|a\right)/p\left(t|a,{\mathrm{\sigma }}^2\right)$$ (14)

The integral of the product of $p(t|a,{\mathrm{\sigma }}^2)$ and $p(w|a)$ is given by

$$p\left(t|a,{\mathrm{\sigma }}^2\right)={\left(2\pi \right)}^{-\mathrm{N}/2}{\left|\mathrm{\Omega }\right|}^{-1/2}\exp \left(-\frac{t^T{\mathrm{\Omega }}^{-1}t}{2}\right)$$ (15)

$$\mathrm{\Omega }={\mathrm{\sigma }}^{2}I+\mathrm{\phi }{A}^{-1}{\mathrm{\phi }}^T,A=diag(a_0,a_1,\dots ,a_N)$$ (16)

$$\begin{array}{l}p\left(w|a,{\mathrm{\sigma }}^2,t\right)={\left(2\pi \right)}^{-\left(N+1\right)/2}{\left|\mathrm{\Sigma }\right|}^{-1/2}\\ \exp \left(-\frac{{\left(w-u\right)}^T\left(w-u\right)}{2}\right)\end{array}$$ (17)

$$\mathrm{\Sigma }={({\mathrm{\sigma }}^{-2}{\mathrm{\phi }}^T\mathrm{\phi }+A)}^{-1}$$ (18)

$$u={\mathrm{\sigma }}^{-2}\mathrm{\Sigma }{\mathrm{\phi }}^{T}t$$ (19)

Because $p(a,{\mathrm{\sigma }}^2|t)\propto p(t|a,{\mathrm{\sigma }}^2)p(a)p({\mathrm{\sigma }}^2)$ and $p(a,{\mathrm{\sigma }}^2|t)$ cannot be solved by means of integration, the solution is approximated using the maximum likelihood method, represented by

$$\left(a_{MP},{\mathrm{\sigma }}_{MP}^2\right)=\underset{a,{\mathrm{\sigma }}^2}{\arg }maxp(t|a,{\mathrm{\sigma }}^2)$$ (20)

The iterative process of $a_{MP}$ and ${\mathrm{\sigma }}_{MP}^2$ given by

$$\{\begin{array}{c}{a}_i^{new}=\frac{{\gamma }_i}{{\mu }_i^2}\\ {({\mathrm{\sigma }}^2)}^{new}=\frac{{\left|\left|t-\mathrm{\phi }\mu \right|\right|}^2}{N-\sum _{i=0}^{\mathrm{N}}{\mu }_i}\\ {\gamma }_i=1-a_i{\sum }^{}i,i\end{array}$$ (21)

Here, ${\mathrm{\Sigma }}^{}i,i$ is $i\mathrm{th}$ element on the diagonal of $\mathrm{\Sigma }$, and the initial values of $a$ and ${\mathrm{\sigma }}^2$ can be decided via the approximation of $a_{MP}$ and ${\mathrm{\sigma }}_{MP}^2$ using formula (21) iteratively. After enough iterations, most of the $a_i$ will be close to infinity, the corresponding parameters in $w_i$ will be zero, and other $a_i$ values will be close to finite. The resulting corresponding parameters $x_i$ of $a_i$ are now referred to as the relevance vector.

Gray wolf optimizer

In recent years, optimization algorithms based on meta-heuristic have been extensively employed to solve many optimization problems in different fields. The meta-heuristics are inspired from nature and animal’s behaviors, typically related to physical phenomena or evolutionary concepts. As a new meta-heuristic algorithm, GWO was first developed by Mirjalili et al.¹⁹ The GWO approach simulates the social leadership and hunting behavior of gray wolves in nature. Gray wolves live in a pack which composes of 5 to 12 wolves on average. The leader of the group is named alpha, whose responsibility is to make a decision about habitat, hunting, and so on. The second in the group is called beta, which can provide a certain help to alpha in decision-making. The lowest ranking gray wolf is called $\mathrm{\rho }$ mega, which usually plays the role of scapegoat. The rest of gray wolves are called delta and dominate the omega. The mathematical model of GWO is defined as follows

$$D=\left|C\cdot X_p\left(t\right)-X\left(t\right)\right|$$ (22)

$$X\left(t+1\right)=X_p\left(t\right)-A\cdot D$$ (23)

where $D$ is the distance between the gray wolf and the food, $t$ represents the current iteration, $X_p$ indicates the position of the prey, $X$ is the position vector of a gray wolf, $A$ and $C$ represent coefficient vectors

$$A=2\mathrm{\alpha }\cdot r_2-\mathrm{\alpha }$$ (24)

$$C=2r_1$$ (25)

where $\mathrm{\alpha }$ linearly decreased from 2 to 0 during the iterations; and $r_1$ and $r_2$ represent random vectors from 0 to 1

$$D_{\mathrm{\alpha }}=\left|C_1\cdot X_{\mathrm{\alpha }}\left(t\right)-X\left(t\right)\right|$$ (26)

$$D_{\mathrm{\beta }}=\left|C_2\cdot X_{\mathrm{\beta }}\left(t\right)-X\left(t\right)\right|$$ (27)

$$D_{\mathrm{\rho }}=\left|C_3\cdot X_{\mathrm{\rho }}\left(t\right)-X\left(t\right)\right|$$ (28)

where $D_{\mathrm{\alpha }}$, $D_{\mathrm{\beta }}$, and $D_{\mathrm{\rho }}$ are the current positions of $\mathrm{\alpha },\mathrm{\beta }$, and $\mathrm{\rho }$, respectively

$$X_1=X_{\mathrm{\alpha }}-A_1\cdot D_{\mathrm{\alpha }}$$ (29)

$$X_2=X_{\mathrm{\beta }}-A_2\cdot D_{\mathrm{\beta }}$$ (30)

$$X_3=X_{\mathrm{\rho }}-A_3\cdot D_{\mathrm{\rho }}$$ (31)

$$X\left(t+1\right)=X_1+X_2+X_3/3$$ (32)

In the GWO approach,$\mathrm{\alpha }$ is the fittest solution, the second solution is $\mathrm{\beta }$, and the third solution is $\mathrm{\rho }$.

RVM based on GWO

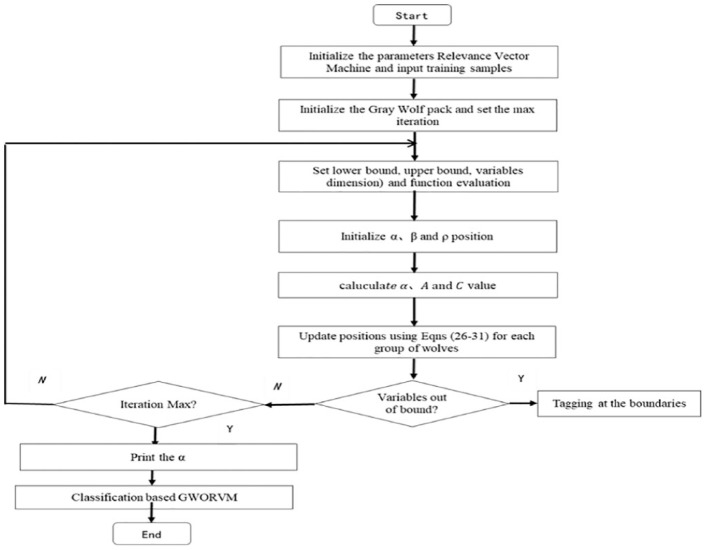
Generally, the kernel parameters of RVM are selected by experience, which may not obtain the optimum solution, affecting the prediction accuracy of RVM. To obtain the optimum solution, many researchers expect to solve the problem using GS, GA,²⁰ and PSO.²¹ In the article, GWO approach was used to obtain the optimum solution of kernel parameters of RVM for the first time. The classification flowchart of RVM based on GWO is given in Figure 1.

Figure 1.

The classification flowchart of GWORVM classification algorithm.

Performance evaluation

In the study, to evaluate the feasibility and effectiveness of the proposed method, we calculated the value of 5 parameters: Accuracy (Ac), Sensitivity (Sn), Specificity (Sp), Precision (Pe), and Matthews correlation coefficient (Mcc). They are expressed as follows

$$\begin{array}{l}\mathrm{Ac}=\frac{TP+TN}{TP+FP+TN+FN}\\ \mathrm{Sn}=\frac{TP}{TP+TN}\\ \mathrm{Sp}=\frac{TN}{FP+TN}\\ \mathrm{Pe}=\frac{TP}{FP+TP}\\ \mathrm{Mcc}=\frac{\left(TP\times TN\right)-\left(FP\times FN\right)}{\sqrt{\left(TP+FN\right)\times \left(TN+FP\right)\times \left(TP+FP\right)\times \left(TN+FN\right)}}\end{array}$$

where TP represents true positives, FP represents false positives, TN represents true negatives, and FN represents false negatives. True positives represent the count of true interacting pairs correctly predicted. True negatives are the number of true noninteracting pairs predicted correctly. False positives defined as the count of true noninteracting pairs falsely predicted, and false negatives represent true interacting pairs falsely predicted to be noninteracting pairs. Moreover, a receiver operating characteristic (ROC) curve was created to evaluate the performance of our proposed method.

Results and Discussion

Performance of the proposed method

To evaluate the efficiency of the GWORVM-BIG, experiments were carried out using the same feature extraction method and a different classifier (GWORVM, GSRVM, GARVM, and PSORVM) on yeast and human data sets, respectively. For averting the overfitting, the data sets were divided into the training sets and independent test sets. More specifically, we randomly selected 1 out of 5 of the data sets as independent test sets and selected the remaining data sets as training sets. Furthermore, we also performed 5-fold cross-validation tests to benchmark the performance of the GWORVM-BIG. In the experiment, the optimum solution of the kernel parameters of RVM was obtained using GWO, GS, GA, and PSO approaches on yeast and human data sets, respectively. The optimum solutions are displayed in Tables 1 and 2. In addition, we selected the Gaussian function as the kernel and set up beta = 0, where beta represents classification or regression. Here, “beta = 0” represents classification. The experimental results are shown in Tables 3 to 10 on yeast and human data sets.

Table 1.

Kernel parameter optimal value of Gauss kernel RVM based on different optimization algorithms on yeast data set.

Method	The optimum solution
GWORVM	2.38
GSRVM	3.96
GARVM	1.58
PSORVM	2.12

Abbreviation: RVM, relevance vector machine.

Table 2.

Kernel parameter optimal value of Gauss kernel RVM based on different optimization algorithm on human data set.

Methods	The optimum solution
GWORVM	1.69
GSVM	1.26
GAVM	2.63
PSORVM	1.98

Abbreviation: RVM, relevance vector machine.

Table 3.

Fivefold cross-validation results shown using RVM based on GWO on yeast data set.

Testing times	Accuracy (%)	Sensitivity (%)	Precision (%)	Mcc (%)
1	96.35	95.87	97.10	91.86
2	97.52	97.89	96.61	94.02
3	97.61	97.84	96.93	93.00
4	496.83	95.32	97.01	92.19
5	97.28	96.91	97.53	93.81
Average	97.12 ± 0.53	96.99 ± 1.20	97.02 ± 0.33	92.97 ± 0.95

Abbreviations: RVM, relevance vector machine; GWO, gray wolf optimizer.

Table 10.

Fivefold cross-validation results shown using RVM based on PSO on human data set.

Testing times	Accuracy (%)	Sensitivity (%)	Precision (%)	Mcc (%)
1	94.03	92.97	97.56	89.58
2	92.58	91.61	94.12	86.94
3	92.80	90.82	96.23	87.26
4	94.89	93.21	97.03	88.21
5	93.21	90.95	97.10	88.12
Average	93.50 ± 0.90	91.91 ± 1.12	96.40 ± 1.38	88.02 ± 1.03

Abbreviations: RVM, relevance vector machine; PSO, particle swarm optimization.

It can be seen from Table 3 that the GWORVM-BIG obtained 97.12%, 96.91%, 97.53%, and 93.81% average accuracy, sensitivity, precision, and Mcc on yeast data set. Table 7 shows that the GWORVM-BIG also achieved good results of average accuracy, sensitivity, precision, and Mcc of 94.567%, 95.55%, 93.08%, and 89.51% on human data set. It can be seen from Tables 4 and 8 that the average accuracy, sensitivity, precision, and Mcc of GSRVM-BIG are 94.79%, 90.58%, 97.11%, and 89.79%; and 92.15%, 91.78%, 91.08%, and 85.45% on yeast and human data sets, respectively. As shown in Tables 5 and 9, the GARVM-BIG obtained 94.79%, 90.58%, 97.11%, and 89.79%; and 92.15%, 91.78%, 91.08%, and 85.45% average accuracy, sensitivity, precision, and Mcc on yeast and human data sets, respectively. Tables 6 and 10 shown that the average accuracy, sensitivity, precision, and Mcc of PSORVM-BIG are 94.79%, 90.58%, 97.11%, and 89.79%; and 92.15%, 91.78%, 91.08%, and 85.45% on yeast and human data sets, respectively.

Table 7.

Fivefold cross-validation results shown using RVM based on GWO on human data set.

Testing times	Accuracy (%)	Sensitivity (%)	Precision (%)	Mcc (%)
1	94.12	95.21	92.24	89.32
2	95.23	97.12	92.68	90.24
3	94.61	95.36	94.86	90.62
4	93.98	94.76	92.26	87.69
5	94.86	94.32	93.35	89.72
Average	94.56 ± 0.52	95.55 ± 0.91	93.08 ± 1.09	89.51 ± 1.14

Abbreviations: RVM, relevance vector machine; GWO, gray wolf optimizer.

Table 4.

Fivefold cross-validation results shown using RVM based on GS on yeast data set.

Testing times	Accuracy (%)	Sensitivity (%)	Precision (%)	Mcc (%)
1	94.33	91.89	97.21	89.12
2	95.29	91.92	97.88	89.94
3	94.58	90.10	97.23	90.21
4	94.86	91.54	96.56	89.65
5	94.92	90.12	96.89	90.03
Average	94.79 ± 0.36	90.58 ± 0.82	97.11 ± 0.67	89.79 ± 0.43

Abbreviations: RVM, relevance vector machine; GS, grid search.

Table 8.

Fivefold cross-validation results shown using RVM based on GS on human data set.

Testing times	Accuracy (%)	Sensitivity (%)	Precision (%)	Mcc (%)
1	92.86	92.02	91.62	86.21
2	93.69	94.00	90.31	88.97
3	91.32	90.32	92.01	83.69
4	92.21	92.16	91.11	85.38
5	90.68	90.36	90.169	82.98
Average	92.15 ± 1.20	91.78 ± 1.52	91.08 ± 0.79	85.45 ± 2.35

Abbreviations: RVM, relevance vector machine; GS, grid search.

Table 5.

Fivefold cross-validation results shown using RVM based on GA on yeast data set.

Testing times	Accuracy (%)	Sensitivity (%)	Precision (%)	Mcc (%)
1	95.65	93.719	97.10	91.36
2	95.29	93.13	96.19	89.92
3	94.66	90.94	96.31	88.96
4	95.91	92.59	98.93	91.25
5	95.10	91.99	97.66	89.86
Average	95.32 ± 0.48	92.36 ± 0.93	97.23 ± 1.12	90.27 ± 1.01

Abbreviations: RVM, relevance vector machine; GA, genetic algorithm.

Table 9.

Fivefold cross-validation results shown using RVM based on GA on human data set.

Testing times	Accuracy (%)	Sensitivity (%)	Precision (%)	Mcc (%)
1	93.85	90.86	96.01	87.59
2	91.56	90.11	91.98	83.76
3	93.00	92.12	93.00	86.29
4	93.32	88.89	96.99	86.00
5	93.45	90.96	95.69	86.96
Average	93.03 ± 0.88	90.59 ± 1.20	94.73 ± 2.13	86.12 ± 1.45

Abbreviations: RVM, relevance vector machine; GA, genetic algorithm.

Table 6.

Fivefold cross-validation results shown using RVM based on PSO on yeast data set.

Testing times	Accuracy (%)	Sensitivity (%)	Precision (%)	Mcc (%)
1	91.17	94.92	98.17	92.94
2	96.16	94.96	97.23	91.16
3	94.85	92.61	96.64	89.01
4	96.66	94.39	98.57	92.54
5	94.61	91.78	97.65	89.21
Average	95.89 ± 1.12	93.73 ± 1.45	97.65 ± 0.76	90.97 ± 1.82

Abbreviations: RVM, relevance vector machine; PSO, particle swarm optimization.

In the experiment, comparing the GWORVM-BIG with GSRVM-BIG, GARVM-BIG and PSORVM-BIG showed that the GWORVM-BIG method is accurate, robust, and effective for predicting PPIs. Similarly, as shown in Figures 2 and 3, the ROC curves of GWORVM-BIG are also significantly better than GSRVM-BIG, GARVM-BIG, and PSORVM-BIG. This clearly proved that the GWORVM is an accurate and robust classifier for predicting PPIs. The major reason is that GWO algorithm has the advantages of less control parameters, strong global optimization ability, and ease of implementation compared with other optimization algorithms. The GWO approach simulates social leadership and hunting behavior of gray wolves in nature, which can obtain the optimal solution position through continuous iteration optimization. It has stronger robustness to the change of its relevant parameters and can adaptively adjust the convergence factor during the process of iteration. The GWO realizes the balance of population between the global search ability and local development ability using feedback mechanism of searching individual information Therefore, the optimization efficiency of GWO algorithm is superior to other intelligent optimization algorithms.

Figure 2.

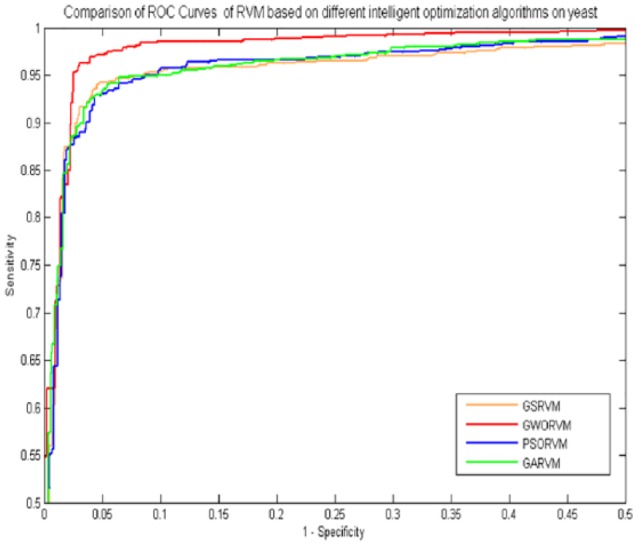
Comparison of ROC curves of RVM based on different intelligent optimization algorithms on yeast data set. ROC indicates receiver operating characteristic; RVM, relevance vector machine.

Figure 3.

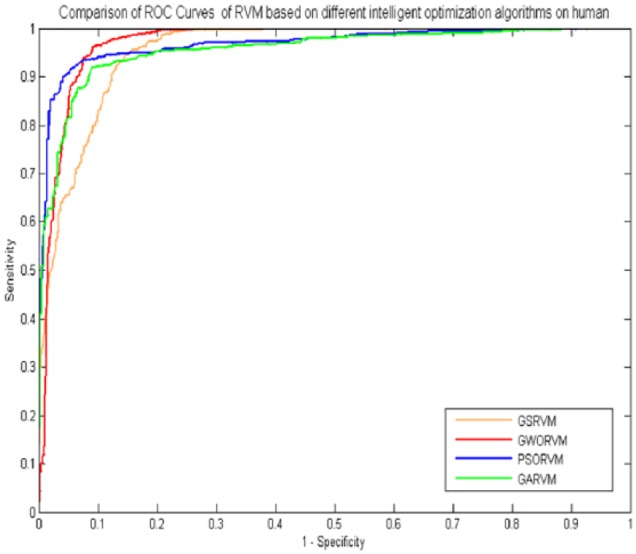
Comparison of ROC curves of RVM based on different intelligent optimization algorithms on human data set. ROC indicates receiver operating characteristic; RVM, relevance vector machine.

Comparison with the SVM based on GWO method

Despite the proposed GWORVM-BIG achieving good predictive performance, for further evaluating the prediction performance of RVM, the comparison of prediction accuracy was implemented between GWORVM classifier and the state-of-the-art SVM based on GWO algorithm on yeast and human data sets using the same feature extraction method (BIG). In the experiment, we used the LIBSVM tool²² to perform classification and GWO algorithm to optimize the RBF kernel parameters of SVM. Here, the optimum solution of kernel parameters was obtained, which were set up c = 0.6 and g = 0.3.

As shown in Table 11, the GWOSVM obtained 92.54% average accuracy, 95.49% average sensitivity, 92.97% average precision, and 89.56% average Mcc on yeast data set. It can be seen from these experimental results that the prediction performance of GWORVM-BIG is significantly better than the GWOSVM-BIG. At the same time, as displayed in Figure 4, the ROC curves of GWORVM classifier are also significantly better than GWOSVM classifier. This clearly proved that the GWORVM classifier is an accurate and robust classifier for predicting PPIs.

Table 11.

Fivefold cross-validation results shown using GWOSVM on yeast data set.

Testing times	Accuracy (%)	Sensitivity (%)	Precision (%)	Mcc (%)
1	93.98	94.96	91.96	89.12
2	95.01	96.69	92.36	90.01
3	94.32	95.12	94.82	90.68
4	94.36	94.86	92.38	88.00
5	94.89	95.52	93.36	89.98
Average	92.54 ± 0.60	95.49 ± 0.88	92.97 ± 1.15	89.56 ± 1.03

Figure 4.

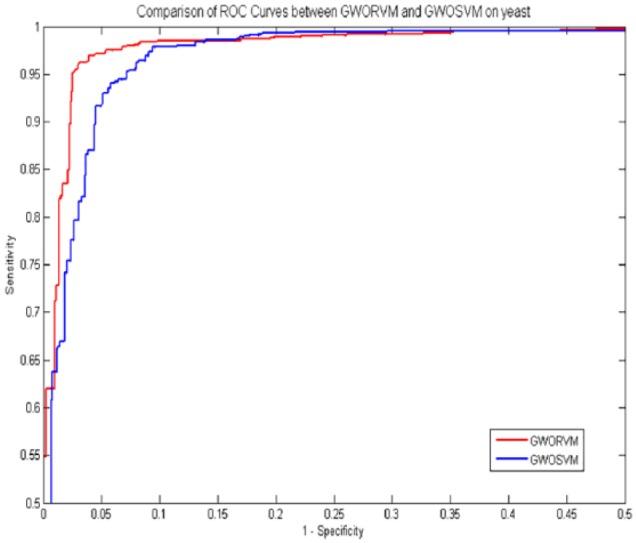
Comparison of ROC curves between GWORVM and GWOSVM on yeast data set. ROC indicates receiver operating characteristic.

In this study, comparing GWORVM with GWOSVM showed that the classification performance of RVM is significantly better than SVM using the same feature extraction method. The major reason is that RVM classifier reduces the amount of calculation of the kernel and overcomes the disadvantage that kernels of SVM required meeting the condition of Mercer. As a result, the experimental results of this study indicate that the GWORVM-BIG prediction model can obtain high accuracy for predicting PPIs.

Comparison with other methods

For demonstrating the effectiveness of the proposed GWORVM-BIG prediction model, we also compared the performance of GWORVM-BIG with existing PPI predictor on yeast and human data sets. It can be found from Tables 12 and 13 that the prediction performance of the GWORVM-BIG model is obviously higher than other prediction models on yeast and human data sets. It is proved from these comparison results that the proposed model called GWORVM-BIG can improve the prediction accuracy relative to current exiting approaches.

Table 12.

The prediction results of different prediction models on yeast data set.

Methods	Accuracy (%)	Sensitivity (%)	Precision (%)	Mcc (%)
Guo et al23	89.33 ± 2.67	89.93 ± 3.60	88.77 ± 6.16	N/A
Zhou et al24	88.56 ± 0.33	87.37 ± 0.22	89.50 ± 0.60	77.15 ± 0.68
Yang et al25	86.15 ± 1.17	81.03 ± 1.74	90.24 ± 1.34	N/A
Wong et al26	93.92 ± 0.36	91.10 ± 0.31	96.45 ± 0.45	88.86 ± 0.63
Huang et al27	96.28 ± 0.52	92.64 ± 1.00	99.92 ± 0.32	92.82 ± 0.97
Li et al28	94.60 ± 0.06	94.80 ± 0.01	94.30 ± 0.05	89.60 ± 0.012
Our method	97.12 ± 0.53	96.99 ± 1.20	97.02 ± 0.33	92.97 ± 0.95

Table 13.

The prediction results of different prediction models on human data set.

Methods	Accuracy (%)	Sensitivity (%)	Precision (%)	Mcc (%)
Nanni29	83.00	86.00	85.10	N/A
Nanni30	84.00	86.00	84.00	N/A
Nanni and Lumin31	86.60	86.70	85.00	N/A
You and colleagues32	92.83	89.32	96.13	86.85
Nanni et al33	93.90	N/A	N/A	N/A
Our method	94.56	95.55	93.08	89.51

The proposed GWORVM-BIG prediction model obtains the good prediction results relative to current exiting approaches. The major reason is that the proposed method adopted effective feature extraction method and classifier. Specifically, there are 3 reasons: (1) the PSSM matrix is a much useful tool for representing protein sequence, which can not only describe the order information but also retain sufficient prior information for the protein sequence. (2) The BIG probabilities represented each protein sequence by its PSSM and calculated the BIG feature using the probability information contained in PSSM. The BIGs features from PSSMs can significantly reduce the sparsity level, which helps in improving the recognition performance. (3) GWO algorithm was employed to obtain the optimal solution of kernel parameters of RVM, which improved prediction performance of RVM. As a result, the experimental results demonstrated that the GWORVM-BIG prediction model is very suitable for predicting PPIs.

Conclusions

In this study, we proposed a computational method called GWORVM-BIG, which used BIG to represent protein sequences on a PSSM and GWORVM classifier to perform classification for predicting PPIs. The experimental results on yeast and human data sets demonstrated the good accuracy and efficiency of the proposed GWORVM-BIG method. The comparisons showed that the proposed GWORVM classifier can significantly improve the prediction performance. The major improvements of the proposed method may attribute to following reasons: (1) the PSSM matrix is a much useful tool for representing protein sequence, which can not only describe the order information but also retain sufficient prior information for the protein sequence. (2) The BIG feature extraction method represented each protein sequence by its PSSM and calculated the BIG feature using the probability information contained in PSSM. The BIGs features from PSSMs can significantly reduce the sparsity level, which helps in improving the recognition performance. (3) GWO algorithm has the advantages of less control parameters, strong global optimization ability, and ease of implementation compared with other optimization algorithms, which were employed to obtain the optimal solution of kernel parameters of RVM and improved prediction performance of RVM.