Multimodal network diffusion predicts future disease–gene–chemical associations

Abstract

Motivation

Precision medicine is an emerging field with hopes to improve patient treatment and reduce morbidity and mortality. To these ends, computational approaches have predicted associations among genes, chemicals and diseases. Such efforts, however, were often limited to using just some available association types. This lowers prediction coverage and, since prior evidence shows that integrating heterogeneous data is likely beneficial, it may limit accuracy. Therefore, we systematically tested whether using more association types improves prediction.

Results

We study multimodal networks linking diseases, genes and chemicals (drugs) by applying three diffusion algorithms and varying information content. Ten-fold cross-validation shows that these networks are internally consistent, both within and across association types. Also, diffusion methods recovered missing edges, even if all the edges from an entire mode of association were removed. This suggests that information is transferable between these association types. As a realistic validation, time-stamped experiments simulated the predictions of future associations based solely on information known prior to a given date. The results show that many future published results are predictable from current associations. Moreover, in most cases, using more association types increases prediction coverage without significantly decreasing sensitivity and specificity. In case studies, literature-supported validation shows that these predictions mimic human-formulated hypotheses. Overall, this study suggests that diffusion over a more comprehensive multimodal network will generate more useful hypotheses of associations among diseases, genes and chemicals, which may guide the development of precision therapies.

Availability and implementation

Code and data are available at https://github.com/LichtargeLab/multimodal-network-diffusion.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Precision medicine is a growing area of research to improve human health and quality of life. To achieve these goals, it seeks to understand which genes drive diseases, and which drugs may target these genes and hence treat these diseases. To support this effort, known associations between diverse types of biological entities have been curated and stored in databases, including, gene–gene (GG; protein–protein) associations in the Search Tool for the Retrieval of Interacting Genes/Proteins (STRING; Szklarczyk et al., 2015), as well as disease–gene (DG), disease–chemical (DC) and gene–chemical (GC) associations in the Comparative Toxicogenomics Database (CTD; Davis et al., 2015). In turn, these databases support algorithms that predict new associations which, if true, may expand the knowledge and speed drug discovery.

Several computational studies predicted pairwise associations among genes, chemicals and diseases (Chen et al., 2016; Li et al., 2016; Piro and Di Cunto, 2012; Shahreza et al., 2017a). A popular approach is network modeling (Shahreza et al., 2017a). Thus, DG associations were predicted by Random walk (RW) (Köhler et al., 2008; Li and Patra, 2010), CIPHER (Wu et al., 2008), Prince (Vanunu et al., 2010), clustering and neighborhood methods (Navlakha and Kingsford, 2010) and a metapath-based approach (Himmelstein and Baranzini, 2015). For GC associations, bipartite graph learning method (Yamanishi et al., 2008), side-effect similarity (Campillos et al., 2008), drugCIPHER (Zhao and Li, 2010), NRWRH (Chen et al., 2012b), DBSI, TBSI, NBI (Cheng et al., 2012), HGBI (Wang et al., 2013) and the within scores and between scores (Shi et al., 2015) were used. As for predicting DC associations, MRS (Suthram et al., 2010), a bipartite graph-based method (Li and Lu, 2012), SNS (Lee et al., 2012), heterogeneous network clustering (Wu et al., 2013) and TTMD (Yu et al., 2017) have been successful.

Interestingly, most such studies focused on just one of three tasks, i.e. either predicting DG, DC or GC associations; they also did not use all of the six possible types of edges (DG, DC, GC, GG, DD and CC; Table 1); and they did not study the impact of sequentially adding information. A few studies (Shahreza et al., 2017b; Wang et al., 2014) investigated more than one tasks. Doing three tasks in one study enables fair comparison among prediction tasks and provides a more complete understanding of precision medicine. On the other hand, it has been suggested that incorporating information into a multimodal network (i.e. a network of more than one mode, also known as type of edges) improves prediction of associations (Chen et al., 2016; Li et al., 2016; Piro and Di Cunto, 2012; Shahreza et al., 2017a). Integrating multiple edge types also helps to model biological systems more completely (Shahreza et al., 2017b). Shahreza et al. (2017b) and Himmelstein et al. (2017) used networks including 6 and 24 edge types, respectively. However, the effect of sequentially adding edge types has not been fully investigated. Therefore, using all six types of information to improve prediction of DG, DC, GC associations is promising, and requires further examination. In addition to potentially improving performance, integrating data provides better prediction coverage of genes, chemicals and diseases allowing for a wider range of predictions for possible associations.

Table 1.

Acronyms used in this paper

D	Disease	DG	Disease–gene	DD	Disease–disease
G	Gene	DC	Disease–chemical	GG	Gene–gene
C	Chemical	GC	Gene–chemical	CC	Chemical–chemical

A common experiment to evaluate predicting DG, DC and GC associations is k-fold cross-validation (e.g. Shahreza et al., 2017b). Since those experiments remove edges randomly, they do not reflect the real-world scenario where edges may be added at different rates depending on network characteristics or the trend of research funding. Researchers usually use the current information to predict the future associations. Therefore, we believe that the time-stamped experiment better resembles the problem, i.e. how to use data from an earlier time to predict data at a later time. Similar experiments have been applied in other link prediction problems (Dunlavy et al., 2011).

In this work, we build a multimodal network of all six types of edges between genes, chemicals (including drugs) and diseases. We then apply three diffusion-based methods to predict the DG, DC and GC associations when varying network information amount. We choose two more modern methods, graph-based information diffusion (GID; Lisewski et al., 2014; Venner et al., 2010) and AptRank (AR; Jiang et al., 2017) and the classical RW (Can et al., 2005; Köhler et al., 2008) for comparison. We test the data consistency through 10-fold cross-validation both within single edge types and across edge types, and examine how the DG, DC and GC edges help in each other’s prediction. In addition, we demonstrate that AR is the best tested method to predict future information.

More importantly, we found that adding information expands network prediction coverage (i.e. possibly predicted edges) up to 3.5 times. Yet, it does so without decreasing performance in most cases. Finally, we show that literature-based validation supports many of our top predictions based on data up to 2016. We conclude that a more comprehensive multimodal network would allow diffusion-based methods to effectively prioritize more associations between genes, chemicals and diseases, to generate testable hypotheses that may accelerate the development of precision medicine.

2 Materials and methods

2.1 Network construction

The network contains three types of nodes (diseases, chemicals and genes), and six types of edges (DG, DC, GC, DD, GG and CC). Chemicals include drugs. Supplementary Table S1 shows the node and edge contributions from each source. We constructed three 1-mode networks for DG, DC and GC, respectively, one 3-mode (DG, DC and GC) network and one 6-mode (DG, DC, GC, DD, GG and CC) network for earlier (up to April 2014) and later (after April 2014) versions (Supplementary Tables S2 and S3), respectively. All networks are symmetric and binary-weighted (zeros and ones). Download links to all networks and the mapping file can be found at https://github.com/LichtargeLab/multimodal-network-diffusion.

2.1.1 Mapping between heterogeneous data sources

All gene IDs in this work were mapped using the HGNC (Yates et al., 2017) custom download tool (September 2017) and Ensembl identifiers from STRING (Szklarczyk et al., 2015). For DG, DC and GC associations, the CTD (Davis et al., 2015) disease and chemical terms were mapped through MeSH term names. If direct mappings could not be obtained, synonyms for genes, chemicals or diseases were used as a secondary method, with the least promiscuous synonyms taking precedence.

2.1.2 DG, DC and GC associations

Curated DG, DC and GC associations were retrieved from the CTD (Davis et al., 2015) (http://ctdbase.org) in April 2014 and April 2016. We chose CTD because it is one of the largest databases with literature-curated associations. We excluded inferred associations, and only included ‘protein form’ and non-nested interactions as performed previously (Regenbogen et al., 2016). The edge weights were set to 1.

2.1.3 DD and CC associations

DD and CC associations were determined and added based on the MeSH hierarchy (Rogers, 1963) tree files (mtrees.bin) from 2013 and 2016 (ftp://nlmpubs.nlm.nih.gov/online/mesh). We chose MeSH because it is one of the largest databases of DD and CC associations, and CTD also provides MeSH identifiers, which alleviates the mapping issue when integrating data. For each pair of diseases or chemicals, an edge confidence of 1 was assigned if both entities were in a parent and child pair. For example, ‘Breast Neoplasms’ (tree number C04.588.180) is a parent of ‘Carcinoma, Ductal, Breast’ (tree number C04.588.180.390). Therefore, an edge with confidence of 1 is assigned between them.

2.1.4 GG associations

We used the experimentally validated human protein–protein interaction data downloaded from STRING (Szklarczyk et al., 2015) (https://string-db.org) versions 9.05 (December 27, 2013) and 10.0a (April 16, 2016). We chose STRING because it has unified the data from six experimental databases, including IntAct (https://www.ebi.ac.uk/intact), DIP (http://dip.mbi.ucla.edu), BioGRID (https://thebiogrid.org), HPRD (https://hprd.org), MINT (https://mint.bio.uniroma2.it) and PDB (https://www.rcsb.org). We only used high-confidence edges (i.e. ≥900) in STRING experimental data, and changed their weights to 1. This binarized the weight of the GG edges to match the other edge types.

2.1.5 Network trimming

We pruned the 1-core graph from the 2-core graph to reduce noise in the experiments, improving predictions. The 1-core of the graph is a tree-like region, which is entirely predictable and uninformative for diffusion-based methods. We removed all nodes whose degrees are 1s in the 6-mode network from all networks used in each experiment. We performed this iteratively such that any node with degree one, because of node removal, was deleted from the graph as well. The removed subgraphs consist mostly of paths or stars. The final network does not contain any degree one nodes.

2.2 Random walk with restart (RW)

We adapted the RW equation (Page et al., 1999; Smedley et al., 2014):

$$f=r{\left(I-\left(1-r\right)W\right)}^{-1}y.$$ (1)

Here, W is the column-normalized adjacency matrix, I is the identity matrix, y is the vector of initial probability, $f$ is the vector of steady-state probability and $r$ is the restart probability.

We constructed $y$ by setting the source node to 1 and 0 otherwise. We set $r$ as 0.75 (Köhler et al., 2008) because it previously outperformed other clustering and neighborhood approaches (Navlakha and Kingsford, 2010).

2.3 Graph-based information diffusion (GID)

GID was previously applied to predict protein function (Lisewski et al., 2014; Venner et al., 2010) using the formula:

$$f={\left(I+\alpha L\right)}^{-1}y.$$ (2)

Here, $L$ is the normalized graph Laplacian, $I$ is the identity matrix, $y$ is a vector of prior labels, $f$ is the label vector after diffusion and $\alpha$ is a factor which balances the tradeoff between loss and smoothness in the diffusion process. We set $\alpha$ as $1/{\parallel L\parallel }_1$, which is a sufficient condition to ensure convexity of the cost function (Lisewski and Lichtarge, 2010).

We consider each entity as a label and diffuse signal from each one to every other entity to predict potential associations. We set the source node to 1 and all other nodes to 0 in $y$.

2.4 AptRank (AR)

AR was used to predict protein functions (Jiang et al., 2017), and we repurposed the method to perform link prediction in this paper. We generated the solution using the formula:

$$f={\displaystyle \sum }_{i=0}^k{\text{γ}}_{\text{*}}^{(i)}{F}^{\text{i}}y.$$ (3)

Here, $F$ is a user-defined diffusion matrix. We chose $F$ to be the adjacency matrix, representing the training graph divided by its spectral radius (i.e. the largest absolute eigenvalue among all eigenvalues of the adjacency matrix), $y$ is the vector of source nodes, $f$ is the result vector after diffusion and ${\gamma }_{\text{*}}^{(\text{i})}$ is the scalar of the adaptive diffusion parameter. The essence of AR is to compute the diffusion parameters from the fitting-validating process instead of directly using a geometric series like the original PageRank (Page et al., 1999), RW or Katz score (Katz, 1953). AR splits non-zero values in $F$ into two subsets for fitting and validating ${\gamma }_{\text{s}}^{(\text{i})}$. Since the process relies on splitting the data into fitting and validation sets, we perform the same experiment S times, each time taking a new random split of the data. We then take ${\gamma }_{\text{*}}^{(\text{i})}$to be the mean of all the diffusion parameters at step i from S trials.

We set $k$ as 8 because terms with large $k$ decay rapidly to 0, we set S as 5 to avoid unnecessarily lengthy evaluations. We choose to use an even split for the fitting and validating process. We set the source node to 1 and all other nodes to 0 in $y$.

3 Results and discussion

3.1 Experimental setup

We test prediction performance with four experiments: (i) 10-fold cross-validation, (ii) leave-one-mode-out (LOMO) (Regenbogen et al., 2016), (iii) time-stamped and (iv) prospective experiments.

3.1.1 Performance metric

To evaluate the prediction performance of each method in 10-fold cross-validation, LOMO and time-stamped experiments, we computed the mean of the bootstrapped area under the receiver operating characteristic curve (AUROC), and the mean of the bootstrapped area under the precision recall curve (AUPRC). Care was taken to balance the classes when bootstrapping since annotated known associations (positive gold standards) are far fewer than non-annotated associations (negative gold standards), which could otherwise impact performance evaluation because of class imbalance (Shahreza et al., 2017a). Each averaged bootstrapped AUROC or AUPRC was computed from 100 samplings. Each sampling randomly took 20% of the positive gold standards and equal amount of negative gold standards for computing AUROC and AUPRC. Prediction ranking is from high to low score in $\text{f}$ for all methods. Furthermore, the same set of edge predictions was evaluated across different networks and algorithms in LOMO and time-stamped experiments in order to facilitate the comparisons of performance among different networks.

As is natural of biological database data, it should be noted that the gold standard negatives are actually unknown and some, and perhaps even many, might be eventually be discovered and turn positive in the future. Therefore, the false positives could either become true positives or remain false positives, and the current performance is a lower bound of estimate.

3.2 10-fold cross-validation

To evaluate whether the multimodal networks improve performance, we performed 10-fold cross-validation for three 1-mode, one 3-mode and one 6-mode networks (Supplementary Table S3) using RW, GID and AR. We added the information sequentially to determine which types of associations were most successfully predicted, and to evaluate whether integrating data improves predictive power. Edges were randomly split into 10 sets of approximately the same size within each type of edge. For the 3-mode and 6-mode networks, edges from different modes were then combined to generate 10 sets of 3-mode or 6-mode subgraphs. Each set of edges was left out and predicted based on the other nine sets, which led to a total of 10 rounds of predictions. All methods used the same 10 sets of data to make them comparable. The final prediction matrix composed of the 10 runs was compared against the initial matrix.

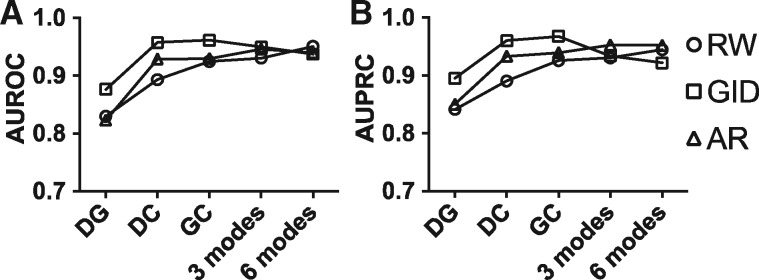
Figure 1 shows that for 3-mode and 6-mode networks, all algorithms converge to mutually consistently high performances, whereas GID outperformed RW and AR in single-mode networks (DG, DC or GC). The performance difference across three single-mode networks suggests that the structure and noise content of those networks are not similar, and, specifically, DG is the least consistent network as compared to DC and GC. Also, RW and AR always benefit from adding other modes, whereas that GID is more sensitive to the noise from multiple modes.

Fig. 1.

Multimodal networks can be recovered better than single-mode networks in 10-fold cross-validation. Network information consistency of single-mode (DG, DC or GC) and multiple modes (3 modes, DG+DC+GC; 6 modes, DG+DC+GC+DD+GG+CC) were tested by three methods. (A) AUROC and (B) AUPRC showed higher performance in multimodal networks for RW and AR but not for GID

3.3 Leave-one-mode-out (LOMO) experiment

Next, we asked whether some of the associations could predict orthogonal ones through LOMO experiments (Regenbogen et al., 2016). These are more stringent tests than simple 10-fold cross-validation or leave-one(‐edge)-out experiments (e.g. Wang et al., 2014) because erasing all the edges from one entire mode precludes the possibility that edge recovery arises trivially from obvious similarities with ones that remained in the network. We therefore removed all DG, DC or GC edges in three separate experiments and tested each time whether they could be recovered by predictions on the remaining network through ‘intermodal transitivity’. We also used 3-mode and 6-mode networks as input to compare the effect of added information.

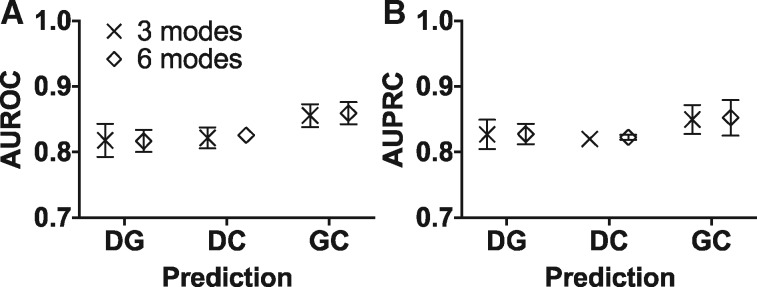
The results show each of the DG, DC and GC modes can be predicted based on the two or five other modes in the network using RW, GID or AR (Fig. 2). Overall, there is little difference in performance between using 3-mode and 6-mode networks. Prediction performance is better for GC, suggesting that associations may be predicted more successfully via disease bridges [i.e. together GD and DC associations (GD $\wedge$DC) predict GC associations] than other cases, e.g. DG predictions from DC$\wedge$CG, or DC predictions from DG$\wedge$GC. This could be because diseases are more specific conditions, while genes and chemicals have protean functions leading to more promiscuous associations and a strong context dependence. Nevertheless, these data show that the AUROC and AUPRC are always above 0.8 (Fig. 2), which suggests gene, chemical and disease network information is transitive across modes; such transfer performs best via diseases.

Fig. 2.

Gene-chemical-disease associations can be retrieved by orthogonal types of information in LOMO experiment. The associations of the prediction type in the input network were left out, and then each method used the remaining information to predict them back. (A) AUROC and (B) AUPRC showed similar performance in 3-mode and 6-mode networks. Each dot and its error bar are the mean and the standard deviation of the results from RW, GID and AR. The error bars were not shown if the error bars are shorter than the height of the symbol. The 3 modes, DG+DC+GC network; 6 modes, DG+DC+GC+DD+GG+CC network

3.4 Time-stamped experiment

To test performance in the most realistic context, we ran time-stamped experiments. We used data from 2014 or before gathered from CTD (2014), STRING (version 9.05) and MeSH (2013) to predict the new edges that were added in the 2016 version of the CTD network (Supplementary Table S2). Three experiments tested the prediction of one edge type, DG, DC or GC, and this was repeated in single-mode, 3-mode and 6-mode networks to compare the effect of adding multimodal information.

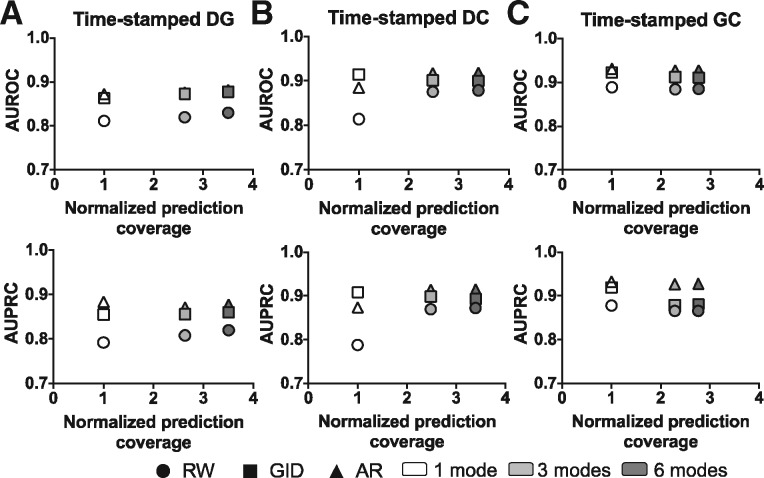
Strikingly, Figure 3 shows that DG, DC and GC associations that were added to CTD in the near future could be predicted readily based on the past information using diffusion-based methods. Much as before, DG is the most difficult mode to predict and GC is easiest. While these differences appear small, the prediction coverage (i.e. the number of edges possible to predict) for DG, DC or GC increased up to 3.5-fold with more modes added (Fig. 3A–C). As an example, the coverage of single-mode DG is computed by multiplying the number of diseases and the number of genes and then subtracting the number of DG pairs which are in different components (i.e. there is no path between the disease and the gene). To distinguish how the performance difference between network inputs compares to a random setting, we ran random simulations (Supplementary Methods; Supplementary Fig. S1; Supplementary Table S4). We found that after adding information into networks, AR often does not change performance significantly, and increases performance significantly in DC; RW sometimes increases performance in DG and DC, and only decreases AUPRC in GC. In contrast, GID does not change performance significantly in DG, but decreases performance significantly in GC and DC when networks changed from 1- to 3-mode or 1- to 6-mode, which can likely be explained by the $\alpha$ parameter computed based on the whole network. In total, there are two metrics, three algorithms, three prediction modes and three network changes. This leads to a total of (2*3*3*3=) 54 experiments. Out of the 54 cases, 10 cases have significantly decreasing performance, 11 cases have significantly increasing performance and 33 cases have no significant changes after adding information into networks (Supplementary Table S4). These data show that the addition of information helps to increase the coverage of the prediction space without significantly decreasing performance in most cases, and AR is the most robust method to accommodate the added information.

Fig. 3.

Network expansion increases prediction coverage without decreasing performance. Network prediction coverage (i.e. the number of possibly predicted edges) was normalized to the 1-mode network of each mode. The 1-mode DG has 9 325 157, 1-mode DC has 12 618 659 and 1-mode GC has 26 910 700 possible edges to predict for the given mode in 2014 networks. The 1 mode, (A) DG, (B) DC, (C) GC; 3 modes, DG+DC+GC network; 6 modes, DG+DC+GC+DD+GG+CC network

Comparing algorithms, AR and GID outperform RW (Fig. 3), likely because both have diffusion parameters adapted to the network, whereas RW is agnostic to the network structure. AR tends to do better than GID in most cases (Fig. 3). Perhaps because the GID diffusion parameter, $\alpha$, relies on an empirical function computed over the entire network, whereas AR, which is closely related to an adaptive RW method, uses a more sophisticated approach that learns its parameters from a fitting-validation process. Overall, AR is the best method for predicting future DG, DC and GC associations.

3.5 Case studies of prospective experiment

To assess performance in practice, we examined the genes and chemicals predicted to be associated with five cancers and five diseases that were leading causes of mortality (American Cancer Society, 2017; World Health Organization, 2017), by literature-based associations. The cancers include lung, colon, pancreatic, breast and liver disease. The other five diseases are coronary artery disease (CAD), stroke, pneumonia, chronic obstructive pulmonary disease and diabetes mellitus. These 10 diseases served as queries in DG and DC predictions.

Because we also would like to examine GC predictions, we chose genes from genes related to those 10 diseases (Supplementary Methods) as queries. The nine unique genes selected were CYP1A2, SLC22A1, CYP2B1, CYP3A4, NR1I3, ESR2, ALB, PARP1 and NR1I2 (Supplementary Table S5). We restricted our validation of chemical predictions to the 1685 FDA-approved drugs from DrugBank (Wishart et al., 2006) version 5.0.3.

Since network-based predictions might have biases in degree, and most of the leading causes of mortality and their related genes have degree more than 100 (Supplementary Table S6), we further randomly chose 10 diseases and 10 genes (Supplementary Table S6), which have <100 edges in the 6-mode network, for comparison.

For each method and query term, we computed precision at 20 by literature-based associations using PubMed. This was based on the top 20 predictions over the 2016 network, a number of putative associations which can eventually be reasonably tested in low-throughput biological experimental assays (e.g. cell line or animal assays) to further validate molecular functions and mechanisms. Adapting a prior method (Ade et al., 2007), we took a predicted association to be true if its Fisher’s exact test (Supplementary Table S7) one-sided P-value was below 0.001, a threshold ensuring that the adjusted P-values corrected for 20 predictions are <0.05. For each query term, we also computed the averaged precision at 20 from 50 times of random predictions. We computed chi-square test of independence to see whether the precision at 20 is significantly higher than random.

First, all algorithms did better than random (Fig. 4A–C; Supplementary Fig. S2A–C; Supplementary Table S8) at predicting DG, DC and GC. Second, the performance of predicting DG associations is the best (Fig. 4A; Supplementary Fig. S2A). This might be because (i) there are relatively fewer studies of those examined diseases/genes in DC and GC and they are not enough to support the predictions. This could be supported by the fact that examined diseases have more articles on PubMed than genes despite their similar degree (Supplementary Fig. S3). (ii) One chemical may be described in the paper by different names, leading to difficulty in searching for literature support. Third, using 3-mode and 6-mode networks often improve the significance for RW and AR but not for GID (Fig. 4D–F; Supplementary Fig. S2D–F; Supplementary Table S8). Fourth, interestingly, the predictions of GID using only DC or GC 1-mode networks still showed overall higher significance than RW and AR using multimodal networks (Supplementary Table S8). Fifth, the entity degree is significantly correlated with precision at 20 for all three modes (rho = 0.63 in DG, 0.42 in DC and 0.48 in GC; Supplementary Fig. S4), and the predictions of most entities are non-random for both low and high degree (i.e. chi-square test P-values <0.05; Supplementary Fig. S4). Sixth, we could not find one combination of method and network that outperforms others in every tested query term, nor one that performs better than random controls in a few cases, e.g. predicting chemicals for ESR2 and NR1I2 (Fig. 4F). These results imply that (i) how to choose the method and the network depends on the specific problem of interest; (ii) ensemble methods based on multiple different algorithms and more comprehensive network information are necessary for improving performance further. Overall, these data show that diffusion-based methods on multimodal networks can generate hypotheses supported by the literature.

Fig. 4.

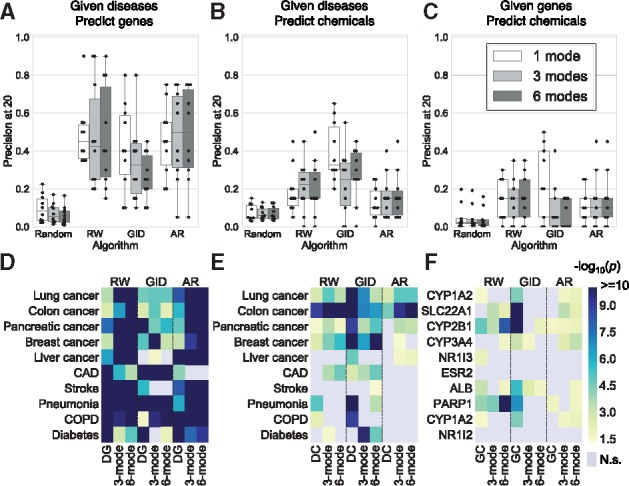
Top predicted entities co-occur with query terms in literature. We validated the top 20 predictions based on 2016 networks for each chosen query term using literature-based associations. We chose 10 diseases of leading cause of mortality as query terms to predict (A, D) associated genes and (B, E) FDA-approved drugs. (C, F) We also chose 10 genes associated with those 10 diseases as query terms and predicted associated FDA-approved drugs. Random control was 50 average experiments of 20 random terms for each query term. We computed (A–C) the precision at 20 and (D–F) chi-square test to determine how different the predictions from random controls. N.s., not significant (i.e. chi-square test P-value >0.05). The 1 mode, (A) DG, (B) DC, (C) GC network; 3 modes, DG+DC+GC network; 6 modes, DG+DC+GC+DD+GG+CC network

We analyzed three queries in greater detail, i.e. CAD for DG, colon cancer for DC and SLC22A1 for GC. For these predictions, we consider each pair of the network and algorithm as a pipeline. Therefore, each task (predicting DG, GC and DC) has nine supporting pipelines. These predictions (Table 2) are in the top 20 predictions from nearly half to all of nine pipeline combinations, and they are also supported by the literature (Fisher’s exact test P-value <0.001). For CAD-related genes, sequence variations of P2RY12 and ADRB2 and DNA methylation levels of MMP9 have been reported to be associated with CAD (Cavallari et al., 2007; Guay et al., 2015; Piscione et al., 2008). For colon cancer-related drugs, tamoxifen was reported to promote a senescence phenotype and reactive oxygen species generation in a colon cancer cell line (Lee et al., 2014). Treating colorectal cancer with tretinoin (all-trans-retinoic acid) reduced tumorigenesis in mice (Bhattacharya et al., 2016). And arsenic trioxide was tested in a clinical trial (NCT00449137) to make colon cancer cells more sensitive to other drugs. For predictions of SLC22A1-related drugs, the administration of cisplatin decreases SLC22A1 (OCT1) protein level in rats (Erman et al., 2014) and nicotine-treated rats have significantly lower SLC22A1 mRNA expressions than control (Syam Das et al., 2018). It has also been reported that SLC22A1 may not be the transporter of cocaine at the blood–brain barrier in mice (Chapy et al., 2014). Although one prediction for SLC22A1 was reported to be non-association, all nine predictions have been hypothesized by scientists, and tested by various assays at different levels. These data show that diffusion-based methods on multimodal networks formulate hypotheses on DG, DC and GC associations that closely mimic those of scientists.

Table 2.

Frequent top predictions for CAD-related genes, colon cancer-related drugs and SLC22A1-related drugs

Query term	Predicted term	# of supporting prediction pipelinesa	Fisher’s exact test P-value	PMID/clinical trialsb id
Coronary artery disease	P2RY12	4	8.3E-127	17803810
	MMP9	4	1.9E-10	25687463
	ADRB2	4	2.9E-04	18940527
Colon cancer	Tamoxifen	9	4.8E-09	24361399
	Tretinoin	9	6.5E-09	27590114
	Arsenic trioxide	8	1.4E-08	NCT00449137
SLC22A1	Cisplatin	7	2.1E-07	24531880
	Nicotine	5	4.0E-05	29740849
	Cocaine	4	4.9E-04	25539501c

^aIn the top 20 predictions of the pipeline.

^b https://clinicaltrials.gov/.

^cNon-association.

4 Conclusion

We have shown that in most cases, adding information into multimodal networks increases the number of edges that can be predicted, without significantly decreasing sensitivity and specificity. Multimodal networks are also more self-consistent than single-mode networks in cases of RW and AR. When stringently removing associations of an entire mode, we demonstrated the effective recovery from the remaining ones, showing information transitivity between diseases, chemicals and genes. In the most realistic test, time-stamped experiments showed GID and AR successfully predict future knowledge, which suggests that both are robust methods for hypothesis generation. This was further confirmed by the literature-supported novel predictions, showing that diffusion methods on multimodal networks could simulate human-formulated hypotheses.

There are several ways this work could be expanded. First, other network-based methods (Himmelstein and Baranzini, 2015; Navlakha and Kingsford, 2010; Shi et al., 2015; Wang et al., 2014), matrix factorization (Hao et al., 2017; Liu et al., 2016; Regenbogen et al., 2016; Žitnik and Zupan, 2015) and supervised learning (Cao et al., 2014; Mei et al., 2013; Napolitano et al., 2013; Wang and Zeng, 2013) could be eventually combined with the diffusion approaches we used here to better prioritize hypotheses through ensemble techniques (e.g. Zhou et al., 2018).

Second, we could also add more data of demonstrated value for the prediction of biological associations, such as, protein domain co-occurrence and gene ontology similarity (Peng et al., 2015), patient exomes (Smedley et al., 2014), drug side effects (Campillos et al., 2008; Yang and Agarwal, 2011), gene pathways (Li and Lu, 2013), diseases phenotypes (Li and Patra, 2010), gene expression data (Jahchan et al., 2013; Piro et al., 2010) and semantic linked data (Chen et al., 2012a). As this work demonstrates, adding high-quality information from multiple sources should improve predictive power and space (i.e. extends predictions to additional entities). A concern remains that adding network information of poor-quality will increase noise and decrease performance. So, care is needed to select an algorithm, such as AR, that is robust enough to tolerate additional noise, and also add only the most reliable data.

Third, an important issue for the future is how to handle the direction and sign of edges. For example, p53 upregulates p21 and not the other way around, so the edge from p53 to p21 is directional. For signed edges, Epinephrine causes tachycardia while metoprolol treats it. In this paper, both directional and signed associations were treated as bidirectional and unsigned associations, clearly a loss of information. How to best represent these attributes of edges in a computable form is an important question and could reduce the noise during data integration.

Ultimately, predictions of entity associations need to be experimentally validated by cell line assays, animal models and even clinical trials. More importantly, those top predictions would assist experimentalists to design their assays to increase the successful rate. The feedback from these validations would guide and improve the computational models. This stresses the need for multidisciplinary collaborations to form a positive feedback loop between algorithms and experiments and spur the rise of precision medicine.

Funding

This work was supported by a training fellowship from the Gulf Coast Consortia, on the Training Interdisciplinary Pharmacology Scientists (TIPS) Program [grant number T32 GM120011]. Additionally, the authors would like to acknowledge funding by National Library of Medicine training fellowship [grant number T15 LM007093] for S.J.W., as well as funding from DARPA [N66001-14-1-4027, SIMPLEX]; National Science Foundation [NSF DBI-1356569, NSF DBI-0851393, CCF-1149756, IIS-1546488, CCF-0939370]; and National Institutes of Health [NIH-GM079656, NIH-GM066099].

Conflict of Interest: none declared.