On the use of min-max combination of biomarkers to maximize the partial area under the ROC curve

Abstract

Background:

Evaluation of diagnostic assays and predictive performance of biomarkers based on the receiver operating characteristic (ROC) curve and the area under the ROC curve (AUC) are vital in diagnostic and targeted medicine. The partial area under the curve (pAUC) is an alternative metric focusing on a range of practical and clinical relevance of the diagnostic assay. In this article, we adopt and extend the min-max method to the estimation of the pAUC when multiple continuous scaled biomarkers are available and compare the performances of our proposed approach with existing approaches via simulations.

Methods:

We conducted extensive simulation studies to investigate the performance of different methods for the combination of biomarkers based on their abilities to produce the largest pAUC estimates. Data were generated from different multivariate distributions with equal and unequal variance-covariance matrices. Different shapes of the ROC curves, false positive fraction ranges, and sample size configurations were considered. We obtained the mean and standard deviation of the pAUC estimates through re-substitution and leave-one-pair-out cross validation.

Results:

Our results demonstrate that the proposed method provides the largest pAUC estimates under the following three important practical scenarios: (1) multivariate normally distributed data for non-diseased and diseased participants have unequal variance-covariance matrices; or (2) the ROC curves generated from individual biomarker are relative close regardless of the latent normality distributional assumption; or (3) the ROC curves generated from individual biomarker have straight-line shapes.

Conclusions:

The proposed method is robust and investigators are encouraged to use this approach in the estimation of the pAUC for many practical scenarios.

1. Introduction

The area under the entire curve (AUC) is one of the most commonly used summary indices in receiver operating characteristic (ROC) analysis and can be interpreted as the average value of sensitivity for all possible values of specificity (Hanley and McNeil, 1982). The empirical estimate of the AUC is closely related to the Mann-Whitney U statistic for comparing ratings of non-diseased and diseased participants (Hanley and McNeil, 1982). Although methods based on the AUC have been well developed and widely implemented (Zhou et al., 2002), (Pepe, 2003), one of the major limitations of the AUC is that it summarizes the performance over the entire curve, including regions that may not be clinically relevant (e.g., the regions with low specificity levels). The partial area under the ROC curve (pAUC) can be used as a summary index of diagnostic/prognostic accuracy over a certain range of specificity that is of clinical interest (McClish, 1989; Jiang et al., 1996). In many applications, tests with false positive rates outside of a particular domain will be of no practical use and hence are irrelevant for evaluating the accuracy of the test. In particular, for a certain disease with low prevalence, the unnecessary follow-up resulting from high false positive rate will burden the health system. There are several proposed methods for analyzing the pAUC (McClish, 1989; Dodd and Pepe, 2003; He and Escobar, 2008; Zhang et al., 2002; Ma et al. 2013; Ma et al., 2015).

When multiple continuous-scaled biomarkers are available in the evaluation of prognostic accuracy, it may be possible to improve the accuracy by combining several biomarkers. The use of linear combination is popular due to its ease of implementation and interpretation. Finding optimal linear combination to maximize the area under the ROC curve has been extensively studied (Su and Liu, 1993; Liu et al., 2005; Jin and Lu, 2009; Kang et al., 2013). By extending the Fisher’s discriminant function, Su and Liu (1993) first proposed the best linear combination to maximize AUC based on the multivariate normality assumption. Su and Liu’s method relies on the strong distributional assumption, and therefore pAUC may have unsatisfactory performance for many practical scenarios when the distributional assumption is not satisfied. Liu et al. (2005) provided an approach to construct the best linear combination that can produce the ROC curve dominating any other ROC curves in some particular specificity ranges. However, this approach depends on the distributional assumption about the mean vectors and the specificity range. Therefore, it may fail to be dominant for a particular range of specificity and sensitivity that may be of clinical interest. In addition, this approach involves the calculation of the eigenvector corresponding to the eigenvalue, and thus the stability of this approach depends on the behavior of eigenvector under small perturbation of the corresponding matrix (Allez and Bouchaud, 2012).

Under the assumption of generalized linear model, Jin and Lu (2009) proved that the combination coefficients from the estimates of logistic regression yielded ROC curve with the highest sensitivity uniformly over the entire range of specificity. Without distributional assumptions on the data, Pepe and Thompson (2000) considered maximizing AUC and pAUC through rank-based estimate, i.e. the Mann-Whitney U statistic (Hanley and McNeil, 1982). They proposed an algorithm to search for optimal linear combinations with number of biomarkers equal to 2. This approach was computationally formidable when the number of biomarkers is greater than or equal to 3 (Pepe et al., 2006). Hsu and Hsueh (2013) and Yu and Park (2015) proposed methods to maximize the partial area under the ROC curve based on the multivariate normality assumption.

Liu et al. (2011) developed a non-parametric min-max approach that reduces data into two dimensions to maximize the Mann-Whitney statistic of the AUC. This approach is robust against distributional assumptions due to its non-parametric nature, and is computationally efficient since the min-max procedure involves searching for only one single coefficient. Although useful, this approach was developed based on the full range of specificity. In many medical areas, the ROC curve is only clinically relevant and of interest when the assay has high specificities. For example, high specificity of an assay is required for screening any healthy population. Similarly, in using diagnostic assay with multiple genes, only high sensitivity and specificity classifiers have clinical utility (Sparano 2015).

We adapt and extend the min-max method to estimating the pAUC when several markers are considered. This article is organized as follows. In Section 2, we provide a thorough review of existing methods that maximize the AUC and pAUC. In Section 3, we extend the min-max combination method to the optimization of the pAUC and discuss the leave-one-pair-out (LOPO) cross validation approach for evaluating of the combination methods based on their accuracy for future observations. In Section 4, we then conduct extensive simulations to investigate the performance of the different combination methods based on their abilities to yield the largest pAUC estimates. In Section 5, two real life examples are presented. We then discuss the results in Section 6 and provide guidelines for practical use of the different approaches.

2. Existing Methods

2.1. Definition

Without loss of generality, we consider the partial area under the ROC curve (pAUC) over the range of high specificity values, i.e.

$$pAU{C}_{t_0}={\int }_0^{t_0}ROC(t)dt.$$

In this article, $t_0$ less than or equal to 0.2, i.e. specificity greater than or equal to 0.8, were considered. This is due to the fact that an assay is unlikely to be used if it has a lower specificity rate.

Let $X_i,i=1,\mathrm{...},n_1$ and $Y_j,j=1,\mathrm{...},n_2$ be the biomarker levels for non-diseased and diseased participants. The corresponding empirical estimate of pAUC by utilizing the Mann-Whitney U statistic is,

$$\widehat{pAUC}=\frac{1}{n_1{n}_2}\sum _{i=1}^{n_1}\sum _{j=1}^{n_2}I\left(X_i<Y_j\mathrm{and}{X}_i>Q\left(1-t_0\right)\right)$$

where $Q\left(1-t_0\right)$ is the $\left(1-t_0\right)$ quantile of the empirical distribution of X.

Assume that we have p diagnostic tests or biomarkers on each subject, n₁ non-diseased participants with ratings

$${\mathbf{X}}_i={\left(X_{i1},X_{i2},\cdots ,X_{ip}\right)}^T,i=1,2,\cdots ,n_1$$

n₂ diseased participants with ratings

$${\mathbf{Y}}_i={\left(Y_{i1},Y_{i2},\cdots ,Y_{ip}\right)}^T,i=1,2,\cdots ,n_2.$$

The best linear combination coefficient $\mathbf{c}={\left(c_1,c_2,\cdots ,c_p\right)}^T$ which maximizes the pAUC can be estimated by maximizing the empirical estimate of pAUC, i.e.,

$$\widehat{pAUC}=\frac{1}{n_1{n}_2}\sum _{i=1}^{n_1}\sum _{j=1}^{n_2}I\left({\mathbf{X}}_i^T\widehat{\mathbf{c}}<{\mathbf{Y}}_j^T\widehat{\mathbf{c}}\mathrm{and}{\mathbf{X}}_i^T\widehat{\mathbf{c}}>Q\left(1-t_0\right)\right)$$

where $Q\left(1-t_0\right)$ is the $\left(1-t_0\right)$ quantile of the empirical distribution of ${\mathbf{X}}_i^T\widehat{\mathbf{c}}$.

2.2. Su and Liu’s Method for pAUC

Assume that ${\mathbf{X}}_i$ and ${\mathbf{Y}}_j$ follow multivariate normal distribution with mean vector ${\mathbf{\mu }}_x,{\mathbf{\mu }}_y\in {\Re }^p$, and $p\times p$ covariance matrix ${\mathbf{\Sigma }}_x$ and ${\mathbf{\Sigma }}_y$, i.e. ${\mathbf{X}}_i~MVN\left({\mathbf{\mu }}_x,{\mathbf{\Sigma }}_x\right)$ and ${\mathbf{Y}}_j~MVN\left({\mathbf{\mu }}_y,{\mathbf{\Sigma }}_y\right)$, respectively. Su and Liu derived the best linear combination coefficient $\mathbf{c}={\left(c_1,c_2,\cdots ,c_p\right)}^T$ that can maximize AUC based on the invariance property of ROC curve to scalar transformation and Fisher’s discriminant coefficient (Su and Liu, 1993). When the two covariance matrices are equal or proportional to each other, the best linear coefficient based on Su and Liu’s method also generates the ROC curve dominating all the others within any range of specificities.

2.3. Liu et al.’s Method for pAUC

By realizing the unsatisfactory performance from the use of Su and Liu’s best linear combination coefficient, Liu et al. considered the scenario where ${\mathbf{\Sigma }}_x\ne {\mathbf{\Sigma }}_y$(Liu et al., 2005). The authors provided an approach to construct best linear combination that can maximizes sensitivity over a certain range of specificities. In particular, if the high specificity region of an ROC curve is of interest, then the best linear combination coefficient is proportional to

$${\mathbf{\Sigma }}_y^{-1/2}{\alpha }_p$$

where ${\alpha }_p$ is the eigenvector corresponding to the smallest eigenvalue of matrix ${\mathbf{\Sigma }}_y^{-1/2}{\mathbf{\Sigma }}_x{\mathbf{\Sigma }}_y^{-1/2}$. It has been showed that this linear combination produces the ROC curve dominating any other ROC curves in some particular specificity ranges.

2.3. Logistic Regression for pAUC

The logistic regression has been widely used to predict binary outcomes by considering linear combination of multiple predictors(Jin and Lu, 2009). It models the probability of disease for a given subject with covariates ${\mathbf{X}}_i$ by using the logit link function, i.e.

$$\mathrm{Pr}\left(D_i=1\right)=\frac{\exp \left({\beta }_0+{\mathbf{X}}_i^T\mathbf{c}\right)}{1+\exp \left({\beta }_0+{\mathbf{X}}_i^T\mathbf{c}\right)}.$$

where ${\beta }_0$ is the intercept and ${\mathbf{X}}_i$ and $\mathbf{c}$ are defined as before. Under the assumption of generalized linear model, the estimate of $c$ followed by the logistic regression can maximize the likelihood function of binary outcomes. Jin and Lu proved that this estimate also provides the highest sensitivity uniformly over the entire range of specificity. This implies that the best linear combination equal $\widehat{\mathbf{c}}$ resulting in an ROC curve which not only have the maximum full AUC, but also dominates any other ROC curves within any range of potential interest, and therefore leads to the maximum pAUC.

2.4. Pepe and Thompon’s Method for pAUC

Without distributional assumptions on the data $\mathbf{X}$ and $\mathbf{Y}$, Pepe and Thompson (Pepe and Thompson, 2000) considered maximizing AUC and pAUC through rank-based estimate, i.e. the Mann-Whitney U statistics (Hanley and McNeil, 1982). For simplicity, they proposed an algorithm to search for optimal linear combinations with number of biomarkers equal to 2 (p=2), i.e., ${\mathbf{X}}_i={\left(X_{i1},X_{i2}\right)}^T$ for $i=1,2,\cdots ,n_1$ and ${\mathbf{Y}}_i=\left(Y_{i1},Y_{i2}\right){}^T$ for $i=1,2,\cdots ,n_2$. Based on the fact that the ROC curve is variant to scale transformation, in order to maximize AUC or pAUC, finding the best combination coefficient $\mathbf{c}={\left(c_1,c_2\right)}^T$, where $c_1,c_2\in \left(-\infty ,+\infty \right)$ is equivalent to finding $\mathbf{c}={\left(1,\alpha \right)}^T$, where $\alpha \in \left(-\infty ,+\infty \right)$. Let [0, fpf₀] denote the range of false positive of potential interest. The estimate of AUC based on the Mann-Whitney U statistics and the estimate of pAUC can be obtained as

$$A\widehat{U}C\left(\alpha \right)=\frac{1}{n_1{n}_2}\sum _{i=1}^{n_1}\sum _{j=1}^{n_2}I\left(X_{i1}+\alpha X_{i2}<Y_{j1}+\alpha Y_{j2}\right)$$

and

$$pA\widehat{U}C\left(\alpha \right)=\frac{1}{n_1{n}_2}\sum _{i=1}^{n_1}\sum _{j=1}^{n_2}I\left(X_{i1}+\alpha X_{i2}<Y_{j1}+\alpha Y_{j2}and{X}_{i1}+\alpha X_{i2}>Q\left(1-fp{f}_0,\alpha \right)\right)$$

respectively, where $Q\left(1-fp{f}_0,\alpha \right)$ is the $\left(1-fp{f}_0\right)$ quantile of $X_{i1}+\alpha X_{i2}$. The authors chose to implement a semiparametric method based on Heagerty and Pepe (1999) to estimate $Q\left(1-fp{f}_0,\alpha \right)$, while they also pointed out that other quantile estimation methods may be applied.

2.5. Min-Max Method for AUC

Liu et al. considered the min-max combination of biomarkers (Liu et al., 2011). Let

$$X_{i,\max }=\underset{1\le k\le p}{\max }{X}_{ik},Y_{i,\max }=\underset{1\le k\le p}{\max }{Y}_{ik}$$

be the maximum value of p biomarkers for non-diseased and diseased participants, respectively. Similarly, let

$$X_{i,\min }=\underset{1\le k\le p}{\min }{X}_{ik},Y_{i,\min }=\underset{1\le k\le p}{\min }{Y}_{ik}$$

be the minimum value of p biomarkers for non-diseased and diseased participants, respectively.

The non-parametric estimate of AUC based on the Mann-Whitney U statistics by linearly combining the minimum and maximum values of p biomarkers for each subject can be obtained as

$$A\widehat{U}C\left(\alpha \right)=\frac{1}{n_1{n}_2}\sum _{i=1}^{n_1}\sum _{j=1}^{n_2}I\left(X_{i,\max }+\alpha X_{i,\min }<Y_{j,\max }+\alpha Y_{j,\min }\right).$$

Since this is not a continuous function of α, a search rather than a derivative-based method is required for the maximization. The searching method for the best value of α is exactly the same as Pepe and Thompson’s method.

3. Methodology Extension: Min-Max Method for pAUC

We extend the min-max method to maximize the pAUC. Let [0, fpf₀] denote the range of false positive of potential interest. By considering only the minimum and maximum values of p biomarkers for each individual, it follows that the non-parametric estimate of pAUC can be obtained as

$$\widehat{pAUC}\left(\alpha \right)=\frac{1}{n_1{n}_2}\sum _{i=1}^{n_1}\sum _{j=1}^{n_2}I\left(X_{i,\max }+\alpha X_{i,\min }<Y_{j,\max }+\alpha Y_{j,\min }and{X}_{i,\max }+\alpha X_{i,\min }>Q\left(1-fp{f}_0,\alpha \right)\right)$$

where $Q\left(1-fp{f}_0,\alpha \right)$ is the $\left(1-fp{f}_0\right)$ quantile of $X_{i,\max }+\alpha X_{i,\min }$. For simplicity, the $\left(1-fp{f}_0\right)$ quantile of the empirical distribution of $X_{i,\max }+\alpha X_{i,\min }$ can be used to estimate $Q\left(1-fp{f}_0,\alpha \right)$. Then the Pepe and Thompson’s (2000) algorithm can be applied to search for the optimal value of α to maximize the estimate of the pAUC.

The new marker $\left(X_{i,\max },Y_{i,\max }\right)$ has larger sensitivity and smaller specificity for any given threshold c than any other individual marker, given that

$$\mathrm{Pr}\left\{Y_{i,\max }>c\right\}=1-\mathrm{Pr}\left\{Y_{i,\max }\le c\right\}=1-\mathrm{Pr}\left\{Y_{ij}\le c,1\le j\le p\right\}\ge 1-\mathrm{Pr}\left\{Y_{ik}\le c\right\}=\mathrm{Pr}\left\{Y_{ik}>c\right\}$$

and

$$\mathrm{Pr}\left\{X_{i,\max }\le c\right\}=\mathrm{Pr}\left\{X_{ij}\le c,1\le j\le p\right\}\le \mathrm{Pr}\left\{X_{ik}\le c\right\}$$

for all $1\le k\le p$; similarly, the new marker $\left(X_{i,\min },Y_{i,\min }\right)$ has smaller sensitivity and larger specificity for any given threshold c than any other individual marker, given that

$$\mathrm{Pr}\left\{Y_{i,\min }>c\right\}=\mathrm{Pr}\left\{Y_{ij}>c,1\le j\le p\right\}\le \mathrm{Pr}\left\{Y_{ik}>c\right\}$$

and

$$\mathrm{Pr}\left\{X_{i,\max }\le c\right\}=1-\mathrm{Pr}\left\{X_{i,\max }>c\right\}=1-\mathrm{Pr}\left\{X_{ij}>c,1\le j\le p\right\}\ge 1-\mathrm{Pr}\le \mathrm{Pr}\left\{X_{ik}>c\right\}=\mathrm{Pr}\left\{X_{ik}\le c\right\}$$

for all $1\le k\le p$. Therefore, we expect that the linear combination of the min-max biomarkers may provide larger partial area under the ROC curve than other methods. We employ simulation study to investigate how well the proposed method performs compared to other established methods.

The cross validation has been widely used to evaluate the generalizability of the statistical results. Huang et al. (2011) proposed a LOPO approach to evaluating the performance of the linear combination coefficient to estimate AUC for future observations. The estimate of AUC based on LOPO cross validation is as follows,

$${\widehat{pAUC}}^{CV}=\frac{1}{n_1{n}_2}\sum _{i=1}^{n_1}\sum _{j=1}^{n_2}I\left({\mathbf{X}}_i^T{\widehat{\mathbf{c}}}^{\left(-ij\right)}<{\mathbf{Y}}_j^T{\widehat{\mathbf{c}}}^{\left(-ij\right)}\right)$$

where ${\widehat{\mathbf{c}}}^{\left(-ij\right)}$ is the best linear combination coefficient based on the observed data without both the ith observation from non-diseased subject and the jth observation from diseased subject. They also demonstrated that the 5-fold and 10-fold cross validation can be computationally efficient and the resulting estimate can be asymptotically unbiased for the future observations.

We implement the LOPO cross validation on the pAUC to evaluate the generalizability of the statistical results. The estimate of the pAUC based on the LOPO cross validation can be obtained as,

$${\widehat{pAUC}}^{CV}=\frac{1}{n_1{n}_2}\sum _{i=1}^{n_1}\sum _{j=1}^{n_2}I\left({\mathbf{X}}_i^T{\widehat{\mathbf{c}}}^{\left(-ij\right)}<{\mathbf{Y}}_j^T{\widehat{\mathbf{c}}}^{\left(-ij\right)}and{\mathbf{X}}_i^T{\widehat{\mathbf{c}}}^{\left(-ij\right)}>Q\left(1-fp{f}_0,\alpha \right)\right)$$

where $Q\left(1-fp{f}_0,\alpha \right)$ is the $\left(1-fp{f}_0\right)$ quantile of ${\mathbf{X}}_i^T{\widehat{\mathbf{c}}}^{\left(-ij\right)}$. For simplicity, in our simulation study the $\left(1-fp{f}_0\right)$ quantile of the empirical distribution of ${\mathbf{X}}_i^T{\widehat{\mathbf{c}}}^{\left(-ij\right)}$ will be used to estimate of $Q\left(1-fp{f}_0,\alpha \right)$.

4. Simulation

Description of Simulations

We conducted extensive simulation studies to investigate the performance of our proposed method with established combination methods based on the partial area under the ROC curves. Ratings of participants were simulated from different multivariate distributions with equal and unequal variance-covariance matrices. We examined false positive fraction ranges 0 – 0.1 and 0 – 0.2 and we considered different samples sizes: 50:50, 50:100, 100:50 and 100:100 for non-diseased and diseased participants, respectively.

For each simulated dataset, we computed the pAUC based on four different approaches: 1) min-max, denoted as MIN-MAX; 2) Su and Liu’s (1993), denoted as SULIU; 3) Liu et al’s (2006), denoted as LIU); and the 4) logistic regression, denoted as LOGISTIC. In addition, we utilized two estimation methods: the re-substitution (denoted as Re-Sub) and 10-fold leave-one-pair-out cross validation (denoted as LOPO) in computing the pAUC. The re-substitution method estimated the pAUC based on the linear combination of the coefficients derived using all the data for each method. The re-substitution method is usually overoptimistic for estimating the diagnostic/prognostic accuracy for future observations due to the reason between training set and validation set in the discipline of machine learning (Huang et al., 2011). We obtained the mean of the pAUC by averaging over the 1,000 simulations, and standard deviation was the square root of the estimated sample variance of the estimated pAUC from 1,000 simulated datasets.

4.1. Multivariate Normal Distributions with Equal Variance-Covariance

We first compared the performance of the min-max approach on the pAUC with the other methods by generating dataset consisting of ratings from multivariate normal distributions (p=4) with different mean vectors and equal variance-covariance matrices (scenario #1). Exploiting the invariance property of the ROC curve to monotonically increasing transformation of the ratings, the distributions of ratings of non-diseased participants were set to be a multivariate normal distribution with mean ${\mathbf{\mu }}_x={\left(0,0,0,0\right)}^T$ and variance covariance matrix

$${\mathbf{\Sigma }}_x=\left(\begin{array}{cccc}1& 0.5& 0.5& 0.5\\ 0.5& 1& 0.5& 0.5\\ 0.5& 0.5& 1& 0.5\\ 0.5& 0.5& 0.5& 1\end{array}\right).$$

Under this scenario, ratings of diseased participants were generated from multivariate normal distributions with variance-covariance matrix ${\mathbf{\Sigma }}_y$ equal to ${\mathbf{\Sigma }}_x$, and the mean vectors were selected to generate the AUC equal to 0.70, 0.73, 0.76, and 0.80 for markers # 1, 2, 3 and 4, respectively (Case #1), and the AUC equal to 0.6, 0.7, 0.8 and 0.9 for markers # 1, 2, 3 and 4, respectively (Case #2).

4.2. Multivariate Normal Distributions with Unequal Variance-Covariance

We also considered multivariate normal distributions with different mean and unequal variance-covariance matrices for non-diseased and diseased participants (scenario #2). The mean settings are the same as the Case 1 and Case 2 as discussed in scenario 1. The variance-covariance matrices were

$${\mathbf{\Sigma }}_x=\left(\begin{array}{cccc}1& 0.2& 0.2& 0.2\\ 0.2& 1& 0.2& 0.2\\ 0.2& 0.2& 1& 0.2\\ 0.2& 0.2& 0.2& 1\end{array}\right),\text{and}{\mathbf{\Sigma }}_y=\left(\begin{array}{cccc}1& 0.8& 0.8& 0.8\\ 0.8& 1& 0.8& 0.8\\ 0.8& 0.8& 1& 0.8\\ 0.8& 0.8& 0.8& 1\end{array}\right).$$

4.3. Multivariate Log-Normal Distributions with Unequal Variance-Covariance

We investigated the performance of the different combination methods by generating dataset consisting of ratings from multivariate log-normal distributions (scenario #3). Ratings were first generated similarly to scenario #2 and then exponentiated to obtain the multivariate log-normal marker values.

4.4. Multivariate Gamma Distributions

We further examined the performance of the different combination methods by generating gamma ROC curves with the AUC settings in Case 1 and Case 2 (scenario #4). The gamma family is one of the well-known families of ROC curves (Egan, 1975; Dorfman et al., 1996; Faraggi et al., 2003; Huang and Pepe, 2009; Ma et al., 2013; Ma et al, 2015). Due to the concavity and flexibility in the shape, Ma et al. (2013) and Ma et al. (2015) demonstrated that the families of gamma ROC curves provided practically reasonable straight-line shaped concave ROC curves, where the statistical inference based on pAUCs is preferable.

The probability density function of the underlying rating model of the gamma ROC curve has the following form:

$$f(x;\kappa ,\theta )=\frac{1}{{\theta }^{\kappa }}\frac{1}{\tau \left(\kappa \right)}{x}^{\kappa -1}{e}^{-\frac{x}{\theta }}.$$

When κ approaches 0, the gamma ROC curve approaches the shape of a straight-line and when κ>1 the shape of the gamma ROC curve resembles an ROC curve with latent normality assumptions. When κ=1 the gamma ROC curve is equivalent to the power-law ROC curve (Egan, 1975; Hanley, 1989). Here we are interested in the investigation of a scenario with straight-line shaped gamma ROC curves (κ=1/3), because this type of ROC curve cannot be generated by the previous scenarios.

Each simulated dataset consisted of ratings generated from multivariate gamma distributions with κ=1/3. Due to the invariance property of the ROC curves, without any loss of generality, we set θ=1 for latent ratings of non-diseased participants. We then selected θ for the latent diseased ratings to reflect the targeted area under the ROC curve in Case #1 and Case #2. The between-modality correlation of 0.5 was established using a Gaussian copula model (Nelsen, 1999). All the programs were written by the first author in R version 2.15.3 and are available: https://duke.box.com/s/u32h7aayxd9bjo41b619xpb21sj1nm67.

4.5. Simulation Results

We compared the performance of the min-max method in estimating the pAUC with three established methods assuming the ratings are from multivariate normal distributions with equal variance-covariance matrices (Table 1). The SULIU and LOGISTIC almost always performed better than the min-max and LIU based on the pAUCs estimated from both the re-substitution and the LOPO cross validation. In addition, the performances of SULIU and LOGISTIC approaches were similar when the AUC were either close or further apart. The min-max approach produced slightly smaller pAUC estimates than that of SULIU and LOGISTIC when the AUCs among biomarkers were relatively close (i.e. Case #1), while this approach became worse when the AUCs were far apart (i.e. Case #2).

Table 1.

Means (standard deviations) of the partial area under the ROC curve for different combination methods based on the dataset consisted of ratings from multivariate normal distributions with equal variance-covariance matrices (scenario#1) with 1000 simulated datasets.

AUCs	Fpf range	Sample Size		MIN-MAX	SULIU	LIU	LOGISTIC
0.7-0.8	0-0.1	50:50	Re-Sub	0.036 (0.010)	0.038 (0.011)	0.024 (0.011)	0.038 (0.011)
			LOPO	0.028 (0.012)	0.030 (0.011)	0.016 (0.011)	0.030 (0.011)
		50:100	Re-Sub	0.036 (0.009)	0.038 (0.010)	0.024 (0.011)	0.037 (0.010)
			LOPO	0.028 (0.011)	0.031 (0.010)	0.016 (0.011)	0.031 (0.010)
		100:50	Re-Sub	0.034 (0.008)	0.036 (0.009)	0.021 (0.010)	0.036 (0.009)
			LOPO	0.028 (0.009)	0.031 (0.009)	0.015 (0.009)	0.030 (0.009)
		100:100	Re-Sub	0.033 (0.007)	0.036 (0.007)	0.021 (0.010)	0.036 (0.007)
			LOPO	0.028 (0.008)	0.031 (0.007)	0.015 (0.009)	0.031 (0.007)
	0-0.2	50:50	Re-Sub	0.094 (0.018)	0.101 (0.020)	0.064 (0.024)	0.101 (0.020)
			LOPO	0.081 (0.022)	0.086 (0.021)	0.049 (0.025)	0.086 (0.021)
		50:100	Re-Sub	0.092 (0.017)	0.099 (0.018)	0.064 (0.024)	0.099 (0.018)
			LOPO	0.081 (0.021)	0.087 (0.019)	0.049 (0.024)	0.087 (0.019)
		100:50	Re-Sub	0.091 (0.015)	0.097 (0.016)	0.059 (0.022)	0.098 (0.016)
			LOPO	0.082 (0.018)	0.087 (0.017)	0.047 (0.022)	0.087 (0.017)
		100:100	Re-Sub	0.089 (0.013)	0.096 (0.013)	0.058 (0.022)	0.096 (0.013)
			LOPO	0.081 (0.016)	0.089 (0.014)	0.047 (0.021)	0.089 (0.014)
0.6-0.9	0-0.1	50:50	Re-Sub	0.047 (0.010)	0.064 (0.011)	0.034 (0.018)	0.065 (0.011)
			LOPO	0.040 (0.012)	0.056 (0.013)	0.026 (0.017)	0.054 (0.012)
		50:100	Re-Sub	0.046 (0.010)	0.063 (0.010)	0.034 (0.018)	0.063 (0.010)
			LOPO	0.041 (0.012)	0.057 (0.012)	0.025 (0.016)	0.056 (0.011)
		100:50	Re-Sub	0.045 (0.009)	0.062 (0.009)	0.029 (0.016)	0.062 (0.009)
			LOPO	0.040 (0.010)	0.057 (0.010)	0.023 (0.014)	0.056 (0.010)
		100:100	Re-Sub	0.044 (0.008)	0.062 (0.008)	0.030 (0.016)	0.062 (0.008)
			LOPO	0.040 (0.009)	0.058 (0.008)	0.024 (0.014)	0.057 (0.008)
	0-0.2	50:50	Re-Sub	0.114 (0.017)	0.148 (0.017)	0.084 (0.037)	0.149 (0.017)
			LOPO	0.106 (0.020)	0.137 (0.019)	0.070 (0.036)	0.135 (0.019)
		50:100	Re-Sub	0.114 (0.017)	0.147 (0.015)	0.085 (0.037)	0.147 (0.015)
			LOPO	0.107 (0.019)	0.138 (0.017)	0.070 (0.034)	0.136 (0.017)
		100:50	Re-Sub	0.112 (0.015)	0.146 (0.014)	0.075 (0.033)	0.146 (0.014)
			LOPO	0.106 (0.017)	0.138 (0.015)	0.065 (0.032)	0.137 (0.015)
		100:100	Re-Sub	0.110 (0.013)	0.146 (0.012)	0.079 (0.035)	0.146 (0.012)
			LOPO	0.106 (0.014)	0.140 (0.012)	0.068 (0.032)	0.139 (0.012)

Moreover, we examined the performance of the four methods, i.e. MIN-MAX, SULIU, LIU and LOGISTIC, assuming ratings are from multivariate normal distributions with unequal variance-covariance matrices (Table 2). When the AUCs were close (Case #1), the min-max method was superior to the other methods in terms of its ability to produce the largest pAUCs based on both the re-substitution and the LOPO cross validation. When the AUCs were far apart (i.e. Case #2), the SULIU and LOGISTIC methods had similar performances superior to the other two methods. The SULIU method was slightly better than the LOGISTIC based on the LOPO cross validation since this takes into account the normality of data with unequal variance-covariance matrices. It should be noted that the difference in the estimates of the pAUCs between the re-substitution and the LOPO cross validation was very small under this scenario.

Table 2.

Means and standard deviation (SD) of the partial area under the ROC curve for different combination methods based on the dataset consisted of ratings from multivariate normal distributions with unequal variance-covariance matrices (scenario#2) with 1000 simulated datasets.

AUCs	Fpf range	Sample Size		MIN-MAX	SULIU	LIU	LOGISTIC
0.7-0.8	0-0.1	50:50	Re-Sub	0.059 (0.011)	0.044 (0.011)	0.046 (0.010)	0.044 (0.011)
			LOPO	0.052 (0.013)	0.035 (0.012)	0.042 (0.010)	0.034 (0.012)
		50:100	Re-Sub	0.058 (0.009)	0.044 (0.009)	0.046 (0.008)	0.042 (0.010)
			LOPO	0.053 (0.012)	0.036 (0.010)	0.042 (0.009)	0.033 (0.010)
		100:50	Re-Sub	0.057 (0.008)	0.043 (0.009)	0.045 (0.008)	0.045 (0.009)
			LOPO	0.052 (0.010)	0.037 (0.009)	0.043 (0.008)	0.039 (0.009)
		100:100	Re-Sub	0.057 (0.007)	0.043 (0.008)	0.044 (0.007)	0.043 (0.008)
			LOPO	0.053 (0.009)	0.038 (0.008)	0.042 (0.007)	0.038 (0.008)
	0-0.2	50:50	Re-Sub	0.136 (0.018)	0.109 (0.019)	0.109 (0.018)	0.109 (0.019)
			LOPO	0.128 (0.021)	0.093 (0.021)	0.102 (0.018)	0.093 (0.021)
		50:100	Re-Sub	0.135 (0.015)	0.109 (0.016)	0.109 (0.015)	0.106 (0.017)
			LOPO	0.129 (0.018)	0.095 (0.018)	0.103 (0.016)	0.090 (0.019)
		100:50	Re-Sub	0.133 (0.014)	0.107 (0.016)	0.107 (0.015)	0.110 (0.015)
			LOPO	0.128 (0.016)	0.098 (0.017)	0.104 (0.015)	0.101 (0.016)
		100:100	Re-Sub	0.133 (0.012)	0.106 (0.013)	0.107 (0.012)	0.107 (0.013)
			LOPO	0.129 (0.013)	0.099 (0.014)	0.104 (0.012)	0.099 (0.014)
0.6-0.9	0-0.1	50:50	Re-Sub	0.051 (0.010)	0.058 (0.012)	0.049 (0.011)	0.059 (0.013)
			LOPO	0.044 (0.012)	0.048 (0.014)	0.045 (0.012)	0.045 (0.014)
		50:100	Re-Sub	0.050 (0.008)	0.059 (0.012)	0.049 (0.010)	0.056 (0.013)
			LOPO	0.044 (0.010)	0.049 (0.013)	0.046 (0.010)	0.045 (0.013)
		100:50	Re-Sub	0.049 (0.008)	0.057 (0.010)	0.048 (0.009)	0.059 (0.010)
			LOPO	0.044 (0.009)	0.051 (0.011)	0.046 (0.009)	0.051 (0.010)
		100:100	Re-Sub	0.049 (0.007)	0.057 (0.009)	0.048 (0.008)	0.056 (0.009)
			LOPO	0.044 (0.008)	0.051 (0.010)	0.046 (0.008)	0.049 (0.010)
	0-0.2	50:50	Re-Sub	0.118 (0.017)	0.143 (0.018)	0.114 (0.020)	0.143 (0.019)
			LOPO	0.108 (0.020)	0.128 (0.021)	0.108 (0.021)	0.124 (0.021)
		50:100	Re-Sub	0.117 (0.014)	0.143 (0.017)	0.115 (0.018)	0.141 (0.018)
			LOPO	0.109 (0.016)	0.129 (0.020)	0.109 (0.019)	0.124 (0.020)
		100:50	Re-Sub	0.116 (0.014)	0.141 (0.016)	0.113 (0.016)	0.143 (0.015)
			LOPO	0.109 (0.016)	0.133 (0.017)	0.110 (0.017)	0.132 (0.016)
		100:100	Re-Sub	0.115 (0.012)	0.140 (0.013)	0.113 (0.014)	0.140 (0.013)
			LOPO	0.109 (0.013)	0.133 (0.014)	0.110 (0.014)	0.131 (0.014)

Furthermore, we studied the performance of the different combination methods assuming multivariate log-normal distributions. From Table 3, under this scenario where data are highly skewed, the min-max approach dominated the other approaches when the AUCs were close (Case #1). On the other hand, the LOGISTIC approach performed better when the AUCs are far apart. It is interesting to observe that the LIU method was suboptimal under both cases in terms of its ability to estimate the pAUC through the LOPO cross validation whereas the SULIU method had the worst performance since the normality assumption was violated.

Table 3.

Means and standard deviation (SD) of the partial area under the ROC curve for different combination methods based on the dataset consisted of ratings from multivariate log-normal distributions with unequal variance-covariance matrices (scenario#3) with 1,000 simulated datasets.

AUCs	Fpf range	Sample Size		MIN-MAX	SULIU	LIU	LOGISTIC
0.7-0.8	0-0.1	50:50	Re-Sub	0.059 (0.011)	0.035 (0.009)	0.040 (0.010)	0.040 (0.010)
			LOPO	0.054 (0.012)	0.026 (0.010)	0.031 (0.011)	0.028 (0.011)
		50:100	Re-Sub	0.058 (0.009)	0.035 (0.008)	0.040 (0.009)	0.039 (0.009)
			LOPO	0.054 (0.011)	0.028 (0.009)	0.032 (0.010)	0.028 (0.010)
		100:50	Re-Sub	0.057 (0.008)	0.033 (0.008)	0.037 (0.008)	0.038 (0.008)
			LOPO	0.054 (0.009)	0.027 (0.008)	0.031 (0.009)	0.030 (0.009)
		100:100	Re-Sub	0.057 (0.007)	0.033 (0.007)	0.036 (0.007)	0.037 (0.007)
			LOPO	0.054 (0.008)	0.028 (0.007)	0.031 (0.008)	0.030 (0.007)
	0-0.2	50:50	Re-Sub	0.136 (0.018)	0.090 (0.018)	0.095 (0.019)	0.099 (0.019)
			LOPO	0.129 (0.020)	0.074 (0.020)	0.082 (0.020)	0.079 (0.020)
		50:100	Re-Sub	0.135 (0.015)	0.091 (0.015)	0.096 (0.017)	0.097 (0.016)
			LOPO	0.129 (0.017)	0.077 (0.017)	0.084 (0.018)	0.079 (0.018)
		100:50	Re-Sub	0.133 (0.014)	0.088 (0.015)	0.091 (0.016)	0.095 (0.016)
			LOPO	0.129 (0.015)	0.077 (0.017)	0.084 (0.016)	0.084 (0.017)
		100:100	Re-Sub	0.133 (0.012)	0.087 (0.013)	0.091 (0.014)	0.094 (0.013)
			LOPO	0.130 (0.013)	0.079 (0.014)	0.084 (0.014)	0.083 (0.014)
0.6-0.9	0-0.1	50:50	Re-Sub	0.050 (0.010)	0.051 (0.012)	0.056 (0.012)	0.059 (0.012)
			LOPO	0.043 (0.012)	0.043 (0.013)	0.048 (0.014)	0.048 (0.013)
		50:100	Re-Sub	0.049 (0.008)	0.050 (0.011)	0.057 (0.011)	0.058 (0.011)
			LOPO	0.043 (0.011)	0.044 (0.012)	0.050 (0.013)	0.050 (0.012)
		100:50	Re-Sub	0.114 (0.014)	0.123 (0.020)	0.128 (0.018)	0.138 (0.016)
			LOPO	0.107 (0.016)	0.115 (0.021)	0.122 (0.019)	0.129 (0.017)
		100:100	Re-Sub	0.047 (0.007)	0.049 (0.010)	0.054 (0.009)	0.056 (0.009)
			LOPO	0.044 (0.008)	0.045 (0.010)	0.050 (0.010)	0.051 (0.009)
	0-0.2	50:50	Re-Sub	0.116 (0.017)	0.126 (0.021)	0.130 (0.022)	0.141 (0.019)
			LOPO	0.106 (0.021)	0.114 (0.023)	0.118 (0.024)	0.125 (0.021)
		50:100	Re-Sub	0.115 (0.014)	0.125 (0.020)	0.131 (0.020)	0.140 (0.018)
			LOPO	0.107 (0.017)	0.114 (0.021)	0.121 (0.022)	0.128 (0.019)
		100:50	Re-Sub	0.048 (0.008)	0.049 (0.011)	0.054 (0.010)	0.057 (0.010)
			LOPO	0.044 (0.009)	0.044 (0.011)	0.050 (0.011)	0.051 (0.010)
		100:100	Re-Sub	0.113 (0.012)	0.124 (0.017)	0.128 (0.016)	0.138 (0.014)
			LOPO	0.108 (0.014)	0.117 (0.018)	0.122 (0.017)	0.130 (0.015)

Lastly, we considered the performance of different combination methods by generating gamma ROC curves. From Table 4, (Scenario #4) where data suggest a straight-line shape ROC curve, when the AUCs were close, the min-max approach performed better than the other three approaches in obtaining the largest pAUCs through both the re-substitution and the LOPO cross validation. When the AUCs were far apart (Case#2), the min-max approach yielded the best pAUC estimates through LOPO cross validation. The LOGITIC approach was best based on the re-substitution.

Table 4.

Means and standard deviation (SD) of the partial area under the ROC curve for different combination methods based on the dataset consisted of ratings from multivariate gamma distributions (scenario#4) with 1000 simulated datasets.

AUCs	Fpf range	Sample Size		MIN-MAX	SULIU	LIU	LOGISTIC
0.7-0.8	0-0.1	50:50	Re-Sub	0.068 (0.007)	0.059 (0.008)	0.052 (0.010)	0.066 (0.008)
			LOPO	0.067 (0.008)	0.056 (0.009)	0.048 (0.011)	0.059 (0.008)
		50:100	Re-Sub	0.068 (0.006)	0.060 (0.007)	0.052 (0.009)	0.065 (0.006)
			LOPO	0.067 (0.006)	0.058 (0.007)	0.049 (0.009)	0.060 (0.007)
		100:50	Re-Sub	0.068 (0.007)	0.059 (0.008)	0.050 (0.009)	0.065 (0.007)
			LOPO	0.067 (0.007)	0.056 (0.008)	0.048 (0.010)	0.060 (0.007)
		100:100	Re-Sub	0.068 (0.005)	0.059 (0.006)	0.051 (0.007)	0.064 (0.005)
			LOPO	0.067 (0.005)	0.057 (0.006)	0.049 (0.008)	0.061 (0.006)
	0-0.2	50:50	Re-Sub	0.145 (0.013)	0.130 (0.015)	0.111 (0.020)	0.141 (0.014)
			LOPO	0.143 (0.014)	0.125 (0.016)	0.105 (0.022)	0.131 (0.015)
		50:100	Re-Sub	0.146 (0.010)	0.132 (0.012)	0.111 (0.017)	0.141 (0.011)
			LOPO	0.144 (0.011)	0.129 (0.013)	0.107 (0.018)	0.133 (0.012)
		100:50	Re-Sub	0.145 (0.012)	0.130 (0.014)	0.109 (0.018)	0.140 (0.013)
			LOPO	0.144 (0.012)	0.125 (0.015)	0.106 (0.020)	0.133 (0.013)
		100:100	Re-Sub	0.145 (0.009)	0.131 (0.011)	0.110 (0.015)	0.139 (0.010)
			LOPO	0.144 (0.009)	0.128 (0.011)	0.108 (0.015)	0.134 (0.010)
0.6-0.9	0-0.1	50:50	Re-Sub	0.081 (0.006)	0.065 (0.009)	0.076 (0.007)	0.084 (0.006)
			LOPO	0.081 (0.006)	0.060 (0.011)	0.076 (0.007)	0.079 (0.008)
		50:100	Re-Sub	0.081 (0.004)	0.066 (0.008)	0.076 (0.005)	0.083 (0.004)
			LOPO	0.081 (0.004)	0.062 (0.009)	0.075 (0.005)	0.080 (0.005)
		100:50	Re-Sub	0.081 (0.005)	0.065 (0.009)	0.076 (0.006)	0.084 (0.005)
			LOPO	0.081 (0.005)	0.061 (0.010)	0.075 (0.006)	0.079 (0.008)
		100:100	Re-Sub	0.081 (0.004)	0.065 (0.008)	0.076 (0.005)	0.083 (0.004)
			LOPO	0.081 (0.004)	0.063 (0.008)	0.075 (0.005)	0.081 (0.004)
	0-0.2	50:50	Re-Sub	0.167 (0.010)	0.141 (0.016)	0.157 (0.013)	0.173 (0.010)
			LOPO	0.167 (0.011)	0.133 (0.018)	0.156 (0.013)	0.164 (0.013)
		50:100	Re-Sub	0.168 (0.008)	0.143 (0.013)	0.157 (0.010)	0.171 (0.008)
			LOPO	0.167 (0.008)	0.137 (0.014)	0.156 (0.010)	0.167 (0.008)
		100:50	Re-Sub	0.167 (0.010)	0.141 (0.016)	0.156 (0.012)	0.172 (0.010)
			LOPO	0.167 (0.010)	0.134 (0.017)	0.155 (0.012)	0.165 (0.013)
		100:100	Re-Sub	0.167 (0.007)	0.142 (0.013)	0.156 (0.009)	0.171 (0.007)
			LOPO	0.167 (0.007)	0.138 (0.013)	0.156 (0.009)	0.167 (0.007)

5. Example

5.1. Example 1

We used data from Cancer and Leukemia Group B study 90206, a Phase III clinical trial of metastatic renal-cell carcinoma (Rini et al., 2008; Rini et al., 2010), to provide an example of our proposed method. The study randomized 732 patients, 369 to anti-VEGF treatment and 363 to a control group (Rini et al., 2008; Rini et al., 2010). The trial was designed with 588 deaths so that the log-rank statistic would have 86% power to detect a hazard ratio of 0.76 for deaths assuming a two-sided significance level of 0.05. The trial collected plasma from patients in order to study the relationship of angiogenic and inflammatory markers with clinical outcomes. A primary objective of the correlative science study was to associate the anti-VEGF biomarkers from the angiome assay with overall survival and build a prognostic model that predicts the clinical outcome (Nixon et al., 2013). Another objective was to correlate the anti-VEGF biomarkers with the best objective response rate (defined as either partial or complete response). The angiome multiplex array has gone through a rigorous evaluation to ensure data quality (Nixon et al., 2013). Markers performed include: Ang-2, bFGF, BMP-9, CRP, Endoglin, Gro-a, HGF, ICAM-1, IGFBP-1, IGFBP-2, IGFBP-3, IL-6, IL-8, MCP-1, OPN, P-selectin, Pai-1-active, Pai-1-total, PDGF-AA, PDGF-BB, PEDF, PlGF, SDF-1, TGFβ1, TGFβ2, TGFβ3- R3, TSP-2, VCAM-1, VEGF, VEGF-C, VEGF-D, VEGF-R1, and VEGF-R2.

We used the random forest, LASSO and adaptive LASSO to select the top three biomarkers of the 33 biomarkers for best objective response. The top three genes (HGF, IL_6 and VEGF_R2) with highest full AUC (0.576, 0.610 and 0.563) were chosen as an example to demonstrate the scenario where the AUCs were close to each other as a potential advantage of the use of the proposed method. The empirical estimates for the pAUC for these three biomarkers are 0.012, 0.012 and 0.028. The correlation matrices for non-responders and responders are

$$Cor{r}_x=\left(\begin{array}{ccc}1& 0.530& 0.319\\ 0.530& 1& 0.273\\ 0.319& 0.273& 1\end{array}\right)\text{and}cor{r}_y=\left(\begin{array}{ccc}1& 0.453& 0.219\\ 0.453& 1& 0.225\\ 0.219& 0.225& 1\end{array}\right).$$

The proposed method provided the following combination:

$$\max \left\{HGF,I{L}_{-}6,andVEG{F}_{-}R2\right\}-\min \left\{HGF,I{L}_{-}6,andVEG{F}_{-}R2\right\}$$

with the estimated pAUC of 0.0427 and the estimated standard deviation of 0.0080 based on 1,000 bootstrap sampling.

In contrast, the SULIU method provided the following combination:

$$HGF+1.36*I{L}_{-}6-1.81*VEG{F}_{-}R2$$

with the estimated pAUC of 0.0426 and the estimated standard deviation of 0.0084.

The LIU method provided the following combination:

$$HGF-1.21*I{L}_{-}6-0.06*VEG{F}_{-}R2$$

with the estimated pAUC of 0.0254 and the estimated standard deviation of 0.0099;

whereas the LOGISTIC’s method had the following combination

$$HGF+1.52*I{L}_{-}6-1.88*VEG{F}_{-}R2$$

with the estimated pAUC of 0.0422 and the estimated standard deviation of 0.0084.

5.2. Example 2

In this section, the proposed method MIN-MAX as well as the SULIU, LIU, and the LOGISTIC are applied to a real data set of 125 females on Duchenne Muscular Dystrophy (DMD) data set. This biomedical data originally containing 209 observations (134 for “normals” and 75 for “carriers”) has been studied by Cox et al. (1982) in order to develop screening methods to identify carriers of a rare genetic disorder based on four measurements made on blood samples. This data set has been widely studied in the literature for improving the classification accuracy by using ROC analysis. The main objective is to combine four markers to increase the diagnostic accuracy of screening females as potential DMD carriers. For example, Kang et al. (2013) applied the stepwise methods to combine four makers in this data to improve AUC, Hsu and Hsueh (2013), and Yu and Park (2015) applied their proposed algorithm to pAUC in this data.

Since four different variables M1- M4 were measured in each blood sample, we processed the data by taking average values for each measurement if one had blood drawn at several different time points. Among the 125 females, there are 87 normals and 38 carriers.

Similarly, we investigated the performance of the four different methods on the pAUC over the range 0–0.2. Since the four measurements are in different scales, we applied the standardization method by dividing each value by the range of that variable before the use of MIN-MAX approach. M1*- M4* denote the standardized marker values. The empirical estimates for the pAUC for these four biomarkers are 0.1472, 0.0436, 0.1086 and 0.1229 for the M1-M4, respectively. The empirical estimates for the full AUC are 0.9034, 0.6057, 0.8232 and 0.8814. The correlation matrices for non-respondents and respondents are

$$Cor{r}_x=\left(\begin{array}{cccc}1& -0.380& 0.012& 0.236\\ -0.380& 1& 0.130& 0.155\\ 0.012& 0.130& 1& 0.281\\ 0.236& 0.155& 0.281& 1\end{array}\right)\text{and}Cor{r}_y=\left(\begin{array}{cccc}1& -0.037& 0.688& 0.625\\ -0.037& 1& -0.222& -0.098\\ 0.688& -0.222& 1& 0.612\\ 0.625& -0.098& 0.612& 1\end{array}\right)$$

The proposed method provided the following combination:

$$max\left\{M{1}^{*},M{2}^{*},M{3}^{*},M4\right\}+6.6667*min\left\{M{1}^{*},M{2}^{*},M{3}^{*},M{4}^{*}\right\}$$

with the estimated pAUC of 0.161 and the estimated standard deviation of 0.0119 based on 1,000 bootstrap sampling.

In contrast, the SULIU method provided the following combination

$$M1+12.6333*M2+7.7165*M3+13.6415*M4$$

with the estimated pAUC of 0.137 and the estimated standard deviation of 0.0157.

The LIU method provided the following combination:

$$M1+0.5248*M2+0.7805*M3-0.1087*M4$$

with the estimated pAUC of 0.151 and the estimated standard deviation of 0.0135;

whereas the LOGISTIC’s method had the following combination

$$M1+0.6950*M2+1.3806*M3+0.2545*M4$$

with the estimated pAUC of 0.156 and the estimated standard deviation of 0.0138.

6. Discussion

In this article, we extend the min-max method to the estimation of the pAUC and compare its performances to three commonly utilized methods. The proposed method has the advantage of both the min-max method and Pepe and Thompson’s method (Pepe and Thompson, 2000). The expected advantages of this approach are threefold. First, it may yield larger partial area under the ROC curves. Second, it is a non-parametric approach and therefore it is robust against distributional assumptions. Lastly, it is computationally feasible and efficient since the min-max procedure involves searching for only one single coefficient. Our works (Ma et al. 2013, 2015) have shown that the use of pAUC is not only clinically useful but is statistically more efficient than the use of the full AUC in the families of area under the ROC curves that are nearly straight-line shaped. Another advantage of this method demonstrated through our simulation study is that in the scenario of a straight-line shaped gamma ROC curves the estimate of pAUC based on re-substitution is close to the estimate based on the LOPO cross validation. This implies that the min-max method on pAUC leads to good generalizability.

As pointed out by several authors (Huang et al., 2011; Copas et al., 2002; Kang et al., 2013), the use of the re-substitution to estimate the area under the ROC curve could usually lead to the overoptimistic result, or upward biased estimates for independent dataset, or future observations. Huang et al. (2011) proposed to use the LOPO cross validation to obtain less biased estimates. Kang et al. (2013) applied the LOPO cross validation to compare different combination methods to maximize the AUC. Because the estimates through cross validation lead to more reliable results in terms of its ability to generalize to an independent dataset, we recommend using cross validation which performs better when decisions based on the re-substitution and the cross validation approaches are different. Based on our simulation results, it is not surprising to observe that the standard deviation of the estimated pAUC decreased as the sample size increased, and that the estimate of the pAUC based on the re-substitution approach was becoming closer to the estimate of the pAUC based on the LOPO cross validation as the sample size increased.

Evaluation of diagnostic assays and prognostic performance of biomarkers will continue to remain an important research topic in several medical areas. This is especially true in oncology where diagnostic assays based on several combinations of biomarkers are developed and validated. For example, a 22-gene model was developed and validated to predict prostate cancer risk (Erho et al, 2013). In addition, identifying predictive markers of clinical outcomes is a hot area of research as finding the optimal treatment to tailor patients is attractive not only to patients but to physicians, insurance company and society as a whole. Currently, several predictors or signature of outcomes are being used to guide therapies in clinical trials (Erho et al, 2013). For example OncotypeDx, a 21 gene expression signature is being used to select treatment in patients with breast cancer based on the recurrence score (Sparano et al, 2015). Recognizing the fact that more predictors will continue to be applied in the clinic, it is critical that when a combination of biomarkers are developed that this would result in the highest pAUC.

Based on our extensive simulations, our recommendations are:

• 1)Use the SULIU or LOGISTIC approach to estimate the pAUC with approximately equal variance multivariate normal data regardless whether the AUCs among biomarkers are relatively close or far apart. The LIU’s approach underestimated the pAUC approximately by 1/3. This is partly due to the instability of the eigenvector of the identity matrix, since LIU’s approach involve the calculation of the eigenvector corresponding to the smallest eigenvalue of ${\mathbf{\Sigma }}_y^{-1/2}{\mathbf{\Sigma }}_x{\mathbf{\Sigma }}_y^{-1/2}$ which is an identity matrix under this scenario when ${\mathbf{\Sigma }}_x={\mathbf{\Sigma }}_y$, and the eigenvector corresponding to the smallest eigenvalue is not stable under small perturbation of the identity matrix (Allez and Bouchaud, 2012).
• 2)Utilize the min-max approach to estimate the pAUC with unequal variance multivariate normal data when the AUCs are relatively close and use the SULIU’s approach when the AUCs are far apart.
• 3)Employ the min-max approach to estimate the pAUC with highly skewed data when the AUCs are relatively close, but use the LOGISTIC method when the AUCs are far apart.
• 4)Use the min-max approach to estimate the pAUC with straight-line shaped ROC curves regardless whether the AUCs are close or far apart.

In summary, the min-max approach seems to be robust and investigators are encouraged to use it in the estimation of the pAUC. It is simple to implement and is computationally feasible. In an era of personalized medicine, it is anticipated that the evaluation of diagnostic assays and the performance of the combination of biomarkers will remain an important area of research not only in diagnosing patients but also in treating patients with the disease.

Figure 1.

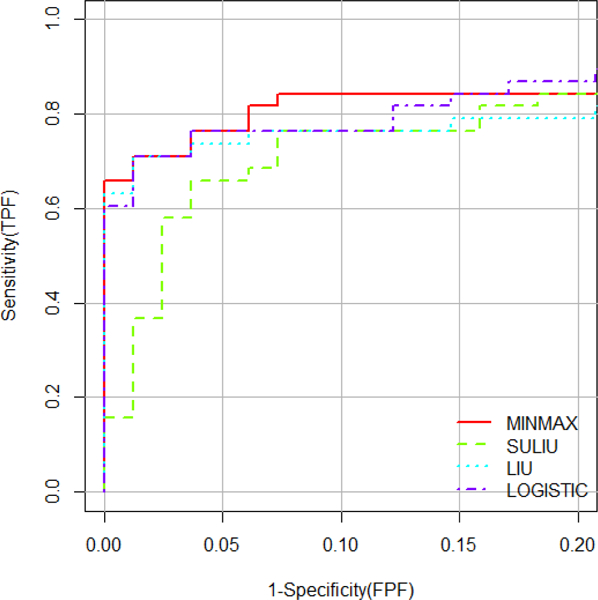
The performance for each method.

Table 5.

The coefficients of the optimal linear combination and the corresponding estimated pAUC

Method	M1	M2	M3	M4	pAUC
MIN-MAX	-	-	-	-	0.161
SULIU	1	12.6333	7.7165	13.6415	0.137
LIU	1	0.5248	0.7805	−0.1087	0.151
LOGISTIC	1	0.6950	1.3806	0.2545	0.156