Deep learning-based three-dimensional segmentation of the prostate on computed tomography images

Abstract.

Segmentation of the prostate in computed tomography (CT) is used for planning and guidance of prostate treatment procedures. However, due to the low soft-tissue contrast of the images, manual delineation of the prostate on CT is a time-consuming task with high interobserver variability. We developed an automatic, three-dimensional (3-D) prostate segmentation algorithm based on a customized U-Net architecture. Our dataset contained 92 3-D abdominal CT scans from 92 patients, of which 69 images were used for training and validation and the remaining for testing the convolutional neural network model. Compared to manual segmentation by an expert radiologist, our method achieved $83\%\pm 6\%$ for Dice similarity coefficient (DSC), $2.3\pm 0.6\mathrm{mm}$ for mean absolute distance (MAD), and $1.9\pm 4.0{\mathrm{cm}}^3$ for signed volume difference ($\mathrm{\Delta }V$). The average recorded interexpert difference measured on the same test dataset was 92% (DSC), 1.1 mm (MAD), and $2.1{\mathrm{cm}}^3$ ($\mathrm{\Delta }V$). The proposed algorithm is fast, accurate, and robust for 3-D segmentation of the prostate on CT images.

1. Introduction

In 2017, prostate cancer (PCa) with more than 161,000 newly diagnosed cases was one of the most frequent cancers diagnosed among men in the United States.¹ Some of the image-guided treatment interventions for PCa management, e.g., radiation therapy, are performed with the prostate border delineated on computed tomography (CT) images. However, the low soft-tissue contrast of CT images challenges manual prostate segmentation performance in terms of accuracy, repeatability, and segmentation time.²

Several computerized algorithms have been developed recently to segment the prostate faster with higher repeatability compared to manual segmentation.^3–15 Some of these algorithms were learning-based segmentation techniques that used manual segmentation information of previously acquired CT images from the same patient for training.^9,10 This approach helps to have a more accurate segmentation. However, as a prerequisite, manual segmentation of previous CT images from the same patient must be available to segment the next image. On the other hand, to evaluate the performance of a computer-assisted algorithm, it is important to consider the high interobserver variability in manual segmentation and compare the results to multiple-observer manual reference, which has not been taken into account in most of the recently published work.

Deep learning-based approaches demonstrate a strong capability for fast prostate segmentation in medical images with high accuracy.^{3,6,11,16–20} However, most of the deep learning algorithms presented in the literature have used either patch-based segmentation, two-dimensional (2-D) slice-by-slice segmentation, or a combination of both. These methods are less complex and decrease the data load on graphics processing units (GPU). However, in patch-based segmentation, some intraslice information is lost, and in slice-by-slice segmentation, the interslice information is missing.

In this study, we present an automatic three-dimensional (3-D) deep learning-based segmentation algorithm to address the need for a fast, accurate, and repeatable 3-D segmentation of the prostate on CT images, which does not depend on the intrapatient data for training. The proposed neural network has not been trained on previously acquired images from the target patient. We evaluated the performance of the algorithm to the manual references from two expert radiologists, and we used the complementary region-based [Dice similarity coefficient (DSC), sensitivity rate (SR), and precision rate (PR)], surface-based [mean absolute distance (MAD)], and volume-based [signed volume difference ($\mathrm{\Delta }V$)] error metrics to measure the segmentation error of our algorithm against manual references. We also compared the results to the measured interexpert observer difference in manual segmentation. The proposed algorithm showed robustness to some of the image artifacts caused by metallic implanted objects.

2. Methods

2.1. Data

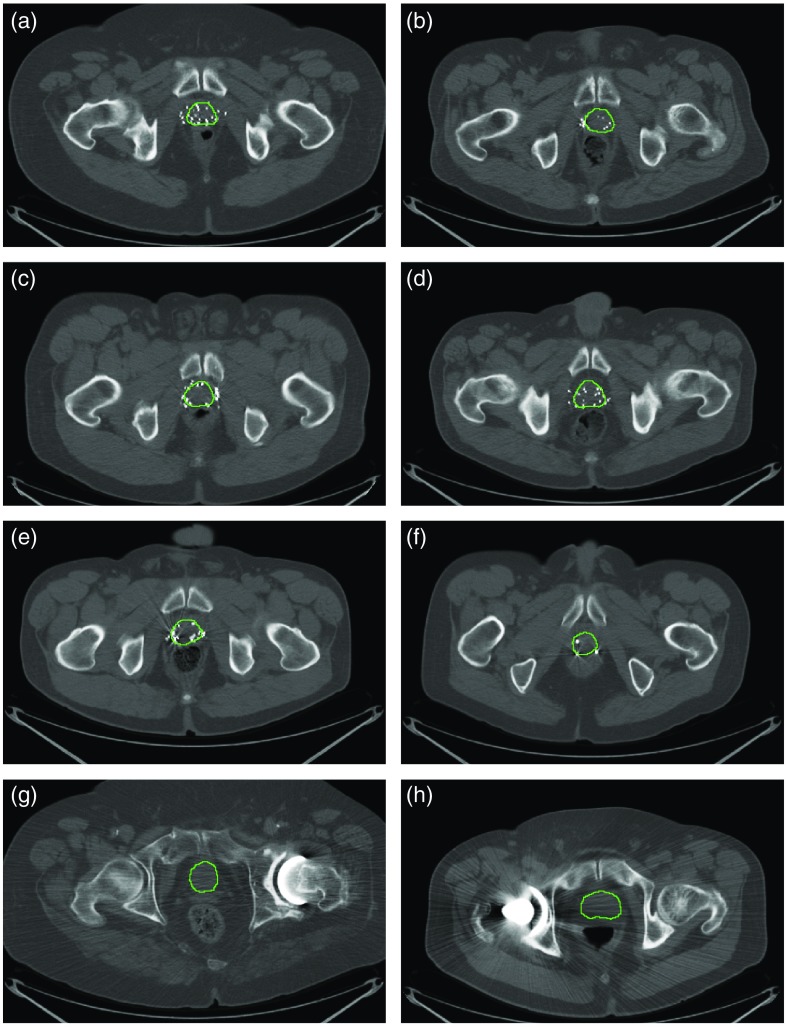
Our dataset contained 92 3-D abdominal CT scans from 92 patients. Each image was originally $512\times 512\times 27\text{voxels}$ in size with a $0.977\times 0.977\times 4.25{\mathrm{mm}}^3\text{voxel}$ size. Thirty-seven (40%) images were from post low-dose brachytherapy patients, with the prostate images distorted by the brachytherapy seeds. For some other cases ($\sim 20\%$), the image quality was affected by other metallic implanted objects, such as fiducial markers and orthopedic implants. Figure 1 shows some of the artifacts in our dataset. In this study, we did not exclude those images with artifacts from the dataset. For each image, two independent manual segmentations were provided by two expert radiologists. We randomly selected 75% of the images (69 patients) for training (65%) and validation (10%) purposes and kept the remaining 25% (23 patients) reserved for final testing of the method.

Fig. 1.

Image artifacts that can affect the segmentation: (a)–(e) low-dose rate brachytherapy seeds image artifacts and (f)–(h) metallic objects interference. The prostate borders manually drawn by a radiologist were overlaid on the images in green contours.

2.2. Preprocessing

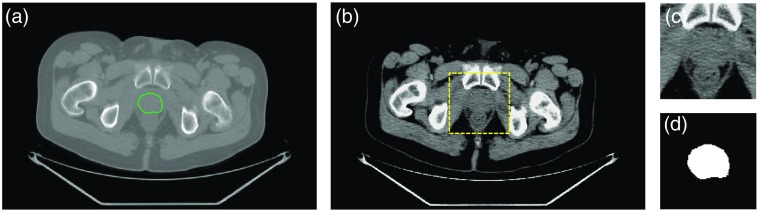
The prostate gland occupied 5 to 13 axial slices and $<0.1\%$ of the whole image volume. Hence, to minimize the data load on the GPU and speed up the training process, we cropped the images to a bounding box of $96\times 96\times 15\text{voxels}$. In the cropped images, the prostate gland occupied $<6\%$ of the image volume on average. We also truncated the Hounsfield unit (HU) range based on the observed range for prostate tissues in the training set. After removing 1% outliers, the lowest and the highest HU values we observed within the prostate tissue across the training set were $-69$ and 165, respectively. For all the images, we replaced those values below $-69$ and above 165 with $-69$ and 165, respectively. This helps to reduce the effect of background tissues, such as bones, adipose tissues, calcifications, brachytherapy seeds, and liquids. Figure 2 shows a sample image after each preprocessing step.

Fig. 2.

Preprocessing steps for the image segmentation. (a) A sample midgland slice of the original CT image with prostate border overlaid in green contour. (b) The image after HU truncation. The selected bounding box is shown in a yellow dashed square. (c) The cropped image and (d) its manual segmentation label.

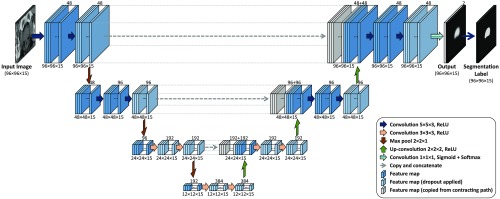
2.3. Fully Convolutional Neural Network Architecture

In this study, we used a customized version of a fully convolutional neural network (FCNN) called U-Net.²¹ The FCNNs are end-to-end networks that produce segmentation maps with the same pixel-wise dimensions as their inputs. We modified the U-Net architecture to make it 3-D and applicable to our images. Figure 3 shows the architecture of the proposed 3-D U-Net. The FCNN is a four-level U-Net model with 21 layers, including 18 convolutional and 3 max pool layers. For 17 convolutional layers, we used rectifier linear unit activation function, and for the last convolutional layer, sigmoid activation function was used. We kept the size of the output channels for all the convolutional layers the same as the input channels by zero-padding the input channel before convolution. For the two upper levels, we used a convolution kernel size of $5\times 5\times 3$, and for the two lower levels, we used kernel size of $3\times 3\times 3$. In the contracting path (left side of the network), we used one $2\times 2\times 1$ max-pooling layer after each pair of convolutional layers. In the expansive path (right side of the network), we used one upconvolutional layer ($2\times 2\times 1$ upsampling followed by $2\times 2\times 2$ convolution) after each pair of convolutional layers. We applied a dropout to 10 of the layers as denoted by the pale blue boxes in Fig 3. In each of the three top levels of the U-Net model, the last feature map of the contracting path is concatenated to the first feature map of the expansive path. Due to a huge imbalance between the number of background and prostate voxels, we used a loss function based on “soft Dice” similarity coefficient:²²

$$L=1-\frac{2{\sum }_i(h(x_i).y_i)}{{\sum }_i[h(x_i)]+{\sum }_i(y_i)},$$

where $h(x_i)$ is the $i$’th probability value of the output probability map and $y_i$ is the $i$’th value of the reference binary mask. For optimization, we used Adadelta²³ gradient-based optimizer.

Fig. 3.

The four-level 3-D U-Net FCNN architecture. The numbers above the feature maps indicate the number of feature channels and the numbers below the feature maps indicate the size of each feature channel.

2.4. Postprocessing

We applied thresholding with the threshold level of 50% to build binary masks out of probability maps. Then we automatically found and kept the largest 3-D object in the image as the prostate label and removed the smaller objects as the false positive objects. During validation, we observed a small amount of oversegmentation of the algorithm on the validation images. Therefore, to compensate the oversegmentation, we applied an erosion operator²⁴ using a $3\times 3$ square shape structuring element to the segmentation results in order to slightly shrink the labels.

2.5. Implementation Details

We used the TensorFlow²⁵ machine learning framework to implement the 3-D U-Net model in Python. We used a desktop computer with 512 GB of memory and an NVIDIA GeForce GTX 1080 Ti GPU. We used a batch size of one and initial learning rate of 1.0. We applied an exponential learning rate decay with a decay rate of 0.99 and decay step of one epoch. We set the dropout rate to 40%, and the decay rate and epsilon conditioning parameters for Adadelta optimizer to 0.9 and $1\times {10}^{-10}$, respectively.

2.6. Data Augmentation

We used data augmentation to double the number of training data using horizontal flipping of the images by exploiting the left-right symmetry of the images.

2.7. Evaluation

We compared the algorithm segmentation results against manual segmentation using a set of segmentation error metrics, including the DSC,²⁶ sensitivity (or recall) rate (SR), PR, MAD, and $\mathrm{\Delta }V$. For details regarding the calculation of the metrics, see Ref. 27. To measure the variability in the results, we used 95% confidence intervals using bootstrapping²⁸ with 10,000 repetitions. We reported the median of the 10,000 means and the 95% confidence interval.

Due to the interobserver variability in manual segmentation of the prostate in CT images,² it is not possible to define a single gold standard for prostate segmentation in CT images. Therefore, we consider the two manual segmentations as two independent manual reference segmentations in this study. We measured the interexpert observer variability in manual prostate segmentation in CT images by comparing the two references using DSC, MAD, and $\mathrm{\Delta }V$ evaluation metrics. To measure the accuracy of the algorithm, we compared the output segmentation label separately to each manual reference segmentation using the evaluation metrics.

3. Experiments and Results

3.1. Interexpert Observer Variation in Manual Segmentation

The interexpert observer differences in ground-truth segmentation were quantified by comparing the two manual references from the test images using DSC, MAD, and $\mathrm{\Delta }V$. The MAD values were calculated in bilateral mode²⁷ (${\mathrm{MAD}}_{\mathrm{b}}$) and absolute volume difference ($\left|\mathrm{\Delta }V\right|$) was calculated because of the lack of a reference in comparison between two manual segmentations. The mean (and 95% confidence interval) for the whole gland were 91.7% ([90.8%, 92.5%]), 1.1 mm ([1.1, 1.2 mm]), and $2.4{\mathrm{cm}}^3$ ([1.9, $3.1{\mathrm{cm}}^3$]), based on DSC, ${\mathrm{MAD}}_{\mathrm{b}}$, and $|\mathrm{\Delta }V|$, respectively.

3.2. Training

We used our two sets of manual reference segmentations by radiologist experts (hereafter referred to as references A and B) and made six different combinations of training, validation, and testing datasets to design three experiments: (1) single-reference training (in-group), (2) single-reference training (out-group), and (3) multireference training. For all the experiments, we used only one of the reference segmentations for validation and test. Additionally, we applied data augmentation to our 60 training images to double the size of our training set for all of the following experiments.

Single-reference training (in-group): We trained the FCNN model using a single-observer manual reference segmentation (e.g., reference A) and validated the training by comparing the results to the same observers’ manual reference segmentation (i.e., reference A). We repeated this experiment using the other observers’ manual segmentation. Therefore, we have two trained models: one trained using reference A (model I) and the other trained using reference B (model II). Since the segmentation of the prostate in CT images is a challenging task even for the expert radiologists, the training accuracy does not approach 100%. Therefore, for each experiment, we trained the FCNN model until the validation accuracy does not improve much. We set the maximum iteration number to 200 training epochs (24,000 iterations). For model I, we got the best performance after 188 epochs (22,560 iterations). For model II, we got the best performance after 139 epochs (16,680 iterations). Training process times for model I and model II were about 31 and 27 h, respectively. Table 1 shows the results.

Table 1.

Training, validation, and testing performance of the three FCNN models in terms of DSC. ${\mathrm{DSC}}_{\mathrm{Tr}}$, ${\mathrm{DSC}}_{\mathrm{v}}$, and ${\mathrm{DSC}}_{\mathrm{Ts}}$ are the means and [95% confidence intervals] of DSC values across the training, validation, and test datasets, respectively.

FCNN model	Training reference (# of samples)	Validation/test reference (# of samples)	${\mathrm{DSC}}_{\mathrm{Tr}}$ (%)	${\mathrm{DSC}}_{\mathrm{V}}$ (%)	${\mathrm{DSC}}_{\mathrm{Ts}}$ (%)
Single-reference training (model I)	A (120)	A (9/23)	92.3 [91.9, 92.7]	82.8 [78.3, 86.3]	82.2 [79.5, 84.1]
Single-reference training (model I)	A (120)	B (9/23)	88.7 [87.6, 89.7]	82.3 [78.3, 85.4]	82.2 [80.2, 83.9]
Single-reference training (model II)	B (120)	B (9/23)	90.7 [90.1, 91.3]	82.3 [78.4, 85.6]	82.4 [80.4, 84.2]
Single-reference training (model II)	B (120)	A (9/23)	89.2 [88.3, 90.0]	80.9 [77.7, 83.5]	82.8 [80.4, 84.5]
Multireference training (model III)	A and B (240)	A (9/23)	92.5 [91.9, 93.1]	82.6 [80.0, 84.9]	83.1 [80.3, 85.0]
Multireference training (model III)	A and B (240)	B (9/23)	90.9 [90.2, 91.5]	83.4 [80.6, 85.6]	82.6 [80.1, 84.6]

Single-reference training (out-group): In this experiment, we performed the FCNN training with the training set with ground truth from one expert’s (e.g., reference A) manual segmentation but used the other expert’s (e.g., reference B) manual segmentation of the testing data for performance evaluation of the testing data. We used the two FCNN models trained during the in-group single-reference-training experiment and tested model I by comparing the segmentation results against reference segmentation B, and model II by comparing the segmentation results against reference segmentation A. Table 1 shows the results.

Multireference training: We used both experts’ manual references to form the ground truth of the training data to train the FCNN model (model III), and validated the trained model by comparing the results once to the reference A and once to the reference B, separately. Therefore, before augmentation, each training image appeared twice: once with ground truth obtained from reference A and once with ground truth obtained from reference B. We set the maximum number of training iterations to 200 epochs (48,000 iterations). We achieved the best performance after 105 epochs (25,200 iterations). Training process time for the model was about 35 h. Table 1 shows the results.

3.3. Testing Results

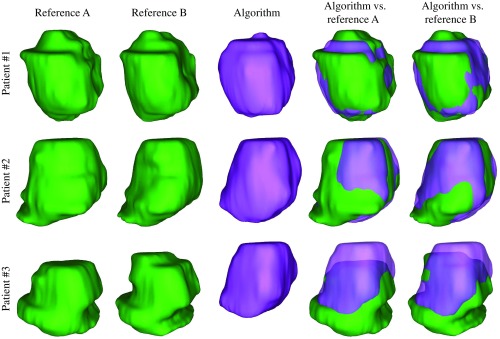
The 23 image testing dataset was segmented using our three trained deep learning models (models I, II, and III), and the performance was stratified from the six different experiments defined in Sec. 3.2. Table 1 shows the training, validation, and testing DSC results for the six experiments. Table 2 shows the performance of the proposed algorithm (model III) against two experts’ manual references (multireference training paradigm) and compares the results of several recently published state-of-the-art segmentation algorithms. Figures 4 and 5 show the segmentation results of the proposed algorithm in 2-D and 3-D, respectively, for three sample test cases using model III (multireference training paradigm). The average $\mathrm{\Delta }V$ values for model III on the test dataset were $1.9\pm 4.0{\mathrm{cm}}^3$ and $3.9\pm 3.6{\mathrm{cm}}^3$ when comparing to reference A and reference B, respectively. The average segmentation time for each 3-D image segmentation was 1.1 s.

Table 2.

The performance of the proposed FCNN (model III) against two expert observers (references A and B) compared to a number of recently published work.

Method, year	$N_{\mathrm{Pat}}$	$N_{\mathrm{Img}}$	$N_{\text{test}}$	MAD (mm)	DSC (%)	SR (%)	PR (%)	Exec. time (s)
Proposed algorithm (reference A)	92	92	23	$2.3\pm 0.6$	$83\pm 6$	$87\pm 8$	$80\pm 9$	$1.1\pm 0.4$
Proposed algorithm (reference B)	92	92	23	$2.4\pm 0.8$	$83\pm 6$	$90\pm 7$	$77\pm 8$	$1.1\pm 0.4$
Kazemifar et al.,3 2018	85	85	$\sim 25$	—	$88\pm 12$	87	92	$\sim 1$
Shahedi et al.,7 2018	70	70	10	$1.9\pm 0.5$	$88\pm 2$	$94\pm 3$	$82\pm 4$	$22\pm 2$
Ma et al.,6 2017	92	92	92	—	84	—	—	—
Ma et al.,4 2016	15	15	15	—	$85\pm 3$	$83\pm 1$	—	—
Shi et al.10, 2016	24	330	258	$1.3\pm 0.8$	$92\pm 4$	$90\pm 5$	—	—
Shi et al.,9 2015	24	330	258	$1.1\pm 0.6$	$95\pm 3$	$93\pm 4$	—	—
Skalski et al.,13 2015	27	27	15	—	$81\pm 5$	—	—	—
Shao et al.,8 2015	70	70	70	$1.9\pm 0.2$	$88\pm 2$	84	86	—

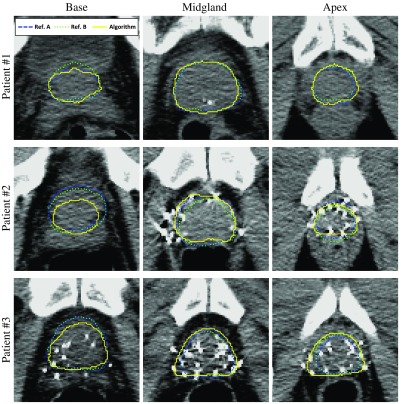
Fig. 4.

Qualitative segmentation results for three sample cases. Each row shows the results for one patient. For each image, the algorithm (model III) segmentation results are shown with yellow contours and the reference contours with blue dashed and green dotted contours on three sample 2-D slices. The bottom row shows the results from the patient in our test dataset with the lowest DSC value (62%).

Fig. 5.

Qualitative segmentation results in 3-D for the three sample cases shown in Fig. 4. Each row shows the results for one patient. The bottom row shows the results from the patient in our test dataset with the lowest DSC value (62%).

3.4. Cross Validation

To test our CNN model on the whole image dataset, we applied a fourfold cross-validation methodology. We randomly divided the 92 image dataset into four subsets of 23 images, and each subset was used as a test set while the remaining data ($3\times 23=69$ images) was used for training. We used the exact same network architecture, hyperparameters, and setup that were used for model III and trained the network four times. We applied flipping data augmentation to all the training images and used manual segmentations from both radiologist experts for each image to yield a total size of 276 training images. We trained each network for up to 150 epochs (41,400 iterations) and stopped training when the training accuracy plateaued. We chose the best trained model determined by minimum training loss. Table 3 shows the performance of the algorithm in terms of DSC for each test fold against the two manual references, separately. The overall DSC on the whole dataset has also been reported in the table.

Table 3.

Fourfold cross-validation results. The mean and 95% confidence intervals of DSC values across the test datasets.

Test set	Number of samples	DSC (%) (reference A)	DSC (%) (reference B)
Test fold 1	23	79.5 [76.0, 82.4]	80.8 [78.0, 83.0]
Test fold 2	23	82.7 [80.3, 84.6]	83.4 [81.3,85.2]
Test fold 3	23	82.6 [81.0, 84.1]	83.4 [81.9, 84.8]
Test fold 4	23	79.9 [76.1, 83.0]	81.0 [77.9, 83.6]
Whole dataset	92	81.1 [79.6, 82.4]	82.1 [80.9, 83.2]

3.5. Quantitative Assessment of the Effect of Image Artifacts

To assess the impact of the image artifacts on the segmentation results, we selected a subset of 43 images that were not affected by imaging artifacts (nonaffected subset) and quantified the segmentation algorithm performance on them. We trained and tested our algorithm on the selected subset using a threefold cross validation with a similar study design used in Sec. 3.4. For this test, we chose batch size of 10. For comparison reasons, we also randomly selected a subset of 43 images from the whole dataset (partially affected subset) and trained and tested the segmentation algorithm on this subset with the same setup used for nonaffected subset. Table 4 shows the performance of the algorithm against the two manual references in terms of DSC for both experiments. The average accuracy of the segmentation on the artifact-affected images based on DSC metric is slightly ($\sim 1.2\%$) dropped compared to the nonaffected images. The variation of the DSC values is also higher for the affected images. However, no statistically significant differences are detected between the DSC values measured from 43 nonaffected images and the DSC values measured from the 43 artifact-affected images, using the one-tailed $t$-test²⁹ ($P<0.05$).

Table 4.

Segmentation accuracy of the FCNN on a subset of 43 images with no imaging artifacts and a subset of 43 images that is partially affected by image artifacts. The mean and 95% confidence intervals of DSC values across the whole subsets.

Test set	Number of samples	DSC (%) (reference A)	DSC (%) (reference B)
Nonaffected data	43	78.9 [76.6, 80.7]	79.5 [77.5, 81.1]
Artifact-affected data	43	77.7 [73.7, 80.4]	78.2 [74.4, 80.8]

4. Discussion

The proposed segmentation technique is able to segment the prostate in 3-D CT image volumes in about 1 s with acceptable segmentation accuracy and high robustness to image distortion by brachytherapy seeds or metallic implants. The algorithm does not need to be trained on previously acquired CT images of the same target patient. Therefore, this segmentation method could be used when there is no previously acquired CT image available for the patient (e.g., for radiation therapy planning).

The proposed method is not a patch-based method and does not use a slice-by-slice technique. It segments the prostate fully in 3-D and takes intra- and interaxial slice information into account for segmentation. The smaller standard deviation of the DSC, in comparison to Kazemifar et al.³, which was a segmentation method based on a 2-D U-Net model, indicates that using interaxial slice information could be useful to have a more robust segmentation. The cross validation also supports this by showing segmentation results on the whole dataset (Table 3) similar to the main test results reported in Table 1. Using both manual references for training the model improved the training process. We also observed a small improvement ($\sim 1\%$ DSC) in the test results.

The maximum meaningful accuracy we could measure on our dataset was limited by the interexpert observer variability measured on the data. It means that in terms of DSC and MAD metrics the highest meaningful accuracy will be about 92% and 1.1 mm, respectively, and our algorithm ($\mathrm{DSC}=83\%$ and $\mathrm{MAD}=1.9\mathrm{mm}$) is about 9% and 0.8 mm off from “perfect” results. For prostate gland volume estimation, the proposed algorithm could achieve a segmentation accuracy ($\mathrm{\Delta }V<4.0{\mathrm{cm}}^3$) close to the observed difference between two manual references ($\mathrm{\Delta }V=2.4{\mathrm{cm}}^3$). The measured segmentation accuracy in terms of DSC, MAD, SR, and PR was lower than some of the recently published results in the literature. According to Table 4, one reason could be that the algorithm has been trained on a dataset in which more than 50% of the CT images are affected by at least one type of image distortion described above, such as brachytherapy seeds or metallic implants. However, most importantly, another explanation for our slightly lower reported results is that our models were not trained using previously acquired CT images from the test patient, unlike Refs. ⁹ and ¹⁰ (ranked the highest DSC and the lowest MAD values in Table 2). Despite the relatively low metric values for some of the test images, visual inspection showed comparable similarity between the manual segmentation and that of the algorithm (e.g., see patient #3 in Fig. 4).

It is important to interpret the results in the context of the strengths and limitations of this study. To the best of our knowledge, this work is the first to apply multiobserver training and evaluation for the prostate CT image segmentation. We reported the interexpert observer difference on the test dataset and compared the algorithm results to the observed range of the metrics in manual segmentation. We also used the complementary region-based (DSC, SR, and PR), surface-based (MAD), and volume-based ($\mathrm{\Delta }V$) error metrics to evaluate the performance of the algorithm. However, this study was limited by the small training sample size we used in this study, with 60 CT images for the main experiment (Table 1) and 69 images for the fourfold cross validation (Table 3). Data augmentation was employed to partially compensate the data size. However, some image artifacts in the test set, such as those produced by some of the metallic implants, were not seen by the network during training. Therefore, to have a more accurate and robust deep learning model, the training set must be more representative.

5. Conclusions

We developed a fast, 3-D fully convolutional deep neural network for the segmentation of the prostate on CT images, which has been demonstrated as robust to image distortions by different image artifacts caused by brachytherapy seeds, metallic fiducial markers, or metallic orthopedic implants. We have used a multiobserver training and testing approach and have evaluated the performance of our algorithm against the observed interexpert difference of manual segmentation to demonstrate the robustness and generality of the proposed method. This algorithm could be used for prostate segmentation in any study that needs to measure prostate volume from CT images. This algorithm is also useful for a quick and reliable initial segmentation to be reviewed and corrected by an expert. As future work, we will improve the performance of this neural network model by adding more levels to the deep learning structure, applying batch normalization, and optimizing the neural network hyperparameters. It is also important to evaluate the impact of the algorithm on the performance of a clinical procedure, such as radiation therapy planning.

Biographies

Maysam Shahedi is a postdoctoral research associate at the University of Texas, Dallas. He received his PhD in biomedical engineering from the University of Western Ontario, Canada. He also holds BSc and MSc degrees in electrical engineering from Isfahan University of Technology. His research interests are medical imaging, medical image processing, image-guided intervention, and machine learning.

Martin Halicek is a PhD candidate in biomedical engineering from Georgia Institute of Technology and Emory University. His PhD thesis research is supervised by Dr. Baowei Fei, who is a faculty member of Emory University and the University of Texas at Dallas. His research interests are medical imaging, biomedical optics, and machine learning. He is also an MD/PhD student from the Medical College of Georgia at Augusta University.

James Dormer is a research engineer at the University of Texas, Dallas. His research interests are using deep learning for medical applications and developing medical imaging devices.

David M. Schuster, MD, is a professor in the Department of Radiology and Imaging Sciences, Emory University, School of Medicine. He serves as a director of the Division of Nuclear Medicine and Molecular Imaging, and is a Georgia Research Alliance distinguished scientist and board certified in radiology and nuclear medicine. He specializes in molecular medicine and integrative imaging. He is a member of the Discovery and Developmental Therapeutics Research Program at Winship Cancer Institute. He is a fellow of the American College of Radiology, and holds professional memberships with Radiological Society of North America, American Roentgen Ray Society, Society of Nuclear Medicine and Molecular Imaging, and American College of Nuclear Medicine.

Baowei Fei is a professor and Cecil H. and Ida Green chair in systems biology science in the Department of Bioengineering, University of Texas (UT), Dallas. He is also a professor of radiology at UT Southwestern Medical Center. He was an associate professor with tenure at Emory University where he was a leader of the Precision Imaging: Quantitative, Molecular & Image-guided Technologies Program in the Department of Radiology and Imaging Sciences. He was recognized as a distinguished investigator by the Academy for Radiology and Biomedical Imaging Research. He was named a distinguished cancer scholar by the Georgia Cancer Coalition and the Governor of Georgia. Since 2017, he has served as a conference chair for the international conference of SPIE Medical Imaging—Image-Guided Procedures, Robotics Interventions, and Modeling. He also served as the chair for the National Institutes of Health (NIH) Study Section ZRG1 SBIB-J (56) on Imaging and Image-guided Interventions. He is a fellow of SPIE and a fellow of the American Institute for Medical and Biological Engineering (AIMBE).

Disclosures

No conflicts of interest, financial or otherwise, are declared by the authors. This study was approved by the research ethics board of our institution, and written informed consent was obtained from all patients prior to enrolment.