Bayesian Network Construction and Genotype-Phenotype Inference Using GWAS Statistics

Abstract

Genome-wide association studies (GWASs) have received an increasing attention to understand how genetic variation affects different human traits. In this paper, we study whether and to what extend exploiting the GWAS statistics can be used for inferring private information about a human individual. We first provide a method to construct a three-layered Bayesian network explicitly revealing the conditional dependency between single-nucleotide polymorphisms (SNPs) and traits from public GWAS catalog. The key challenge in building a Bayesian network from GWAS statistics is the specification of the conditional probability table of a variable with multiple parent variables. We employ the models of independence of causal influences which assume that the causal mechanism of each parent variable is mutually independent. We then formulate three inference problems based on the dependency relationship captured in the Bayesian network, namely trait inference given SNP genotype, genotype inference given trait, and trait inference given known traits, and develop efficient formulas and algorithms. Different from previous work, the possible target of these inference problems we study may be any individual, not limited to GWAS participants. Empirical evaluations show the effectiveness of our proposed methods. In summary, our work implies that meaningful information can be inferred from modeling GWAS statistics, and appropriate privacy protection mechanisms need to be developed to protect genetic privacy not only of GWAS participants but also regular individuals.

1. Introduction

GENOME-WIDE association studies (GWASs) have received intensive attention due to the rapid decrease of genotyping costs and promising potential in genetic diagnostics. GWASs typically focus on associations between single-nucleotide polymorphisms (SNPs) and human traits including common diseases. It has been shown that many common diseases such as various cancer types, have genetic disposition factors.

High-density genotyping microarrays, and recently next-generation sequencing technologies, have been utilized to identify common genetic variants that predispose an individual to diseases. Genotype data is usually classified as sensitive and should be handled by complying with specific restrictions. For example, the Health Insurance Portability and Accountability Act of 1996 (HIPAA) protects the privacy of individually identifiable health information in the USA. It was shown that only 30–80 out of 30 million SNPs are needed to uniquely identify an individual [25]. Therefore, in addition to the HIPPA privacy rule, the USA Genetic Information Nondiscrimination Act of 2008 (GINA) requires data collectors and supervisory organizations must guarantee that data analysts meet privacy restrictions, and organizations should protect against all forms of genetic discrimination from using individuals’ genetic information. Hence, genotype profiles for GWAS participants are only accessible to researchers after confidentiality agreements are signed. However, in biomedical community, there is a considerable push to make experimental data publicly available so that the data can be combined with other studies or reanalyzed by other researchers. As a result, most of the GWAS statistics and SNP-trait associations are publicly accessible. To capture such information, the GWAS catalog [47] collects and publicly releases literature-derived GWAS statistics, including pair-wise SNP-trait associations and related statistics (risk allele frequency, odds ratio, p-value, etc.).

Several studies [14], [17], [36], [37], [43], [45] have investigated how to make use of the publicly released GWAS statistics to infer an individual’s identity or other private information of GWAS participants. Homer et al. [14] developed a method to determine whether a person with known genotypes at a number of markers was part of a sample from which only allele frequencies are known. They showed that the probability a person who participated in a particular GWAS cohort can be assessed. In [45], the authors examined the use of local linkage disequilibrium structures in their inference attacks. By searching for the co-occurrence of two relatively uncommon alleles in different haplotype blocks, the authors demonstrated that individuals can actually be identified from even a relatively small set of statistics, e.g., routinely published in GWAS papers. In [36], the authors further showed that high-order single nucleotide variance correlations can be exploited to breach genomic privacy.

In this paper, we investigate a related but different problem, i.e., exploiting GWAS statistics to infer private information of unrelated regular individuals who are not participants of GWAS. To this end, we propose to construct a Bayesian network explicitly revealing the conditional dependency between SNPs and traits from the GWAS statistics. Bayesian networks have been demonstrated to be powerful for such modeling to dissect complex (e.g. gene interactions) or causal relationships between SNPs and associated traits [10], [19], [49]. However, these methods require raw genotypes of SNPs and such information is not publically available in the GWAS catalog. On the contrary, we develop a method to build a Bayesian network using only GWAS statistics for characterizing SNP-trait associations. In order to utilize the GWAS statistics, the constructed network is composed of three layers, the genotype layer, the allele layer, and the trait layer. Edges only go from an upper layer to a lower layer, and all edges among nodes within the same layer are prohibited.

The key challenge in specifying the Bayesian network is that, when the dependent variable (i.e., trait) has associations with multiple independent variables (i.e., SNPs), the Bayesian network needs to specify the conditional probability table (CPT) of the trait conditional on every value combination of its associated SNPs. However, GWAS statistics only provide the information for each trait-SNP association pair. The information about epistatic interactions among multiple SNPs that bring about joint effect on a trait is rather limited. Additionally, complex traits are commonly associated with many SNPs. Therefore, it is a combinatorial problem for specifying CPTs because the number of the conditional probability distribution values in the CPT is exponential to the number of SNPs associated with a trait.

To deal with this issue, we propose to adopt the models of independence of causal influences (ICI), a family of models which are widely used in building Bayesian networks [12], [13]. The ICI models assume that, when there are multiple parent variables, the causal mechanism of each parent variable is mutually independent. Hence, the combined influence of multiple parents is decomposable into a series of independent influence of each parent variable. Thus, an ICI model enables us to specify the CPT of a variable given its parents in terms of an associative and commutative operator on the contribution of each parent. The learning process of an ICI model generally requires raw data in order to find the parameters that make the model fit the data best [32], [44]. In this study, we investigate a scenario that the raw data (genotypes) are unknown and only GWAS statistics are available. This makes it challenging to build an ICI model for constructing a Bayesian network from only statistics. In order to do this, we derive a formulation based on the Noisy-Or model [21], one best known example of the ICI models, that can be used to specify the CPT from the released GWAS statistics where the underlying genotypes can be unknown. We prove that, the specified CPT is accurate as long as the individual-level genotype profile follows the Noisy-Or model. Then, we empirically evaluate the fitness of the Noisy-Or model to validate the proposed method.

As applications of the constructed Bayesian network, we propose three inference problems: 1) trait inference given SNP genotype that aims to infer the probability of a target developing certain traits when the target’s genotype profile is given; 2) genotype inference given trait that aims to infer the probability of a target having a certain genotype profile when some traits of the target are given; and 3) trait inference given trait that aims to infer the probability of having a new trait given known traits of the target. We study efficient inference methods to solve these problems using the constructed Bayesian network. To evaluate the derived inference methods, we simulate three scenarios accordingly. In the first scenario, we assume that an individual has taken a genetic test and wants to infer his/her probability of having some sensitive trait (e.g., disease) based on the genotype profile. For example, companies like Family Tree DNA, 23 and Me, and Ancestry offer genotyping and analyzing service for various SNPs and traits. In the second scenario, we assume that an attacker such as an outsider has access to an anonymized genotype profile database which contains the target individual’s record and aims to identify the target individual’s record from the anonymized dataset. For example, private traits and attributes of individuals can be predictable from easily accessible digital records of behavior such as Facebook Likes [22]. Other patient social networks and online communities like ‘patientlikeme.com’ provide a platform for users (mostly patients) to connect with others who have the same disease or condition and share their own experiences. Online publishing platform such as openSNP [8] also allows customers to share and publish their genotype and phenotype profiles. In the third scenario, we also assume the attacker knows some traits of the target individual, but the attacker aims to derive new traits. We evaluate how the derived inference methods perform in these scenarios, and compare with previous methods such as [16] for re-identifying users from anonymized genotype databases.

The contributions of our study are as follows. 1) We apply the classic Bayesian network approach [7], [11], [18] to build a three-layered Bayesian network from the released GWAS statistics. The constructed Bayesian network explicitly reveals the conditional dependency between SNPs and traits, and can be used to compute the probability distribution for any subset of network variables given the values or distributions for any subset of the remaining variables. 2) We formulate three inference problems based on the dependency relationship captured in the Bayesian network and develop efficient formulas and algorithms to infer the posterior probabilities. 3) We conduct empirical evaluations and the results show the effectiveness of our proposed methods, implying that meaningful private information can be inferred from public GWAS statistics on both participants and non-participants of GWAS. Our results imply that privacy protection mechanisms may need to be developed to protect genetic privacy of both GWAS participants and the general population.

2. Background

2.1. GWAS Catalog and Statistics

GWASs are usually conducted in a case-control setting, where cases are individuals with the trait under investigation and controls are matched individuals without the trait. Each individual is genotyped by microarray or sequencing platforms. Dependent on genotyping platform, the number of SNPs genotyped in a GWAS setting typically ranges from tens of thousands to tens of millions. In a GWAS framework, we assume we study biallelic SNPs. Each biallelic SNP has two possible nucleotide variations in this base position, referred to as alleles (e.g., A/G). The allele that is more frequent in the case group comparing with the control group is called the risk allele (e.g., A), and the other one is called the non-risk allele (e.g., G). Each individual carries a pair of alleles inherited from both parents and the genotype refers to the two alleles an individual has for a particular SNP. The genotype that contains two risk alleles is called the homozygote for risk allele (e.g., AA),the genotype that contains two non-risk alleles is called the homozygote for non-risk allele (e.g., GG), and the genotype that contains one risk allele and one non-risk allele is called the heterozygote (e.g., AG).

A GWAS is then to assess the difference of the frequency of alleles in the case and control groups. The typical process of a GWAS is described as follows. First, a genotype profile dataset is generated by genotyping the individuals in the case group and the control group. For each SNP, the genotype frequency is counted over the two groups to obtain a 3 × 2 contingency table, as shown in Table 1. Here, r0 denotes the number of individuals in the case group with genotype AA and so forth. Then, the genotype frequency is transformed into the allele frequency represented by a 2 × 2 contingency table as shown in Table 2. To be specific, each homozygote for risk/non-risk allele is counted as 2 copies of risk/non-risk alleles, and each heterozygote is counted as 1 risk allele and 1 non-risk allele. After that, statistical tests such as chi-square test, are performed on the allele contingency table to investigate whether there is an association between the SNP and the trait. In addition to a p-value indicating the significance of the association, the GWAS also reports odds ratios that measure the difference of frequency of an allele in the case versus control group. Specifically, the odds ratio is defined as the ratio between the proportion of individuals with a specific allele in the case group, and the proportion of individuals with the same allele in the control group. If the odds ratio is larger than 1, it indicates that the risk allele is more frequent in the case group than it is in the control group. Finally, the trait and its significantly associated SNPs are reported, along with the risk allele type and corresponding statistics (odds ratios, p-values, etc.). The GWAS catalog [47] extracts these information from literature and releases curated GWAS statistics to the public. An example of entries in the GWAS catalog is illustrated in Figure 1. It shows two records added on 1-May-15 by Kristiansen, which are extracted from the paper (Kristiansen W, 2015) experimented on 8,013 Europeans about the relationship between germ cell tumor and two SNPs. The risk allele type, risk allele frequency in controls, p-value, odds ratio, etc. are presented.

TABLE 1:

The genotype frequency

	AA	AG	GG	Total
Cases	r0	r1	r2	R
Controls	s0	s1	s2	S
Total	n0	n1	n2	N

TABLE 2:

The allele frequency

	A	G	Total
Cases	2r0+r1	r1+2r2	2R
Controls	2s0+s1	s1+2s2	2S
Total	2n0+n1	n1+2n2	2N

Fig. 1.

GWAS catalog.

2.2. Bayesian Network Revisited

Bayesian networks are widely used for reasoning under uncertainty and its representation rigorously describes probabilistic relationships among variables of interest [7], [11], [18]. A Bayesian network G = (V,E) is a Directed Acyclic Graph (DAG), where the nodes in V represent the variables and the edges in E represent the dependence relationships among the variables. The dependence/independence relationships are graphically encoded by the presence or absence of direct connections between pairs of variables. Hence a Bayesian network shows the (in) dependencies between the variables qualitatively, by means of the edges, and quantitatively, by means of conditional probability distributions which specify the relationships. In general, a Bayesian network represents the joint probability distribution by specifying a set of conditional independence assumptions together with sets of local conditional probabilities. An edge in the network represents the assertion that an variable is conditionally independent of its nondescendants in the network given its immediate predecessors. A conditional probability table is given for each variable, describing the probability distribution for that variable given the values of its immediate predecessors. Formally, for each variable X_i ∈ V, we have a family of conditional probability distributions P(X_i|Par(X_i)), where Par(X_i) represents the parent set of the variable Xi in G. From these conditional distributions we can compute the joint probability for any desired assignment of values < x₁,x₂,···,x_n > to the tuple of network variables X₁,X₂,···,X_n by the factorization formula:

$$P(x_1,x_2,\hspace{0.17em}\cdots \hspace{0.17em},x_n)=\prod _{i=1}^{n}P(x_i|Par(X_i))$$ (1)

Note the values of P(x_i|Par(X_i)) are precisely the values stored in the conditional probability table associated with variable X_i. Bayesian networks can be used to perform efficiently reasoning tasks. There are several algorithms (including exact inference methods and approximate inference methods) to compute the posterior probability for any variable given the observed values of the other variables in the graph [33].

2.3. Independence of Causal Influence

We describe the models of independence of causal influence that are widely used in building a Bayesian network. Consider a set of independent variables A = {A₁,···,A_m} and a dependent variable C. In our context, we assume C is a binary variable. The CPT P(C|A) that exhibits ICI is defined as follows. First, each independent variable A_j is connected with a hidden variable X_j, which represents the “effective value” of A_j on C. The connection between A_j and X_j can be defined via various stochastic or deterministic functions. Then, the resulting hidden variables X_js are combined using certain deterministic function f(·). Usually, in order to be a decomposable function, f(·) is required to be associative and commutative. Besides, an additional hidden variable X₀ is added to represent background knowledge, resulting a combination function X = f(X₀,X₁,···,X_m). Finally, another stochastic or deterministic function is applied to X to obtain the value of C. The structure of the general formulation of the ICI models is shown in Figure 2. In general, learning an ICI model requires the raw data for estimating parameters in the presence of hidden variables.

Fig. 2.

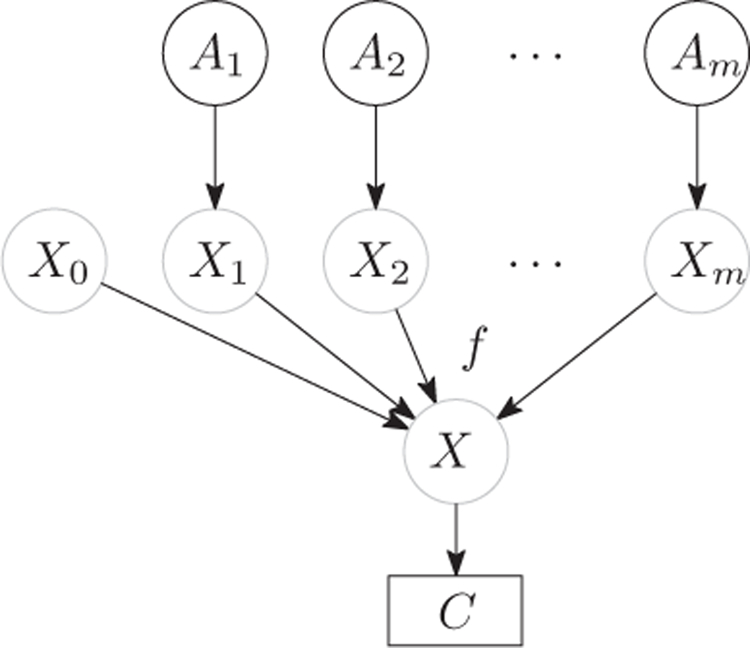
The ICI model

In the following, we introduce the Noisy-Or model, one best known example of the ICI models. The Noisy-Or model can be considered as a generalization of the deterministic Or relation since it is an ICI model where the combination function is the Or function. In this model, each hidden variable X_j is a binary variable taking values of 0 and 1. The connection between each pair of A_j and X_j is defined as the following probabilistic distribution:

$$\text{for}\hspace{0.17em}\text{each}\hspace{0.17em}j,\hspace{0.17em}P(X_j=0|A_j=a_j)=\{\begin{array}{ll}1\hfill & \text{if}\hspace{0.17em}{a}_j=0,\hfill \\ {\theta }_j(a_j)\hfill & \text{otherwise,}\hfill \end{array}$$

where θ_j(a_j) is called the noise parameter representing the probability that the presence of A_j (i.e., A_j ≠ 0) would be effective if the occurrence of C is true (i.e., C = 1). It is also defined that

$$P(X_0=0)={\theta }_0,$$

which is called a leak probability that allows C to occur when all the A_js are absent. Then, f(·) is defined as the deterministic Or function that takes all X_js as the input, i.e.,

$$f(X_0=x_0,X_1=x_1,\hspace{0.17em}\cdots \hspace{0.17em},X_m=x_m)=x_0\vee x_1\vee \hspace{0.17em}\cdots \hspace{0.17em}\vee x_m.$$

Finally, C directly takes the value of the output of f(·). Straight forwardly, C equals 0 if and only if all X_js take the value of 0. Thus, the probability of C = 0 given A = a is calculated by

$$\begin{array}{l}P(C=0|\mathbf{A}=\mathbf{a})=P(X_0=0)\prod _{j:a_j\ne 0}P(X_j=0|A_j=a_j)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}={\theta }_0\prod _{j:a_j\ne 0}{\theta }_j(a_j).\end{array}$$

By defining an indicator function

$$𝟙(a_j)=\{\begin{array}{ll}0\hfill & \text{if}\hspace{0.17em}{a}_j=0\hfill \\ 1\hfill & \text{otherwise}\hfill \end{array}$$

the above probability can be rewritten more compactly as

$$P(C=0|\mathbf{A}=\mathbf{a})={\theta }_0\prod _{j=1}^m{\theta }_j{(a_j)}^{𝟙(a_j)}.$$ (2)

To learn the Noisy-Or model, assume that we are given a dataset $\mathcal{D}=\{\cdots ,{\mathbf{d}}^l,\cdots \}$, where each tuple d^l = {c^l,a^l} represents the values of C and A. The objective function is typically formalized as maximizing the log-likelihood of the model given the observed data, i.e., ${\sum }_{l=1}^{\left|\mathfrak{D}\right|}\log P(\{C,\mathbf{A}\}={\mathbf{d}}^l)$ Following the procedure in [44], the Noisy-Or model can be learned using an EM algorithm [30]. The EM algorithm with the derived formulas is included in Appendix A of the supplementary file.

3. Construct Bayesian Network from Gwas Statistics

In this section, we elaborate how to build a three-layered Bayesian network. In general, we extract summary statistics of risk alleles from the GWAS catalog [47], build a three-layered Bayesian network from the aforementioned GWAS catalog, and prove the derived formula based on the Noisy-Or model for constructing a Bayesian network from GWAS statistics. The constructed Bayesian network, which explicitly captures the conditional dependency between SNPs and their associated traits, will be used as background knowledge for inference. Throughout this paper, we use upper-case alphabets, e.g., X, to represent a variable; bold upper-case alphabets, e.g., X, to represent a subset of variables. We use lower-case alphabets, e.g., x, to represent a value assignment of X; bold lower-case alphabets, e.g., x to represent a value assignment of X. Thus, the probability of the value assignment X = x is given by P(X = x), or simply P(x) if there is no ambiguity.

3.1. Knowledge from GWAS Catalog

We use the information publicly available from the GWAS catalog [47] to construct the Bayesian network. As illustrated in Figure 1, such information includes trait/disease name, the associated SNPs and corresponding risk allele type, the risk allele frequency in control group, and statistics (e.g., odds ratio and p-value) in the association test of each SNP. Specifically, we extract the following data from the GWAS catalog: a trait set $\mathcal{T}$, which contains m traits, and an SNP set $\mathcal{S}$, which contains n SNPs. For each specific trait $T_k\in \mathcal{T}$, we have a subset of associated SNPs S_k. For each associated SNP S_kj ∈ S_k, we can extract its corresponding risk allele type (r_kj) associated trait T_k, the odds ratio O_kj of the association test, and the risk allele frequency in the control group $f_{kj}^t(r)$.

Though not directly given in the GWAS catalog, the risk allele frequency in the case group can be derived from the corresponding odds ratio and the risk allele frequency in the control group. For an SNP S_kj associated with a trait T_k, its odds ratio is

$$O_{kj}=\frac{f_{kj}^c(r)(1-f_{kj}^t(r))}{f_{kj}^t(r)(1-f_{kj}^c(r))}.$$ (3)

With the released values of the odds ratio (O_kj) and the risk allele frequency in the control group $f_{kj}^t(r)$, the risk allele frequency in the case group $f_{kj}^c(r)$ can be derived as

$$f_{kj}^c(r)=\frac{O_{kj}\cdot f_{kj}^t(r)}{O_{kj}\cdot f_{kj}^t(r)+1-f_{kj}^t(r)}.$$ (4)

In summary, the background knowledge that an attacker can obtain from the GWAS catalog [47] includes: a trait set $\mathcal{T}$, an SNP set $\mathcal{S}$, the risk allele type (r_kj), the odds ratio O_kj, and the risk allele frequency in the control group $f_{kj}^t(r)$ and in the case group $f_{kj}^c(r)$ for each pair of trait and its associated SNPs.

3.2. Three-layered Bayesian Network Construction

To construct a Bayesian network to represent the conditional dependencies between traits and SNPs, we treat each trait $T_k\in \mathcal{T}$ as a binary random variable taking values in the set {1,0}. Here, value 1 stands for the presence of the trait of a participant and value 0 stands for the absence. For each SNP $S_j\in \mathcal{S}$, its allele and genotype are represented as two different random variables. We denote S _j’s allele by $S_j^a$ taking values in{1,0}, where 1 stands for that the SNP has the risk allele and 0 otherwise; denote S _j’s genotype by $S_j^g$ taking values in {0,1,2}, where 0 represents the homozygote for non-risk allele, 2 represents the homozygote for risk allele, and 1 represents the heterozygote. Similarly, for a set of SNPs S, the set of their alleles are denoted by S^a, and the set of their genotypes are denoted by S^g.

We construct the Bayesian network with background knowledge shown in Section 2.3. The constructed network is composed of three layers, from top to bottom, the SNP genotype layer, the SNP allele layer, and the trait layer, based on the procedure of GWAS. Edges only go from an upper layer to a lower layer, as shown in Figure 3. For each SNP S _j, two nodes $S_j^g$ and $S_j^a$ are at the top two layers respectively to denote its genotype and allele. The edge is pointing from $S_j^g$ to $S_j^a$ to represent the transformation of the genotype frequency to the allele frequency. For each trait T_k, there is a node at the bottom level of the network. If an SNP S _kj is associated with a trait T_k in the GWAS catalog, then an edge is added pointing from $S_{jk}^a$ to T_k to represent this SNP-trait pair. Under the context of GWAS catalog analysis, we cannot acquire the SNP-SNP correlation or the trait-trait association. Thus, we prohibit the edges among SNP genotype nodes, the edges among SNP allele nodes, and the edges among trait nodes.

Fig. 3.

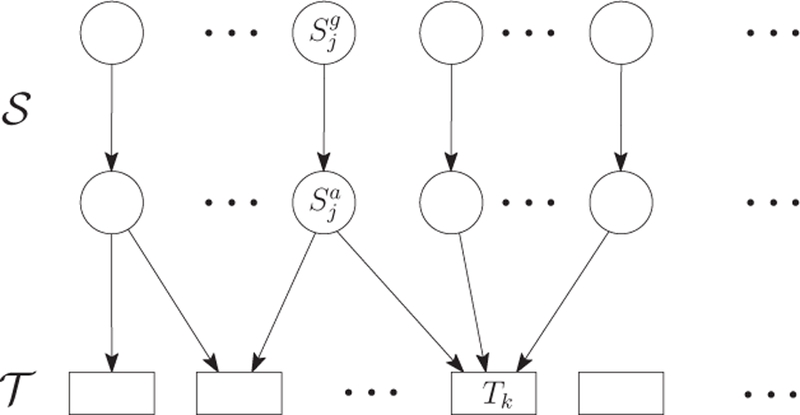
A three-layered Bayesian network of traits and associated SNPs

The next step to completely specify a Bayesian network is to determine the CPT stored at each node. We aim to accomplish all specifications by using only the background knowledge obtained from the GWAS catalog plus some prior information. Firstly, we need to acquire the prior probability $P(S_j^g)$ of each SNP genotype $S_j^g$ at the top level of the network. Since the comprehensive knowledge of the frequency of every SNP in a population is limited, we first estimate the allele prior probability $P(S_j^a)$, and then estimate $P(S_j^g)$ using the Hardy-Weinberg principle [4]. It is straightforward to estimate $P(S_j^a)$ as follows.

$$P(S_j^a=s_j)=P(S_j^a=s_j|T=0)P(T=0)+P(S_j^a=s_j|T=1)P(T=1).$$

By the Hardy-Weinberg principle, $P(S_j^g)$ is estimated as

$$P(S_j^g=s_j)=\{\begin{array}{ll}P{(S_j^g=1)}^2\hfill & s_j=2,\hfill \\ P{(S_j^g=0)}^2\hfill & s_j=0,\hfill \\ 2P(S_j^g=1)P(S_j^g=0)\hfill & s_j=1.\hfill \end{array}$$

Secondly, we need to specify the conditional probability $P(S_j^a|S_j^g)$ for each SNP, which represents how the genotype frequency is transformed into the allele frequency in GWAS. For the typical procedure as shown in Section 2.1, we can directly define $P(S_j^a|S_j^g)$ as

$$P(S_j^a=s_1|S_j^g=s_2)=\{\begin{array}{ll}1\hfill & 2s_1=s_2,\hfill \\ 0.5\hfill & s_2=1,\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}$$ (5)

Note that $P(S_j^a|S_j^g)$ typically represents the assumption of the genetic effect in the data. The definition in Equation (5) is known as the additive model, which means that 2 copies of risk alleles impose twice genetic effect of a single risk allele on the trait. Our model can be easily extend to represent other assumptions. For example, to represent the dominant model where having one or more risk alleles imposes the same increased risk compared to the homozygote for non-risk allele, we can transform the heterozygote completely into the risk allele in Equation (5).

Finally, we need to specify the CPT of each trait T_k given its associated SNPs S_k which represents the SNP-trait association. It is challenging to estimate the combined effect of multiple independent variables on a dependent variable, especially when the raw data is not available. We compute $P(T_k=0|{\mathbf{S}}_k^a={\mathbf{s}}^a)$ as given by Equation (6) which is derived from the Noisy-Or model presented in the Section 3.3. We prove that, the computation in Equation (6) is accurate as long as the genotype profile follows the Noisy-Or model.

$$P(T_k=0|{\mathbf{S}}_k^a={\mathbf{s}}^a)=\frac{P(T_k=0){\prod }_{S_{kj}\in \hspace{0.17em}{\mathbf{S}}_k}P(S_{kj}^a=s_j^a|T=0)}{{\prod }_{S_{kj}\in \hspace{0.17em}{\mathbf{S}}_k}{\sum }_{S_{kj}^g}P(S_{kj}^g)P(S_{kj}^a|S_{kj}^g)}.$$ (6)

As can be seen, the knowledge required for accomplish all above specifications only includes: 1) conditional probability P(S^a|T), and 2) prior probability P(T). The former can be estimated from the allele frequencies f^t(·) and f^c(·) according to the maximum likelihood estimate, and the latter can be acquired from literature or internet.

3.3. Modeling SNP-Trait Associations

This subsection derives the CPT specification formulation shown in Equation (6). Specifically, given a trait T and its associated SNP S, we assume that a Noisy-Or model holds for conditional probability of T given S’s genotype S^g, i.e., P(T|S^g), which will later be empirically validated using raw genotype data. This means that P(T = 0|S^g = s) can be represented as

$$P(T=0|{\mathbf{S}}^g=\mathbf{s})={\theta }_0\prod _{j=1}^m{\theta }_j{(s_j)}^{\mathrm{𝟙}(s_j)}.$$

Then, we derive Equation (6) from the obtained model.

Lemma 1. Let P(T|S^g) follow the Noisy-Or model. Then for S^g we have

$$P({\mathbf{S}}^g=\mathbf{s}|T=0)=\prod _{j=1}^{m}P(S_j^g=s_j|T=0).$$

Lemma 2. Let P(T|S^g) follows the Noisy-Or model. Then for S^a we also have

$$P({\mathbf{S}}^a=\mathbf{s}|T=0)=\prod _{j=1}^{m}P(S_j^a=s_j|T=0).$$

Please refer to Appendices B and C in the supplementary file for the proofs.

Theorem 1. Let P(T|S^g) follow the Noisy-Or model. Then we have

$$P(T=0|{\mathbf{S}}^a=\mathbf{s})=\frac{P(T=0){\prod }_{j=1}^{m}P(S_j^a=s_j|T=0)}{{\prod }_{j=1}^m{\sum }_{S_j^g}P(s_j^g)P(s_j^a|s_j^g)}.$$

Proof: It directly follows Lemma 2 that

$$\begin{array}{l}P(T=0|{\mathbf{S}}^a=\mathbf{s})=\frac{P(T=0)P({\mathbf{S}}^a=\mathbf{s}|T=0)}{P({\mathbf{S}}^a=\mathbf{s})}\\ =\frac{P(T=0){\prod }_{j=1}^{m}P(S_j^a=s_j|T=0)}{{\prod }_{j=1}^{m}P(S_j^a=s_j)}.\end{array}$$

4. Inference Based on the Constructed Bayesian Network

With the three-layered Bayesian network constructed from the GWAS catalog, we can calculate the joint probability for any desired assignment of values to variable sets S^g of SNPs S and traits T, which reflects the relationship among genotypes and traits. We first develop the general formula for any inference on the constructed Bayesian network. Then we consider three specific inference problems, namely trait inference given SNP genotype, genotype inference given trait, and trait inference given trait. Finally, we present a typical application using the derived inference methods.

4.1. General Inference Formula

Theorem 2. The joint probability for any value assignment to S^g of $\mathbf{S}\subseteq \mathcal{S},\mathbf{T}\subseteq \mathcal{T}$, i.e., P(s^g,t), is given by

$$\begin{gathered} P({\mathbf{S}}^g,\mathbf{t}) \\ =\prod _{S_j\in \hspace{0.17em}{\mathbf{S}}_1}P(s_j^g)\sum _{{\mathbf{S}}_2^a,{\mathbf{S}}_3^g,{\mathbf{S}}_3^a}\left(\prod _{S_j\in \hspace{0.17em}{\mathbf{S}}_2\cup \hspace{0.17em}{\mathbf{S}}_3}P(s_j^g)P(s_j^a|s_j^g)\prod _{T_k\in \mathbf{T}}P(t_k|Par(T_k))\right), \end{gathered}$$

where S₁ denotes the SNPs in S but not associated with T, S₂ denotes the SNPs in S and also associated with T, S₃ denotes the SNPs associated with T but not in S. Note that ${\sum }_{\mathbf{x}}f(\mathbf{x})$ means to sum up all f(x) going through all value assignments to attributes X.

Proof: The joint probability can be written as

$$P({\mathbf{s}}^g,\mathbf{t})=\sum _{{\mathbf{S}}^a,{\overline{\mathbf{s}}}^g,{\overline{\mathbf{s}}}^a,\overline{\mathbf{T}}}P({\mathbf{s}}^g,{\overline{\mathbf{s}}}^g,{\mathbf{s}}^a,{\overline{\mathbf{s}}}^a,\mathbf{t},\overline{\mathbf{t}}),$$

where $\overline{\mathbf{S}}=\mathcal{S}\backslash \mathbf{S}$ and $\overline{\mathbf{T}}=\mathcal{T}\backslash \mathbf{T}$.

According to the Markov property, the joint probability can be factorized as

$$\begin{gathered} P(\mathbf{s},\mathbf{t}) \\ =\sum _{{\mathbf{S}}^a,{\overline{\mathbf{S}}}^g,{\overline{\mathbf{S}}}^a,\overline{\mathbf{T}}}\left(\prod _{S_j\in \hspace{0.17em}\mathbf{S}\cup \hspace{0.17em}\overline{\mathbf{S}}}P(s_j^g)P(s_j^a|s_j^g)\prod _{T_k\in \mathbf{T}}P(t_k|Par(T_k))\prod _{T_l\in \overline{\mathbf{T}}}P(t_l|Par(T_l))\right), \end{gathered}$$

which follows that

$$\begin{gathered} P({\mathbf{s}}^g,\mathbf{t}) \\ =\sum _{{\mathbf{S}}^a,{\overline{\mathbf{S}}}^g,{\overline{\mathbf{S}}}^a}\left(\prod _{S_j\in \hspace{0.17em}\mathbf{S}\cup \hspace{0.17em}\overline{\mathbf{S}}}P(s_j^g)P(s_j^a|s_j^g)\prod _{T_k\in \mathbf{T}}P(t_k|Par(T_k))\sum _{\overline{\mathbf{T}}}\prod _{T_l\in \overline{\mathbf{T}}}P(t_l|Par(T_l))\right) \\ =\sum _{{\mathbf{S}}^a,{\overline{\mathbf{S}}}^g,{\overline{\mathbf{S}}}^a}\left(\prod _{S_j\in \hspace{0.17em}\mathbf{S}\cup \hspace{0.17em}\overline{\mathbf{S}}}P(s_j^g)P(s_j^a|s_j^g)\prod _{T_k\in \mathbf{T}}P(t_k|Par(T_k))\right). \end{gathered}$$

Then, we divide $\mathcal{S}$ into four disjoint subsets: S₁ denotes the SNPs in S but not associated with T, S₂ denotes the SNPs in S and also associated with T, S₃ denotes the SNPs associated with T but not in S, and S₄ denotes all the other SNPs. Thus, S = S₁∪S₂, $\overline{\mathbf{S}}={\mathbf{S}}_3\cup {\mathbf{S}}_4$, and Par(T_k) for T_k ∈ T only involves SNPs in S₂ and S₃. It follows that

$$\begin{gathered} P({\mathbf{s}}^g,\mathbf{t}) \\ =\sum _{{\mathbf{S}}^a,{\overline{\mathbf{S}}}^g,{\overline{\mathbf{S}}}^a}\left(\prod _{S_j\in \hspace{0.17em}\mathbf{S}\cup \hspace{0.17em}{\mathbf{S}}_3}P(s_j^g)P(s_j^a|s_j^g)\prod _{S_j\in {\mathbf{S}}_4}P(s_j^g)P(s_j^a|s_j^g)\prod _{T_k\in \mathbf{T}}P(t_k|Par(T_k))\right) \\ =\sum _{{\mathbf{S}}^a,{\mathbf{S}}_3^g,{\mathbf{S}}_3^a}\left(\prod _{S_j\in \hspace{0.17em}\mathbf{S}\cup \hspace{0.17em}{\mathbf{S}}_3}P(s_j^g)P(s_j^a|s_j^g)\prod _{T_k\in \mathbf{T}}P(t_k|Par(T_k))\sum _{{\mathbf{S}}_4^g,{\mathbf{S}}_4^a}\prod _{S_j\in {\mathbf{S}}_4}P(s_j^g)P(s_j^a|s_j^g)\right) \\ =\sum _{{\mathbf{S}}^a,{\mathbf{S}}_3^g,{\mathbf{S}}_3^a}\left(\prod _{S_j\in \hspace{0.17em}\mathbf{S}\cup \hspace{0.17em}{\mathbf{S}}_3}P(s_j^g)P(s_j^a|s_j^g)\prod _{T_k\in \mathbf{T}}P(t_k|Par(T_k))\right) \\ =\sum _{{\mathbf{S}}^a,{\mathbf{S}}_3^g,{\mathbf{S}}_3^a}\left(\prod _{S_j\in \hspace{0.17em}{\mathbf{S}}_2\cup \hspace{0.17em}{\mathbf{S}}_3}P(s_j^g)P(s_j^a|s_j^g)\prod _{S_j\in {\mathbf{S}}_1}P(s_j^g)P(s_j^a|s_j^g)\prod _{T_k\in \mathbf{T}}P(t_k|Par(T_k))\right) \\ =\sum _{{\mathbf{S}}_2^a,{\mathbf{S}}_3^g,{\mathbf{S}}_3^a}\left(\prod _{S_j\in \hspace{0.17em}{\mathbf{S}}_2\cup \hspace{0.17em}{\mathbf{S}}_3}P(s_j^g)P(s_j^a|s_j^g)\prod _{T_k\in \mathbf{T}}P(t_k|Par(T_k))\sum _{{\mathbf{S}}_1^a}\prod _{S_j\in {\mathbf{S}}_1}P(s_j^g)P(s_j^a|s_j^g)\right) \\ =\sum _{{\mathbf{S}}_2^a,{\mathbf{S}}_3^g,{\mathbf{S}}_3^a}\left(\prod _{S_j\in \hspace{0.17em}{\mathbf{S}}_2\cup \hspace{0.17em}{\mathbf{S}}_3}P(s_j^g)P(s_j^a|s_j^g)\prod _{T_k\in \mathbf{T}}P(t_k|Par(T_k))\prod _{S_j\in {\mathbf{S}}_1}P(s_j^g)\right) \\ =\prod _{S_j\in {\mathbf{S}}_1}P(s_j^g)\sum _{{\mathbf{S}}_2^a,{\mathbf{S}}_3^g,{\mathbf{S}}_3^a}\left(\prod _{S_j\in \hspace{0.17em}{\mathbf{S}}_2\cup \hspace{0.17em}{\mathbf{S}}_3}P(s_j^g)P(s_j^a|s_j^g)\prod _{T_k\in \mathbf{T}}P(t_k|Par(T_k))\right). \end{gathered}$$

Note that in Theorem 2, we apply marginalization to sum out ‘irrelevant’ variables so that we do not need to involve all variables in our summation to calculate P(s^g,t). As a result, the computation only involves variables in T, S₁, S₂ and S₃.

Additionally, we can calculate the conditional joint probability for any desired assignment of values to variable sets ${\mathbf{S}}_x^g$, T_x given the observed assignment of variable sets ${\mathbf{S}}_y^g$, T_y following Theorem 3. Note that ${\mathbf{S}}_x^g$ and ${\mathbf{S}}_y^g$ denote the set of SNP genotypes; while T_x, T_y denote the set of traits.

Theorem 3. The probability for any desired assignment of values ${\mathbf{s}}_x^g$, t_x to variables in ${\mathbf{S}}_x^g$, T_x given the (observed) assignment of values ${\mathbf{s}}_y^g$, t_y to variables in, T_y can be directly derived

$$P({\mathbf{s}}_x^g,{\mathbf{t}}_x|{\mathbf{s}}_y^g,{\mathbf{t}}_y)=\frac{P({\mathbf{s}}_x^g,{\mathbf{t}}_x,{\mathbf{s}}_y^g,{\mathbf{t}}_y)}{P({\mathbf{s}}_y^g,{\mathbf{t}}_y)}$$ (7)

where the joint probability $P({\mathbf{s}}_x^g,{\mathbf{t}}_x,{\mathbf{s}}_y^g,{\mathbf{t}}_y)$ and $P({\mathbf{s}}_y^g,{\mathbf{t}}_y)$ can be calculated following Lemma 2.

A given Bayesian network can be used to derive the posterior probability distribution of one or more variables in the network given the values observed for other variables in the network. Theorem 2 and Theorem 3 show the simple and brute-force formulae, which have exponential time complexity and are not computationally tractable. Researchers have developed various efficient exact inference algorithms that take advantage of independence relationships represented in a Bayesian network, and stochastic approximation algorithms to estimate exact inference results when exact inference is prohibitively time consuming [33].

4.2. Trait Inference Given SNP Genotype

We assume that we have been given the genotype profile of the target and aim to derive the probability that the target has a specific trait using the constructed Bayesian network. The probability of the prevalence of a specific trait, which is retrievable from literature or internet, is used as the prior probability that the target has the specific trait. We then calculate the posterior probability of the target having the trait by inferring from the target’s genotypes. Formally, we represent the genotypes of a target v as a vector, ${\mathbf{s}}_v^g=(s_{v1}^g,s_{v2}^g,\hspace{0.17em}\cdots \hspace{0.17em},s_{vn}^g)$, with each entry $s_{vj}^g$ denoting the genotype of SNP j.

Definition 1. The problem of trait inference given SNP genotype, aims to learn the posteriori probability $P(t|{\mathbf{s}}_v^g)$ that the target has a specific trait T given the target’s genotype profile ${\mathbf{s}}_v^g$ using the constructed Bayesian network.

The posteriori probability $P(t|{\mathbf{s}}_v^g)$ can be calculated following Equation (7), specifically with ${\mathbf{s}}_x^g=\mathrm{Ø}$, t_y = Ø, t_x = {t}, and ${\mathbf{s}}_y^g={\mathbf{s}}_v^g$. In Lemma 3, we show our simplified formula where the calculation only involves SNPs that are associated with trait T.

Lemma 3. The posteriori probability $P(t|{\mathbf{s}}_v^g)$ can be calculated as:

$$P(t|{\mathbf{s}}_v^g)=\sum _{{\mathbf{Q}}^a}\left(\prod _{S_j\in \mathbf{Q}}P(s_j^a|s_{vj}^g)P(t|{\mathbf{q}}^a)\right),$$ (8)

where Q denotes the SNPs that are associated with trait T.

Proof: Denote by Q the SNPs that are associated with trait T. We have $P(t|{\mathbf{s}}_v^g)=\frac{P(t,{\mathbf{s}}_v^g)}{P({\mathbf{s}}_v^g)}$ and apply Lemma 2 to compute $P(t|{\mathbf{s}}_v^g)$. Note that ${\mathbf{S}}_1=\overline{\mathbf{Q}}$, S₂ = Q, and S₃ = Ø. Thus, we have

$$P(t|{\mathbf{s}}_v^g)=\prod _{S_j\in \overline{\mathbf{Q}}}P({\mathbf{s}}_{vj}^g)\sum _{{\mathbf{Q}}^a}\left(\prod _{S_j\in \mathbf{Q}}P(s_{vj}^g)P(s_j^a|s_{vj}^g)P(t|{\mathbf{q}}^a)\right).$$

Therefore, it results that

$$\begin{gathered} P(t|{\mathbf{s}}_v^g)=\frac{P(t,{\mathbf{s}}_v^g)}{P({\mathbf{s}}_v^g)} \\ =\frac{{\prod }_{S_j\in \overline{\mathbf{Q}}}P(s_{vj}^g){\sum }_{{\mathbf{Q}}^a}\left({\prod }_{S_j\in \mathbf{Q}}P(s_j^g)P(s_j^a|s_{vj}^g)P(t|{\mathbf{q}}^a)\right)}{{\prod }_{S_j\in \mathbf{S}}P(s_{vj}^g)} \\ =\frac{{\prod }_{S_j\in \overline{\mathbf{Q}}}P(s_{vj}^g){\prod }_{S_j\in \mathbf{Q}}P(s_{vj}^g){\sum }_{{\mathbf{Q}}^a}\left({\prod }_{S_j\in \mathbf{Q}}P(s_j^a|s_{vj}^g)P(t|{\mathbf{q}}^a)\right)}{{\prod }_{S_j\in \mathbf{S}}P(s_{vj}^g)} \\ =\sum _{{\mathbf{Q}}^a}\left(\prod _{S_j\in \mathbf{Q}}P(s_j^a|s_{vj}^g)P(t|{\mathbf{q}}^a)\right). \end{gathered}$$

Specifically, according to Equation (6), we have

$$P(T=0|{\mathbf{s}}_v^g)=P(T=0)\sum _{{\mathbf{Q}}^a}\left(\prod _{S_j\in \mathbf{Q}}\frac{P(s_j^a|s_{vj}^g)P(s_j^a|T=0)}{{\sum }_{S_j^g}P(s_j^g)P(s_j^a|s_j^g)}\right),$$

which shows how the prior probability is updated to obtain the posteriori probability. Note that $P(T=1|{\mathbf{s}}_v^g)=1-P(T=0|{\mathbf{s}}_v^g)$ and $P(T=1|{\mathbf{s}}_v^g)$ is often of more interest to users.

Lemma 3 implies that, instead of conducting inference based on the whole Bayesian network G, we can simply identify a subgraph G′ that contains all associated SNPs of trait T, and then calculate the posterior probability following Equation (8).

Trait inference can help an individual discover the risk of having a certain disease based on his/her genotype profile. If the genotype profile of an individual has been stolen, then it introduces genetic privacy concerns since the genotype can be used to infer private trait information of the target by attackers.

4.3. Genotype Inference Given Trait

In this problem, we aim to acquire the probability that an individual has specific genotypes for a set of SNPs given his/her associated trait information, with the Bayesian network constructed. Formally, we denote by ${\mathbf{s}}_i^g=(s_{i1}^g,s_{i2}^g,\hspace{0.17em}\cdots \hspace{0.17em},s_{in}^g)$ an arbitrary genotype profile. A subset of a target’s trait T_v with its value assignment t_v is given.

Definition 2. The problem of genotype inference given trait aims to learn the posteriori probability $P({\mathbf{s}}_i^g|{\mathbf{t}}_v)$ that the target has a genotype profile given the target’s traits t_v using the constructed Bayesian network.

Lemma 4. The posterior probability $P({\mathbf{s}}_i^g|{\mathbf{t}}_v)$ is

$$\begin{gathered} P({\mathbf{s}}_i^g|{\mathbf{t}}_v) \\ =\frac{{\prod }_{S_j\in \mathbf{Q}}P(s_{ij}^g){\sum }_{{\mathbf{Q}}^a}\left({\prod }_{S_j\in \mathbf{Q}}P(s_{ij}^g)P(s_j^a|s_{ij}^g){\prod }_{T_k\in {\mathbf{T}}_v}P(t_k|Pa(T_k))\right)}{{\sum }_{{\mathbf{Q}}^g,{\mathbf{Q}}^a}\left({\prod }_{S_j\in \mathbf{Q}}P(s_j^g)P(s_j^a|s_j^g){\prod }_{T_k\in {\mathbf{T}}_v}P(t_k|Pa(T_k))\right)}, \end{gathered}$$

Where Q denotes the SNPs that are associated with traits in T_v, and $P(t_k|Pa(T_k))$ is computed according to Equation (6).

Proof: We have $P({\mathbf{s}}_i^g|{\mathbf{t}}_v)=\frac{P({\mathbf{s}}_i^g|{\mathbf{t}}_v)}{P({\mathbf{t}}_v)}$ and apply Theorem 2 to compute the probabilities. For $P({\mathbf{s}}_i^g|{\mathbf{t}}_v)$, similar to the proof to Lemma 3, we obtain

$$P({\mathbf{s}}_i^g|{\mathbf{t}}_v)=\prod _{S_j\in \mathbf{Q}}P(s_{ij}^g)\sum _{{\mathbf{Q}}^a}\left(\prod _{S_j\in \mathbf{Q}}P(s_{ij}^g)P(s_j^a|s_{ij}^g)\prod _{T_k\in {\mathbf{T}}_v}P(t_k|Pa(T_k))\right),$$

where Q denotes the SNPs that are associated with traits in T_v. For P(t_v), when applying Theorem 2, note that S = Ø and $\overline{\mathbf{S}}=\mathbf{Q}$. Thus we have

$$P({\mathbf{t}}_v)=\sum _{{\mathbf{Q}}^g,{\mathbf{Q}}^a}\left(\prod _{S_j\in \mathbf{Q}}P(s_j^g)P(s_j^a|s_j^g)\prod _{T_k\in {\mathbf{T}}_v}P(t_k|Pa(T_k))\right).$$

4.4. Trait Inference Given Trait

A straightforward extension to the above two inferences is that, we can also infer other trait information of the target individual. Assume that we are given some of the target’s traits t_v. Then Lemma 5 gives the probability that the target has a new trait T_new.

Lemma 5. The probability that the target has a new trait T_new given some of the target’s traits t_v can be derived as

$$P(t_{new}|{\mathbf{t}}_v)=\sum _{{\mathbf{Q}}^g}P(t_{new}|{\mathbf{q}}^g)P({\mathbf{q}}^g|{\mathbf{t}}_v),$$

where Q is the set of SNPs associated with t_new and t_v.

The proof is straightforward by applying the d-separation criterion [34]. We can see that P(t_new|q^g) can be derived following Lemma 3, and P(q^g|t_v) can be derived following Lemma 4.

4.5. Application: Identity Attack

We present an attack that aims to infer the probability of a record in an anonymized genotype database that belongs to a target, when some traits of the target are available. As shown in Figure 4, assume that an attacker has access to an anonymized genotype dataset $\mathcal{R}$ that contains the target’s genotype record ${\mathbf{s}}_v^g$. The attacker also knows a subset of traits t_v the target has. Then the attacker can learn the posteriori probability $P({\mathbf{s}}_i^g=={\mathbf{s}}_v^g|{\mathbf{t}}_v)$ that each genotype record ${\mathbf{s}}_i^g$ in the database corresponds to the target, as shown in Lemma 6. As a result, the attacker may be able to identify the target’s record from the anonymized dataset.

Fig. 4.

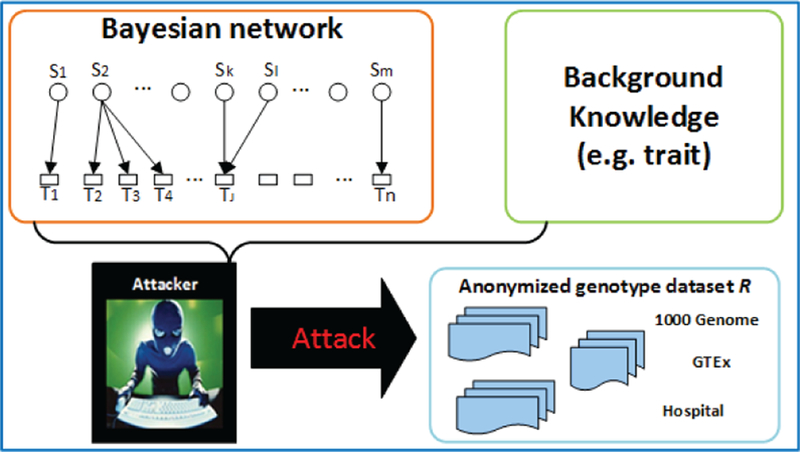
Identity attack

Lemma 6. The posteriori probability that the genotype record ${\mathbf{s}}_i^g$ corresponds to the target given his trait t_v is given by

$$P({\mathbf{s}}_i^g=={\mathbf{s}}_v^g|{\mathbf{t}}_v)=\frac{P({\mathbf{s}}_v^g|{\mathbf{t}}_v)}{{\sum }_{i=1}^{\left|\mathcal{R}\right|}P({\mathbf{s}}_i^g|{\mathbf{t}}_v)}.$$

5. Further Considerations

5.1. Dealing with SNP-SNP Correlations

In this paper we treat SNPs as they are mutually independent since the SNP-SNP correlations cannot be obtained from the GWAS catalog. However, in some situations the SNP-SNP correlations may be obtained, e.g., being provided by some biomedical studies. In this subsection, we briefly discuss how to integrate the SNPSNP correlations into our model.

When the SNP-SNP correlations are available, we assume that in addition to the allele frequency in the case and control groups, we also know the joint genotype frequency of the correlated SNPs. Then, a straightforward extension of our model can be given as follows. For two or more correlated SNPs, we cluster their corresponding nodes in the genotype layer as a single super node. The super node represents the combination of the SNP genotypes, and takes value as the cross-product of the sets of values of the genotypes. There is an edge pointing from the super node to each corresponding allele node. The clustered Bayesian network represents the same joint probability distribution as the original Bayesian network.

Figure 5 shows an example, where SNPs S₁ and S₂ are correlated. Thus, we cluster nodes $S_1^g$, $S_2^g$ as a single node $S_{1,2}^g$, i.e., $S_{1,2}^g=S_1^g\times S_2^g$ Node $S_{1,2}^g$ has two emanating edges pointing to $S_1^a$ and $S_2^a$ respectively. Denoting the value combination $(s_1^g,s_2^g)$ by $s_{1,2}^a$ according to Equation (1), the joint probability of $P(s_{1,2}^g,s_3^g,t_1,t_2)$ in the clustered Bayesian network is given by

$$\begin{array}{l}P(s_{1,2}^g,s_3^g,t_1,t_2)=\\ \sum _{S_1^a,S_2^a,S_3^a}P(s_{1,2}^g)P(s_3^g)P(s_1^a|s_{1,2}^g)P(s_2^a|s_{1,2}^g)P(s_3^a|s_3^g)P(t_1|s_1^a,s_2^a)P(t_2|s_2^a,s_3^a).\end{array}$$ (9)

In Equation (9), $P(s_{1,2}^g)=P(s_1^g,s_2^g)$ is assumed to be given representing the SNP-SNP correlation. For $P(s_1^a,s_{1,2}^g)$ (resp. $P(s_2^a,s_{1,2}^g)$), as shown in Section 3.2 it represents for SNP S₁ (resp. S₂) how the genetic effect of the genotype is obtained from the genetic effects of its two alleles, hence has no connection with other SNPs. Thus, we have and $P(s_2^a|s_{1,2}^g)=P(s_1^a|s_2^g)$. For $P(t_2|s_2^a,s_3^a)$, it can be accurately computed using Theorem 1 since $S_{1,2}^g$ and $S_3^g$ are independent. The only issue of exactly computing Equation (9) lies in the computing of $P(t_1|s_1^a,s_2^a)$. Since $P(t_1|s_1^a,s_2^a)$ can be represented as $\frac{P(t_1)}{P(s_1^a,s_2^a)}P(s_1^a,s_2^a|t_1)$, and we can easily obtain that $P(s_1^a,s_2^a)={\sum }_{S_{1,2}^g}P(s_1^a|s_1^g)P(s_2^a|s_2^g)P(s_{1,2}^g)$, we focus on the computing of $P(s_1^a,s_2^a|t_1)$.

Fig. 5.

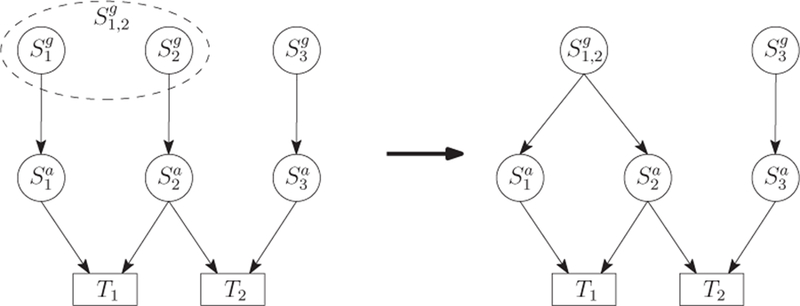
An example network where S₁ and S₂ are correlated.

If $P(s_1^a,s_2^a|t_1)$ is also given, then Equation (9) can be exactly computed. If not, we can estimate $P(s_1^a,s_2^a|t_1)$ as follows. We have

$$\begin{array}{l}P(s_1^a,s_2^a)-P(s_1^a)P(s_2^a)\\ =\sum _{T_1}P(s_1^a,s_2^a|t_1)P(t_1)-\sum _{T_1}P(s_1^a|t_1)P(t_1)\sum _{T_1}P(s_2^a|t_1)P(t_1).\end{array}$$

Usually, P(T₁ = 0) is much larger than P(T₁ = 1). Thus, by approximating $\frac{P(T_1=1)}{P(T_1=0)}$ and $\frac{P(T_1=1)}{\sqrt{P(T_1=0)}}$ as zero, it follows that

$$\begin{array}{l}P(s_1^a,s_2^a)-P(s_1^a)P(s_2^a)\\ \approx P(T_1=0)\left(P(s_1^a,s_2^a|T_1=0)-P(s_1^a|T_1=0)P(s_2^a|T_1=0)P(T_1=0)\right),\end{array}$$

which leads to

$$\begin{array}{l}P(s_1^a,s_2^a|T_1=0)\\ \approx \frac{P(s_1^a,s_2^a)-P(s_1^a)P(s_2^a)}{P(T_1=0)}+P(s_1^a|T_1=0)P(s_2^a|T_1=0)P(T_1=0).\end{array}$$

It should be noted that, the above extension cannot deal with the situation where the SNP-SNP correlations have overlaps, e.g., in Figure 5 S₂ is correlated with both S₁ and S₃ but the correlation among the three SNPs are not available. In this case, we can resort to the factor graph model [26] to represent the SNP-SNP correlations. We leave the detailed study to the future work.

5.2. Dealing with Numerical Traits

In this paper we assume that all traits are categorical. When numerical traits are involved into analysis, the variables become a mixture of discrete (SNPs and categorical traits) and continuous (numerical traits) variables, and hence cannot be handled by the traditional Bayesian network. Many research has been devoted to extend the Bayesian network to contain both discrete and continuous variables. One effort is called the Conditional Linear Gaussian (CLG) Bayesian network [23]. This subsection briefly discuss how the CLG Bayesian network can be used to deal with numerical traits.

Similar to the Bayesian network, an CLG Bayesian network also consists of an DAG. The difference is that the variables are partitioned into two sets, the set of continuous variables and the set of discrete variables. For each discrete variable, it is associated with a conditional probability distribution. For each continuous variable, there is a CLG distribution conditional on each value assignment of its parent variables. One limitation of the CLG Bayesian network is that, a discrete variable is not allowed to have continuous parents. This limitation will not affect the network construction in our case since only the traits can be continuous.

Inference in the CLG Bayesian network is well-studied, and many algorithms have been proposed in the literature (e.g., [2], [23], [28]), which can facilitate the genotype and phenotype inference in our network. To learn the CLG Bayesian network from the GWAS catalog, we can first construct the network structure and then specify the conditional probability distributions for SNPs and discrete traits similarly to Section 3.2. The next step is to specify the CLG distributions for continuous traits. We leave the detailed study to the future work.

6. Experiments

We first validate the Noisy-Or model in Section 6.1. Then we construct the Bayesian network from the GWAS catalog in Section 6.2. The inference methods and their applications are evaluated in Sections 6.3 and 6.4.

6.1. Noisy-Or Model Validation

To evaluate the fitness of the Noisy-Or model in modeling the SNP-trait association, we use raw data from openSNP [8] where more than two thousand users over the world share their genotype profiles and trait information. The genotype file contains the results of the genetic test taken by each user. Each line in the file corresponds to one SNP with its identifier (rsid), its location on the reference human genome and alleles provided. Besides, users also contribute their phenotypes to openSNP, such as what the color of their eyes, whether they have astigmatism, or whether they are suffering from irritable bowel syndrome.

6.1.1. Data Setup

In the experiments, we use openSNP of version 20151231. The genetic test results provided by users are taken from different genetic screening services. We focus on the genotyping files from 23andMe, Ancestry and FamilyTreeDNA. The data from these services account for more than 99% of the whole dataset. Among the 341 traits from the original data, there are 129 binary traits, 136 non-binary categorical traits, 39 numeric traits and 14 traits with unknown values. In align with GWAS case-control settings, we focus on the 129 binary traits to evaluate our models.

The data in openSNP is highly sparse and contains a mass of missing values due to various genetic testing platforms and varying willingness of individuals to share their traits. To ensure that the statistic tests in the model construction are meaningful, we further filter the data as follows. For each trait, we extract the individuals that belong to the control group and the case group. If the number of individuals contained in both groups for a trait is less than 10, we exclude this trait from our experiment. As a result, we obtain 71 traits satisfying the requirement. Then, following a typical GWAS procedure [42], from all associated SNPs for each trait, we remove the SNPs with:1)low minor allele frequency(i.e., <1%); 2) call rate less than 90%; and 3) the number of records containing the risk allele less than 10. After that, we discard the traits with no associated SNPs left after filtering. Finally, we obtain a dataset which contains 23 traits and 256,845 SNPs.

6.1.2. Results

To build the Bayesian network, we extract for each trait the associated SNPs along with risk allele types, risk allele frequencies and odds ratios. For each SNP, the allele frequencies in the case group and the control group and odds ratios are computed. If the odds ratio is larger than 1, the corresponding allele is considered as the risk allele. Then, we perform the Fisher’s exact test of independence to test whether the association between the trait and the SNP is significant. The threshold of the p-value is set as 4 × 10⁻⁵. We discard the traits with zero associated SNP, as well as the traits with only one associated SNP as they have no effect in testing ICI model. As a result, we obtain 7 traits and 34 associated SNPs for building the Bayesian network, as shown in Table 3.

TABLE 3:

SNP-Trait associations

Traits	SNPs	Traits	SNPs
Eye with blue halo	rs6913354	Irritable bowel syndrome	rs8039023
	rs10460585		rs2948814
Hair on fingers	rs1239925	Do you grind your teeth	rs3923767
	rs11715867		rs2531864
	rs2302025		rs2042279
ADHD	rs1496496		rs12094507
	rs4619		rs9809185
	rs7235392	Enjoy driving a car	rs2409764
	rs664510		rs12564559
	rs1910236		rs10882959
	rs6922476		rs6601522
Astigmatism	rs747644		rs1002399
	rs1466410		rs6993841
	rs11680053		rs958648
	rs12358733		rs3808513
	rs1400390		rs6601518
	rs10508470		rs357281

We then evaluate the fitness of the Noisy-Or model. For each trait, we predict the observed number of individuals with a specific trait and specific SNP genotypes, i.e., n(T,S^g), by computing the predicted value as $\widehat{n}(T,{\mathbf{S}}^g)=P(T|{\mathbf{S}}^g)n({\mathbf{S}}^g)$, where n(S^g) is the observed total number of individuals with the SNP genotypes. Since the data is highly sparse, when computing the chi-square value we only sum up the cells where n(S^g) does not equal to 0. We then compute the p-value to show the significance. The degree of freedom is computed as “total number of predictions the number of non-zero n(S^g) - the number of model parameters”. The null hypothesis H0 assumes that there is no relationship between the data and the model. Thus, the model is not rejected if p-value >0.05. In addition, we further compute the Root Mean Square Error of Approximation (RMSEA) values [27] which is an absolute measure of fit, to show the degree of the fitness. The RMSEA values are categorized into four levels: close fit (.00 .05), fair fit (.05 - .08), mediocre fit (.08-.10) and poor fit (over .10). Note that RMSEA is applicable only when the chi-square value is larger than the degree of freedom (df), and is labelled as ‘NA’ otherwise. The results are shown in Table 4. As can be seen, the Noisy-Or model is accepted for all traits according to the p-values, which indicates the model is a good fit. The values of RMSEA show a close fit in general. Therefore, we validate the use of the Noisy-Or model in modeling SNP-trait association.

TABLE 4:

The chi-square value, degree of freedom (df), p-value, RMSEA of the Noisy-or model

Trait	Chi-square	df	p-Value	RMSEA
Eye with blue halo	6.73	4	0.15	0.10
Hair on fingers	14.46	14	0.41	0.02
Irritable bowel syndrome	5.24	4	0.26	0.05
ADHD	55.32	53	0.38	0.02
Astigmatism	132.55	123	0.26	0.02
Do you grind your teeth	50.13	49	0.42	0.02
Enjoy driving a car	96.33	98	0.52	NA

6.2. Bayesian Network Construction

With the justified Noisy-Or model for constructing a Bayesian network, we set out to construct a Bayesian network captured in GWAS statistics. Specifically, we construct a Bayesian network using data extracted from the online GWAS catalog [47] as of Feb 25th, 2016. This version of the GWAS catalog includes 2,347 publications and 23,152 records (SNP-trait pairs) about 17,781 SNPs associated with 1,457 traits. Publications included in such a catalog are limited to those attempted to assay at least 100,000 SNPs in the initial stage. SNP-trait pairs listed are limited to those with p-values less than 10⁻⁵. For each record, the odds ratio or beta coefficient is provided to indicate the association of the trait-SNP pair, depending on whether the trait is categorical (e.g., some disease) or numerical (e.g., height). The two values are contained in the same field in the dataset.

In this paper, we target for categorical variables only. Thus, we focus on a subset of data published as the interactive diagram by the GWAS catalog, where an additional attribute “orType” is used to clearly indicate whether the odds ratio is provided. This subset of data includes 5,047 records with 791 traits associated with 4,250 SNPs, and SNP-trait pairs are limited to those with p-values less than 5 × 10⁻⁸. We extract the records with the odds ratio provided. As a result, we obtain 2,325 records with 266 traits associated 2,177 SNPs. Among these SNPs, there are 1,941 SNPs associated with a single trait, 122 SNPs associated with two traits, and at the most, one SNPs associated with 7 traits. Finally, we build a knowledge database for all extracted traits and associated SNPs including the risk allele type, risk allele frequency in the control group, and the odds ratio.

Based on the knowledge database, we build the Bayesian network according to Section 3.2. Particularly, to acquire the prior probability (prevalence) of each trait, we classify all the traits into 17 categories (e.g., immune system disease, nervous system disease), and retrieve the average prevalence of each category from the Wikipedia [48]. We use the average prevalence of a category as the prior probability of each trait belonging to the category. Our constructed Bayesian network can be refined by assigning the accurate prior probability for each trait when available.

6.3. Simulated Scenario: Trait Inference

We evaluate the constructed Bayesian network using two simulated scenarios. In the first scenario, we infer the probability of an individual of having a trait given his/her genotype profile using the constructed Bayesian network. We use the genotype profiles in the 1000 Genomes Project [40] and extract a dataset referred to as ‘CEU’ for our experiment. It consists of 99 HapMap individuals from Utah residents with Northern and Western European ancestry (CEU) in the 1000 Genomes Project, which are treated as targets of trait inference in this study.

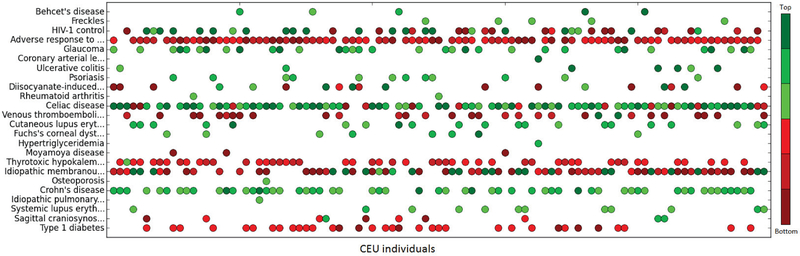
For each CEU individual v, we compute his/her posterior probability $P(T_k=1|{\mathbf{s}}_v^g)$ of having each trait T_k given the SNP genotype profile ${\mathbf{s}}_v^g$ according to Lemma 3. Then, we compute the relative difference rd between the prior probability and the posterior probability of each trait, i.e., $rd=\frac{P(T_k=1|{\mathbf{s}}_v^g)-P(T_k=1)}{P(T_k=1)}$, and rank the traits according to the rd for each individual. Figure 6 shows for top-3 and bottom-3 traits of each individual. A total of 24 traits are included as illustrated in Figure 6, each of which is represented as a row. Each column shows the top traits of an individual, where the green and red dots represent the traits with the most positive and negative rd respectively.

Fig. 6.

Top-3 and bottom-3 traits of each CEU individual

Tables 5 and 6 show the information of a snapshot of the constructed Bayesian network and the computed posterior probabilities. There are 7 traits and 9 SNPs. In Table 5, the risk allele type, risk allele in the control group and the odds ratio of each each SNP-trait pair are shown in Columns 3–5. Note that SNP rs2187668 is associated with two traits. The calculated risk allele frequency in the case group for each SNP-trait is shown in Column 6. Note that there is a big gap between the risk allele frequency in the case group and that in the control group. The prior probability (prevalence) of each trait is shown in Column 7. In Table 6, each index corresponds to the trait with the same index in Table 5. Columns ${\mathbf{s}}_v^g$ and Count respectively show the genotypes of the associated SNPs and the number of individuals who have the genotypes. As before, 0 denotes the genotype of two non-risk alleles, 2 denotes the genotype of two risk alleles, and 1 denotes the genotype of one risk allele and one non-risk allele. Column $P(t|{\mathbf{s}}_v^g)$ shows the posterior probability of one individual has a trait given his SNP genotype profile. The last column rd shows the relative difference between the prior probability and the posterior probability of each trait. As can be seen, all the posterior probabilities are significantly different from the corresponding prior probability of having a trait. In general, the posterior probability of a trait is larger if the individual has more risk alleles. Hence, the constructed Bayesian network is useful to infer new trait information. We also observe that, when there are multiple associated SNPs, the effect of each SNP can be different. For example, Trait 1 is associated with two SNPs. The posterior probability when the genotypes are (0,1) is larger than that when the genotypes are (2,0), implying that the second SNP has greater effect than the first one.

TABLE 5:

Trait-SNP association

Index	Trait	SNP-risk allele	$f_{kj}^t(r)$	Okj	$f_{kj}^c(r)$	P(tk)
1	Type 1 diabetes	rs9272346-G	0.13	8.3	0.55	0.25
		rs2647044-A	0.61	5.49	0.90
2	Behcet’s disease	rs17482078-T	0.02	4.56	0.09	0.04
3	Crohn’s disease	rs11924265-C	0.02	3.99	0.08	0.26
		rs76418789-G	0.93	2.06	0.97
		rs2066847-G	0.06	2.27	0.13
4	Fuchs’s corneal dystrophy	rs613872-G	0.15	5.47	0.49	0.09
5	Freckles	rs1805007-T	0.05	4.37	0.19	0.05
6	Celiac disease	rs2187668-T	0.26	6.23	0.68	0.26
7	Immunoglobulin A		0.13	2.53	0.27	0.05

TABLE 6:

Posterior probability of certain trait considering associated SNPs

Index	${\mathbf{s}}_v^g$	Count	$P(t|{\mathbf{s}}_v^g)$	rd	Index	${\mathbf{s}}_v^g$	Count	$P(t|{\mathbf{s}}_v^g)$	rd
1	(0,0)	28	0.149	−0.403	3	(0,2,2)	89	0.349	0.341
	(1,0)	30	0.198	−0.208		(1,2,2)	7	0.367	0.411
	(2,0)	22	0.247	−0.012		(2,2,2)	3	0.385	0.481
	(0,1)	10	0.269	0.078	4	(0)	66	0.056	−0.379
	(1,1)	6	0.311	0.245		(1)	27	0.150	0.670
	(2,1)	3	0.353	0.413		(2)	6	0.245	1.718
2	(0)	55	0.037	−0.064	5	(0)	75	0.043	−0.138
	(1)	36	0.094	1.351		(1)	23	0.104	1.076
	(2)	8	0.151	2.766		(2)	1	0.164	2.289
6	(0)	80	0.129	−0.501	7	(0)	80	0.024	−0.511
	(1)	19	0.305	0.174		(1)	19	0.108	1.162

6.4. Simulated Scenario: Identity Inference

In this scenario, we evaluate whether a target individual can be identified from an anonymized genotype database by an attacker given some traits of the target individual using the Bayesian network. For comparison we also include Humbert’s de-anonymizing method proposed in [16]. This method also aims to identify the genotypes that correspond to the given traits, making use of the single SNP-single trait correlation. The difference lies in that this method relies upon some invalidated independence assumption, whereas our method is based on the independence of causal influence, which is shown to have a good fitness in modeling the SNPtrait associations in Section 6.1. We compare the identification accuracy of the Humbert’s method to our method.

We consider the 7 trait-SNPs pairs listed in Table 7 whose odds ratios are larger than 10. The ‘CEU’ dataset is used to serve as the anonymized genotype database. To simulate an attack, we first designate a target individual whose traits t_v and genotypes are known. Then we blend the genotype profile of the target into the ‘CEU’ dataset(containing the genotype records of the 99 unrelated CEU individuals), and attempt to re-identify it assuming that the attacker only knows the target’s traits t_v. To define the target, we assume that the target has a 50% chance to have each trait, i.e., P(T_k = 1) = 0.5 for each trait T_k. We then randomly generate the genotype record for the target individual. The generating strategy is that for each SNP S _kj associated with one trait T_k, we generate $S_{kj}^g=s_{kj}^g$ with the probability $P(S_{kj}^g=s_{kj}^g|T_k)$. In this way we simulate a scenario where the target is randomly selected from the case and control groups . Finally, we calculate the probability that the generated record is correctly identified as belonging to the target individual, given the background trait information, according to Lemma 6. We also compare the identification capability with different amount of background knowledge, i.e., with the size of trait set t_v ranging from one to four.

TABLE 7:

Trait-SNP pairs

Trait	SNP-risk allele	Okj
Exfoliation glaucoma	rs893818-A	20.94
	rs3825942-G	20.1
Response to hepatitis C treatment	rs11697186-A	33.33
	rs8099917-G	27.1
	rs6139030-T	25
Blue vs. brown eyes	rs1667394-T	29.43
Skin pigmentation	rs1834640-G	12.5

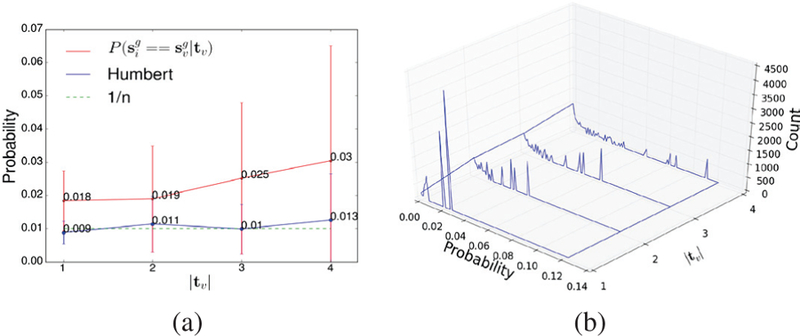
We run this whole process 10,000 times for each trait set. Figure 7a shows the average value of the resulted probabilities. As shown in Figure 7a, the green line is the baseline representing the probability 1/100 (100 = 99 ‘CEU’ individuals + 1 target) that the generated record is inferred as belonging to the target individual without any background knowledge. The blue line represents the inferred probability based on the Bayesian network, and the red line represents the inferred probability using the Humbert’s method. The first points in the blue and red lines represent the results given the value of the first trait (according to the trait index in Table 5) of the target. Similarly, the second points represent the results given both values of the first two traits of the target, and so on. The bar at each point shows the standard deviation of the resulting probabilities of 10,000 times of test. We can see that in general, the probabilities of correctly identifying the target individual of both methods increase as the background knowledge increases, and the identification probability our method is significantly larger than that of the situation without any background knowledge (i.e., 0.01). Comparing the two methods, our method consistently outperforms the Humbert’s method (the p-value of the t-test is 0.005). In addition, the identification probability given only one trait of our method is even larger than that given all four traits of the Humbert’s method, showing that our method significantly improves the identification accuracy over the Humbert’s method.

Fig. 7.

(a) Average Probability of Identification; (b) Probability Distribution of Identification

Figure 7b shows the distribution of the inference probability among the 10,000 times of identifications of our method. As the amount of background traits increases, the peaks of the process count would be located at positions with larger identifying probabilities. This indicates that in general, the more background knowledge we have, the more probably that the target individual’s record is correctly identified. On the other hand, multiple peaks in each line represent different identifying probabilities due to different combinations of background traits, as well as different possible genotype records being randomly generated.

As an alternative method of defining the target, we leverage the openSNP users as they share both of their trait and genotype profiles online. By blending the profile of an openSNP user into the ‘CEU’ dataset and re-identifying it, we evaluate the risk of privacy leak of the openSNP users although their profiles are anonymized. One issue here is that the sets of traits and SNPs contained in the GWAS catalog and those contained in openSNP are not identical. In order to perform the attack, we select the target individuals from openSNP who have reported the traits and SNPs which are also contained in the GWAS catalog. Thus, we first identify the overlapped traits and SNPs contained in both the GWAS catalog and openSNP. Among all the identified traits and SNPs, we further require that the odds ratio of the trait-SNP pair to be larger than 2 so that the effect of the SNP on the trait is significant. We have 3 traits and 7 associated SNPs satisfying the requirement, which are shown in Table 8. Then, we select the openSNP users who have reported at least one of the three traits and all the SNPs associated with the reported traits. As a result, we obtain a total of 101 openSNP users who are considered as targets in the experiment.

TABLE 8:

Trait-SNP association

Index	Trait	SNP-risk allele	$f_{kj}^t(r)$	Okj	$f_{kj}^c(r)$	P(tk)
1	Rheumatoid arthritis	rs6457617-T	0.49	2.36	0.69	0.01
		rs9275406-T	0.17	2.1	0.30
2	Hypertriglyceridemia	rs964184-G	0.14	3.28	0.35	0.30
3	Multiple sclerosis	rs3129889-G	0.2	2.97	0.43	0.01
		rs3129934-T	0.1	2.34	0.21
		rs3135388-A	0.22	2.75	0.44
		rs9271366-G	0.15	2.78	0.33

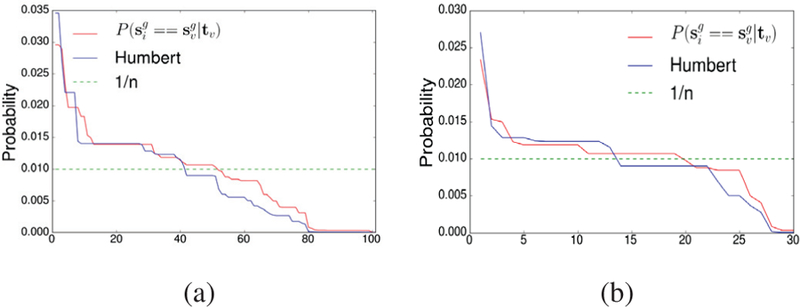
We compute the probability for each target to be correctly identified from the database. The results for all targets are shown in Figure 8a. As can be seen, nearly half (51/101 for our method and 41/101 for the Humbert’s method) of the targets have the probability of identification higher than 0.01. In this case, it shows that there is no obvious risk for openSNP users. This is probably due to the difference between the openSNP users and the population represented by the GWAS catalog. However, as shown in Figure 8b, if we confine the targets to those who have at least reported the trait of “Hypertriglyceridemia”, they have higher chances to be more accurately identified (19/30 for our method and 13/30 for the Humbert’s method). These results show that, for certain openSNP users there are higher risk of privacy leak. Under what circumstance the openSNP users may face higher risk of privacy leak is worthy of further study. Comparing the two methods, it can be seen that our method still outperforms the Humbert’s method in term of the identification accuracy.

Fig. 8.

Probability of identification: (a) all targets; (b) targets with hypertriglyceridemia

7. Related Work

The detection of SNP-trait associations by building Bayesian networks has been studied in biomedical fields, where a Bayesian network is used to address the high computationally complex and high dimensional problems. In [19] the authors used a score-based Bayesian network structure learning algorithm to detect epistasis or interactions among SNPs. In [10], the same problem is addressed by using a new information-based score and a branch-and bound search algorithm to discover the structure of the Bayesian network. As an extension to the work of [19], a recent study [49] proposed an exhaustive search on a Bayesian network to detect high order associations of SNPs with traits, without requiring marginal effects on low dimensional datasets. All of the related work aforementioned requires a raw genotype dataset to construct a Bayesian network. Our work is novel in that we build a Bayesian network from the publicly released GWAS statistics where the underlying genotypes are not publicly available.

Our previous work [46] showed that the released GWAS statistics can be used to build a two-layered Bayesian network for inference. Nonetheless, this work suffers from significant limitations. First, the constructed Bayesian network contains only the nodes representing traits and nodes representing SNP alleles. Thus, it cannot directly characterize the associations between the traits and the genotypes which are the combinations of two alleles. Second, the orientation of the arcs are pointing from trait nodes to SNP nodes, which contradicts to the fact that in GWAS researchers usually treat the traits as the dependent variables and the SNPs as the independent variables. Finally, it assumes that the SNPs are conditionally independent given the traits that they are associated with. However, this assumption has not been validated. In our work, we overcome all these limitations and study how to build an accurate Bayesian network from GWAS statistics.

Our method is based on the models of Independence of Causal Influence. ICI is proposed to overcome the problem of specifying a large number of conditional probability distributions in the CPT for a node with multiple parents in the Bayesian network. Examples of widely used ICI models include Noisy-Or, Noisy-Max, Linear-Gaussian, etc. [13]. The Noisy-Max model is equivalent to the Noisy-Or model in our situation where each hidden variable X_j is binary. The Linear-Gaussian model is proposed for modeling numeric variables. Therefore, these two models are not discussed in this paper.

Genetic privacy has also been actively studied in the literature (refer to survey papers [5], [31], [38]). For example, Homer et al. developed a method that can identify whether a target with some known SNPs comes from an population with known allele frequency[14]. It attracted more and more attention on the privacy disclosure of the public dissemination of the genotype-related data and aggregate statistics from the genome-wide association studies (GWAS) [17], [29], [36], [37], [43], [45], [51]. Another work [9] showed that full identities of personal genomes can be exposed via surname inference from recreational genetic genealogy databases followed by Internet searches. They considered a scenario in which the genomic data are available with the target’s year of birth and state of residency, two identifiers that are not protected by HIPAA. In our previous work [46], we also studied whether and to what extent the unperturbed GWAS statistics can be exploited by attackers to breach the privacy of regular individuals who are not GWAS participants. Two attacks, namely trait inference attack and identify inference attack were formalized based on the 2-layer Bayesian network inference and empirically evaluated. In [39], the authors developed a likelihood-ratio test that uses allele presence or absence responses from a Web service called beacon to derive whether a target individual genome is present in the database. In [35], the authors proposed practical strategies including obscuration and access control for reducing re-identification risks in beacons. In [16], Humbert et al. studied the use of phenotypic traits to re-identify users in anonymized genomic databases such as openSNP and demonstrated the privacy risks due to genotype-phenotype associations. The posterior probability of a set of traits given a set of SNPs is computed as a product of the conditional probability for each trait given each of its associated SNP. As shown in our experiments, our method generally has a higher identification accuracy than the Humbert’s method, although at the cost of higher computational complexity. In [15], it was proposed to build a Bayesian network to represent the genotype and phenotype dependencies among family members, so that the genotype of a family member can be inferred from the genotypes and phenotypes of his relatives. When the correlation among genotypes are considered, the factor graph are further adopted instead of the Bayesian network to represent the familial dependencies.

Several research works [6], [20] have been conducted for the safe release of aggregate GWAS statistics without compromising a participant’s privacy. Their ideas were based on differential privacy [3]. Differential privacy is defined as a paradigm of post processing the output and provides guarantees against arbitrary attacks. A differentially private algorithm provides an assurance that the output cannot be exploited by the attacker to derive whether or not any individual’s record is included. The privacy parameter controls the amount by which the distributions induced by two neighboring data sets may differ(smaller values enforce a stronger privacy guarantee). A general method for achieving differential privacy for a query f is to compute the sum of the true output and random noise generated from a Laplace distribution. The magnitude of the noise distribution is determined by the sensitivity of the query and the privacy parameter specified by the data owner. The sensitivity of a computation bounds the possible change in the computation output over any two neighboring data sets (differing at most one record). For example, the sensitivity values of chi-square statistic and p-value were derived in [6]. For those statistics with large sensitivity values (e.g., the sensitivity of odds ratio is infinity), the authors in [6] adapted the idea of releasing the most significant patterns together with their frequencies in the context of frequent pattern mining [1] to release K most significant SNPs. In [20], the authors developed distance-score based privacy preserving algorithms for computing the number and location of SNPs that are significantly associated with the trait, the significance of any statistical test between a given SNP and the trait, correlation between SNPs, and the block structure of correlations. In [41], the authors developed methods for releasing differentially private χ²-statistics in GWAS while guaranteeing membership privacy in adversarial settings [24].

8. Conclusions and Future Work

In this paper, we studied whether and to what extend exploiting public GWAS statistics can be used to infer private information about general population, not limited to GWAS participants. We first studied the construction of Bayesian networks from publicly released GWAS catalog. We employed the models of independence of causal influences (ICI) which assume that the causal mechanism of each parent variable is mutually independent. We derived a formulation from the Noisy-Or model, one of the ICI models, to specify the CPT using GWAS statistics, and developed a Bayesian Network construction algorithm based on the CPT specification formulation. We proved that, the specified CPT is accurate as long as the underlying individual-level genotype and phenotype profile data follows the Noisy-Or model. In the experiments, we empirically validated the fitness of the Noisy-Or model. Then, we developed three inference problems based on the constructed Bayesian network, namely trait inference given SNP genotype, genotype inference given trait, and trait inference given trait. We developed efficient formulas and algorithms to infer posterior probabilities. Finally, we empirically evaluated the derived inference methods for two applications. In the first application, we showed that significant amount of knowledge regarding traits can be inferred from the genotype profiles. In the second application, we showed that the probability of an individual to be identified from an anonymized genotype database is increasing given some traits of the individual. In the future work, we will develop methods to enable researchers to safely release aggregate GWAS data without compromising the anonymity of both GWAS participants and the general population.

Biographies

Lu Zhang received the BEng degree in computer science and engineering from the University of Science and Technology of China, in 2008, and the PhD degree in computer science from Nanyang Technological University in 2013. He is currently a postdoctoral researcher in the Computer Science and Computer Engineering Department, University of Arkansas. His research interests include distributed computing, fairness-aware data mining, and causal inference.

Qiuping Pan is currently pursuing the Master degree in computer science at University of Arkansas, USA. She received the B.S. degree in network engineering from Huaqiao University, China, in 2009. Her research interests include bioinformatics and genetic privacy.

Yue Wang is a Senior Software Engineer at AcuSys, Inc. She received her Ph.D. degree in Information Technology from the University of North Carolina at Charlotte in 2015 and a B. Eng degree in Computer Science from University of Science and Technology of China in 2011. Her research interest is in privacy preserving data mining, big data analysis, bioinformatics and business intelligence.

Xintao Wu is a Professor in the Department of Computer Science and Computer Engineering at the University of Arkansas. He held a faculty position at the College of Computing and Informatics at the University of North Carolina at Charlotte from 2001 to 2014. He got his Ph.D. degree in Information Technology from George Mason University in 2001. He received his BS degree in Information Science from the University of Science and Technology of China in 1994, an ME degree in Computer Engineering from the Chinese Academy of Space Technology in 1997. His major research interests include data mining and knowledge discovery, bioinformatics, data privacy and security.

Xinghua Shi is an assistant professor in the Department of Bioinformatics and Genomics, College of Computing and Informatics, University of North Carolina at Charlotte. Before joining UNC Charlotte in 2013, she was a postdoctoral research fellow at Brigham and Women’s Hospital and Harvard Medical School (2009–2012). She received her Ph.D. (2008) and M.S. (2003) degrees in Computer Science from the University of Chicago, and M.Eng (2001) and B. Eng (1998) degrees in Computer Science from Beijing Institute of Technology, China. Her research interest is in bioinformatics, genetic privacy, network science, and big data analytics in biomedical research.