Marand et al. use a high-resolution recombination map to dissect the genetic components of yield in diploid potato. Regions of recalcitrant heterozygosity in the inbred parent co-localized with elevated recombination rates, signatures of selection, and tissue-specific gene expression...
Keywords: yield, epistasis, QTL, heterozygosity, sequencing, potato, outcrossed
Abstract
Deconvolution of the genetic architecture underlying yield is critical for understanding bases of genetic gain in species of agronomic importance. To dissect the genetic components of yield in potato, we adopted a reference-based recombination map composed of four segregating alleles from an interspecific pseudotestcross F1 potato population (n = 90). Approximately 1.5 million short nucleotide variants were utilized during map construction, resulting in unprecedented resolution for an F1 population, estimated by a median bin length of 146 kb and 11 genes per bin. Regression models uncovered 14 quantitative trait loci (QTL) underpinning yield, average tuber weight, and tubers produced per plant in a population exhibiting a striking 332% average midparent-value heterosis. Nearly 80% of yield-associated QTL were epistatic, and contained between 0 and 44 annotated genes. We found that approximately one-half of epistatic QTL overlap regions of residual heterozygosity identified in the inbred parental parent (M6). Genomic regions recalcitrant to inbreeding were associated with an increased density of genes, many of which demonstrated signatures of selection and floral tissue specificity. Dissection of the genome-wide additive and dominance values for yield and yield components indicated a widespread prevalence of dominance contributions in this population, enriched at QTL and regions of residual heterozygosity. Finally, the effects of short nucleotide variants and patterns of gene expression were determined for all genes underlying yield-associated QTL, exposing several promising candidate genes for future investigation.
YIELD is regarded as the most important agricultural trait in efforts to breed superior crops. Owing to its multifaceted nature, genetic dissection of the fine-scale architecture controlling yield has remained a challenge in most agriculturally relevant species. For example, in rice, yield is a manifestation of individual yield components such as panicle number, grains per panicle, and grain weight [reviewed in Xing and Zhang (2010) and Jeon et al. (2011)]. Each yield component can be further deconstructed into a finer grid of quantitative measurements. For instance, rice grain weight is largely determined by the relative height, width, depth, and density of each individual grain (Xing and Zhang 2010). Considering that most yield components are quantitative in nature, the number of genetic elements controlling each of these individual traits can range from one to thousands comprising an intricate network (Lippman and Zamir 2007; Xing and Zhang 2010; Yan et al. 2011). Individually, each gene or genetic element is likely to have a small effect on yield, but collectively, these loci can account for a substantial proportion of phenotypic variation (Mackay 2009). Yield quantitative trait loci (QTL) represent genomic regions with statistically significant effects on yield as a result of segregating alleles. A limiting factor in the detection of QTL is the power of the population to detect small-effect loci, which depends on population characteristics such as size and structure. Indeed, QTL mapping from multiple segregating pig and dairy populations were shown to bias for fewer, large-effect QTL (Hayes and Goddard 2001). This is in part due to overly stringent detection thresholds precluding the identification of anything other than large-effect regions (Zeng 1994). The contributions of QTL to yield variation are also strongly influenced by the genetic background and environment, further restricting the identification of QTL to those with large effects (Xing and Zhang 2010). Another important consideration is the degree of recombination and the density of markers composing a genetic map. The effective resolution of a genetic map—or how precise QTL can be demarcated—is directly determined by the number recombination events and the density of markers surrounding breakpoints (Zeng 1994).
Introgression of novel QTL into existing germplasm provides an important basis to improve crop production. Traditionally, the improvement of plants and animals through breeding required the identification and selection of genetically superior individuals in segregating populations. In potato breeding, selection was carried out in open-pollinated populations until the 20th century. Most seedlings were likely products of self-pollination, as the majority of potato cultivars are self-compatible autotetraploids. Contemporary breeding is carried out using controlled crosses between superior heterozygous tetraploid clones followed by phenotypic selection across sequential asexual generations (Jansky 2018). Clonal propagation improves selection accuracy but limits opportunities for recombination, a process central to purifying deleterious alleles. This has important consequences for both the development of improved cultivars and the mapping of agronomically important traits.
Potato yield is typically measured as the total weight of tubers harvested from a given growing area, such as pounds per hectare. Potato cultivars developed over the last century in North America produce similar yields under modern field management practices, indicating minimal genetic gains in yield after several decades of breeding and selection (Douches et al. 1996). The absence of marked genetic gain has been largely attributed to the complex genetics associated with autotetraploid potato, such as high heterozygosity, genetic load, and severe inbreeding depression (Douches et al. 1996; Hirsch et al. 2013). As a result, the autotetraploid nature of potato has impeded the dissection of the genetic components underlying yield compared to diploid crop species (Douches et al. 1996; Hirsch et al. 2013). To overcome these obstacles, recent trends have seen the adoption of diploid breeding schemes for the production of mapping populations in potato (Jansky et al. 2016). Since most diploid potatoes are self-incompatible, numerous studies have developed segregating outcross populations by mating two heterozygous dihaploids (2n = 2x = 24) derived from cultivated potato (Hutten et al. 1995; Śliwka et al. 2017; Manrique-Carpintero et al. 2018). Alternate population structures, such as testcross populations, have also been realized by utilizing crosses between heterozygous material and inbred wild potato species—which contain alleles for self-compatibility—or a synthetic doubled monoploid (DM) that suffers from severe inbreeding depression (Hosaka and Hanneman 1998; Felcher et al. 2012; Manrique-Carpintero et al. 2015). Several diploid potato populations have demonstrated the utility of genome reduction for identifying QTL for yield and other tuber traits (Lindqvist-Kreuze et al. 2015; Manrique-Carpintero et al. 2015, 2018; Hara-Skrzypiec et al. 2018). However, genotyping uncertainties and coarse genetic maps hampered past efforts to clearly define discrete genomic intervals underlying important agronomic traits. In cereal crops such as rice and maize, these challenges have been addressed by the adoption of sequencing-based genotyping (Huang et al. 2009; Yu et al. 2011; Li et al. 2015; Su et al. 2017). These methods have demonstrated remarkable accuracy and utility for QTL mapping. However, implementation of sequencing-based genetic maps for populations derived from outbred crosses has lagged behind.
Outcrossed populations offer several salient advantages over traditional inbred line-based strategies in biparental crosses. First, the presence of two additional alleles allows for greater allelic diversity, potentially revealing trait-associated loci that may be lost during parental inbreeding. Small-effect loci may be particularly affected, as selection during inbred line generation may bias toward large-effect regions and result in the unintentional loss of less significant contributors. Second, outcrossed populations inherently contain greater levels of observable recombination (Solberg Woods 2014). Recombination (for the purpose of QTL mapping) within inbred line populations cannot be observed until the F2 generation, as recombination events between homologous chromosomes in the inbred parents are invisible without distinguishing molecular markers. In mice, QTL resolution of F2 intercross or backcross populations is typically in the order of 40–60 Mb, a stark comparison to the average of ∼1 Mb in outbred mice from the Collaborative Cross (Churchill et al. 2004; Valdar et al. 2006; Durrant et al. 2011). Third, outbred populations provide an opportunity to combine multiple genetic backgrounds. Such increased genetic diversity diminishes the role of genetic background, aiding the identification of QTL present across multiple haplotypes. Outcrossed populations also gain the benefit of increased genetic and phenotypic variability, allowing investigation of a wide array of traits in comparison to traditional F2 populations derived from inbred parents on the basis of single-trait divergence. However, the use of low marker densities and the lack of existing methods to resolve highly accurate haplotypes is a current bottleneck for the precise determination of complex trait QTL.
In the present study, we utilized whole-genome resequencing of a pseudotestcross diploid potato population derived from two widely divergent genetic backgrounds. Integration of maternal and paternal reference-based haplotype recombination maps afforded unparalleled resolution, validated via simulations and empirical mapping of a well-known maturity gene to a physical interval of 250 kb. Application of this map to potato yield and its components uncovered widespread epistatic QTL, and elevated relative dominance overlapping regions of residual heterozygosity. Collectively, our analysis provides novel insight into the genetic, and transcriptional, architecture of residual heterozygosity and yield-associated QTL at an unprecedented resolution in potato.
Materials and Methods
Plant material and phenotypic data curation
Two diploid potato clones, US-W4 and M6 (ABxCD), were crossed to create a population of 90 F1 individuals. This population was planted in the plain field loamy sand soil at the University of Wisconsin Hancock Agricultural Research Station, Hancock, WI for four consecutive years (2014–2017) using a randomized complete block design, with three replicates for each genotype plot and five hills (plants) per plot at 30-cm spacing. Rows were separated by 90 cm. A single Red Norland seed tuber was placed 60 cm from either end of a plot for the final 3 years to separate plots and to allow for simplified collection of tubers during harvest. All plots were planted across all years in the first week of May. Height was measured (from stem base to the highest point) on each plant weekly throughout the growing season. Height data were analyzed as a function of days after planting and based on the median value among all five plants within a plot. Yield was determined following hand harvesting as the total weight of all tubers within a plot. Tuber number reflects the total number of tubers collected from a single plot. Average tuber weight was determined by dividing the total weight by the tuber number for each plot. Yield, average tuber weight, and tuber number data were evaluated ∼120–133 days after planting.
Construction of a four-allele recombination haplotype map
To construct the recombination map of the inbred parent M6, short nucleotide variants (SNVs) heterozygous in M6 and homozygous in US-W4 were selected from an initial set of 3.9 million SNVs. To remove false-positive variants, SNVs demonstrating low levels of linkage disequilibrium (LD) with nearby markers were removed. To this end, we estimated local r2 values for each SNV using the nearest 100 SNVs. Local r2 values were taken as the average r2 value across the 100 comparisons, filtering SNVs with mean r2 values < 0.1. The remaining markers were used as input for phaseLD (flags set: -q) (Marand et al. 2017). Following haplotype reconstruction of M6, we merged the haplotype maps from US-W4 (AB) and M6 (CD), producing a four-allele (ABCD) recombination map where each bin was separated by a single recombination event stemming from either parent.
Identification of residual heterozygosity
A bimodal distribution of local LD r2 values was observed across all chromosomes, suggesting a mixture of false-positive and true heterozygous M6-specific SNVs. Reasoning that heterozygous SNVs should segregate together, we implemented a two-state hidden Markov model (HMM) to redefine homozygous and heterozygous M6 SNVs using the R package, depmixS4 (Visser and Speekenbrink 2010). Specifically, SNV r2 values were used as input to build an unsupervised HMM model separately for each chromosome. Posterior probabilities for each state (heterozygous and homozygous) at a particular SNV were then estimated from the fitted models. To define broader domains exhibiting residual heterozygosity, the genome was parsed into 10-kb windows, shifting at 2.5-kb intervals using BEDtools (Quinlan and Hall 2010). A 10-kb window size was selected to optimize resolution based on the average SNV density in this data set (227,530 M6-specific SNVs per 725 Mb = 3.14 SNVs per 10 kb). We then counted the occurrence of HMM-defined heterozygous SNVs within each 10-kb window, merging overlapping windows containing at least one heterozygous SNV. It is important to note that defining larger windows will result in fewer heterozygous regions that span relatively larger domains. The use of a sliding window also has a smoothing effect that provides an opportunity to merge overlapping windows with similar features, minimizing the effects of sampling errors and ascertainment bias.
Overlap analysis using permutations
Monte Carlo simulations were used to construct null distributions for comparison to parameters of interest. As an example, to test for an association between gene density and the occurrence of residual heterozygosity (n = 23 regions), we first collected 23 random regions of the genome (excluding regions of residual heterozygosity and gaps in the reference assembly) matched with the same length distribution as regions of residual heterozygosity. Then, the average density of protein coding genes within these 23 random sites was estimated by defining overlap as coordinates that intersect by at least 1 bp using BEDtools (Quinlan and Hall 2010). To build a distribution of random gene densities, the process of identifying 23 random matched regions and estimating their gene densities was repeated (permuted) 10,000 times. Thus, the empirical P-value was determined as the fraction of permutations with gene densities greater than or equal to the gene density of residual heterozygous regions. We also applied this general approach to determine the significance of overlap between genes under selection or QTL with regions of residual heterozygosity that were greater than expected by chance.
Gene ontology term enrichment
Gene ontology (GO) enrichment tests were performed assuming a hypergeometric distribution using the software agriGO (Tian et al. 2017). The false discovery rate (FDR) was controlled using the Benjamini–Hochberg P-value correction, with FDR < 0.05 considered significant. Due to a lack of power from low sample size, blocks with < 50 genes were excluded from the analysis of individual blocks. However, these genes were included when assessing GO enrichment across all heterozygous regions. Only molecular function ontologies were considered during the analysis.
RNA-sequencing analysis of residual heterozygosity
RNA-sequencing (RNA-seq) data derived from M6 tissues were acquired from a previous study (Leisner et al. 2018). Raw RNA-seq reads were quality (-q 20) and adapter trimmed using cutadapt (Martin 2011). Trimmed reads were aligned using HISAT2 (Pertea et al. 2016), allowing for an intron size of 15,000 bp in parallel with known gene annotation coordinates (Potato Genome Sequencing Consortium et al. 2011) to the DM v4.04 reference genome (Hardigan et al. 2016), keeping the remaining parameters default. Alignments were conducted using a single-end read mode and only considering forward reads for libraries constructed using paired-end chemistry. Raw counts per transcript were developed using HTSeq count with default parameters (Anders et al. 2015). Raw counts were then converted to reads per kilobase by accounting for transcript length, adjusting by the total reads per kilobase for each tissue, and finally scaling the sum across genes to 1 M, yielding transcripts per million (TPM) (Li et al. 2010).
Analysis of phenotypic data
Best linear unbiased predictors (BLUPs) for tuber number, average tuber weight, and yield were calculated as the predictions of genotypic effects from the model (Equation 1):
| (1) |
where is the phenotype of the clone i, grown in year j, in block k; represents the effect of the clone i; is the effect of the year j; is the interaction between clone i and year j; represents the effect of the block k in the year j; and is an independent and identically distributed error term.
The year and block terms were treated as fixed, while clone was treated as a random effect. Plant height, measured longitudinally within each year, was modeled using a random regression model (Equation 2).
| (2) |
Equation 2 includes all the same terms as listed above (Equation 1) as well as linear, quadratic, and cubic fixed effects for days after planting , and a random slope term for each clone . The in Equation 2 has a heterogeneous first-order autocorrelation structure with a continuous time variable, allowing different variances for each time point and correlated residuals within each clone.
Model selection was performed using Akaike information criterion (AIC) and visual assessment of model assumptions. Broad-sense heritability values for each trait were derived using the BLUP genotypic effects (Equation 3) (Bernardo 2014).
| (3) |
where are the estimated genotypic, genotype by year, and residual variances, l is the number of years, and r is the number of blocks.
Clones were clustered into two groups using k-means clustering on the predicted slope and intercept terms from random regression models, which represent predicted genotypic effects in the middle of the growing season and differential growth rates for each genotype, respectively. The resulting clusters corresponded with the two distinct growth habits. All random regression models were fitted with the lme() function in the R package nlme (Pinheiro et al. 2018). Significance tests for midparent heterosis were estimated using the average yield BLUPs across all clones against the null hypothesis of 0% heterosis in yield with Welch’s t-test (unequal variance).
Power and precision simulations
Simulations to determine the power and precision of our reference-based haplotype recombination map were carried out using R/qtl (Arends et al. 2010). Phenotypic heritability was allowed to range from 0.05 to 0.95 for a single fixed-position additive QTL. We further allowed the size of the population to range from 20 to 200 individuals. Power was defined as the proportion of simulations where the QTL was detected, while precision was estimated as the proportion of simulations capturing the precise bin with the designated QTL.
QTL mapping
QTL mapping was conducted using the BLUPs from yield, average tuber weight, tuber number, cluster affiliation for growth type (group), and the random slope and intercept predictions for plant height as response variables. QTL mapping was performed by fitting a single multiple linear model to each recombination bin containing a term for the US-W4 allele, the M6 allele, and their interaction. For bins where one parent was not segregating, that parent and the interaction dropped from the model, as those coefficients went to zero. P-values and F-statistics for the model overall, each parental haplotype effect, and the interaction between parental haplotypes (when applicable) were recorded for each bin. Significance thresholds (α = 0.05) for single-QTL scans were estimated by 1000 permutations. LOD scores were calculated using F-statistics derived from the multiple linear regression models (Equation 4) (Broman and Sen 2009):
| (4) |
where is the number of haplotypes ( for an intercross).
LOD scores were then used to estimate the percent variance explained (PVE) (Equation 5):
| (5) |
QTL mapping using covariates was performed in R/qtl with cross type coded as a “4way.” The function “scanone” with slopes from random regression models used as additive covariates was used for single-marker regression analysis. Two-dimensional scans for interacting and additive QTL were performed using the function “scantwo,” again with the slopes from random regression models specified as additive covariates, using single-marker regression. One-thousand permutations per trait were carried out using identical model parameters as for QTL detection, set to an α of 0.05 for single-QTL mapping and an α of 0.1 for two-dimensional scans. Additive and dominance values for each haplotype combination were estimated following a published method (Da 2015). To ease visualization, we define relative dominance as the log2 transformed ratio of dominance to additive values with correction (Equation 6).
| (6) |
Where and are the dominance and additive values for the genotype with haplotypes and .
Fine-scale genetic dissection of tuber number and weight QTL
Phased SNVs overlapping QTL bins were assessed for potential effects using snpEff (Cingolani et al. 2012) and the DM v4.03 gene annotation (Potato Genome Sequencing Consortium et al. 2011). Counts of various polymorphism effects were scaled from zero to one for each effect type. Expression values [reads per kilobase of exon model per million mapped reads (FPKM)] for various tissue types and treatments were obtained from the potato genome public repository (Potato Genome Sequencing Consortium et al. 2011). Gene expression data were first converted to TPM by normalizing FPKM values by the total FPKM in each tissue. For heatmap plots, TPM values were normalized by centering to zero.
Data availability
The software used to generate phased haplotypes is freely available in the software package phaseLD (https://github.com/plantformatics/phaseLD). Haplotype bins, phenotypes, and scripts for QTL mapping can be found on GitHub at the following open access repository (https://github.com/joegage/diploid_potato_qtl_mapping). Raw sequencing data for the F1 population and parental genotypes can be found under BioProject number PRJNA356643. All supplemental figures and tables are available on figshare in files Figures_S1-12.pdf and Supplemental_Tables.xls. Supplemental material available at https://doi.org/10.25386/genetics.7312142.
Results
Development of a maternal reference-based haplotype recombination map
We previously performed an interspecific cross between US-W4, a heterozygous Solanum tuberosum group Tuberosum dihaploid clone (2n = 2x = 24), and M6, a seventh-generation inbred of the wild diploid S. chacoense species (2n = 2x = 24) (Jansky et al. 2014) to construct a pseudoone-way testcross population consisting of 90 F1 individuals (Marand et al. 2017). The F1 population was genotyped using whole-genome resequencing (∼2× coverage per individual), resulting in the identification of ∼3.9 million (M) SNPs and insertion/deletions (SNVs). A subset of segregating markers (∼1.3 M) were identified as heterozygous in the maternal parent, US-W4. These markers were subsequently utilized to produce a maternal reference-based haplotype recombination map with a median crossover breakpoint resolution of 880 bp and a total of 1055 recombinations (Marand et al. 2017).
Haplotype reconstruction of the inbred paternal diploid clone M6
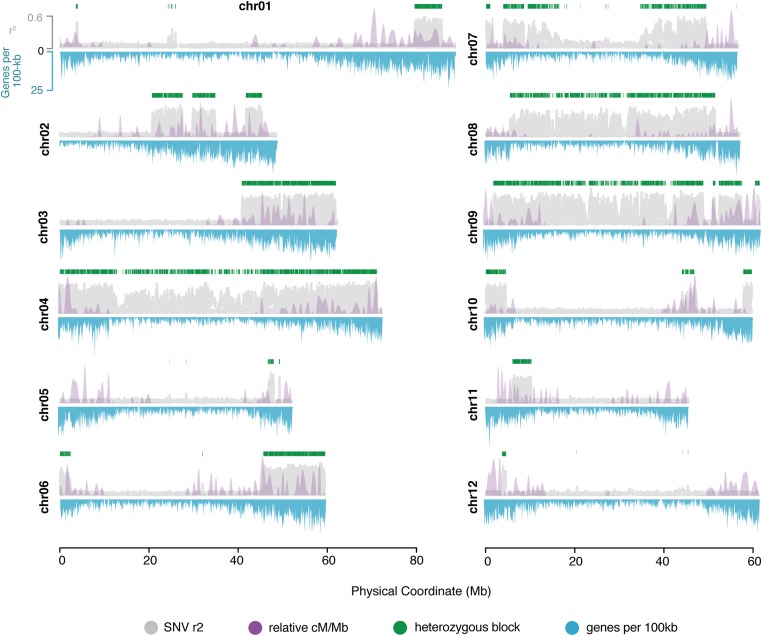
A recent report revealed residual heterozygosity in our inbred paternal parent M6 (Leisner et al. 2018). We aimed to leverage this residual heterozygosity to identify paternal segregating haplotypes. Conditioning on SNVs in the F1 population that were heterozygous in M6 and homozygous in US-W4 revealed a total of 227,530 M6-specific SNVs. To remove artifactual SNVs and determine regions of residual heterozygosity, we estimated the local LD for each SNV by averaging r2 values from estimates with 100 flanking SNVs. We identified a total of 144,245 M6-specific SNVs delimiting whole-chromosome-level residual heterozygosity for chromosomes 4, 7, 8, and 9, consistent with the previous report (Figure 1) (Leisner et al. 2018). In addition, this approach uncovered the presence of several short blocks of recalcitrant heterozygosity that may have been previously overlooked (Figure 1). To uncover the patterns of paternal haplotype inheritance, we used the 144,245 M6-specific SNVs as input for the LD-based haplotyping method, phaseLD (Marand et al. 2017), resulting in a total of 650 uniquely segregating haplotype bins (Supplemental Material, Figure S1).
Figure 1.
Recalcitrant residual heterozygous SNVs in a seven-generation inbred. Genome-wide map of local LD based on the mean r2 centered on windows of 100 SNVs (gray) and the coincidence of elevated recombination rates (relative recombination rates, purple overlay). Top y-axis, average r2 per marker. Bottom y-axis, genes per 100 kb (blue). Green blocks, regions with elevated LD, heterozygous blocks in M6. chr, chromosome; LD, linkage disequilibrium; SNV, short nucleotide variant.
Residual heterozygosity coincides with elevated gene density, recombination rate, and functional annotations suggestive of gametic selection
The widespread prevalence of residual heterozygosity in M6 may play a key role in distributing phenotypic variation in our progeny. Because chromosomes 4, 7, 8, and 9 were almost entirely heterozygous, we focused on characterizing the shorter heterozygous blocks embedded within homozygous regions on the remaining chromosomes. These heterozygous blocks (n = 23) spanned ∼11% (76.8/725 Mb) of the potato genome, with a median block length of 1300 kb (range: 17–21,000 kb) (Table S1). Unlike chromosome-level heterozygosity, these short regions overlapped regions with increased recombination rates relative to the genome-wide average (Wilcoxon rank sum test; P < 4.8e−10), leading us to posit that recalcitrant heterozygosity over short blocks is likely associated with selective forces rather than inefficient purification mediated by the absence of recombination (Figure 1).
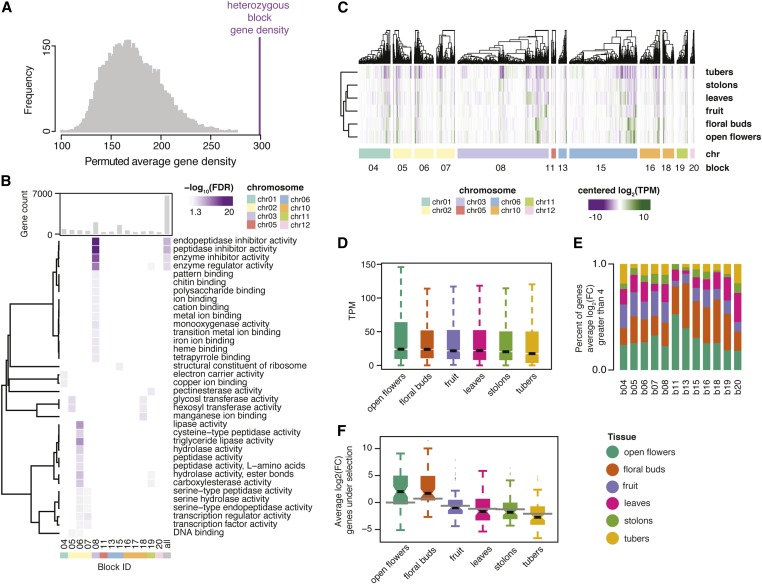
Characterization of the genetic composition underlying heterozygous regions revealed a total of 6878 genes, providing a mean of 299 genes per block (range: 0–1920). Comparison with 10,000 random permutations of the same number and length (excluding assembly gaps) as heterozygous blocks uncovered a significant association between recalcitrant heterozygosity and elevated gene density (empirical; P < 1.0e−4) (Figure 2A). Considering a twofold overall enrichment of genes at heterozygous blocks (heterozygous blocks = 90 genes Mb−1, genome-wide = 51 genes Mb−1), we were interested to determine if regions of residual heterozygosity harbor genes with distinct functional annotations. Focusing on GO annotations for blocks with sufficient power for discovery (number genes ≥ 50), we found that terms related to peptidase, transferase, and transcription factor activity were prevalent across multiple heterozygous blocks (Figure 2B). Functional characterization of peptidases has highlighted roles in reproductive development, including embryogenesis, pollen development, and gametophyte survival [reviewed in van der Hoorn (2008)], suggesting that persistent heterozygosity may be associated with the production of functional gametes.
Figure 2.
Recalcitrant heterozygosity is associated with increased gene density and floral-specific gene expression in potato. (A) Permuted distribution (10,000×) of gene density from random regions (gray) compared with gene density of heterozygous blocks (purple line). (B) Heatmap of significant GO terms enriched within the heterozygous blocks in M6. Nonsignificant terms are colored as white squares, while significant terms [−log10 (FDR) > 1.3] range in color from gray to dark purple. (C) Hierarchically clustered heatmap of centered gene expression values (log2 TPM) across six different tissues at heterozygous blocks. (D) Distribution of gene expression values across six different tissues for genes underlying heterozygous blocks. (E) Distribution of tissue-specific gene expression for genes transcribed in distinct tissue types for individual heterozygous blocks. (F) Average log2 (FC) for genes under selection. The gray bar over each boxplot represents the average log2 (FC) for all genes. chr, chromosome; FC, fold change; FDR, false discovery rate; GO, gene ontology; ID, identifier; TPM, transcripts per million.
Patterns of gene expression and selection underlie regions of recalcitrant heterozygosity
We further posited that genes within heterozygous blocks may demonstrate patterns of tissue-specific expression. Approximately 81% of genes (5594/6878) within heterozygous blocks were expressed (TPM ≥ 1) in at least one tissue type (tubers, stolons, leaves, fruit, floral buds, and open flowers) derived from the paternal inbred parent M6. Generally, genes underscoring heterozygous blocks were expressed at greater levels in floral tissues (floral buds and open flowers) (Figure 2, C and D and Figure S2). To gain insight into tissue-specific expression, we estimated the average log2 fold change for each gene across tissue types and defined tissue specificity as genes with an average log2 fold change > 4 in a single tissue (Figure S3A). Interestingly, 12% (685/5594) of expressed genes within heterozygous blocks exhibited tissue-specific expression, 63% of which were overrepresented within floral and fruit tissues consistently across heterozygous blocks (Figure 2E and Figure S3, B and C).
Positing a potential relationship between residual heterozygosity and targets of selection, we scanned published data sets of genes demonstrating signatures of selection in potato (Hardigan et al. 2017). Remarkably, genes under selection (20%, 509/2622) were highly enriched within M6 heterozygous blocks (empirical, 10,000 permutations; P < 1.0e−4). Conditioning for tissue-specific expression resulted in a total of 64 tissue-specific genes under selection (Figure S3D). Nearly 75% (47/64) of tissue-specific genes were expressed exclusively in floral tissues, substantially greater than the genome-wide average (Figure 2F). Taken together, residually heterozygous regions demonstrate a persistent relationship with genes under selection and floral tissue specificity.
A high-resolution four-allele recombination bin map
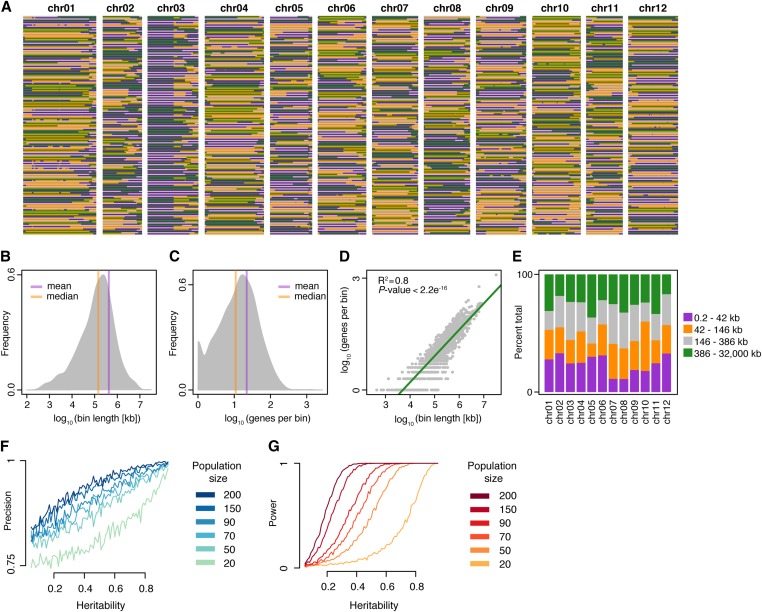
To achieve maximal resolution and power for downstream QTL mapping, we merged the haplotype recombination maps from US-W4 and M6 to create a comprehensive reference-based recombination bin map composed of 1714 uniquely segregating bins, representing distinct combinations of four different alleles (Figure 3A). The outcrossed haplotype structure of this map resembles that of a four-way cross population. Considering that this recombination bin map was generated with a segregating F1 population, we found that our map demonstrated exceptional resolution, revealed by a median and average physical bin length of ∼146 and 423 kb, respectively (Figure 3B). Additionally, > 80% of recombination bins spanned intervals < 500 kb in length. To determine the resolution of this map for the identification of candidate genes, we investigated the distribution of gene counts across bins. This analysis revealed a median and mean of 11 and 22 genes per bin, respectively, with 80% of bins containing < 33 genes (Figure 3C). We also characterized bin lengths and gene density across chromosomes, highlighting the applicability of this map for QTL analysis (Figure 3, D and E).
Figure 3.
Construction and analysis of a four-allele reference-based haplotype recombination bin map in diploid potato. (A) Haplotype distribution of a four-allele reference-based haplotype recombination bin map in diploid potato. Orange and purple, US-W4 haplotypes 1 and 2, respectively. Green and gray, M6 haplotypes, respectively. (B) Distribution of recombination bins based on the physical bin length. (C) Distribution of genes per bin genome-wide. (D) Scatter plot depicting the density of genes as a function of bin length. (E) Proportion of chromosome recombination bins composed of different physical bin lengths (split into quartiles). (F) Simulation estimates of precision across a range of heritability values (x-axis) and population sizes (dark blue to light green lines). (G) Simulation estimates of power across a range of heritability values (x-axis) and population sizes (dark red to orange lines). chr, chromosome.
xWe were then interested to determine the power and precision of our merged map for QTL analysis. To this end, we assessed the power (proportion of simulations detecting the QTL) and precision (proportion of simulations capturing the correct QTL position) of our bin map by simulating different population sizes with variable phenotypic heritability associated with a QTL. We employed a single fixed additive QTL model using broad-sense phenotypic heritability estimates ranging from 0.05 to 0.95, and population sizes between 20 and 200 individuals. Analysis of these simulations indicated that our map (population size = 90) can detect QTL with > 90.4% power and 91.2% precision when the phenotypic heritability of an additive QTL is 0.5 (Figure 3, F and G). Overall, this analysis indicates that our comprehensive recombination map provides exceptional resolution in an F1 potato population established by the low gene counts and short physical lengths per bin, and the reliable detection and localization of QTL for phenotypes of modest heritability.
Prevalent heterosis for yield component traits in a diploid potato population
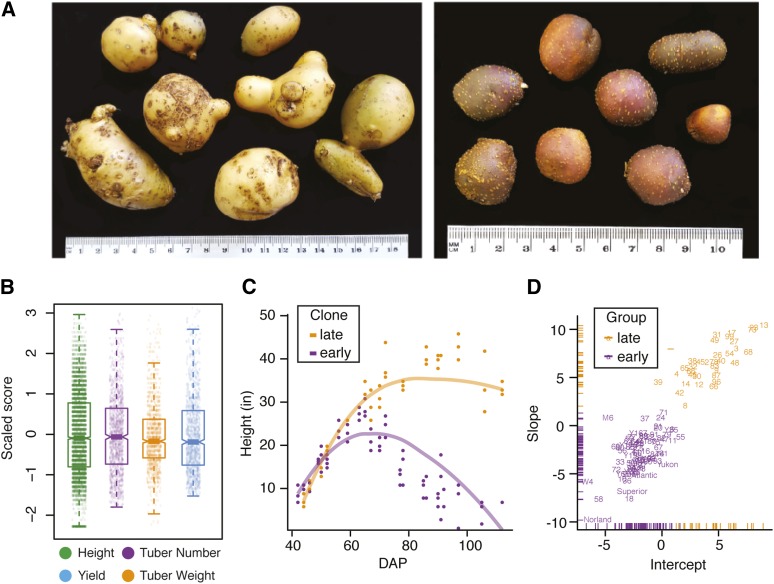
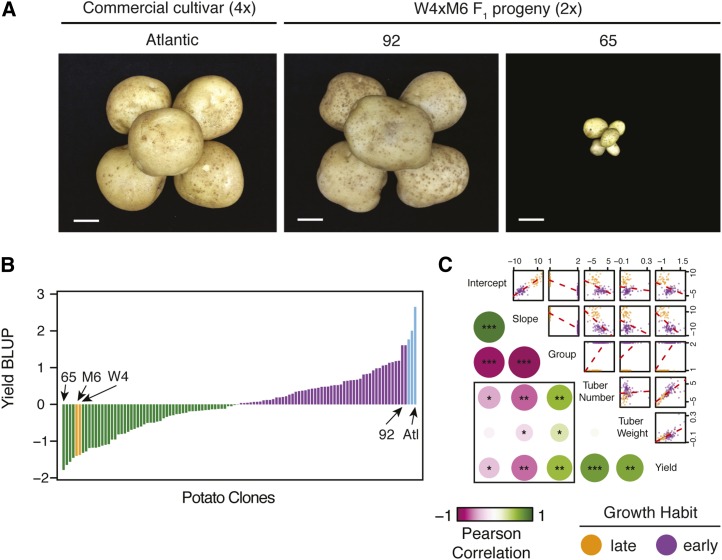
Outbred populations display remarkable phenotypic diversity and occasionally substantial heterosis over parental genotypes (Svenson et al. 2012). Both parents, US-W4 and M6, produce small tubers (Figure 4A), typical of diploid potato germplasm. Our initial evaluation of a few F1 progeny revealed remarkable heterosis in tuber size, prompting an evaluation of a larger F1 population. To assess the degree of yield heterosis, clonally propagated tubers from the F1 population and four commercial tetraploid cultivars (Atlantic, Red Norland, Superior, and Yukon) were planted in the field for four consecutive years (2014–2017). We collected data on yield, tuber number, and average tuber weight following harvest. We also measured plant height weekly for individual plots throughout the growing seasons. Phenotypic analysis indicated the presence of substantial variation for all collected traits (Figure 4B). Because plant height was measured longitudinally within years, we used random regression models to fit growth curves. Visual inspection of these models suggested two main growth habits, which we label as “early” maturity for determinate growth and “late” maturity for indeterminate growing clones (Figure 4C). We used unsupervised k-means clustering to assign early and late maturity labels to the F1 progeny, parental genotypes, and commercial tetraploids using the clone-specific slope and intercept estimates from the random regression models, highlighting the occurrence of two distinct groups based on patterns of senescence (Figure 4D).
Figure 4.
Analysis of phenotypic variance and maturity segregation in potato. (A) Comparison of tuber size between the maternal parent US-W4 (left) and the paternal parent M6 (right). Bar, 2.54 cm (1 inch). (B) Distributions of scaled phenotypic values for plant height, tuber number, average tuber weight, and overall yield. (C) Example of different growth habits for two genotypes demonstrating early (purple) and late (orange) maturity. The purple and orange lines were derived from random regression models for each clone. DAP, days after planting. (D) K-means clustering of all F1 individuals, parental genotypes, and commercial tetraploid cultivars. Early-maturing clones are illustrated in purple, while late-maturing clones are labeled in orange.
An extreme range of tuber sizes was observed across the F1 population, consistent with initial observations (Figure 5A). To control for variation due to year and replication, we derived breeding values for all phenotypes using BLUP models. Ranking clones by yield BLUPs uncovered a proliferation of extreme high-parent (HPH) and midparent heterosis (MPH), as several F1 clones produced yields comparable to commercial tetraploid cultivars (average MPH = 332%, average HPH = 325%) (Figure 5B). We additionally observed heterosis for tuber number (average MPH = 147%, average HPH = 71%) and average tuber weight phenotypes (average MPH = 50%, average HPH = 37%). Furthermore, all tuber traits were highly heritable, with broad-sense heritability values of 0.85, 0.89, and 0.9 for tuber number, average tuber weight, and yield, respectively. These observations suggest that multiallelic states in tetraploids may not be responsible for the yield barrier commonly associated with diploid potatoes. Because commercial tetraploid cultivars demonstrated early maturation and senescence, we were interested to determine if the yield, tuber number, and average tuber weight phenotypes exhibit a statistical relationship with the maturity parameters derived from the random regression model. Pairwise correlation analysis across phenotypic data sets revealed significant correlations for slope, intercept, and group with overall yield (Pearson’s r = 0.4–0.6) and tuber number (Pearson’s r = 0.45–0.62), and while still significant, less predictability for average tuber weight (Pearson’s r = 0.1–0.3) (Figure 5C). Interestingly, we did not find a correlation between tuber number and average tuber weight, although both traits were associated with overall yield. These results imply genetic independence between average tuber weight and maturity, and strong correlations between early senescence, increased tuber number, and overall yield.
Figure 5.
Persistent heterosis in tuber size is independent of maturity in potato. (A) Comparison of tuber size among a commercial tetraploid cultivar (left), a high-yielding diploid clone (middle), and a low-yielding diploid clone (right). Bar, 2.54 cm (1 inch). (B) Ordered yield BLUPs across the F1 population, the parental genotypes, and tetraploid cultivars. Orange bars indicate the two parental genotypes. Blue bars represent the commercial tetraploid cultivars. Green bars indicate clones with below-average yield BLUP values. Purple bars represent clones with above-average yield BLUP values. (C) Pairwise correlations between maturity and yield components. A linear regression model is plotted as a red line in pairwise comparisons. Early- and late-growing labels are assigned to clones as purple and orange colors, respectively. Significance denoted as * P < 5.0e−10, ** P < 5.0e−20, and *** P < 5.0e−50. BLUP, best linear unbiased prediction.
Identification of novel yield-associated QTL
To reveal the genetic constituents governing yield-related traits in this population, we performed QTL mapping using the BLUPs from yield, tuber number, average tuber weight, and the three maturity components (slope, intercept, and group) as response variables. Because of the four-allele structure of this population, we developed a mapping approach that separately estimates the individual effects of each parent, the interaction between parent haplotypes, and a full model incorporating all terms (see Materials and Methods). Past reports have suggested that yield increases may be driven by interactions between parental genomes (overdominance) (Lippman and Zamir 2007). However, in this study, modeling of the parental haplotype interactions failed to uncover significant effects (Figure S4). Although several loci were suggestive (nearly significant) of haplotype interactions, these results suggest that yield components in this diploid potato population are instead likely associated with additive, dominance, or epistatic effects.
Given the absence of significant interspecific parental effects, we sought to characterize effects of the full model in addition to parent-specific terms. This analysis uncovered multiple significant QTL with varying positions on chromosome 05 for all traits (Figure S4). Significant QTL for maturity components (PVE: 36.4–44.7%), tuber number (PVE: 24.4%), and overall yield (PVE: 28.5%) mapped to the same 256-kb recombination bin (chromosome 05: 4,344,170–4,599,697), which also contains the well-characterized potato maturity locus gene StCDF1 (chromosome 05, ∼4.5 Mb) (Kloosterman et al. 2013), providing further evidence supporting the accuracy and resolution of our bin map. Visual assessment of the –log10 (P-value) profiles indicated that a second significant QTL peak from the full model for tuber number (PVE: 25.4%) was located ∼1 Mb upstream of the maturity locus, separated by four crossover events (Figure S5A). For convenience, we denote this genomic interval as the tuber number (tn1) locus (167 kb; chromosome 05: 3,436,979–3,603,744). Furthermore, we identified a significant QTL for average tuber weight (PVE: 18.6%) originating from US-W4 (184-kb; chromosome 05: 9,694,035–9,877,748) shifted downstream relative to the bin containing StCDF1 and label this interval as the average tuber weight (tw1) locus (Figure S5A). Analysis of marker effects at tn1 and tw1 indicated that the same US-W4 allele is the major contributor to increases in both average tuber weight and number in this population (Figure S5B).
To evaluate the possibility that LD with the maturity locus results in tn1 and tw1 QTL, we estimated pairwise LD between all bins on chromosome 05 (Figure S5C). Analysis of LD between the maturity locus and the tn1 and tw1 bins revealed the presence of recombination among these loci, and the maturity locus, indicated by r2 values of 0.9 and 0.7, for tn1 and tw1, respectively. The relatively high LD between the maturity locus and these bins is expected given the physical proximity of < 5 Mb in both cases. The observation of 4 and 11 crossover events between the maturity locus and tn1 and tw1, respectively, suggests sufficient recombination for identification of independent QTL.
Controlling for maturity reveals prevalent epistasis and relative dominance over additive action overlapping residual heterozygosity
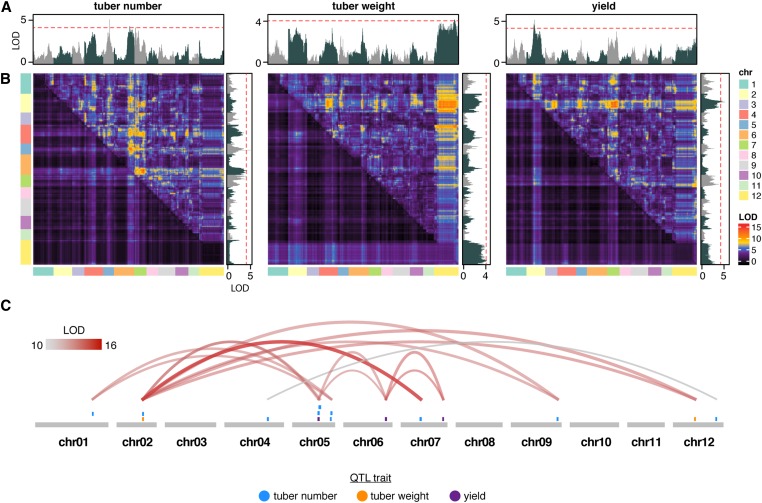
To control for the correlated effects of maturity on yield-associated traits, we performed additional one- (Figure 6A) and two-dimensional genome-wide scans (Figure 6B) using maturity group (early vs. late maturing) as a covariate during QTL detection. This resulted in the identification of several significant (FDR < 0.1) QTL, with substantial contributions from epistatic interactions for all traits (Figure 6C). Several QTL were consistent among yield-associated traits, resulting in a total of 14 novel QTL regions (including tn1 and tw1). Interestingly, we found that 79% (11/14) of QTL regions were epistatic (Table S2). To ensure that interacting QTL were not due to misplaced scaffolds or translocations, we estimated LD for all epistatic interactions, revealing r2 values < 0.1 for all interactions (Figure S6 and Table S2). Multiple QTL models controlling for maturity as a covariate explained 74.6, 58.3, and 88.6% of the total phenotypic variance for tuber number, average tuber weight, and yield, respectively. Visual inspection of QTL peaks suggested that these genomic regions may preferentially colocalize with sites of residual heterozygosity. Indeed, enrichment analysis indicated a near-significant relationship between regions of residual heterozygosity in M6 and epistatic yield-associated QTL peaks (46%, 5/11 overlap; empirical, 1 million permutations: P < 0.057).
Figure 6.
QTL detection accounting for maturity as a covariate in potato. (A) Single-marker regression scan for QTL associated with tuber number (left), average tuber weight (middle), and yield (right). The red line indicates significance thresholds for α = 0.05. (B) Two-dimensional QTL scans for epistatic interactions associated with tuber number (left), average tuber weight (middle), and overall yield (right). The top half of the matrix indicates LOD scores from the full model (two QTL and their interaction). The bottom of the matrix represents LOD scores from the additive model of two QTL. (C) A summary of all significant epistatic interactions among QTL for various traits. chr, chromosome.
To gain insight into the contribution of distinct haplotype combinations toward phenotypic variation, we estimated the additive and dominance values for each allelic combination for each bin. We found widespread prevalence of elevated dominance values relative to additive values for all traits (defined as the average log2 transformed ratio between dominance and additive values; see Materials and Methods), suggesting that dominance action predominantly influences yield and its components in this population (Figure S7–S9). In addition, relative dominance values at yield (Wilcoxon rank sum test; P < 1.0e−4) and tuber number (Wilcoxon rank sum test; P < 0.02) QTL were significantly greater than genome-wide estimates, while average tuber weight QTL were not (Wilcoxon rank sum test; P = 0.12). To determine if residual heterozygosity contributes to dominance, we evaluate the relative dominance to additive value ratio at heterozygous compared to the whole genome. Heterozygous blocks were associated with significantly greater relative dominance than the genome average for tuber number (Wilcoxon rank sum test; P < 5.8e−5) and yield (Wilcoxon rank sum test; P < 0.001), but not for average tuber weight (Wilcoxon rank sum test; P = 0.72) (Figure S10). Taken together, epistatic QTL underlying yield-related traits contribute to a large proportion of the phenotypic variance, are associated with elevated relative dominance values, and overlap with regions of residual heterozygosity.
Fine-scale genetic and transcriptional dissection of yield-associated candidate genes
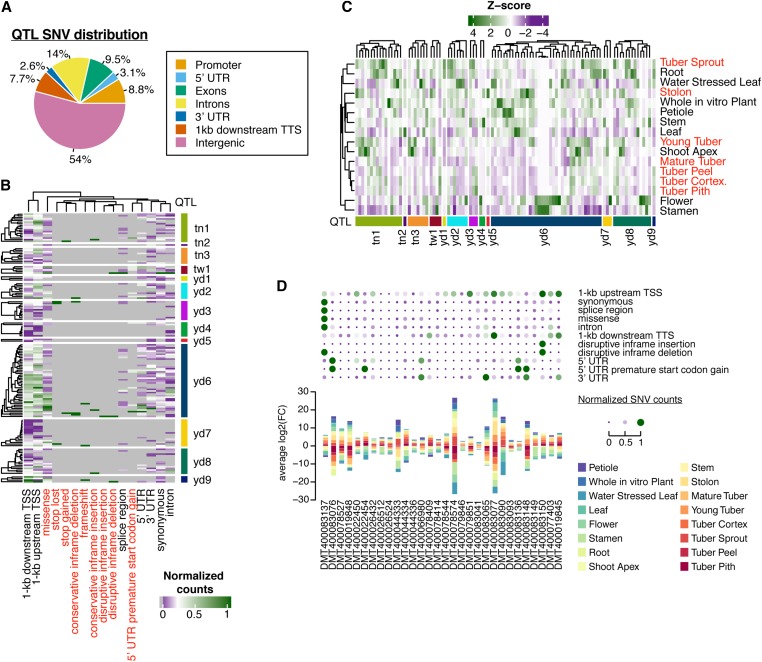
The high resolution of our genetic map affords the opportunity to dissect the fine-scale genetic and transcriptional architecture underlying yield-associated QTL. QTL intervals ranged in length from 22.7 to 681 kb, contained between 0 and 44 annotated genes per bin, and harbored a total of 159 genes. Since QTL mapping was performed on large haplotype bins and ignored fine-scale polymorphisms, we speculated that sequence variation among haplotypes within coding, splicing, or regulatory regions of key trait-related genes may lead to phenotypic differences. To this end, we identified a total of 10,272 SNVs, ranging from 25 to 4001 SNVs per QTL interval. Approximately one-half (46%) of these SNVs were located within genes and their 1-kb flanking regions (Figure 7A and Figure S11). On average, each QTL-localized gene contained ∼18 and 57 SNVs within the gene body and 1-kb flanking regions, respectively. After accounting for variation in gene length, we found that the level of genetic diversity both within and surrounding yield-associated QTL genes was significantly greater compared to all genes genome-wide (gene body: Wilcoxon rank sum test; P < 0.009, 1-kb flanking: Wilcoxon rank sum test; P < 2.2e−4), suggesting that regions related to yield may harbor significantly greater levels of genetic diversity around genes. Focusing on SNVs with putative functional implications revealed that of the 159 genes, 94% contained at least one polymorphism predicted to potentially affect transcription (up- and downstream SNVs), alter the cognate peptide sequence, or impact RNA splicing, editing, or translation (Figure 7B and Table S3). Approximately 60% (95/159) of genes contained at least one SNV predicted to affect peptide sequence, highlighting the abundance of potential functional genetic diversity underlying yield-associated QTL.
Figure 7.
Fine-scale analysis of the genetic and expression regulation architecture of yield-associated QTL in potato. (A) Distribution of SNVs relative to genes across all 14 QTL regions. (B) Normalized (0–1) counts of different SNV effects types (columns) across all 159 QTL genes (rows). (C) Normalized (z-scores) expression values of all 159 QTL genes (rows) across 16 different tissue types (columns). (D) Coincidence of tuber- or stolon-specific QTL genes (bottom plot) with various SNV effects (top bubble plot). Counts of SNV effects were scaled to range from 0 to 1. Tuber- and stolon-specific QTL genes were determined by the tissue type with the greatest TPM average log2 (FC). FC, fold change; SNV, short nucleotide variant; TPM, transcripts per million; TSS, transcription start site; TTS, transcription termination site.
Leveraging published RNA-seq data (Potato Genome Sequencing Consortium et al. 2011), we profiled gene expression (TPM) for all genes contained within each QTL. Of the 159 QTL-localized genes, 61% (97/159) were expressed in at least one profiled tissue type (Figure 7C and Table S4). Reasoning that candidate genes related to tuber number or average tuber weight would be preferentially expressed within tuber or stolon tissues, we searched for genes demonstrating evidence of tuber or stolon-specific gene expression. We estimate the degree of tissue specificity for each gene by taking the average log2 fold change across tissues. By considering genes where the greatest average log2 fold change occurred within tuber or stolon tissue types, a total of 30 genes over 9 QTL regions were identified (tuber- and stolon-specific expression = 19% of QTL genes; 30/159) (Figure S12 and Table S5). Yield-associated QTL contained a greater proportion of genes with tuber- or stolon-specific expression compared to the genome average, but the enrichment was not significant (Fisher’s exact test; QTL-localized genes = 19% vs. genome-wide genes = 12%, P = 0.066). To further delineate potential candidate genes, we assessed SNV effects for genes found in yield-associated QTL specifically expressed in tuber and stolon tissues. A total of 28 tuber- or stolon-specific expressed genes were associated with at least one SNV with the potential to alter transcription regulation, peptide sequence, or RNA splicing/translation (Figure 7D). Taken together, this analysis has revealed numerous candidate genes expressed in tuber and stolon tissues that underly genomic regions affiliated with yield QTL.
Discussion
It is commonly believed that tetraploidy is necessary for high yield in potato due to the potential for complex genetic interactions (Mendoza and Haynes 1973; Mendiburu and Peloquin 1977; Hermsen 1984). Here, we report the production of diploids that produce yields comparable to tetraploid potato cultivars. It is important to note that, while this study challenges the concept that competitive cultivars must have four sets of chromosomes, it does support extensive earlier literature suggesting that interlocus (epistasis) and intralocus (dominance) interactions are important for high yield in potato (Mendoza and Haynes 1973; Mendiburu and Peloquin 1977; Ortiz et al. 1997). The diploids in this study are interspecific hybrids between cultivated potato and the wild potato relative S. chacoense. The production of high-yielding individuals carrying a large proportion of wild germplasm has important implications for the use of this germplasm resource in potato. Notably, most of the 107 wild potato species are sexually compatible with the cultivated potato (Jansky 2018). This provides breeders with an expansive array of genetic variability for cultivar improvement. Allele mining within the wild and cultivated diploid germplasm has the potential to enhance yields and ease breeding efforts.
We have identified and carried out a comprehensive analysis of 14 novel QTL underlying potato yield. Identification of QTL was afforded by the construction of a high-resolution reference-based haplotype recombination map of an outcrossed population, maximizing the power of low-coverage whole-genome resequencing. The haplotype structure of a seventh-generation inbred paternal parent was revealed by leveraging residual heterozygosity present at greater levels than expected in most inbred genotypes (McMullen et al. 2009), enabling the identification of crossovers at high resolution and precise demarcation of recombination bin coordinates. The accuracy and precision of our reference-based mapping approach was validated via simulations, and mapping, of the well-known potato maturity locus gene StCDF1 to the center of a discrete recombination bin ∼250 kb in length. These findings represent a substantial improvement in terms of resolution over past QTL mapping studies in potato, which relied on relatively few (< 10,000) markers resulting in large QTL intervals often containing hundreds of genes (Lindqvist-Kreuze et al. 2015; Manrique-Carpintero et al. 2015; Hara-Skrzypiec et al. 2018). In addition, identification of novel genomic loci associated with yield has been impeded by the extreme proportion of variance harbored by the maturity locus on chromosome 05 (Manrique-Carpintero et al. 2015). By performing QTL detection with maturity explicitly defined as a covariate, we were able to uncover several novel QTL, including those involved in epistatic interactions. Although much speculated, only a handful of QTL studies in potato have identified epistatic QTL, likely due to a lack of marker resolution, genotyping accuracy, and power necessary to capture such effects (Mok and Peloquin 1975; van den Berg et al. 1996; Manrique-Carpintero et al. 2015). In contrast to past studies, most QTL regions in this population were associated with epistatic interactions, while only three QTL were the result of additive effects. Backward selection examining multiple QTL models indicated that most of the phenotypic variation could be explained by a modest number of large-effect QTL. One of our initial hypotheses was that the interspecific nature of this population might be a major contributor toward the observed yield heterosis (Mendoza and Haynes 1974; Mok and Peloquin 1975). Although we were unable to detect significant interactions between parental haplotypes, we did identify an increase in relative dominance across all yield-associated traits localizing to regions of recalcitrant heterozygosity in the inbred parent. Additional populations from divergent genetic backgrounds will be necessary to determine if these observations are a unifying feature of the potato genome.
The identification of recalcitrant heterozygosity in the inbred parent has important implications for future mapping and breeding efforts. The occurrence of residual heterozygosity has been largely attributed to a lack of recombination (Gore et al. 2009; Leisner et al. 2018), noting that recombination the enables purification of deleterious alleles and aids in selection efforts. However, other reports have indicated that localized regions may be a result of other more complex population forces (Liu et al. 2018). We demonstrate that the persistence of residual heterozygosity in discrete euchromatic regions does not arise from the absence of recombination, but may be in part due to gametic selection necessitating maintained heterozygosity at specific loci. These conclusions, although speculative, are supported by the enrichment of genes carrying signatures of selection, of floral-specific expression profiles, and GO annotations consistent with gametic function and development. It is attractive to consider these genes as potential players in the developmental transition from vegetative to reproductive stages, a process that profoundly impacts metabolic resource allocation during tuber development (Martin et al. 2009). However, future work characterizing the functional roles of such genes will be necessary to determine their part in recalcitrant heterozygosity. We also found that regions with elevated heterozygosity were affiliated with greater ratios of dominance to additive values for yield and tuber number. Considering that secondary tubers are equivalent to asexually propagated progeny, the number of tubers produced per individual plant can be regarded as a general proxy for fitness (Hardigan et al. 2017). This suggests that maintained heterozygosity may be important for overall fitness and is consistent with severe inbreeding phenotypes in potato. The majority of epistatic QTL identified by two-dimensional QTL scans overlapped regions of residual heterozygosity, which further implicates a potential relationship between increased allelic variation, epistatic contributions to yield, and overall fitness.
The short physical QTL bin lengths allowed for the examination of putative candidate genes at a fine scale. Among the 28 tuber- or stolon-specifically expressed genes underpinning yield QTL, several emerged as promising candidates for further consideration. A gene underlying an epistatic QTL for both yield and tuber number, annotated as a gibberellin-regulated protein (PGSC0003DMT400083077), was expressed sevenfold greater in stolon tissues and threefold greater in young tubers compared to other tissue types. Gibberellin plays a well-documented role in plant development and structural architecture, providing further support for a putative function of this gene in tuber initiation (Daviere and Achard 2013). Gibberellin-regulated protein was coincident with 1-kb upstream, 1-kb downstream, and missense SNVs, indicating that there are multiple segregating alleles present in our population. A gene (PGSC0003DMT400019845) located within the tw1 average tuber weight QTL was annotated as a starch granule-bound R1 protein (SGBR1). SGBR1 proteins, when bound to the surface of granules, have been shown to elicit starch degradation in potato leaves (Ritte et al. 2000b). However, SGBR1 proteins are also speculated to be involved in starch synthesis when encapsulated within granules, a case observed predominantly in tubers ((Ritte et al. 2000a,b). This gene is expressed mainly within the tuber pith and cortex in the genotype “RH” and demonstrates a threefold expression increase in the tubers of M6 relative to other tissue types. The abundance of putative cis-regulatory SNVs and 11 missense mutations highlights the genetic diversity in this gene. These genes represent candidate genes based on a priori annotations, patterns of transcription, and the presence of more than one allele. Further experiments will be necessary to validate the functional contributions of these genes toward yield-related phenotypes.
Acknowledgments
This research was supported by National Science Foundation grant ISO-1237969 to J.J.
Author contributions: S.H.J. and J.J. designed the research; A.P.M. and A.J.H. performed experiments; A.P.M., S.H.J., J.L.G., N.d.L, and J.J. analyzed data; and A.P.M. and J.J. wrote the article.
Footnotes
Supplemental material available at https://doi.org/10.25386/genetics.7312142.
Communicating editor: P. Andrew
Literature Cited
- Anders S., Pyl P. T., Huber W., 2015. HTSeq-a Python framework to work with high-throughput sequencing data. Bioinformatics 31: 166–169. 10.1093/bioinformatics/btu638 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arends D., Prins P., Jansen R. C., Broman K. W., 2010. R/qtl: high-throughput multiple QTL mapping. Bioinformatics 26: 2990–2992. 10.1093/bioinformatics/btq565 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernardo R., 2014. Essentials of Plant Breeding. Stemma Press, Woodbury, MN. [Google Scholar]
- Broman K. W., Sen S., 2009. Introduction, in A Guide to QTL Mapping with R/qtI. Springer-Verlag, New York. [Google Scholar]
- Churchill G., Airey D. C., Allayee H., Angel J. M., Attie A. D., et al. , 2004. The Collaborative Cross, a community resource for the genetic analysis of complex traits. Nat. Genet. 36: 1133–1137. 10.1038/ng1104-1133 [DOI] [PubMed] [Google Scholar]
- Cingolani P., Platts A., Wang le L., Coon M., Nguyen T., et al. , 2012. A program for annotating and predicting the effects of single nucleotide polymorphisms, SnpEff: SNPs in the genome of Drosophila melanogaster strain w1118; iso-2; iso-3. Fly (Austin) 6: 80–92. 10.4161/fly.19695 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Da Y., 2015. Multi-allelic haplotype model based on genetic partition for genomic prediction and variance component estimation using SNP markers. BMC Genet. 16: 144 10.1186/s12863-015-0301-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daviere J. M., Achard P., 2013. Gibberellin signaling in plants. Development 140: 1147–1151. 10.1242/dev.087650 [DOI] [PubMed] [Google Scholar]
- Douches D. S., Maas D., Jastrzebski K., Chase R. W., 1996. Assessment of potato breeding progress in the USA over the last century. Crop Sci. 36: 1544–1552. 10.2135/cropsci1996.0011183X003600060024x [DOI] [Google Scholar]
- Durrant C., Tayem H., Yalcin B., Cleak J., Goodstadt L., et al. , 2011. Collaborative Cross mice and their power to map host susceptibility to Aspergillus fumigatus infection. Genome Res. 21: 1239–1248. 10.1101/gr.118786.110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felcher K. J., Coombs J. J., Massa A. N., Hansey C. N., Hamilton J. P., et al. , 2012. Integration of two diploid potato linkage maps with the potato genome sequence. PLoS One 7: e36347 10.1371/journal.pone.0036347 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gore M. A., Wright M. H., Ersoz E. S., Bouffard P., Szekeres E. S., et al. , 2009. Large-scale discovery of gene-enriched SNPs. Plant Genome 2: 121–133. 10.3835/plantgenome2009.01.0002 [DOI] [Google Scholar]
- Hara-Skrzypiec A., Śliwka J., Jakuczun H., Zimnoch-Guzowska E., 2018. QTL for tuber morphology traits in diploid potato. J. Appl. Genet. 59: 123–132. 10.1007/s13353-018-0433-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hardigan M. A., Crisovan E., Hamilton J. P., Kim J., Laimbeer P., et al. , 2016. Genome reduction uncovers a large dispensable genome and adaptive role for copy number variation in asexually propagated Solanum tuberosum. Plant Cell 28: 388–405. 10.1105/tpc.15.00538 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hardigan M. A., Laimbeer F. P. E., Newton L., Crisovan E., Hamilton J. P., et al. , 2017. Genome diversity of tuber-bearing Solanum uncovers complex evolutionary history and targets of domestication in the cultivated potato. Proc. Natl. Acad. Sci. USA 114: E9999–E10008. 10.1073/pnas.1714380114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayes B., Goddard M. E., 2001. The distribution of the effects of genes affecting quantitative traits in livestock. Genet. Sel. Evol. 33: 209–229. 10.1186/1297-9686-33-3-209 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hermsen J. G. T., 1984. Nature, evolution and breeding of polyploids. Iowa State J. Res. 58: 411–412. [Google Scholar]
- Hirsch C. N., Hirsch C. D., Felcher K., Coombs J., Zarka D., et al. , 2013. Retrospective view of North American potato (Solanum tuberosum L.) breeding in the 20th and 21st centuries. G3 (Bethesda) 3: 1003–1013. 10.1534/g3.113.005595 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hosaka K., Hanneman R. E., Jr., 1998. Genetics of self-compatibility in a self-incompatible wild diploid potato species Solanum chacoense. 2. Localization of an S locus inhibitor (Sli) gene on the potato genome using DNA markers. Euphytica 103: 265–271. 10.1023/A:1018380725160 [DOI] [Google Scholar]
- Huang X., Feng Q., Qian Q., Zhao Q., Wang L., et al. , 2009. High-throughput genotyping by whole-genome resequencing. Genome Res. 19: 1068–1076. 10.1101/gr.089516.108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutten R. C. B., Soppe W. J. J., Hermsen J. G. T., Jacobsen E., 1995. Evaluation of dihaploid populations from potato varieties and breeding lines. Potato Res. 38: 77–86. 10.1007/BF02358072 [DOI] [Google Scholar]
- Jansky S. H., Spooner D. M., 2018. The evolution of potato breeding. Plant Breeding Rev 41: 169–214 .
- Jansky S. H., Chung Y. S., Kittipadukal P., 2014. M6: a diploid potato inbred line for use in breeding and genetics research. J. Plant Regist. 8: 195–199. 10.3198/jpr2013.05.0024crg [DOI] [Google Scholar]
- Jansky S. H., Charkowski A. O., Douches D. S., Gusmini G., Richael C., et al. , 2016. Reinventing potato as a diploid inbred line-based crop. Crop Sci. 56: 1412–1422. 10.2135/cropsci2015.12.0740 [DOI] [Google Scholar]
- Jeon J. S., Jung K. H., Kim H. B., Suh J. P., Khush G. S., 2011. Genetic and molecular insights into the enhancement of rice yield potential. J. Plant Biol. 54: 1–9. 10.1007/s12374-011-9144-0 [DOI] [Google Scholar]
- Kloosterman B., Abelenda J. A., Gomez Mdel M., Oortwijn M., de Boer J. M., et al. , 2013. Naturally occurring allele diversity allows potato cultivation in northern latitudes. Nature 495: 246–250. 10.1038/nature11912 [DOI] [PubMed] [Google Scholar]
- Leisner, C. P., J. P. Hamilton, E. Crisovan, N. C. Manrique-Carpintero, A. P. Marand et al., 2018 Genome sequence of M6, a diploid inbred clone of the high-glycoalkaloid-producing tuber-bearing potato species Solanum chacoense, reveals residual heterozygosity. Plant J. 94: 562–570 (erratum: Plant J. 96: 482). 10.1111/tpj.13857 10.1111/tpj.13857 [DOI] [PubMed]
- Li B., Ruotti V., Stewart R. M., Thomson J. A., Dewey C. N., 2010. RNA-Seq gene expression estimation with read mapping uncertainty. Bioinformatics 26: 493–500. 10.1093/bioinformatics/btp692 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li C., Li Y., Bradbury P. J., Wu X., Shi Y. S., et al. , 2015. Construction of high-quality recombination maps with low-coverage genomic sequencing for joint linkage analysis in maize. BMC Biol. 13: 78 10.1186/s12915-015-0187-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindqvist-Kreuze H., Khan A., Salas E., Meiyalaghan S., Thomson S., et al. , 2015. Tuber shape and eye depth variation in a diploid family of Andean potatoes. BMC Genet. 16: 57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lippman Z. B., Zamir D., 2007. Heterosis: revisiting the magic. Trends Genet. 23: 60–66. 10.1016/j.tig.2006.12.006 [DOI] [PubMed] [Google Scholar]
- Liu N., Liu J., Li W., Pan Q., Liu J., et al. , 2018. Intraspecific variation of residual heterozygosity and its utility for quantitative genetic studies in maize. BMC Plant Biol. 18: 66 10.1186/s12870-018-1287-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mackay T. F., 2009. Q&A: genetic analysis of quantitative traits. J. Biol. 8: 23 10.1186/jbiol133 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manrique-Carpintero N. C., Coombs J. J., Cui Y. H., Veilleux R. E., Buell C. R., et al. , 2015. Genetic map and QTL analysis of agronomic traits in a diploid potato population using single nucleotide polymorphism markers. Crop Sci. 55: 2566–2579. 10.2135/cropsci2014.10.0745 [DOI] [Google Scholar]
- Manrique-Carpintero N. C., Coombs J. J., Pham G. M., Laimbeer F. P. E., Braz G. T., et al. , 2018. Genome reduction in tetraploid potato reveals genetic load, haplotype variation, and loci associated with agronomic traits. Front. Plant Sci. 9: 944 10.3389/fpls.2018.00944 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marand A. P., Jansky S. H., Zhao H. N., Leisner C. P., Zhu X. B., et al. , 2017. Meiotic crossovers are associated with open chromatin and enriched with Stowaway transposons in potato. Genome Biol. 18: 203 10.1186/s13059-017-1326-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin A., Adam H., Diaz-Mendoza M., Zurczak M., Gonzalez-Schain N. D., et al. , 2009. Graft-transmissible induction of potato tuberization by the microRNA miR172. Development 136: 2873–2881. 10.1242/dev.031658 [DOI] [PubMed] [Google Scholar]
- Martin M., 2011. Cutadapt removes adapter sequences from high-throughput sequencing reads. EMBnet.journal 17: 10–12. [Google Scholar]
- McMullen M. D., Kresovich S., Villeda H. S., Bradbury P., Li H. H., et al. , 2009. Genetic properties of the maize nested association mapping population. Science 325: 737–740. 10.1126/science.1174320 [DOI] [PubMed] [Google Scholar]
- Mendiburu A. O., Peloquin S. J., 1977. Bilateral sexual polyploidization in potatoes. Euphytica 26: 573–583. 10.1007/BF00021683 [DOI] [Google Scholar]
- Mendoza H. A., Haynes F. L., 1973. Some aspects of breeding and inbreeding in potatoes. Am. Potato J. 50: 216–222. 10.1007/BF02851773 [DOI] [Google Scholar]
- Mendoza H. A., Haynes F. L., 1974. Genetic basis of heterosis for yield in the autotetraploid potato. Theor. Appl. Genet. 45: 21–25. 10.1007/BF00281169 [DOI] [PubMed] [Google Scholar]
- Mok D. W., Peloquin S. J., 1975. Breeding value of 2n pollen (diplandroids) in tetraploid x diploid crosses in potatoes. Theor. Appl. Genet. 46: 307–314. 10.1007/BF00281153 [DOI] [PubMed] [Google Scholar]
- Ortiz R., Iwanaga M., Peloquin S. J., 1997. Evaluation of FDR diploid and tetraploid parents in potato under two different day-length environments. Plant Breed. 116: 353–358. 10.1111/j.1439-0523.1997.tb01011.x [DOI] [Google Scholar]
- Pertea M., Kim D., Pertea G. M., Leek J. T., Salzberg S. L., 2016. Transcript-level expression analysis of RNA-seq experiments with HISAT, StringTie and Ballgown. Nat. Protoc. 11: 1650–1667. 10.1038/nprot.2016.095 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pinheiro J., Bates D., DebRoy S., Sarkar D., R Core Team , 2018. nlme: linear and nonlinear mixed effects models, R Package 3.1. Available at https://cran.r-project.org/web/packages/nlme/nlme.pdf.
- Potato Genome Sequencing Consortium. Xu X., Pan S., Cheng S., Zhang B., et al. , 2011. Genome sequence and analysis of the tuber crop potato. Nature 475: 189–195. 10.1038/nature10158 [DOI] [PubMed] [Google Scholar]
- Quinlan A. R., Hall I. M., 2010. BEDTools: a flexible suite of utilities for comparing genomic features. Bioinformatics 26: 841–842. 10.1093/bioinformatics/btq033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ritte G., Eckermann N., Haebel S., Lorberth R., Steup M., 2000a Compartmentation of the starch-related R1 protein in higher plants. Starke 52: 145–149. [DOI] [Google Scholar]
- Ritte G., Lorberth R., Steup M., 2000b Reversible binding of the starch-related R1 protein to the surface of transitory starch granules. Plant J. 21: 387–391. 10.1046/j.1365-313x.2000.00683.x [DOI] [PubMed] [Google Scholar]
- Śliwka J., Brylińska M., Stefańczyk E., Jakuczun H., Wasilewicz-Flis I., et al. , 2017. Quantitative trait loci affecting intensity of violet flower colour in potato. Euphytica 213: 254. [Google Scholar]
- Solberg Woods L. C. S., 2014. QTL mapping in outbred populations: successes and challenges. Physiol. Genomics 46: 81–90. 10.1152/physiolgenomics.00127.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Su C., Wang W., Gong S., Zuo J., Li S., et al. , 2017. High density linkage map construction and mapping of yield trait QTLs in maize (Zea mays) using the genotyping-by-sequencing (GBS) technology. Front. Plant Sci. 8: 706 10.3389/fpls.2017.00706 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Svenson K. L., Gatti D. M., Valdar W., Welsh C. E., Cheng R., et al. , 2012. High-resolution genetic mapping using the mouse diversity outbred population. Genetics 190: 437–447. 10.1534/genetics.111.132597 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tian T., Liu Y., Yan H., You Q., Yi X., et al. , 2017. agriGO v2.0: a GO analysis toolkit for the agricultural community, 2017 update. Nucleic Acids Res. 45: W122–W129. 10.1093/nar/gkx382 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valdar W., Flint J., Mott R., 2006. Simulating the collaborative cross: power of quantitative trait loci detection and mapping resolution in large sets of recombinant inbred strains of mice. Genetics 172: 1783–1797. 10.1534/genetics.104.039313 [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Berg J. H., Ewing E. E., Plaisted R. L., McMurry S., Bonierbale M. W., 1996. QTL analysis of potato tuber dormancy. Theor. Appl. Genet. 93: 317–324. 10.1007/BF00223171 [DOI] [PubMed] [Google Scholar]
- van der Hoorn R. A. L., 2008. Plant proteases: from phenotypes to molecular mechanisms. Annu. Rev. Plant Biol. 59: 191–223. 10.1146/annurev.arplant.59.032607.092835 [DOI] [PubMed] [Google Scholar]
- Visser I., Speekenbrink M., 2010. depmixS4: an R package for hidden Markov models. J. Stat. Softw. 36: 1–21. 10.18637/jss.v036.i07 [DOI] [Google Scholar]
- Xing Y., Zhang Q., 2010. Genetic and molecular bases of rice yield. Annu. Rev. Plant Biol. 61: 421–442. 10.1146/annurev-arplant-042809-112209 [DOI] [PubMed] [Google Scholar]
- Yan J. B., Warburton M., Crouch J., 2011. Association mapping for enhancing maize (Zea mays L.) genetic improvement. Crop Sci. 51: 433–449. 10.2135/cropsci2010.04.0233 [DOI] [Google Scholar]
- Yu H., Xie W., Wang J., Xing Y., Xu C., et al. , 2011. Gains in QTL detection using an ultra-high density SNP map based on population sequencing relative to traditional RFLP/SSR markers. PLoS One 6: e17595 (erratum: PLoS One 6). 10.1371/journal.pone.0017595 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng Z. B., 1994. Precision mapping of quantitative trait loci. Genetics 136: 1457–1468. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The software used to generate phased haplotypes is freely available in the software package phaseLD (https://github.com/plantformatics/phaseLD). Haplotype bins, phenotypes, and scripts for QTL mapping can be found on GitHub at the following open access repository (https://github.com/joegage/diploid_potato_qtl_mapping). Raw sequencing data for the F1 population and parental genotypes can be found under BioProject number PRJNA356643. All supplemental figures and tables are available on figshare in files Figures_S1-12.pdf and Supplemental_Tables.xls. Supplemental material available at https://doi.org/10.25386/genetics.7312142.