Dirac nodal surfaces and nodal lines in ZrSiS

Photoemission demonstrates that the Dirac-like band crossings form 1D nodal lines and 2D nodal surfaces in the bulk of ZrSiS.

Abstract

Topological semimetals are characterized by symmetry-protected band crossings, which can be preserved in different dimensions in momentum space, forming zero-dimensional nodal points, one-dimensional nodal lines, or even two-dimensional nodal surfaces. Materials harboring nodal points and nodal lines have been experimentally verified, whereas experimental evidence of nodal surfaces is still lacking. Here, using angle-resolved photoemission spectroscopy (ARPES), we reveal the coexistence of Dirac nodal surfaces and nodal lines in the bulk electronic structures of ZrSiS. As compared with previous ARPES studies on ZrSiS, we obtained pure bulk states, which enable us to extract unambiguously intrinsic information of the bulk nodal surfaces and nodal lines. Our results show that the nodal lines are the only feature near the Fermi level and constitute the whole Fermi surfaces. We not only prove that the low-energy quasiparticles in ZrSiS are contributed entirely by Dirac fermions but also experimentally realize the nodal surface in topological semimetals.

INTRODUCTION

When two bands cross each other, a hybridized gap is opened if without symmetry protection. However, band crossings can be protected by certain symmetries in a class of materials called topological semimetals (TSMs). In Dirac and Weyl semimetals, the band crossings with four- and twofold degeneracies occur at zero-dimensional (0D) nodal points, where the quasiparticle excitations are analogous to relativistic Dirac and Weyl fermions, respectively. Dirac and Weyl semimetals have been theoretically predicted (1–6) and experimentally confirmed (7–12). Moreover, band theory has predicted three-, six-, and eightfold degenerate nodal points (13–17), where the quasiparticles have no counterparts in high-energy physics, and the threefold degenerate points have been confirmed experimentally very recently (18, 19).

On the other hand, band theory has shown that additional crystalline symmetries can protect the band crossings along the 1D line in the Brillouin zone (BZ) (20). In contrast to isolated nodal points, nodal lines have much richer topological configurations, and they can constitute nodal ring, nodal chain, nodal link, or nodal knot (21). Band calculations have predicted numerous nodal-line semimetals (22, 23), while a few candidates have been experimentally confirmed (24–26). Recent advances in band theory have proposed that the band crossings can be preserved on the 2D surface in 3D BZ (27, 28), further expanding the scope of TSMs. To date, only a few nodal-surface semimetals have been predicted (27–29), and none of them are experimentally confirmed.

ZrSiS has been proposed to have both nodal lines and nodal surfaces protected by crystalline symmetries (30, 31). It crystallizes in a nonsymmorphic space group P4/nmm (no. 129), which is isostructural to the “111”-type iron-based superconductor LiFeAs (Fig. 1A). Owing to weak interlayer coupling, the electronic structures of ZrSiS are quasi-2D, and the band dispersions are very similar in all k_x-k_y planes. In an arbitrary k_x-k_y plane, band inversion occurs at the BZ center, resulting in band crossings on a closed ring surrounding the center of the k_x-k_y plane. However, in the 3D BZ, the band crossings are protected only in the horizontal and vertical high-symmetry planes, forming multiple interconnected nodal lines (red dashed lines in Fig. 1B). Very recently, band theory has pointed out that the nonsymmorphic symmetries in ZrSiS enforce band degeneracies in the k_x = π and k_y = π planes, forming the nodal surfaces on the BZ boundary (yellow planes in Fig. 1B) (31). They are present in the absence of spin-orbit coupling (SOC) but generally gapped when SOC is considered, which is common in systems with the $\mathcal{T}\mathcal{P}$ symmetry. However, because of small SOC effects in ZrSiS, the millivolt-level gaps can be ignored in most of the experimental work.

Fig. 1. Comparison between the (001) surface and bulk states of ZrSiS.

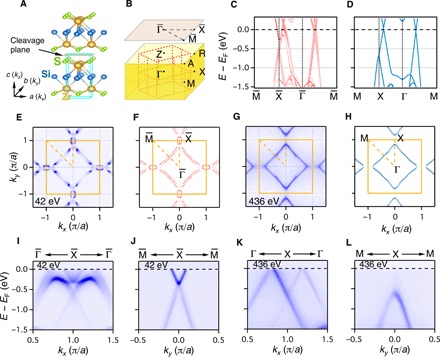
(A) Crystal structure of ZrSiS. (B) Schematic of the locations of the nodal surfaces (yellow planes) and nodal lines (red dashed lines) of ZrSiS in the bulk BZ. (C) Calculated surface band structures. (D) Calculated bulk band structures at k_z = 0. (E) FSs measured with hν = 42 eV. (F) Calculated surface FSs. (G) FSs measured with hν = 436 eV. (H) Calculated bulk FSs at k_z = 0. (I and J) Band dispersions along the $\overline{\mathrm{\Gamma }}$-$\overline{\mathrm{X}}$ and $\overline{\mathrm{M}}$-$\overline{\mathrm{X}}$ lines, respectively, measured with hν = 42 eV. (K and L) Band dispersions along the Γ-X and M-X lines, respectively, measured with hν = 436 eV.

RESULTS

The electronic structures of ZrSiS have been studied by angle-resolved photoemission spectroscopy (ARPES) (31–35). In Fig. 1 (E, I, and J), we present the Fermi surfaces (FSs) and band dispersions measured with vacuum ultraviolet (VUV) lights, which reproduce the previous results. The VUV data show negligible dispersions along k_z, as shown in the Supplementary Materials. They are inconsistent with the calculated bulk electronic structures in Fig. 1 (D and H) but well reproduced by our slab calculations with spectral weights projected onto the topmost unit cell in Fig. 1 (C and F), indicating that these ARPES data mainly reflect the surface states in the topmost unit cell.

The most remarkable discrepancy between the surface and bulk states is the surface electron FS pocket around the $\overline{\mathrm{X}}$ point, which arises from the surface floating bands caused by symmetry reduction at the (001) surface (31). The symmetry reduction generally lifts the band degeneracies on both nodal surfaces and nodal lines (31). Therefore, the surface states are essentially different from the electronic states in the bulk. The surface states are robust even in the bulk-sensitive soft x-ray ARPES experiments (31), seriously hindering from the investigation of the intrinsic bulk electronic structures.

We found that when the samples were cleaved in air or in very few cases in vacuum, the surface states could be eliminated. But using soft x-ray, we observed clear band dispersions, which represent the bulk electronic structures. In Fig. 1 (G, K, and L), we present the FSs and band dispersions measured with photon energy hv = 436 eV, in which the surface electron pocket and associated surface floating bands disappear. By contrast, we observe a diamond-shaped FS enclosing the Γ point and linearly dispersive bands along the Γ-X line, which are well consistent with the calculated bulk electronic structures at k_z = 0 in Fig. 1 (D and H). The elimination of the surface states allows us to systematically investigate the nodal surfaces and nodal lines in the bulk states of ZrSiS.

The electronic structures of the nodal surfaces of ZrSiS are summarized in Fig. 2. Figure 2 (D to F) shows the calculated bands in the k_z = 0, π/2, and π planes. The bands are doubly degenerate on the BZ boundary R-A, L-H, and X-M, while SOC is not considered. There are two degenerate bands in the energy range within 3 eV below E_F, which are indicated with red and green colors, respectively. The nonsymmorphic symmetries enforce that all bands are doubly degenerate at all k_z’s on the BZ boundary, forming the nodal surfaces in the vertical X-M-A-R planes, as indicated with yellow color in Fig. 2A. Figure 2C plots a schematic band structure in an arbitrary k_x-k_y plane near the nodal surface. The degenerated band splits into two away from the nodal surface, and the bands show a Dirac-like crossing in the normal direction of the nodal surface. As discussed later, these features are observed in our experimental data.

Fig. 2. Electronic structures of the nodal surfaces of ZrSiS.

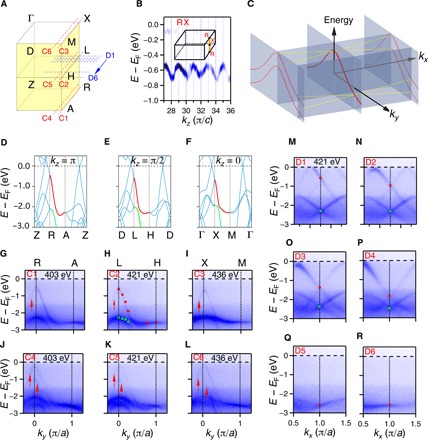
(A) Schematic of momentum locations of cuts C1 to C6 and D1 to D6 in the bulk BZ. (B) Intensity plot of second derivatives of the ARPES data along X-R measured in a range of hν from 405 to 730 eV. (C) Schematic plot of the band structure in an arbitrary k_x-k_y plane near the nodal surface. Thick and thin red curves represent the degenerate band on the nodal surface and the nondegenerate bands away from the nodal surfaces, respectively. Yellow lines represent the bands with Dirac-like crossing in the normal direction of the nodal surface. (D to F) Calculated bulk bands at k_z = π, π/2, and 0, respectively. The red and green lines indicate the degenerate bands on the BZ boundary. (G to L) Band dispersions along cuts C1 to C6, respectively. Arrows in (J) to (L) indicate the band splitting when the cuts deviate off the BZ boundary. (M to R) Band dispersions along cuts D1 to D6, respectively. Red and green dots in (M) to (R) indicate the band crossings, whose positions in the degenerate bands are marked in (H).

We first measured the band dispersions along X-R by varying photon energy. The measured band in Fig. 2B corresponds to the top of the upper degenerate band (red curves in Fig. 2, D to F). It oscillates between −0.5 and −0.7 eV along k_z with a period of 2π/c, which is consistent with the band calculations. This indicates that our measurements can probe the bulk states of ZrSiS.

On the basis of the data in Fig. 2B, we can determine the k_z location for each photon energy. We then selected three photon energies to measure the band dispersions in the k_z = 0, π/2, and π planes, respectively. Figure 2 (G to I) plots the experimental bands along cuts C1 to C3 on the BZ boundary, which are well consistent with the calculations in Fig. 2 (D to F). In Fig. 2 (J to L), we observe band splitting along cuts C4 to C6, which slightly deviate from the BZ boundary.

Figure 2 (M to R) plots the measured bands along cuts D1 to D6, which are perpendicular to the BZ boundary, as indicated in Fig. 2A. The bands along cuts D1 to D5 exhibit Dirac-like crossings on the BZ boundary. When sliding the cut to D6 (Fig. 2R), the Dirac bands become degenerate because D6 is located on the BZ boundary. These crossing points constitute the degenerate bands on the L-H line in Fig. 2H. Owing to the quasi-2D electronic structures of ZrSiS, the band dispersions are very similar in all k_x-k_y planes. The Dirac-like band crossings on the BZ boundary are protected by the nonsymmorphic symmetries for all k_z locations, forming the Dirac nodal surfaces.

The electronic structures of the nodal lines of ZrSiS are summarized in Fig. 3. The calculations show that the band crossings of the nodal lines lie around E_F. The interconnected nodal lines in the vertical and horizontal high-symmetry planes (Fig. 1B) constitute 3D “cage”-like FSs (Fig. 3N). Note that the FSs have finite volumes because the band crossings do not reside exactly at E_F. We measured all FSs in the four high-symmetry planes, as shown in Fig. 3 (C, D, G, and H). The experimental FSs are well consistent with the calculations in Fig. 3 (A, B, E, and F).

Fig. 3. Electronic structures of the Dirac nodal lines of ZrSiS.

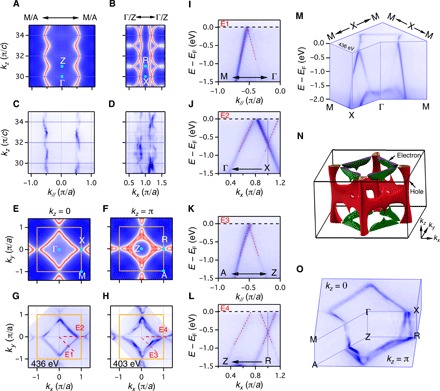
(A and B) Calculated FSs in the Γ-M-A-Z and Γ-X-R-Z planes, respectively. (C and D) Experimental FSs in the Γ-M-A-Z and Γ-X-R-Z planes, respectively, measured in a range of hν from 466 to 691 eV. (E and F) Calculated FSs in the k_z = 0 and π planes, respectively. (G and H) Experimental FSs in the k_z = 0 and π planes measured with hv = 436 and 403 eV, respectively. (I to L) Band dispersions along cuts E1 to E4, respectively. (M) 3D intensity plot of the ARPES data measured with hν = 436 eV, showing the band structure of the nodal ring in the k_z = 0 plane. (N and O) Calculated and experimental FSs in the 3D bulk BZ, respectively.

Figure 3 (I to L) plots the measured bands along four high-symmetry lines. These bands disperse almost linearly in an energy range within 1.5 eV below E_F and cross each other near E_F. In Fig. 3M, we show a 3D plot to illuminate the band structure of the nodal ring in the k_z = 0 plane. The near-E_F band crossings extend along a closed trajectory, forming a diamond-shaped FS. As the band crossings are very close to E_F in the horizontal plane k_z = 0 and vertical plane Γ-M-A-Z, the FSs in these two planes are very thin (Fig. 3, A, C, E, and G). By contrast, the band crossings are slightly away from E_F in the other two planes k_z = π and X-Γ-Z-R, where the FSs have finite sizes (Fig. 3, B, D, F, and H).

In Fig. 3O, we combine the measured FSs in the high-symmetry planes of the BZ, which are well consistent with the calculated cage-like FSs in Fig. 3N. The two nodal-ring FSs in the horizontal planes k_z = 0 and π are connected by the nodal-line FSs in the vertical planes Γ-M-A-Z and Γ-X-R-Z. The measured FSs are distinct from the previous ARPES results, which show surface electron pockets around the $\overline{\mathrm{X}}$ point (31–35). Our results demonstrate unambiguously that the whole FSs of ZrSiS are composed of the nodal lines near E_F, and therefore, the carriers are contributed entirely by the Dirac fermions with nearly zero effective masses (36). This makes ZrSiS a promising platform to study the physical properties governed by Dirac fermions. The Shubnikov–de Haas measurements on ZrSiS have revealed unusual field-induced mass enhancement (37) and a sharp topological phase transition as a function of angle of fields (38), which were associated with the Dirac nodal-line band structures near E_F.

DISCUSSION

Our results have revealed that ZrSiS has both Dirac nodal surfaces and nodal lines in its bulk electronic structures. On the basis of the formation mechanisms, the band crossings in TSMs can be classified as accidental or guaranteed. The nodal lines in ZrSiS belong to the first class, which requires band inversion. All experimentally identified TSMs so far have accidental band crossings, such as the Weyl points in TaAs (9–12), Dirac points in Na₃Bi (7) and Cd₃As₂ (8), triple points in MoP and WC (18, 19), and nodal lines in PbTaSe₂ (24) and TiB₂ (25, 26). By contrast, the nodal surfaces in ZrSiS belong to the second class, in which the band crossings are guaranteed by specific space-group symmetries. ZrSiS is the first experimental example that realizes the guaranteed band crossings. Band theory has proposed that the second class can host more exotic types of excitations at band degeneracies, such as spin-1 and spin-3/2 chiral fermions (14, 39). The discovery of these exotic fermions in TSMs calls for future experimental efforts.

MATERIALS AND METHODS

Sample growth and preparations

Polycrystalline powders of ZrSiS were first synthesized by mixing high-purity zirconium (99.99%), silicon (99.999%), and sulfur (99.99%) and sintering at 1000°C for 5 days. From the polycrystalline precursor, the single crystals were grown by chemical vapor transport method with iodine as agent. The polycrystalline powders and iodine in a mass ratio of 1:0.07 were sealed in silica tubes under vacuum. Then, the silica tubes were put in a gradient tube furnace with the source powders at 1050°C and the cold end at around 950°C for 7 days. Rectangular plane-like crystals were obtained from the cold end of the silica tubes.

ARPES experiments

Soft x-ray ARPES measurements were performed at the Advanced Resonant Spectroscopies (ADRESS) beamline at the Swiss Light Source with a SPECS PHOIBOS-150 analyzer (40) and the “Dreamline” beamline of the Shanghai Synchrotron Radiation Facility (SSRF) with a Scienta Omicron DA30L analyzer. Most of the soft x-ray ARPES data were taken at the ADRESS beamline, with the overall energy resolution varied from 40 to 100 meV. VUV ARPES measurements were performed at the Dreamline beamline of SSRF with a Scienta Omicron DA30L analyzer and at the 13U beamline of the National Synchrotron Radiation Laboratory at Hefei with a Scienta Omicron R4000 analyzer. In the soft x-ray ARPES experiments, to eliminate the surface states, the samples were cleaved in air and then transferred to the vacuum chamber. However, we found that the surface states could also be eliminated for very few samples cleaved in high vacuum. In the VUV ARPES experiments, all the samples were cleaved in high vacuum. The measurements were performed at 20 K with vacuum condition better than 5 × 10⁻¹¹ torr.

First-principles calculations of the band structure

We performed first-principles calculations based on density functional theory (41) within the Perdew-Burke-Ernzerhof exchange-correlation (42) implemented in the Vienna ab initio simulation package (43). The plane-wave cutoff energy was 500 eV with a 12 × 12 × 6 k-mesh in the BZ for bulk band and slab calculations. All the calculations were in the absence of SOC. We used maximally localized Wannier functions (44) to obtain the tight-binding model of the bulk ZrSiS and used it for the FS calculations. The lattice constants a = b = 3.544 Å and c = 8.055 Å and the atomic sites are in agreement with the experimental values.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/5/eaau6459/DC1

Fig. S1. ARPES data collected with VUV lights.