Emulating a trial of joint dynamic strategies: an application to monitoring and treatment of HIV-positive individuals

Abstract

Decisions about when to start or switch a therapy often depend on the frequency with which individuals are monitored or tested. For example, the optimal time to switch antiretroviral therapy depends on the frequency with which HIV-positive individuals have HIV-RNA measured. This paper describes an approach to use observational data for the comparison of joint monitoring and treatment strategies, and applies the method to a clinically relevant question in HIV research: when can monitoring frequency be decreased and when should individuals switch from a first-line treatment regimen to a new regimen?

We outline the target trial that would compare the dynamic strategies of interest, and then describe how to emulate it using data from HIV-positive individuals included in the HIV-CAUSAL Collaboration and the Centers for AIDS Research Network of Integrated Clinical Systems. When, as in our example, few individuals follow the dynamic strategies of interest over long periods of follow-up, we describe how to leverage an additional assumption: no direct effect of monitoring on the outcome of interest. We compare our results with and without the no direct effect assumption. We found little differences on survival and AIDS-free survival between strategies where monitoring frequency was decreased at a CD4 threshold of 350 cells/μl compared with 500 cells/μl and where treatment was switched at an HIV-RNA threshold of 1000 copies/ml compared with 200 copies/ml. The no direct effect assumption resulted in efficiency improvements for the risk difference estimates ranging from a 7- to 53- fold increase in the effective sample size.

1. Introduction

Many clinical guidelines recommend starting, stopping, or switching a therapy when a clinical marker crosses a certain threshold. For example, some guidelines recommend that adults initiate statin therapy if LDL-Cholesterol is greater than 190 mg/dL ^[1], and others that HIV-positive individuals switch treatment (antiretroviral therapy) if HIV-RNA is greater than 500 copies/ml ^[2]. These guidelines are examples of dynamic strategies because the decision to start or switch therapy depends on an individual’s time-varying covariates (LDL-cholesterol or HIV-RNA).

When randomized trials are not available to inform guidelines, observational data can be used to try to emulate a hypothetical randomized trial—a target trial ^[3] —of dynamic strategies. For example, previous observational analyses have emulated target trials in which HIV-positive individuals were assigned to different treatment initiation and switching strategies ^[4–10]. Adjustment for measured time-varying confounders was achieved via inverse-probability weighting ^{[4, 6]} or the parametric g-formula ^[8–10].

But recommendations about when to start or switch a therapy generally depend on the frequency with which individuals are monitored or tested ^[11]. For example, the optimal time to switch therapy may be the first time HIV-RNA crosses above 500 copies/ml if HIV-positive individuals are monitored every 6 months, but at a different threshold, lower than 500 copies/ml, if individuals were monitored every 12 months. Therefore, clinical guidelines for starting or switching a treatment based on the results of a test need to specify both the frequency of monitoring/testing and the threshold at which treatment is started or switched.

In this paper, we extend the methodology to emulate a target trial of joint monitoring and treatment strategies using observational data, and describe how to leverage an additional assumption: no effect of monitoring on the outcome except through aiding decisions concerning when to switch antiretroviral therapy ^[11]. Exploiting this no direct effect assumption may drastically decrease the estimates’ variance without requiring additional modeling assumptions. Section 2 outlines the key components of the target trial and how to emulate it using observational data from HIV-positive individuals. In Section 3, we describe how to estimate the per-protocol effect, first in the target trial and then using observational data. Section 4 introduces the no direct effect assumption and compares the efficiency of the results estimated with and without the additional assumption.

2. Specification and emulation of the target trial

Table 1 summarizes the key components of the protocol of the target trial in which participants are randomly assigned to one of four joint monitoring and treatment strategies, based loosely on current clinical guidelines ^{[2, 12–14]}. The goal of the trial is to determine the joint strategy with the greatest 5-year survival and AIDS-free survival for HIV-positive individuals who achieve virologic suppression within 12 months of initiating an eligible ART regimen.

Table 1.

Key components of the protocol of the target trial of joint monitoring and treatment strategies

Component	Target trial	Emulation using observational data
Eligibility criteria	Confirmed virologic suppression (two consecutive HIV-RNA ≤ 200 copies/ml) within 12 months of initiating an eligible treatment regimen in 2000 or later while remaining on an eligible treatment regimen (Appendix Table 4) 18 years or older, no history of AIDS-defining illness [25], a CD4 cell count measurement, no pregnancy	Same, except pregnancy information is not available for all individuals
Joint monitoring and treatment strategies	CD4 threshold 350/tight control: CD4 cell count and HIV-RNA are monitored every 3–6 months when CD4 is below a threshold of 350 cells/μl and every 9–12 months when CD4 is above the threshold, and individuals switch treatment (Appendix Table 4) within 3 months of HIV-RNA crossing above 200 copies/ml CD4 threshold 350/loose control: same as (1) except that the HIV-RNA threshold is 1000 copies/ml CD4 threshold 500/tight control: same as (1) except that the CD4 cell count threshold is 500 cells/μl CD4 threshold 500/loose control: same as (3) except that the HIV-RNA threshold is 1000 copies/ml All four strategies further require individuals to be monitored once every 3–6 months (± 1 month) when HIV-RNA>200 copies/ml or after diagnosis of an AIDS-defining illness. Individuals cannot switch after the initial treatment switch.	Same, except changes to new regimens lasting fewer than 14 days were not considered treatment switches and the person-time was assigned to the previous regimen of duration 14 days or longer (sensitivity analyses with periods other than 14 did not materially change the results).
Outcomes	All-cause mortality Combined endpoint of AIDS-defining illness or death	Same. The date of death was identified using a combination of national and local mortality registries and clinical records, as described elsewhere [15, 16], and AIDS-defining illnesses were ascertained by the treating physicians.
Follow-up period	Individuals are followed from baseline (confirmed virologic suppression while otherwise eligible, when randomization occurs) until the event of interest, pregnancy, loss to follow-up (12 months after the most recent laboratory measurement), or five years of follow-up, whichever occurred earlier.	Same, except that the cohort-specific administrative end of follow-up may be less than 5 years from baseline and pregnancy information not available for all individuals.
Causal contrast(s) of interest	Intention-to-treat effect Per-protocol effect, i.e. the effect that would have been observed if all individuals were monitored and switched treatment as indicated by their randomization arm	Per-protocol-effect effect only. Since all individuals included in our study had data consistent with each of the four joint monitoring and treatment strategies at baseline, an intention-to-treat analysis would compare groups consisting of the same individuals.
Analysis plan	Intention-to-treat analysis Per-protocol analysis (see text)	Same per-protocol analysis with replication

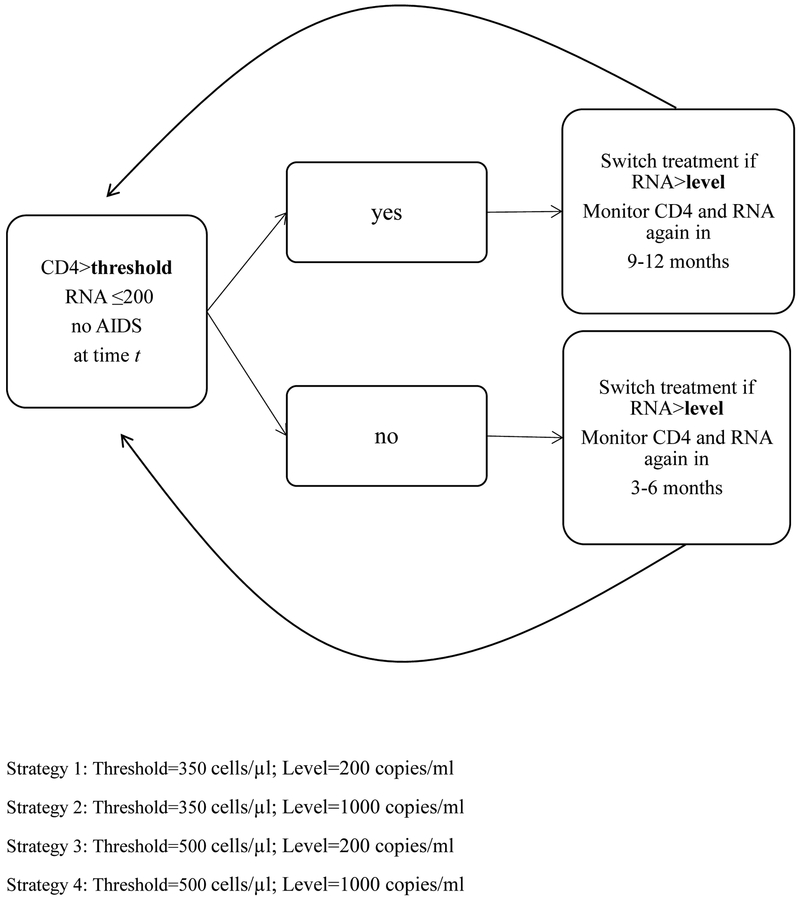
Strategy (1) “CD4 threshold 350/tight control” is as follows: CD4 cell count and HIV-RNA are monitored every 3–6 months when CD4 is below a threshold of 350 cells/μl and every 9–12 months when CD4 is above the threshold, and individuals switch treatment within 3 months of HIV-RNA crossing above 200 copies/ml (tight-control) and do not switch again.

Strategy (2) “CD4 threshold 350/loose control” is the same as (1) except that the HIV-RNA threshold is 1000 copies/ml (loose-control).

Strategy (3) “CD4 threshold 500/tight control” is the same as (1) except that the CD4 cell count threshold is 500 cells/μl.

Strategy (4) “CD4 threshold 500/loose control” is the same as (3) except that the HIV-RNA threshold is 1000 copies/ml. All four strategies further require individuals to be monitored every 3–6 months when HIV-RNA>200 copies/ml or after diagnosis of an AIDS-defining illness (Figure 1).

Figure 1.

Schematic of 4 dynamic monitoring and treatment strategies to be followed at each time t of follow-up. By considering the combinations of 2 CD4 cell count thresholds (350 and 500 cells/μl) and 2 HIV-RNA levels (200 and 1000 copies/ml), 4 strategies are defined.

Any treatment change was classified as a non-switch, ineligible switch, or switch (Appendix Table 4). For example, a change from one protease-inhibitor based regimen to another protease-inhibitor based regimen was not considered a switch whereas a change from a protease-inhibitor based regimen to an integrase-inhibitor based regimen was considered a switch. Any changes to monotherapy or dual-therapy or stopping therapy altogether were considered ineligible switches as they are not consistent with current guidelines ^[7]. The switching thresholds were based on current clinical guidelines and to maximize the number of individuals following distinct strategies (in practice, switching also occurs for reasons other than treatment failure).

We consider two clinical endpoints: all-cause mortality and a combined endpoint of AIDS-defining illness or death. Our goal is to estimate the per-protocol effect, that is, the effect that would have been observed if all individuals were monitored and switched treatment as indicated by their assigned strategy.

We emulated this target trial using observational data from two collaborations of prospective studies from high-income countries. The HIV-CAUSAL Collaboration includes prospective cohort studies from Europe and the Americas ^[15]. The individual cohort studies are FHDH-ANRSC04 (France), ANRS PRIMO (France), ANRS SEROCO (France), ANRS CO3-Aquitaine (France), UK CHIC (United Kingdom), UK Register of HIV Seroconverts (United Kingdom), ATHENA (the Netherlands), SHCS (Switzerland), PISCIS (Spain), CoRIS/CoRIS-MD (Spain), GEMES (Spain), VACS (United States), AMACS (Greece), IPEC (Brazil) and SAC (Canada). The Center for AIDS Research (CFAR) Network of Integrated Clinical Systems (CNICS) contains clinical data from inpatient and outpatient encounters of HIV-positive individuals at 8 U.S. sites: Case Western Reserve University, Fenway Community Health Clinic, Johns Hopkins University, University of Alabama at Birmingham, University of California at San Diego, University of California at San Francisco, University of North Carolina, and University of Washington ^[16]. All cohorts included in the HIV-CAUSAL and CNICS Collaborations were assembled prospectively and are based on data collected for clinical purposes.

To emulate the target trial, we identified HIV-positive individuals who met the eligibility criteria, classified them into the four strategies (see below), and followed them until the event of interest, pregnancy, loss to follow-up (12 months after the most recent laboratory measurement), five years of follow-up, or the cohort-specific administrative end of follow-up, whichever occurred earlier. To allow more individuals to follow each strategy over time, our primary analysis included an additional month before and after each monitoring window (e.g. 3–6 ± 1), so that the monitoring grace period was 5 months. In the next sections, we describe how to estimate the per-protocol effect in the target trial and using observational data.

3. Estimating the per-protocol effect

Specification of per-protocol analysis in the target trial

Eligible individuals are randomized at enrollment in the trial to one of the four joint monitoring and treatment strategies. We define the per-protocol effect as the difference in 5-year survival and AIDS-free survival between the four strategies if all individuals have followed their assigned strategies as indicated in the protocol of the target trial. We describe a three-step procedure to estimate the per-protocol effect in the target trial.

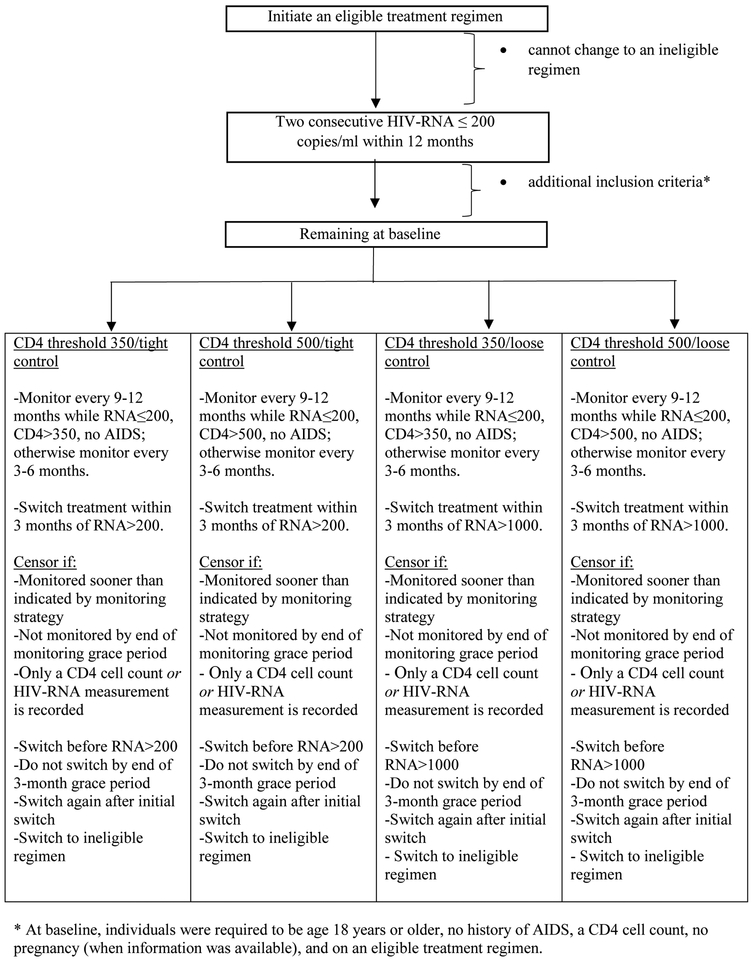
First, censor individuals when they deviate from their assigned strategy. Specifically, censor individuals when they are monitored sooner than indicated by their strategy, when they are not monitored soon enough, when they change treatment sooner than indicated by their strategy, when they have not switched at the end of the 3-month treatment switching grace period, when they switch treatment again after their initial treatment switch, when only a CD4 cell count or HIV-RNA measurement is recorded (uneven monitoring), or when they switch to an ineligible treatment regimen (Figure 2).

Figure 2.

Flow diagram for the eligibility criteria and censoring process, CNICS and HIV-CAUSAL Collaboration 2000–2015

Second, fit a discrete-time hazards model and use its predicted values to estimate standardized survival and AIDS-free survival curves ^{[6, 17, 18]}. For example, the discrete-time hazard at each month t can be estimated by fitting a pooled logistic model such as $logit\text{\hspace{0.05em}Pr}\left(D_{t+1}=1|D_t=0,C_t=0,X,V\right)={\theta }_0+h\left(t\right)+{\theta }_1^{\text{'}}V+{\theta }_2{X}_{350-tightcontrol}+{\theta }_3{X}_{350-loosecontrol}+{\theta }_4{X}_{500-loosecontrol}+{\theta }_5^{\text{'}}{X}_{350-tightcontrol}h\left(t\right)+{\theta }_6^{\text{'}}{X}_{350-loosecontrol}h\left(t\right)+{\theta }_7^{\text{'}}{X}_{500-loosecontrol}h\left(t\right)$, where θ₀ + h(t) is a time-varying intercept with h(t) defined as a restricted cubic spline for follow-up time (4 knots at 1, 6, 12, and 24 months), D_t is an indicator for developing the outcome by month t (1: yes, 0: no), V is a vector of baseline prognostic factors that predict adherence, the X’s are indicators for the corresponding strategy (1: yes, 0: no) with strategy CD4 threshold 500/tight control as the reference, and C_t = 0 is an indicator for remaining uncensored through t. We use prime notation to denote vectors since V is a vector of baseline covariates and h(t) includes 3 covariates. We include product terms between h(t) and the X’s so that the estimated hazard ratios can vary over time. The model uses a smooth function to combine information from each strategy, producing more stable estimates than a non-parametric estimate of the survival function (e.g. Kaplan-Meier) ^[6]. This model adjusts for baseline (time-fixed) prognostic factors, but not for post-baseline (time-varying) factors because the inclusion of post-baseline covariates in the model for the outcome may introduce selection bias ^[19].

Third, estimate inverse-probability (IP) weights to adjust for post-baseline prognostic factors. To describe the weights, we need to introduce some additional notation. Let A_t = 2 indicate that the individual switches to an eligible regimen at time t, A_t = 1 indicate that the individual switches to an ineligible regimen during time t, and A_t = 0 indicate that the individual does not switch treatment during time t. Let N_t = 2 indicate that the individual has both CD4 cell count and HIV-RNA measurements during time t, N_t = 1 indicate that the individual has either a CD4 cell count or an HIV-RNA measurement during time t but not both, and N_t = 0 indicate that the individual has neither a CD4 cell count nor an HIV-RNA measurement during time t. We use overbars to denote the history of a time-dependent variable:${\stackrel{-}{N}}_t$ is the individual’s monitoring history through time t, ${\stackrel{-}{A}}_t$ is the individual treatment switching history through time t, and ${\stackrel{-}{L}}_t$ is the individual time-varying covariate history through time t.

The non-stabilized IP treatment switching weight for each uncensored individual at each time t is $W_t^A={\prod }_{k=0}^t\frac{1}{Pr\left(C_k=0|C_{k-1}=0,D_k=0,X=x,{\stackrel{-}{L}}_k,{\stackrel{-}{N}}_k,{\stackrel{-}{A}}_{k-1}\right)}$.$Pr\left(C_k=0|C_{k-1}=0,D_k=0,X=x,{\stackrel{-}{L}}_k,{\stackrel{-}{N}}_k,{\stackrel{-}{A}}_{k-1}\right)\mathrm{i}\mathrm{s}\mathrm{e}\mathrm{q}\mathrm{u}\mathrm{a}\mathrm{l}\mathrm{t}\mathrm{o}f\left(A_k|{\stackrel{-}{A}}_{k-1},D_k=0,{\stackrel{-}{L}}_k,{\stackrel{-}{N}}_k\right)$ before and after the treatment switching grace period where $f\left(A_k|{\stackrel{-}{A}}_{k-1},D_k=0,{\stackrel{-}{L}}_k,{\stackrel{-}{N}}_k\right)$ is the conditional probability density function $f_{A_k|{\stackrel{-}{A}}_{k-1},D_k=0,{\stackrel{-}{L}}_k,{\stackrel{-}{N}}_k}\left(a_k|{\stackrel{-}{a}}_{k-1},d_k=0,{\stackrel{-}{l}}_k,{\stackrel{-}{n}}_k\right)$ with $\left(a_k|{\stackrel{-}{a}}_{k-1},d_k=0,{\stackrel{-}{l}}_k,{\stackrel{-}{n}}_k\right)$ evaluated at the random argument $\left(A_k|{\stackrel{-}{A}}_{k-1},D_k=0,{\stackrel{-}{L}}_k,{\stackrel{-}{N}}_k\right)$ and is equal to $1-Pr\left(A_k=1|{\stackrel{-}{A}}_{k-1},D_k=0,{\stackrel{-}{L}}_k,{\stackrel{-}{N}}_k\right)$ during the treatment switching grace period ^{[6, 20]}.

We estimate $Pr\left(A_k=a_k|{\stackrel{-}{A}}_{k-1},D_k=0,{\stackrel{-}{L}}_k,{\stackrel{-}{N}}_k\right)$ via a pooled multinomial logistic regression model fit in the original data. Alternatively, we could fit two nested logistic models: a model for ineligible treatment switching and a model for an eligible treatment switch (versus no switch) conditional on not having an ineligible treatment switch (Appendix 1).

Similarly, the non-stabilized IP monitoring weights are $W_t^N={\prod }_{k=0}^t\frac{1}{Pr\left(C_k=0|C_{k-1}=0,D_k=0,X=x,{\stackrel{-}{L}}_{k-1},{\stackrel{-}{N}}_{k-1},{\stackrel{-}{A}}_{k-1}\right)}$.

$Pr\left(C_k=0|C_{k-1}=0,D_k=0,X=x,{\stackrel{-}{L}}_{k-1},{\stackrel{-}{N}}_{k-1},{\stackrel{-}{A}}_{k-1}\right)$ is equal to $f\left(N_k\right|{\stackrel{-}{N}}_{k-1},D_k=0,{\stackrel{-}{L}}_{k-1},{\stackrel{-}{A}}_{k-1})$ before and after the monitoring grace period where $f\left(N_k|{\stackrel{-}{N}}_{k-1},D_k=0,{\stackrel{-}{L}}_{k-1},{\stackrel{-}{A}}_{k-1}\right)$ is the conditional probability mass function $f_{N_k|{\stackrel{-}{N}}_{k-1},D_k=0,{\stackrel{-}{L}}_{k-1},{\stackrel{-}{A}}_{k-1}}\left(n_k\right|{\stackrel{-}{n}}_{k-1},d_k=0,{\stackrel{-}{l}}_{k-1},{\stackrel{-}{a}}_{k-1})$ with $\left(n_k\right|{\stackrel{-}{n}}_{k-1},d_k=0,{\stackrel{-}{l}}_{k-1},{\stackrel{-}{a}}_{k-1})$ evaluated at the random argument $\left(N_k\right|{\stackrel{-}{N}}_{k-1},D_k=0,{\stackrel{-}{L}}_{k-1},{\stackrel{-}{A}}_{k-1})$ and is equal to $1-Pr(N_k=1|{\stackrel{-}{N}}_{k-1},D_k=0,{\stackrel{-}{L}}_{k-1},{\stackrel{-}{A}}_{k-1})$ during the monitoring grace period. We estimate $Pr(N_k=n_k|{\stackrel{-}{N}}_{k-1},D_k=0,{\stackrel{-}{L}}_{k-1},{\stackrel{-}{A}}_{k-1})$ via a pooled multinomial logistic model fit in the original data. Alternatively, we could fit two nested logistic models: a model for uneven monitoring (only a CD4 cell count or HIV-RNA measurement is recorded) and a model for CD4 and RNA monitoring (versus no monitoring) conditional on not having uneven monitoring (Appendix 1).

All models include a time-varying intercept, monitoring history ${\stackrel{-}{N}}_k$ summarized by the proportion of months of follow-up from baseline to time k with a CD4 cell count measurement (restricted cubic splines with 3 knots at 0.2, 0.3 and 0.5), the proportion of months of follow-up from baseline to time k with an RNA measurement (restricted cubic splines with 3 knots at 0.2, 0.3 and 0.5), months between time k and the last CD4 cell count measurement (restricted cubic splines with 3 knots at 1, 4 and 7), and months between time k and the last RNA measurement (restricted cubic splines with 3 knots at 1, 4 and 7), treatment switching history ${\stackrel{-}{A}}_k$ summarized by V V and L_k, which includes the most recently recorded values of CD4 cell count (restricted cubic splines with 5 knots at 200, 350, 500, 650, and 1000 cells/μl), HIV-RNA (≤200, 201–999, 1,000–9,999, ≥10,000 copies/ml), and diagnosis of an AIDS-defining illness (when the outcome was all-cause mortality) at time k.

The non-stabilized IP weight W_t for each person-month is the product of the treatment switching weight and the monitoring weight $W_t=W_t^A*W_t^N$. We truncate the estimated weights W_t at the 99^th percentile to protect against potential model misspecification and near violations of positivity.

Under the assumptions of sequential exchangeability, positivity, and consistency for monitoring and treatment switching conditional on the measured time-fixed and time-varying covariates ^[11], the parameters of the IP weighted discrete-time hazards model consistently estimate the parameters of a dynamic marginal structural discrete-time hazards model

$$logit\text{\hspace{0.05em}Pr}\left(D_{t+1}^x=1|D_t^x=0,V\right)={\beta }_0+h\left(t\right)+{\beta }_1^{\text{'}}V+{\beta }_2{\text{x}}_{350-tightcontrol}+{\beta }_3{x}_{350-loosecontrol}+{\beta }_4{x}_{500-loosecontrol}+{\beta }_5^{\text{'}}{x}_{350-tightcontrol}h\left(t\right)+{\beta }_6^{\text{'}}{x}_{350-loosecontrol}h\left(t\right)+{\beta }_7^{\text{'}}{x}_{500-loosecontrol}h\left(t\right)$$

where $D_t^x$ is, for each individual, a (counterfactual) indicator for developing the outcome by month t (1: yes, 0: no) under strategy X= x for monitoring and treatment. The validity of this procedure also requires no misspecification of the models used to estimate the weights and of the discrete-time hazards model.

The non-stabilized IP weights defined above imply strategies under which individuals who were not monitored or did not switch during the corresponding grace period are forced to be monitored or switch treatment at the end of the grace period ^[6]. Since this can lead to unstable estimates and may not be consistent with clinical practice, we also consider IP weights that estimate strategies under which individuals are monitored with a uniform probability during the monitoring grace period and switch treatment with a uniform probability during the treatment switching grace period ^[6]. Appendix 1 shows the contributions to the monitoring and treatment switching weights at different time points for both the non-stabilized and uniform IP weights. We used nonparametric bootstrapping with 500 samples to compute 95% confidence intervals around our estimates.

Even if the data on monitoring and treatment strategy assignment had been inadvertently erased from the analysis file in the target trial, one can still construct consistent estimators of the per-protocol effects under exchangeability, consistency, and positivity. In fact, Robins (1986) shows that the most efficient estimator of the per-protocol effect ignores data on assignment even when available ^[21]. The following section describes estimators that ignore data on assignment to emulate the per-protocol analysis of a target trial using observational data.

Emulation of the per-protocol analysis using observational data

The observational per-protocol analysis is the same as described above for the target trial except that data on monitoring and treatment strategy assignment is absent as no such assignment occurred. In fact, an individual’s data at baseline may be consistent with more than 1 of the 4 strategies of interest. As previously described in detail ^{[6, 7, 22]}, we solved this problem by creating an expanded dataset with 4 exact replicates of each individual (1 per strategy), each following one of the strategies of interest. We censored each replicate, as described above, when the individual’s data were no longer consistent with the strategy assigned to the replicate. Appendix 2 describes data for three hypothetical individuals and the strategies they followed over 24 months of follow-up time. To estimate the per-protocol effect, we used the same IP weighted pooled logistic model described for the target trial, except that we fitted the model to the expanded dataset. The models for the weights were fit in the original unexpanded dataset.

Data from each participating study can be requested from the sponsoring institution in accordance with the applicable laws or regulations in each country. SAS programs are available at https://www.hsph.harvard.edu/causal/hiv.

Data analysis results

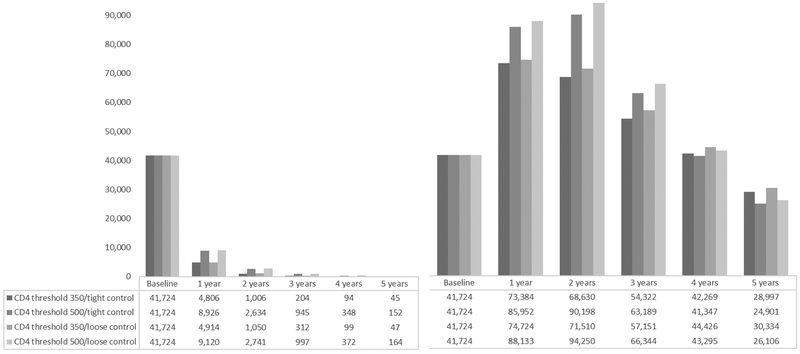
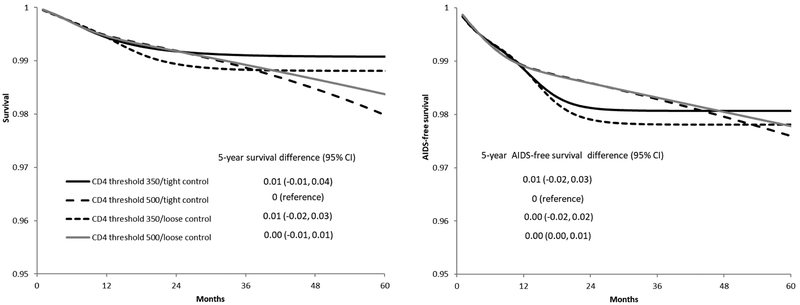
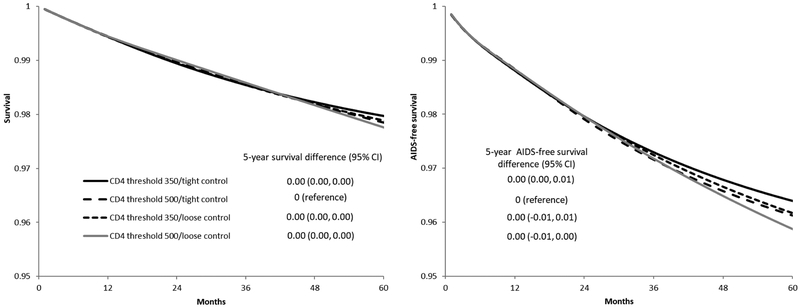
41,724 individuals met the eligibility criteria and were included in our analysis. After two years of follow-up, 1,006 individuals were following the CD4 threshold 350/tight control strategy, 2,634 individuals were following the CD4 threshold 500/tight control strategy, 1,050 individuals were following the CD4 threshold 350/loose control strategy, and 2,741 individuals were following the CD4 threshold 500/loose control strategy. After five years of follow-up, these numbers were 45, 152, 47, and 164, respectively (Figure 3). Over the five-year follow-up, there were 455 deaths and 1,151 cases of AIDS-defining illness or death (Table 2). The median (IQR) time from baseline to death among individuals who died was 5 (2, 10) months. Figure 4 plots the estimated 5-year survival and 5-year AIDS-free survival. Compared with the CD4 threshold 500/tight control strategy, the five-year survival difference was 0.01 (-0.01, 0.04) for CD4 threshold 350/tight control, 0.01 (-0.02, 0.03) for CD4 threshold 350/loose control, and 0.00 (-0.01, 0.01) for CD4 threshold 500/loose control. The five-year AIDS-free survival difference was 0.00 (-0.02, 0.03) for CD4 threshold 350/tight control, 0.00 (-0.02, 0.02) for CD4 threshold 350/loose control, and 0.00 (0.00, 0.01) for CD4 threshold 500/loose control, compared with CD4 threshold 500/tight control (Table 2).

Figure 3.

Number of replicates following each monitoring and treatment strategy over follow-up time, without (left) and with (right) the no direct effect assumption, CNICS and HIV-CAUSAL Collaboration 2000–2015

Table 2.

Estimated 5-year survival and AIDS-free survival^* under each monitoring and treatment strategy, CNICS and HIV-CAUSAL Collaboration, 2000–2015

“No direct effect” assumption	Strategy	No. of deaths	5-year survival (95% CI)	5-year survival difference (95% CI)	No. of deaths/AIDS	5-year AIDS-free survival (95% CI)	5-year AIDS-free survival difference (95% CI)
No	CD4 threshold 350/tight control	101	0.99 (0.99, 1.00)	0.01 (-0.02, 0.04)	262	0.98 (0.97, 0.99)	0.01 (-0.02, 0.03)
	CD4 threshold 500/tight control	123	0.98 (0.95, 1.00)	0 (reference)	309	0.98 (0.95, 1.00)	0 (reference)
	CD4 threshold 350/loose control	105	0.99 (0.98, 1.00)	0.01 (-0.02, 0.04)	267	0.98 (0.97, 0.99)	0.00 (-0.02, 0.03)
	CD4 threshold 500/loose control	126	0.98 (0.96, 1.00)	0.00 (-0.01, 0.01)	313	0.98 (0.96, 1.00)	0.00 (0.00, 0.01)
Yes	CD4 threshold 350/tight control	1,375	0.98 (0.97, 0.98)	0.00 (0.00, 0.01)	2,224	0.96 (0.96, 0.97)	0.00 (0.00, 0.01)
	CD4 threshold 500/tight control	1,478	0.98 (0.97, 0.98)	0 (reference)	2,514	0.96 (0.95, 0.97)	0 (reference)
	CD4 threshold 350/loose control	1,455	0.98 (0.97, 0.98)	0.00 (0.00, 0.00)	2,353	0.96 (0.95, 0.97)	0.00 (-0.01, 0.01)
	CD4 threshold 500/loose control	1,578	0.98 (0.97, 0.99)	0.00 (0.00, 0.00)	2,667	0.96 (0.95, 0.97)	0.00 (-0.01, 0.00)

These estimates were standardized by the baseline covariates: sex, CD4 cell count (≤200, 201–350, 351–500, ≥501 cells/μl), years since HIV diagnosis (<1, 1 to 4, ≥5 years, unknown), race (white, black, other or unknown), geographic origin (N. America/W. Europe, Sub-Saharan Africa, other, unknown), acquisition group (heterosexual, homosexual or bisexual, injection drug use, other or unknown), calendar year (restricted cubic splines with 3 knots at 2001, 2007 and 2011), age (restricted cubic splines with 3 knots at 25, 39 and 60), cohort, and months from treatment initiation to virologic suppression (2–4, 5–8, ≥9).

^*All estimates rounded to the nearest hundredth

Figure 4.

Survival (left) and AIDS-free survival (right) under each monitoring and treatment strategy, CNICS and HIV-CAUSAL Collaboration 2000–2015. The curves are standardized by the baseline covariates: sex, CD4 cell count (≤200, 201–350, 351–500, ≥501 cells/μl), years since HIV diagnosis (<1, 1 to 4, ≥5 years, unknown), race (white, black, other or unknown), geographic origin (N. America/W. Europe, Sub-Saharan Africa, other, unknown), acquisition group (heterosexual, homosexual or bisexual, injection drug use, other or unknown), calendar year (restricted cubic splines with 3 knots at 2001, 2007 and 2011), age (restricted cubic splines with 3 knots at 25, 39 and 60), cohort, and months from treatment initiation to virologic suppression (2–4, 5–8, ≥9).

4. Estimating the per-protocol effect with a “no direct effect” assumption

In many settings, it can be argued that monitoring has no direct effect on the outcome except through aiding decisions regarding switching treatment. For example, in our study, we can assume that having a lab measurement can only affect the risk of AIDS or death by triggering treatment changes. More precisely, consider a target trial with two arms in which both arms are assigned the same static treatment strategy but different monitoring strategies. Then, the no direct effect assumption says that the two arms will have the same survival curves. By emulating this type of target trial with observational data it is in principle possible to test the no direct effect assumption under sequential exchangeability, positivity, and consistency ^[23].

Under the assumption of no direct effect of monitoring measurements inconsistent with the monitoring strategy have no effect on survival. Therefore CD4 and HIV-RNA measurements at months not consistent with the monitoring strategy can be ignored and replicates need not be censored at those times. Because these individuals are not censored, we will have more individuals continuing to follow the strategies of interest at any given time and therefore more precise effect estimates. Under the no direct effect assumption, individuals can no longer be censored for being monitored too frequently but can still be censored for not being monitored frequently enough. In fact, it is possible for the counterfactual survival curve under a particular monitoring and treatment strategy to be identified under the no direct effect assumption but to be unidentified (due to lack of positivity) without the assumption ^[11]. For example, if all subjects in the observational data were monitored every month, it would not be possible to identify the effect of any less frequent monitoring strategy without the no direct effect assumption.

To implement the modified per-protocol analysis that incorporates the no direct effect assumption, we construct a “no direct effect” version of the data using the following algorithm, formalized previously by Robins and colleagues ^[11]: (1) recode the monitoring indicator at each month t to 0 when an individual is monitored at a time t inconsistent with his or her randomization arm’s monitoring strategy (including when only CD4 cell count or HIV-RNA is measured; (2) delete the CD4 cell count and HIV-RNA recorded at month t whenever the monitoring indicator at time t has been recoded to 0; and (3) carry forward the previous CD4 cell count and HIV-RNA until the next time that individual is monitored (Appendix 3). In this “no direct effect” dataset, we then proceed to censor individuals when they deviate from their assigned strategy and to estimate the survival and AIDS-free survival for each strategy as described above. To emulate the target trial using the observational data, we modify the expanded dataset in the same way to construct a “no direct effect” dataset.

The algorithm described above can be extended to strategies with grace periods, which allows even more individuals to follow the strategies of interest over a long period of time. The algorithm can be adapted to handle more than one monitoring time during a grace period. To extend the algorithm, replicates monitored during the monitoring grace period are further replicated, as a way of simulating monitoring trajectories where replicates are monitored at different times during the monitoring grace period ^[11]. Specifically, a replicate monitored during the grace period is cloned at the point of their first measurement in the grace period into two new replicates 1_t and 2_t where t denotes the time in the grace period the cloning occurred. For replicate 1_t, the new CD4 cell count and HIV-RNA measurements are revealed (recorded for data analysis) and the replicate exits the monitoring grace period in the usual way. For replicate 2_t, the new CD4 cell count and HIV-RNA measurements are ignored, i.e., the monitoring indicator is recoded to 0, the CD4 and HIV-RNA measurements are deleted, the previous CD4 and RNA measurements are carried forward, and replicate 2_t moves to the next month of the grace period. Replicates are only censored if they are not monitored at least as frequently as required by the strategy. As an example, replicate 2_t will be censored if she receives no further monitoring during the grace period. Appendix 3 describes the “no direct effect” dataset for one hypothetical individual, first under strategies that require individuals to be monitored exactly every 6 months if their CD4 cell count falls below the strategy’s threshold and exactly every 12 months otherwise and second under strategies with grace periods.

Under the no direct effect assumption, the monitoring weights $W_t^N$ are equal to ${\prod }_{k:N^{*}\left(k\right)=2}^t\frac{1}{f\left(N_k\right|{\stackrel{-}{N}}_{k-1},D_k=0,{\stackrel{-}{L}}_{k-1},{\stackrel{-}{A}}_{k-1})}$ where N*(k)=2 denotes times k when a replicate’s CD4 and HIV-RNA values are revealed. The factors in the denominator of $W_t^N$ are 1 at all times when a replicate’s CD4 and HIV-RNA values are not revealed. (Appendix 1) ^[11]. The treatment weights remain as before. Note that different replicates from a single person will have different weights. Below, we compare the efficiency of the estimates with and without the no direct effect assumption when using uniform IP weights (Table 2).

Data analysis results

After five years of follow-up, 28,997 individuals were following the CD4 threshold 350/tight control strategy, 24,901 individuals were following the CD4 threshold 500/tight control strategy, 30,334 individuals were following the CD4 threshold 350/loose control strategy, and 26,106 individuals were following the CD4 threshold 500/loose control strategy (Figure 3). Over the five-year follow-up, there were 5,886 deaths and 9,758 cases of AIDS-defining illness or death (Table 2). The median (IQR) time to death among individuals who died was 14 (6, 28) months. Figure 5 plots the estimated 5-year survival and 5-year AIDS-free survival. Compared with the CD4 threshold 500/tight control strategy, the five-year survival difference was 0.00 (0.00, 0.00) for CD4 threshold 350/tight control, 0.00 (0.00, 0.00) for CD4 threshold 350/loose control, and 0.00 (0.00, 0.00) for CD4 threshold 500/loose control. The five-year AIDS-free survival difference was 0.00 (0.00, 0.01) for CD4 threshold 350/tight control, 0.00 (-0.01, 0.01) for CD4 threshold 350/loose control, and 0.00 (-0.01, 0.00) for CD4 threshold 500/loose control, compared with CD4 threshold 500/tight control (Table 2).

Figure 5.

Survival (left) and AIDS-free survival (right) under each monitoring and treatment strategy with the no direct effect assumption, CNICS and HIV-CAUSAL Collaboration 2000–2015. The curves are standardized by the baseline covariates: sex, CD4 cell count (≤200, 201–350, 351–500, ≥501 cells/μl), years since HIV diagnosis (<1, 1 to 4, ≥5 years, unknown), race (white, black, other or unknown), geographic origin (N. America/W. Europe, Sub-Saharan Africa, other, unknown), acquisition group (heterosexual, homosexual or bisexual, injection drug use, other or unknown), calendar year (restricted cubic splines with 3 knots at 2001, 2007 and 2011), age (restricted cubic splines with 3 knots at 25, 39 and 60), cohort, and months from treatment initiation to virologic suppression (2–4, 5–8, ≥9).

These estimates under the no direct effect assumption were more precise than the ones in the previous section. For example, the standard errors for the 5-year survival difference estimates ranged from 0.0046 to 0.0131 without the no direct effect assumption and from 0.0017 to 0.0019 with the no direct effect assumption, implying the ratio of the effective sample size under the no direct effect assumption to that without the assumption ranged from 7 to 53.

5. Discussion

This paper describes the use of observational data to emulate a target trial of joint monitoring and treatment strategies. We applied the method to strategies for the management of HIV-positive individuals and found no differences on survival and AIDS-free survival between strategies with monitoring at a CD4 threshold of 350 cells/μl compared with 500 cells/μl and with treatment switching at an HIV-RNA threshold of 1000 copies/ml compared with 200 copies/ml.

Like for any other observational study, the validity of our estimates relies on the untestable assumption that the measured covariates were sufficient to adjust for confounding and selection bias. In our analysis, we adjusted for several joint predictors of monitoring and the outcome as well as of treatment switching and the outcome. If physicians monitor individuals perceived to have lower adherence with greater frequency or make different decisions about treatment switching based on perceived adherence, which we did not directly adjust for, this assumption may not hold. However, we were able to adjust for several potential proxies of adherence, such as HIV-RNA. Also, our results could be biased if both the monitoring frequency and survival vary by site. However, the monitoring frequency was similar between the countries included in our analysis (data not shown).

One challenge in estimating the effect of complex treatment strategies using observational data is that few individuals may have data consistent with the strategies of interest over an extended period of follow-up. We described how to ameliorate this by incorporating the often plausible assumption that monitoring has no direct effect on the outcome, except through aiding decisions regarding when to switch treatment. The no direct effect assumption is advantageous because it increases the number of individuals whose data are consistent with the strategies of interest and does not require additional modeling assumptions. In fact, our survival and AIDS-free survival estimates were similar with and without the no direct effect assumption, but the estimates under the no direct effect assumption were more precise.

The no direct effect assumption may not be met if contact with health facilities improves outcomes through interventions that are either unrecorded in the database or not included as additional types of ‘treatments’ in addition to treatment switching. For example, if HIV care is integrated with other services like screening for cancer or cardiovascular disease, or if physicians use the results of a CD4 cell test to initiate treatments other than the one under consideration (e.g., prophylaxis for opportunistic infections), the assumption may not hold (unless the strategy includes screening and/or prophylaxis as additional ‘treatments’). However, under the strategies of interest individuals with low CD4 cell counts were monitored frequently (every 2–7 months) and so few CD4 tests were deleted for these individuals when creating the modified dataset (in the analysis without the no direct effect assumption, only 4% of replicates censored for being monitored too frequently had a CD4 cell count ≤ 200 cells/μl at the time they were censored).

The monitoring and treatment strategies in our primary analysis did not consider treatment switches after the initial treatment switch. While strategies that allow arbitrary treatment switches would be more realistic ^[24], they are also computationally harder to implement under the no direct effect assumption. In a sensitivity analysis without the no direct effect assumption, we considered modified strategies that allowed treatment switches both before virologic failure and after the initial treatment switch. This analysis yielded similar results (five-year survival difference compared with CD4 threshold 500/tight control: 0.01 (-0.01, 0.02) for CD4 threshold 350/tight control, 0.01 (-0.01, 0.04) for CD4 threshold 350/loose control, and 0.01 (0.00, 0.01) for CD4 threshold 500/loose control).

The methods described in this paper can be extended to other joint monitoring and treatment strategies analyzed in health research. The no direct effect assumption can be a useful tool in settings where individuals are monitored or tested often but inferences about less frequent monitoring or testing are desired. For example, this approach may be particularly useful when data from a high-resource population with frequent testing is available but researchers want to apply the estimates to a low-resource population with infrequent testing ^[11].