Self-organized nuclear positioning synchronizes the cell cycle in Drosophila embryos

Abstract

The synchronous cleavage divisions of early embryogenesis require coordination of the cell cycle oscillator, the dynamics of the cytoskeleton and the cytoplasm. Yet, it remains unclear how spatially restricted biochemical signals are integrated with physical properties of the embryo to generate collective dynamics. Here, we show that synchronization of the cell cycle in Drosophila embryos requires accurate nuclear positioning, which is regulated by the cell cycle oscillator through cortical contractility and cytoplasmic flows. We demonstrate that biochemical oscillations are initiated by local Cdk1 inactivation and spread through the activity of phosphatase PP1 to generate cortical myosin II gradients. These gradients cause cortical and cytoplasmic flows that control proper nuclear positioning. Perturbations of PP1 activity and optogenetic manipulations of cortical actomyosin disrupt nuclear spreading, resulting in loss of cell cycle synchrony. We conclude that mitotic synchrony is established by a self-organized mechanism that integrates the cell cycle oscillator and embryo mechanics.

eTOC Blurb

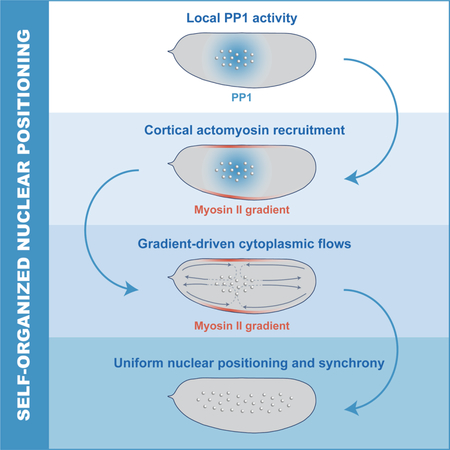
Synchronization of the cell cycle in syncytial Drosophila embryos is controlled by a self-organized mechanism that drives accurate nuclear positioning by integrating localized cell cycle oscillations, actomyosin cortical contractility and cytoplasmic flows.

Graphical Abstract

Introduction

Embryonic development is controlled by dynamic biochemical signals which trigger changes in the organization of the cytoskeleton and of the cytoplasm, and thereby of the mechanical properties of the embryo (Gilmour et al., 2017; Gross et al., 2017). Changes in the physical properties of the embryo can, in turn, feedback to biochemical dynamics, suggesting that morphogenesis requires the integration of biochemical and mechanical signals, possibly through the generation of self-organized circuits (Gross et al., 2017; Maitre et al., 2016; Samarage et al., 2015). However, the molecular principles underlying this integration remain poorly understood, making it difficult to quantitatively and predictably describe embryonic development on a macroscopic scale.

A powerful model system to dissect the integration of biochemistry and mechanics during morphogenesis is provided by the cleavage divisions of the Drosophila embryo. After fertilization, the fruit fly embryo undergoes 13 rounds of DNA replication and mitosis without cytokinesis, resulting in a multinucleated syncytium containing about 6,000 nuclei (Farrell and O’Farrell, 2014; Rabinowitz, 1941) (Figure 1A). These nuclear cycles are controlled by oscillations in the activity of cyclin-dependent kinase 1 (Cdk1) and mitotic phosphatases, PP1 and PP2A (Heim et al., 2017; Mochida et al., 2010; Morgan, 2007; Wu et al., 2009). The first cleavage divisions are accompanied by a series of nuclear movements; by cycle 10, movements result in a hollow shell at the surface of the embryo where nuclei are uniformly distributed (Figure 1A) (Foe and Alberts, 1983). Following the first 3 rounds of division, where no significant nuclear movement is observed, nuclei spread along the anterior-posterior (AP) axis during cell cycles 4–6 in a process called axial expansion (Zalokar and Erk, 1976). Subsequently, in cell cycles 7–9 nuclei migrate progressively to the embryo surface (Baker et al., 1993) where they undergo 4 rounds of blastoderm divisions, which gradually slow down without losing synchrony.

Figure 1. Nuclei provide a spatial landmark for the oscillations of Cdk1 and PP1.

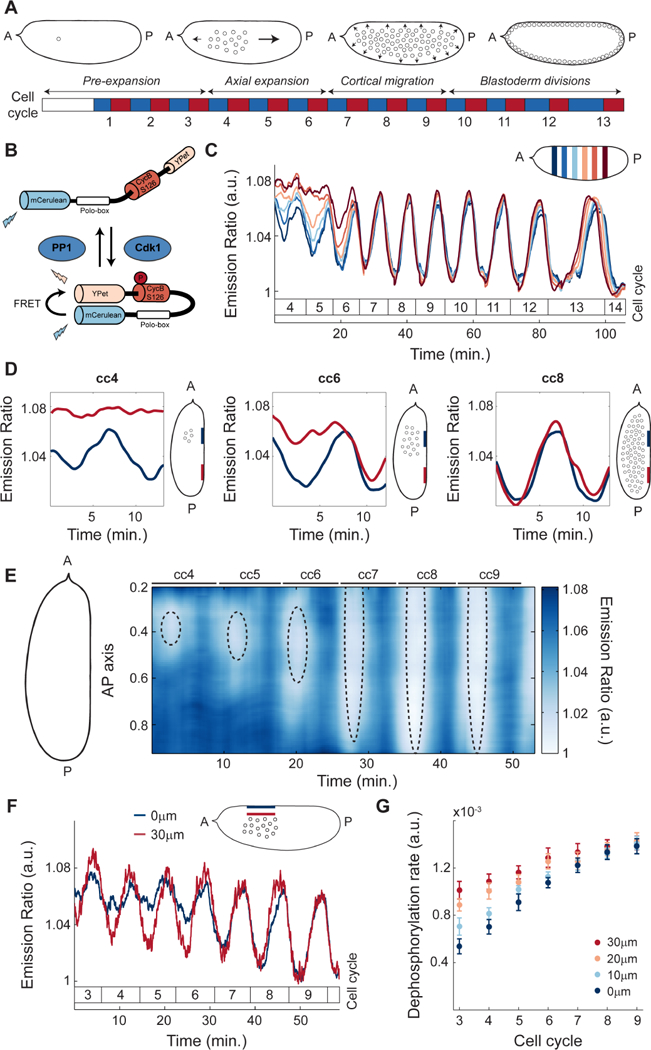
A) After fertilization, the Drosophila embryo undergoes 13 syncytial divisions characterized by four different stages of nuclear movement: pre-expansion (cc1–3), axial expansion (cc4–6), cortical migration (cc7–9), and blastoderm divisions (cc10–13). Embryo diagrams show mid-plane position of nuclear cloud during interphase of cell cycle 1, 6, 8 and 11, respectively. Blue boxes: S-phase; red boxes: mitosis. B) Diagram of Cdk1 to PP1 FRET sensor. C) Emission ratio of Cdk1/PP1 FRET sensor averaged in different regions of the surface of one embryo at cell cycles 4–14. Mitotic exit marks start of a new cycle. Inset, embryo outline with shaded boxes indicating the positions along the AP axis and at the surface of the embryo where the signal was averaged. D) Cdk1 to PP1 activity ratio in anterior (navy) or posterior (red) regions at the surface of an embryo for cell cycles 4 (left), 6 (middle), and 8 (right). Embryo diagrams show mid-plane position of the nuclear cloud as well as regions at the surface (navy and red) where measurements were taken. E) Heat map of Cdk1 to PP1 activity as a function of time along the AP axis of an embryo for cell cycles 4–9. Black dotted ellipses: nuclear cloud border. F) Emission ratio of Cdk1/PP1 FRET sensor for cell cycles 3–9 at embryo surface (blue) and 30μm from the surface (red); p<10⁻¹⁰ (χ² test). G) Quantification of the dephosphorylation rate of Cdk1/PP1 FRET sensor in different axial planes for cell cycles 3–9. Error bars, sem; a.u., arbitrary units.

Two conceptually distinct, although not mutually exclusive, models have been proposed for how nuclei spread across the AP axis (Royou et al., 2002; von Dassow and Schubiger, 1994), a process known to be driven by actomyosin contractility (Hatanaka and Okada, 1991; Zalokar and Erk, 1976). The first model, here referred to as the local disassembly model, proposes that actin around nuclei partially disassembles during interphase and this local decrease in tension causes streaming of the cytoplasm and the nuclei toward the poles (von Dassow and Schubiger, 1994). The second model, here referred to as the cortical contraction model, proposes that cycles of myosin II-driven cortical contraction generate cytoplasmic flows that push nuclei along the AP axis (Royou et al., 2002). These two models require different assumptions about the mechanisms coupling cell cycle dynamics and nuclear movement, which have been shown to be tightly linked (Foe, 1993). In the first model, local cell cycle dynamics are sufficient to couple nuclear cycles and cytoskeletal rearrangements; conversely, the second model requires a mechanism that couples nuclear dynamics and cortical contractility over the relatively large distance (about 40 microns) separating nuclei from the cortex.

Our current understanding of the spatial regulation of the cell cycle is unable to distinguish between these two models. On the one hand, Cdk1 activity is high in most of the cytoplasm during the first 9 cell cycles (Edgar et al., 1994; Su et al., 1998), while it is locally inactivated through degradation of a small pool of cyclins around the nuclei (Huang and Raff, 1999). Consistent with the local disassembly model of nuclear spreading, local oscillations of Cdk1 can drive actin disassembly in a small region surrounding the nuclei (von Dassow and Schubiger, 1994). On the other hand, pharmacological perturbations of Cdk1 dynamics, which have been shown to interfere with cortical myosin II dynamics (Royou et al., 2002), argue in favor of the cortical contraction model. It remains unclear how cortical and cell cycle dynamics are coupled and whether this involves waves of Cdk1 activity, similar to those observed at the later blastoderm cycles (Deneke et al., 2016; Vergassola et al., 2018). Alternatively, the coupling could be mediated by the activity of mitotic phosphatases PP1 and PP2A. During mitosis, the activity of Cdk1 is high, while PP1 and PP2A activities are low (Grallert et al., 2015; Heim et al., 2017). The decrease in Cdk1 activity at mitotic exit results in activation of mitotic phosphatases, which is further sharpened by several feedback mechanisms (Grallert et al., 2015; Mochida et al., 2010; Wu et al., 2009). How the activities of PP1 and PP2A are regulated spatially, and whether they play a role in nuclear positioning remains unknown.

Cytoplasmic flows represent a mechanism for large scale coordination of nuclear movements, provided their directionality and strength are regulated to ensure precise nuclear positioning. Nuclear spreading could potentially feedback on cell cycle synchrony since the distribution of nuclei across the embryo determines the nuclear to cytoplasmic ratio (NC ratio), which correlates with the duration of the nuclear divisions (Farrell and O’Farrell, 2014; Foe and Alberts, 1983; Sibon et al., 1997). During the later blastoderm cycles, an increase in the NC ratio reduces the DNA replication capacity of the embryo and triggers the activation of the DNA replication checkpoint, which causes a gradual slowdown of the cell cycle (Farrell and O’Farrell, 2014; Foe and Alberts, 1983; Sibon et al., 1997) and plays an important role in the regulation of mitotic synchrony (Deneke et al., 2016).

Here, we have generated imaging and computational tools to determine the mechanisms of nuclear positioning and cell cycle synchronization during early Drosophila development. We demonstrate that cell cycle synchronization emerges from the ability of nuclei to self-organize their positioning by regulating the spatiotemporal dynamics of the cell cycle, cortical contractions, and cytoplasmic streaming. We show that local Cdk1 downregulation at mitotic exit initiates the damped spreading of PP1 activity, which is responsible for recruiting myosin II to cortical regions that surround the nuclei, where gradients of contractility are generated. These gradients drive cortical and cytoplasmic flows that properly position the nuclei across the embryo. Such spatial organization ensures a homogeneous NC ratio and synchronous embryo-wide oscillations of Cdk1 and PP1 activities at the maternal-to-zygotic transition.

Results

Nuclei provide a spatial landmark for the oscillations of Cdk1 and PP1

To elucidate the mechanisms that regulate the emergence of cell cycle synchronization in the Drosophila embryo, we first measured detailed spatiotemporal activity profiles of major cell cycle regulators. To this end, we used a biosensor which undergoes a conformational change increasing Fluorescence Resonance Energy Transfer (FRET) efficiency upon phosphorylation by Cdk1 (Figure 1B) (Deneke et al., 2016; Gavet and Pines, 2010). In addition, we found that the dephosphorylation of the biosensor and the consequent decrease in FRET efficiency was triggered by PP1 activity (STAR Methods; Figure S1A-B). Thus, at each time interval during the cell cycle, the biosensor (referred to as Cdk1/PP1 biosensor) reports the ratio of Cdk1 to PP1 activities. Quantification of the emission ratio of the Cdk1/PP1 biosensor near the embryo surface shows that the Cdk1/PP1 ratio exhibited a disorganized pattern of activity in cell cycles 4–6 (Figure 1C). After cell cycle 6, oscillations became synchronous and persisted until cell cycle 14 (Figure 1C). Spatial analysis of the Cdk1/PP1 biosensor dynamics revealed that oscillations were restricted to regions of the cortex surrounding the nuclei (Figure 1D). To display Cdk1/PP1 activity in both space and time, we used a heat map representation where color indicates activity, the x-axis is the time coordinate and the y-axis the coordinate along the AP axis. We found that the oscillatory pattern of Cdk1/PP1 activity at the surface of the embryo gradually spreads along the AP axis during cell cycles 4–6 (Figure 1E). By cell cycle 7, the Cdk1/PP1 biosensor oscillated synchronously throughout the entire embryo (Figure 1E). Importantly, even though nuclei are located at the embryo mid-plane during the first 9 cycles, the region that displayed localized oscillations near the cortex is located 40 μm above the nuclei (Figure 1E, dotted ellipses and Figure S1C). The Cdk1/PP1 oscillations expanded in a manner that closely mirrors the expansion of the nuclear cloud (Figure 1E). Taken together our measurements argue that during the early cell cycles the oscillations in the Cdk1 to PP1 activity ratio at the surface of the embryo closely follow the position of the nuclei located at embryo mid-plane.

To further elucidate the relation between the Cdk1 to PP1 oscillations at the cortex and around the nuclei, we performed measurements of the Cdk1/PP1 biosensor activity in the axial direction (Figure 1F). Biosensor oscillations in the cytoplasm close to the cortex were damped compared to oscillations in a region 30 μm inside the embryo (Figure 1F), as well as along the AP axis (Figure S1D). To obtain further quantitative insights on the spatiotemporal dynamics of the Cdk1/PP1 biosensor, we measured the dephosphorylation rate, defined as the slope of the temporal decrease of the FRET signal at mitotic exit. Quantification of this rate in the axial direction showed a gradual decrease moving from the inner-most plane to the surface of the embryo (Figure 1G), confirming that the Cdk1/PP1 activity oscillations are the strongest around the nuclei and reduce as the surface of the embryo is approached. To further test the role of nuclei, we imaged activated, unfertilized eggs, which did not undergo nuclear proliferation. Importantly, newly laid unfertilized eggs did not show effective oscillations of the biosensor (Figure S1E), highlighting the importance of nuclei in initiating oscillations in the Cdk1/PP1 activity ratio. Collectively, our results demonstrate that local oscillations of Cdk1 to PP1 initiate around the nuclei and spread radially in a damped manner. These oscillations reach the surface of the embryo and could couple nuclear and cortical dynamics.

The dynamics of the cell cycle oscillator is characterized by a graded distribution of PP1 activity.

To confirm and elucidate the coupling between nuclear and cortical dynamics, we dissected the respective contribution of Cdk1 and PP1 to the oscillations of the biosensor. To determine whether oscillations at the surface of the embryo were due to downregulation of Cdk1 activity through cyclin degradation, we measured cyclin-B dynamics using 2-photon and confocal imaging of a functional GFP-cyclin-B trap line. Consistent with previous findings, cyclin-B levels only oscillated in a small region around the nuclei (Figure 2A, blue line; Figure S2A) (Huang and Raff, 1999). At the cortex, cyclin-B levels did not oscillate until the nuclei reached the surface of the embryo at cell cycle 9 (Figure 2A, red line). Spatial analysis of cyclin-B dynamics at the surface confirmed lack of local oscillations during early divisions (Figure S2B). Finally, we found that the dynamics of the Cdk1/PP1 biosensor was unaltered in embryos mutant for Wee1, a kinase playing a major role in the regulation of Cdk1 activity (Morgan, 2007) (Figure S2C). The upshot is that the local cytoplasmic oscillations of the Cdk1/PP1 biosensor are not due to cyclin degradation or post-translational regulation of Cdk1, thus pointing at the role of PP1 activity.

Figure 2. The dynamics of the cell cycle oscillator is characterized by a graded distribution of PP1 activity.

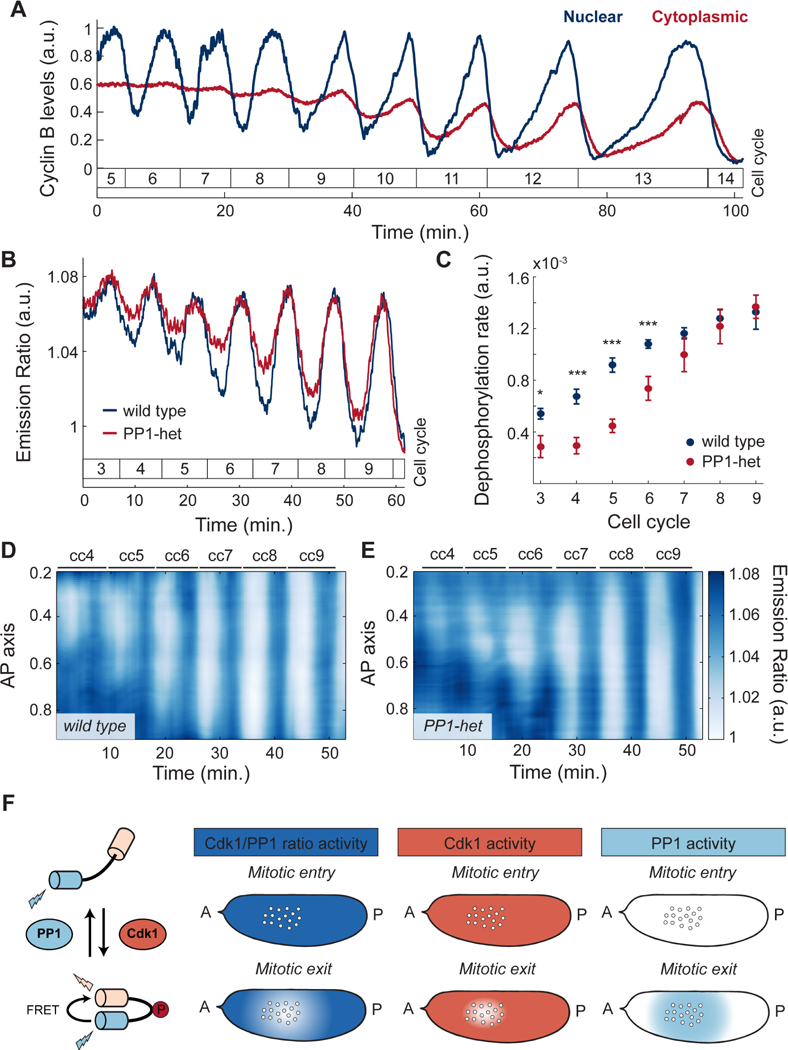
A) Quantification of cyclin-B levels in the cytoplasm near the embryo cortex (red) and around nuclei (blue). B) Emission ratio of Cdk1/PP1 FRET sensor at the surface of a wild type (blue) or a PP1-het (red) embryo; p<10⁻¹⁰ (χ² test). C) Quantification of the dephosphorylation rate of Cdk1/PP1 FRET sensor in wild type (blue) vs. PP1-het embryos (red). p<10⁻¹⁰ (χ² test). D-E) Heat map of Cdk1 to PP1 activity along the AP axis of an embryo for cell cycles 4–9 near the cortex of a wild type (D) and a PP1-het (E) embryo. F) Diagram summarizing the activity of Cdk1 and PP1 in the early embryo. First panel from left: Simplified diagram of Cdk1 to PP1 FRET sensor. Second panel from left: Measured Cdk1 to PP1 activity ratio during mitotic entry and mitotic exit. Third panel from left: Cdk1 (coral shaded region) activity is downregulated only in a small region around nuclei during mitotic exit. Fourth panel from left: PP1 activity (light blue shaded region) shows a graded, damped distribution from nuclei to cortex during mitotic exit. Error bars, sem; a.u., arbitrary units. *p < 0.05, **p < 0.001, ***p < 0.0001.

To test this hypothesis, we analyzed the dynamics of the biosensor in embryos heterozygous for two genes encoding maternally expressed PP1 α (hereby referred as PP1-heterozygous) (Kirchner et al., 2007). We observed that oscillations of the biosensor near the surface during the early cell cycles were damped in PP1-heterozygous embryos compared to wild type embryos (Figure 2B). This was due to reduced dephosphorylation rates (Figure 2C), indicating that PP1 is rate-limiting for dephosphorylation of the sensor. Spatial analysis of the Cdk1/PP1 biosensor showed delayed oscillations at the poles compared to wild type (Figure 2D-E). The importance of PP1 in the spatial regulation of the cell cycle was further supported by decreasing the levels of Inhibitor-2, a major regulator of PP1 activity (Figure S2D).

The above results collectively support the following model for the spatial regulation of the cell cycle. Upon mitotic entry, Cdk1 activity is uniformly high in the embryo, while PP1 activity is uniformly low (Figure 2F). At mitotic exit, cyclins are degraded in a small region surrounding the nuclei, which results in a local decrease of Cdk1 activity (Figure 2F) and PP1 activation. PP1 is then able to stimulate its own activity, which extends to a spatial region of about 50 μm that reaches cortical regions surrounding the nuclear cloud (Figure 2F). Thus, our experiments argue that, similarly to the Cdk1/PP1 biosensor, other mitotic targets are dephosphorylated by PP1 in a region extending from the nuclei to the surrounding surface of the embryo (Figure 2F). Based on these data, we hypothesize that PP1 is responsible for coupling nuclear and cortical dynamics by driving the recruitment of myosin II to regions of the cortex surrounding the nuclear cloud.

Local PP1 activity couples nuclear and cortical dynamics by regulating cortical myosin II recruitment.

To demonstrate the role of PP1 activity in the recruitment and positioning of myosin II at the cortex, we measured both Cdk1/PP1 and Myosin II Light Chain dynamics (Video S1) simultaneously in early embryos. Spatial analysis of cortical myosin II dynamics showed that myosin II accumulated in regions where the Cdk1/PP1 biosensor featured oscillations (Figure 3A-D). In addition, myosin II recruitment closely followed the expansion of the Cdk1/PP1 oscillations along the AP axis (Figure 3A, C). Using a Moesin-ABD-GFP transgenic line, we visualized and quantified F-actin dynamics at the cortex, which closely matched myosin II dynamics both in space and time (Figure S3A-B). Cortical recruitment of F-actin and myosin II depend on Rho1 (Royou et al., 2002). Using a biosensor of Rho activity (Munjal et al., 2015), we found that Rho activity displayed spatial dynamics that closely matched that of myosin II (Figure 3E-F). Rho activity peaks simultaneously with PP1 activity, as revealed by the low Cdk1/PP1 ratios at the maximum of Rho activity (Figure 3G, dotted line). The peak in Rho activity is followed by a peak in myosin II with a delay of 1–2 minutes (Figure 3G). This suggests that the delay between PP1 activation and myosin II accumulation is largely due to the time needed for myosin II activation by Rho. Both activation of Rho and recruitment of myosin II were reduced in PP1-heterozygous embryos (Figure 3H; Figure S3I), which further establishes the importance of PP1 in regulating actomyosin cortical contractility during the early cycles.

Figure 3. Local PP1 activity couples nuclear and cortical dynamics by regulating cortical myosin II recruitment.

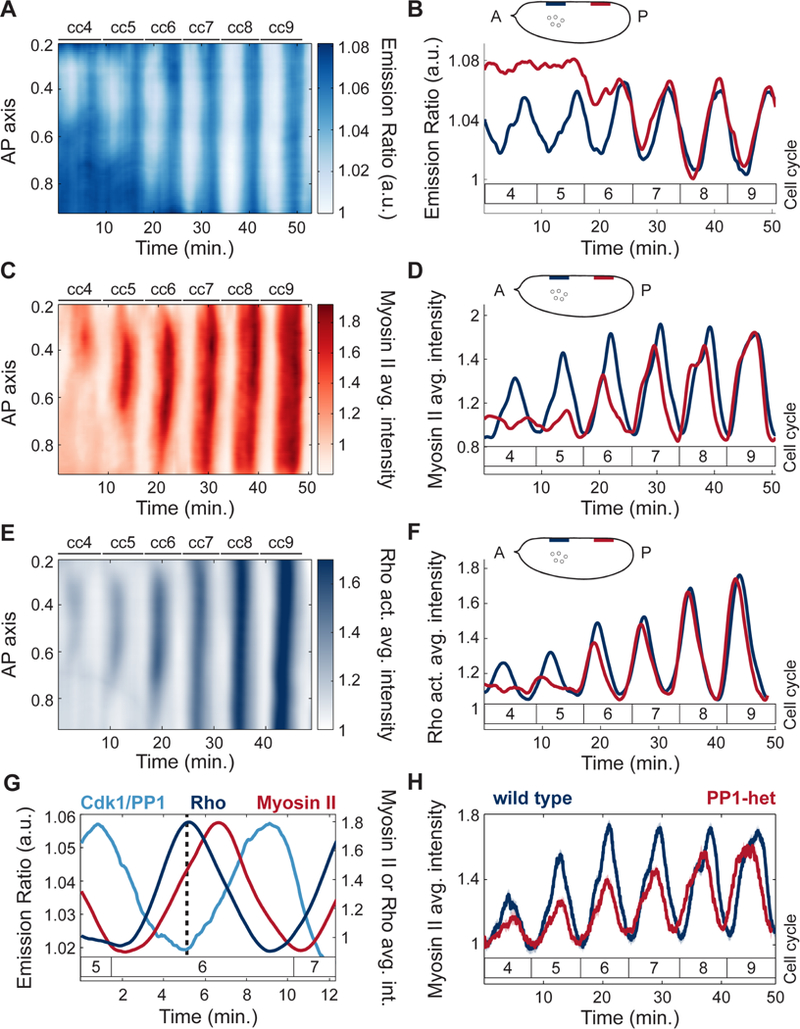
A) Heat map of Cdk1 to PP1 activity as a function of time along the AP axis at the surface of a wild type embryo for cell cycles 4–9. B) Cdk1 to PP1 activity ratio in anterior (navy) or posterior (red) regions at the surface of an embryo for cell cycles 4–9. Inset, embryo outline with shaded boxes indicating the positions along the AP axis at the surface of the embryo where the signal was averaged (nuclear cloud at cell cycle 4 is depicted for reference). C) Heat map of myosin II levels as a function of time along the AP axis at the surface of a wild type embryo for cell cycles 4–9. D) Myosin II levels in anterior (navy) or posterior (red) regions at the surface of an embryo for cell cycles 4–9. Inset, same as in B. E) Heat map of Rho activity as a function of time along the AP axis at the surface of the embryo for cell cycles 4–9. F) Rho activity in anterior (navy) and posterior (red) regions at the surface of an embryo for cell cycles 4–9. G) Dynamics of Cdk1/PP1 FRET sensor, Rho activity, and myosin II levels averaged in regions surrounding nuclei at cell cycle 6. Dotted line: local Rho activity maximum and Cdk1/PP1 activity minimum. Delay between Rho activity and myosin level peak: 1.3 min. (p<10⁻⁶, t-test). H) Myosin II levels at surface averaged in regions surrounding nuclei for wild type (blue line) and PP1-het (red line) embryos at cell cycles 4–9. Shaded regions, sem; p<10⁻¹⁰ (χ² test); a.u., arbitrary units.

Myosin II gradients drive cortical contractions

One possible function of coupling cell cycle dynamics and cortical actomyosin accumulation is the generation of cycles of cortical contractility and flow during interphase, which could in turn control cytoplasmic flow and nuclear positioning. Spatial analysis of myosin II recruitment revealed that myosin II accumulated locally and formed gradients along the AP axis during cycles 4–6 (Figure 4A, top panel). The region of myosin II accumulation gradually expanded until cycle 7, while at the following cycles myosin II accumulated uniformly across the AP axis (Figure 4A, bottom panel). The transition to a uniform myosin II accumulation coincided with the time when nuclei occupied the entire AP axis in the interior of the embryo and Cdk1/PP1 oscillations became uniform. To dissect the relationship between myosin II dynamics and cortical flows, we performed particle image velocimetry (PIV) in embryos co-expressing His2Av-GFP and MLC-mCherry (see STAR Methods and Video S2). The His2Av-GFP signal was sufficiently particulate to be tracked by PIV and could be used to measure the flow of the cytosol, that is the soluble aqueous component of the cytoplasm, as confirmed by FRAP (Fluorescence Recovery After Photobleaching) measurements of soluble GFP (see Figure S4A-C and STAR Methods). Trajectories of the flow field during cell cycle 6 showed a polarized movement of the cytoplasm from the poles towards a point of zero velocity (stagnation point) at around 40% egg length (Figure 4B, light to dark red trajectories, inset). In contrast, once nuclei distributed across the AP axis by cell cycle 7, no net flow was evident (Figure 4C, light to dark red trajectories, inset). Quantification of the velocities during cortical contractions along the AP axis allowed the generation of a spatiotemporal cortical flow map, where flows to the posterior side are represented as positive velocities (Figure 4D, blue shades) and flows towards the anterior side as negative velocities (Figure 4D, red shades). Geometry and strength of the cortical flows demonstrated a tight correlation with myosin II gradients. First, cell cycles 4–6, which exhibited gradients of myosin II (Figure 4A, top panel), also displayed cycles of polarized contraction (Figure 4D, cell cycles 4–6). Second, the speed of cortical flow increased as myosin II accumulation levels increased and expanded (Figure 4D, cc4–6; Figure 4G, left panel, solid lines). Third, during cycles 7–9, when myosin II accumulated uniformly at the cortex, embryos did not undergo polarized contractions and showed little to no net flow (Figure 4D, cc7–9; Figure 4G, right panel, solid lines). To test quantitatively whether cortical flows could be predicted by myosin II gradients, we measured myosin II gradients during the contraction phases of cycles 5–7 (Figure S4D-F) and compared the cortical speed along the AP axis to predictions of a viscoelastic model (Mayer et al., 2010). In the model, cortical tension results from the combination of tension imbalances between neighboring regions, which are linked to myosin II gradients, and viscous effects, which characterize the physical nature of cortical flows (see STAR Methods). We found that speed and direction of cortical flows were in good agreement with theoretical predictions (Figure 4E). These data strongly suggest that myosin II gradients at the embryo cortex drive cortical contractions and cortical flows during cell cycles 4–6. Furthermore, assuming that the cytoplasm behaves as an incompressible fluid, inward flows at the cortex must generate outward flows in the mid-embryo. In this manner, cytoplasmic flows could achieve the proper geometry and magnitude to facilitate nuclear spreading.

Figure 4. Myosin II gradients drive cortical contractions.

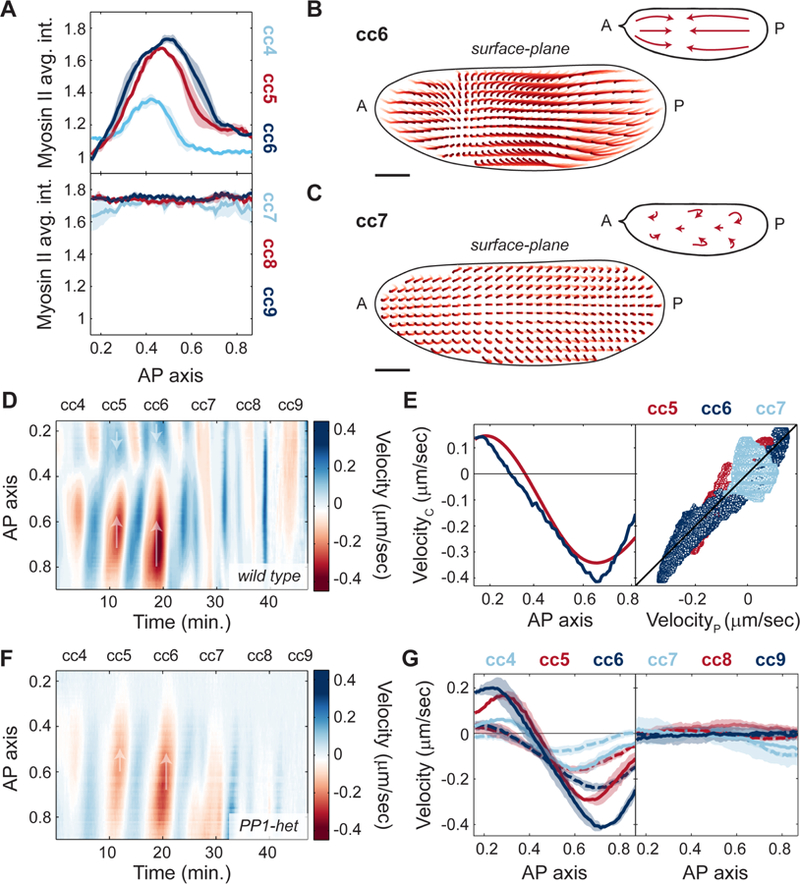
A) Myosin II intensity profiles across AP axis during maximum myosin II recruitment for cell cycles 4–6 (top) and cell cycles 7–9 (bottom). B-C) Cortical flow trajectories (light to dark red) for contraction phase of an embryo during cell cycle 6 (B) and cell cycle 7 (C). Insets, schematic of streamlines showing direction of cortical flows. D) Heat map of cortical flow velocity along the AP axis of an embryo for cell cycles 4–9. Arrows indicate the direction of movement along the AP axis. E) Left: Measured cortical velocity (blue line) for a cycle 6 embryo and predicted velocity (red line) from myosin II gradients. Right: Cortical velocity versus predicted velocity using a gradient-driven flow model for cell cycle 5 (red), 6 (navy blue) and 7 (light blue). Black line: least squares regression line (R²=0.82). F) Heat map of cortical flow velocity along the AP axis of a PP1-het embryo for cell cycles 4–9. Arrows as in D). G) Velocity profiles across AP axis during contraction phases of cell cycles 4–6 (left panel) and cell cycles 7–9 (right panel) for wild type (solid lines) and PP1-het embryos (dashed lines). For cell cycles 4–6, p<10⁻¹⁰ (χ² test); for cell cycles 7–9, not significant. Shaded regions, sem. Scale bars, 50μm.

To evaluate the role of localized PP1 oscillations in the regulation of cortical contractions, we measured myosin II gradients and cortical flows in PP1-heterozygous embryos. Myosin II spatial profiles retained a similar geometry in PP1-heterozygous embryos to that observed in wild type embryos, but with reduced amplitude (Figure S4G). Consistently, flows at the cortex were reduced by about 2-fold in PP1-heterozygous embryos during cycles 4–6 (Figure 4F-G, cc4–6, dotted lines). Thus, cortical contractions damped when PP1 levels decreased, yet the geometry of the flow remained unaltered (Figure 4F-G; Figure S4H). Therefore, PP1 activity plays a crucial role in coupling cell cycle and cortical dynamics by regulating myosin II gradients at the cortex and, consequently, the magnitude and geometry of cortical contractions.

Nuclear movements correlate with cytoplasmic flows

To test the role of cytoplasmic flows in nuclear positioning, we measured and reconstructed mid-embryo flows using a technique to stain yolk granules (Quinlan, 2016) and PIV analysis (Video S3-4), which provided a reliable measurement of cytosolic flow as confirmed by FRAP measurements of soluble cytosolic RFP (Figure S5A-C). Nuclei were tracked using a PCNA-TagRFP transgenic line, whose high expression levels enabled deep tissue imaging of nuclei during interphase by confocal microscopy. In interphase of cycle 6, embryos displayed cytoplasmic flows characterized by features compatible with nuclear spreading. In the middle of the embryo where nuclei are located, the cytoplasm flowed from the center of the nuclear cloud toward the poles (Figure 5A, light to dark red trajectories, inset). Nuclei closely followed the direction of the cytoplasmic flows and spread to the same extent (Figure 5A, light to dark blue trajectories). Consistent with data shown in Figure 4, flows were also visible near the cortex of the embryo, moving from the poles toward the center and meeting at a position along the AP axis closely matching the center of the nuclear cloud. The bidirectional flow both at the cortex and mid-embryo created four vortices and a stagnation point that arose near the center of the nuclear cloud where cortical flows converged and ingressed (Figure 5A, inset) (von Dassow and Schubiger, 1994). In cycle 7, once nuclei were uniformly spread along the AP axis, cytoplasmic flows were significantly reduced (Figure 5B, light to dark red trajectories) and nuclei also showed little movement (Figure 5B, light to dark blue trajectories). Quantitative analysis of cytoplasmic and nuclear speed during cycles 4–8 showed a high degree of correlation (Figure 5C). Additionally, the direction of the nuclear and cytoplasmic movements throughout the embryo was strongly correlated (Figure 5D), thus demonstrating that nuclear movements closely followed the flow of the cytoplasm.

Figure 5. Nuclear movements correlate with cytoplasmic flows.

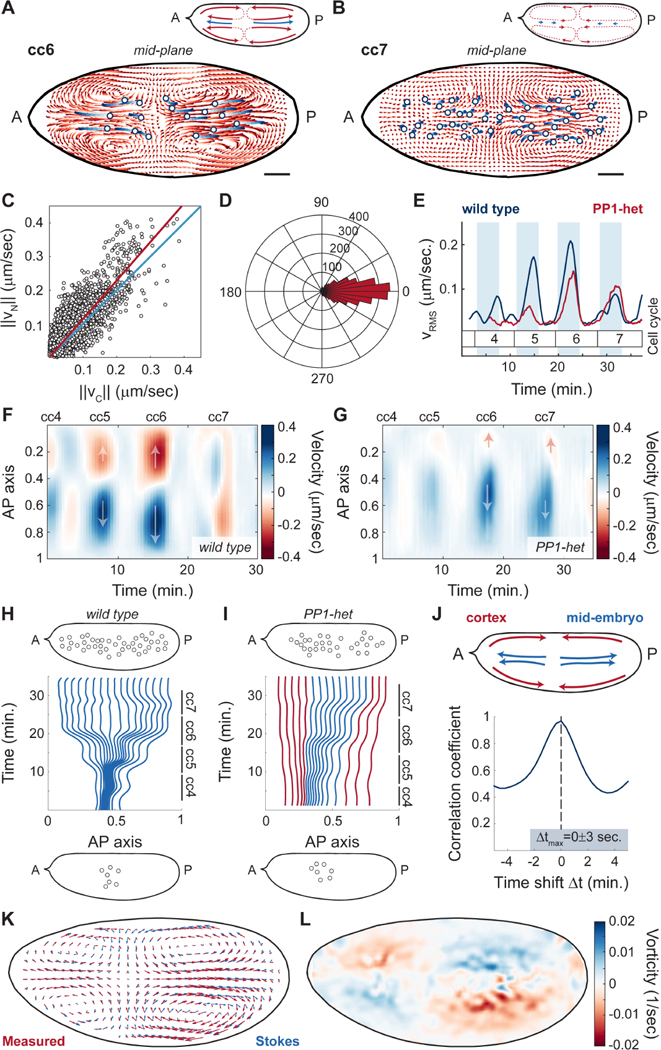
A-B) Cytoplasmic flow trajectories (light to dark red) and nuclear trajectories (light to dark blue) during interphase of cell cycle 6 (A) and cell cycle 7 (B). Insets, schematic of streamlines showing direction of cortical and cytoplasmic flows (red) and nuclear movement (blue). Scale bars, 50μm. C) Modulus of nuclear versus cytoplasmic flow velocities for embryos in cell cycles 4–7. Blue line: identity line; red line: best fit. D) Histogram in polar coordinates of the angle between nuclear and cytoplasm velocities. E) Root mean square velocity across a wild type embryo (blue) and a PP1-het (red) embryo in cell cycles 4–7. Shaded blue regions: interphase. p<10⁻¹⁰ (χ² test). F-G) Heat map of cytoplasmic flow in a 50 μm region in the center of a wild type (F) and a PP1-het embryo (G) for cell cycles 4–7. Arrows indicate the direction of movement along the AP axis. H-I) Computationally reconstructed flow trajectories needed for uniform nuclear distribution at the end of cell cycle 7 in a wild type (H) and a PP1-het embryo (I). Blue lines represent trajectories that at cell cycle 4 initiate in the region where nuclei are present, while red lines represent trajectories outside of the nuclear cloud. Top and bottom insets: nuclear distribution in embryos at cell cycle 4 (bottom) and cell cycle 7 (top) from experimental data. J) Cross-correlation analysis of cortical flows and mid-embryo cytoplasmic flows. K) Comparison between the measured flow (red arrows) and the best-fitted Stokes’ flow (blue arrows). L) Heat map showing the vorticity field (ω = ∇ × v) of the measured flow.

Similar to cortical flows, cytoplasmic speed increased gradually in magnitude from cycles 4–6 but was significantly reduced by cycle 7 (Figure 5E, blue line). Since embryos heterozygous for PP1 showed reduced cortical contractions, we hypothesized that cytoplasmic flows should also be reduced. In agreement with our prediction, PP1-heterozygous embryos showed damped cytoplasmic flows during cycles 4–6 (Figure 5E, red line, Video S5). Spatial analysis of mid-embryo movements showed that flows in PP1-het embryos followed the same polarized geometry as those in wild type embryos during cycles 4–6 (Figure 5F-G; Figure S5D-G). However, at cycle 7, when wild type embryos no longer show polarized flows, PP1-het embryos still showed polarized cytoplasmic flows (Figure 5G, cell cycle 7; Figure S5D-G), consistent with the fact that nuclei were not uniformly distributed at cycle 7 in mutant embryos.

To assess the ability of the measured flows to position nuclei uniformly, we quantified the extent to which cytoplasmic flows could drive separation of initially proximal particles. We asked whether nuclei distributed uniformly at the end of cycle 7 would start from a small cloud at the beginning of cycle 4 according to the measured flow. To this aim, we computationally positioned uniformly-distributed particles in the mid-embryo along the AP axis at the end of cycle 7. We then used the measured cytoplasmic flows to evolve their position back in time until the beginning of cycle 4. Wild type flow trajectories were able to transform a cloud of nuclei similar to the one observed at cycle 4 into a uniform distribution by the end of cycle 7 (Figure 5H, bottom panel). By contrast, in PP1-heterozygous embryos flows were unable to disperse the nuclei properly and the only possibility to obtain a uniform nuclear distribution by cycle 7 was to start with partially dispersed nuclei (Figure 5I, red lines). Altogether, this quantitative analysis argues that flows in wild type embryos are effective at nuclear spreading, while flows in PP1-heterozygous are not sufficient to spread nuclei uniformly, as it is indeed observed in experimental data (Figure 5I, top panel).

Optogenetic control of Rho signaling shows that cytoplasmic flows and nuclear movements are mainly driven by cortical contractions.

Cytoplasmic flows are synchronized with the cell cycle and occur predominantly during interphase (Figure 5E). However, the respective contributions to the generation of flows by actomyosin contractility in the bulk cytoplasm or at the cortex remain to be determined, as both contractile modes are regulated by the cell cycle. To distinguish between these two possibilities, first we performed a correlation analysis between the dynamics of cortical and mid-embryo cytoplasmic flows in the same embryo, and found that they are essentially simultaneous (Figure 5J), arguing that flows of cytoplasm near the cortex and in the mid-embryo might be directly coupled. Second, we assayed the contribution of the contractile cortical actomyosin to the motion of the cytoplasm by an experimental approach that allows specific control over cortical contractility. To this end, we made use of an optogenetic tool to activate Rho signaling specifically at the embryo cortex (Izquierdo et al., 2018). Upon blue light activation, the catalytic domain of RhoGEF2, tagged with the photosensitive protein domain CRY2, was recruited to the plasma membrane of the illuminated area, via a CIB1 localized plasma membrane anchor (Figure 6A, Figure S6A-D), where it triggered Rho signaling and myosin II activation (Izquierdo et al., 2018) (Figure S6E-G). Embryos expressing RhoGEF2::CRY2 were imaged in the presence of uniform blue light, which resulted in uniform recruitment of myosin II at the cortex (Figure S6F-G), which overrode endogenous cortical myosin II gradients that were present during the contraction cycles (Figure 4B). Embryos exposed to uniform blue light showed dramatic dampening both of cortical contractions (Figure 6B) and of mid-embryo cytoplasmic flows (Figure 6C-D, Video S6). Importantly, in embryos exposed to uniform blue light, nuclei failed to spread along the AP axis during interphase (Figure 6E). Therefore, actomyosin gradients at the cortex are necessary to generate cortical contractions which then facilitate cytoplasmic flows and nuclear spreading.

Figure 6. Optogenetic control of Rho signaling shows that cytoplasmic flows and nuclear movements are mainly driven by cortical contractions.

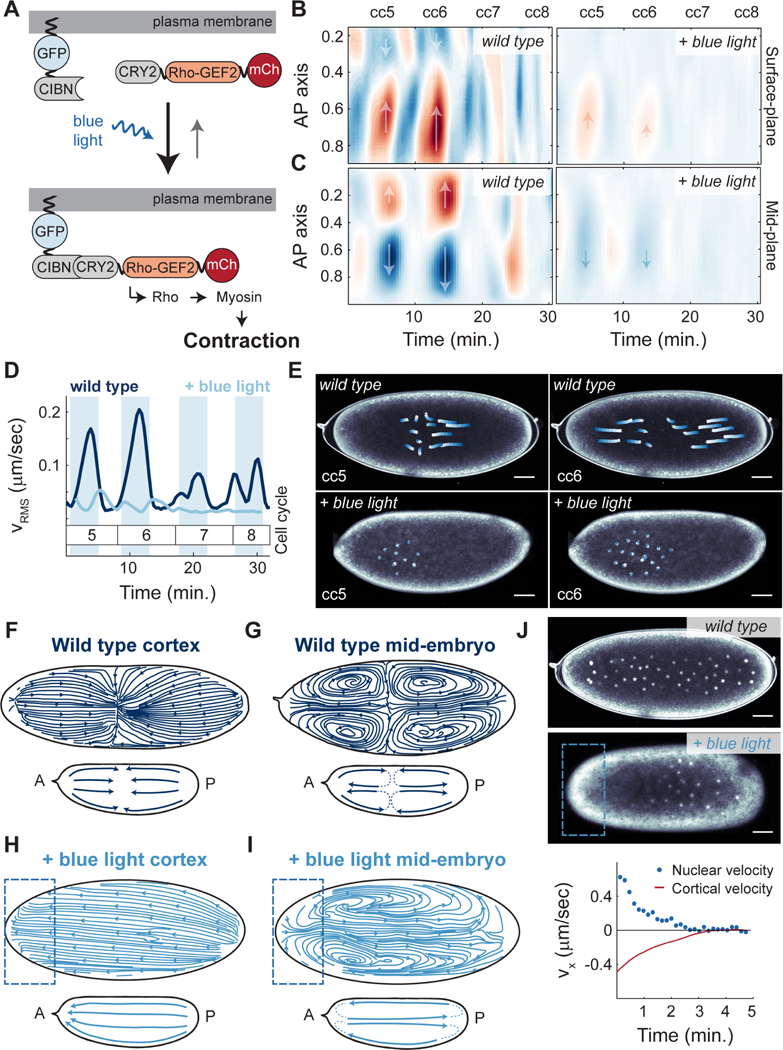
A) Schematic view of the RhoGEF2 optogenetic tool. B) Heat map of cortical velocities in a wild type (top) and embryo expressing RhoGEF2 optogenetic system exposed to constant blue light (bottom) for cell cycles 5–8. Arrows indicate the direction of movement along the AP axis. C) Heat map of mid-embryo cytoplasmic velocities in a wild type (top) and embryo expressing RhoGEF2 optogenetic system exposed to constant blue light (bottom) for cell cycles 5–8. Arrows as in B). D) Root mean square cytoplasmic velocity of a wild type embryo (navy blue) and an optogenetic RhoGEF2 embryo exposed to blue light (light blue). Shaded blue regions: interphase. E) Nuclear trajectories (white to blue) for contraction phase of a wild type (top) or optogenetic RhoGEF2 embryo exposed to blue light (bottom) during cell cycle 5 (left) and cell cycle 6 (right). F-G) Streamlines showing direction of cortical (F) or cytoplasmic (G) flows in a wild type embryo during cell cycle 6. Inset, summary diagram of flows. H-I) Streamlines showing direction of cortical (H) or cytoplasmic (I) flows in an optogenetic RhoGEF2 embryo that was activated with blue light on the anterior pole. Inset, summary diagram of flows. J) Top two panels: Nuclear distribution for a wild type (top) and a pole-activated embryo (middle) at cell cycle 7 expressing PCNA-TagRFP to mark nuclei. Bottom panel: average cortical velocity during one contraction phase (red line) with corresponding nuclear velocity (blue points) of an optogenetic RhoGEF2 embryo activated on anterior pole. Scale bars, 50μm.

To test whether cortical myosin II gradients were also sufficient to control nuclear spreading, we locally recruited RhoGEF2::CRY2 to different cortical regions of the embryo along the AP axis and assessed whether flows and nuclear movements could be induced in a predictable manner. Specifically, we reasoned that, if RhoGEF2::CRY2 was recruited to one pole, cortical flows would be directed toward that pole, while mid-embryo cytoplasmic flows and nuclear movements would be directed toward the opposite pole. In wild type embryos, flows at the cortex at cycle 6 were directed towards a point along the AP axis that corresponded to the center of the nuclear cloud (Figure 6F). In the middle of the embryo, flows were directed out from the center of the nuclear cloud and towards the poles (Figure 6G). Upon light-mediated recruitment of RhoGEF2 to the anterior pole of the embryo, myosin II was recruited to the activated area (Figure S6J-K), and cortical flows were now re-directed towards the anterior pole (Figure 6H). As expected, mid-embryo flows displayed unidirectional flows toward the posterior side of the embryo (Figure 6I) and nuclei were consequently shuttled to the posterior side of the embryo (Figure 6J, top 2 panels, Video S7). By simultaneously measuring cortical flow velocities and nuclear movement velocities in anteriorly-activated embryos, we observed that, as the cortex moves toward the anterior pole (negative velocity), nuclei move at a similar rate towards the posterior pole (positive velocity) (Figure 6J, red line vs. blue points, respectively). Taken together, these results demonstrate that the positioning of myosin II at the cortex and the consequent gradients that are formed upon activation of contractility determine the geometry of the cortical and cytoplasmic flows, which in turn control the movement and distribution of nuclei in the embryo.

Viscous dynamics captures the large-scale features of cytoplasmic flows

The cytoplasm is a complex medium that features at least two phases, an active actomyosin gel and a fluid cytosol (Mogilner and Manhart, 2018). The permeation of the fluid through the gel is important in a number of biological phenomena, which have motivated the development of multi-phase models, for example poroelastic, that are poised to capture the relative motion and conditions for equilibration between the two phases (Charras et al., 2005; Mitchison et al., 2008). Our experiments suggest a simpler physical model for Drosophila cytoplasmic flows. Indeed, while relative motion between the actomyosin gel and the cytosol is possible and expected at small scales, our data show that the motion of the two phases in Drosophila embryos is strongly correlated on timescales of tens of seconds (Figures 4 and 5; Figure S4A-C and Figure S5A-C). Furthermore, the general circulation patterns of the flow in Figure 6G are on spatial scales comparable to the embryo size, which are larger than the expected microscopic length scales. These observations argue that the large-scale dynamics of the bulk flow is consistent with the phases being equilibrated, and that the dynamics may then lend to an approximate description by a single, effectively continuum phase. In principle, such phase should be modeled as a viscoelastic fluid (Mogilner and Manhart, 2018). Yet, our optogenetic experiments argue that contractility effects in the bulk, which are responsible for elastic behaviors, are small (Figure 6B-D). We conclude that the simplest physical model that recapitulates our experimental observations has an active actomyosin gel generating cortical contractions at the boundary of the embryo, which, in turn, drive a large-scale flow in the bulk that can be described by a single effective fluid that is passive and incompressible.

The flow of such fluid is characterized by its Reynolds number, which for our observed flows is small ($Re=\frac{VL}{v}\approx {10}^{-5}$, where V ≈ 0.3μm/s is the observed typical velocity of the flow, L ≈ 100μm is a characteristic length related to the size of the embryo and v ≈ 3 10⁶μm²/s is an estimate of the kinematic viscosity (Swaminathan et al., 1997)). A low Reynolds number implies that viscous forces dominate over inertial forces. The resulting viscous dynamics is consistent with the experimentally observed absence of delays between the motion at the cortex and in the bulk (Acheson, 1990). Since the major active mechanisms act near the embryo boundary, mathematically we account for the effects of cortical contractions by boundary conditions. In other words, the flow in the bulk is obtained by solving the fluid dynamics (Stokes) equations for a passive viscous fluid and the effects of cortical activity are introduced by setting the velocity at the boundary. Flows predicted by this procedure are similar to cytoplasmic flows measured experimentally (Figure 5K). Specifically, both direction and speed of the observed and the best-fitted Stokes flow are comparable (Figures S5H-J).

While the above description is appropriate at large scales, deviations are expected at small scales, which we could detect. For instance, the vorticity field features maxima and minima inside the embryos (Figure 5L), which is not possible for a Stokes flow since its extrema can be proved to be restricted at the boundary of the embryo (see STAR Methods and Figure S5K). Vorticity is the mathematical quantity that locally measures the rotation of fluid elements with respect to their center of mass, and it involves derivatives of the velocity that highlight characteristic structures at small scales. The observed deviations are likely due to a combination of active mechanisms in the bulk, for instance of the type identified previously for the cytoplasmic actomyosin network (Field et al., 2011; von Dassow and Schubiger, 1994) (Figure S3E-F), and multi-phase effects that are not captured by our simplified model. In summary, our analysis suggests that, at the relatively large scales relevant for nuclear positioning, the flow in the bulk is mainly controlled by viscous effects. As a consequence, despite the complex actomyosin dynamics, the large-scale features of the flow are well captured by the dynamics of a viscous, incompressible fluid passively responding to active contractions at the cortex.

Proper nuclear positioning is required for synchronous cell cycles

Our results point towards a self-organized process by which nuclei drive their positioning in the early Drosophila embryo. Nuclei initiate the oscillations of PP1 that drive the recruitment of myosin II at the cortex, which then generates cortical gradients (Figure 7A, left panel). These gradients lead to stereotypical cortical contractions which in turn give rise to mid-embryo cytoplasmic flows that spread nuclei along the AP axis and control to their positioning across the embryo (Figure 7A, middle and right panel). Nuclear positioning locally determines the NC ratio, which regulates multiple aspects of embryonic development, including the cell cycle remodeling events that accompany the maternal-to-zygotic transition (Farrell and O’Farrell, 2014; Ferree et al., 2016). Specifically, the NC ratio is a major determinant of the duration of DNA replication and, as a consequence, cell cycle timing. Thus, we predicted that altering nuclear spreading may give rise to differential activation of the DNA replication checkpoint across the embryo. As a consequence, cell cycle timing would be spatially perturbed, resulting in loss of mitotic synchrony as embryos approached the maternal-to-zygotic transition.

Figure 7. Proper nuclear positioning is required for synchronous cell cycles.

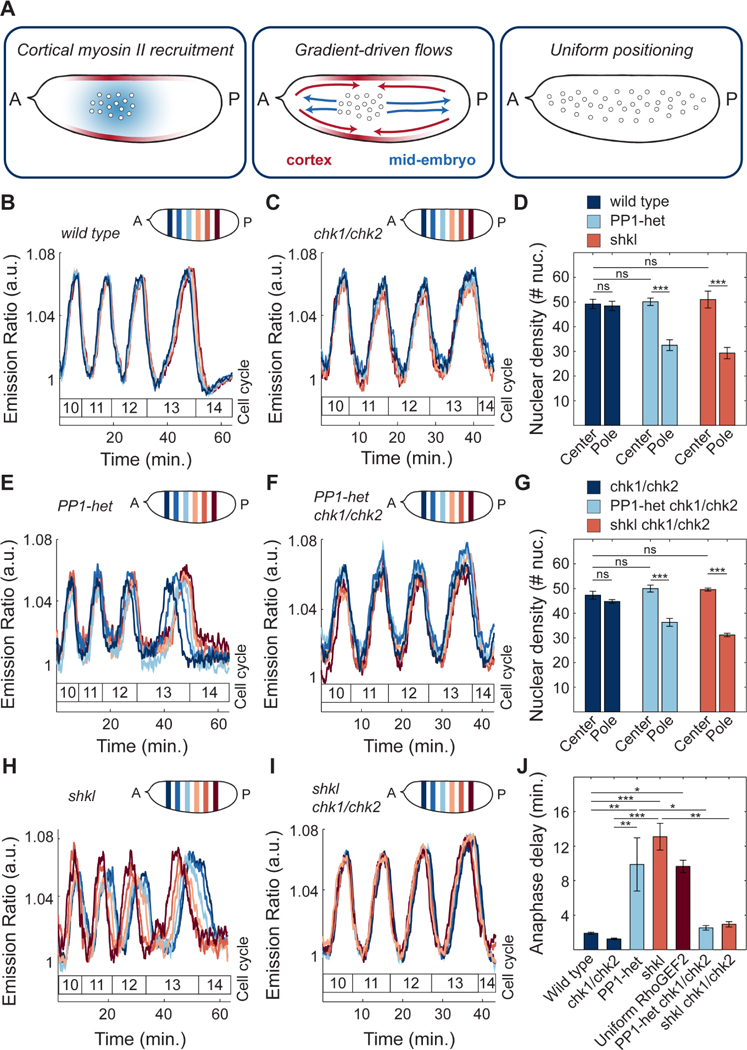
A) Model of nuclear spreading in early Drosophila embryos. Left embryo: local oscillations of PP1 activity (blue faded region) spread in a damped manner from the nuclear cloud and position myosin II at the cortex (red faded outline). Middle embryo: gradients of myosin II drive cortical contractions (red arrows) which result in mid-embryo cytoplasmic flows (blue arrows). Right embryo: Cytoplasmic flows push nuclei toward poles and distribute them along the AP axis. B-C) Emission ratio of Cdk1/PP1 FRET sensor averaged in different regions of the surface of a wild type (B) and chk1/chk2 (C) embryo at cell cycles 10–13. D) Nuclear density in a 50μm by 50μm region in center or pole region of a wild type, PP1-het and shkl embryo in cell cycle 13. E-F) Emission ratio of Cdk1/PP1 FRET sensor averaged in different regions of the surface of a PP1-het (E) and PP1-het chk1/chk2 (F) embryo at cell cycles 10–13. G) Nuclear density in a 50μm by 50μm region in center or pole region of a chk1/chk2, PP1-het chk1/chk2 and shkl chk1/chk2 embryo in cell cycle 13. H-I) Emission ratio of FRET sensor averaged in different regions of the surface of a shkl (H) and shkl chk1/chk2 (I) embryo at cell cycles 10–13. J) Quantification of delay between first nucleus to enter anaphase to last nucleus in cell cycle 13. Error bars, sem. *p < 0.05, **p < 0.001, ***p < 0.0001; a.u., arbitrary units.

In wild type embryos, at cycle 13, the last syncytial cycle, the dynamics of the Cdk1/PP1 biosensor across different regions of the embryos were synchronous (Figure 7B). This synchrony was observed starting from the end of cycle 6/beginning of cycle 7, when nuclei underwent the last axial spreading movement (Figure 1C). In fact, wild type embryos showed uniform nuclear density in the center and pole regions (Figure 7D, navy bars). In a fraction of PP1-heterozygous embryos (7 out of 11), reduced cortical and cytoplasmic flows disrupted nuclear spreading (Figure 7D, light blue bars). This subset of embryos showed significant asynchronies in the blastoderm cell cycles that became very prominent in cycle 13 (Figure 7E). Therefore, by halving the dose of PP1, embryos featured damped, and spatially more confined, oscillations in the Cdk1 to PP1 activity ratio (Figure 2E), reduced cortical contractions (Figure 4F-G) and cytoplasmic flows (Figure 5E, G), non-uniform positioning and tissue-wide asynchronies (Figure 7D-E). To verify that cell cycle asynchronies in PP1-heterozygous were the result of uneven nuclear distribution, we performed analogous experiments in shackleton mutants, a mutant defective in nuclear spreading (Yohn et al., 2003), but not in cell cycle regulation (STAR Methods; Figure S7A-B). shkl mutants showed a non-uniform distribution of nuclei along AP axis (Figure 7D, orange bars) and a significant degree of asynchrony, which increased during blastoderm divisions (Figure 7H). A large spread in the timing of mitosis 13 was also observed in optogenetic RhoGEF2 embryos, in which nuclear spreading was impaired by uniform blue light illumination during cycles 4–8 (Figure 7J, dark red bar). Finally, embryos with nuclear spreading defects often have large regions undergoing an extra mitosis (Figure S7C-D). Collectively, these observations argue that a non-uniform NC ratio generates a lack of tissue-wide synchrony and improper control in the number of nuclear divisions preceding the maternal-to-zygotic transition.

To test the hypothesis that the cell cycle asynchronies in PP1-heterozygous and shkl embryos were due to asymmetries in nuclear distribution, we introduced these mutants in genetic backgrounds that made embryos unable to respond to changes in the NC ratio. We generated PP1-heterozygous and shkl mutant embryos which were also mutant in chk1 and chk2, the two main effectors kinases of the DNA replication checkpoint. These genetic manipulations render embryos unable to sense the NC ratio and slow down the cell cycle during the blastoderm divisions (Farrell and O’Farrell, 2014; Sibon et al., 1997). Embryos heterozygous for PP1 and mutant for chk1 and chk2 and shkl/chk1/chk2 triple mutants, while displaying similar nuclear spreading defects as PP1-het and shkl embryos (Figure 7G, light blue and orange bars), retained cell cycle synchrony (Figures 7F and 7I). These experiments confirm that uniform nuclear positioning is required for uniform activation of the DNA replication checkpoint and cell cycle synchronization. This is demonstrated by the quantification of the time delay between the first nucleus to enter anaphase and the last nucleus in cell cycle 13. Wild type and chk1/chk2 mutants showed a delay of at most 2 minutes (Figure 7J, navy blue bars). On the contrary, embryos with perturbations that resulted in non-uniform nuclear spreading, such as PP1-heterozygous, shkl, or optogenetic RhoGEF2 embryos exposed to uniform blue light, showed significantly longer anaphase delays of 10–13 minutes (Figure 7J). These delays were reduced to 3–4 minutes in embryos which also lacked chk1 and chk2 (Figure 7J), confirming that they were mainly due to asymmetries in the NC ratio.

Discussion

The cleavage divisions of early embryogenesis require precise coordination of biochemical signals and mechanical properties of the cytoskeleton and of the cytoplasm. We have uncovered how the cell cycle oscillator drives changes in the mechanical properties of the Drosophila embryo, thereby ensuring accurate nuclear positioning and maintenance of mitotic synchrony at the maternal-to-zygotic transition.

Our experiments reveal insights into the spatial regulation of the cell cycle. Previous models of cell cycle synchrony have proposed that nuclei are either coordinated independently by oscillations that are very restricted in space (Su et al., 1998) or that waves synchronize the entire cytoplasm (Chang and Ferrell, 2013). Here, we demonstrate that the spreading of PP1 activity to couple nuclear and cortical dynamics is required for mitotic synchrony. Moreover, forcing the system to trigger wave-like spreading of PP1 throughout the entire embryo is also incompatible with proper nuclear positioning (Figure S7E-J). Thus, we propose that the morphogenetic processes needed for the establishment of mitotic synchrony require that PP1activity spreads across length scales similar to the distance between nuclei and the cortex.

The functional significance of localized activation of PP1 is to drive the activation of cortical actomyosin in a spatially restricted manner, which results in myosin II gradients closely linked to the position of the nuclear cloud. Myosin II gradients can drive cortical and cytoplasmic flows by causing tension imbalances at the cortex (Mayer et al., 2010). The precise spatiotemporal relationship between the position of nuclei, the cell cycle oscillator and the accumulation of myosin II provide features important for proper positioning. Indeed, cortical flows converging toward the top of the nuclear cloud have exactly the directionality needed to generate cytoplasmic flows inside the embryo and distribute nuclei along the embryo. Consistently, contractions are only observed prior to uniform nuclear positioning. Once nuclei have filled the embryo, myosin II recruitment becomes uniform and unable to generate significant flows, as demonstrated also by uniform optogenetic activation of Rho signaling (Fig. 6). This implies that the self-organized mechanism driving nuclear spreading is intrinsically robust, automatically adjusting the strength and properties of cortical and cytoplasmic flows to the degree of nuclear spreading. Moreover, this mechanism yields accurate nuclear positioning in the face of variability in the position of the nucleus at fertilization (Figure S7E).

Two non-mutually exclusive models had been previously proposed for nuclear spreading. In the local disassembly model actin dynamics in the cytoplasm drive nuclear movements (von Dassow and Schubiger, 1994), while in the cortical contraction model nuclear movements are driven by cortical actomyosin (Royou et al., 2002). These studies relied on pharmacological perturbations, which have the pitfall of influencing both cytoplasmic and cortical components. To distinguish the contribution of the two mechanisms to nuclear spreading, we used optogenetics to precisely control cortical contractility in space and time (Izquierdo et al., 2018). This approach allowed us to demonstrate that nuclear positioning is mainly driven by cortical contractions through the generation of cytoplasmic streaming. Quantitatively, the speed, the direction and the duration of the cytoplasmic flows are very close to the physical parameters needed for uniform nuclear distribution, suggesting that the generated cortical forces have the correct amplitude to guarantee mitotic synchrony.

Cytoplasmic flows are ubiquitous in biology (Goldstein and van de Meent, 2015; Quinlan, 2016), yet whether they are functionally relevant during early embryogenesis or are an epiphenomenon, simply arising as a consequence of cortical flows, is moot. Here, we have demonstrated an important function for cytoplasmic flows in regulating nuclear spreading, ensuring that all nuclei undergo the same number of divisions and that the cell cycle remains synchronous at the maternal-to-zygotic transition. This synchrony guarantees that all nuclei in the embryo initiate cellularization and gastrulation at the same time, thus favoring proper coordination of morphogenesis.

The integration of biochemical and mechanical signals is a common feature of biological systems and must be achieved across very different spatial and temporal scales. Studying this integration in large embryos allowed us to gain rigorous, quantitative insights on the mechanisms by which biochemical signals and mechanical properties of tissues can be integrated over large spatial scales (order 1 mm). Since both chemical and physical mechanisms of cell communication are emerging as general properties for the regulation of collective tissue dynamics (Deneke and Di Talia, 2018; Gross et al., 2017; Munjal et al., 2015), we speculate that their understanding in the regulation of early embryogenesis reveals general principles for the integration of biochemical and mechanical signals in complex tissues.

STAR METHODS

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Stefano Di Talia (stefano.ditalia@duke.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

All Drosophila melanogaster stocks that were used to generate the lines for this study are described in the Key Resources Table. Flies in a y¹ w¹ background were crossed to the desired transgenes and used as wild type controls and are referred to as wild type in the manuscript. For PP1-heterozygous experiments, we used a stock in which 2 genes encoding PP1α are mutated (PP1–87B and PP1–96A). To image unfertilized and activated eggs, we crossed males expressing a dominant mutation in β2 tubulin (betaTub85D), which produces immotile sperm that is unable to fertilize eggs, to wild type females. For all experiments, adult female and male flies were raised at 25°C on standard molasses food. For embryo collection, flies were placed in cages with apple juice agar plates and yeast paste. Embryos were collected on apple juice agar plates after 0–1 hr at 25°C. Genetic crosses and cages of flies expressi ng optogenetic constructs were kept in the dark.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, Peptides, and Recombinant Proteins
Citra Solv Concentrated Cleaner & Degreaser	www.citrasolv.com	N/A
Trypan Blue Solution, 0.4%	Gibco	Cat #: 15250061
Halocarbon Oil 27	Sigma	Cat #: 9002–83-9
Deep Golden Amber Filter	www.leefilters.com	No: 135
Experimental Models: Organisms/Strains
D. melanogaster: w; Cdk1-FRET; His2Av-mRFP	S. Di Talia	(Deneke et al., 2016)
D. melanogaster: y[1] w[*]; P{w[+mC]=PTT-GC}CycB[CC01846]	Bloomington Drosophila Stock Center	BDSC: 51568; FlyBase: FBst0051568
D. melanogaster: w[*];; Pp1–87B[87Bg-3] e[1] Pp1alpha-96A[2]/TM6B, Tb[1]	Bloomington Drosophila Stock Center	BDSC: 23699; FlyBase: FBst0023699
D. melanogaster: w[*];; P{w[+mC]=sqh-mCherry.M}3	Bloomington Drosophila Stock Center	BDSC: 59024; FlyBase: FBst0059024
D. melanogaster: w; AniRBD-GFP	T. Lecuit	(Munjal et al., 2015)
D. melanogaster: w*; P{His2Av-mRFP1}II.2	Bloomington Drosophila Stock Center	BDSC: 23651; FlyBase: FBst0023651
D. melanogaster: w*;; P{His2Av-mRFP1}III.1	Bloomington Drosophila Stock Center	BDSC: 23650; FlyBase: FBst0023650
D. melanogaster: w;; PCNA-TagRFP-T	S. Di Talia	(Deneke et al., 2016)
D. melanogaster: w[*]; If/Cyo; P[w+,UASp>RhoGEF2-CRY2::mCherry]/TM3, Ser	S. De Renzis	(Izquierdo et al., 2018)
D. melanogaster: w[*]; If/CyO; P[w+, UASp>RhoGEF2- CRY2]/TM3, Ser	S. De Renzis	(Izquierdo et al., 2018)
D. melanogaster: w[*]; P[w+, UASp>CIBN::pmGFP]/Cyo; Sb/TM3, Ser.	S. De Renzis	(Guglielmi et al., 2015)
D. melanogaster: w1118; P{osk-GAL4::VP16}A11/CyO	Bloomington Drosophila Stock Center	BDSC: 44241; FlyBase: FBst0044241
D. melanogaster: w; grp209 lok30/grpz5170 lok30	J. Sekelsky	N/A
D. melanogaster: w;; shklGM130/shklGM163	R. Lehmann	(Yohn et al., 2003)
D. melanogaster: w[*]; P{ry[+t7.2]=neoFRT}82B P{w[+mC]=ovoD1–18}3R/st[1] betaTub85D[D] ss[1] e[s]/TM3, Sb[1]	Bloomington Drosophila Stock Center	BDSC: 2149; FlyBase: FBst0002149
D. melanogaster: Df(3L)AC1, rn[roe-1] p[p]/TM3, Sb[1]	Bloomington Drosophila Stock Center	BDSC: 997; FlyBase: FBst0000997
D. melanogaster: y[1] w[1118]; PBac{y[+mDint]=3HPy[+]}I-2[C362]	Bloomington Drosophila Stock Center	BDSC: 16350; FlyBase: FBst0016350
D. melanogaster: w; sqh::GFPmoesinABD	D. Kiehart	N/A
D. melanogaster: w[*]; P{w[+mC]=UAS-I-2.HA}G; P{w[+mC]=UAS-Pp1–87B.HA}H-1/TM6B, Tb[1]	Bloomington Drosophila Stock Center	BDSC: 24101; FlyBase: FBst0024101
D. melanogaster: w[1118];; P{w[+mC]=GAL4::VP16-nos.UTR}CG6325[MVD1]	Bloomington Drosophila Stock Center	BDSC: 4937; FlyBase: FBst0004937
D. melanogaster: w; twine-GFP His2Av-mRFP	S. Di Talia	This study
Software and Algorithms
MATLAB R2018a	Mathworks	N/A
ImageJ	https://imagej.nih.gov/ij/	N/A
Adobe Illustrator CC 2018	Adobe.com	N/A
Ilastik	www.ilastik.org	N/A
JMP	www.jmp.com	N/A

METHOD DETAILS

Embryo Manipulations

Following collection, embryos were dechorionated with 50% bleach for 1 min, rinsed with water and mounted in halocarbon oil on a gas-permeable membrane and covered with a glass coverslip. To visualize cytoplasmic flows, yolk granules were stained by permeabilizing embryos with a solution of 10% CitraSolv in water for 2 minutes and immersing them in Trypan Blue for 1 minute.

Microscopy

Imaging experiments were performed with an upright Leica SP8 confocal microscope, a 20×/0.75 numerical aperture oil-immersion objective, an argon ion laser, and a 561-nm diode laser, unless stated otherwise. For the analysis of the Cdk1/PP1 sensor activity at the surface, as well as cortical contractions, we acquired images (800 × 300 pixels, pixel size: 0.56 μm) with a frame rate of 1/2.89 s. For analysis of the Cdk1/PP1 sensor along the axial direction, z-stack images (296 × 80 pixels, pixel size 1.51 μm) were acquired in 10 μm steps with a frame rate of 1/1.41 s. For the analysis of cytoplasmic flow, we acquired stacks of raw confocal sections (800 × 400 pixels, pixel size: 0.727 μm) of cytoplasm (Trypan Blue) and nuclei (PCNA-TagRFP) with an axial distance of about 50–60 microns and sampling of about 20 seconds. Multiphoton imaging of CyclinB-GFP His2Av-mRFP embryos was performed on an Olympus FV1000 using a 25×/1.05 water immersion lens (512 × 256 pixels, pixel size: 1.25 μm) with a frame rate of 1/2s.

For optogenetic experiments, imaging was performed with a Zeiss LSM 780 NLO confocal microscope equipped with a 561-nm diode laser, and an argon laser. A 32×/0.85 NA water immersion objective was used for image acquisition. For sample location, bright field illumination was filtered through a Deep Amber lighting filter. The microscope was controlled through the Zen Black software whereas photo-activation protocols were carried out with the Pipeline Constructor Macro (Izquierdo et al. 2018).

For FRAP experiments, imaging was performed with an upright Leica SP8 confocal, a 20×/0.75 numerical aperture oil-immersion objective, an argon ion laser, and a 561-nm diode laser. For embryos co-expressing Cdc25^Twine-GFP and His2Av-mRFP, 75 μm × 75 μm square areas were bleached for 1.5 min. with a 488-nm laser (pinhole: 7 AU) spanning 20 μm axially. We acquired fluorescence recovery images (800 × 300 pixels, pixel size: 0.56 μm, pinhole: 1 AU) with a frame rate of 1/2 s. For embryos expressing PCNA-TagRFP, 115 μm × 115 μm square areas were bleached for 1.5 min. with both a 488-nm laser and a 561-nm laser (pinhole: 7 AU) spanning 20 μm axially. We acquired fluorescence recovery images (800 × 300 pixels, pixel size: 0.727 μm, pinhole: 1 AU) with a frame rate of 1/2 s.

Production of endos^S68D and I-2 mRNA

Endos-S68D ssRNA was synthesized by in vitro transcription of a DNA template containing the T7 promoter sequence on the 5’ end. The DNA template was generated by introducing Endos-S68D in pBluescript vector via Gibson assembly following PCR amplification of genomic DNA from w¹¹¹⁸ flies using Q5 High-Fidelity DNA Polymerase. The S68D point mutation was generated by fusing (in the Gibson assembly reaction) two PCR fragments in which the mutation was incorporated through the primers. Amplified DNA templates were in vitro transcribed (Ambion Megascript Kit) and diluted to a final concentration of 1 mg/mL. The primers used for PCR amplification were: T7-endos-fwd (5’ - CTC ACT ATA GAT GAG CTC CGC GGA AGA AAA C - 3’), T7-endos-rev (5’ - TCC GCG GAG CTC ATC TAT AGT GAG TCG TAT TAC AAT TC - 3’), endos-S68D-fwd (5’ - GCA GAA GGG GCA AAA GTT CTT CGA CGA CGG C - 3’), endos-S68D-rev (5’- AGA ACT TTT GCC CCT TCT GCA GCC TTT TC - 3’), pBSK-T7-fwd (5’ – TAT CGA TAA GCT TGA TAT CGG ATT AAG TTG GGT AAC GC - 3’), S68D-pBSK-rev (5’ - TGG ATC CCC CGG GCT GCA GGT TAG CTC GTC GCC GGG AAC - 3’).

I-2 mRNA was synthesized by in vitro transcription of a DNA template containing the T7 promoter sequence on the 5’ end. The DNA template was assembled by PCR amplification of a pGEX plasmid including human Inhibitor-2 sequence (gift from S. Kornbluth). Amplified DNA templates were in vitro transcribed (Ambion Megascript Kit) and diluted to a final concentration of 1 mg/mL. The primers used for PCR amplification were: Inh2-T7-fwd (5’ – TAA TAC GAC TCA CTA TAG GGA TGG CGG CCT CGA CGG CC - 3’), Inh2-rev (5’ – CTA TGA ACT TCG TAA TTT GTT TTG CTG - 3’).

QUANTIFICATION AND STATISTICAL ANALYSIS

Image analysis

All computational operations and image analysis steps were performed with custom-written MATLAB algorithms with the Image Processing Toolbox unless otherwise noted.

Identification of the phosphatase regulating the FRET biosensor

Previous work argued that a mitotic phosphatase must be important in the regulation of the biosensor (Gavet and Pines, 2010). To identify it, we used injection of mRNA encoding inhibitors specific for the two major mitotic phosphatases, PP2A and PP1. To inhibit PP2A, we injected mRNA encoding a mutant version of Endosulfine (Endos-S68D), a phosphomimetic mutant that strongly suppresses PP2A (see below for Methods). Upon injection of endos^S68D mRNA, we observed significant mitotic exit defects (data not shown). However, the biosensor was still fully dephosphorylated, albeit at a slightly lower rate (Figure S1A). By contrast, injection of mRNA encoding Inhibitor-2 (I-2) (see below for Methods), a specific inhibitor of PP1 activity when highly over-expressed, caused the biosensor to remain in a phosphorylated state (Figure S1B) and nuclei to arrest in metaphase, consistent with previous observations that PP1 is required for mitotic exit (Wu et al., 2009). The role of PP1 in the dephosphorylation of the biosensor was further supported by genetic manipulations reducing the levels of I-2, which cause a decrease in the level of phosphorylation of the biosensor in mitosis (Figure S2D). We conclude that the Cdk1 biosensor is mainly dephosphorylated by PP1, so we refer to it as Cdk1/PP1 biosensor.

Quantification of the Cdk1/PP1 biosensor

The Cdk1/PP1 activity ratio was estimated as in (Deneke et al., 2016). To generate heat maps, the Emission Ratios were averaged over regions of 4.48 μm along the AP axis. Slight differences in the plane of focus across the embryo, as well as small drifts during imaging, cause trends in the data that were reduced using the following procedure. First, we normalized the emission ratio for each region with the average in that region during cell cycle 12, when the amplitude of Cdk1/PP1 oscillations is essentially uniform is space. Then, we de-trended the data by subtracting the dynamics in each region with that obtained using Smoothing Splines with a very high smoothing parameter (1/p=10⁹) to extrapolate the low frequency behavior of the average FRET signal across the embryo. Normalized and de-trended data were then smoothened in time and space using the Savitsky-Golay filter (3^rd order polynomial over 55 points in time and 1^st order polynomial over 7 points in space). Similar smoothing with Savitsky-Golay filters was used to generate the myosin II and Rho activity heat maps.

Quantification of cortical and cytoplasmic flows

Stacks of raw confocal sections of Trypan Blue stained yolk granules and nuclear marker (PCNA-TagRFP) were sum-projected and Gaussian-filtered (width of 10 μm and standard deviation 6 μm) in order to increase signal-to-noise ratio as a pre-processing image analysis step. Nuclear tracking was performed by means of Ilastik trained on several embryo datasets. Binary images obtained with segmentation were labeled and centroids were used to extract the position of nuclei which was then fed to a tracking algorithm based on minimum distance criterion. Cytoplasmic velocity fields were measured by means of Particle-Image-Velocimetry. Briefly, stripes of 35 μm (Anterior-Posterior direction) by 15 μm (Dorsal-Ventral or lateral direction) were used as templates and probed within regions of 60 μm by 30 μm to find best correlation spots, with a threshold correlation coefficient of 0.7. PIV was calculated for ten thousand unique points randomly distributed within the embryo at each time interval. A sampling of around 20 to 30 seconds was used to get reliable local displacements yet maintaining high correlations. The obtained velocity fields were time-averaged over a range of 10 seconds and then linearly interpolated on a square grid with 4 μm spacing. One-dimensional heat maps were generated by averaging the AP component of the velocity over the whole embryo and on a stripe 100 μm-thick, centered on the AP axis and interpolating it on a dense uniformly spaced one dimensional grid with spacing equivalent to 500 points on the length of the embryo. Each time interval was then used as a column in a matrix represented with the appropriate color-map.

Lagrangian trajectories of particles such as those shown in Figures 4 and 5 were computed by seeding uniformly spaced points and integrating numerically the equation $\dot{x}\left(t\right)=v\left(x\left(t\right)\right)$) with Euler’s scheme using spatially interpolated velocity fields from PIV data at each time interval. Integration was performed for the whole duration of each interphase. Backward integration of particle trajectories along the AP axis was performed by integrating $\dot{x}\left(t\right)=v\left(x\left(t\right)\right)$ with the mid-point method backward in time and using interpolated 1-D values of the AP velocity as described above. Integration was performed for the whole duration of each shown dataset. The vorticity ω = ∇ × v was computed using the curl function in MATLAB, after having verified that on simulated Stokes flows maxima and minima are on the boundary, as expected.

Validation of cortical and bulk cytoplasmic flow measurements

In order to verify the effectiveness of our approach for visualizing and quantifying cytoplasmic flows, we compared the velocities obtained with PIV of His2Av and yolk granules (stained with Trypan Blue) with those obtained using a Fluorescence Recovery After Photobleaching (FRAP) method on cytosolic proteins (Carroll et al., 2014), which should act as soluble tracers (Cdc25^Twine-GFP or PCNA-TagRFP). Particle Image Velocimetry (PIV) provides an accurate methodology for the reconstruction of flows with high spatiotemporal resolution. However, since PIV is based on cross-correlation between images, it can detect movements of structures with size of at least a few units of digital resolution, in our case not smaller than a few microns. As a consequence, it does not allow the tracking of featureless tracers, such as signals coming from a soluble molecule which is uniformly distributed. Therefore, it is possible that the movement detected with our signal and methods (His2Av, yolk granules and PIV) reflects the movement of larger scale structures, either bound to the actomyosin network or influenced by its mesh size. Indeed, in response to an external impulsive pressure, during blebbing the soluble aqueous component of the cytoplasm (cytosol) and the actomyosin gel have been shown to move relative to each other on timescales of few seconds across several microns (Mitchison et al., 2008). To validate our measurements, we compared the movement obtained for both His2Av-mRFP and yolk granules to that of soluble markers (Cdc25^Twine-GFP and PCNA-TagRFP). The latter was assessed by adapting a FRAP method for measuring flow using soluble fluorescent proteins (Carroll et al., 2014). Following photobleaching, the movement of the dark bleached region is described by an advection-diffusion equation. In the absence of advection, the bleached region remains close to its initial location and fluorescence recovery follows purely diffusive dynamics. In the presence of advection, the bleached area is transported by the flow and flow velocity can be obtained by tracking the bleached area (Carroll et al., 2014). We optimized the bleaching conditions to follow reliably the bleached area for 2–3 minutes and could observe that it moves (Figures S4A-B and Figure S5A-B), strongly supporting that the cytosol is being advected during cell cycles 4–6. To measure velocity, we inferred the position of the bleached area by fitting the front of the fluorescence prolife across space with a sigmoidal function of the form: $I\left(x\right)=C\ast \left(1-\text{erf}\left(\frac{x-a}{w}\right)\right)+B$, where a is the inferred position at a particular time, B is the background, C is the amplitude, and w is the width of the sigmoid, which is linked to diffusion (Figure S4B and Figure S5B). From the derivative of a smoothing spline fit (parameter p=1/100) of the position a, we extrapolated velocity as a function of time. Since we performed these experiments in embryos co-expressing Cdc25^Twine-GFP and His2Av-mRFP (for cortical flows) and PCNA-TagRFP and stained yolk granules (for cytoplasmic flows), we could directly correlate flow measurements from PIV and FRAP. Figures S4C and S5C show that there is a strong 1:1 agreement between the two measurements, confirming that our PIV-based approaches measure the flow of cytosol both at the cortex and in the bulk of early Drosophila embryos.

Prediction of cortical velocity from myosin gradients

To determine the relation between cortical flows and myosin spatial distribution, we used a mathematical model previously proposed by (Mayer et al., 2010). To keep presentation self-contained, we repeat the derivation of the model (Mayer et al., 2010). The central assumption of the model is that cortical tension is proportional to myosin levels and a viscous term, characterizing the physical nature of cortical flows:

$$T\left(x\right)=C\left(x\right)+\eta \frac{\partial v}{\partial x}$$

where T is the tension, C is the force (contractility) generated by myosin, which we take to be proportional to myosin concentration, and η is the viscosity of the cytoplasm near the cortex. Flows arise from gradients in tension and are related to those gradients through an overdamped relationship characterized by a friction coefficient γ:

$$\frac{dT}{dx}=\gamma v$$

From these relationships, one obtains:

$$\frac{{\partial }^{2}v}{\partial x^2}-\frac{1}{{\lambda }^2}v=-\frac{1}{\eta }\frac{\partial C}{\partial x}$$ (Equation 1)

which can be used to fit cortical flows from measured myosin gradients. Myosin spatial profiles were fitted using Smoothing Splines with smoothing parameter 1/p=100 and gradients were evaluated using the differentiate function in MATLAB. These gradients were then used to solve Equation 1 using standard numerical methods. An important parameter of the model is the length scale: $\lambda \equiv \sqrt{\eta /\gamma }$, which gives the spatial decay length of velocity in response to a step change in myosin levels (contractility), thus providing a length scale over which actomyosin contractility is correlated. We found that cortical flows can be fit well with $\lambda ~100\mu m$ and used this value to generate the data shown in Figure 4E.

Cytoplasmic F-actin and myosin II dynamics

To understand the dynamics of F-actin and myosin II in the cytoplasm, we imaged embryos expressing Moesin-ABD-GFP (F-actin marker) and myosin II-mCherry in the same embryos at different depths from the surface of the embryo (Figure S3E-F). These imaging experiments show several important features of actomyosin dynamics. First, the dynamics of F-actin and myosin II are strongly correlated both at the cortex and in the cytoplasm (Figure S3E-F). Second, the oscillations at the cortex are much more pronounced that cytoplasmic oscillations (Figure S3E-F). Third, the cytoplasmic and cortical oscillations have different timing. Cytoplasmic F-actin and myosin II levels have dynamics similar to that of the Cdk1/PP1 biosensor and increase during mitosis, as previously observed in vertebrate embryos (Field et al., 2011). On the contrary, cortical levels increase about 2 minutes earlier and are highest in interphase (Figure S3E-F and Figure 3). Finally, spatial regulation of cytoplasmic F-actin and myosin II is also coupled to nuclear positioning with oscillations observed in cytoplasmic regions surrounding nuclei, but not in regions away from the nuclear cloud (Figure S3G-H).

Analysis of the physical nature of cytoplasmic flows

To characterize the physical properties of cytoplasmic flows, we first computed the Reynolds number (Re). Using typical values for the speed of cytoplasmic flows, the dimension of the embryo and using the kinematic viscosity of water $\left(V=0.3\frac{\mu m}{s};L=100\mu m;v=3\cdot {10}^6\mu m^2/s\right)$, we obtain $Re\approx {10}^{-5}$. At low Reynolds number, fluids are dominated by viscous forces, undergo laminar flows and can be described by Stokes’ equation:

$$v{\nabla }^{2}v=-\frac{1}{\rho }\nabla p$$ (Equation 2)

where ρ is the density of the fluid and p is the pressure. We used this equation to compare the measured flows with those predicted assuming that the cytoplasm behaves as a passive viscous fluid. Predicted flows were computed using the boundary method to solve Equation 2 (Pozrikidis, 2011). We used the single-layer formulation of the boundary integral equations:

$$u_j\left({\overrightarrow{x}}_0\right)={\int }_D{f}_i\left(\overrightarrow{x}\right)G_{ij}\left(\overrightarrow{x},{\overrightarrow{x}}_0\right)dS\left(\overrightarrow{x}\right)$$ (Equation 3)

where ${\overrightarrow{x}}_0$ is any point in the domain of interest, $\overrightarrow{x}$ is a point located on the boundary of the domain, ƒ_i is the force density in the i direction, u_j is the j-th component of the fluid velocity vector, dS is the surface element on the boundary of the domain of interest (here the cortex), G_ij is the two-dimensional Green’s function Stokeslet.

Determining the force densities $f_i\left(\overrightarrow{x}\right)$ along the cortex is equivalent to determining the velocity field $\overrightarrow{v}\left(\overrightarrow{x}\right)$ along the cortex. The flow in the interior of the embryo (our domain of interest) depends on $\overrightarrow{v}\left(\overrightarrow{x}\right)$ via Equation 3. Our goal is to identify the cortical velocity ${\overrightarrow{v}}^{\ast }\left(\overrightarrow{x}\right)$ which minimizes the difference between the experimentally measured velocity profile ${\overrightarrow{u}}_{Measured}$ and the Stokes flow ${\overrightarrow{u}}_{Stokes}$ as expressed by Equation 3. In other words, the following optimization was done:

$${\overrightarrow{v}}^{\ast }\left(\overrightarrow{x}\right)=ar{g}_{v\left(\overrightarrow{x}\right)}\min ‖{\overrightarrow{u}}_{Stokes}\left({\overrightarrow{x}}_0\right)-{\overrightarrow{u}}_{Measured}\left({\overrightarrow{x}}_0\right)‖$$

where the error is quantified by the L2 quadratic norm between the velocities in the interior of the embryo and minimization was performed by convex optimization using CVX (Grant and Boyd, 2013).

For practical purposes, the cortical velocities were constrained to be of the form:

$$\overrightarrow{v}\left(\overrightarrow{x}\right)=\left(\sum _{j=1}^4{a}_j\sin \left(j\varphi \right)\cos \left(\theta \right),\sum _{j=1}^4{a}_j\sin \left(j\varphi \right)\sin \left(\theta \right)\right)$$

where θ is the angle subtended by the tangent to the embryo at the point $\overrightarrow{x}$, and ϕ is the angle subtended by $\overrightarrow{x}$ with respect to the center of the embryo. No major difference was observed if the number of harmonics is increased. This analysis demonstrates that the flows observed inside the embryos are similar to those expected for a viscous fluid (Figures 5 and S5), arguing that forces at the cortex are mainly responsible for generating cytoplasmic flows, a theoretical hypothesis confirmed experimentally using optogenetic regulation of cortical contractility (Figure S6).

Since we expect a viscous description to be relevant at large scales only, we next performed a more detailed analysis to determine whether deviations from the behavior of a viscous fluid are observed at small scales. Comparisons of the predicted velocity fields with the measured ones indicate that deviations are indeed observed, pointing that flows deviate from the simple behavior of a viscous fluid. To strengthen this conclusion, we computed the vorticity of the velocity field ω = ∇ × v and analyzed its geometrical characteristics, which reflect the properties of the flow at small scales. Taking the curl of Stokes’ equation (4), the following equation for the vorticity is obtained:

$${\nabla }^2\omega =0$$

implying that ω is a harmonic function. The mean-values property of harmonic functions implies that the maximum or minimum of the vorticity can only be attained at the boundary of the embryo. We observe that the pseudo-vector ω is three dimensional and that computing its components in all 3 dimensions is experimentally very difficult. However, since the equation above must be respected by each component of the vorticity, we focused on the axial direction ω_z, which can be readily computed from our data. In contrast with the prediction of Stokes flow, we observed that extremal values of the vorticity are observed in four regions inside the embryo. Thus, we conclude that, while cytoplasmic streaming is in large part captured by the behavior of a viscous fluid responding to cortical forces, deviations from a Stokes flow are readily observed in the cytoplasm. A likely interpretation is that active or multi-phase mechanisms provide additional contributions that shape the flows.

Characterization of shackleton mutant

The gene shackleton (shkl) was identified in a screen for mutants affecting the specification of germ cells during early embryonic development (Yohn et al., 2003). It was found that the decrease in germ cells was probably explained by defects in nuclear spreading, as nuclear positioning at the posterior of the embryo is required for germ cell specification (Yohn et al., 2003). Using imaging of both fixed and living embryos, we confirmed that indeed shkl mutant embryos are defective in nuclear spreading (Figure 7D). Since the cell cycle drives nuclear spreading, we asked whether these defects could be due to defects in cell cycle regulation. Three main lines of evidence argue against this scenario: 1. The oscillations of the Cdk1/PP1 biosensor in the region of the nuclei are very similar to those observed in wild type, suggesting that the core of the cell cycle oscillator is not influenced (Figure S7A; Figure 7B, 7H); 2. Cell cycle timing is normal for each NC ratio (Figures S7A-B); 3. No morphological mitotic defects are observed. Collectively, these observations argue that shkl does not encode a gene product important for cell cycle regulation. Thus, shkl mutants provide an experimental system to test the effect of impaired nuclear spreading on mitotic synchrony.

Analysis of traveling waves of Cdk1/PP1 activity

Our experiments indicate an important role for the local spreading of PP1 activity in the coordination of the early cell cycles. To further elucidate the importance of this spatial dynamics, we sought conditions that would force PP1 activity to spread through the entire embryo. We found that embryo-wide oscillations of the Cdk1/PP1 biosensor could be generated in a fraction of embryos, in which expression of an UAS-I-2 construct was driven maternally by the nanos-Gal4 driver (maternal genotype: w; UAS-Inh-2/Cdk1-FRET His2AvRFP; Cdk1-FRET His2AvRFP/nanos-Gal4). Specifically, we observed global oscillations of the Cdk1/PP1 biosensor, which spread through the entire embryo as traveling waves (Figure S7F). Even though the mechanism by which I-2 can facilitate embryo-wide oscillations of PP1 activity is unclear, we speculate that this is due to its function as an inhibitory chaperone, arguing that it might work as an inhibitor during mitotic entry and as an activator during mitotic exit (Heim et al., 2017). Our ability to generate traveling waves of Cdk1/PP1 activity allowed us to test whether such waves are compatible with efficient nuclear spreading and mitotic synchrony. To elucidate how waves of Cdk1/PP1 drive the recruitment of actomyosin at the cortex, we quantified both the biosensor and myosin II dynamics. We found that in these embryos there are traveling waves of myosin II that closely follow the Cdk1/PP1 waves (Figure S7G). In fact, myosin II waves showed the same propagating dynamics as the Cdk1/PP1 waves, as evidenced by comparing the Cdk1/PP1 propagation front during mitotic exit (Figure S7G, dotted line, top left panel) to the myosin II recruitment wave front (Figure S7G, dotted line, bottom left panel), which was shifted by the same time delay of 1–2 minutes observed in wild type. These waves have the consequence of generating alternating myosin II gradients, a gradient in one direction along the anterior-posterior axis at mitotic entry and an opposite one at mitotic exit (Figure S7G, right panel). These alternating gradients generate cortical contractions that are no longer linked to nuclear position. Instead cortical flows are directed toward one pole at mitotic entry and towards the other pole at mitotic exit (Figure S7H-I). As expected, cytoplasmic flows respond to changes in cortical flows and also show a pattern in which the entire cytoplasm flows towards one pole during mitotic entry and towards the other pole during interphase (Figure S7J). This pattern of cytoplasmic flows would move more or less uniformly the entire nuclear cloud toward alternating poles and would not facilitate nuclear spreading. In fact, we observe a strong disruption of nuclear spreading in many of these embryos with nuclei occupying a small fraction of the surface of the embryo at cell cycle 10. Similar to PP1 heterozygous and shkl embryos, non-uniform positioning of nuclei results in significant asynchronies in the cell cycle at the maternal-to-zygotic transition (Figure S7K). Based on all these observations, we conclude that traveling waves in the activity of Cdk1/PP1 are incompatible with mitotic synchrony during early Drosophila embryogenesis.

Statistical analysis

All statistical analyses were performed using JMP Pro. Statistical comparisons between multiple samples was by one-way ANOVA followed by Tukey’s test to compare all pairs. For all measurements, at least three biological replicates were used unless otherwise noted.

Supplementary Material

1

Figure S1. Identification of PP1 as the phosphatase driving dephosphorylation and spatiotemporal dynamics of the Cdk1/PP1 biosensor. Related to Figure 1. A) Dynamics of biosensor in a control-injected blastoderm embryo (navy line) and embryo injected with phospho-mimetic endos-S68D mRNA (red line), which inhibits PP2A. B) Dynamics of biosensor in a control-injected blastoderm embryo (navy line) and embryo injected with I-2 mRNA (red line), which inhibits PP1. C) Emission ratio of Cdk1/PP1 FRET sensor averaged in regions 30μm from the surface on anterior side (blue line) and posterior side (red line). Note that the early positioning of nuclei is on the anterior side. Inset, embryo outline with shaded boxes indicating position of plotted regions along the anterior-posterior axis and 30μm from the surface of the embryo. D) Cdk1 to PP1 activity ratio in anterior (navy line) or posterior (red line) regions at the surface of an embryo for cell cycle 4. Inset, embryo outline with shaded boxes indicating the positions along the anterior-posterior axis and at the surface of the embryo where the signal was averaged. E) Cdk1 to PP1 activity ratio in anterior region and at the surface of a fertilized (navy line) in cell cycles 4–9 and unfertilized (red line) embryo of similar age. Error bars, sem; a.u., arbitrary units.

5

Figure S5.Cytoplasmic flows in wild type and PP1-heterozygous embryos. Related to Figure 5. A) Snapshots of an embryo expressing soluble PCNA-TagRFP 0 min. (top) and 1.5 min. (bottom) after fluorescence recovery of bleached region. White box: bleached region at t=0 min. Dotted white box: bleached region at t=1.5 min. B) Heat map of TagRFP fluorescence intensity along the AP axis following photobleaching. Dotted black line: calculated position of front edge of bleached area. C) Velocity measured by PIV on yolk granules versus velocity measured by FRAP on PCNA-TagRFP for 10 embryos during cell cycles 4–8. Solid red line: best fit line (slope: 0.98+−0.02). D-E) Heat map of cytoplasmic flow in a 50 μm region in the center of a wild type (D) and a PP1-heterozygous embryo (E) for cell cycles 4–7. Arrows indicate the direction of movement along the AP axis. F-G) Heat map of cytoplasmic flow in a 50μm region in the center of a wild type (F) and a PP1-heterozygous embryo (G) for cell cycles 5–7. Arrows indicate the direction of movement along the AP axis. H) Probability density of the difference between the speed predicted by Stokes’ flow and the measured speed. As a reference, the experimental resolution is 1 pixel/ 2 frames~0.025 μm/s. Red line: Gaussian fit. I) Heat map showing the cosine of the angle θ defined by the measured velocity and the velocity predicted by Stokes’ flow. J) Heat map showing the difference between the speed predicted by Stokes’ flow and the measured speed normalized by the root-mean-square in a posterior region in the mid-embryo where flows are strong. K) Vorticity (ω = ∇ × v) for a simulated Stokes’ flow, demonstrating that maxima and minima are located at the embryo cortex.

6

Figure S6.Optogenetic RhoGEF2-CRY2 recruitment to plasma membrane drives myosin II cortical accumulation upon blue light illumination. Related to Figure 6. A) Snapshot of an embryo co-expressing CIBN::pmGFP and RhoGEF2-CRY2::mCherry before (top) and after global blue light illumination (bottom). B) Quantification of RhoGEF2 average intensity across the embryo before (navy line) and after (red line) global blue light illumination. C) Snapshot of an embryo co-expressing CIBN::pmGFP and RhoGEF2-CRY2::mCherry before (top) and after local blue light illumination on posterior side of embryo (bottom). Dotted box: illuminated region. D) Quantification of RhoGEF2 average intensity across the embryo before (navy line) and after (red line) global blue light illumination. Dotted lines: illuminated region. E) Quantification of myosin II average intensity dynamics of embryos co-expressing CIBN::pmGFP, RhoGEF-CRY2, and myosin II::mCherry. Navy line, no blue light illumination control embryo showing endogenous myosin II recruitment at cell cycle 7. Light blue line, embryo illuminated with blue light globally. Red line, embryo illuminated only in local center region. Light peach line, embryo illuminated on posterior side. Top panel, diagrams of all illumination conditions with illuminated regions shown in dotted black line and averaged region shown in colored regions. F) Snapshot of an embryo co-expressing CIBN::pmGFP, RhoGEF2-CRY2, and myosin II::mCherry before (top) and after global blue light illumination (bottom). G) Quantification of average myosin II intensity across an embryo before (navy line) and after (red line) global blue light illumination. H) Snapshot of an embryo co-expressing CIBN::pmGFP, RhoGEF2-CRY2, and myosin II::mCherry before (top) and after center blue light illumination (bottom). Dotted box: illuminated region. I) Quantification of average myosin II intensity across an embryo before (navy line) and after (red line) center blue light illumination. Dotted lines: illuminated region. J) Snapshot of an embryo co-expressing CIBN::pmGFP, RhoGEF2-CRY2, and myosin II::mCherry before (top) and after local blue light illumination in anterior side of embryo (bottom). Dotted box: illuminated region. K) Quantification of average myosin II intensity across an embryo before (navy line) and after (red line) local blue light illumination on anterior side of embryo. Dotted lines: illuminated region. All scalebars, 50μm.

7

Figure S7.shackleton controls nuclear spreading without affecting the cell cycle; characterization of traveling waves of Cdk1/PP1 activity in early embryos. Related to Figure 7. A) Emission ratio of FRET sensor averaged in different regions of the surface of a shkl embryo at cell cycles 6–13. Boxes delineate cell cycle timing for shkl and wild type embryos. B) Top: nuclear density in anterior and posterior regions of a shkl embryo in cell cycle 13. Bottom: nuclear density in anterior and posterior regions of a wild type embryo in cell cycle 12 and 13. Inset, number of nuclei in region. Scale bars, 10μm. Right panel: Cdk1 to PP1 activity plotted for wild type cell cycle 12 (blue solid line), wild type cell cycle 13 (red solid line), the anterior side of a shkl embryo at cell cycle 13 (red dotted line), and the posterior side of a shkl embryo at cell cycle 13 (dotted blue line). C-D) Snapshot of anterior side of a PP1-het (C) and a shkl (D) embryo undergoing an extra division. Red dotted line: extra division boundary. Scale bars, 20μm. E) Histogram of cell cycle 1 nuclear distribution along AP axis measured from fixed wild type embryos stained with DAPI (n=11). F) Heat map of Cdk1 to PP1 activity along the AP axis of a UAS-I2 overexpressing embryo for cell cycles 4–9. Dashed line: mitotic entry wave front; solid line: mitotic exit wave front. G) Heat maps of Cdk1 to PP1 activity (top left) and myosin levels (bottom left) along the AP axis of a cell cycle 6 UAS-I2 overexpressing embryo with corresponding Cdk1 and myosin gradients during mitotic entry and exit (right panels). Blue points and lines: gradients during mitotic entry with best fit; red points and lines: gradients during mitotic exit with best fit; dashed line: mitotic entry wave front; solid line: mitotic exit wave front. H) Heat map of cortical flow velocity along the AP axis of an embryo with intermediate I-2 overexpression for cell cycles 4–9. I) Myosin intensity profiles across AP axis during mitotic entry (top left panel) and mitotic exit (bottom left panel) of a UAS-I2 embryo. Streamlines showing direction of cortical flows (red arrows) during mitotic entry (top right panel) and exit (bottom right panel) in a UAS-I2 embryo. J) Heat map of cytoplasmic flow velocity along the AP axis of an embryo with intermediate I-2 overexpression for cell cycles 4–9. K) Emission ratio of FRET sensor averaged in different regions of the surface of an embryo with intermediate I-2 overexpression at cell cycles 6–13.

8

Video S1. Cortical recruitment of Rho sensor and myosin II in early cycles. Time-lapse video of an embryo expressing anillin-rbd (Rho binding domain) tagged with GFP and the Regulatory Light Chain of myosin II tagged with mCherry (sqh-mCherry) during cell cycles 3–10. Images were acquired with 1/2.89 s. frame rate. Video was resampled to show one in every five images and are shown at 15 frames/s. Embryo orientation: left, anterior; right, posterior; up, dorsal; bottom, ventral. Scale bar, 50 μm. Related to Figure 3.

9

Video S2. Visualization and quantification of cortical flows. Time-lapse video of the surface of an embryo expressing His2Av-GFP (top) and overlay of cortical flow quantification using PIV (bottom) during cell cycles 3–10. Arrows indicate the flow velocities. Images were acquired with 1/2.89 s. frame rate. Video was resampled to show one in every three images and are shown at 10 frames/s. Embryo orientation: left, anterior; right, posterior; up, dorsal; bottom, ventral. Related to Figure 4.

10

Video S3. Visualization of cytoplasmic flows and nuclear movements in the early embryo. Time-lapse video of an embryo expressing PCNA-TagRFP (to mark nuclei) and stained with Trypan Blue (to visualize yolk granules) during cell cycles 3–10. Arrows indicate flow patterns in cell cycles 4–6. Images were acquired with 1/22.86 s. frame rate and are shown at 7 frames/s. Embryo orientation: left, anterior; right, posterior; up, dorsal; bottom, ventral. Related to Figure 5.

11

Video S4. Quantification of cytoplasmic flows and nuclear spreading. Time-lapse video of an embryo expressing PCNA-TagRFP from cell cycles 4–8. Nuclei were segmented and are represented in red. Cytoplasmic flows were quantified using PIV and are represented as arrows indicating flow magnitude and direction. Images were acquired with 1/14.4 s. frame rate and are shown at 7 frames/s. Embryo orientation: left, anterior; right, posterior; up, dorsal; bottom, ventral. Related to Figure 5.

12

Video S5. PP1-heterozygous embryos show defects in nuclear spreading. Time-lapse video of a PP1-heterozygous embryo expressing PCNA-TagRFP (to mark nuclei) in cell cycles 4–9. Images were acquired with 1/21.53 s. frame rate and are shown at 7 frames/s. Embryo orientation: left, anterior; right, posterior; up, dorsal; bottom, ventral. Related to Figure 5.

13

Video S6. Optogenetic uniform recruitment of RhoGEF2 to the cortex inhibits contractions and disrupts nuclear spreading. Time-lapse video of an embryo co-expressing PCNA-TagRFP (nuclear marker) and the RhoGEF2 optogenetic system exposed to constant blue light for cell cycles 5–8. Images were acquired with 1/23.1 s. frame rate and are shown at 7 frames/s. Embryo orientation: left, anterior; right, posterior; up, dorsal; bottom, ventral. Related to Figure 6.

14

Video S7. RhoGEF2 cortical activation at poles drives nuclear movement toward opposite pole. Time-lapse video of an embryo co-expressing PCNA-TagRFP (nuclear marker) and the RhoGEF2 optogenetic system. Embryo was activated with blue light 3 independent times at opposing poles (anterior activation, posterior activation, anterior activation). Dotted rectangles show activated region. Images were acquired with 1/10.3 s. frame rate and are shown at 7 frames/s. Embryo orientation: left, anterior; right, posterior; up, dorsal; bottom, ventral. Related to Figure 6.

2

Figure S2.Biosensor dynamics near the surface of early embryos is regulated by PP1 activity rather than Cdk1. Related to Figure 2. A) APC activity at mitotic exit as a function of distance from chromosomes in 2 embryos. APC activity was estimated as the relative rate of cyclin B degradation, that is $APCactivity=\frac{d\left[CycB\right]}{dt}/\left[CycB\right]=\frac{d}{dt}ln\left[CycB\right]$. B) Heat map of cyclin B levels along the anterior-posterior axis at the surface of a wild type embryo for cell cycles 3–13. C) Emission ratio of Cdk1/PP1 FRET sensor at the surface of a wild type (blue line) or wee1 mutant (red line) embryo. wee1 mutant embryos fail to slow down the cell cycle during cc10–13 and as a result have 2 extra divisions. Nonetheless, the Cdk1/PP1 ratio shows very similar dynamics (the same amplitude and period) in both wee1 mutants and wild type embryos during the pre-blastoderm cycles (cc 4–9). D) Emission ratio of Cdk1/PP1 FRET sensor at the surface of a wild type embryo (blue line) or an embryo in which I-2 levels are highly reduced by mutations (red line). p<10−10 (χ2 test).

3

Figure S3.Quantification of myosin II, F-actin and Rho activities in early development. Related to Figure 3. A) Myosin II and F-actin (measured by Moesin-ABD-GFP) levels as a function of time in anterior (left) or posterior (right) regions at the surface of an embryo for cell cycle 5. B) Myosin II and F-actin level dynamics in anterior (left) or posterior (right) regions at the surface of an embryo for cell cycle 7. C-D) Heat map of Rho activity (C) and myosin II levels (D) along the anterior-posterior axis at the surface of a wild type embryo for cell cycles 4–9. E-F) Myosin II (E) and F-actin (F) level dynamics for cell cycles 5–6 at embryo surface (blue line) and varying distances from the surface (see legend). Dotted black line: Cdk1 to PP1 activity dynamics. G-H) Myosin II (G) and F-actin (H) level dynamics averaged in regions with and without nuclei and at different depths from the surface (see legend). I) Rho activity at the surface averaged across oscillating regions for wild type (blue line) and PP1-heterozygous (red line) embryos. Shaded regions, sem.; p<10−10 (χ2 test).

4

Figure S4.Prediction of cortical velocity from myosin II gradients and quantification of gradients and cortical flows in PP1-heterozygous embryos. Related to Figure 4. A) Snapshots of an embryo expressing soluble Cdc25Twine-GFP 0 min. (top) and 1.5 min. (bottom) after fluorescence recovery of bleached region. White box: bleached region at t=0 min. Dotted white box: bleached region at t=1.5 min. B) Heat map of GFP fluorescence intensity along the AP axis following photobleaching. Dotted black line: calculated position of front edge of bleached area. C) Velocity measured by PIV of His2Av-mRFP images versus velocity measured by FRAP for 10 embryos during cell cycles 4–8. Solid green line: best fit line (slope: 0.96+−0.02). D) Measured myosin II intensity profile across AP axis for one embryo in cell cycle 6 (blue line) and fitted curve (red line). E) Myosin II gradient across AP axis. F) Measured cortical velocity (blue line) for a cycle 6 embryo and predicted velocity (red line) from myosin II gradients. G) Myosin II intensity profiles across AP axis during maximum myosin II recruitment for cell cycle 5 (top) and cell cycle 6 (bottom) in wild type (solid lines) vs. PP1-heterozygous (dotted lines) embryos. H) Cortical flow trajectories (light to dark red) for contraction phase of a wild type (top) and PP1-heterozygous (bottom) embryo during cell cycle 6. Insets, schematic of streamlines showing direction of cortical flows. Scale bars, 50μm.

Highlights.

• PP1 activity couples cell cycle dynamics and cortical actomyosin contractility

• Myosin gradients drive cortical contractions and cytoplasmic flows

• Cytoplasmic flows distribute nuclei uniformly across the embryo

• Uniform nuclear positioning is required for cell cycle synchrony