Using the Proton Energy Spectrum and Microdosimetry To Model Proton Relative Biological Effectiveness

Abstract

Purpose:

We introduce a methodology to calculate the microdosimetric quantity dose-mean lineal energy for input into the microdosimetric kinetic model (MKM) to model the relative biological effectiveness (RBE) of proton irradiation experiments.

Methods and Materials:

The data from seven individual proton RBE experiments were included in this study. In each experiment, the RBE at several points along the Bragg curve was measured. Monte Carlo (MC) simulations to calculate the lineal energy probability density function of 172 different proton energies were carried out with use of Geant4 DNA. We calculated the fluence-weighted lineal energy probability density function (f_w(y)), based on the proton energy spectra calculated through MC at each experimental depth, calculated $\overline{y_D}$ for input into the MKM, and then computed the RBE. The radius of the domain (r_d) was varied to reach the best agreement between the MKM-predicted RBE and experimental RBE. A generic RBE model as a function of dose averaged linear energy transfer (LET_D) with one fitting parameter was presented and fit to the experimental RBE data as well, to facilitate a comparison to the MKM.

Results:

Both the MKM and LET_D based models modeled the RBE from experiments well. Values for r_d were similar to those of other cell lines under proton irradiation that were modeled with the MKM. Analysis of the performance of each model revealed neither model was clearly superior to the other.

Conclusions:

Our three key accomplishments include the following: (1) Developed a method that uses the proton energy spectra and lineal energy distributions of those protons to calculate dose-mean lineal energy. (2) Demonstrated that our application of the MKM provides theoretical validation of proton irradiation experiments that show that RBE is significantly greater than 1.1. (3) Showed that there is no clear evidence that the MKM is better than LET_D based RBE models.

Summary

Using Monte Carlo simulations, the microdosimetric kinetic model (MKM) was applied to three previously published proton relative biological effectiveness (RBE) studies. The MKM fitting was compared to a generic RBE model as a function of dose averaged linear energy transfer (LET_D). Analysis of the fittings reveal no clear advantage to using one model over the other and we conclude that both the MKM and LET_D based proton RBE models are appropriate.

Introduction

With increased adoption of proton therapy in clinics around the world, researchers are increasingly focusing on the issue of relative biological effectiveness (RBE). In proton therapy, RBE is defined as the ratio of x-ray dose to proton dose needed to reach a specified biological end point, most often clonogenic cell survival. Based on early experiments, and summarized by Paganetti et al. [1], RBE in proton therapy was set to a constant value of 1.1 at all points along the beam and for all end points. Experiments, however, have shown a wide range of RBE values and demonstrate RBE’s dependency on factors such as dose, cell type, point in the cell cycle, biological end point, etc. An updated, comprehensive study of proton RBE performed by Paganetti [2], using the available experimental data from published literature, revealed that due to a lack of standardization across experiments and large uncertainties, RBE values on average are ~1.1 but increase at the end of the proton beam’s range. This increased RBE at the end of the range may have clinical consequences, as demonstrated by Peeler et al. and Underwood et al. [3, 4]. Thus, it is important to take into account variable RBE during the treatment planning process.

Several phenomenological RBE models have been developed [5-11], based on in vitro experiments, in order to model the observed variable RBE. Dose-averaged linear energy transfer (LET_D) is often used as input for these models. However, as summarized by Mohan et al. [12], for a broad spectrum of proton energies, protons with higher LET should, in theory, contribute more to cell killing than do the lower LET protons in the spectrum for the same dose deposited if RBE is not linear with LET. At the Bragg peak and distal edge of a proton beam, the proton energy spectrum is indeed broad, meaning there is a correspondingly large spread in LET. This large variability in LET could make use of LET_D and the reference radiation α and β values alone an inappropriate measure of biological effect. One purpose of this study was to compare an RBE model as a function of LET_D to that of the MKM. This allows the comparison of RBE models with different underlying expressions for radiation quality: LET_D and $\overline{y_D}$.

The microdosimetric kinetic model (MKM) proposed by Hawkins [13, 14], in contrast, uses lineal energy probability density function f(y) as an input. In this work, we present a method with which to calculate f(y) for a monoenergetic proton beam with use of Monte Carlo simulation. Then, we calculated a fluence-weighted lineal energy probability density function (f_w(y)) for a polyenergetic proton beam, calculated the dose mean lineal energy $(\overline{y_D})$ and used this as input into the MKM to predict RBE. Finally, we varied a fitting parameter in the MKM to achieve a best-fit between the MKM and RBE experiments. Our work showed that the MKM can be applied to explain the increase in RBE as a function of $\overline{y_D}$ in recent proton irradiation experiments. To compare the MKM fitting of RBE as a function of $\overline{y_D}$ to an RBE model that is a function of LET_D, we propose a generic RBE model with one fitting parameter. This parameter was varied to achieve the best fit to experimental data, and then the generic RBE model and the MKM fits were compared using Akaike Information Criterion (AIC) [15] to determine which of the two models best described the data.

Methods and Materials

RBE data

The RBE data and proton energy spectra corresponding to the RBE measurements were obtained from the three studies by Chaudhary and Marshall et al. [16], Guan and Bronk et al. [17], and Patel and Bronk et al. [18]. In all three studies, the authors measured RBE at various depths along a proton beam. In addition, they simulated their beam geometry with Geant4 [19], calculating LET_D and the proton energy spectrum at each measurement point. Together, these three studies represent seven total experiments across three different beamlines and four cell lines. Pristine Bragg peaks were used for all three studies, and Chaudhary and Marshall et al. also included spread-out Bragg peak investigations in their study.

Lineal energy (y):

Lineal energy y is defined as the quotient of the energy deposited into a volume of interest ε and the mean chord length through that volume $\stackrel{‒}{l}$ by a single energy deposition event [20], and is expressed as

$$y=\frac{\epsilon }{\overline{l}}.$$ (1)

In this work the volume of interest is called the domain and is defined as a sphere with radius r_d. In microdosimetry, y is a stochastic quantity that follows a distribution, called the lineal energy probability density function (f(y)) [21]. The second moment of f(y) is the dose-mean lineal energy and is expressed as

$$\overline{y_D}=\frac{\int y^{2}f(y)dy}{\int yf(y)dy}.$$ (2)

Calculating y

Geant4 DNA version 10.2.0 was used to calculate the f(y) for 172 proton energies. The basis for the selection was to ensure adequate sampling of y values at all proton energies used in the RBE experiments. The Geant4 DNA extension [22, 23] was used to simulate 100 tracks at each energy in a liquid water cube geometry of 5-μm side lengths. 5-μm was chosen to match the voxel size that LET_D was scored in. To calculate f(y) at a particular energy, a Matlab script was developed to score the lineal energy y at randomly generated locations around the proton track, inside spherical domains with a radius (r_d) of 500 nm for each track. The scored y values were then binned into a histogram with a bin width of 0.1 keV/μm, with a range of [0.01, 300] keV/μm.

Calculating $\overline{y_D}$

For a proton of a given energy, the lineal energy follows a distribution rather than holding a single, fixed value. Therefore, to get an accurate account of the energy loss across a spectrum of proton energies, the lineal energy probability density function of a polyenergetic proton beam (f_w(y)) has to take into account the various constituent f(y) values and their respective weights in the proton energy spectrum. We calculated f_w(y) with use of a fluence-weighting technique. At each point along the Bragg curve where RBE was measured, the proton energy fluence (Φ(E)) was calculated via Monte Carlo simulation. Using the fluence at energy i and f(y)_i, f_w(y) was calculated as follows:

$$f_w(y)=\frac{{\sum }_i\Phi (E{)}_{i}f(y){}_i}{{\sum }_i\Phi (E{)}_i}.$$ (3)

The calculation of $\overline{y_D}$ for a polyenergetic beam is then straightforward

$$\overline{y_D}=\frac{\int y^2{f}_w(y)dy}{\int y{f}_w(y)dy}.$$ (4)

Uncertainty analysis of f(y)

We assumed that the number of scored y values in each bin follows a Poissonian distribution, and the fractional error per bin can be calculated as $\frac{\sqrt{nsamples}}{nsamples}$. Since calculating $\overline{y_D}$ is essentially a sum over all scored y values, as shown in Eqs. 2 and 4, the total fractional error of each $\overline{y_D}$ value is the quadrature sum of the fractional errors from each bin, divided by the sum of all y samples scored. The number of scores per track was increased until the maximum fractional uncertainty for any f(y) was approximately 1.5×10⁻⁴. Table S2 contains the number of scores per track that was performed.

Modeling RBE with the MKM

MKM builds upon the theory of dual radiation action, which was proposed by Kellerer and Rossi [24]. It uses the linear-quadratic (LQ) framework and predicts the α parameter as a function of $\overline{y_D}$. We calculated α_p by using the method proposed by Kase et al. [25]:

$${\alpha }_p={\alpha }_x+{\beta }_x\frac{\overline{y_D}}{\rho \pi r_d^2}$$ (5)

where α_x and β_x are the linear and quadratic fitting parameters from the reference radiation survival curve, ρ is the mass density of water and r_d is the radius of the domain. Eqs. 3 and 4 show how we calculated $\overline{y_D}$ at each point along the Bragg curve in each experiment. Since RBE is defined as the ratio of doses of two radiation types to reach a specified biological endpoint – in this case, a given surviving fraction (SF) - we calculate RBE by solving for both doses from the LQ model. To calculate the experimental RBE, we use the LQ parameters from each clonogenic survival experiment from Refs. 16-18. The values used for α_x and β_x are given in S1 and the reader is referred to Refs. 16-18 for the LQ parameters for the proton experiments. The MKM assumes β_p = β_p, and α_p is calculated from Eq. 5. Thus RBE can be calculated by solving the LQ model SF = e^−α−βD2 for the corresponding dose in each irradiation modality, giving

$$RBE=\frac{\sqrt{{\alpha }_x^2-4{\beta }_x\text{ln}SF}-{\alpha }_x}{\sqrt{{\alpha }_p^2-4{\beta }_p\text{ln}SF}-{\alpha }_p}\times \frac{{\beta }_p}{{\beta }_x}.$$ (6)

Other works have derived similar expressions for RBE as a function of dose or survival fraction [7]. In this work, all RBE values were calculated for a survival fraction (SF) of 10%. To find the best r_d for each experiment, r_d was varied in Eq. 5 through the least squares method. We assume that $\overline{y_D}$ is independent of r_d for sufficiently small domains so that even changing the value of r_d on the order of a 200-300 nanometers will not change the underlying microdosimetric distributions.

Comparing the MKM to a generic RBE model

In order to compare the MKM with a model based on LET_D we propose an RBE model whose β is constant (β_p = β_x) and whose α parameter varies linearly with LET_D:

$${\alpha }_p={\alpha }_x+k\times LE{T}_D.$$ (7)

This approach is similar to the one taken by Chaudhary and Marshall et al. [16]. This model and the MKM are only approximately correct because the LET_D of an x-ray beam is nonzero, around 0.2 keV/μm. However as LET_D increases, Eq. 5 and Eq. 7 become a better model of biological response. We applied this model to each RBE experiment and varied the k term to reach a best fit for the data, through the least squares method. The sum of squares from each model and experiment combination were input into the Akaike Information Criterion [15] to determine which model best describes the data.

Results

Calculating $\overline{y_D}$

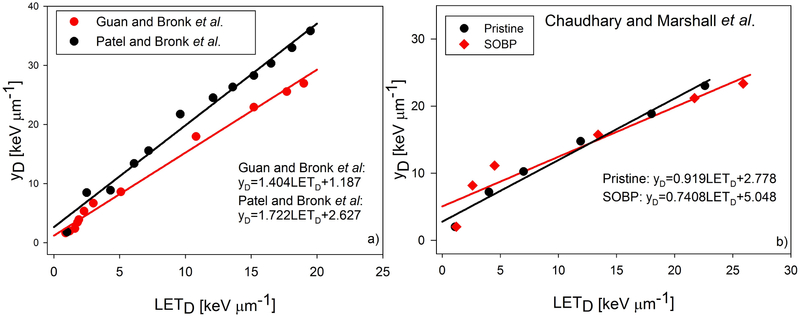
The proton energy spectrum at each point along the Bragg curve for each experiment was used to calculate both the LET_D and $\overline{y_D}$, with $\overline{y_D}$ being calculated according to Eq. 3 and 4, and the resulting relationship between the two quantities is noted in Fig. 2. For each experiment, $\overline{y_D}$ appears to be an approximately linear function of LET_D.

Fig. 2.

Plots of $\overline{y_D}$ as a function of LET_D for each of the three experiments. Our results indicate an approximately linear relationship between $\overline{y_D}$ and LET_D. The equation of $\overline{y_D}$ as a linear function of LET_D for each of the four beam configurations are shown in the panels.

Uncertainty analysis of f(y)

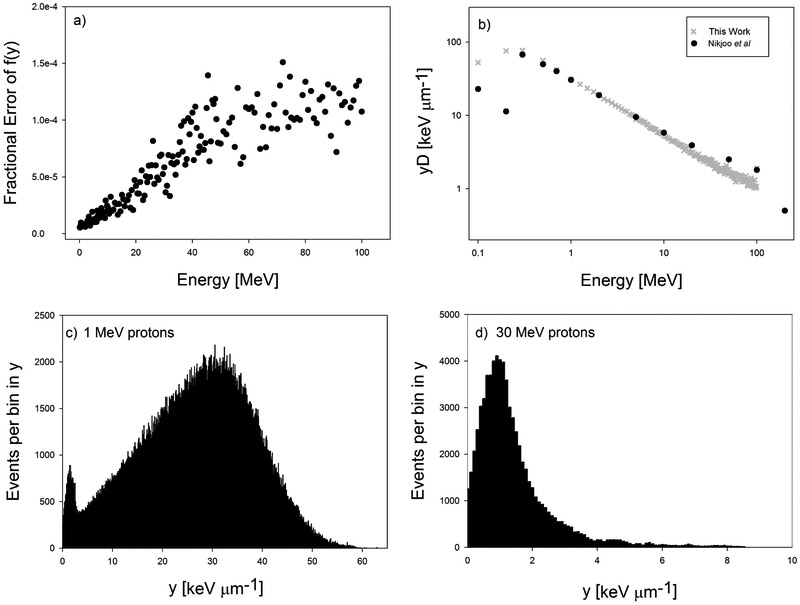
In Fig. 1a, the fractional errors for each f(y) scored is plotted. We input each of our scored f(y) functions into Eq. 2, calculated $\overline{y_D}$, and compared our $\overline{y_D}$ to those reported by Nikjoo et al. [26] in Fig. 1b.

Fig. 1.

(a) Total fractional error from each f(y) scored using Geant4 DNA. (b) Comparison of our values of $\overline{y_D}$, using our scored probability density functions (f(y)), to those from Nikjoo et al [26]. (c, d) Histograms for the distribution of y values for 1 MeV and 30 MeV protons, respectively. These histograms were normalized and thus became the f(y) functions.

Modeling RBE with MKM

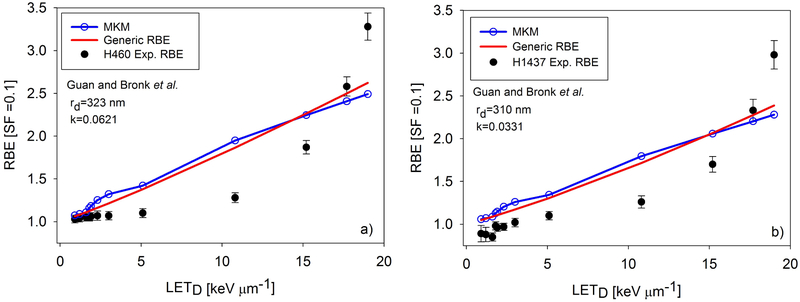
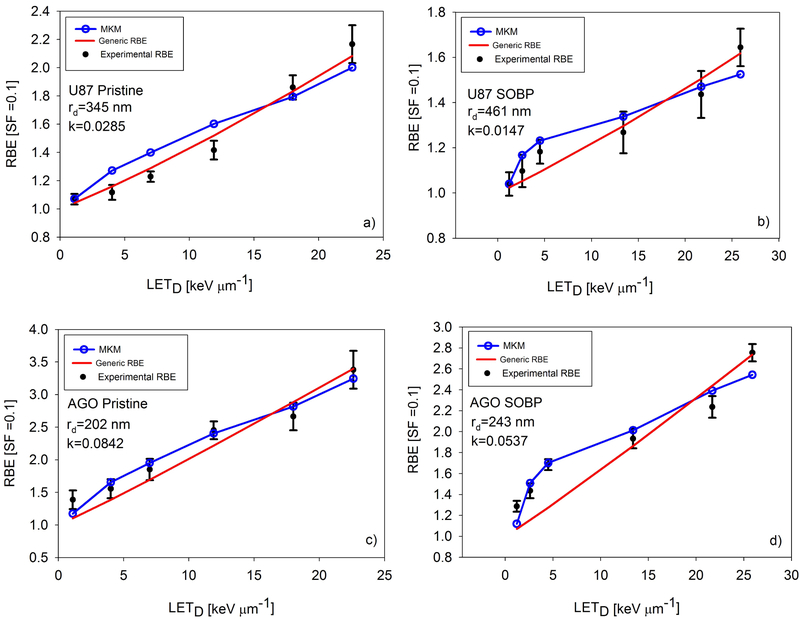
By varying r_d, we were able to fit the experimental RBE data well by using the MKM, as shown in Figs. 3-5. Values for the best-fit r_d are shown on the plots and in Table 1. Note that in Figs. 3-5, the RBE modeled by the MKM is plotted as a function of LET_D, even though the MKM is a function of $\overline{y_D}$. This was done to be consistent with past practice and to enable plotting both the MKM and generic RBE model on one plot. While Fig. 2 shows the linear fit for $\overline{y_D}$ as a function of LET_D for each beamline, $\overline{y_D}$ values were not directly transformed via these equations. Rather, the points were plotted directly against the calculated LET_D values.

Fig. 3.

Results of fitting the generic RBE model and the MKM, with fitting parameters. Panel a) contains the experimental data and fits for the H460 data from Guan and Bronk et al, while panel b) contains the data and fits for the H1437 data. The experimental data was performed at MDACC.

Fig. 5.

The results of fitting the generic RBE model and the MKM for the data from Chaudhary and Marshall et al. Panels a) and c) show the pristine Bragg peak irradiations for cell lines U87 and AGO1522, respectively. Panels b) and d) show the spread out Bragg peak irradiations experiments for the U87 and AGO1522 cell lines, respectively. In the low LET_D and low $\overline{y_D}$ region, MKM was better able to model RBE than the generic RBE model. Experiments performed at CATANA, Italy.

Table 1.

Results of AIC analysis between the MKM and generic RBE model. r_d: radius of the domain; CI: confidence interval; SS: sum of squares; RL: relative likelihood.

Guan and Bronk etal
H460
MKM	Generic
rd=323 nm	k=0.0621
CI=[286.7-379.3]	CI=[0.04798-0.07578]
SS1=1.473	SS2=1.061
RL = 0.140
H1437
MKM	Generic
rd=310 nm	k=0.0330
CI=[274.8-368.8]	CI=[0.02511-0.04073]
SS1=1.271	SS2=0.9396
RL = 0.1632
Patel and Bronk et al
H460
MKM	Generic
rd=426 nm	k=0.045
CI=[397.5-461.9]	CI=[0.03987-0.05014]
SS1=0.3606	SS2=0.2169
RL = 0.0474
Chaudhary and Marshall et al
Pristine Bragg Peak, AGO1522
MKM	Generic
rd=202 nm	k=0.08423
CI=[192.4-213.9]	CI=[0.07092-0.09746]
SS2=0.1096	SS1=0.2404
	RL = 0.0948
Pristine Bragg Peak, U87
MKM	Generic
rd =345 nm	k=0.0285
CI=[311.3-394.7]	CI=[0.02554-0.0313]
SS1=0.1189	SS2=0.02386
RL = 0.0081
SOBP, AGO1522
MKM	Generic
rd=243 nm	k=0.0537
CI=[227.2-262.8]	CI=[0.03957-0.06765]
SS2=0.1086	SS1=0.3402
	RL = 0.0325
SOBP, U87
MKM	Generic
rd = 461 nm	k=0.0147
CI=[420.0-518.0]	CI=[0.01318-0.0194]
SS2=0.02759	SS1=0.01614
RL = 0.2002

Comparing the MKM to a generic RBE model

Table 1 contains the values of each of the k parameters for the generic RBE model given in Eq. 7. The output of the AIC calculation is the relative likelihood that a given model is a better fit than another model and are given in Table 1. In two experiments, the MKM was found to fit the data better than the generic RBE model, while five experiments were better modeled by the generic RBE model. However, in the majority of the experiments the AIC analysis also suggests that there is little evidence to choose between the models as the differences in AICs were typically small.

Discussion

In the present study we calculated $\overline{y_D}$ at various depths along the Bragg curve, based on the proton energy spectra at that depth. By inputting $\overline{y_D}$ at various depths along the Bragg curve into the MKM and varying r_d we were able to find a best-fit r_d that modeled the experimental RBE data well. We then compared this fit of the MKM to a generic RBE model with one fitting parameter to determine if RBE was better modeled by the MKM or a generic RBE model that includes LET_D as a measure of radiation quality. AIC analysis indicated that for two experiments, MKM was the superior model and for five experiments, the generic RBE model was better. However in most experiments there was not strong evidence favoring either model.

The values published by Nikjoo et al. [26] provide a useful reference for our $\overline{y_D}$ values, since both our method and Nikjoo et al.’s published data are modeled with use of a domain radius of 500 nm. When comparing our values to those of Nikjoo et al. in Fig. 1b), we see excellent agreement except the lowest two proton energies, 0.1 and 0.2 MeV. However these energies contribute so little dose in a clinical proton beam spectrum that they do not have a significant impact on our microdosimetric calculations. Our $\overline{y_D}$ calculations also agree well with those reported by Lindborg et al [27]. The low fractional error and agreement with the values published by Nikjoo et al. and Lindborg et al. give us confidence in the accuracy of the values of our calculations for $\overline{y_D}$. Figure 2 shows that $\overline{y_D}$ and LET_D increase in a linear relationship. This relationship has been derived by Kellerer and is $\overline{y_D}=\frac{9}{8}LE{T}_D+\frac{3{\delta }_2}{2d}$ where δ₂ is the weighted energy loss per collision and d is the diameter of the domain [28].Confidence intervals for the linear relationships between $\overline{y_D}$ and LET_D plotted in Fig. 2 are reported in the Supplementary Data. Recently, a series of microdosimetric measurements were conducted by Anderson et al. [29] where they measured $\overline{y_D}$ at various depths along a 71.3 MeV and 159.9 MeV proton beam and compared those measurements to calculations of LET_D. They found a similar, linear relationship between LET_D and $\overline{y_D}$, and our values of $\overline{y_D}$ at similar LET_D are similar to theirs. It is important to highlight the differences between LET_D and $\overline{y_D}$. LET_D is calculated by sampling the stopping power, known as the unrestricted LET, of each proton that passes through the scoring volume and averaging the LET values by weighing them according to how much energy was deposited by those protons in the scoring volume. $\overline{y_D}$ is a measure of the energy deposited into a volume, called a domain. The energy deposited into the domain can come from the primary proton and delta rays. When calculating $\overline{y_D}$, we include instances when the proton passes near the domain, but not through it, and delta rays deposit energy into the domain.

In this study, r_d was varied for each experiment to achieve a best fit between the MKM and experiments. The values for r_d for these experiments range between 0.202 μm and 0.461 μm. Work by Kase et al. [30] showed that when fitting the MKM to other proton RBE data, r_d values were 0.26 μm, 0.34 μm, and 0.35 μm for V79, HSG, and T1 cell lines, respectively. Mairani et al. [31] conducted a similar fitting utilizing proton and helium ion irradiation data and found their best fitting r_d value was 0.300 μm . We concluded that our r_d values were similar to previous studies that applied the MKM to proton RBE experiments. Patel and Bronk and Guan and Bronk used the same cell line, H460, in their experiments. We were able to fit both of them by using the MKM. However, the value of r_d to get a best fit was different for each experiment. Based on Guan et al.’s data, r_d was 0.323 μm and for Patel et al.’s data, r_d was 0.426 μm. The Guan and Bronk et al. data show RBE as a much more nonlinear function of LET_D than the similar studies performed by Patel and Bronk et al. and Chaudhary and Marshall et al., and it remains unclear why. Both the generic RBE model and the MKM fit this data set poorly when compared to the fits shown in Figs. 4 and 5. Three RBE models were applied to the Guan and Bronk et al. data by McNamara et al. [9], and Mohan et al. [12] and their models were unable to account for the highest experimental RBE, though their models were better able to fit the RBE at 15 keV/μm and below. The study in Ref. 18 highlights the importance and sensitivity of the settings used in Monte Carlo simulations, particularly when the LET_D and dose values from simulations are used for calculating RBE. We suggest that the difference in Monte Carlo settings in the different studies is the reason for the large difference in r_d values for the same cell line in two different experiments, and why both the MKM and generic RBE model fit the Patel and Bronk et al. data, and Chaudhary and Marshall et al. data better. In the high gradient region distal to the Bragg peak, there may be significant uncertainties in delivered dose, which may be quite different among the different experiments. To address these issues, we are further investigating the relationship between RBE, $\overline{y_D}$ and LET_D by performing cell irradiation experiments using ramp fields and SOBPs with different dose and LET_D combinations [32, 33]. What is also striking about the experimental data in Figs. 3 and 4 is the RBE at LET_D > ~15 keV/μm seems to be increasing nonlinearly. This is in contrast to heavy ion studies that show RBE as a linear function of LET_D up to around 100 keV/ μm [34]. This nonlinearity at high proton LET_D may also point to modifications of the MKM and other RBE models, such as including a variable β term or higher-order terms in the relationship between LET and α.

Fig. 4.

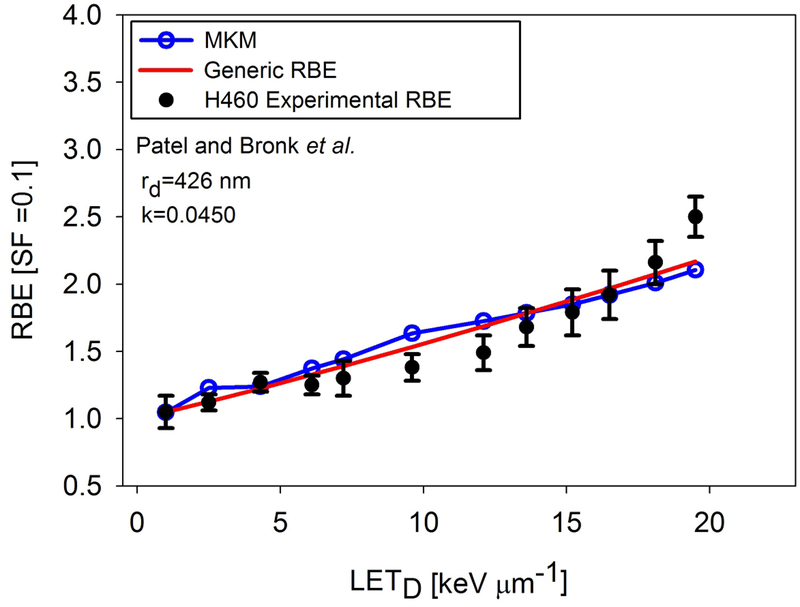
Results of fitting the generic RBE model and the MKM to the Patel and Bronk et al. data. Experimental data was performed at HIT, Germany.

The results of fitting the MKM and the generic RBE model to the experimental data are shown in Figs. 3-5. Overall, both models gave very similar fits to the data. Particularly in the U87 and AGO1522 pristine Bragg peak experiments in the Chaudhary and Marshall et al. data, and the Patel and Bronk et al. data, RBE appears to be a linear function of LET_D. For the SOBP experiments from Chaudhary and Marshall et al., the MKM better models the RBE at the lowest three LET_D points. The difference in the two models can be significant, as seen in Fig. 5b) and 5d). Others have suggested that LET_D may not be the best surrogate for biological response [12]. The superior fit of the MKM shown in Fig. 5b) and 5d) support the hypothesis that $\overline{y_D}$ better encapsulates biological effect than LET_D, particularly in an SOBP, supporting the soundness of its underlying assumptions. However, more studies similar to the one presented here are needed to fully determine the relative merits of MKM or LET_D based models in a proton SOBP. To determine which RBE model fits the data best, the AIC analysis in Table 1 was used. Overall, the generic RBE model was preferred in five experiments and the MKM in two. A minor caveat is the relatively weak preference for the generic RBE model in the Guan and Bronk et al. data, where the relative likelihood of MKM being the better model was 0.140 and 0.163 for the H460 and H1437 experiments, respectively.

Based on the AIC analysis between the generic RBE model and the MKM, there is no clear evidence that the MKM models RBE better than a generic LET_D based model. We have demonstrated that the MKM can be used to model proton RBE experiments whose RBE values are much higher than the clinically accepted RBE=1.1 model, however we have not demonstrated a clear superiority by using the MKM. Thus we conclude that there is not enough evidence to move away from LET_D based RBE models. There may be some end of range proton RBE nonlinearity but at present we conclude that both the MKM and LET_D based models provide an accurate model of RBE, even if the underlying RBE model is more complex.

An advantage of this MKM fitting procedure is that its use is not restricted to protons. Any radiation type, such as helium or carbon, whose f_w(y) can be calculated, can apply this method to modeling RBE. A modified version of the MKM was incorporated into a treatment planning system for carbon ions by Inaniwa et al. [35] and our group is developing this MKM algorithm to be implemented in a treatment planning system for proton therapy. Future studies will examine the differences in treatment plans optimized by using the traditional RBE=1.1 paradigm and those optimizing on biological effect by using the MKM.

Conclusions

Using data from three independent proton RBE studies, we have presented a method to calculate the dose mean lineal energy $(\overline{y_D})$ of a polyenergetic proton beam and apply the microdosimetric kinetic model (MKM) to the RBE experiments. To our knowledge, this fluence-based method of calculating the probability density function f_w(y) based on the proton energy distribution and f(y) for monoenergetic proton beams is unique. This study provides a theoretical basis for modeling the increase in RBE along the distal edge of a proton beam. We also applied a generic LET_D based RBE model to the same data and compared the MKM and generic RBE model fittings with AIC analysis. Based on this analysis there is no clear evidence that the MKM, using radiation quality represented by $\overline{y_D}$, is superior to a generic model using LET_D as a measure of the radiation quality. Given the wide ranges of LET values in a spread out Bragg peak and the concern about the quantity LET_D, measuring f(y) distributions and $\overline{y_D}$ with a tissue equivalent proportional counter may be the preferred way to characterize proton beam quality in the clinic, at least as a calibration of Monte Carlo simulation settings.