Digital Staining of High-Definition FTIR Images Using Deep Learning

Abstract

Histological stains, such as hematoxylin and eosin (H&E), are routinely used in clinical diagnosis and research. While these labels offer a high degree of specificity, throughput is limited by the need for multiple samples. Traditional histology stains, such as immunohistochemical labels, also rely only on protein expression and cannot quantify small molecules and metabolites that may aid in diagnosis. Finally, chemical stains and dyes permanently alter the tissue, making downstream analysis impossible. Fourier transform infrared (FTIR) spectroscopic imaging has shown promise for label-free characterization of important tissue phenotypes, and can bypass the need for many chemical labels. FTIR classification commonly leverages supervised learning, requiring human annotation that is tedious and prone to errors. One alternative is digital staining, which leverages machine learning to map infrared spectra to a corresponding chemical stain. This replaces human annotation with computer-aided alignment. Previous work relies on alignment of adjacent serial tissue sections. Since the tissue samples are not identical at the cellular level, this technique cannot be applied to high-definition FTIR images. In this paper, we demonstrate that cellular-level mapping can be accomplished using identical samples for both FTIR and chemical labels. In addition, higher-resolution results can be achieved using a deep convolutional neural network that integrates spatial and spectral features.

Introduction

Histology relies heavily on expert interpretation of staining patterns produced by chemical contrast agents. Tissue staining is a critical component of modern clinical practice, since it is extremely difficult to differentiate structure and morphology in unstained tissue. Accurate disease diagnosis, prognosis, and prediction therefore requires reliable labeling.

The most common clinical labels include hematoxylin and eosin (H&E),^1–3 periodic acid-Schiff (PAS), and Masson’s trichrome. Selecting the appropriate label largely depends on tissue type, and panels requiring 3+ labels of serial tissue sections is common clinical practice.^4,5 Although staining protocols have been widely adopted, variability makes automated analysis difficult.^6–8 Clinical diagnosis therefore still relies on manual assessment by experts, increasing cost and reducing throughput.

Vibrational spectroscopy provides a label-free alternative for pathological assessment that is comparable to traditional histology for many applications.^9–13 Raman and infrared (IR) spectroscopy are highly specific techniques for molecular identification. However, Raman spectroscopy is limited by the weak signal.^14–17 Infrared (IR) absorbance spectroscopy has routinely demonstrated the ability to differentiate tissues relevant to disease^18–22 without significantly perturbing the sample,²³ providing the potential for augmenting traditional histology. IR spectroscopy can also probe changes associated with abnormal tissue that are difficult to determine using histology alone.^24–28

Motivation

While chemical staining is the current standard, it is non-quantitative and prone to human error and inter-observer disagreement.¹⁶ Our goal is to leverage the quantitative infrared spectroscopy to provide consistent molecular maps that aid pathological inspection. The most common approach leverages annotated IR images to train supervised machine learning (ML) algorithms for automated classification.^29–33 This approach would require additional training for experts to integrate quantitative IR maps with existing clinical practice. For example, immunohistochemical labels frequently rely on counterstains to label tissue landmarks that are currently difficult to identify in IR images. This landmark challenge also effects the annotated ground truth used for ML training, since experts are likely to limit annotations to pixels that have a high degree of certainty. Critically, this introduces a bias in validation, making classifiers appear more accurate than they actually are.

Related Work

Many research works have been conducted to classify tissues in IR images, including unsupervised techniques such as K-means clustering^6,34 or hierarchical cluster analysis³⁴ and supervised techniques such as random forests,^33,35 Bayesian,^30,32 artificial neural network (ANN)^32,36 and support vector machines (SVMs)^32,37.

We have previously shown that many traditional stains and counterstains can be digitally applied using artificial neural networks (ANNs) to map molecular spectra to RGB values.³⁶ This technique limits spatial resolution based on two critical factors: First, training requires aligned input/target pairs. Previous work uses adjacent sections, making cellular-level mapping impossible because adjacent images are fundamentally different at this scale. Second, an ANN uses pixel-independent spectra to determine the output color. Since a large amount of molecular information is embedded within the fingerprint region (500 to 1500 cm⁻¹), the resulting digital stain is diffraction limited to this region (6.5 to 20µm).

In this paper, we demonstrate digital staining of high-definition FTIR images to provide cellular-level labeling that mimics traditional histology.³⁸ Our proposed algorithm relies on improved standard protocols for imaging, labeling, and aligning the sample, allowing accurate generation of input/target training pairs that reflect micrometer-scale features. We use a convolutional neural network (CNN)³⁹ to leverage both spatial and spectral image features, allowing us to take advantage of scattering at higher wavenumbers to overcome limitations in chemical resolution.

Materials and methods

Sample preparation

Tissue samples, consisting of pig kidney, pig skin, mouse kidney and mouse brain, were fixed for 24 hours in 10% neutral buffered formalin. The tissue was then embedded in paraffin using standard clinical techniques, which include dehydration in graded ethanol baths, clearing with xylene, and finally infiltration with paraffin at 6°C. The tissue sections were cut into thin sections (2 to 5µm) and mounted on calcium fluoride (CaF₂) substrates. The tissue was then deparaffinized with xylene and graded ethanol, followed by re-hydration using phosphate buffered saline.⁴⁰

After imaging, samples were labeled with either hematoxylin and eosin (H&E) or 4,6-diamidino-2-phenylindole (DAPI) to provide chemical contrast.

Data collection

Deparaffinized sections were imaged using a Cary 600 FTIR spectroscopic microscope (Agilent Technologies) in the range of 800 to 4000 cm⁻¹ at 8 cm⁻¹ spectral resolution and focal plane array with a size of 128 × 128 . Imaging was performed using a 15X 0.62NA Cassegrain objective with a projected pixel size of 1.1 µm for high magnification and 5.5 µm for standard magnification in transmission mode. A smaller projected pixel size allows diffraction-limited in high-wavenumber regions. After staining, samples were imaged using a Nikon optical microscope with a 10X 0.3NA objective. H&E stains were imaged in brightfield mode, while DAPI was imaged using a 390 ± 9nm excitation filter and 460 ± 30nm emission filter.

Data preprocessing

FTIR images were preprocessed using standard protocols,⁴⁰ including piece-wise linear baseline correction and band normalization to Amide I (1650 cm⁻¹). These methods help to mitigate spatial effects introduced by scattering within heterogeneous samples, however peak shifts introduced at interfaces with differing refractive index can still impact the positions of resonance peaks. Principle component analysis (PCA) was employed to reduce the number of bands to 60 components representing 97.7% of the overall variance. Dimension reduction was necessary in order to mitigate memory constraints when using a CNN.

Image alignment

In order to perform semantic (pixel-wise) segmentation, IR spectra must be assigned input and target values for training. The input was selected from the IR image at position p = [x, y]^T and the target color is selected from the associated location in the stained image. While the tissue samples in both images are identical, the staining process introduces deformation and tearing. Both images must be aligned using an elastic deformation transform T such that the position x within the absorbance image A(p) maps to the stained image S(Tp) at a transformed position Tp. This requires pixel-level alignment of both IR and brightfield images to extract the corresponding positions. Using the same tissue sample for both images facilitated alignment, however distortions were introduced through chemical staining, due to required rehydration and chemical manipulation of the sample. Alignment was performed manually using the GIMP open-source editing software (Figure 1) to apply affine transformations to sub-regions of the sample used for training and validation. Regions that had undergone significant distortion (e.g. tearing) were excluded.

Figure 1.

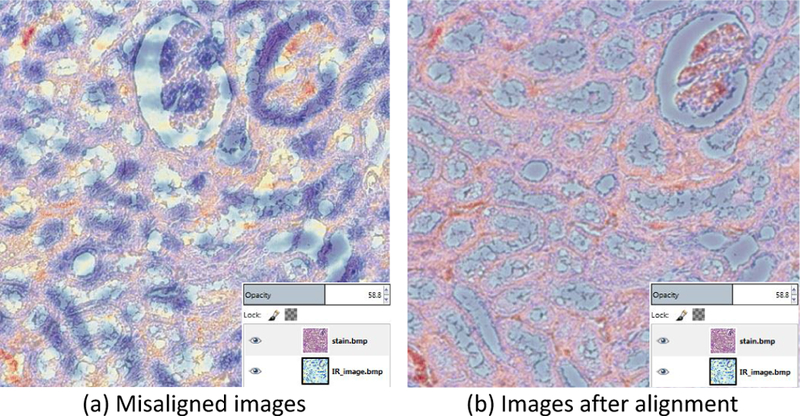
Image alignment using GIMP. A single FTIR band was used for manual alignment. A transparency value was assigned to the H&E image in order to visualize the degree of misalignment (a), which was then corrected using affine transformations (b).

Convolutional neural network architecture

Our CNN architecture is composed of alternating convolutional and pooling layers followed by a fully connected ANN.

Convolutional layer:

Convolutional layers apply a kernel with a small receptive field^41,42 to extract spatial features. Required hyper-parameters for optimization include filter size, padding, and stride. The filter size is equivalent to the spatial region considered to contain a viable image feature. The output of a convolutional layer is always smaller than the input by the filter size. The input is therefore padded with zeros at the borders to preserve spatial extent (width and height). The stride hyper-parameter controls the shifting step size for the convolution filters.

A point-wise nonlinear activation function is applied to the output of each convolution layer. The activity of feature map j in layer l is given by:

$${\mathbf{\text{X}}}_j^l=g\left(\sum _i^{N_{l-1}}{\mathbf{\text{k}}}_{i,j}^l\ast {\mathbf{\text{X}}}_i^{l-1}+{\mathbf{\text{b}}}_j^l\right),$$

where N_l−1 indicates the number of feature maps in layer (l − 1), ${\mathbf{\text{X}}}_i^{l-1}$ is the feature map i in layer (l − 1), ${\mathbf{\text{k}}}_{i,j}^l\in {ℝ}^{k\times k}$ is a convolutional kernel applied to ${\mathbf{\text{X}}}_i^{l-1}$, and ${\mathbf{\text{b}}}_j^l$ is a bias term that facilitates learning. The transfer function g( ) is a nonlinear activation function, such as a sigmoid, tanh, or a rectified linear unit (relu). The * denotes the discrete convolution.

Local response normalization:

In case of using the relu activation function, local response normalization (LNR) is employed to mitigate problems introduced with an unbounded activation function by enforcing local competition among features in different feature maps at the same spatial location.⁴³ The normalization response, $b_{x,y}^i$, of a neuron activity at location (x, y) after applying kernel i and activation function g(.), denoted as $a_{x,y}^i$ is computed as³⁹

$$b_{x,y}^i=a_{x,y}^i/{\left(k+\alpha \sum _{j=\max (0,i-n/2)}^{\min (N-1,i+n/2)}{\left(a_{x,y}^j\right)}^2\right)}^{\beta },$$

where n is the number of adjacent feature maps around that kernel i. k, n, α and β are constant hyper-parameters. They are chosen to be k = 1, n = 5, α = 1 and β = 0.5.

Pooling layer:

The normalized output of each convolution layer is passed through a pooling layer to summarize local features.⁴⁴ By using a stride (stepping size over input pixels) greater than 1, the pooling layer sub-samples the feature maps to merge semantically similar features to provide invariant representation.^45,46 This further improves the computational time by reducing the number of parameters. The Pooling Layer operates independently on every depth slice of the input and resizes it spatially. The depth dimension remains unchanged. If the feature map volume size is m × n × d, The pooling layer with filter dimension of q and stride s produces output with volume size of m′ × n′ × d where:

$$m\prime =\frac{1}{s}(m-q)+1$$

$$n\prime =\frac{1}{s}(n-q)+1$$

Fully connected layer:

Our CNN is followed by a fully connected layer composed of a traditional artificial neural network (ANN) to facilitate deep learning.⁴⁷ The input of fully connected layer is the output of previous layer flatten into a feature vector (X^l−1).⁴⁸ The output vector of the fully connected layer l is:

$$X^l=f({\mathbf{\text{W}}}^l{\mathbf{\text{X}}}^{l-1}+{\mathbf{\text{b}}}^l)$$

Connections between neurons in the layer l − 1 and l are stored in the weight matrix W^l with bias vector b^l.

Loss function:

The resulting supervised optimization minimizes the difference between network predictions and target values provided through a training set. For regression with linear output, the mean square error is used as a loss function:

$$L=\sum \frac{1}{2}{(t-p)}^2$$

where t is the expected output and p is the value predicted by the most recent model.

Training:

Training the network model starts with weight initialization in convolutional and fully-connected layers. This step is important because bad initialization leads to a slow training or no convergence training.⁴⁹ Then the network is fed with training set to determine the activation of each neuron(forward propagation). The loss function compares the network output with the actual value and is optimized to adjust the weights so that the loss decreases(back propagation). Different gradient descent based optimization algorithms, such as stochastic gradient descent, Adam,⁵⁰ and Adadelta,⁵¹ have been proposed and employed for ANN optimization.⁵² Our method uses the Adam optimizer for back-propagation.

Regularization:

A regularization term with/without dropout prevents the model from over-fitting on training data and provides better generalization on test data.⁵³ We use ℓ₁ regularization without dropout.

Batch training:

Most neural network training is based on mini-batch stochastic gradient optimization. In this optimization method, training data set is split into small batches to calculate the loss function and update the parameters (weights and biases). Small batch training provides more robust convergence by avoiding local minima and also facilitate training on system with small memory.

Implementation

The network’s input $\mathbf{\text{X}}\in {ℝ}^{m\times n\times b}$ is a hyperspectral image with a spatial size of m × n and b spectral bands, which in our case are composed of the 60 principle components chosen from PCA. The trained CNN takes an input image to create a chemical map. In order to satisfy CNN requirements, we crop an s × s area around each pixel of X to create a s × s × b patch volume centered at p_i. We use a spatial crop size of 9 × 9 around each pixel. The intensity value I_i of pixel p_i in the color image is assigned to this volume path.

The experimental design of our CNN consists of four convolution layers with 32, 32, 64, 64 feature maps, respectively, and 3 × 3 kernel windows with a stride of 1 for all convolution layers. Every other convolution layer is followed by a pooling layer with a kernel size of 2 × 2 to reduce the spatial dimension by the factor of 2. The network is followed by two fully connected layers: one with 128 neurons and the other with three neurons that provide the color channels for the output color image. An overview of the proposed CNN architecture used is shown in Figure 2.

Figure 2.

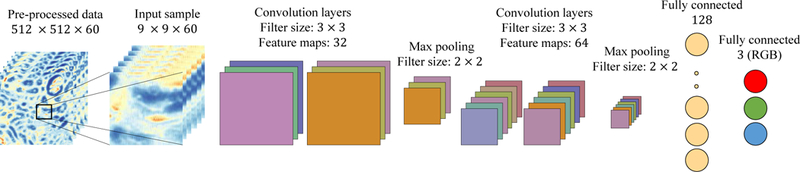
Schematic presentation of our CNN model composed of convolution and pooling layers followed by two fully connected layers (a). The network is fed by a data cube of size 9 × 9 × 60, which is a spatial crop around each pixel.

This network requires the adjustment of many hyperparameters, including the choice of optimizer, learning rate, and regularization factor, which are tuned on a validation set. Training is carried out using batch optimization with a batch size of 128. We use the Adam⁵⁰ optimizer with a learning rate of 0.01 to minimize our mean squared error (MSE) performance metric.⁵² To reduce the generalization error, we add L₂ regularization to the weights, with the parameter set to 0.001. We use the softplus activation function for each layer except the output, which is a smoother version of relu. If x is the output of a neuron, then softplus is defined as:

$$\text{softplus}(x)=\ln (1+e^x).$$

The output layer passes through the linear function that returns the incoming tensor without changes.

We initialized the weights in our model using a normal distribution with a 0 mean and standard deviation of 0.02.

Results

Our network is used for pixel-level mapping of large high- resolution images of normal pig kidney. In order to mitigate over-fitting due to biological variation, random sampling was used to select training data from larger images without the need to use every pixel in the training data. We used 16000 samples, each with the tensor size of 9 × 9 × 60 data points. Training and testing were performed using a Tesla k40M GPU. The average training time for 7 epochs was 33 seconds, and the CNN required 20 seconds to digitally stain a 512 × 512 × 60 pixels hyperspectral image.

MSE was computed after each iteration (mini-batches) to evaluate model convergence on the training data (Figure 3a), and after each epoch for random samples on validation data (Figure 3b).

Figure 3.

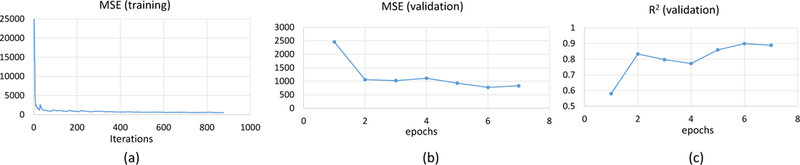
MSE plot convergence (a) with respect to iteration numbers during training on training data (b) with respect to epoch numbers for validation data. (c) Coefficient of determination (R²) of validation data during training process computed after each epoch

Model performance was evaluated using the coefficient of determination R² ∈ [0, 1] to measure the goodness of fit on an independent validation set. This metric indicates better performance as R² approaches 1:

$$R^2=1-\frac{{\sum }_{i=1}^N{({\widehat{y}}_i-y_i)}^2}{{\sum }_{i=1}^N{(y_i-\overline{y})}^2}$$

where y and $\widehat{y}$ are target and predicted images respectively, $\overline{y}=\frac{1}{N}{\sum }_{i=1}^N{y}_i$ is mean value of target image over all pixels(N ). The parameter R² is computed after each epoch for validation data (Figure 3c).

The network was tested on independent images and compared to previously published algorithms³⁶ (Figure 4) using the same imaging system. Applying a pixel level ANN (1 hidden layer with 7 nodes) to the high-magnification data does not provide a significant improvement in resolution, likely due to reliance on chemical information in the fingerprint region of the spectrum (900 to 1500cm⁻¹) where the diffraction limited resolution is comparable to a standard-magnification optical path (Figures 4a and 4b). The introduction of spatial features available at higher wavenumbers using a CNN provides significantly better spatial resolution in the output image (Figure 4c) compared to the chemically stained tissue (Figure 4d).

Figure 4.

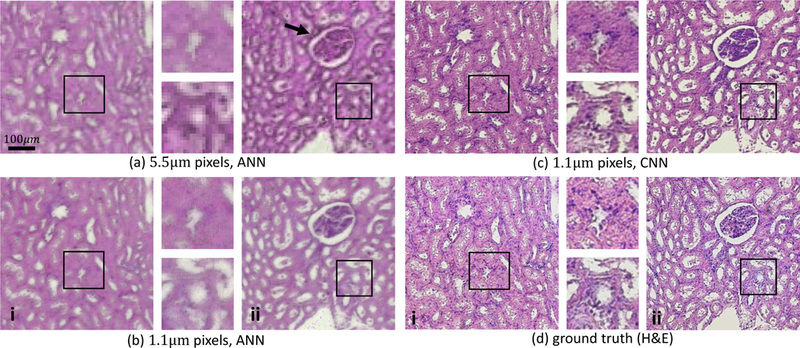
Molecular imaging reproduced by chemical imaging using different digital staining methods and varying spatial resolutions for two pig kidney tissue sections i and ii. Standard digital H&E staining is shown using an ANN³⁶ on (a) standard-magnification (5.5 µm pixel size) and (b) high-magnification (1.1 µm pixel size) images. (c) Digital H&E using the proposed CNN framework on high-magnification data shows greater cellular-level detail when compared to the ground truth (d) chemically-stained H&E images collected with a bright-field microscope. Improved spatial resolution provided by the CNN is clear in the magnified insets, as well as in the kidney glomerulus (black arrow), where boundries are more clearly defined. Note that some deformations were introduced between the FTIR (a-c) and bright-field (d) images because chemical staining was performed between these two steps.

We presented the result of the digital staining networks qualitatively. The generated images from proposed CNN simply resemble the ground truth images visually. Due to color variation and local deformation happening during physical staining (ground truth), the synthesized images cannot be fully overlapped with the ground truths and quantitative evaluation is challenging. We quantified the visibility of differences between the digitally generated staining patterns and the chemically stained images using structural similarity (SSIM) index (Table 1). The SSIM index measures the similarity in case of luminance, contrast and structure.^54,55 SSIM between two images x and y is defined as:

$$SSIM(x,y)=\frac{(2{\mu }_x{\mu }_y+C_1)(2{\sigma }_{xy}+C_2)}{({\mu }_x^2+{\mu }_y^2+C_1)({\sigma }_x^2+{\sigma }_y^2+C_2)}$$ (1)

Table 1.

SSIM index for the different digital staining method outputs shown in Figure 4.

SSMI	Low mag. ANN	High mag. ANN	High mag. CNN
Test Image (i)	0.61	0.62	0.70
Test Image (ii)	0.58	0.63	0.71

where µ_x, µ_y, σ_x, σ_y and σ_xy are the local means, standard deviation, and cross-covariance for images x and y. C₁ and C₂ are regularization constants to avoid division by zero where the local means or standard deviations are close to zero.

In addition, the proposed CNN was trained and tested on different mouse kidney, mouse brain, and pig skin tissue samples to digitally mimic DAPI staining (Figure 5) to demonstrate that high-magnification infrared can capture the morphological features of cell nuclei and often individual cell positions.

Figure 5.

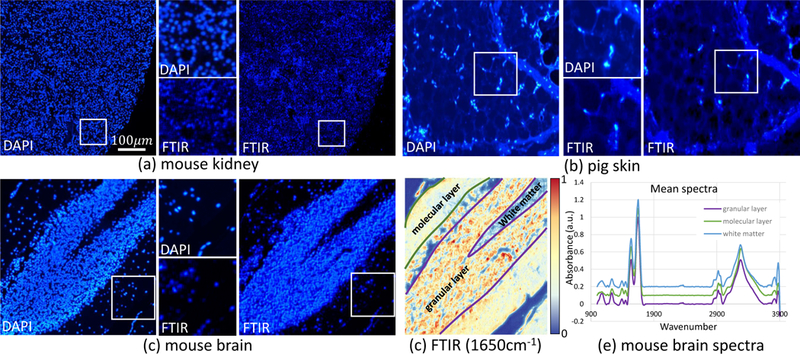
Digital DAPI staining of (a) mouse kidney, (b) pig skin, and (c) mouse brain respectively using our CNN framework. Digitally stained FTIR images are shown on the right, with close-ups on the bottom. (d) FTIR absorbance image at 3300 cm⁻¹ indicating the regions used to collect average spectra. (e) Mean spectra were extracted using SIproc⁵⁶ from masks of the molecular layer (green), granular layer (purple), and white matter (blue) of the cerebellum. Spectra are baseline corrected, normalized to Amide I, and offset for clarity.

Conclusion

We propose a method to reproduce high-resolution staining patterns based on direct molecular imaging using mid- infrared spectroscopy. These digital stains can be applied without the use of chemical labels or dyes and provide results similar to those used in traditional histology. We have developed a tissue preparation protocol that can be used to acquire input/target pairs for training. Unlike previous methods, our approach relies on the same tissue sample as the source of both input and target data. While these protocols allow a more accurate mapping between IR spectra and the desired output, a large amount of the relevant lportion of the spectrum. When relying only on spectral features, the low spatial resolution of the fingerprint region in the absorbance spectrum limits the corresponding spatial resolution of the output image. This is likely due to the abundance of biological information encoded in wavenumbers below 1800 cm⁻¹. CNNs are able to combine the chemistry within the fingerprint region with spatial features from higher wavenumbers that provide greater spatial resolution. This approach clearly produces a more accurate duplication of the desired staining patterns, based on a subjective assessment (Figure 4).

While we are able to capture broad features produced by clusters of nuclei, and often individual cells, the diffraction limit imposed by IR is not yet competitive with bright field or fluorescence imaging. Other spectroscopic contrast mechanisms that do not perturb the sample, such as second harmonic generation (SHG) may also be used to extract more accurate target values. In addition, our current analysis relies on subjective criteria to evaluate output quality. Clinical application will require extensive validation, potentially as a double-blind experiment coordinated with trained histologists. Given the increase in image acquisition time over brightfield microscopy, it will also be important to identify spectral characteristics provided by FTIR that are unavailable or inaccessible to standard clinical practice. Finally, the higher resolution output achieved in our experiments relies on high spatial frequencies encoded in bands collected at higher wavenumber. Therefore, the results described here are likely incompatible with imaging systems using quantum cascade laser (QCL) sources.