Machine learning in neuroimaging: Progress and challenges

1. Introduction

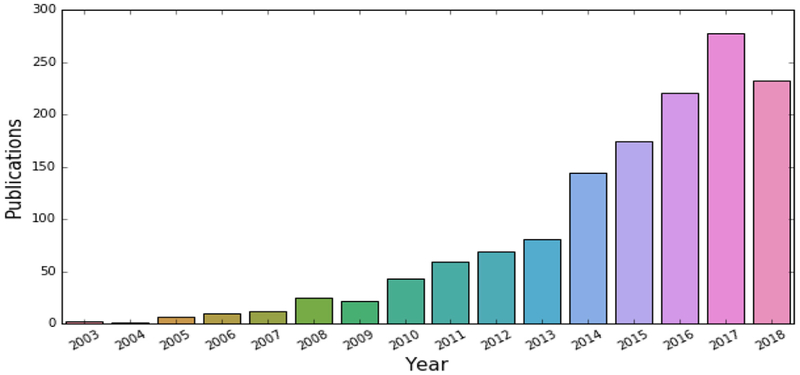
It has been a privilege to serve the Neuroimage community as a Handling Editor, with primary focus on machine learning, over the past six years. As I step down, I was asked to provide my thoughts on the evolution of the field over the past 10–15 years, as well as its potential future challenges and directions. It is exciting to reflect back on the spectacular growth of this field over the past decade (Fig. 1), and to ponder on some of the challenges faced currently by the field, and which are likely to become central points of investigation in the upcoming decade.

Fig. 1.

Publications obtained from Pubmed with the following search query: ("MRI” OR “Magnetic Resonance Imaging” OR "Structural Magnetic Resonance Imaging" OR "Functional Magnetic Resonance Imaging" OR "Diffusion Tensor Imaging" OR "FDG-PET” OR "Amyloid-PET” OR “multimodal" OR "neuroimaging") AND (“brain”) AND (“Machine learning” OR “pattern classification”), on September 5, 2018. This plot reflects the exponential growth of adoption of these methods in neuroimaging.

2. From mass univariate to multi-variate methods

The mid-90's brought the revolution of statistical parametric mapping and voxel-based analysis methods (Friston et al., 1994), which allowed us to form detailed spatial maps of brain structure and function under various conditions, and hence explore data-driven analyses oriented toward knowledge discovery. However, these methods were limited primarily to group analyses, i.e. to exploring anatomical and functional differences between groups or to investigating correlations between imaging and clinical/cognitive variables at the population level. As was discussed in a commentary (Davatzikos, 2004), such mass-univariate methods can fail to reveal disease effects, brain activations, and other imaging patterns, when these are not focal but are rather diffuse, in nature. Therefore, group comparisons generally don't allow us to develop individually-based imaging indices, the latter being essential for establishing biomarkers and diagnostic/prognostic indices at the individual level.

As a consequence, the early 2000's brought the revolution of the application of machine learning methods to neuroimaging studies, thereby enabling the development of imaging signatures of brain function and structure which can be detected at a single individual. Some the earlier studies focused on support vector machines (SVM) (Golland et al., 2002; Lao et al., 2003), whose development and understanding had matured over the 90's, based on structural risk minimization principles (Vapnik, 1998), which ensured good generalization of learned models to new data. SVM has been a cornerstone in this field, largely because of its robustness and ease of use with a variety of kernels, which allow it to learn nonlinear boundaries via kernel mapping (Schölkopf and Smola, 2002). Another family of methods that gained popularity was that of random forests (BREIMAN, 2001), which built on extensive research over a decade on ensemble methods. Ensembles are very powerful approaches, as they tend to reduce error by combining many models built in partly based on random feature (and sample) selection. They have been another cornerstone of this field, largely due to their good generalization properties and ability to weed out noise in favor of true signal, by virtue of model averaging/voting. Ensembles remain a cornerstone currently, oftentimes used along with stronger classifiers, such as deep learning models. The latter have been the latest development in the field, and they offer a great deal of promise, for various reasons. In particular, deep architectures can learn complex features in a hierarchical way, thereby obviating the need to construct the right features upfront. Moreover, deep learning architectures are able to build highly nonlinear boundaries, albeit often at the risk of data overfitting and poor generalization, unless very large amounts of data are available for training. Therefore, some of the most successful examples of deep learning in neuroimaging have been using ensembles of deep learners (Kamnitsas et al., 2018), in order to combine the benefits of depth and breadth in model building.

The applications of these and other methods to neuroimaging studies have been numerous. For example, in clinical neuroimaging, machine learning studies revealed imaging signatures for a number of diseases and disorders, such as Alzheimer's Disease ((Kloppel et al., 2008; Zhang et al., 2011); see (Rathore et al., 2017) for a recent review), brain development and aging (Franke et al., 2010; Habes et al., 2016; Xia et al., 2018), preclinical states (Davatzikos et al., 2009), schizophrenia (Davatzikos et al., 2005a) and its prodromal stages (Koutsouleris et al., 2009), mood disorders (Koutsouleris et al., 2015), and autism (Ecker et al., 2010), amongst others. In cognitive neuroscience, machine learning methods offer promise to provide functional fingerprints that identify individual brains (Finn et al., 2015) and brain states (Poldrack et al., 2010; Haynes and Rees, 2006; Davatzikos et al., 2005b).

3. Current challenges, future directions

Despite the promises, and often over-promises, made by various publications, reliable application of machine learning methods in neuroscience is still in its infancy, as many challenges are currently present. Below, I try to offer my opinion about several aspects of machine learning that should be kept in mind, as these methods mature into reliable tools for clinical and cognitive neuroscience.

3.1. The no-free-lunch theorem (NFLth)

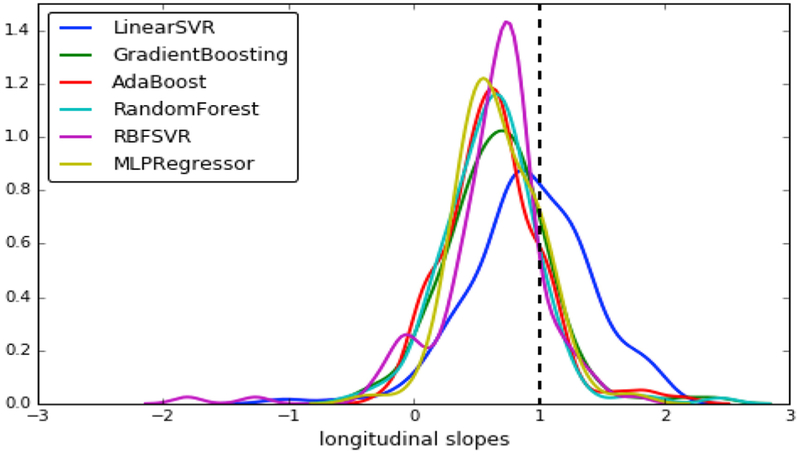
Professors and students briefly discuss the NFLth in machine Learning 101 courses, before forgetting about it in order to study their favorite method(s). Loosely speaking, the NFLth states that no machine learning method is better than the others, on average, over a broad family of problems. This theorem tends to be considered of primarily theoretical and not practical importance, since real problems might relate to specific distributions that are amenable to specific machine learning methods. Nonetheless, the NFLth must always be kept in mind, especially in an era of over-excitement about deep learning methods. One practical implication of the NFLth is that, if a certain biological problem of interest relates to simply-separable distributions, such as linearly separable distributions of patients and controls, then a simpler linear model will likely perform better in this problem, compared to more complex models. Fig. 2 shows an example from my own laboratory's experiments.

Fig. 2.

Different Brain-age regressors were fit to data of an aging population, using as features a simple set of approximately 150 ROI volumes parcelating the brain. All models gave relatively good cross-validated accuracy on cross-sectional datasets, with correlation coefficients varying from 0.8 to 0.84 (r = 0.84 was achieved via the linear SVR and the multi-layer perceptron artificial neural network using 5 hidden layers). However, when these models were applied prospectively to longitudinal data, only the linear SVR gave a distribution of rate of change of the brain-age scores centered around 1. Although ground truth is not available for these datasets, it is reasonable to assume that these brains age by approximately 1 year per year, plus/minus some range that defines accelerated/resilient brain aging. Of all these models, the simpler linear SVR regressor is therefore the best one, for this specific problem.

It is therefore mundane to keep looking for new methods that will be universally better, since different problems might be better tackled by different machine learning models, often dictated by the underlying biology. We should therefore view machine learning research as a process that generates an increasingly richer toolbox out of which we can draw the methods that are best for a given problem. Promises of the type “this method is the best” could be considered as fundamentally misleading.

3.2. Overfitting

Machine learning 101: a model that fits the data well doesn't necessarily generalize well. Appropriate split-sample, replication to new samples, or cross-validation schemes must always be used to obtain a proper estimate of accuracy of a method. Although there have been numerous violations of this rule in the literature in the earlier years of this field, more recent studies generally tend to adhere to these rules for proper evaluation. However, the over-excitement with deep learning seems to have somewhat brought us back into the overfitting realm. Deep learning models tend to fit the data exceptionally well, however this doesn't mean that they generalize well. Even though most researchers cross-validate their deep learning models, they fail to … “cross-validate” the numerous efforts of a dedicated student or postdoc who tries numerous architectures and parameters prior to finding one that works when “cross-validated”. Conventional machine learning studies were less vulnerable to this issue, since one would typically calculate in advance a general set of features to be used, and would cross-validate the process of feature selection and model building using nested cross-validation with a training, validation, and test set. However, deep learning effectively allows you to extract different features as you tweak the architectures, and hence this process, which can be manual and spread over months of experimental work, must also be properly cross validated by single replication to unseen samples. More generally, as our community adopts increasingly nonlinear and high-flexibility models, it needs to become increasingly vigilant about proper evaluation of good generalization. In the era of big data, generalization should be tested in separate samples, or else using split-sample approaches in which one split is kept completely hidden until the very final application of a model.

3.3. Patient or healthy control?

The overwhelming majority of machine learning studies in clinical neuroscience have focused on correctly classifying individual patients from healthy controls. Although this is a good starting point, its practical value is very limited, since those patients are presumably already “correctly” classified via simpler clinical examinations, hence they are used as ground truth. The real clinical value of machine learning methods, and associated biomarkers, would come from our ability to detect subtle imaging signatures before disease is clinically detectable (Davatzikos et al., 2009; Koutsouleris et al., 2009), or to refine clinical categories according to imaging phenotypes of clinical relevance (Rathore et al., 2018). It is therefore important to shift our focus from correct classification of patients vs. controls to more clinically useful investigations of imaging patterns in early pre-clinical states, and in normal-appearing aging or development. This is a much tougher problem.

3.4. The black box: what information is statistically significant for classification?

There is certainly some utility in a black box that gives the right answer when presented with a set of images: it is a tool or device that derives a biomarker that can be used for diagnostic and/or predictive purposes, or for classification of a brain state. However, a black box doesn't further our understanding of disease, brain function, or pathology, unless it also provides us with maps and relationships of brain regions or features that are significant contributors to an imaging signature. ROC analyses, sensitivity, specificity and accuracy of a classifier don't provide such information. Surprisingly little attention has been paid to deriving statistical significance maps of imaging patterns. This problem becomes increasingly more profound, as difficult-to-interpret deep learning methods spread through the field. The literature has provided some solutions for relatively simple linear SVM models (Gaonkar and Davatzikos, 2013), however similar efforts should be made for other, especially nonlinear models. At the very least, the use of permutation experiments should be used routinely, in order to establish whether or not the weight of a voxel or a deep feature is a statistically significant contributor to a machine learning model. Even though permutation tests are extremely costly, and potentially prohibitive for complex models and analyses, they should become the norm rather than the exception.

3.5. Heterogeneity

A classifier or regressor seeks to find a pattern that separates or fits the data. However, in most applications, there might be multiple patterns that characterize disease (subtypes) or brain activation. Nonlinear models of course deal with his heterogeneity, albeit in a way that makes them difficult to interpret. Clinical adoption of these tools might require approaches that capture such heterogeneity in relatively simple and interpretable ways. For example, disease subtypes could be captured by two or more imaging signatures, allowing for clinical refinement of a diagnosis. Even for diseases like Alzheimer's that are thought to have a fairly consistent pattern, multiple studies have elucidated important heterogeneity that calls for multiple imaging signatures, with differential clinical characteristics (Dong et al., 2017; Noh et al., 2014; Nettiksimmons et al., 2014). The use of semi-supervised learning methods might be an area of promise (Varol et al., 2017; Filipovych et al., 2011; Bzdok et al., 2015), since it offers the potential to have a clear label, e.g. healthy control, and a fuzzy label, e.g. patient, which potentially comprises multiple subclasses to be estimated in a data-driven way. The subcategorization of a patient into one of several subtypes would be easier for clinicians to adopt, rather than a complex and difficult to interpret nonlinear decision boundary. More generally, interpretable and easy-to-adopt machine learning models that refine diagnostic and prognostic categories would be important segues to precision diagnostics.

3.6. Big multi-site data, new challenges

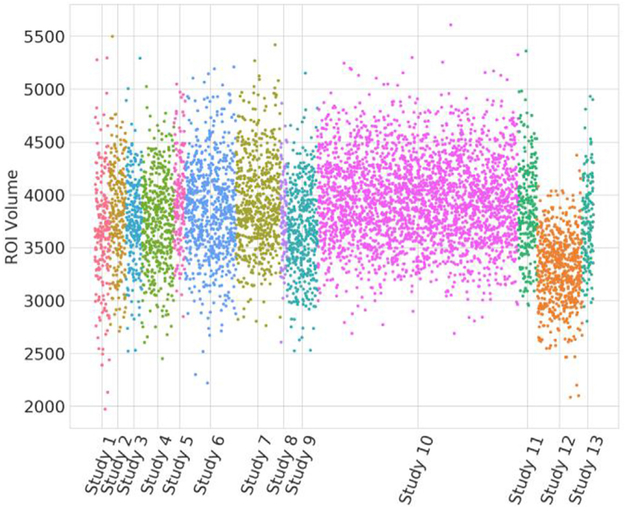
The era of focused studies of a few dozens or even a few hundred subjects, using tightly controlled image acquisition protocols that yield consistent data throughout the study, is gradually yielding to the new era of big data and integration of thousands of datasets across multiple sites, scanners and populations. This is a very exciting era for machine learning, since it will finally provide sufficiently rich datasets to train complex models on, which is very much needed (Varoquaux, 2017). However, it also raises a new challenge: data from different sites and sub-studies are typically acquired in different ways, via different types of scanners, acquisition protocols or scanner software and hardware versions. The image characteristics can be remarkably different, thereby amplifying the problem of overfitting and poor generalization. Our own experiments have shown that even when state of the art image analysis methods specifically designed to minimize vulnerability of extracted features to scanner variations are used, confounding heterogeneity still remains (see Fig. 3 below, for a simple example).

Fig. 3.

Volumetric measurements of the hippocampus from 13 different studies. (ROI volumes were obtained via an optimized multi-atlas, multi-warping consensus method (Doshi et al., 2016), which topped the challenge of (Asman, 2013)). Inter-study differences render it difficult to combine data into a single training set. Application of statistical harmonization methods (taking into consideration various covariates, such as age and sex, as well as the nonlinearity in brain aging trajectories) must be applied, prior to being able to leverage the power of such large databases for machine learning methods.

The effects of this heterogeneity can become very detrimental in high-dimensional models that tend to fit the data tightly. Appropriate statistical harmonization methods must therefore be applied, prior to applying machine learning methods. The science of statistical harmonization has only recently begun to grow substantially in neuroimaging (Fortin et al, 2017, 2018), and it should be followed very closely by those wanting to merge large datasets from multiple sources.

3.7. Interpretability and generative-discriminative learning

The most commonly used machine learning tools involve some kind of discriminative learning (e.g. patients vs. controls, progressors vs. non-progressors, or activation during task 1 vs. task 2). In item (4), above, I briefly discussed the need to derive statistical significance maps, in order to understand which brain regions and features contribute to the best discrimination among classes/labels. Even if such practice is followed, discriminative models hide an often ignored interpretation trap: the discriminative model can happily utilize only a fraction of the image in order to make the right decision. For example, a large region of 1000 voxels might be activated during a given brain state. A machine learning model might happily use only 5 of these voxels, as long as it can make the right decision, and discard everything else. Although this is fine from the black-box perspective, it is very misleading if we interpret this machine learning model as a pattern of just 5 voxels being activated during the task. Some solutions to this problem have been proposed in the literature under certain assumptions (e.g. (Haufe et al., 2014; Diedrichsen et al., 2018)). In general, increased interpretability of discriminative machine learning models is likely to come from hybrid generative-discriminative models, in which not only a discriminative pattern is sought, but also a pattern that describes as much of the data as possible. The literature certainly uses such models (Brodersen et al., 2011), and adaptations of GAN deep networks might hold promise, however the development of machine learning methods that seek primarily to provide insights into the biology of disease processes or brain function, in addition to making the right decision, is still in its infancy.

4. Conclusion

The application of machine learning methods to neuroimaging has risen more rapidly than could have been predicted 15 years ago. It has been a very exciting new direction in neuroimaging, as it has expanded the field from population-based analyses into individualized biomarkers of diseases or functional brain states. From a clinical perspective, this expansion is obviously of fundamental importance in diagnosis, prognosis, and patient stratification. However, the enthusiasm for this growth has also overshadowed a great deal of challenges that need to be addressed, some of which I discussed in the current commentary. Most importantly, this enthusiasm has led to over-promises and to frequent lack of reproducibility of published results. Proper evaluation of generalization ability, especially of powerful nonlinear models, is of very high importance, and should constantly be in the minds of authors and reviewers. Moreover, application of these methods to small datasets should be avoided at any cost, since it is known to have resulted in potentially spurious results that don't replicate well (Varoquaux, 2017). The availability of large datasets in our days renders it easier to adhere to this rule. Even though smaller studies will continue to be published and break into new frontiers, results should always be presented and received with caution, until replicated in larger studies. Regardless of all these challenges, machine learning offers one of the most exciting directions in the field of neuroimaging, as it speaks directly to precision diagnostics, in clinical neuroscience, and to identification of distinct brain states, in cognitive neuroscience. Perhaps more importantly, machine learning is likely to ultimately lead to a better form of dimensional neuroimaging (Davatzikos, 2018), i.e. to our ability to place a brain scan into a succinct, yet highly comprehensive and informative reference system, dimensions of which will reflect patterns associated with normal or pathologic brain structure or function. Such development will significantly facilitate the clinical adoption of advanced neuroimaging, by reducing the vast information conveyed by these images into a small yet comprehensive, interpretable, and highly informative panel of measurements. Each of these measurements will reflect the presence or absence of a relatively distinct imaging pattern associated with different diseases, their subtypes, various risk factors, likelihood of responding to a treatment, likelihood of clinical progression, or with other clinically relevant information.