Abstract
The aim of this research is to automatically detect lumbar vertebras in MRI images with bounding boxes and their classes, which can assist clinicians with diagnoses based on large amounts of MRI slices. Vertebras are highly semblable in appearance, leading to a challenging automatic recognition. A novel detection algorithm is proposed in this paper based on deep learning. We apply a similarity function to train the convolutional network for lumbar spine detection. Instead of distinguishing vertebras using annotated lumbar images, our method compares similarities between vertebras using a beforehand lumbar image. In the convolutional neural network, a contrast object will not update during frames, which allows a fast speed and saves memory. Due to its distinctive shape, S1 is firstly detected and a rough region around it is extracted for searching for L1–L5. The results are evaluated with accuracy, precision, mean, and standard deviation (STD). Finally, our detection algorithm achieves the accuracy of 98.6% and the precision of 98.9%. Most failed results are involved with wrong S1 locations or missed L5. The study demonstrates that a lumbar detection network supported by deep learning can be trained successfully without annotated MRI images. It can be believed that our detection method will assist clinicians to raise working efficiency.
Keywords: Convolutional network, Deep learning, Lumbar detection, The similarity function
Introduction
Magnetic resonance imaging (MRI) is one of the main medical imaging methods to check lumbar diseases. Automatic vertebra detection and location will play an important role in medical image diagnoses, therapeutic schedule, and a follow-up check. For example, lumbar disc herniation usually results from the nerve damage generated by direct compression of the spinal canal [1]. Clinicians often diagnose lumbar disc herniation through physical signs in medical images, such as displacement and transformation [2]. A radiologist works redundantly to label every lumbar vertebra per patient for further diagnoses. Automatic vertebra detection can assist clinicians with etiological diagnoses, such as scoliosis, lumbar canal stenosis, and vertebra degeneration. This will help radiologists recognize each lumbar spine and relieve from duplicate works to annotate each new medical image. However, it remains to be a challenging task to detect automatically in a lumbar image. Imaging mode and patient movement usually result in a high variance or shadow in the image. It is difficult to automatically label every vertebra because characteristics between vertebras are in high resemblance.
Researches have been conducted to make medical images easier to analyze. Several studies focus on special deformation or injury in spine images [3, 4], and other studies aim to automatically detect vertebras [5, 6]. In previous studies, methods with support vector machine, classification forests, and other feature extraction algorithm showed great performance. Since Hilton et al. [7] proposed deep learning in 2006, deep learning has a rapid development in the medical image area. Most recent researches require either fully segmented training data or annotated vertebras in the form of bounding boxes and vertebra positions. For example, Masudur et al. [8] used fully segmented images to train the convolutional neural network to segment cervical or lumbar vertebras. Kim et al. [9] and Oktay et al. [10] trained networks to detect lumbar vertebras on labeled images with bounding boxes and object positions. Han et al. [11] and Wang et al. [12] trained networks to analyze lumbar neural foraminal stenosis with fully segmented lumbar images. However, there exists no recognized lumbar dataset with segmented labels or bounding boxes. Most deep learning tasks of detecting and locating vertebras in medical images rely on an annotated dataset [13]. Making training datasets requires multiple manual works. Moreover, training dataset labeled by their team impacts somewhat on the accuracy of detection and location [14]. Regarding other network frameworks, we propose a new framework to detect MRI lumbar spine via a transfer learning method [15] without using annotated MRI training images.
This paper presents a convolutional neural network [16] with transfer learning to locate the lumbar spine from L1 to S1. The strength of our method is that it does not require annotated vertebra training images. Firstly, the detection network is trained on a recognized video dataset. It is trained to learn to compare the similarity between the contrast image and search images. We recognize the target position according to the high similarity value in the score map. Secondly, we fine-tune parameters when the network is tested on thousands of MRI images. We detect each lumbar image twice. Vertebra S1 is firstly detected and a region based on it is used to search for L1–L5. Thirdly, the contrast image will not update during detection. The experiment shows that our method can receive a better accuracy than others.
The organization of this paper is scheduled as follows. The significance of our work and several successful medical image detections are arranged in the “Introduction” section. Convolutional neural network for detection and training details are introduced in the “Methods” section. Experiment results and evaluations tested on MRI dataset are arranged in the “Experimental Results” section. Finally, the discussion and conclusion are proposed in the “Discussion” and “Conclusion” sections.
Methods
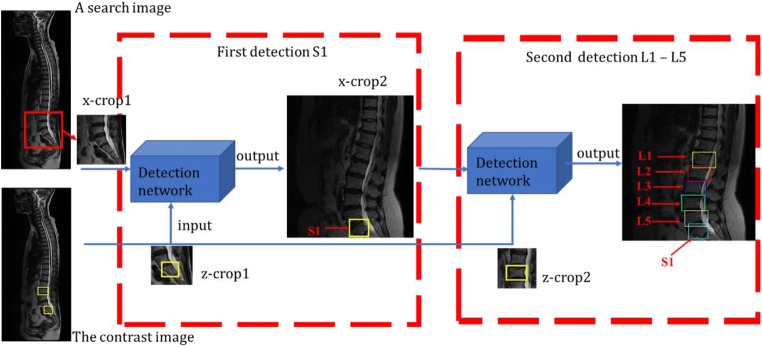
A similarity function g(z, x) is proposed to compute the similarity between a contrast image z and a search image x. If two images describe the same object, the function will return a high value, a low value otherwise. The z-crop out of a contrast image is labeled with a bounding box. The search image is one of the rest images where we search for L1–S1. The x-crop1 is centered at the previous target position. As shown in Fig. 1, we detect twice in the experiment, one for S1, another for L1–L5. In the first detection, an x-crop1 from a search image and the z-crop1 with a labeled S1 are inputted into the convolutional network. Another x-crop2 including S1 will generate immediately after S1 is found. In the second detection, a larger x-crop2 and a z-crop2 with another label are inputted to the same network to search for L1–L5. Figure 1 demonstrates the flow of lumbar detection of L1–S1. The contrast image with two bounding boxes is provided beforehand, acting as a reference for vertebra detection. Six detected vertebras are marked with rectangles. The x-crop1 and x-crop2 are 255 × 255 and 431 × 431 pixels. Z-crops both are 127 × 127 pixels. The specific layer’s settings and training details of the detection network will be discussed in the “Convolutional Neural Architecture” section.
Fig. 1.
The whole framework of lumbar detection. The image with two bounding boxes is the contrast image provided in advance. Instructions in red indicate six target vertebras to be detected
Convolutional Neural Architecture
Model: Framework Design
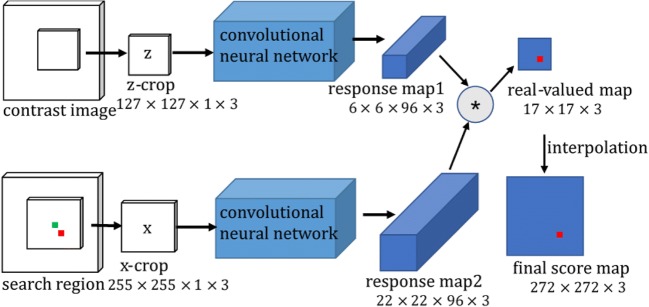
We both input the contrast image z and a search region x to the convolutional neural network, then obtain a score map which indicates the similarities between the corresponding sub-windows. To be more specific, Fig. 2 shows a straightforward relationship between a contrast image z and a search region x. The search region centered at the previous target is a rough and large region. The z-crop is cut out from the first frame with an annotated object position. The x-crop centers at the previous object position, combined with three scales. The z-crop is compared with three scaled x-crops. Since the object will not deviate too much between frames, we believe the object is still in the larger x-crop so we can find it. After inputting three same z-crops and three scaled x-crops into the network, we will receive three response map1 with 6 × 6 × 96 pixels and three response map2 with 22 × 22 × 96 pixels. The smaller response map acts as a convolutional kernel to convolve the larger ones. The symbol * represents a convolution function between two response maps, affecting on the size of the output map. A red pixel in the real-value map is the maximum value position of three maps, which indicates the object position. The green pixel in the center is the previous object position. The experiment demonstrates that amplifying the real-value map with bicubic interpolation leads to a more accurate object position. The final score map is interpolated from 17 × 17 to 272 × 272. According to the red pixel position in the final score map, we can calculate the target position in the search region. Layer settings for the detection convolutional neural network are provided in Fig. 3, including batch normalization layers and ReLU non-linear layers.
Fig. 2.
Convolutional neural network for detection. The z-crop is compared with 3 scaled x-crops. The outputs are 3 final score maps, where we search for the highest similarity value. The maximum pixel in red in the final score map indicates the most possible object position. The green pixel is the center of a search region
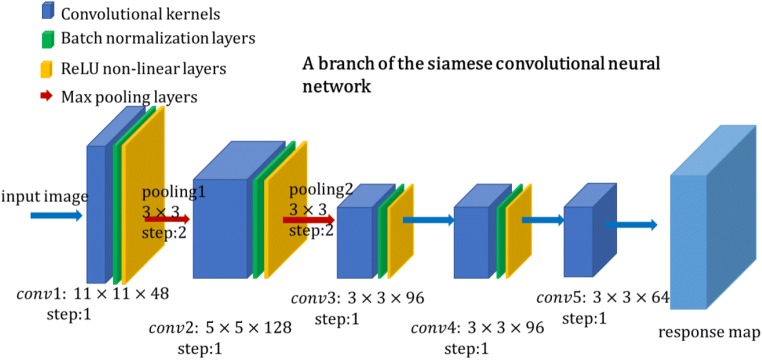
Fig. 3.
A branch of the siamese convolutional neural network. The construction shows kernel parameters of each layer, which is viewed in different colors
Our network has five convolutional layers and two max-pooling layers. Each convolutional layer is followed by a batch normalization layer and a non-linear activation layer excluding the final layer, conv5. The total stride of our network is 8, which will be used to compute the final target position in search images.
Convolutional layers extract high-level feature maps through parameter w. Assuming that represents the output of cell i in layer l, and represents the weighted sum of cell i in layer l, including bias cell, for the given weight parameters wi and biases bi, the function of convolutional layers can be written as:
| 1 |
| 2 |
where function f means a non-linear activation function. We use rectified linear units (ReLU) here in activation layers, which can be expressed as the following formula:
| 3 |
It extremely decreases the number of parameters in the network and increases the running speed. Compared with other non-linear activation functions such as sigmoid and tanh function, ReLU function requires lower calculation cost and less training time. Max-pooling layers down-sample the size of feature maps by a 3 × 3 neighboring window, which effectively avoids overfitting. More specific parameters and feature map sizes are listed in Table 1. The size of the convolutional kernels resembles that of Krizhevsky et al. [17]. Channel and map represent the number of output and input feature maps in convolutional layers.
Table 1.
Architecture of the convolutional neural network except for batch normalization layers and ReLU non-linear layers
| Feature map size | |||||
|---|---|---|---|---|---|
| Layer | Support | Stride | Chan*Map | For z-crop | For x-crop |
| 127 × 127 × 1 | 255 × 255 × 1 | ||||
| Conv1 | 11 × 11 | 2 | 48 × 1 | 59 × 59 × 48 | 123 × 123 × 48 |
| Pool1 | 3 × 3 | 2 | 29 × 29 × 48 | 61 × 61 × 48 | |
| Conv2 | 5 × 5 | 1 | 128 × 48 | 25 × 25 × 128 | 57 × 57 × 128 |
| Pool2 | 3 × 3 | 2 | 12 × 12 × 128 | 28 × 28 × 128 | |
| Conv3 | 3 × 3 | 1 | 96 × 128 | 10 × 10 × 96 | 26 × 26 × 96 |
| Conv4 | 3 × 3 | 1 | 96 × 96 | 8 × 8 × 96 | 24 × 24 × 96 |
| Conv5 | 3 × 3 | 1 | 64 × 96 | 6 × 6 × 64 | 22 × 22 × 64 |
Training Dataset
We train the network with the ImageNet Video dataset from the 2015 edition of the ImageNet Large Scale Visual Recognition Challenge (ILSVRC) [18]. All images were carefully annotated with a bounding box. In this paper, we ignore the object classes. The dataset contains 4417 videos of 30 categories, including millions of labeled frames. The massive size dataset can be successfully applied to object detection via deep learning.
Model: Train
Considering that MRI lumbar images are grayscale images, we extract the G channel of each training image. This change happens before the image inputting. The z-crop and x-crops are 127 × 127 and 255 × 255 pixels. The object position in the z-crop is depicted in advance. A real-value map will be obtained after a z-crop and an x-crop are inputted into the network. The ground truth labels of positive and negative pairs are described as + 1 and − 1. We employ the logistic regression loss to evaluate positive and negative pairs during training:
| 4 |
where y ∈ {+1, −1} is a true label of training pairs and v is a valued score. This will generate a score map . The logistic regression loss can be written as:
| 5 |
To optimize the parameters w in the convolutional network, we adopt stochastic gradient descent (SGD) to the problem:
| 6 |
In detail, we set z-crops at 127 × 127 and x-crop at 255 × 255 pixels. Target sizes in the original annotations are non-uniform. Thus, the scale of targets in video frames needs to be normalized. On this account, training crops need to be fixed with a scale sz and contextual margin pz. If the size of a bounding box is (w, h) and the fixed area is 127 × 127, we can give the equation:
| 7 |
where pz is a quarter of the perimeter of a bounding box pz = (w + h)/4. We can also write it as
| 8 |
We can get a z-crop with a fixed size according to sz and pz.
Considering the size of an x-crop is about twice bigger than that of a z-crop, we need to add more contextual margin px to resize it. The size x can be computed as the following expressions:
| 9 |
| 10 |
| 11 |
After adding three scales 1.0375{−1, 0, 1} to the G channel in a search region, we can get three scaled x-crops. The z-crop is compared with three x-crops.
Model: Test
In our network, the z-crop will not update after finding a target position. Other image characteristics are not extracted in this study, such as histogram and optical flow. We only compare a contrast image with a larger search image to find the target position. The real-value map is a similarity metric of 17 × 17 pixels. As shown in Fig. 2, the real-value map is relatively coarse and vague. We found that the score map leads to a more accurate position when the similarity metric is amplified 16 times with bicubic interpolation to 272 × 272. The maximum value of three score maps indicates the object position. Assuming that the coordinates of the maximum value are T(rmax, cmax), we can give the distance from the maximum value position to the score map center C.
| 12 |
The search region and x-crop are centered at the previous object position. According to the total network stride 8 mentioned in the “Model: Framework” section and the interpolation size 16, we can calculate the relative position displacement from the previous target position to the current position. It can be written as:
| 13 |
where O indicates the previous object position, also the center position of the x-crop. Finally, we can describe the current object position based on in the search region.
Experimental Results
MRI Dataset
In this section, our MRI dataset contains 1318 healthy and unhealthy samples, about 2739 images, ranging from different age groups. The dataset comes from the Department of Orthopedics Traumatology of Hong Kong University. We use the sagittal lumbar spine acquired through the T2-weighted sequence slices.
Experimental Setup
As mentioned above, x-crops are scaled to deal with dimension change in lumbar spines. We take advantages of the detection network twice here. S1 and another vertebra in the contrast image need to be labeled with rectangles. First, we detect S1 which is special and easy to be found. The z-crop1 with a labeled S1 are 127 × 127 pixels and the x-crop1 are 255 × 255 pixels. Immediately, after the S1 is found in the first detection, the x-crop2 containing several vertebras will be extracted. The size of 255 × 255 pixels is too small to detect L1–L5 in the network. Thus, the x-crop2 are 431 × 431 pixels. The z-crop2 with a labeled L3 still are 127 × 127 pixels. We will finally obtain a real-value map with the size of 39 × 39 pixels.
The second score map is resized to 624 × 624 by bicubic interpolation, where we can find five maximum values. According to positions of a maximum value in the first detection and five maximum values in the second detection, we can calculate positions of L1–S1 with Eq. 13. It should be noted that our detection network is to compare the similarity between a search image and a contrast image. If we just clear the maximum point in the second time, the next maximum value is probably beside it, leading to a wrong position. Several high-value points around the maximum value are possible to exceed that of the rest object positions. The foreseeable result is that two bounding boxes will find the same position. Therefore, a small rectangle centered at the maximum value need to be cleared once finding a maximum value. Only in this way can we find the rest maximum values around the target position found.
Results and Evaluation
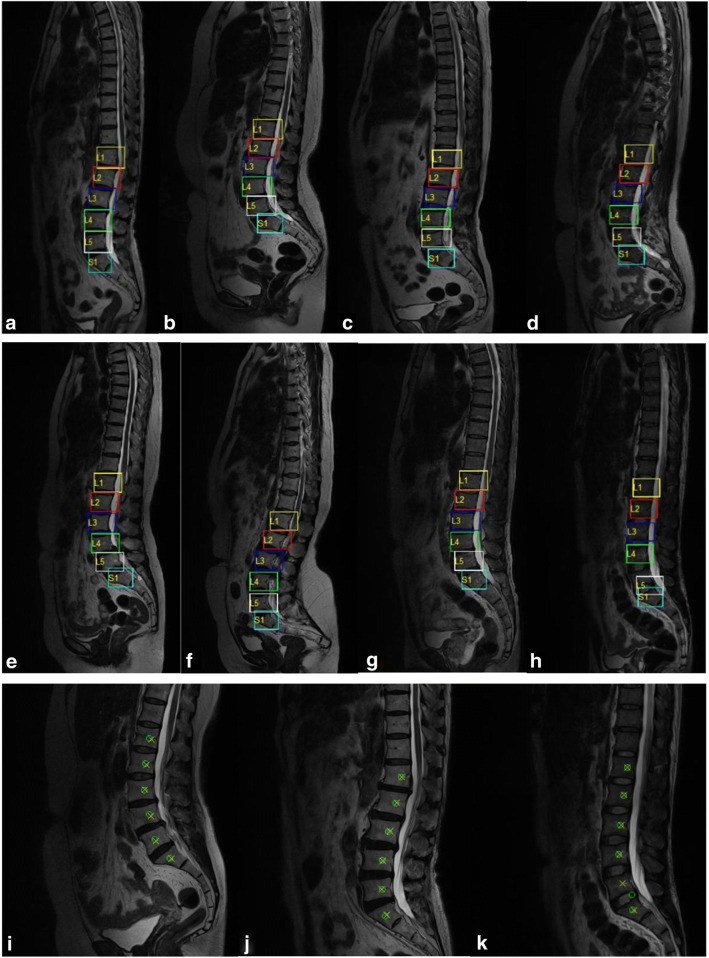
Several detection and identification results are exhibited in Fig. 4. Six vertebra detection results are presented with bounding boxes in different colors. From top to end, they are called L1, L2, L3, L4, L5, and S1. Successful detections are presented in Fig. 4a–g, while failed ones are in Fig. 4h and k. Figure 4i–k shows corresponding positions of detection results and manually annotated centers. Detection positions in green “o” are the centers of bounding boxes. Manual annotations in yellow “x” are the annotated centers of vertebras together with spine canals. The result in Fig. 4k misses L5 and finds an extra vertebra.
Fig. 4.
Lumbar detection results based on deep learning. Each lumbar vertebra is outlined with bounding boxes in a–h together with their classes. Successful locations are demonstrated in the first four examples a–g, failed results in the h and k. i–k show detection and labeled positions in MRI regions
A threshold is set to compare detection positions with labeled positions. Regions beyond the threshold are negative. If the absolute distance of those two positions is below the threshold, then it is a true positive (TP) sample, otherwise a false positive (FP) or false negative (FN) sample. Our detection results are evaluated with every location accuracy of L1–S1 in Table 2. False detection results are associated with wrong L5 or S1 position to a large degree. General evaluation indexes and comparative results are provided in Table 3. We define precision, specificity, sensitivity, and accuracy as follows:
| 14 |
| 15 |
| 16 |
| 17 |
Table 2.
Detection accuracy of the specific vertebra. Our method has a better accuracy in most vertebras
| Accuracy (%) | L1 | L2 | L3 | L4 | L5 | S1 |
|---|---|---|---|---|---|---|
| Ours | 99.0 | 99.2 | 99.0 | 98.9 | 98.5 | 98.6 |
| Cai [19] | 98.3 | 95.1 | 98.2 | 97.4 | 98.4 | 99.1 |
Table 3.
Comparative results reported by other methods
Error mean and standard deviation (STD) in Table 3 are calculated through the absolute distance of corresponding annotation and detection position pairs. Other reported results in Table 2 and Table 3 are tested on their dataset, while their evaluation indexes have a difference. Compared with other results, our method receives a better accuracy in most vertebras, and a high sensitivity (98.9%) and accuracy (98.6%). Our error mean and STD are much smaller than other methods. Although our network is not trained on annotated lumbar spine images, detection results in this paper show a better performance than some other methods.
In the experiment, we have 2739 lumbar MRI samples in total, 2701 samples detected correctly and 38 samples detected mistakenly. We receive a lower precision and sensitivity than Forsberg [14] in Table 3. However, Forsberg [14] tested their network on about 700 MRI images, far less than the number of ours. Positive results are successfully located and classified on six vertebral bodies. Most failed results are related to either a wrong S1 detection or a missed vertebra in MRI images. We identify lumbar spines according to bounding boxes. In some conditions, two bounding boxes will overlap partly on a vertebra. Hence, a displacement rectification is posed to it. However, mistaken recognition of S1 will result in a subjective failure, for example, if L5 or S2 is erroneously identified as S1.
Discussion
A novel detection method is presented in this paper based on deep learning. Firstly, the detection network is trained on an acknowledged video dataset instead of labeled MRI images. Secondly, we fine-tune the parameters when the network is tested on the MRI dataset. For example, we amplify the size of input images as well as the final score map. The similarity function will output six score values, according to which we can locate lumbar positions. Thirdly, the object feature remains unchanged in the first image. There is only one contrast image with two bounding boxes in vertebra detection. It guarantees that our method can run at a high speed.
Different from most detection methods of learning to distinguish between vertebras, our network learns to compare the similarity between vertebras. The characteristic merely concerned about is target position. The detection result is compared with that of Suzaini [20], Cai et al. [19], Kim [9], and Forsberg et al. [14]. They trained and tested their convolutional networks with their datasets. However, there exists no recognized annotated lumbar dataset. Forsberg et al. [14] trained on MRI dataset annotated by picture archiving and communication system (PACS). Cai et al. [19] trained with several hundreds of images. They distinguished vertebras based on annotations. Their performance is somewhat restricted by label precision. Our method reaches a quite or even better accuracy and performs a better precision. Most methods detect a vertebral body with a bounding box. In our method, both vertebral body and spine canal are included in the bounding box. Several lumbar diseases like lumbar intervertebral disc result from the compression of the spinal canal. Further image analysis with one or several vertebras can build on the detection result. However, our method cannot locate a quite precise position. We only can know where it is and what it is, rather than a specific size. In total, an accuracy of 98.6% is received from the detection network.
Conclusion
In this paper, we realize the possibility of lumbar detection based on the convolutional neural work. A similarity function is successfully applied to the detection task. Deep learning network in our work extracts lumbar spines instantly and efficiently. The network is successfully tested on more than two thousand patient cases. We can identify vertebras with stable locations and classifications in MRI slices. This method can assist clinicians with repetitive and basic work.
Funding Information
The research is supported by National Natural Science Foundation of China (Grant no. 11503010, 11773018), the Fundamental Research Funds for the Central Universities (Grant no. 30916015103), and the Qing Lan Project and Open Research Fund of Jiangsu Key Laboratory of Spectral Imaging & Intelligence Sense (Grant no. 3091601410405).
References
- 1.Choi KC, Kim JS, Dong CL, et al. Percutaneous endoscopic lumbar discectomy: minimally invasive technique for multiple episodes of lumbar disc herniation. Bmc Musculoskelet Disord. 2017;18:329–324. doi: 10.1186/s12891-017-1697-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Li X, Dou Q, Hu S, Liu J, Kong Q, Zeng J, Song Y. Treatment of cauda equina syndrome caused by lumbar disc herniation with percutaneous endoscopic lumbar discectomy. Acta Neurologica Belgica. 2016;116(2):185–190. doi: 10.1007/s13760-015-0530-0. [DOI] [PubMed] [Google Scholar]
- 3.Anitha H, Prabhu GK. Identification of Apical Vertebra for Grading of Idiopathic Scoliosis using Image Processing. J Digit Imaging. 2012;25(1):155–161. doi: 10.1007/s10278-011-9394-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kumar S, Nayak KP, Hareesha KS. Improving Visibility of Stereo-Radiographic Spine Reconstruction with Geometric Inferences. J Digit Imaging. 2016;29(2):226–234. doi: 10.1007/s10278-015-9841-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kumar VP, Thomas T. Automatic estimation of orientation and position of spine in digitized X-rays using mathematical morphology. J Digit Imaging. 2005;18(3):234–241. doi: 10.1007/s10278-005-5150-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Benjelloun M, Mahmoudi S. Spine localization in X-ray images using interest point detection. Journal of Digital Imaging. 2009;22(3):309–318. doi: 10.1007/s10278-007-9099-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hinton GE, Salakhutdinov R. Reducing the dimensionality of data with neural networks. Science. 2006;313(5786):504–507. doi: 10.1126/science.1127647. [DOI] [PubMed] [Google Scholar]
- 8.Al Arif SMMR, Knapp K, Slabaugh G. Fully automatic cervical vertebrae segmentation framework for X-ray images. Comput Methods Prog Biomed. 2018;157:95–111. doi: 10.1016/j.cmpb.2018.01.006. [DOI] [PubMed] [Google Scholar]
- 9.Kim K, Lee S. Vertebrae localization in CT using both local and global symmetry features. Comput Med Imaging Graph. 2017;58:45–55. doi: 10.1016/j.compmedimag.2017.02.002. [DOI] [PubMed] [Google Scholar]
- 10.Oktay AB, Akgul YS. Simultaneous Localization of Lumbar Vertebrae and Intervertebral Discs With SVM-Based MRF. IEEE Trans Biomed Eng. 2013;60(9):2375–2383. doi: 10.1109/TBME.2013.2256460. [DOI] [PubMed] [Google Scholar]
- 11.Han Z, Wei B, Leung S, et al. Automated pathogenesis-based diagnosis of lumbar neural foraminal stenosis via deep multiscale multitask learning. Neuro informatics. 2018;1:1–13. doi: 10.1007/s12021-018-9365-1. [DOI] [PubMed] [Google Scholar]
- 12.Wang J, Fang Z, Lang N, Yuan H, Su MY, Baldi P. A multi-resolution approach for spinal metastasis detection using deep Siamese neural networks. Comput Biol Med. 2017;84(C):137–146. doi: 10.1016/j.compbiomed.2017.03.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Celik AN, Muneer T. Neural network based method for conversion of solar radiation data. Energy Convers Manag. 2013;67(1):117–124. doi: 10.1016/j.enconman.2012.11.010. [DOI] [Google Scholar]
- 14.Forsberg D, Sjöblom E, Sunshine JL. Detection and labeling of vertebrae in mr images using deep learning with clinical annotations as training data. J Digit Imaging. 2017;30(4):1–7. doi: 10.1007/s10278-017-9945-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gao J, Ling H, Hu W et al.: Transfer Learning Based Visual Tracking with Gaussian Processes Regression. Computer Vision – ECCV 2014. Springer International Publishing, 2014, pp. 188–203
- 16.Bertinetto L, Valmadre J, Henriques J F, et al. Fully-Convolutional Siamese Networks for Object Tracking. European Conference on Computer Vision – ECCV2016, 2016:850–865.
- 17.Krizhevsky A, Sutskever I, Hinton G E. ImageNet classification with deep convolutional neural networks. International Conference on Neural Information Processing Systems. Curran Associates Inc. 60(2):1097–1105, 2012.
- 18.Russakovsky O, Deng J, Su H, Krause J, Satheesh S, Ma S, Huang Z, Karpathy A, Khosla A, Bernstein M, Berg AC, Fei-Fei L: ImageNet Large Scale Visual Recognition Challenge. IJCV, 2015
- 19.Cai Y, Landis M, Laidley DT, Kornecki A, Lum A, Li S. Multimodal vertebrae recognition using transformed deep convolution network. Computerized Medical Imaging and Graphics. 2016;51:11–19. doi: 10.1016/j.compmedimag.2016.02.002. [DOI] [PubMed] [Google Scholar]
- 20.Suzani A, Seitel A, Liu Y, et al. Fast Automatic Vertebrae Detection and Localization in Pathological CT Scans - A Deep Learning Approach. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015, 9353:678–686, 2015.